Идентификация и классификация электрической нагрузки горных предприятий на основе методов декомпозиции сигналов
- 1 — д-р техн. наук заведующий кафедрой Санкт-Петербургский горный университет императрицы Екатерины II ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 2 — аспирант Санкт-Петербургский горный университет императрицы Екатерины II ▪ Orcid ▪ Elibrary ▪ Scopus
Аннотация
В исследовании рассматривается возможность применения метода сингулярного разложения в качестве инструмента для разложения исходного временного ряда потребления электроэнергии отходящих присоединений с целью идентификации и последующей классификации электрической нагрузки горных предприятий. Необходимость постоянного повышения эффективности процессов продиктована современными трендами и тенденциями повышения потребления ископаемых и энергетических ресурсов. Рассмотренный алгоритм позволяет определять подобие характера потребления электроэнергии по укрупненным группам нагрузок, исходя из результатов разложения временного ряда потребления электроэнергии. По результатам анализа данных потребления электроэнергии по двум независимым фидерам выявлен факт формирования подобных повторяющихся характерных изменений нагрузки (временных паттернов) с периодом, равным трем суткам. Применение результатов исследования актуально при автоматизированной типизации профилей нагрузки для решения задач, связанных с интеграцией экономических стимулов при управлении спросом на электроэнергию, а также при оценке целесообразности вовлечения и потенциала участия потребителя в регулировании графика нагрузки. Предложенные алгоритмы позволяют использовать полученные типовые профили потребления электроэнергии для расчетов квазидинамических электрических режимов при решении задач перспективного развития систем энергообеспечения горных предприятий и повышения энергетической эффективности.
Финансирование
Работа выполнена в рамках Государственного задания Министерства науки и высшего образования Российской Федерации № FSRW-2023-0002 «Фундаментальные междисциплинарные исследования недр Земли и процессов комплексного освоения георесурсов».
Введение
Необходимость повышения эффективности ведения горных работ продиктована современными трендами и тенденциями, в частности увеличением потребления полезных ископаемых [1-3]. Цифровая трансформация, базирующаяся на применении цифровых технологий и математических методов, которые позволяют обрабатывать и анализировать большие объемы данных, генерируемые горнопромышленным оборудованием, позволяет повысить эффективность технологических процессов всей цепочки добычи полезных ископаемых от геологоразведки до потребления ресурсов [4-6]. Аналогично задачам повышения качества электроэнергии [7, 8], для обеспечения достаточного уровня энергетической эффективности необходимо использовать методы, базирующиеся на моделях объекта исследования [9, 10].
В статье рассматривается подход к повышению эффективности электроснабжения горного предприятия на основе идентификации и классификации электрической нагрузки путем декомпозиции сигналов. Декомпозиция сигнала – разложение исходного сигнала (временного ряда) на составляющие, представленные в виде мод, компонент и др. Методы декомпозиции сигнала определяются, исходя из характеристик анализируемого временного ряда [11, 12] (табл.1).
Таблица 1
Характеристика декомпозиционных методов в электротехнических комплексах
|
Метод |
Область применения |
Недостатки |
Литературный источник |
|
Преобразование Фурье |
Анализ гармоник в электрической сети (THD, гармонические искажения). Выделение сезонных компонент в нагрузке. Обнаружение неисправностей в оборудовании по спектру тока/напряжения |
Предполагает стационарность сигнала, что редко бывает в реальных нагрузках. Не подходит для анализа нелинейных и нестационарных процессов, часто встречающихся в горной промышленности |
[13-16] |
|
Сингулярное разложение (Singular value decomposition, SVD) |
Разложение временных рядов нагрузки на трендовые и циклические компоненты. Очистка сигналов от шума. Анализ нестационарных процессов в электросетях |
В описываемом контексте не обнаружено |
[17-20] |
|
Разложение сигнала на эмпирические моды (Empirical mode decomposition, EMD) |
Анализ нестационарной нагрузки на шахтах и карьерах. Диагностика оборудования по вибрациям и токам. Улучшение прогнозирования нагрузки в реальном времени |
Склонен к модальному смешиванию (разные частоты в одной IMF). Высокая чувствительность к шуму |
[13, 21-23] |
|
Вариационное разложение моды (Variational mode decomposition, VMD) |
Анализ и прогнозирование электрической нагрузки в условиях переменной добычи. Выделение аномальных режимов работы оборудования. Совместное использование с ИИ-моделями (например, LSTM) для прогнозирования |
Зависимость от начальных параметров. Высокая вычислительная сложность, проблемы с обработкой сигналов с резкими скачками или импульсами. Не гарантирует полного разделения перекрывающихся частотных компонент |
[24, 25] |
|
Преобразование Гильберта – Хуанга (HHT) |
Анализ переходных процессов в сетях горных предприятий. Диагностика неисправностей в электродвигателях и насосах. Мониторинг качества электроэнергии |
Проблема модального смешивания. Краевые эффекты. Высокая чувствительность к шуму. Сложность автоматизации и стандартизации |
[26-28] |
В различных технологических процессах, связанных с энергообеспечением горных предприятий, применяются различные декомпозиционные методы [29, 30]. Выбор конкретного метода зависит от объема данных, их статистических характеристик и прочих факторов, которые не являются предметом исследования.
Исследования, включающие преобразование Фурье как метод изучения, чаще всего посвящены анализу параметров качества электроэнергии в сетях электроснабжения. В работах отечественных и зарубежных ученых применение сингулярного разложения в последнее время весьма популярно и сопряжено с решением большого количества задач. Так, например, в исследовании [24] метод сингулярного разложения применяется как часть комплекса анализа сингулярного спектра при решении задач прогнозирования потребления электроэнергии в изолированном гибридном электротехническом комплексе.
Несмотря на то, что в горной промышленности значительная часть исследований по анализу состояния электромеханического оборудования основана на применении методов спектрального анализа, таких как преобразование Фурье и сингулярное разложение, в большинстве случаев они используются для диагностики состояния отдельных узлов, например подшипников, или анализа вибрационных характеристик оборудования в целом. Вместе с тем остается недостаточно изученным влияние структуры и параметров электропривода, включая тип двигателя, систему управления, режимы работы и взаимодействие с технологическим процессом, на характер потребления электроэнергии из сети. Это ограничивает возможности комплексного анализа электрических режимов и снижает точность прогнозирования нагрузок, особенно при использовании адаптивных методов анализа сигналов. Таким образом, в дальнейших исследованиях целесообразно учитывать не только внешние проявления сигналов (вибрации, ток, напряжение), но и внутренние параметры электропривода, влияющие на формирование нагрузки в электрической сети.
Методы
Методы разложения сигналов – важнейшие аналитические приемы, используемые в различных дисциплинах, включая обработку сложных сигналов, анализ данных и инженерию, для извлечения значимых компонент. Среди известных методов – преобразование Фурье, SVD, EMD, многомасштабное сингулярное разложение (Multi-scale singular value decomposition, MSVD) [31, 32], VMD, HHT. Эти методы позволяют получить ценные сведения о характеристиках сигналов при решении таких проблем, как нелинейность, нестационарность, шум и мультимодальные данные, что делает их незаменимыми инструментами в современном анализе. Области применения методов отличаются и имеют свои особенности в приложении к задачам разного типа.
SVD – основополагающий метод линейной алгебры, который позволяет разложить матрицу на три составляющие, выявляя внутренние свойства исходной матрицы. Этот метод широко используется для уменьшения размерности, подавления шума и сжатия данных в различных областях, таких как обработка изображений и машинное обучение. SVD особенно эффективен для выявления скрытых структур в данных, позволяет понять глубинные закономерности и взаимосвязи. Однако данный метод чувствителен к выбросам данных, а разложения больших матриц должны проводиться с учетом требований значительных вычислительных ресурсов.
EMD – метод, основанный на данных, разбивает сигнал на собственные моды (IMF), которые отражают различные частотные компоненты сигнала, не полагаясь на заранее определенные базисные функции. Этот метод особенно эффективен для анализа нелинейных и нестационарных сигналов, что делает его пригодным для применения в мониторинге состояния объектов и других областях. Процесс EMD включает алгоритм отсеивания, который итеративно извлекает IMF из исходного сигнала до остатка без явных вариаций. В недавних исследованиях метод EMD был расширен до двумерной эмпирической модовой декомпозиции (BEMD), что позволило применять его к двумерным сигналам и изображениям.
VMD – относительно новый метод, направленный на разложение сигнала на набор ограниченных по частотной полосе собственных модовых функций. Он устраняет некоторые ограничения EMD и SVD, применяя вариационный подход, который оптимально разделяет моды на основе их собственных частот пропускания. Этот метод особенно полезен для сигналов с близко расположенными частотными компонентами и обеспечивает улучшенную производительность при оценке несущей частоты и анализе сигналов.
HHT объединяет EMD и преобразование Гильберта для обеспечения временно-частотного анализа сигналов. Применяя преобразование Гильберта к IMF, полученным с помощью EMD, HHT, позволяет генерировать спектр Гильберта, который показывает мгновенное распределение частоты и энергии сигнала во времени. Этот подход особенно эффективен для анализа сложных сигналов с изменяющимися во времени характеристиками.
Общие ограничения и критерии выбора для любого метода:
- Нестационарность и нелинейность. Многие реальные сигналы обладают нестационарными и нелинейными характеристиками. Наличие этих характеристик может усложнить анализ и интерпретацию сигналов. Традиционные методы обработки сигналов часто предполагают, что сигналы являются стационарными, что приводит к неточным выводам при применении к нестационарным данным.
- Шум и выбросы данных – еще одна серьезная проблема при обработке сигналов. Они могут исказить истинный сигнал и привести к недостоверным результатам. Методы декомпозиции помогают решить эту проблему, выделяя из шума значимые компоненты сигнала.
- Разрешение и извлечение признаков. Методы разложения сигналов также направлены на улучшение их разрешения, что позволяет извлечь большее количество информации. Такие методы, как дискретное вейвлет-преобразование (DWT), повышают частотное разрешение при одновременном снижении временного разрешения, обеспечивая комплексное представление сигнала в различных масштабах.
- Обработка мультимодальных данных. В современных приложениях по обработке сигналов все чаще возникает необходимость в анализе мультимодальных данных, объединяющих различные типы сигналов. Методы декомпозиции сигналов способствуют эффективному объединению этих модальностей, повышая эффективность классификации и позволяя более полно понять процессы, лежащие в их основе.
Для получения составляющих оригинального временного ряда потребления электроэнергии было принято решение использовать метод SVD по причине устойчивости метода к зашумленным данным. Также метод позволяет обрабатывать нестационарные сигналы (каким является исследуемый временной ряд), извлекая трендовую составляющую.
В соответствии с методом сингулярного анализа необходимо получить траекторную матрицу из исходного временного ряда. Для этого исходный временной ряд, имеющий N значений {p1, …, pN}, подвергают вложению в пространство, имеющее размерность L. В российской литературе данный метод получения траекторной матрицы из временного ряда получил название «Гусеницы», в зарубежной – Embedding. Значение L определяет размерность траекторной матрицы и называется длиной окна. Порядок определения величины длины окна является отдельной научной задачей, однако при рассмотрении временных рядов, имеющих заранее известные периодики, длина окна выбирается, исходя из продолжительности известного периода. Например, при рассмотрении зависимости солнечной радиации от времени на протяжении недели целесообразно определить длину окна, равную или кратную одному дню (полному периоду изменения значений). В остальных случаях следует решать дополнительные научные задачи для обоснования размера окна.
Результатом вложения временного ряда в пространство размерности L является матрица размерности Ln (матрица является Ганкелевой):
где p1, p2, …, pn – значения параметра в момент времени t = 1, 2, 3, …, N; n = N – L + 1 – количество столбцов матрицы (размер вектора вложения); количество строк должно удовлетворять условию L≤[(N+1)/2].
В соответствие с данными [33] любую матрицу можно представить в виде:
где матрица U состоит из левых сингулярных векторов, т.е. столбцы матрицы U состоят из собственных векторов матрицы AAT; матрица V состоит из правых сингулярных векторов, т.е. столбцы матрицы V состоят из собственных векторов матрицы ATA; σN – сингулярные числа матрицы AAT(σ=√λ, λ – собственное число матрицы AAT), сингулярные числа расположены на главной диагонали в порядке убывания.
Примем, что λ1...λL – собственные числа матрицы AAT, при этом λ1≥λ2...≥λL. Также примем U1...UL как столбцы матрицы U, взятые в соответствии с сингулярными числами λ.
Если записать Vi=XTUi/√λi при этом i=1,...,rank(A), то сингулярное разложение матрицы A может быть записано таким образом:
где Ai=√λiUiViT.
Каждая из матриц Ai имеет ранг 1, поэтому их можно назвать элементарными матрицами. Каждый из √λi,Ui,Vi называют i-й сингулярной тройкой разложения.
На заключительном этапе алгоритма каждая из матриц Аi из разложенных преобразуется обратно в форму исходного объекта. Эта операция осуществляется с помощью ганкелизации матриц (диагонального усреднения),
Посредством диагонального усреднения компонент из полученной матрицы получаем восстановленные временные ряды. Таким образом, исходный ряд раскладывается в сумму восстановленных рядов.
Оригинальное исследование временных рядов потребления электрической энергии (ЭЭ) представлено в статье [34]. В данном исследовании были использованы графики электрических нагрузок восьми фидеров подстанции за год наблюдений. Данные были получены напрямую со счетчика электрической энергии и мощности (счетчик коммерческого учета марки «Меркурий», класс точности 0,5). Временные ряды имеют степень дискретизации, равную 30 мин, т.е. значения потребляемой мощности усреднены на участке в 30 мин.
Исходный временной ряд состоит из 17520 точек. Весь набор данных включает 140160 значений в соответствии с количеством отходящих от подстанции присоединений. Увеличенный по оси времени участок исходного временного ряда для первого фидера в масштабе одного месяца представлен фиолетовой кривой на рис.1. Также отображены результат SVD-разложения в виде первых 12 компонент исходного временного ряда.
Перед применением каких-либо математических преобразований была проведена нормировка данных по методу min-max. Исходный временной ряд специально не очищался от шумов и отклонений для проверки алгоритма на устойчивость к качеству входных данных.
Трассировка алгоритма
Весь алгоритм был реализован в среде разработки Jupyter Notebook на языке Python. За исключением служебных этапов в виде введения библиотек, задания функций и пр., основными этапами работы алгоритма являются:
- Импорт и предобработка данных для дальнейшей работы с массивом данных. Формирование таблицы Pandas с датой/временем и значениями мощности потребления по каждому фидеру.
- Введение дополнительных признаков в исходную таблицу на основании информации о дате и времени. Получение столбцов с порядковым номером дня в месяце, днем недели, порядковым номером месяца, номером квартала и др. Данное действие необходимо для дальнейшей группировки данных и поиску зависимостей в разных временных срезах.
- Проведение предварительного корреляционного анализа данных с расчетом коэффициента корреляции по методу Пирсона (рис.2). Необходимо для определения линейной зависимости между фидерами при помощи их попарного сравнения.
- Задание ширины окна L. При анализе всего года ширина окна задается равной Lгод = 1460 ед. данных, исходя из среднего количества точек за месяц. При рассмотрении масштаба месяца длина окна была определена как количество данных за неделю, т.е. Lмес = 336. Аналогично при рассмотрении отдельной недели размер окна был задан равным Lнед = 48 в соответствии с количеством данных за день.
- Создание траекторной матрицы для отдельного фидера (рис.3).
- Сингулярное разложение созданной ранее траекторной матрицы, проверка корректности разложения путем суммирования всех элементарных матриц с последующим сравнением результата с исходной матрицей.
- Расчет относительного и кумулятивного вклада компонент в исходный временной ряд для последующего определения необходимого объема компонент при их группировке (рис.4).
- Обратное преобразование. Преобразование элементарных матриц во временные ряды при помощи создания Ганкелевых матриц. Сохранение компонент в отдельный файл для дальнейшего анализа.
- Построение матрицы W-корреляции и сортировка компонент по главной диагонали с учетом вклада компоненты в исходный временной ряд.
- Группировка компонент на основании построенной матрицы W-корреляции. Формирование паттернов потребления каждого фидера (рис.5).
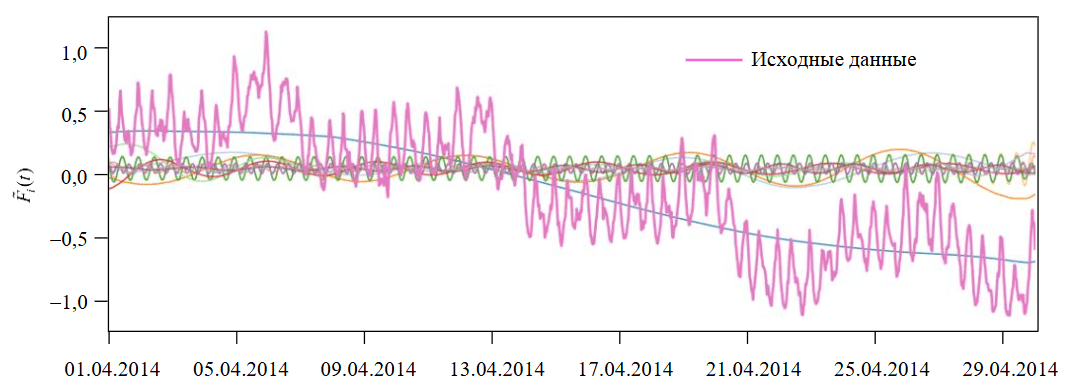
Рис.1. График потребления ЭЭ в апреле 2014 г. и 12 компонент временного ряда [34]
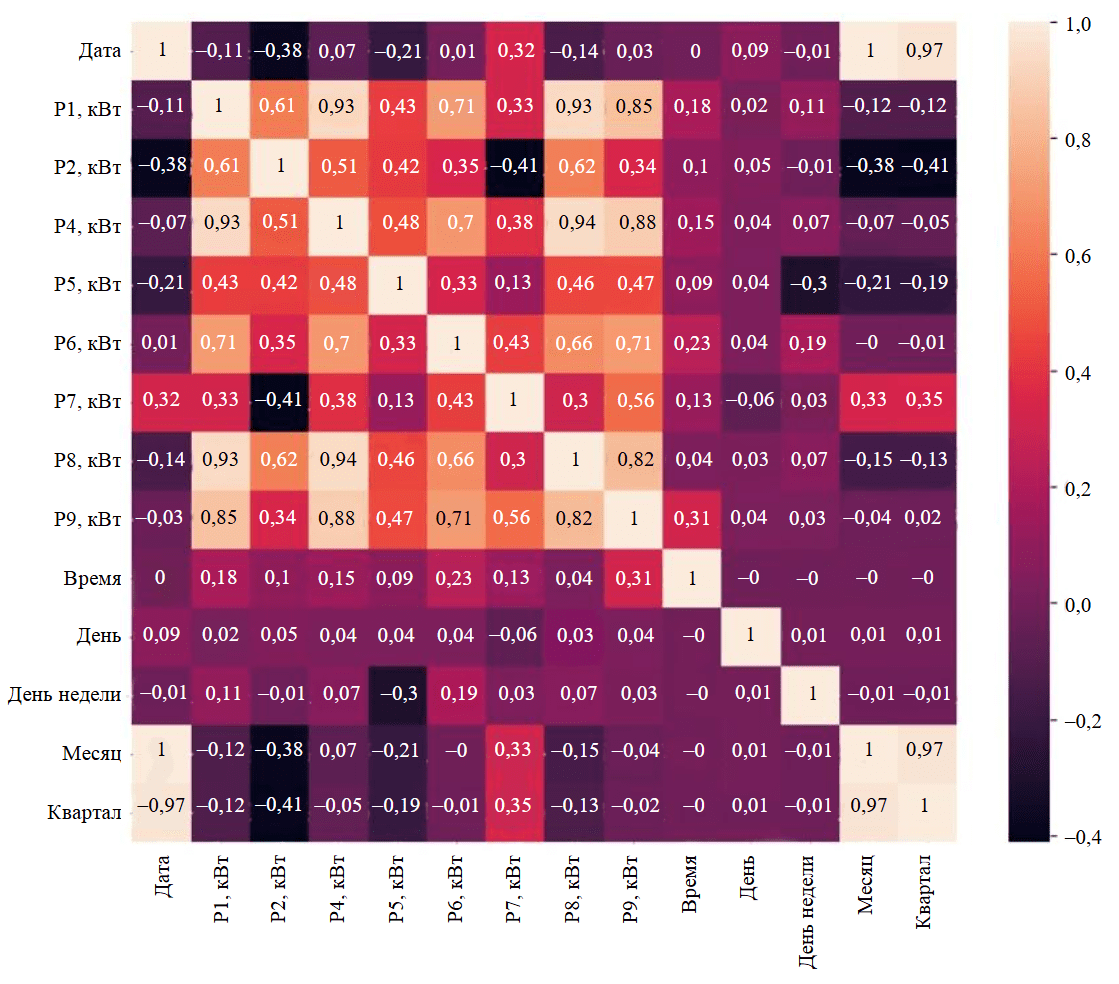
Рис.2. Матрица корреляции исходных данных по методу Пирсона
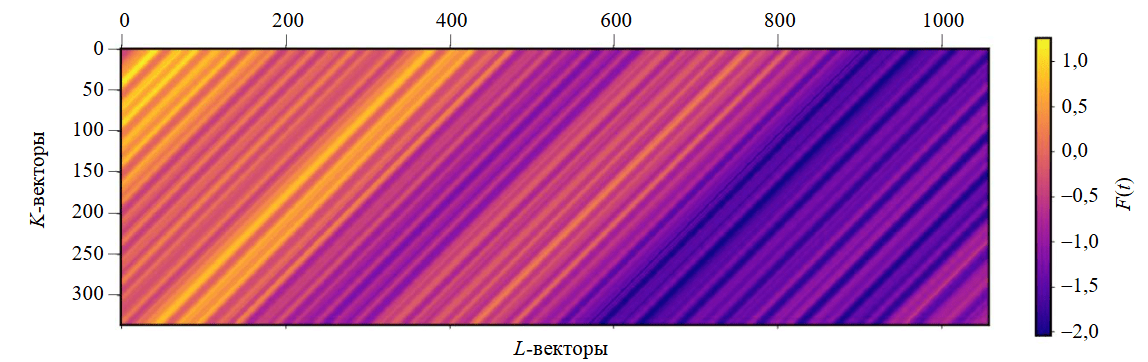
Рис.3. Траекторная матрица нормированных исходных данных. Временной ряд фидера 1 представлен в виде матрицы
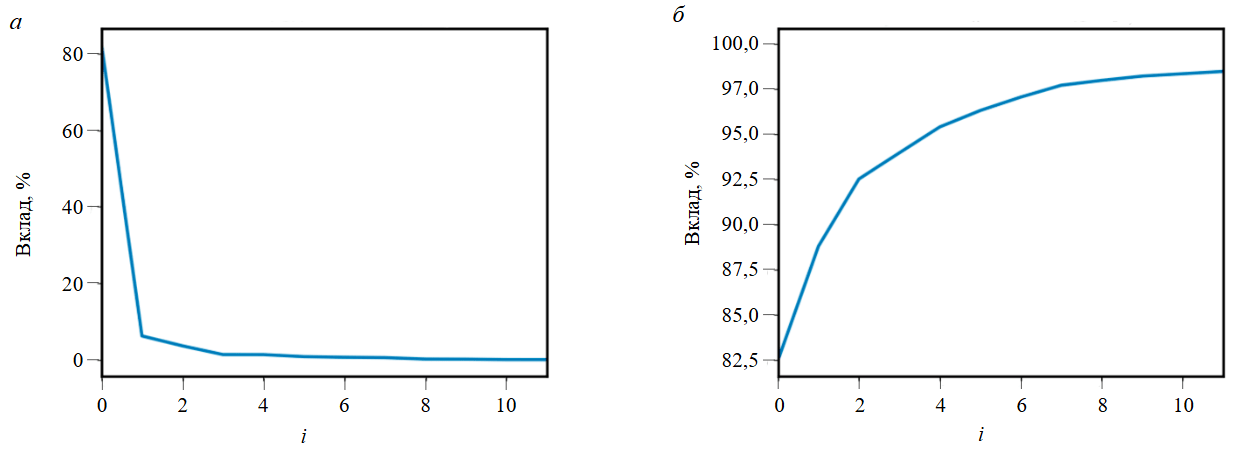
Рис.4. Относительный (а) и кумулятивный (б) вклады компонент на примере фидера 1
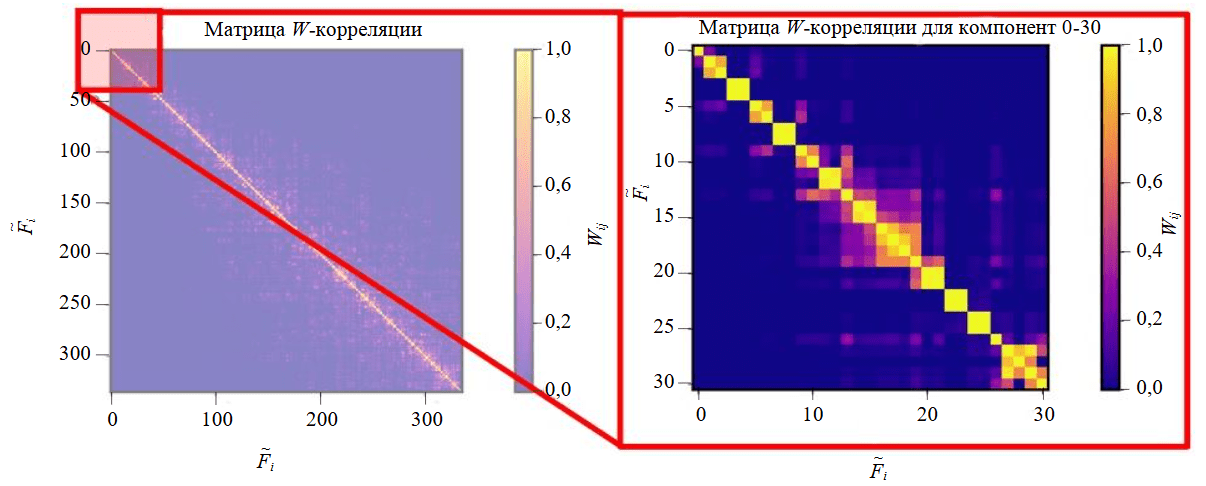
Рис.5. Матрица W-корреляции компонент фидера 1 [34]
Из матрицы W-корреляции видно, что некоторые пары компонент имеют высокую степень корреляции. Дальнейшая группировка проводится на основании интенсивности корреляции. Так, например, компоненты 2 и 3 группируются с компонентами 5 и 6, а компоненты 3 и 4 – с компонентами 7 и 8 (также с компонентами 11 и 12).
Обсуждение результатов
Статья [34] содержит результаты ручной группировки компонент при помощи матрицы W-корреляции (рис.6). Расширен принцип группировки на основе матрицы W-корреляции с применением амплитудно-частотной кластеризации и учетом множества фидеров (рис.7). Для фидера 1 в рамках рассматриваемого временного промежутка компоненты были сгруппированы следующим образом:
- трендовая группа: 0;
- периодическая группа 1: 1, 2, 5, 6, 9, 10;
- периодическая группа 2: 3, 4, 7, 8, 11, 12;
- периодическая группа 3: 19, 20, 21, 27, 28, 29.
Для трендовой группы характерна демонстрация недельного паттерна графика потребляемой мощности. В то же время при рассмотрении исходного временного ряда данный паттерн является трудноразличимым.
Для периодической группы 1 характерна демонстрация суточного паттерна потребления с ярко выраженными утренним и вечерним максимумами потребления. Вместе с тем форма кривой остается неизменной даже при серьезном изменении характера потребляемой мощности и увеличении количества шума.
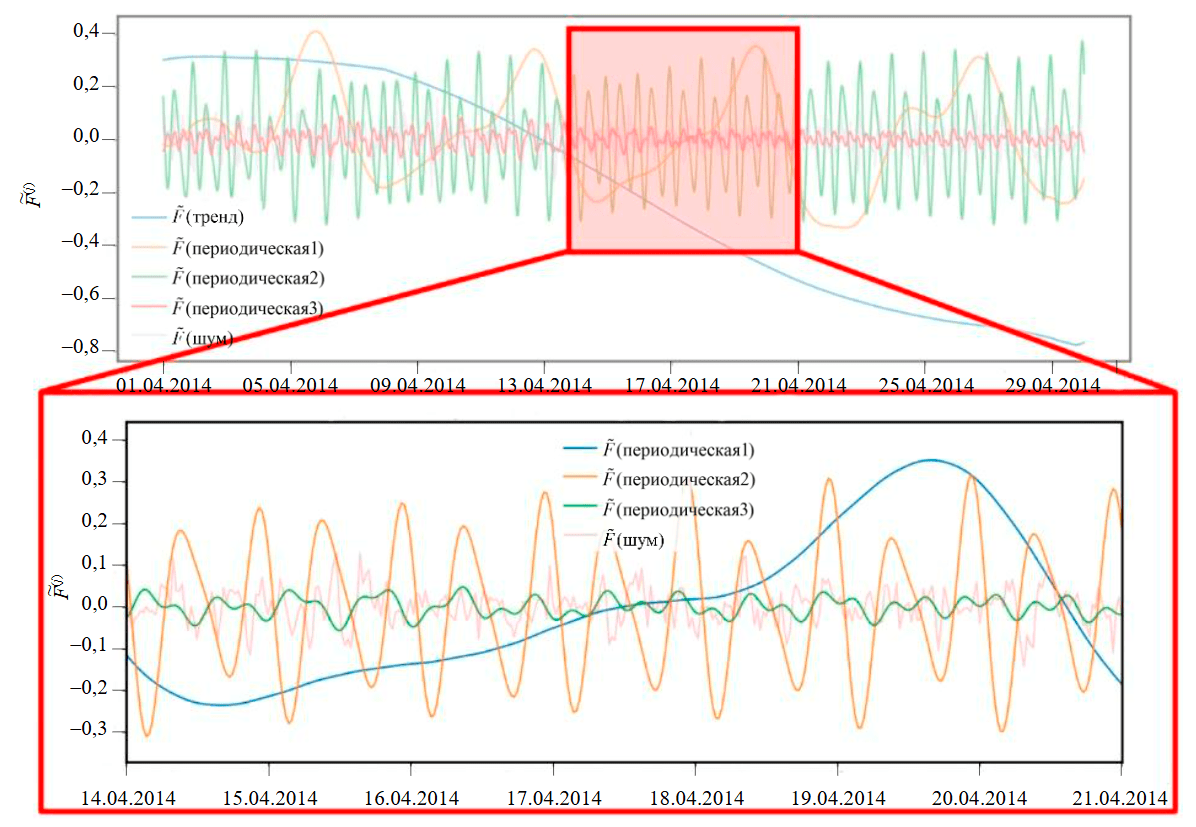
Рис.6. Сгруппированные компоненты временного ряда: одна компонента тренда и три группы периодических компонент [34]
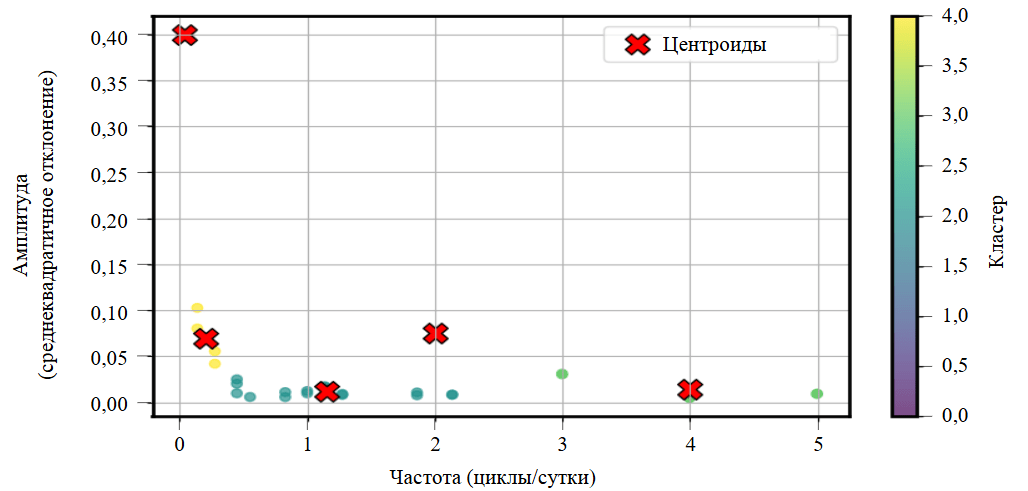
Рис.7. Кластеризация по частоте и амплитуде первых 10 компонент восьми фидеров
Для периодической группы 2 происходит формирование паттерна с периодом появления дважды в сутки. Паттерн визуально напоминает суточный, однако амплитуда его максимумов в несколько раз меньше.
Показанный пример справедлив для фидера 1 при рассмотрении месячного объема данных. Однако формирование ярко выраженных паттернов с некоторой периодичностью справедливо для каждого из рассматриваемых в исследовании набора данных. При этом для каждого фидера паттерны уникальны и меняются в зависимости от типа подключенной нагрузки. В табл.2 приведены результаты анализа для всего набора данных.
На основании допущения о постоянстве частоты и амплитуды компоненты на всем рассматриваемом участке было проведено построение амплитудо-частотной плоскости, где по вертикали находится ось RMS-значения компоненты, а по горизонтали – частоты, рассчитанные при помощи преобразования Фурье. В результате анализа компонент фидеров таким методом было получено семейство точек на плоскости, где каждая точка – отдельная компонента фидера (рис.7).
Таблица 2
Результаты применения метода SVD и группировки компонент по матрице W-корреляции
|
Фидер |
Компонента |
Характеристика |
Группа |
Описание группы |
Примечание |
|
9 |
0 |
Тренд |
0 |
– |
Формирование суточного паттерна. Девиантные значения определяются провалом потребления на протяжении 1,5 ч в четверг 17.04.2014 в середине суток. График мощности не зависит от дня недели |
|
1 |
Период – 1/2 сут., максимум совпадает с утренним пиком |
1 |
Формирование суточного паттерна потребления |
||
|
2 |
1 |
||||
|
3 |
Период – 1 сут. для обеих компонент. Сильная взаимная W-корреляция |
1 |
|||
|
4 |
1 |
||||
|
5 |
– |
2 |
Характерно формирование гармонической составляющей с частотой 3,5 раза в сутки |
||
|
6 |
– |
2 |
|||
|
8 |
0 |
Тренд |
0 |
– |
Минимум потребления в вечерний период с достижением первого максимума к полуночи. Снижение потребления наблюдается в полдень |
|
1 |
Период – 1 сут., максимум совпадает с утренним периодом |
1 |
Формирование суточного паттерна потребления |
||
|
2 |
1 |
||||
|
3 |
Период – 1/2 сут., максимум наступает в момент полудня и полуночи |
1 |
|||
|
4 |
1 |
||||
|
5 |
– |
2 |
Формирование гармонической составляющей с частотой три раза в сутки |
||
|
6 |
– |
2 |
|||
|
7 |
0 |
Тренд |
0 |
– |
Формирование ярко выраженного суточного паттерна с повторяющимися участками в дневной период будних дней, которые были выделены в отдельную пару компонент 7 и 8 |
|
1 |
Период – 1/2 сут., максимумы совпадают с пиками потребления |
1 |
Формирование суточного паттерна потребления |
||
|
2 |
1 |
||||
|
3 |
Период – 1 сут., максимум совпадает с дневным пиком нагрузок |
1 |
|||
|
4 |
1 |
||||
|
5 |
Период – 1/3 сут., максимум совпадает с полуночью |
1 |
|||
|
6 |
1 |
||||
|
7 |
Период – 1/5 сут., максимум совпадает с 23.00 |
2 |
Амплитуда меняется в зависимости от дня. В выходные дни амплитуда уменьшается до нуля |
||
|
8 |
2 |
||||
|
9 |
Период – 1/4 сут., минимум совпадает с полуночью |
3 |
Амплитуда и частота меняются в узких пределах незначительно в зависимости от дня недели |
||
|
10 |
3 |
||||
|
6 |
0 |
Тренд |
0 |
– |
Формирование практически не меняющейся во времени кривой потребления ЭЭ. Визуально отсутствует суточная периодика. В будние дни потребление находится в пределах 800-1000 кВт. В выходные дни значения превышают данные пределы |
|
1 |
0 |
– |
|||
|
2 |
Период – 1/2 сут., максимум наступает в момент полудня и полуночи |
1 |
Группа, вопреки ожиданиям, не формирует суточный паттерн. Частота и амплитуда группы изме-няется в широких пределах |
||
|
3 |
1 |
||||
|
4 |
Компонента слабо коррелирует с трендом |
0 |
– |
||
|
5 |
Период – 1/4 сут., максимум совпадает с полуднем |
2 |
Группа компонент формирует осцилляции с амплитудой менее 3 % от базового сигнала со стабильной частотой и с амплитудой, изменяющейся в широких пределах |
||
|
6 |
2 |
||||
|
7 |
2 |
||||
|
8 |
2 |
||||
|
9 |
Период – чуть больше 1/7 сут., минимум совпадает с полуночью |
3 |
Группа компонент формирует гармоническую составляющую сигнала с высокой частотой |
||
|
10 |
3 |
||||
|
5 |
0 |
Тренд |
0 |
– |
Формирование суточного паттерна. Потребление имеет зависимость от дня недели: в выходные дни суточный паттерн пропадает. Увеличение потребления ЭЭ сконцентрировано в дневное и вечернее время. Для 13.00-14.00 характерен провал в потреблении ЭЭ. Амплитуда всех рассматриваемых компонент и групп компонент падает до нуля в выходные дни |
|
1 |
Период – 1 сут., максимум совпадает с дневным пиком потребления |
1 |
Группа компонент формирует суточный паттерн потребления ЭЭ. Может быть использована для типизации вида нагрузки как группа компонент, очищенная от шумов |
||
|
2 |
1 |
||||
|
3 |
Период – 1/2 сут., максимум наступает в момент полудня и полуночи |
1 |
|||
|
4 |
1 |
||||
|
5 |
Период – 1/4 сут., минимум совпадает с полуночью |
2 |
Группа компонент меняет свою амплитуду несущественно. Минимумы совпадают с провалами потребления в период 13.00-14.00 |
||
|
6 |
2 |
||||
|
7 |
2 |
||||
|
8 |
Период – 1/10 сут. Высокочастотная компонента |
3 |
Группа компонент формирует гармоническую составляющую сигнала с высокой частотой |
||
|
9 |
3 |
||||
|
4 |
0 |
Тренд |
0 |
– |
Для временного ряда характерна ярко выраженная периодика на протяжении суток с небольшим отклонением от среднесуточного потребления ЭЭ. Наблюдается снижение потребления ЭЭ в воскресенье |
|
1 |
Период – 1/2 сут., максимум совпадает с утренним и вечерним пиками |
1 |
Группа компонент формирует суточный паттерн потребления ЭЭ |
||
|
2 |
1 |
||||
|
4 |
Период – 1/3 сут., максимум совпадает с полуночью |
1 |
|||
|
5 |
1 |
||||
|
7 |
Период – 1/5 сут., максимум совпадает с полуночью |
2 |
Группа компонент формирует осцилляции с малой амплитудой и средней частотой |
||
|
8 |
2 |
||||
|
2 |
0 |
Тренд |
0 |
– |
Для временного ряда характерна неявно выраженная периодика на протяжении суток с небольшим отклонением от среднесуточного потребления ЭЭ. Наблюдается выброс значений от среднего на протяжении 7 ч в середине недели |
|
1 |
Период – 1/2 сут., максимум наступает в момент полудня и полуночи |
1 |
Группа компонент формирует суточный паттерн потребления ЭЭ |
||
|
2 |
1 |
||||
|
3 |
1 |
||||
|
4 |
1 |
||||
|
5 |
Период – 1/3 сут., максимум совпадает с полуночью |
2 |
Компоненты имеют стабильную частоту вне зависимости от различия данных. Амплитуда увеличивается при возникновении существенных отклонений |
||
|
6 |
2 |
||||
|
1 |
0 |
Тренд |
0 |
– |
Для временного ряда характерна ярко выраженная периодика с небольшим отклонением от среднесуточного потребления ЭЭ. Наблюдается снижение потребления ЭЭ в конце недели на протяжении одного дня |
|
1 |
Период – 1/2 сут., максимум наступает за 2 ч до полудня и полуночи |
1 |
Группа компонент формирует суточный паттерн потребления ЭЭ |
||
|
2 |
1 |
||||
|
4 |
Период – 1/3 сут., максимум совпадает с полуночью |
1 |
|||
|
5 |
1 |
||||
|
7 |
Период – 1/5 сут., максимум наступает за 2 ч до полуночи |
2 |
Группа компонент имеет переменную амплитуду. Частота на протяжении рассматриваемого интервала постоянна. Амплитуда минимальна во второй день |
||
|
8 |
2 |
В результате исследований было определено следующее:
- При использовании метода SVD в задаче анализа временного ряда потребления мощности по фидеру подстанции формируются компоненты исходного сигнала, имеющие в первом приближении установившиеся частоту и амплитуду.
- Нулевая компонента разложения всегда является трендовой и как правило составляет более 70 % от исходного сигнала в соответствии с метрикой относительного вклада компонент в исходный сигнал.
- При группировке компонент при помощи матрицы W-корреляции в соответствии с интенсивностью корреляции происходит формирование недельного, суточного, дневного и более высокочастотных паттернов, уникальных для каждого фидера.
- Для формирования паттерна достаточно трех-четырех первых пар компонент, обратное преобразование матрицы и восстановление компоненты во временной ряд следует проводить только для первых 30 компонент.
- Для повышения информативности графиков при рассмотрении нанесенных на амплитудо-частотную плоскость компонент необходимо использовать экспоненциальный масштаб оси OY.
- При анализе рис.7 и аналогичных ему с различными временными интервалами было обнаружено, что компоненты группируются в зоне характерных частот, что косвенно указывает на наличие подобия на компонентном уровне групп потребителей рассматриваемых фидеров. Данная информация может быть использована при различных сценариях: от прогнозирования потребления до выработки управляющих воздействий алгоритма управления спросом на электроэнергию.
Заключение
Применение результатов исследования актуально в задачах автоматизированной типизации профилей нагрузки при этом приложение может меняться в зависимости от условий и исходных данных. Результаты могут быть применимы в задачах, связанных с интеграцией экономических стимулов в розничный рынок, при оценке пригодности и потенциала потребителя с точки зрения управления спросом на электроэнергию, а также при автоматизации процесса определения места несанкционированного доступа к электроэнергии. Метод будет демонстрировать изменение компонентного состава временного ряда и появление изменений в профиле нагрузки. В таком случае для большей эффективности применения данного метода целесообразно разработать систему с внедрением классификатора на основе искусственной нейронной сети [35] с целью использования в различных направлениях.
Создание «балансового портрета» или «типового профиля потребления» также необходимо для решения задач, связанных с интеграции экономических стимулов при управлении спросом. Информацию о профиле потребления необходимо использовать для формирования индивидуальных запросов для управления группой нагрузок, имеющих созависимый и/или общий характер потребления, и таким образом формировать стратегию управления, основанную на мотивации [36] к активному участию в процессе управления спросом на электроэнергию.
Использование результатов группировки компонент одного фидера позволяет оценить пригодность и потенциал потребителя с точки зрения управления спросом на электроэнергию. Также внедрение результатов кластеризации компонент на амплитудо-частотной плоскости возможно в приложении к решению вопроса подобия фидеров в динамике, т.е. не в целом подобие формы графиков, а их подобие на компонентном уровне, например практически полное совпадение графиков потребления по определенным дням недели.
Помимо прочего, метод SVD может быть применен в решении задачи анализа трендов генерации стохастических источников энергии, например ветроэлектростанции или солнечные электростанции. Адаптации метода не требуется, как описано в [37], для прогнозирования генерации ВИЭ необходимо получить периодические составляющие из общего состава компонент с использованием матрицы W-корреляции как индикатора отбора периодических компонент.
Предложенные алгоритмы позволят использовать полученные типовые профили потребления электроэнергии для расчетов квазидинамических электрических режимов при решении задач перспективного развития электротехнических комплексов и выборе рациональных способов энергообеспечения и повышения энергетической эффективности горных предприятий [38].
Литература
- Николаев А.В., Фёт Ш., Кычкин А.В. Использование кибернетического подхода к ценозависимому управлению спросом на потребляемую подземным горно-добывающим предприятием электроэнергию // Записки Горного института. 2023. Т. 261. С. 403-414. DOI: 10.31897/PMI.2022.33
- Рыльникова М.В., Клебанов Д.А., Макеев М.А., Кадочников М.В. Применение искусственного интеллекта и перспективы развития аналитических систем больших данных в горной промышленности // Горная промышленность. 2022. № 3. С. 89-92. DOI: 10.30686/1609-9192-2022-3-89-92
- Скамьин А.Н., Добуш В.С., Жопри М.Х. Определение сопротивления электрической сети при расчете режимов с искажениями в напряжении // Записки Горного института. 2023. Т. 261. С. 443-454. DOI: 10.31897/PMI.2023.25
- Shklyarskiy Ya., Skvortsov I., Sutikno T., Manap M. The optimization technique for a hybrid renewable energy system based on solar-hydrogen generation // International Journal of Power Electronics and Drive Systems. 2024. Vol. 15. № 1. P. 639-650. DOI: 10.11591/ijpeds.v15.i1.pp639-650
- Shklyarskiy Ya., Andreeva Iu., Sutikno T., Jopri M.H. Energy management in hybrid complexes based on wind generation and hydrogen storage // Bulletin of Electrical Engineering and Informatics. 2024. Vol. 13. № 3. P. 1483-1494. DOI: 10.11591/eei.v13i3.6757
- Beloglazov I., Plaschinsky V. Development MPC for the Grinding Process in SAG Mills Using DEM Investigations on Liner Wear // Materials. 2024. Vol. 17. Iss. 4. № 795. DOI: 10.3390/ma17040795
- Sychev Yu.A., Aladin M.E., Aleksandrovich S.V. Developing a hybrid filter structure and a control algorithm for hybrid power supply // International Journal of Power Electronics and Drive Systems. 2022. Vol. 13. № 3. P. 1625-1634. DOI: 10.11591/ijpeds.v13.i3.pp1625-1634
- Сериков В.А., Костин В.Н., Сычев Ю.А., Хайдар С. Метод оценки качества электроэнергии в системах электроснабжения горных предприятий с мощными высоковольтными частотно-регулируемыми электроприводами // Горный информационно-аналитический бюллетень. 2024. № 12. С. 162-177. DOI: 10.25018/0236_1493_2024_12_0_162
- Жуковский Ю.Л., Сусликов П.К. Оценка потенциального эффекта применения технологии управления спросом на горных предприятиях // Устойчивое развитие горных территорий. 2024. Т. 16. № 3 (61). С. 895-908. DOI: 10.21177/1998-4502-2024-16-3-895-908
- Xiang Jing, Wenping Qin, Hongmin Yao et al. Resilience-oriented planning strategy for the cyber-physical ADN under malicious attacks // Applied Energy. 2024. Vol. 353. Part 4. № 122052. DOI: 10.1016/j.apenergy.2023.122052
- Zarate-Perez E., Rosales-Asensio E., González-Martínez A. et al. Battery energy storage performance in microgrids: A scientific mapping perspective // Energy Reports. 2022. Vol. 8. Suppl. 9. P. 259-268. DOI: 10.1016/j.egyr.2022.06.116
- Fedorova E., Morgunov V., Lobko K., Pupysheva E. Review: Axial Motion of Material in Rotary Kilns // Eng. 2025. Vol. 6. Iss. 6. № 106. DOI: 10.3390/eng6060106
- Beloglazov I. Review of Advanced Digital Technologies, Modeling and Control Applied in Various Processes // Symmetry. 2024. Vol. 16. Iss. 5. № 536. DOI: 10.3390/sym16050536
- Котелева Н.И., Вальнев В.В., Королев Н.А. Технология дополненной реальности как средство технического обслуживания оборудования металлургических производств // Цветные металлы. 2023. № 4. С. 14-23. DOI: 10.17580/tsm.2023.04.02
- Skamyin A., Shklyarskiy Ya., Lobko K. et al. Impedance analysis of squirrel-cage induction motor at high harmonics condition // Indonesian Journal of Electrical Engineering and Computer Science. 2024. Vol. 33. № 1. P. 31-41. DOI: 10.11591/ijeecs.v33.i1.pp31-41
- Кваснiков В.П., Стахова А.П. Спектральний аналiз сигналу вiбраiï з використанням перетворення Фур’є // Збiрник наукових праць Одеськоï державноï академiï технiчного регулювання та якостi. 2022. № 2 (21). С. 28-33. DOI: 10.32684/2412-5288-2022-2-21-28-33
- Yingguan Lu. Applications of Fourier transforms in engineering // Theoretical and Natural Science. 2024. Vol. 43. P. 26-32. DOI: 10.54254/2753-8818/43/20241142
- Zihui Yin, Rongwen Guo, Hang Chen. Multi-station Magnetotelluric Data Processing Based on Singular Value Decomposition // Journal of Physics: Conference Series. 2023. Vol. 2651. № 012067. DOI: 10.1088/1742-6596/2651/1/012067
- Zhukovskiy Y., Buldysko A., Revin I. Induction Motor Bearing Fault Diagnosis Based on Singular Value Decomposition of the Stator Current // Energies. 2023. Vol. 16. Iss. 8. № 3303. DOI: 10.3390/en16083303
- Javadnejad F., Sharifi M.R., Basiri M.H., Ostadi B. Optimization Model for Maintenance Planning of Loading Equipment in Open Pit Mines // European Journal of Engineering and Technology Research. 2022. Vol. 7. Iss. 5. P. 94-101. DOI: 10.24018/ejeng.2022.7.5.2907
- Zeyang Zhou, Mingzhu Zhang, Jie Tian, Jingwen Huang. Experimental study on classification and identification method for fault signals of mining steel wire ropes // Journal of Physics: Conference Series. 2024. Vol. 2798. № 012043. DOI: 10.1088/1742-6596/2798/1/012043
- MingAng Guo, Xiaotong Tu, Abbas S. et al. Time-frequency analysis-based impulse feature extraction method for quantitative evaluation of milling tool wear // Structural Health Monitoring. 2024. Vol. 23. Iss. 3. P. 1766-1778. DOI: 10.1177/14759217231192003
- Ninawe S., Deshmukh R. Efficient vibration analysis system using empirical mode decomposition residual signal and multi-axis data // Journal of Vibration and Control. 2025. Vol. 31. Iss. 15-16. P. 2993-3006. DOI: 10.1177/10775463241262117
- Guolong Fu, Jintian Yin, Shengyi Wu et al. Composite Fault Signal Detection Method of Electromechanical Equipment Based on Empirical Mode Decomposition // Advanced Hybrid Information Processing: 6th EAI International Conference, 29-30 September 2022, Changsha, China. Springer, 2023. Part 2. P. 1-13. DOI: 10.1007/978-3-031-28867-8_1
- Харченко К.В., Зубец А.Ж., Москвитина Е.И. и др. Анализ эффективности внедрения предиктивного обслуживания горнодобывающего оборудования на основе технологий Индустрии 4.0 // Горная промышленность. 2024. № 4. С. 130-138. DOI: 10.30686/1609-9192-2024-4-130-138
- Zexian Sun, Mingyu Zhao, Guohong Zhao. Hybrid model based on VMD decomposition, clustering analysis, long short memory network, ensemble learning and error complementation for short-term wind speed forecasting assisted by Flink platform // Energy. 2022. Vol. 261. Part B. № 125248. DOI: 10.1016/j.energy.2022.125248
- Khalkhali Shandiz S., Khezrzadeh H. Application of moving vehicle response and variational mode decomposition (VMD) for indirect damage detection in bridges // Modares Civil Engineering journal. 2021. Vol. 21. Iss. 1. P. 31-46.
- Ahmad Zaki Maulana, Subekti Subekti, Nur Indah. Detecting damage on engine mounts using hilbert-huang transform vibration analysis // JTTM: Jurnal Terapan Teknik Mesin. 2024. Vol. 5. № 2. P. 235-240. DOI: 10.37373/jttm.v5i2.1108
- Prasshanth C.V., Venkatesh S.N., Mahanta T.K. et al. Deep learning for fault diagnosis of monoblock centrifugal pumps: a Hilbert–Huang transform approach // International Journal of System Assurance Engineering and Management. 2024. DOI: 10.1007/s13198-024-02447-z
- Ziyu Guo. Robot terrain classification based on improved Hilbert-Huang transform and long short-term memory network // Applied and Computational Engineering. 2024. Vol. 95. P. 49-56. DOI: 10.54254/2755-2721/95/2024BJ0060
- Hong Lu, Wei Zhang, Zhimin Chen et al. Rotating machinery early fault detection integrating variational mode decomposition and multiscale singular value decomposition // Measurement Science and Technology. 2024. Vol. 35. № 12. № 126128. DOI: 10.1088/1361-6501/ad7a1f
- Khan M.U., Hasan M.A.H. Hybrid EEG-fNIRS BCI Fusion Using Multi-Resolution Singular Value Decomposition (MSVD) // Frontiers in Human Neuroscience. 2020. Vol. 14. № 599802. DOI: 10.3389/fnhum.2020.599802
- Golyandina N. Particularities and commonalities of singular spectrum analysis as a method of time series analysis and signal processing // WIREs Computational Statistics. 2020. Vol. 12. Iss. 4. № e1487. DOI: 10.1002/wics.1487
- Сусликов П.К., Жуковский Ю.Л. Определение скрытых зависимостей множественных временных рядов потребления электроэнергии с целью классификации и управления профилями нагрузки // Электроэнергетика глазами молодежи – 2024: Материалы XIV Международной научно-технической конференции, 1-4 октября 2024, Ставрополь, Россия. В 2 томах. Т. 2. Ставрополь: Северо-Кавказский федеральный университет, 2024. С. 127-130.
- Ustinov D.A., Aysar Abou Rashid. Using Artificial Neural Network Methods to Increase the Sensitivity of Distance Protection // International Journal of Engineering – Transactions B: Applications. 2024. Vol. 37. Iss. 11. P. 2192-2199. DOI: 10.5829/IJE.2024.37.11B.06
- Shushpanov I., Suslov K., Ilyushin P., Sidorov D.N. Towards the Flexible Distribution Networks Design Using the Reliability Performance Metric // Energies. 2021. Vol. 14. Iss. 19. № 6193. DOI: 10.3390/en14196193
- Kavakci G., Cicekdag B., Ertekin S. Time Series Prediction of Solar Power Generation Using Trend Decomposition // Energy Technology. 2024. Vol. 12. Iss. 2. № 2300914. DOI: 10.1002/ente.202300914
- Ilyushin P., Papkov B., Kulikov A., Suslov K. Algorithm and Methods for Analyzing Power Consumption Behavior of Industrial Enterprises Considering Process Characteristics // Algorithms. 2025. Vol. 18. Iss. 1. № 49. DOI: 10.3390/a18010049
