Application of machine learning to modeling Herschel – Bulkley drilling fluid parameters for optimizing wellbore cleaning
- 1 — Ph.D. Scientific Supervisor of Laboratory Empress Catherine II Saint Petersburg Mining University ▪ Orcid ▪ Scopus ▪ ResearcherID
- 2 — Ph.D., Dr.Sci. Scientific Supervisor of Scientific Center, Head of Department Empress Catherine II Saint Petersburg Mining University ▪ Orcid ▪ Scopus
- 3 — Ph.D. Executive Director of Scientific Center Empress Catherine II Saint Petersburg Mining University ▪ Orcid ▪ Scopus ▪ ResearcherID
- 4 — Lead Engineer of Laboratory Empress Catherine II Saint Petersburg Mining University ▪ Orcid
Abstract
Water- and oil-based drilling fluids are polydisperse non-Newtonian systems, the stress state of which is adequately described by the Herschel – Bulkley rheological model. This study hypothesizes that cuttings transport efficiency can be improved by selecting the most effective combination of the three parameters of the rheological model – yield stress, consistency index, and flow behavior index – when designing drilling fluid properties. The effective parameter combination of the Herschel – Bulkley model for achieving a uniform velocity profile was determined using correlation and regression analysis methods as well as machine learning techniques. The computational part of the work was performed in the Wolfram Mathematica symbolic calculation package. Deterministic regions of the dependence of the velocity profile uniformity index on the rheological coefficients were identified. For practical engineering calculations, a linear mathematical model was constructed to represent the relationship between the modified excess coefficient and the parameters of the three-parameter Herschel – Bulkley rheological equation. The proposed methodology can be recommended for designing new drilling fluid systems and testing existing ones under given wellbore cleaning conditions.
Introduction
One of the most important functions of drilling fluids is to transport drilled cuttings to the surface. Cuttings transport efficiency is governed by annular flow velocity, fluid density, and its rheological characteristics. The correct selection of rheological parameters significantly enhances the rate of penetration [1]. Control of drilling fluid rheology is achieved through the selection of chemical additives and their concentrations [2, 3]. The velocity profile of drilling fluids has a significant impact on cuttings transport efficiency [4]. A flat velocity profile in the wellbore annulus provides a more uniform momentum transfer to the particles in the direction of flow. When fluids flow in pipes, the velocity profile exhibits a symmetric distribution with maximum velocity at the center of the flow [5]. In annular flow, however, the maximum velocity shifts toward the pipe axis. This leads to uneven cuttings transport and the formation of stationary cuttings beds along the wellbore walls [6, 7]. These effects are confirmed by both analytical and numerical solutions of the governing flow equations [8, 9]. Experimental data also validate the non-uniformity of velocity profiles in both pipes and annular geometries [10]. Research [11] demonstrates strong agreement between numerical simulations of cuttings-laden flows and laboratory-scale experimental results. Similar solutions can be obtained using the control volume method implemented in software packages such as ANSYS Fluent and OpenFOAM [12, 13]. These computational tools also enable modeling of wellbore cleaning while accounting for drillstring rotation [14] and thermal effects [15]. Temperature effects become particularly significant during well construction and production operations in Arctic environments [16, 17]. Research [18] addresses the modeling of cuttings transport in deviated and horizontal wells under high-temperature and high-pressure conditions. At the same time, considerable attention is currently being given to drilling fluid losses. The calculation of flow velocities and pressures for specific wellbore conditions contributes to improving hole-cleaning practices in cases of drilling fluid loss [19].
When modeling the flow of drilling fluids, the choice of a rheological model plays a critical role. The rheological behavior of modern drilling fluids is best represented by the Herschel – Bulkley model [20-22]. This model is applicable both to fluids containing solid phases and to formulations without them [23]. The least-squares method is the most reliable approach for determining the coefficients of a rheological model. It is applied to approximate the experimental dependence of shear stress on shear rate [24]. The mathematical formulation of fluid flow in the wellbore annulus includes the governing equations of motion, the rheological model of the fluid, and boundary conditions. The choice of the rheological model is of particular importance, since adjusting its coefficients allows control over velocity and pressure distributions. The mathematical model of drilling fluid flow in the wellbore annulus was adopted from [24]. In this research, a numerical method is presented to determine the velocity distribution of a non-Newtonian fluid represented by the Herschel – Bulkley model in annular geometries. In contrast to the Ostwald – de Waale model, it contains three coefficients:
where τ0 – yield stress; γ – shear rate; K – consistency index; n – flow index.
The stationary modified Navier – Stokes differential equation for determining the velocity field:
where ρ – fluid density; r – radial coordinate; g – gravitational acceleration; ∂p/∂z – pressure gradient along the length L.
For the boundary conditions of the wellbore annulus:
where w – fluid layer velocity; R1 – external radius of drill pipe; R2 – well radius.
The assumptions include fluid incompressibility ρ = const, one-dimensional flow, and steady-state conditions:
Research [24] compared the solutions obtained under the Newtonian fluid approximation with the analytical solution for Poiseuille flow in an annular gap. The physical adequacy of the numerical solution was confirmed when varying the input parameters. The numerical solution was implemented in Wolfram Language as an interpolating function that enables velocity values to be represented as a function of the coordinate. In addition, a numerical indicator of velocity profile uniformity, referred to as the modified excess coefficient, was introduced:
where μ2, μ4 – the central moments applied to the velocity distribution in the flow.
A minimum value of this parameter indicates the presence of the most uniform velocity profile. The use of program code makes it possible to obtain numerical solutions for the velocity profile. The corresponding modified excess coefficient characterizes the uniformity of the velocity distribution. For a more accurate visual assessment, the velocity distribution is plotted in a dimensionless form. This form represents the ratio of point velocity to the mean flow velocity – The plotting domain is located between the drill pipe wall R1 and the wellbore wall R2. Examples of velocity distributions and the corresponding values of the excess coefficient are shown in Fig.1. The most elongated and shifted profile corresponds to the highest value of parameter E.
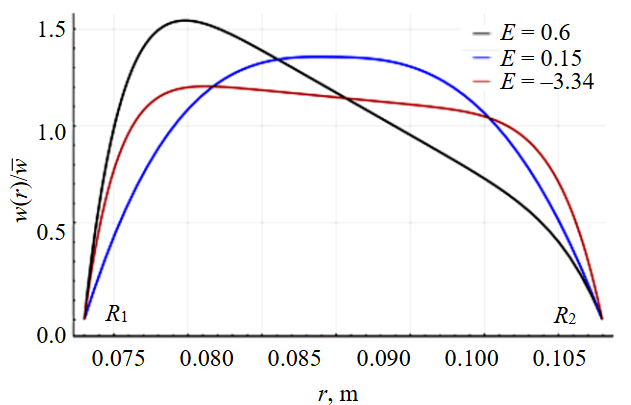
Fig.1. The flattest and most elongated velocity profiles
It is known that in the Shvedov – Bingham model, the value of yield stress influences the uniformity of the velocity distribution, while plastic viscosity determines the average flow velocity. In the Ostwald – de Waale power-law model, a reduction in the flow behavior index n leads to the formation of a flatter velocity profile. A drawback of this approximation is that it does not account for the yield stress of the drilling fluid τ0 The rheological equation of the power-law fluid is expressed as:
Research [24] showed that in the Herschel – Bulkley model, no explicit correlation is observed between the parameters τ0, K, n and the modified excess coefficient E. This confirms that the velocity distribution of the fluid cannot be controlled by adjusting τ0, K, n independently of one another. Controlling only the flow behavior index n, as in the power-law model, does not yield a positive result [4, 8]. Considering these limitations, the objective of this work is to develop a method for determining the interrelations among the three rheological parameters of the Herschel – Bulkley model, with a tendency toward forming a more uniform velocity profile. The uniformity can be numerically assessed using the modified excess coefficient.
Methodology
To determine the effect of the parameter combination of the Herschel – Bulkley model (1) on the uniformity of the velocity profile, it is necessary to establish the dependence of the modified excess coefficient E on the parameters τ0, K, n. Since E depends on the velocity distribution obtained from the numerical solution of the momentum equation with specified geometric conditions, pressure drops, and fluid parameters, the problem reduces to identifying the relationship among these numerical parameters. A nonlinear form of dependence is assumed:
To establish such a dependence, it is necessary to construct a table of values for E, τ0, K, and n, that correspond to the physical and technological parameters of the wellbore cleaning process. When preparing this table, wide parameter ranges are proposed as constraints for τ0, K, and n, corresponding to the properties of drilling fluids [25]: yield stress 0.1 ≤ τ0 ≤ 5 Pa; consistency index 2 ≤ K ≤ 15 Pa·sⁿ; and flow behavior index 0.15 ≤ n ≤ 1. For the most promising fluids, rheological parameters are assumed that ensure efficient cuttings transport under laminar flow conditions. These parameters are calculated according to the methodology presented in [26]. Under laminar flow conditions, dynamic pressures are lower than in turbulent flow, which reduces the risk of formation fracturing during hole cleaning. Therefore, the critical velocity of the drilling fluid is calculated, above which the flow regime transitions from laminar to turbulent [27].
Next, the cuttings transport quality index for the critical velocity of the drilling fluid is calculated by determining the cuttings transport velocity based on the difference between the flow velocity and the particle settling velocity. Shear stresses and the flow regime in the vicinity of the particle, which may be either laminar or turbulent, must be taken into account. For the parameters τ0, K, and n, corresponding to high values of the cleaning index, the velocity profile is calculated at pressures associated with the critical velocity of the drilling fluid. The calculated modified excess coefficient E is entered into a table for further processing.
The three-factor dependence E= f (τ0, K, n) may exhibit a pronounced nonlinear character. The next task involves identifying the deterministic sections of dependence (2) with the possibility of determining linear segments, after which a linear multifactor regression can be constructed:
where ai – the regression coefficients.
The advantage of isolating linear segments lies in the possibility of obtaining an analytical form of the dependence, which is preferred by drilling hydraulics designers for evaluating velocity profile uniformity when selecting a drilling fluid.
Machine learning methods have been successfully applied to describe multifactor nonlinear dependencies. For example, in [28] it is described the use of a neural network to evaluate equivalent circulating density based on large datasets. In [29], a neural network approach was employed to predict the plastic and effective viscosities of oil-based drilling fluids. Research [30] utilized a Gaussian process model to forecast drilling fluid rheological properties from six factors: Marsh funnel viscosity, density, volumetric content of water, oil and solids, and temperature. The coefficient of determination exceeded 0.9, indicating high predictive accuracy. The authors of [31] applied hybrid machine learning to achieve rapid prediction of rheological and filtration properties of water-based drilling fluids. Research [32] employed machine learning methods to predict porosity and permeability during drilling. Research [33] proposed a neural network training approach (Python programming language) for forecasting drilling fluid properties under high-pressure and high-temperature conditions. The results were compared with the Herschel – Bulkley and power-law rheological models. Yield stress values were predicted using three input parameters: shear rate, pressure, and temperature. In [34], the authors developed a script in Wolfram Language to implement a logarithmic-linear (L-L) mathematical model. Using this code, a mathematical model was realized for analyzing the rheological properties of drilling fluids, based on a nonlinear relationship between measured shear stress and shear rate values in fluids used for drilling oil and geothermal wells. Machine learning methods have also proven effective in addressing problems related to wellbore complications during field operations [35, 36]. Such approaches are particularly suitable for processing field data with high levels of noise caused by random factors.
Based on the objectives of this study, Wolfram Language was selected for the full calculation cycle, including the numerical solution of the momentum equation with respect to the velocity profile and the identification of deterministic sections of dependence (3). Using the Predict function, a machine learning method is selected – Random Forest, Nearest Neighbors, Decision Tree, and others [37]. A drawback of predictive models is the inability to construct an analytical form of the dependence. The identification of linear sections of the dependence makes it possible to transition to a linear multifactor regression model. The LinearRegression option within the Predict function enables the construction of multifactor linear dependencies of the form (4). To select the most effective method of the Predict function for processing the initially compiled data table, a predefined template is applied to test each method and compare the coefficient of determination R2. For identifying deterministic sections potentially suitable for constructing the analytical form (4), the method with the highest R2 value is used. The presence of deterministic sections can be readily determined by analyzing the ComparisonPlot and ResidualPlot graphs, which illustrate the deviation between actual and predicted values as well as the magnitude of deviation across different segments of the predicted values.
A methodology has been developed to determine the most effective parameter combinations of the Herschel – Bulkley model for ensuring high-quality wellbore cleaning, including through the formation of the most uniform velocity profile. The methodology consists of the following steps:
- Using the procedure for calculating the cuttings transport efficiency index, establish the initial requirements for the rheological characteristics of the drilling fluid under the power-law rheological approximation while maintaining laminar flow conditions.
- Determine the type of velocity profile by calculating the modified excess coefficient for a Herschel – Bulkley fluid with K and n values that satisfy the initial requirements.
- Identify the combinations of τ0, K, and n that meet the requirement of high cuttings transport efficiency and provide a uniform velocity profile with the lowest value of the modified excess coefficient E.
- Apply machine learning methods to establish the relationship between τ0, K, n and the quantitative indicator of velocity profile uniformity – the modified excess coefficient E.
- For the sections selected for constructing an analytical form of linear multifactor regression, calculate the regression coefficients.
- Develop methodological recommendations for the design of drilling fluids with effective combinations of rheological parameters τ0, K, and n to ensure high-quality cuttings transport in laminar flow while maintaining a uniform velocity profile.
Discussion
Using Wolfram Language, 9235 combinations of the parameters τ0, K, and n were generated within the specified bounds and step size Δ:
The cuttings transport efficiency index was calculated for the critical velocity of the drilling fluid, defined as the velocity above which the fluid transitions to turbulent flow. This choice is justified by the requirement to remain within safe drilling parameters under laminar flow, which is characterized by significantly lower hydrodynamic pressures. The common input parameters for the calculations are as follows: drilling fluid density – 1200 kg/m3; cuttings density – 2300 kg/m3; diameter of the spherical coarse cuttings model – 7.6 mm; wellbore diameter – 215.9 mm; and outer diameter of the drill pipe – 146 mm.
Out of the total combinations, 7980 provide cuttings transport efficiency greater than 70 %, while 7582 combinations exceed 80 %. The highest efficiency is observed at n = 1; however, modern drilling fluids for directional and horizontal wells exhibit pronounced pseudoplastic properties, and the parameter n << 1 [38]. A graph characterizing the trend of cuttings transport efficiency as a function of the rheological coefficients K and n is shown in Fig.2. With increasing values of the consistency index K and the flow behavior index n, the particle settling velocity decreases, since in the power-law rheological model the consistency index serves as an analogue of viscosity. Consequently, an increase in viscosity reduces the particle settling velocity due to the enhanced ability of the fluid flow to suspend particles. This conclusion is consistent with Stokes’ theory through the viscous characteristics of the fluid [39].
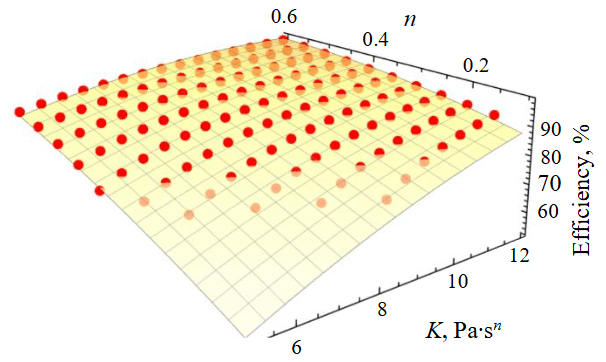
Fig.2. Dependences of the efficiency coefficient of cuttings transport on the coefficients K and n of the rheological model of a power-law liquid
The flow behavior index in the power-law rheological model reflects the non-Newtonian behavior of the medium: with increasing shear rate, viscosity decreases at low values of the exponent. Consequently, when n → 1 viscosity shows a lower tendency to decline; at n = 1 viscosity remains constant; and when n > 1 the fluid can be considered dilatant, although such fluids are not used in drilling. An increase in viscosity enhances suspension capacity; therefore, its reduction, reflected by a decrease in the parameter n, is undesirable for cuttings transport. As these coefficients increase, the critical velocity of the drilling fluid also rises. The turbulent regime occurs at higher velocities, which is favorable for the drilling process, since the flow rate can be increased while avoiding transition to turbulent flow with high pressure [40].
The occurrence of turbulent flow is influenced by the hydraulic diameter of the wellbore annulus, the rheological characteristics of the drilling fluid, and its density. The most effective method for preventing the onset of turbulence is to reduce the drilling fluid flow rate and maintain its parameters within the range specified by the designed drilling hydraulics program. In well construction projects, pressure control is also carried out in terms of equivalent circulating density [41].
The values of the modified excess coefficient were calculated for each velocity distribution while varying the parameters τ0, K, and n under pressure drops corresponding to the critical flow velocity. According to the two-sigma statistical rule, profiles with the most uniform velocity distribution were identified with a probability of 95 %. A total of 4845 cases with cuttings transport efficiency greater than 70 % and n ≤ 0.8 correspond to the currently relevant formulations of drilling fluids. For these cases, the values of the velocity profile uniformity index were determined. The test was carried out for fluids with cuttings transport efficiency greater than 70 % and n ≤ 0.8. The next step was to determine the dependence of type (3) of the modified excess coefficient on the parameters of the rheological model. Based on the results of [24], it can be assumed that the relationship is nonlinear. Due to the multifactorial nature of the approximation task, a machine learning method selection template was used. The data were randomly divided into training and test sets in an 80/20 ratio. The input parameters were τ0, K, n the output parameters were the modified kurtosis coefficient E. According to the coefficient of determination, the Neural Network method in Wolfram Language proved to be the most effective for this task, with R2 = 0.996 (Fig.3). The distribution of deviations (Fig.3, b) also indicates the high quality of the approximation. Analysis of the graphs showed that deterministic sequences were identified for the modified excess coefficient starting from 0.9. Further consideration of the problem continues exclusively within this interval.
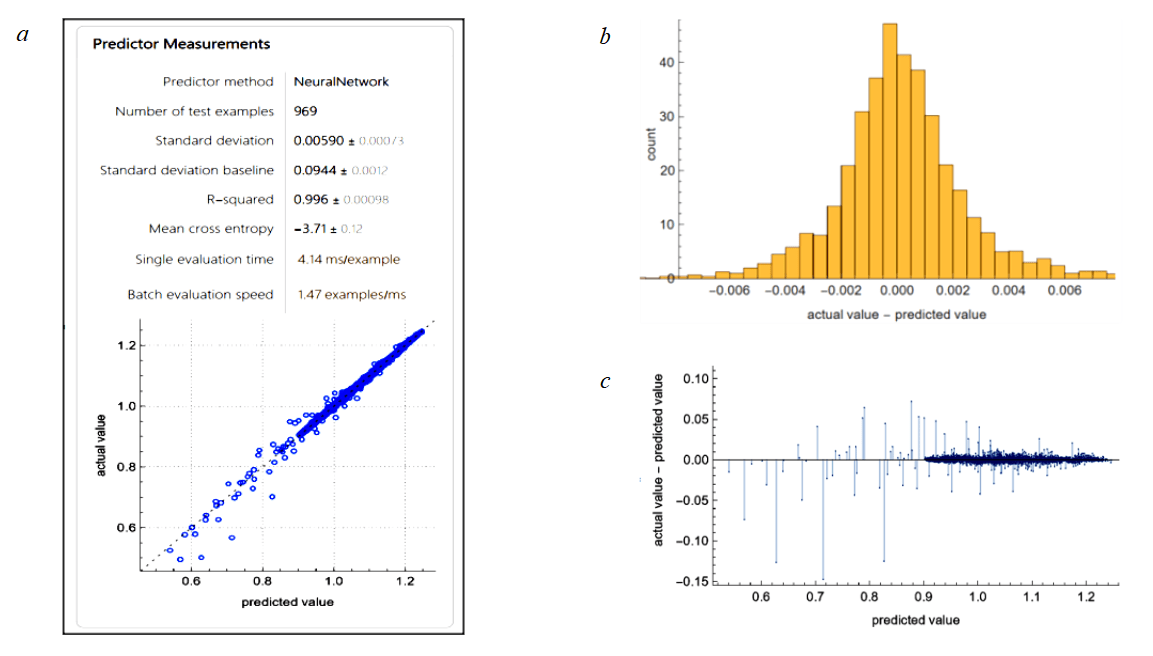
Fig.3. Characteristics of the neural network method: a – dialog of the method characteristics; b – histogram of deviations ResidualHistogram; c – distribution of deviations by areas ResidualPlot
The most uniform velocity profile from the deterministic values is 0.9 ≤ Е ≤ 0.95. The parameter constraints (5) become more stringent due to the requirements of achieving high cuttings transport efficiency:
According to [24], controlling these parameters independently within the Herschel – Bulkley rheological model to achieve a uniform velocity profile is not possible. Analysis of parameter combinations of the rheological model that are effective for cuttings transport under laminar flow with the presence of the most uniform velocity profiles showed the necessity of fulfilling conditions for n and τ0 depending on K:
Thus, it has been established that when using a bit and drill pipes with diameters of 215.9 mm and 146 mm, respectively, the most uniform velocity distributions of fluids modeled by the Herschel – Bulkley rheological model correspond to calculated parameter values in the range 0.9 ≤ 𝐸 ≤ 0.95. To achieve these values, the permissible limits of the rheological parameters were determined as (6) and (7).
The presented sequence of calculations requires sufficiently advanced engineering skills and specialized software for data processing, which makes its application challenging in industrial practice. Therefore, for the end user, such as a drilling fluids engineer, a final calculation formula accompanied by practical recommendations for its application would be of significant value.
In the deterministic range of values (6) within 0.9 ≤ 𝐸 ≤ 0.95, it is proposed to construct a linear multifactor regression model of type (4), which can be used to calculate the modified excess coefficient and predict the velocity profile when testing drilling fluid formulations. For the values satisfying conditions (6) and (7), the LinearModelFitfunction of Wolfram Language was applied to perform linear multifactor regression. The coefficient of determination was R2 = 0.83, with the highest number of deviations recorded around zero. To predict the uniformity of the velocity profile in order to improve cuttings transport efficiency, the applicability of the constructed regression equation is confirmed:
The graphs (Fig.4) show projections of the four-dimensional model (8) onto three-dimensional space at fixed values of the rheological parameters. The response surfaces provide an approximation of the initial data in the examined regions. Low deviation values and R2 = 0.83 are explained by the weak manifestation of nonlinearity in the vicinity of the response surface. Neglecting this minor nonlinearity, equation (8) can be used for sufficiently simple calculations. For the most uniform profile, E will assume the lowest values when conditions (6)-(7) are satisfied.
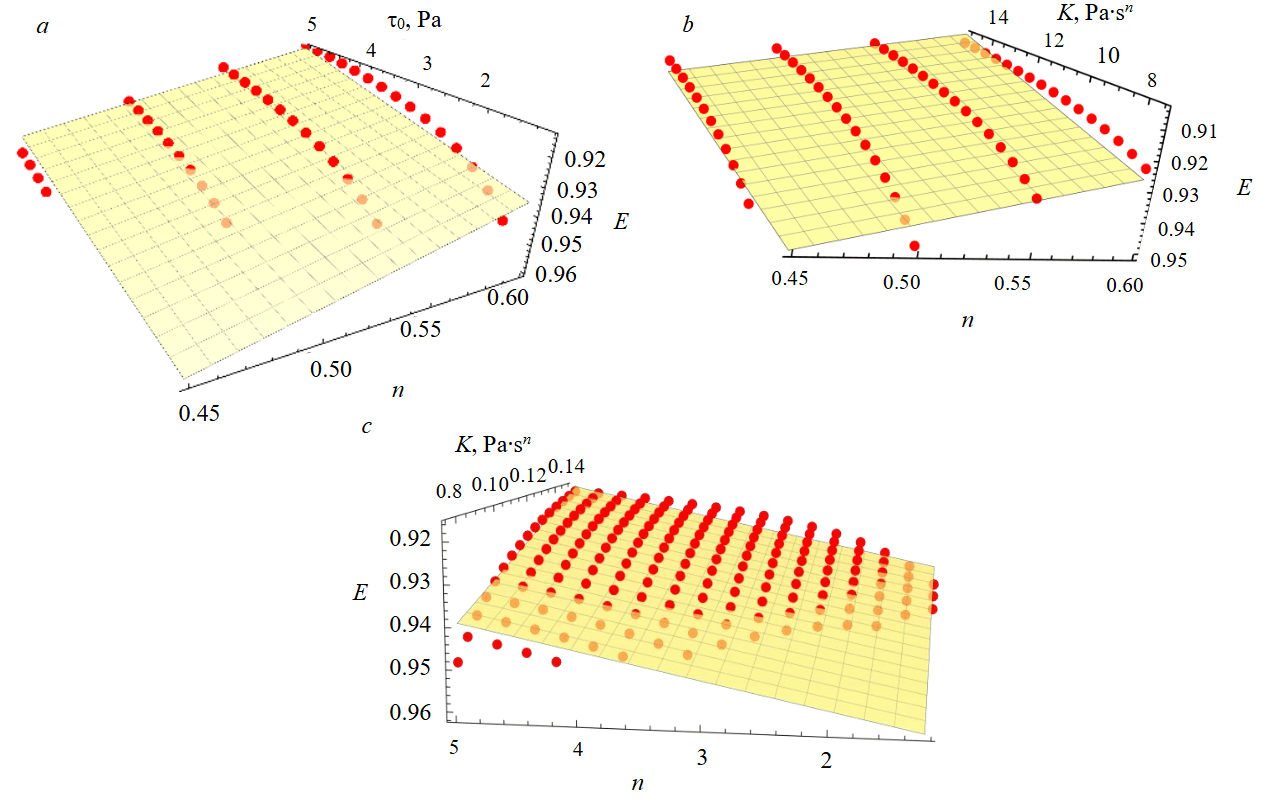
Fig.4. Three-dimensional projections of linear regression: a – τ0, n, E at K = 8 Pa∙sn; b – K, n, E at τ0 = 3 Pa; c – K, τ0, E at n = 0.45
The proposed modeling method is validated by comparing two parameter sets of the rheological model for velocity distribution simulation: one obtained by numerical solution and the other using the control volume method in Ansys Fluent. The advantage of CFD software lies in its high calculation accuracy, which accounts for various influencing factors [42]. The calculation conditions are as follows: wellbore diameter – 215.9 mm; outer pipe diameter – 146 mm; fluid density – 1200 kg/m3. For the Herschel – Bulkley model, two parameter sets are tested:
1) τ0 = 3.5 Pa, n = 0.6, K = 7, satisfying conditions (6), (7);
2) τ0 = 2 Pa, n = 0.4, K = 7, not satisfying conditions (6), (7).
When calculating the modified excess coefficient using the approximate formula (8), E = 0.928 for parameter set 1 and E = 0.967 for parameter set 2. It has been established that the velocity profile of parameter set 1 is more uniform compared to parameter set 2. Analysis of the graphs (Fig.5) shows agreement between the solutions obtained by the numerical method and those obtained using the control volume method. The minor deviation can be explained by differences between the computational algorithms of Wolfram Language, which constructs an interpolating function of the numerical solution, and the solver in Ansys Fluent. At the same time, it is evident that the hypothesis of a flatter velocity profile for parameter set 1 is confirmed by both calculation methods.
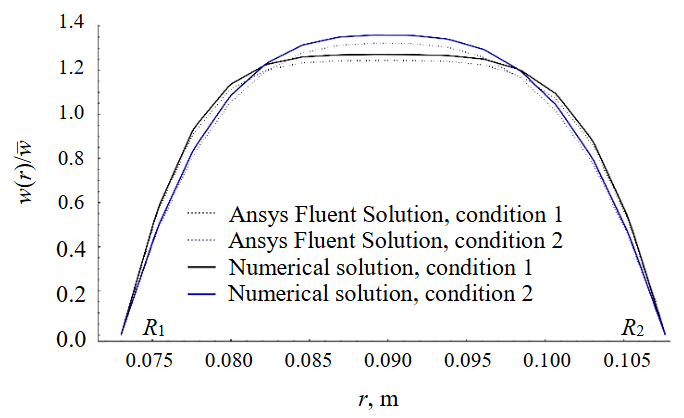
Fig.5. Comparison of velocity distributions obtained using a numerical solution and using the Ansys Fluent package
Conclusions
This work presents a method for establishing the relationship between the parameters of the Herschel – Bulkley model and the modified excess coefficient in order to ensure a uniform velocity profile of the drilling fluid in the wellbore annulus. The scientific novelty of this study lies in the simultaneous consideration of all three parameters of the Herschel – Bulkley rheological model and the derivation of compatibility conditions for them. The hypothesis concerning the possibility of controlling the velocity distribution of a non-Newtonian fluid in the wellbore annulus through the selection of parameter combinations of the rheological model is analyzed. Improving cuttings transport efficiency can be achieved by maintaining the most effective combination of Herschel – Bulkley model parameters when designing the properties of a drilling fluid to ensure a more uniform velocity profile.
The analysis of the influence of the Herschel – Bulkley model coefficients on the uniformity of the velocity profile revealed a qualitatively new behavior compared to the use of simplified rheological models. While in the Shvedov – Bingham model velocity profile uniformity is achieved by controlling the yield stress, and in the Ostwald – de Waale power-law model by the flow behavior index n, in the Herschel – Bulkley model the simultaneous influence of τ0, K, n, has been established, which necessitates determining the interrelation among them.
This study demonstrates a method for determining the interdependence of the three rheological model parameters with the uniformity index of the velocity profile. As an example, combinations of the most favorable rheological parameters for cleaning the annular space between the pipe and the wellbore with diameters of 146 and 215.9 mm, respectively, are considered. Compatibility conditions have been defined for the flow behavior index τ0, n with the consistency index K. A linear mathematical model E=f(τ0, K, n), has been constructed, reflecting the relationship between the quantitative indicator used to evaluate velocity profile uniformity and the coefficients of the three-parameter Herschel – Bulkley rheological equation.
The implementation of these recommendations for designing drilling fluid parameters can result in the formation of a uniform velocity profile, thereby improving cuttings transport. The developed model makes it possible to numerically compare the uniformity of velocity profiles when testing potentially recommended fluids. For comparison of the calculation results, the Ansys Fluent package was used.
Using the described methodology, it is possible to analyze changes in the velocity profile for the most common combinations of annular space geometries. The presence of cuttings in the drilling fluid alters its density and rheological characteristics. Measuring the parameters of drilling fluid with cuttings under reservoir temperature ranges makes it possible to model the process under conditions close to those in the wellbore. These data can also be obtained using a continuous drilling fluid monitoring system at the rig. A promising direction is the development of nomograms for the rheological parameters of the Herschel – Bulkley model as a function of diameter ratios. The availability of such functional relationships enables more efficient selection of fluid parameters to ensure a uniform velocity profile in the wellbore annulus.
References
- Jalakani R., Tabatabaee Moradi S.S., Morenov V. Reliability Analysis of a Drilling Bit Penetration Model in Oil and Gas Wells: A Case Study. International Journal of Engineering – Transactions B: Applications. 2024. Vol. 37. Iss. 11, p. 2213-2222. DOI: 10.5829/ije.2024.37.11b.08
- Raupov I., Rogachev M., Sytnik J. Design of a Polymer Composition for the Conformance Control in Heterogeneous Reservoirs. Energies. 2023. Vol. 16. Iss. 1. N 515. DOI: 10.3390/en16010515
- Zubkova O.S., Kuchin V.N., Toropchina M.A., Ivkin A.S. Potential Application of Saponite Clay for Production of Drilling Fluids. International Journal of Engineering – Transactions B: Applications. 2024. Vol. 37. Iss. 11, p. 2142-2149. DOI: 10.5829/ije.2024.37.11b.01
- Ferroudji H., Rahman M.A., Hadjadj A. et al. 3D numerical and experimental modelling of multiphase flow through an annular geometry applied for cuttings transport. International Journal of Multiphase Flow. 2022. Vol. 151. N 104044. DOI: 10.1016/j.ijmultiphaseflow.2022.104044
- Ashena R., Badrouchi F., Elmgerbi A. et al. Stepwise mathematical derivation of the Herschel–Bulkley laminar fluid flow equations – in pipes. Journal of Petroleum Exploration and Production Technology. 2023. Vol. 13. Iss. 2, p. 625-643. DOI: 10.1007/s13202-022-01566-2
- Belimane Z., Hadjadj A., Ferroudji H. et al. Modeling surge pressures during tripping operations in eccentric annuli. Journal of Natural Gas Science and Engineering. 2021. Vol. 96. N 104233. DOI: 10.1016/j.jngse.2021.104233
- Chandrasekhar S.V. Annular Couette–Poiseuille flow and heat transfer of a power-law fluid – analytical solutions. Journal of Non-Newtonian Fluid Mechanics. 2020. Vol. 286. N 104402. DOI: 10.1016/j.jnnfm.2020.104402
- Xiaofeng Sun, Kebo Zhang, Ye Chen et al. Study on the settling velocity of drilling cuttings in the power law fluid. Powder Technology. 2020. Vol. 362. P. 278-287. DOI: 10.1016/j.powtec.2019.11.025
- Roberts T.G., Cox S.J. An analytic velocity profile for pressure-driven flow of a Bingham fluid in a curved channel. Journal of Non-Newtonian Fluid Mechanics. 2020. Vol. 280. N 104278. DOI: 10.1016/j.jnnfm.2020.104278
- Lin Zhang, Yigang Wang, Dake Chen, Cheng Chen. Prediction and correction of scaling effects on velocity profile in hydraulic laboratory experiments. Desalination and Water Treatment. 2019. Vol. 149. 2019. P. 31-42. DOI: 10.5004/dwt.2019.23848
- Sirui Tong, Bin Miao, Mengsong Shen et al. Experimental and numerical analysis of granular phase flow behavior in a rotary bed reactor: Velocity profile study. Powder Technology. 2024. Vol. 444. N 119992. DOI: 10.1016/j.powtec.2024.119992
- Kharlamov S.N., Janghorbani M., Bryskin M.R. Aspects of Computer Simulation of Transport and Cleaning Processes from Cuttings in Horizontal Well Sections. Mathematical Models and Computer Simulations. 2023. Vol. 15. N 3, p. 502-519. DOI: 10.1134/S2070048223030080
- Muangput B., Zin T., Namchanthra S. et al. CFD elucidation of high-pressure subcooled boiling flow towards effects of variable refrigerant properties using OpenFOAM empirical closures. Applications in Engineering Science. 2024. Vol. 19. N 100187. DOI: 10.1016/j.apples.2024.100187
- Alade O., Mahmoud M., Al-Nakhli A. Rheological studies and numerical investigation of barite sag potential of drilling fluids with thermochemical fluid additive using computational fluid dynamics (CFD). Journal of Petroleum Science and Engineering. 2023. Vol. 220. Part A. N 111179. DOI: 10.1016/j.petrol.2022.111179
- Gulraiz S., Gray K.E. A model for investigating wellbore hydraulics of thermo-thixotropic drilling fluids. Geothermics. 2021. Vol. 96. N 102214. DOI: 10.1016/j.geothermics.2021.102214
- Litvinenko V.S., Dvoynikov M.V., Trushko V.L. Elaboration of a conceptual solution for the development of the Arctic shelf from seasonally flooded coastal areas. International Journal of Mining Science and Technology. 2021. Vol. 32. Iss. 1, p. 113-119. DOI: 10.1016/j.ijmst.2021.09.010
- Leusheva E., Morenov V. Effect of Temperature Conditions in Arctic Offshore Oil Fields on the Rheological Properties of Various Based Drilling Muds. Energies. 2022. Vol. 15. Iss. 5. N 5750. DOI: 10.3390/en15155750
- Al-Shargabi M., Davoodi S., Wood D.A. et al. Hole-cleaning performance in non-vertical wellbores: A review of influences, models, drilling fluid types, and real-time applications. Geoenergy Science and Engineering. 2024. Vol. 233. N 212551. DOI: 10.1016/j.geoen.2023.212551
- Buslaev G.V., Belkin A.S. Development and Field Testing of the Downhole Multi-Purpose Thrusting Device for Drilling of Deep Vertical and Directional Wells. SPE Russian Petroleum Technology Conference, 26-28 October 2015, Moscow, Russia. OnePetro, 2015. N SPE-176539-MS. DOI: 10.2118/176539-MS
- Abdullah A.H., Ridha S., Mohshim D.F., Maoinser M.A. An experimental investigation into the rheological behavior and filtration loss properties of water-based drilling fluid enhanced with a polyethyleneimine-grafted graphene oxide nanocomposite. RSC Advances. 2024. Vol. 14. Iss. 15, p. 10431-10444. DOI: 10.1039/D3RA07874D
- Saasen A., Ytrehus J.D. Viscosity Models for Drilling Fluids – Herschel-Bulkley Parameters and Their Use. Energies. 2020. Vol. 13. Iss. 20. N 5271. DOI: 10.3390/en13205271
- Bavoh C.B, Ofei T.N., Lai B. et al. Assessing the impact of an ionic liquid on NaCl/KCl/polymer water-based mud (WBM) for drilling gas hydrate-bearing sediments. Journal of Molecular Liquids. 2019. Vol. 294. N 111643. DOI: 10.1016/j.molliq.2019.111643
- Leusheva E., Brovkina N., Morenov V. Investigation of Non-Linear Rheological Characteristics of Barite-Free Drilling Fluids. Fluids. 2021. Vol. 6. Iss. 9. N 327. DOI: 10.3390/fluids6090327
- Nikitin V.I. Problem solution analysis on finding the velocity distribution for laminar flow of a non-linear viscous flushing fluid in the annular space of a well. Journal of Mining Institute. 2022. Vol. 258, p. 964-975. DOI: 10.31897/PMI.2022.93
- Heidari M., Shahbazi Kh., Fattahi M. Experimental study of rheological properties of aphron based drilling Fluids and their effects on formation damage. Scientia Iranica. Transactions C: Chemistry and Chemical Engineering. 2017. Vol. 24. Iss. 3, p. 1241-1252. DOI: 10.24200/sci.2017.4108
- Tabatabaee Moradi S.Sh. A probabilistic study on hole cleaning optimization. Journal of Mining Institute. 2022. Vol. 258, p. 956-963. DOI: 10.31897/PMI.2022.67
- Nikolaev A., Goluntsov A., Breff A.T. Determination of the coefficient of hydraulic resistance when using anti-turbulence additives. Reliability: Theory & Applications. 2024. Vol. 19. Special Issue 6 (81), p. 107-124. DOI: 10.24412/1932-2321-2024-681-107-124
- Alkinani H.H., Al-Hameedi A.T.T., Dunn-Norman S., Lian D. Application of artificial neural networks in the drilling processes: Can equivalent circulation density be estimated prior to drilling? Egyptian Journal of Petroleum. 2020. Vol. 29. Iss. 2, p. 121-126. DOI: 10.1016/j.ejpe.2019.12.003
- Alsabaa A., Gamal H., Elkatatny S., Abdelraouf Y. Machine Learning Model for Monitoring Rheological Properties of Synthetic Oil-Based Mud. ACS Omega. 2022. Vol. 7. Iss. 18, p. 15603-15614. DOI: 10.1021/acsomega.2c00404
- Song Deng, Bingzhao Huo, Shoukun Xu et al. Prediction of water-in-oil emulsion drilling fluids rheological properties based on GPR-Bagging ensemble learning. Colloids and Surfaces A: Physicochemical and Engineering Aspects. 2024. Vol. 686. N 133336. DOI: 10.1016/j.colsurfa.2024.133336
- Davoodi S., Mehrad M., Wood D.A. et al. Hybridized machine-learning for prompt prediction of rheology and filtration properties of water-based drilling fluids. Engineering Applications of Artificial Intelligence. 2023. Vol. 123. Part C. N 106459. DOI: 10.1016/j.engappai.2023.106459
- Jian Sun, Rongjun Zhang, Mingqiang Chen et al. Identification of Porosity and Permeability While Drilling Based on Machine Learning. Arabian Journal for Science and Engineering. 2021. Vol. 46. Iss. 7, p. 7031-7045. DOI: 10.1007/s13369-021-05432-x
- Quitian-Ardila L.H., Garcia-Blanco Y.J., Rivera A. De J. et al. Developing a machine learning-based methodology for optimal hyperparameter determination – A mathematical modeling of high-pressure and high-temperature drilling fluid behavior. Chemical Engineering Journal Advances. 2024. Vol. 20. N 100663. DOI: 10.1016/j.ceja.2024.100663
- Andaverde J.A., Wong-Loya J.A., Vargas-Tabares Y., Robles M. A practical method for determining the rheology of drilling fluid. Journal of Petroleum Science and Engineering. 2019. Vol. 180. P. 150-158. DOI: 10.1016/j.petrol.2019.05.039
- Tananykhin D.S., Struchkov I.A., Khormali A., Roschin P.V. Investigation of the influences of asphaltene deposition on oilfield development using reservoir simulation. Petroleum Exploration and Development. 2022. Vol. 49. Iss. 5, p. 1138-1149. DOI: 10.1016/S1876-3804(22)60338-0
- Podoprigora D.G., Byazrov R.R., Lagutina M.A. et al. A novel integrated methodology for screening, assessment and ranking of promising oilfields for polymer floods. Advances in Geo-Energy Research. 2024. Vol. 12. N 1, p. 8-21. DOI: 10.46690/ager.2024.04.02
- Villalobos Alva J. Beginning Mathematica and Wolfram for Data Science. Apress, 2021, p. 416. DOI: 10.1007/978-1-4842-6594-9
- Misbah B., Elgaddafi R., Malhas R.N. et al. Exploring the rheology characteristics of Flowzan and Xanthan polymers in drilling water based fluids at high-temperature and high-shear rates. Geoenergy Science and Engineering. 2024. Vol. 243. N 213309. DOI: 10.1016/j.geoen.2024.213309
- Phirommark P., Namchanthra S., Chaiyanupong J. et al. CFD elucidation of microscopic particles in a low-volumetric classifier towards effects of Stokes number and density ratio. International Journal of Thermofluids. 2023. Vol. 20. N 100497. DOI: 10.1016/j.ijft.2023.100497
- Singh R., Ahmed R., Karami H. et al. CFD Analysis of Turbulent Flow of Power-Law Fluid in a Partially Blocked Eccentric Annulus. Energies. 2021. Vol. 14. Iss. 3. N 731. DOI: 10.3390/en14030731
- Badrouchi F., Rasouli V., Badrouchi N. Impact of hole cleaning and drilling performance on the equivalent circulating density. Journal of Petroleum Science and Engineering. 2022. Vol. 211. N 110150. DOI: 10.1016/j.petrol.2022.110150
- Tananykhin D.S. Scientific and Methodological Support of Sand Management During Operation of Horizontal Wells. International Journal of Engineering – Transactions A: Basics. 2024. Vol. 37. Iss. 7, p. 1395-1407. DOI: 10.5829/ije.2024.37.07a.17
