Экспериментальное исследование термомеханических эффектов  в водонасыщенных известняках при их деформировании

Д. И. Блохин; П. Н. Иванов; О. Л. Дудченко

doi:10.31897/PMI.2021.1.1

Том 247

Страницы:

1-10

Скачать том:

RUS ENG

Горное дело

Экспериментальное исследование термомеханических эффектов в водонасыщенных известняках при их деформировании

Авторы:

Д. И. Блохин¹

П. Н. Иванов²

О. Л. Дудченко³

Об авторах

1 — канд. техн. наук Институт проблем комплексного освоения недр РАН ▪ Orcid ▪ Scopus
2 — аспирант Национальный Исследовательский Технологический Университет "МИСиС" ▪ Orcid ▪ Scopus
3 — канд. техн. наук доцент Национальный Исследовательский Технологический Университет "МИСиС" ▪ Orcid ▪ Scopus

Дата отправки:

2020-07-30

Дата принятия:

2021-03-02

Дата публикации:

2021-04-21

Аннотация

Контроль устойчивости элементов каменных конструкций различных сооружений является обязательным условием их безопасной эксплуатации. Использование современных методик неразрушающей диагностики напряженно-деформированного состояния таких конструкций – эффективный, а во многих случаях единственный способ контроля. Исследования сопутствующего процессам деформирования твердых тел теплового излучения позволили обосновать и разработать метод, позволяющий бесконтактно получать информацию об изменениях напряженно-деформированного состояния в различных типах геоматериалов, включая известняки. Однако исследования влияния водонасыщенности горных пород на фиксируемые таким образом параметры теплового излучения в настоящее время носят поверхностный характер. Учет степени водонасыщения горных пород необходим при контроле механического состояния каменных сооружений, находящихся в непосредственном контакте с водой. Основной целью данной работы является исследование зависимостей изменений интенсивности теплового излучения с поверхности образцов известняка с различной влажностью в условиях одноосного сжатия. Полученные результаты показали ожидаемое значительное снижение механических свойств (предела прочности при одноосном сжатии и модуля упругости) водонасыщенных образцов в сравнении с сухими. При этом зафиксировано существенное увеличение интенсивности теплового излучения подвергаемых сжатию образцов известняка при повышении их водонасыщения, что обусловливает необходимость учета выявленной закономерности при идентификации изменений во времени напряженного состояния каменных конструкций, установленных по данным бесконтактной ИК-диагностики в реальных условиях.

Ключевые слова:

каменные строительные конструкции известняк водонасыщенность осевые напряжения деформация мониторинг ИК-излучение лазерно-ультразвуковая диагностика

10.31897/PMI.2021.1.1

Введение. Природный камень, из которого построены самые древние сооружения, в настоящее время так же эффективно используется при возведении объектов промышленного и гражданского назначения [3], например исторические здания, культовые постройки, памятники, мосты, подпорные стены, тоннели и другие. Эти инженерные сооружения могут подвергаться различным динамическим нагрузкам как природного, так и техногенного характера (ветер, землетрясения, вибрации и другие) [3, 17]. Такие нагрузки негативно влияют на устойчивость сооружений, являясь катализаторами деструктивных механических процессов в материале. В связи с этим оценка надежности рассматриваемых сооружений является актуальной задачей, для решения которой необходимо использовать процедуры мониторинга деформационных процессов в каменных конструкциях.

Стандартные методы измерения изменений параметров напряженно-деформированного состояния (НДС) строительных конструкций подразумевают использование различных модификаций деформометров, которые размещаются либо на свободных поверхностях конструкций, либо в их теле [1, 6, 9]. Однако в отличие от бетонных конструкций, имеющих относительно гладкую поверхность, подобное размещение измерительных датчиков на поверхности каменных сооружений может быть затруднительно, а расположение их в теле элементов конструкций требует проведения нарушающих их целостность специальных работ, что может быть недопустимо при обследовании исторических или мемориальных сооружений. Указанные обстоятельства и определяют необходимость использования методов неразрушающей диагностики при обследовании каменных конструкций.

В настоящее время в системах мониторинга состояния строительных конструкций и массивов горных пород достаточно эффективно применяются методы, включающие измерения вариаций параметров физических полей различной природы, сопутствующих процессам деформирования и разрушения материалов [1, 9, 10, 17]. К активно развиваемым методам неразрушающей диагностики механического состояния геоматериалов относится метод ИК-радиометрии, использующий результаты бесконтактных измерений изменений интенсивности инфракрасного излучения с поверхности горных пород при их деформировании [21, 15, 19, 22]. Интерпретация результатов терморадиационных ИК-измерений основана на описании известных термодинамических эффектов: изменения температуры твердого тела при ее адиабатическом деформировании (термоупругий и термопластический эффекты [2, 18]) и зависимости интенсивности инфракрасного излучения с поверхности тела от температуры [25].

В работах [21, 15, 19, 22] была обоснована эффективность ИК-радиометрии для идентификации стадий деформирования горных пород различных типов. Однако для получения достоверной информации о протекании деформационных процессов по данным терморадиационных измерений в реальных условиях необходимы исследования по оценке влияния изменчивости физико-механических свойств горных пород на регистрируемые параметры теплового излучения, в частности учет степени влагонасыщения исследуемых материалов при интерпретации терморадиационных измерений, которая оказывает существенное влияние на физико-механическое состояние горных пород [11, 20, 12, 27].

Цель настоящей работы – исследование с использованием бесконтактных ИК-измерений проявлений указанных термомеханических эффектов в образцах структурно-неоднородных горных пород с различной влажностью в условиях одноосного сжатия.

Методология. Эксперименты проводились на образцах известняка – наиболее часто используемого материала каменных конструкций [3, 20]. Поскольку известняк относится к горным породам, обладающим высокой степенью неоднородности, для получения качественных и обоснованных результатов при выполнении описываемых исследований была создана выборка образцов с близкими значениями физико-механических параметров и схожими структурными особенностями. Для этого был проведен комплекс предварительных испытаний, включающий как стандартные методы определения физико-механических свойств горных пород, так и методы, основанные на интроскопических способах исследования, например растровую электронную микроскопию и лазерную ультразвуковую диагностику [4, 14, 24].

Цельный блок известняка был распилен на более 100 параллелепипедов размером 25х25х55 мм.

Минеральный и элементный анализы были выполнены на серии аншлифов площадью 25х25 мм с использованием сканирующего электронного микроскопа Phenom ProX, работающего как в режиме оптического изображения для петрографического анализа, так и электронного изображения, по которому на базе энергодисперсионной системы определялся элементный состав. Анализ показал, что для большинства образцов среднее содержание составляет, %: кальция 40,0-42,3, углерода 12,1-13,9, кислорода 45,1-47,5. Было обнаружено незначительное присутствие различных минеральных компонентов и примесей, %: кремния 0,2-0,3, магния 0,1-0,2, железа 0,1. Примеси были распределены равномерно по всей поверхности исследуемых образцов.

Поверхность исследованных аншлифов представлена зернистой структурой. На границе контактов зерен зафиксированы системы пор, занимающие 5-7 % от общей площади поверхности, значения характерных размеров пор лежат в пределах 40-450 мкм. Минеральный состав представлен кальцитом, содержание которого колебалось в пределах 97,5-98,3, незначительным количеством кварца – 1,5-2,3 и доломитом – менее 0,5 %. Суммарный вклад остальных минералов мал (менее 0,1 %).

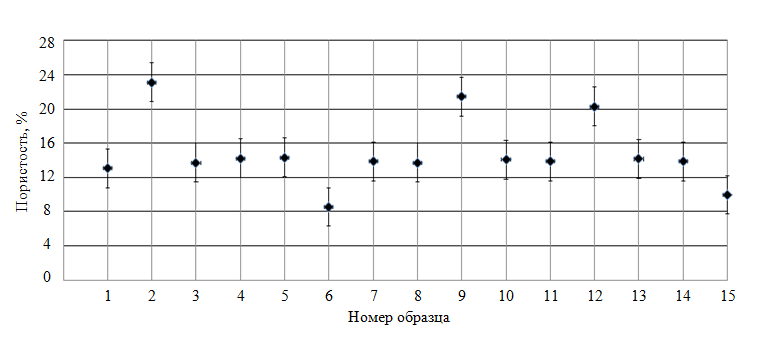
С учетом данных электронной микроскопии из первоначальной серии были отобраны 15 образцов со схожими структурными особенностями. На втором этапе уже из этой серии необходимо было отобрать образцы с примерно одинаковыми значениями пористости. Оценка пористости осуществлялась с использованием лазерной ультразвуковой структуроскопии [4, 14, 23], проведенной на автоматизированном дефектоскопе УДЛ-2М на 15 пластинах размером 50х25 мм и толщиной около 4-5 мм, изготовленных из отобранных образцов.

Рис.1. Схема (а) и внешний вид (б) лазерно-ультразвукового структуроскопа УДЛ-2М 1 – отраженные сигналы; 2 – аналого-цифровой преобразователь; 3 – короткий лазерный импульс; 4 – оптоволоконный кабель; 5 – лазерно-ультразвуковой преобразователь; 6 – зондирующие акустические импульсы; 7 – исследуемый образец

Принцип действия структуроскопа (рис.1) основан на регистрации сигналов, полученных в результате рассеяния широкополосных акустических импульсов на различных неоднородностях образцов [4].

Сканирование проводилось по поверхности пластины с шагом 1 мм. С учетом толщины и времени двойного пробега акустического импульса по образцу в каждой точке сканирования рассчитывались скорости распространения продольных волн V_l. По времени задержки сдвиговой волны относительно опорного сигнала определялась ее скорость V_t. Были получены локальные значения скоростей упругих волн в 100 точках каждого образца. В табл.1 представлены значения средних скоростей продольных и сдвиговых волн.

Таблица 1

Результаты измерения скоростей упругих волн

Скорость волн, м/с	Номер образца
Скорость волн, м/с	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
V_l	4506	4185	4540	4520	4517	4758	4534	4501	4245	4526	4575	4289	4523	4534	4696
V_t	2409	2098	2420	2447	2408	2531	2403	2367	2006	2394	2454	2043	2336	2315	2574

По приведенным данным, можно рассчитать локальную пористость образцов [13]:

$$P_{общ}=\Biggl(1-\Biggl(\frac{V_1}{V_0}\Biggl)^2\Biggl)^{\frac{3}{2}}, \tag*{(1)}$$

где V₀ – скорость распространения продольной волны в материале при P_общ, то есть при отсутствии пористости.

Для вычисления V₀ был разработан следующий алгоритм. Известно, что основные минералы, содержащиеся в известняке (кальцит и кварц), принадлежат к тригональному классу симметрии [5]. В кристаллах тригональной сингонии только вдоль трех кристаллографических осей [100], [010] [001] распространяются чисто продольные волны, скорости V₁, V₂, V₃ которых определяются диагональными элементами матрицы жесткости C33, C11 [5]:

$$\rho V_1^2=C_{33}; \tag*{(2)}$$

$$\rho V_2^2=\rho V_3^2=C_{11}, \tag*{(3)}$$

где $\rho$ – плотность кристалла.

Во всех остальных направлениях распространяются квазипродольные волны, фазовые скорости которых определяют из уравнения Грина – Кристоффеля [5], а их значения могут существенно отличаться от значений скоростей чистых мод. Поскольку в известняке минералы кальцита и кварца хаотически ориентированы, то для вычисления скорости V₁₀ необходимо выполнить усреднение по всем направлениям, что является достаточно трудоемкой процедурой. Поэтому для оценки V₀ по известным значениям коэффициентов матрицы жесткости $ \{ C_{ij}\}, i,j=1..,6 $ для кальцита и кварца, приведенным в табл.2, были найдены скорости V₁, V₂, V₃ вдоль кристаллографических осей [100], [010], [001] и дополнительно в направлениях [110], [011] [101] скорости V₁₂, V₂₃, V₁₃ для каждого минерала [5]. Далее было выполнено усреднение по всем шести направлениям с учетом вклада кальцита и кварца.

Таблица 2

Коэффициенты матрицы жесткости для кальцита и кварца

Порода	C₁₁, GPa	C₁₂, GPa	C₄₄, GPa	C₃₃, GPa	C₁₃, GPa	C₆₆, GPa	$\rho$, кг/м³
Кальцит	137	45,2	34,2	79,2	44,8	45,9	2980
Кварц	86,8	7,1	58,3	105,9	–11,9	39,9	2650

В результате проведенных расчетов среднее значение скорости V₀ в образце известняка без пор составило 4900 м/с. На рис.2 представлены результаты расчета значений пористости образцов, проведенные по формуле (1). Показатели общей пористости P_общ образцов 1, 3, 4, 5, 7, 8, 10, 11, 13, 14 принадлежат одному интервалу, который составляет 13-14 %. Указанные образцы в дальнейшем были подвергнуты механическим испытаниям.

Рис.2. Значения пористости для исследуемых образцов известняка

Рис.3. Сухие (а) и водонасыщенные (б) образцы известняка

Результаты. Для проведения экспериментов по оценке влияния водонасыщения образцов известняка на кинетику теплового излучения, сопутствующего их деформированию, были отобраны образцы 1, 3, 4, 5, 7, 8, 10, 11, 13, 14, которые разделили две группы (по 5 образцов в каждой) (рис.3). Образцы одной группы помещались в воду на семь суток. После этого определялась масса образцов и рассчитывалась их плотность, значения которых представлены в табл.3.

Таблица 3

Геометрические и плотностные параметры образцов известняка

Номер образца	m, г	a, мм	b, мм	S = ab, мм²	h, мм	V_общ = Sh	r, кг/м³
Сухие образцы
1с	67,18	25,65	23,50	603,28	50,29	30131	2216
2с	67,05	25,06	24,34	585,90	49,95	29215	2294
3с	66,98	25,15	24,10	581,02	50,07	29088	2312
4с	67,46	25,32	25,07	584,77	50,01	29212	2299
5с	67,05	25,50	25,50	650,25	50,27	32688	2251
Водонасыщенные образцы
1м	70,15	24,64	24,03	592,10	49,97	29587	2370
2м	69,26	24,42	24,36	594,87	50,28	29910	2315
3м	70,25	23,61	24,63	581,51	50,13	29151	2409
4м	70,09	24,50	24,56	601,72	50,54	30410	2304
5м	69,55	25,65	23,46	601,75	50,22	30219	2299

Средние значения плотностей сухих и водонасыщенных образцов составили 2274 и 2340 кг/м³ соответственно.

Измерения выполнялись на испытательной машине LFM-50 с помощью автоматизированно-го комплекса [22], позволяющего вести синхронную регистрацию механических и терморадиа-ционных параметров (рис.4).

В экспериментах в качестве первичного приемника ИК-излучения использовался детектор РТН-31 [21, 22], предназначенный для бесконтактного измерения изменений интенсивности оп-тического излучения в инфракрасном диапазоне частот. Датчик ИК-излучения 1 устанавливается примерно в середине высоты образца 2 на расстоянии 0,5-1 см от поверхности.

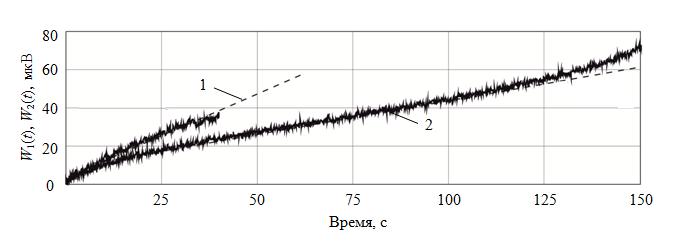
Графики изменений во времени значений выходных сигналов, получаемых в результате прохождения первичного сигнала с ИК-радиометра (детектора РТН-31) через измерительно-вычислительный тракт, при деформировании сухого W₁(t) и водонасыщенного W₂(t) образцов известняка в режиме одноосного сжатия при постоянной скорости нагружения $(d\sigma_1/dt=const)$ представлены на рис.5. Зависимости W₁(t) и W₂(t) демонстрируют характер изменения интенсивности ИК-излучения во временных интервалах, соответствующих промежуткам протекания линейной стадии деформирования образцов известняка.

Диаграммы $\sigma_1-\epsilon_1,$, полученные в ходе эксперимента, показаны на рис.6. Графики $\sigma_1(\epsilon_1),$ подтверждают наличие существенной зависимости изменений прочностных и деформационных характеристик образцов известняка от степени их водонасыщения [22, 12]. В частности, определенные по графикам, представленным на рис.6, значения пределов прочности для сухого $\sigma_{D_{\epsilon}}$ и водонасыщенного $\sigma_{w_{\epsilon}}$ образцов известняка отличаются примерно в 2,5 раза ($\sigma_{D_{\epsilon}}\asymp$74 МПа, а $\sigma_{W_{\epsilon}}\asymp$30 МПа).

Рис.4. Экспериментальный стенд

Обсуждение результатов. Анализируя зависимости W₁(t) и W₂(t), можно сделать вывод, что угол наклона прямой, аппроксимирующей график W2(t), существенно больше угла наклона соответствующей прямой для графика W₁(t), что свидетельствует о более высокой термоактивности водонасыщенного образца известняка. Полученный результат согласуется с выводами работ [8, 26], в которых также фиксируется увеличение интенсивности ИК-излучения подвергаемых сжатию образцов горных пород при повышении их водонасыщения. Изменения как теплофизических, так и физико-механических характеристик образцов под влиянием водонасыщения являются основным фактором, обуславливающим наблюдаемый термомеханический эффект.

Рис.5. Выходные сигналы ИК-радиометрии для образцов известняка 1 – сухого; 2 – водонасыщенного

В ходе анализа полученных результатов для подтверждения их адекватности можно провести оценочные расчеты приращений температуры DT для сухих и водонасыщенных образцов. Для этого применено известное приближение [2, 18], связывающее приращения напряжений твердого тела с изменениями температуры при его одноосном адиабатическом деформировании,

$$\Delta T=\frac{\alpha}{\rho c}T_0\Delta \sigma_1, \tag*{(4)}$$

где T₀ – абсолютное значение температуры до начала деформирования; $\alpha$ – коэффициент линейного расширения; с – удельная теплоемкость при постоянном давлении; $\rho$ – плотность материала.

Тогда, как следует из выражения (4), при одинаковом приращении напряжений твердого тела $\Delta \sigma_1$ при его одноосном адиабатическом деформировании связь между изменениями темпера-туры $\Delta T$ для сухих и водонасыщенных образцов примет следующий вид [16]:

$$\frac{\rho_cc_c}{\alpha_c}\frac{\Delta T_c}{T_0}=\frac{\rho_Bc_B}{\alpha_B}\frac{\Delta T_B}{T_0}, \tag*{(5)}$$

В работе [16] для различных типов твердых тел показана справедливость соотношения

$$\alpha \sim \ const/\sqrt E, \tag*{(6)}$$

где E – модуль упругости материала при одноосной деформации.

Значения модулей E_c и E_B для сухих и водонасыщенных образцов соответственно рассчитывались по графикам $\sigma_1-\epsilon_1,$, представленным на рис.6. Тогда формула (5) приобретет следующий вид:

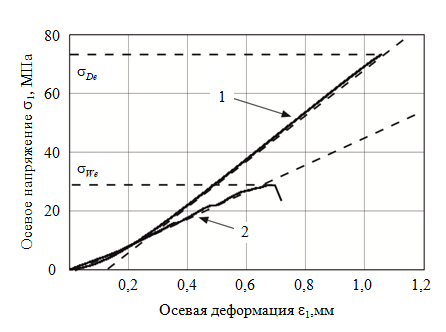
Рис.6. Зависимость напряжения от деформаций $\sigma_1-\epsilon_1,$ для образцов известняка 1 – сухого; 2 – водонасыщенного

$$\rho_cc_c\sqrt{E_c}\Delta T_c=\rho_Bc_B\sqrt{E_B}\Delta T_B, \tag*{(7)}$$

Результаты вычислений величин модулей упругости: E_c= 69 и E_B = 42 ГПа

Для вычислений по формуле (7) использовались данные табл.3.

С целью получения ориентировочных значений удельной теплоемкости с для водо-насыщенных и сухих образцов известняка следует воспользоваться известным определением [7], в котором под удельной теплоемкостью гетерогенной среды понимается арифметическое средневзвешенное всех присутствующих в среде минеральных компонент с долей k_i и их удельной теплоемкостью c_i:

$$c=\sum c_ik_i, \tag*{(8)}$$

Поскольку основным компонентом материала испытываемых образцов является кальцит, то из уравнения (8) была получена формула расчета удельной теплоемкости водонасыщенного известняка:

$$c_B=\sum c_ik_i=\frac{c_{кальц}\rho_{кальц}V_{кальц}+c_{воды}\rho_{воды}V_{воды} P_{откр}}{\rho_{изм.в}V_{обр}}, \qquad\qquad\qquad\qquad\qquad\tag*{(9)}$$

где с_кальц– удельная теплоемкость, $\rho_{кальц}$ – плотность, V_кальц – объем кальцита, с_воды – удельная теплоемкость, $\rho_{воды}$ – плотность, V_воды – объем воды, Р_откр – открытая пористость, $\rho_{изм.в}$ – экспериментально измеренная плотность водонасыщенного образца, V_обр – объем образца

Определение открытой пористости производилось по методу Архимеда в соответствии с ASTM C830-00(2016). Объем пор был определен по разнице в массе сухого и водонасыщенного образца, а открытая пористость по формуле

$$P_{откр}=\frac{V_{пор\ ср.}}{V_{ср}}, \tag*{(10)}$$

По результатам расчетов, среднее значение открытой пористости составило 9,5 %, при этом общая пористость Р_общ составляла 13,7 %. Учитывая, что объем кальцита связан с суммарной пористостью Р_общ, включающей открытую Р_откр и закрытую $\ (P_{общ}- P_{откр})$, т.е. $\ V_{кальц}= V_{обр}(1- P_{откр})$ , получено

$$c_B=\sum c_ik_i=\frac{c_{кальц}\rho_{кальц}(1-P_{общ})+c_{воды}\rho_{воды} P_{откр}}{\rho_{изм.в}}, \qquad\qquad\qquad\qquad\tag*{(11)}$$

Аналогично получено выражение для расчета удельной теплоемкости сухого известняка:

$$c_с=\sum c_ik_i=\frac{c_{кальц}\rho_{кальц}(1-P_{общ})}{\rho_{изм.с}}, \qquad\qquad\tag*{(12)}$$

Теплоемкость воздуха, который сосредоточен в порах сухого образца, не учитывается. Результаты расчета удельных теплоемкостей для сухих cc и водонасыщенных cв образцов по формулам (11) и (12) представлены в табл.4.

Таблица 4

Результаты расчета удельной теплоемкости для образцов

Сухие образцы		Водонасыщенные образцы
Номер образца	c, Дж/(кг∙К)	Номер образца	c, Дж/(кг∙К)
1с	1059	1м	1149
2с	1023	2м	1177
3с	1015	3м	1131
4с	1021	4м	1182
5с	1044	5м	1185
Среднее значение	1032	Среднее значение	1165

В дальнейших расчетах по формуле (6) участвуют средние значения удельных теплоемко-стей для сухих и водонасыщенных образцов, приведенные в табл.4. Кроме того, в расчетах Т₀ = 300 К.

Подставив в формулу (7) значения необходимых для расчета величин, получим, что прира-щение температуры для водонасыщенных образцов составляет $\ \Delta T_B\asymp1,2 \Delta T_c$, что подтверждают полученные экспериментальные зависимости, представленные на рис.5.

Таким образом, проведенные комплексные экспериментальные исследования, подкреплен-ные выполненными оценочными расчетами, демонстрируют значительное влияние водонасы-щенности пористых материалов на их механические и теплофизические характеристики, выра-жающиеся в существенном увеличении термоактивности, инициируемой происходящими в них деформационными процессами.

Заключение. Проведенные исследования демонстрируют комплексный подход к лабораторному исследованию термомеханических процессов в подвергаемых деформированию сложно структурированных неоднородных материалах, каковыми и являются образцы известняка.

С использованием стандартных методов электронной растровой микроскопии проведен петрографический анализ и выявлены структурные особенности исследуемых образцов. Показана эффективность использования данных лазерно-ультразвуковой структуроскопии для количественной экспресс-оценки пористости горных пород.

Получены зависимости изменений интенсивности теплового излучения W(t) с поверхности образцов известняка с различной влажностью в условиях одноосного сжатия. Существенным элементом проводимых экспериментов являлась синхронная регистрация вариаций интенсивно-сти теплового излучения и изменений механических параметров. Анализ данных совместных измерений осевых напряжений и деформаций показал ожидаемое значительное снижение механических свойств (предела прочности при одноосном сжатии и модуля упругости) водонасыщенных образцов по сравнению с сухими. Результаты ИК-радиометрических измерений показали однозначную зависимость характера графиков W(t) от степени водонасыщенности испытываемых образцов, что обуславливает необходимость учета выявленной закономерности при идентификации изменений во времени напряженного состояния элементов каменных конструкций в реальных условиях.

Литература

1. Басов А.Д. Экспериментальные исследования напряженно-деформированного состояния горных пород и конструкций крепи при строительстве тоннеля на участке Северокавказской железной дороги Сочи-Адлер / А.Д.Басов, К.В.Романевич // Инженерная геология. 2013. № 6. С. 28-37.

2. Гиляров В.Л. Описание термоупругого эффекта в твердых телах в широкой области температур / В.Л.Гиляров, А.И.Слуцкер // Физика твердого тела. 2014. Т. 56. Вып. 12. C. 2407-2409. Описание термоупругого эффекта в твердых телах в широкой области температур

3. Использование природного камня человеком: путь от древности к современной архитектуре / М.С.Уляков, И.С.Сорокин, А.В.Маганева, Р.Ф.Иштакбаев // Добыча, обработка и применение природного камня: Сборник научных трудов. Т. 14. Магнитогорск: МГТУ им. Г.И.Носова, 2014. 263 с.

4. Исследование структуры и упругих свойств геоматериалов с помощью контактной широкополосной ультразвуковой структуроскопии / В.А.Винников, Е.Б.Черепецкая, В.Н.Захаров, О.Н.Малинникова // Горный журнал. 2017. № 4. С. 29-32. DOI: 10.17580/gzh.2017.04.05

5. Капитонов А.М. Физические свойства горных пород западной части Сибирской платформы / А.М.Капитонов, В.Г.Васильев. М.: Инфра-м, 2018. 424 с.

6. Методы и измерительные приборы для моделирования и натурных исследований нелинейных деформационно-волновых процессов в блочных массивах горных пород / В.Н.Опарин, Б.Д.Аннин, Ю.В.Чугуй и др. Новосибирск: Издательство Сибирского отделения Российской академии наук, 2007. 330 с.

7. Определение эффективных теплофизических характеристик композиционного материала / П.А.Люкшин, Б.А.Люкшин, Н.Ю.Матолыгина, С.В.Панин // Физическая мезомеханика. 2008. Т. 11. № 5. С. 103-110. Определение эффективных теплофизических характеристик композиционного материала

8. An Experimental Study on Infrared Radiation Characteristics of Sandstone Samples Under Uniaxial Loading / L.Ma, Y.Zhang, K.Cao, Z.Wang // Rock Mechanics and Rock Engineering. 2019. Vol. 52. P. 3493-3500. DOI: 10.1007/s00603-018-1688-6

9. Damage monitoring of masonry structure under in-situ uniaxial compression test using acoustic emission parameters / Y.Wu, S.Li, D.Wang, G.Zhao // Construction and Building Materials. 2019. Vol. 215. P. 812-822. DOI: 10.1016/j.conbuildmat.2019.04.192

10. Electromagnetic and neutron emissions from brittle rocks failure: experimental evidence and geological implications / A.Carpinteri, G.Iacidogna, O.Borla, A.Manuello, G.Niccolini // Sadhana. 2012. Vol. 37. № 1. P. 59-78. DOI: 10.1007/s12046-012-0066-4

11. Experimental study of water saturation effect on acoustic velocity of sandstones / W.Si, B.Di, J.Wei, Q.Li // Journal of Natural Gas Science and Engineering. 2016. Vol. 33. P. 37-43. DOI: 10.1016/j.jngse.2016.05.002

12. Experimental study of the influence of water and temperature on the mechanical behavior of mudstone and sandstone / Y.Lu, L.Wang, X.Sun, J.Wang // Bulletin of Engineering Geology and the Environment. 2017. Vol. 76. P. 645-660. DOI: 10.1007/s10064-016-0851-0

13. Karabutov A.A. Measuring the dependence of the local Young's modulus on the porosity of isotropic composite materials by a pulsed acoustic method using a laser source of ultrasound / A.A.Karabutov, N.B.Podymova, E.B.Cherepetskaya // Journal of Applied Mechanics and Technical Physics. 2013. Vol. 54. P. 500-507. DOI: 10.1134/S0021894413030218

14. Karabutov A.A. Determination of uniaxial stresses in steel structures by the laser-ultrasonic method / A.A.Karabutov, N.B.Podymova, E.B.Cherepetskaya // Journal of Applied Mechanics and Technical Physics. 2017. Vol. 58. P. 503-510. DOI: 10.1134/S0021894417030154

15. Lou Q. Experimental study on infrared radiation temperature field of concrete uniaxial compression / Q.Lou, X.He // Infrared Physics & Technology. 2018. Vol. 90. P. 20-30. DOI: 10.1016/j.infrared.2018.01.033

16. Multifunctionalization of novolac epoxy resin and its influence on dielectric, thermal properties, viscoelastic, and aging behavior / S. Zhao, G. Zhang, R. Sun, C. Wong // Journal of Applied Polymer Science. 2014. Vol. 131. Iss. 8. DOI: 10.1002/app.40157

17. Ohtsu M. Overview of visualized NDE for on-site measurement // Innovative AE and NDT Techniques for On-Site Measurement of Concrete and Masanry Structures: State-of-the-Art Reports of the RILEM Technical Commitee 239-MCM. Springer, 2016. P. 173-176. DOI: 10.1007/978-94-017-7606-6_10

18. Plekhov O.A.Experimental study of thermodynamics of plastic deformation by infrared thermography // Technical Physics. The Russian Journal of Applied Physics. 2011. Vol. 56. № 2. P. 301-304.

19. Precursors for Fracturing and Failure. Part II: IRR T – Curve Abnormalities / L.Wu, S.Liu, Y.Wu, C.Wang // International Journal of Rock Mechanics and Mining Sciences. 2006. Vol. 43. Iss. 3. P. 483-493. DOI: 10.1016/j.ijrmms.2005.09.001

20. Rabat Á. Effect of water saturation on strength and deformability of building calcarenite stones: Correlations with their physical properties / Á.Rabat, M.Cano, R.Tomás // Construction and Building Materials. 2020. Vol. 232. 117259. DOI: 10.1016/j.conbuildmat.2019.117259

21. Sheinin V.I. Features of thermomechanical effects in rock salt samples under uniaxial compression / V.I.Sheinin, D.I.Blokhin // Journal of Mining Science. 2012. Vol. 48. Iss. 1. P. 39-45. DOI: 10.1134/S1062739148010054

22. Study of Limestone Deformation Stages on The Basis of Acoustic Emission and Thermomechanical Effects / V.I.Sheinin, D.I.Blokhin, E.A.Novikov, L.V.Mudretsova // Soil Mechanics and Foundation Engineering. 2020. Vol. 56. № 6. P. 398-401. DOI: 10.1007/s11204-020-09621-y

23. The progress in photoacoustic and laser ultrasonic tomographic imaging for biomedicine and industry: A review / A.Bychkov, V.Simonova, V.Zarubin et al. // Applied Sciences (Switzerland). 2018. Vol. 8 (10). DOI: 10.3390/app8101931

24. Victorov S.D. Experimental study of the microstructural characteristics of the surfaces and volumes of granite samples / S.D.Victorov, A.N.Kochanov, A.A.Pachezhertsev // Bulletin of the Russian Academy of Sciences: Physics. 2018. Vol. 82. № 7. P. 786-788. Experimental study of the microstructural characteristics of the surfaces and volumes of granite samples

25. Vavilov V.P. Review of pulsed thermal NDT: Physical principles, theory and data processing / V.P.Vavilov, D.D.Burleigh // NDT and E International. 2015. Vol. 73. P. 28-52. DOI: 10.1016/j.ndteint.2015.03.003

26. Water Saturation Effects on Thermal Infrared Radiation Features of Rock Materials During Deformation and Fracturing / X.Cai, Z.Zhou, L.Tan et al. // Rock Mechanics and Rock Engineering. 2020. P. 1-18. DOI: 10.1007/s00603-020-02185-1

27. Weakening laws of rock uniaxial compressive strength with consideration of water content and rock porosity / X.Shi, W.Cai, Y.Meng et al. // Arabian Journal of Geosciences. 2016. Vol. 9. № 5. P. 1-7. DOI: 10.1007/s12517-016-2426-6

Экспериментальное исследование термомеханических эффектов в водонасыщенных известняках при их деформировании

Аннотация

Похожие статьи