Experimental study of thermomechanical effects in water-saturated limestones during their deformation
- 1 — Ph.D. Institute of Comprehensive Exploitation of Mineral Resources Russian Academy of Sciences ▪ Orcid ▪ Scopus
- 2 — Postgraduate Student National University of Science and Technology MISiS ▪ Orcid ▪ Scopus
- 3 — Ph.D. Associate Professor National University of Science and Technology MISiS ▪ Orcid ▪ Scopus
Abstract
Stability control of elements of stone constructions of various structures is a prerequisite for their safe operation. The use of modern methods of non-destructive diagnostics of the stress-strain state of such constructions is an effective, and in many cases the only way to control it. Studies of thermal radiation accompanying the processes of solid bodies deformation allowed to justify and develop a method that allows to obtain non-contact information about changes in the stress-strain state in various types of geomaterials, including limestones. However, studies of the water saturation influence of rocks on the thermal radiation parameters recorded in this way are currently superficial. Taking into account the water saturation degree of rocks is necessary when monitoring the mechanical condition of stone structures that are in direct contact with water. The main purpose of this work is to study the dependences of changes in the intensity of thermal radiation from the surface of limestone samples with different humidity under conditions of uniaxial compression. The obtained results showed the expected significant decrease in the mechanical properties (uniaxial compressive strength and elastic modulus) of water-saturated samples in comparison with dry ones. At the same time, a significant increase in the intensity of thermal radiation of limestone samples subjected to compression with an increase in their water saturation was recorded, which makes it necessary to take into account the revealed regularity when identifying changes in the stress state of stone structures established according to non-contact IR diagnostics in real conditions.
Introduction. Natural stone, from which the most ancient structures are built, is now also effectively used in the construction of industrial and civil objects [3], for example, historical buildings, religious buildings, monuments, bridges, retaining walls, tunnels, and others. These engineering structures can be subjected to various dynamic loads of both natural and man-made nature (wind, earthquakes, vibrations, etc.) [3, 17]. Such loads negatively affect the stability of structures, being catalysts for destructive mechanical processes in the material. In this regard, the reliability assessment of the considered structures is an urgent task, for which it is necessary to use the procedures for monitoring the deformation processes in stone constructions.
Standard methods for measuring changes in the parameters of the stress-strain state (SSS) of building constructions involve the use of various modifications of deformometers that are placed either on the free surfaces of structures or in their body [1, 6, 9]. However, unlike concrete structures that have a relatively smooth surface, such placement of measuring sensors on the surface of stone structures can be difficult, and their location in the body of structural elements requires special work that violates their integrity, which may be unacceptable when analyzing historical or memorial structures. These circumstances determine the need for the use of non-destructive diagnostic methods in the investigation of stone constructions.
Currently, monitoring systems for the state of building constructions and rock masses use the methods that include measurements of variations in the parameters of physical fields of different nature that accompany the processes of deformation and destruction of materials [1, 9, 10, 17]. Among the actively developed methods of non-destructive diagnostics of the mechanical state of geomaterials is the method of IR radiometry, which uses the results of non-contact measurements of changes in the intensity of infrared radiation from the surface of rocks during their deformation [21, 15, 19, 22]. The interpretation of the thermoradiative IR measurements results is based on the description of the known thermodynamic effects: changes in the temperature of a solid body during its adiabatic deformation (thermoelastic and thermoplastic effects [2, 18]) and the dependence of the infrared radiation intensity from the body surface on the temperature [25].
In [21, 15, 19, 22] the effectiveness of IR radiometry for identifying the stages of deformation of various types of rocks was justified. However, in order to obtain reliable information about the course of deformation processes based on thermoradiation measurements in real conditions, it is necessary to study the variability influence of the physical and mechanical properties of rocks on the recorded thermal radiation parameters, in particular, taking into account the degree of water saturation of the studied materials when interpreting thermoradiation measurements, which has a significant impact on the physical and mechanical state of rocks [11, 20, 12, 27].
The purpose of this work is to study the phenomenon of these thermomechanical effects in structurally inhomogeneous rock samples with different humidity under uniaxial compression using non-contact IR measurements.
Methodology. Experiments were carried out on limestone samples – the most commonly used material of stone constructions [3, 20]. Since limestone belongs to rocks with a high degree of heterogeneity, a selection of samples with similar values of physical and mechanical parameters and similar structural properties was created in order to obtain high-quality and reasonable results when performing the described studies. For this purpose, a set of preliminary tests was carried out, including both standard methods for determining the physical and mechanical properties of rocks, and methods based on introscopic methods of investigation, such as scanning electron microscopy and laser ultrasonic diagnostics [4, 14, 24].
A solid block of limestone was cut into more than 100 parallelepipeds measuring 25 x 25 x 55 mm.
The mineral and elemental analyses were carried out on a series of 25 ´ 25 mm anslips using a Phenom ProX scanning electron microscope, which operates both in the optical image mode for petrographic analysis and in the electronic image mode, from which the elemental composition was determined on the basis of an energy-dispersion system. The analysis showed that for most samples the average content is, %: calcium 40.0-42.3, carbon 12.1-13.9, oxygen 45.1-47.5. A slight presence of various mineral components and impurities was found, %: silicon 0.2-0.3, magnesium 0.1-0.2, iron 0.1. The impurities were distributed evenly over the entire surface of the studied samples.
The surface of the studied anslips is represented by a granular structure. Pore systems occupying 5-7 % of the total surface area are recorded at the grain contact boundary; the values of characteristic pore sizes are in the range of 40-450 microns. The mineral composition is represented by calcite, the content of which varied in the range of 97.5-98.3, an insignificant amount of quartz-1.5-2.3 and dolomite-less than 0.5 %. The total contribution of the remaining minerals is small (less than 0.1 %). Taking into account the electron microscopy data, 15 samples with similar structural properties were selected from the original series. At the second stage, it was necessary to select samples with approximately the same porosity values from this series. The porosity was evaluated using laser ultrasonic structurescopy [4, 14, 23], performed on an automated structuroscope UDL-2M on 15 plates with a size of 50 ´ 25 mm and a thickness of about 4-5 mm, made from selected samples.

The principle of the structurescope operation (Fig.1) is based on the registration of signals obtained as a result of the dispersal of broadband acoustic pulses on various inhomogeneities of samples [4].
Scanning was performed on the surface of the plate in 1 mm increments. Taking into account the thickness and time of the double path of the acoustic pulse along the sample, the distribution velocities Vl. of the longitudinal waves were calculated at each scanning point. The velocity of the shear wave Vt was determined by the delay time of the shear wave relative to the reference signal. Local values of elastic wave velocities at 100 points of each sample were obtained. Table 1 shows the values of the average velocities of longitudinal and shear waves.
Table 1
Results of measurement of elastic wave velocities
| Wave velocity, m/s | Sample number | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| Vl | 4506 | 4185 | 4540 | 4520 | 4517 | 4758 | 4534 | 4501 | 4245 | 4526 | 4575 | 4289 | 4523 | 4534 | 4696 |
| Vt | 2409 | 2098 | 2420 | 2447 | 2408 | 2531 | 2403 | 2367 | 2006 | 2394 | 2454 | 2043 | 2336 | 2315 | 2574 |
According to the given data, it is possible to calculate the local porosity of the samples [13]:
where V0 – is the distribution velocity of the longitudinal wave in the material at Ptotal, that is in the absence of porosity.
To calculate V0 the following algorithm was developed. It is known that the main minerals contained in limestone (calcite and quartz) belong to the trigonal symmetry class [5]. In crystals of trigonal syngony only along three crystallographic axes [100], [010] [001] purely longitudinal waves propagate, the velocities V1, V2, V3 of which are determined by the diagonal elements of the stiffness matrix C33, C11 [5]:
where \(\rho\) – is the crystal density.
In all other directions, quasi-longitudinal waves spread, the phase velocities of which are determined from the Green-Christoffel equation [5], and their values can differ significantly from the values of the velocities of pure modes. Since calcite and quartz minerals in limestone are chaotically oriented, it is necessary to perform averaging in all directions to calculate the velocity V10 which is a rather time-consuming procedure. Therefore, to estimate V0 from the known values of the stiffness matrix coefficients \(\{ C_{ij}\}, i,j=1..,6\) for calcite and quartz, given in Table.2, the velocities V1, V2, V3 were found along the crystallographic axes [100], [010], [001] and additionally in the directions [110], [011] [101] the velocities are V12, V23, V13 for each mineral [5]. Next, averaging was performed in all six directions, taking into account the contribution of calcite and quartz.
Table 2
Stiffness matrix coefficients for calcite and quartz
| Rock | C11, GPa | C12, GPa | C44, GPa | C33, GPa | C13, GPa | C66, GPa | \(\rho\), kg/m3 |
| Calcite | 137 | 45,2 | 34,2 | 79,2 | 44,8 | 45,9 | 2980 |
| Quartz | 86,8 | 7,1 | 58,3 | 105,9 | –11,9 | 39,9 | 2650 |
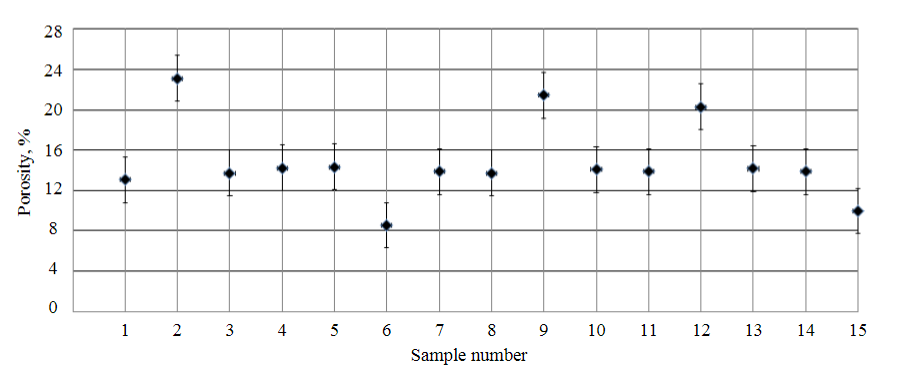
As a result of the calculations, the average velocity V0 in a limestone sample without pores was 4900 m/s. Figure 2 shows the results of the calculation of the porosity values of the samples, carried out according to the formula (1). Indicators of the total porosity Ptotal of the samples 1, 3, 4, 5, 7, 8, 10, 11, 13, 14 belong to a single interval, which is 13-14 %. These samples were subsequently subjected to mechanical tests.
Results. To conduct experiments to assess the effect of water saturation of limestone samples on the kinetics of thermal radiation accompanying their deformation, samples 1, 3, 4, 5, 7, 8, 10, 11, 13, 14 were selected and then divided into two groups (5 samples in each) (Fig. 3). Samples of one group were placed in water for seven days. After that, the mass of the samples was determined and their density was calculated, the values of which are presented in Table 3.
Table 3
Geometric and density parameters of limestone samples
| Sample number | m, g | a, mm | b, mm | S = ab, mm2 | h, mm | Vtotal = Sh | r, kg/m3 |
| Dry samples | |||||||
| 1с | 67,18 | 25,65 | 23,50 | 603,28 | 50,29 | 30131 | 2216 |
| 2с | 67,05 | 25,06 | 24,34 | 585,90 | 49,95 | 29215 | 2294 |
| 3с | 66,98 | 25,15 | 24,10 | 581,02 | 50,07 | 29088 | 2312 |
| 4с | 67,46 | 25,32 | 25,07 | 584,77 | 50,01 | 29212 | 2299 |
| 5с | 67,05 | 25,50 | 25,50 | 650,25 | 50,27 | 32688 | 2251 |
| Water-saturated samples | |||||||
| 1м | 70,15 | 24,64 | 24,03 | 592,10 | 49,97 | 29587 | 2370 |
| 2м | 69,26 | 24,42 | 24,36 | 594,87 | 50,28 | 29910 | 2315 |
| 3м | 70,25 | 23,61 | 24,63 | 581,51 | 50,13 | 29151 | 2409 |
| 4м | 70,09 | 24,50 | 24,56 | 601,72 | 50,54 | 30410 | 2304 |
| 5м | 69,55 | 25,65 | 23,46 | 601,75 | 50,22 | 30219 | 2299 |
The average densities of dry and water-saturated samples were 2274 and 2340 kg/m3 respectively.
The measurements were performed on the LFM-50 test machine using an automated system [22], which allows simultaneous recording of mechanical and thermoradiative parameters (Fig. 4).
In the experiments, the RTN-31 detector was used as the primary receiver of IR radiation [21, 22], designed for non-contact measurement of changes in the intensity of optical radiation in the infrared frequency range. The IR radiation sensor 1 is installed approximately in the middle of the height of the sample 2 at a distance of 0.5-1 cm from the surface.
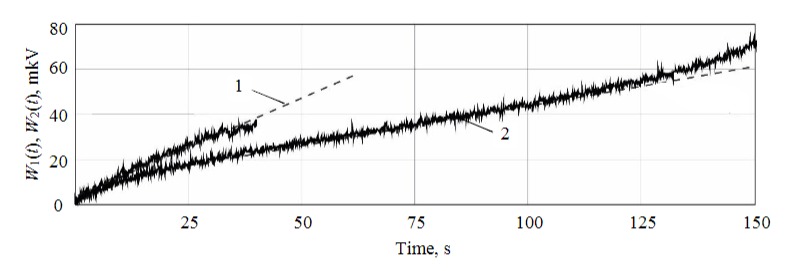
Graphs of changes in the time values of the output signals obtained as a result of the passage of the primary signal from the IR radiometer (RTN-31 detector) through the measuring and computing path during the deformation of dry W1(t) and water-saturated W2(t) limestone samples in the uniaxial compression mode at a constant loading rate \((d\sigma_1/dt=const)\) are shown in Fig.5. The dependences W1(t) and W2(t) demonstrate the nature of changes in the intensity of IR radiation in time intervals corresponding to the intervals of the linear stage of limestone samples deformation.
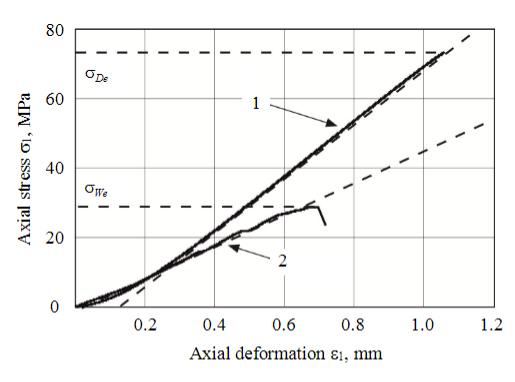
The diagrams \(\sigma_1-\epsilon_1,\), obtained during the experiment are shown in Figure 6. The graphs \(\sigma_1(\epsilon_1),\) confirm the existence of a significant dependence of changes in the strength and deformation characteristics of limestone samples on the degree of their water saturation [22, 12]. In particular, the values of the ultimate strength for dry \(\sigma_{D_{\epsilon}}\) and water-saturated \(\sigma_{w_{\epsilon}}\) limestone samples determined from the graphs shown in Figure 6 differ by about 2.5 times (\(\sigma_{D_{\epsilon}}\asymp\)74 MPa, а \(\sigma_{W_{\epsilon}}\asymp\)30 MPa).
Discussion of the results. Analyzing the dependences W1(t) and W2(t), we can conclude that the angle of inclination of the straight line approximating the graph W2(t), is significantly greater than the angle of inclination of the corresponding straight line for the graph W1(t), which indicates a higher thermal activity of the water-saturated limestone sample. The obtained result is consistent with the conclusions of [8, 26], which also record an increase in the IR radiation intensity of rock samples subjected to compression with an increase in their water saturation. Changes in both the thermophysical and physico-mechanical characteristics of samples under the influence of water saturation are the main factor determining the observed thermomechanical effect.
During the analysis of the obtained results, to confirm their adequacy, it is possible to perform estimated calculations of temperature increments \(\Delta T\) for dry and water-saturated samples. For this purpose, the well-known approximation [2, 18], is used, which relates the increments of the solid body stresses with temperature changes during its uniaxial adiabatic deformation,
where T0 – absolute value of the temperature before the start of deformation; \(\alpha\) – linear expansion coefficient; с – specific heat capacity at constant pressure; \(\rho\) – material density.
Then, as follows from the expression (4), with the same increment of the solid body stresses \(\Delta \sigma_1\) under its uniaxial adiabatic deformation, the relationship between the temperature changes \(\Delta T\) for dry and water-saturated samples will take the following form [16]:
In [16] the validity of the relation is shown for different types of solid bodies
where E – is the elastic modulus of the material under uniaxial deformation.
The values of the Ec and EB modules for dry and water-saturated samples, respectively, were calculated using the graphs \(\sigma_1-\epsilon_1,\), shown in Figure 6. Then the formula (5) will take the following form:
The results of calculations of the elastic modulus values: Ed= 69 и Ew = 42 GPa
For the calculations according to formula (7), the data from Table 3 were used.
In order to obtain approximate values of the specific heat capacity с for water-saturated and dry limestone samples, it is necessary to use the well-known definition [7], in which the specific heat capacity of a heterogeneous medium is understood as the arithmetic weighted average of all mineral components present in the medium with a fraction of ki and their specific heat capacity ci:
Since the main material component of the test samples is calcite, the formula for calculating the specific heat capacity of water-saturated limestone was obtained from equation (8):
where сcalc– specific heat capacity of calcite, \(\rho_{calc}\) – calcite density, Vcalc – calcite volume, сwater – specific heat capacity of water, \(\rho_{water}\) – water density, Vwater – water volume, Рopen – open porosity, \(\rho_{m.w.}\) – experimentally measured density of a water-saturated sample, Vs – sample volume
The open porosity was determined by the Archimedes method in accordance with ASTM C830-00 (2016). The pore volume was determined by the difference in the mass of the dry and water-saturated sample, and the open porosity was determined by the formula
According to the results of calculations, the average value of the open porosity was 9.5 %, while the total porosity Рtotal was 13.7 %. Considering that the calcite volume of is related to the total porosity Рtotal, including open Рopen and closed \(\ (P_{total}- P_{open})\), i.e. \(\ V_{calc}= V_{s}(1- P_{open})\) , получено
Similarly, an expression is obtained for calculating the specific heat capacity of dry limestone:
The heat capacity of the air, which is concentrated in the pores of the dry sample, is not taken into account. The results of calculating the specific heat capacities for dry сd and water-saturated сw samples according to formulas (11) and (12) are presented in Table 4.
Table 4
Results of calculation of specific heat capacity for samples
| Dry samples | Water-saturated samples | ||
| Sample number | c, J/(kg*K) | Sample number | c, J/(kg*K) |
| 1с | 1059 | 1м | 1149 |
| 2с | 1023 | 2м | 1177 |
| 3с | 1015 | 3м | 1131 |
| 4с | 1021 | 4м | 1182 |
| 5с | 1044 | 5м | 1185 |
| Average value | 1032 | Average value | 1165 |
Further calculations using formula (6) involve the average values of specific heat capacities for dry and water-saturated samples, shown in Table 4. In addition, in the calculations, Т0 = 300 К.
Substituting in formula (7) the values necessary for the calculation, we obtain that the temperature increment for water-saturated samples is \(\ \Delta T_w\asymp1,2 \Delta T_d\), which is confirmed by the experimental dependences shown in Figure 5.
Thus, the conducted complex experimental studies, supported by the performed estimated calculations, demonstrate a significant influence of the water saturation of porous materials on their mechanical and thermophysical characteristics, which are expressed in a significant thermal activity increase initiated by the deformation processes occurring in them.
Conclusion. The conducted studies demonstrate a comprehensive approach to the laboratory study of thermomechanical processes in complexly structured heterogeneous materials subjected to deformation, which are limestone samples.
Using standard methods of scanning electron microscopy, a petrographic analysis was carried out and the structural features of the studied samples were revealed. The efficiency of using the data of laser-ultrasonic structroscopy for quantitative rapid assessment of the porosity of rocks is shown.
The dependences of changes in the intensity of thermal radiation W(t) from the surface of limestone samples with different humidity under uniaxial compression conditions are obtained. An important element of the conducted experiments was the synchronous registration of variations in the intensity of thermal radiation and changes in mechanical parameters. Analysis of the data of combined measurements of axial stresses and deformations showed an expected significant decrease in the mechanical properties (uniaxial compressive strength and elastic modulus) of water-saturated samples compared to dry ones. The results of IR-radiometric measurements showed a clear dependence of the W(t) graphs nature on the degree of water saturation of the test samples, which makes it necessary to take into account the revealed regularity when identifying changes in the stress state of the stone constructions elements in real conditions.