Оптимизация взрывного дробления горных пород с использованием гибридных методов искусственного интеллекта на алмазном руднике Орапа (Ботсвана)
- 1 — магистр научный сотрудник Ботсванский международный университет науки и технологий ▪ Orcid
- 2 — Ph.D. преподаватель Ботсванский международный университет науки и технологий ▪ Orcid
- 3 — Ph.D. заведующий кафедрой Ботсванский международный университет науки и технологий ▪ Orcid
- 4 — Ph.D. заведующий кафедрой Ботсванский международный университет науки и технологий ▪ Orcid
Аннотация
В данном исследовании демонстрируются различные методы искусственного интеллекта для прогнозирования и оптимизации взрывного дробления породы на алмазном руднике Орапа в Ботсване. Эти методы включают искусственные нейронные сети (ИНС/ANN), адаптивную нейро-нечеткую систему вывода (ANFIS), генетический алгоритм с ИНС (GA-ANN) и метод роя частиц с ИНС (PSO-ANN). Для выполнения задачи была использована база данных, включающая информацию о 120 взрывных работах на руднике с девятью входными параметрами. Результаты показывают, что модель PSO-ANN превосходит другие в прогнозировании взрывного дробления породы. Оптимальная модель включает девять входных параметров, два скрытых слоя с 65 и 30 нейронами и один выходной параметр (7-65-30-1). Это десятимерное пространство решений исследовалось с использованием градиентного спуска для определения оптимизированных параметров проектирования взрыва, и достигнуто оптимальное значение дробления приблизительно 86 %. Результаты анализа чувствительности показывают, что входными параметрами, имеющими наибольшее влияние на дробление, являются коэффициент крепости породы (15,3 %), индекс взрываемости (14,7 %) и коэффициент сближения скважин (14,7 %). Наименьшее влияние на дробление оказывает коэффициент жесткости (6,3 %).
Финансирование
Исследовательский проект финансировался алмазной компанией Debswana, грант № P00064.
Введение
Буровзрывные работы признаны наиболее эффективным методом дробления пород в горнодобывающей и строительной отраслях. Это означает, что производственные взрывные работы в горно-добывающей промышленности играют важную роль в последующих операциях, включая погрузку, транспортировку и дробление. Получение обломков с оптимальным распределением частиц по размерам повышает эффективность указанных операций [1]. В связи с этим точное прогнозирование дробления породы после взрывных работ имеет решающее значение для повышения общей экономической эффективности горных работ и производственных операций [2]. На дробление породы влияют как контролируемые, так и неконтролируемые факторы. Контролируемые факторы включают параметры проектирования взрывных работ и свойства взрывчатых веществ, а неконтролируемые – геомеханические свойства породы [3, 4].
Существует множество эмпирических моделей, разработанных для прогнозирования дробления породы [5-7]. Однако эти модели часто не обладают надежностью и точностью, поскольку не учитывают нелинейные взаимосвязи между всеми релевантными параметрами. Это привело к применению методов искусственного интеллекта в горном деле и механике горных пород [8-13]. Н.Гаэини и соавторы [14] использовали метод взаимной информации (MI) для прогнозирования дробления породы при взрывных работах на медном руднике Мейдук. Для сравнения также применялась модель Кузнецова – Раммлера (KuzRam). Входные данные модели включали десять параметров при наборе данных по 36 взрывам. Исследование показало, что метод MI оказался наиболее эффективным с R2 = 0,81. В другом исследовании С.Шамс и соавторы [15] использовали систему нечеткого вывода (FIS), множественный регрессионный анализ (MRA) и эмпирические модели Кузнецова и SveDeFo для прогнозирования дробления породы. Модель FIS превзошла статистические и эмпирические модели, достигнув коэффициента детерминации R2 = 0,922.
П.Асл и соавторы [16] применили искусственную нейронную сеть (ИНС) с оптимизацией по «алгоритму светлячков» (FFA) для прогнозирования и оптимизации дробления породы взрывными работами в известняковом руднике Таджарех. Рассматриваемые параметры включали расстояние между скважинами, диаметр и длину скважины, подбуривание, забойку, расход взрывчатого вещества, заряд на каждый интервал замедления и геомеханический индекс прочности (GSI). Значение R2 для ИНС в исследовании составило 0,94, а анализ чувствительности показал, что наибольшее влияние на дробление оказали GSI и расстояние между скважинами. Л.Димитраки и соавторы [17] использовали набор данных 100 взрывов для прогнозирования размера частиц при дроблении породы посредством взрывов. Они применяли ИНС со следующими входными параметрами: расход взрывчатого вещества, индекс взрываемости и количество взорванной горной породы. При прогнозировании дробления ИНС имела значение R2, равное 0,80. Метод опорных векторов (SVR) показал превосходные результаты с наивысшей точностью и наименьшей ошибкой, в то время как метод Кузнецова имел наименьшую точность и наибольшую ошибку. Наконец, Е.Эбрахими и др. [18] использовали ИНС с алгоритмом оптимизации искусственного пчелиного роя (ABC) для прогнозирования и повышения эффективности обратного разлета породы и дробления. В качестве эталона для прогнозирования среднего размера обломков использовалась эмпирическая модель KuzRam. Результаты показали превосходную способность алгоритма ABC оптимизации дробления породы по сравнению с другими моделями.
Данная работа вносит значительный вклад в изучаемую область. Во-первых, в исследовании рассматриваются данные о взрывных работах алмазной компании Debswana, расположенной в Орапа, Ботсвана. Во-вторых, исследование использует набор данных, собранный на основе 120 взрывных операций. В-третьих, в исследование включены девять входных параметров: коэффициент сближения скважин S/B, коэффициент жесткости H/B, забойка T, диаметр скважины D, расход взрывчатого вещества Pf, заряд на интервал замедления C, глубина скважины L, коэффициент крепости породы Rf, индекс взрываемости BI. В-четвертых, в работе применяются четыре метода машинного обучения: искусственные нейронные сети (ANN), адаптивная нейро-нечеткая система вывода (ANFIS), генетический алгоритм с нейронными сетями (GA-ANN), метод роя частиц с нейронными сетями (PSO-ANN). В-пятых, в исследовании моделируется восьмимерная поверхность решений с помощью PSO-ANN для прогнозирования, оптимизации и нахождения обратного решения по дроблению породы при взрывных работах методом градиентного спуска. Наконец, проводится анализ чувствительности с использованием весов сети модели PSO-ANN, который подтверждается методом SHapley Additive exPlanations (SHAP). Предложенная в статье методология сравнивается с двумя аналогичными исследованиями.
М.Хасанипанах и соавторы [19] провели прогнозирование дробления породы при взрывных работах в районе плотины р. Шур, расположенной в южной части провинции Керман, Иран. В исследовании использовался набор данных, включающий 72 взрыва и пять входных параметров: максимальный заряд на интервал замедления, забойка, линия наименьшего сопротивления (ЛНС), расстояние между скважинами, удельный заряд. В работе применялись три алгоритма машинного обучения: ANFIS, PSO-ANFIS, SVR, а также статистический метод нелинейной множественной регрессии. Анализ чувствительности проводился с использованием метода амплитуды косинуса.

Рис.1. Алмазный рудник Орапа
Дж.Чжоу и соавторы [20] также провели прогнозирование дробления породы при взрывных работах в районе плотины р. Шур в Иране. Использовался набор данных, включающий 88 взрывов и шесть входных параметров: максимальный заряд на замедление, ЛНС, расход взрывчатого вещества, расстояние между скважинами, забойка, характеристика породной толщи RMR. В исследовании применялись пять алгоритмов машинного обучения: ANFIS-GA, ANFIS с оптимизацией по «алгоритму светлячков», ANFIS, SVR, ANN. Анализ чувствительности проводился с использованием метода амплитуды косинуса.
Исследование месторождения
Алмазный рудник Орапа расположен в Ботсване, Южная Африка (рис.1). Месторождение включает единую вулканическую трубку, которая разделяется в глубине на северную и южную части, проходя через отложения Трансвааля и осадочные породы Кару, сформировавшиеся более 200 млн лет назад. В процессе взрывных работ применяется шахматный порядок бурения, при этом используются два типа взрывчатых веществ: А и В. Высота уступа составляет 15 м, скважины имеют диаметры 127, 165 и 250 мм. Типичный ряд содержит от 40 до 60 скважин, а каждый взрыв включает 15-25 рядов. Взорванную массу в карьере обрабатывают с помощью экскаваторов, погрузчиков и самосвалов с задней разгрузкой. В настоящее время горные работы на руднике Орапа достигают глубины 305 м, к 2026 г. планируется достичь отметки в 350 м. Добыча варьируется в зависимости от плана разработки месторождения и в среднем составляет около 2000 кг в год.
Методы
В данном разделе рассматриваются набор данных и методики, используемые в настоящем исследовании. Основное внимание уделяется наборам собранных в ходе горных работ данных, применяемых в методах машинного обучения, и реализованным процессам оптимизации.
Набор данных
Данные о взрывных работах (всего 120 взрывных событий) были извлечены из шахтерской документации для обучения и тестирования моделей, предложенных в настоящем исследовании. Параметры с диапазонами приведены в табл.1.
Таблица 1
Входные и выходные параметры
|
Параметр |
Тип |
Min |
Max |
|
Коэффициент жесткости Н/В |
Ввод |
2,5 |
3,75 |
|
Коэффициент сближения скважин S/B |
Ввод |
1,17 |
1,25 |
|
Глубина забойки Т, м |
Ввод |
4 |
5 |
|
Глубина скважины L, м |
Ввод |
12,73 |
15,34 |
|
Диаметр скважины D, мм |
Ввод |
165 |
250 |
|
Заряд на интервал замедления C, кг |
Ввод |
235,71 |
634,88 |
|
Расход взрывчатого вещества Pf, кг/м3 |
Ввод |
0,3 |
1,2 |
|
Коэффициент крепости породы Rf |
Ввод |
3,26 |
7,62 |
|
Индекс взрываемости BI |
Ввод |
22 |
66 |
|
Дробление Fr, % |
Вывод |
70 |
81 |
Предварительная обработка данных была выполнена в первую очередь для обеспечения качества и согласованности набора данных. В нее вошли очистка, в ходе которой обрабатывались пропущенные или несогласованные значения, а также нормализация, при которой все входные параметры приводились к единому диапазону для предотвращения доминирования в процессе обучения характеристик с большими величинами. Набор данных был разделен на две подвыборки: 80 % для обучения и 20 % для тестирования. Обучающая часть дополнительно подвергалась шестикратной кросс-валидации, при которой данные разделялись на шесть равных частей (примерно по 20 образцов в каждой), пять частей использовались для обучения модели, а одна часть – для валидации. Процесс повторялся шесть раз, чтобы каждый образец участвовал как в обучении, так и в валидации. Предварительная обработка данных также включала построение корреляционной матрицы и анализ главных компонент. Для оценки моделей использовались показатели эффективности – среднеквадратичная ошибка (СКО), R2 и средняя абсолютная ошибка (САО). Программное обеспечение Split Desktop применялось при анализе и построения кривой распределения частиц по размерам (PSD) для оценки степени дробления (с помощью изображений, полученных с цифровой камеры). Качество дробления на руднике оценивается на основе показателя 76 %-ного прохождения через сито частиц размером 150 мм, при этом размер менее 50 мм считается мелким, а более 150 мм – крупным. На рис.2 представлены изображение отвала горной массы и кривая PSD, полученная с помощью программного обеспечения Split Desktop.
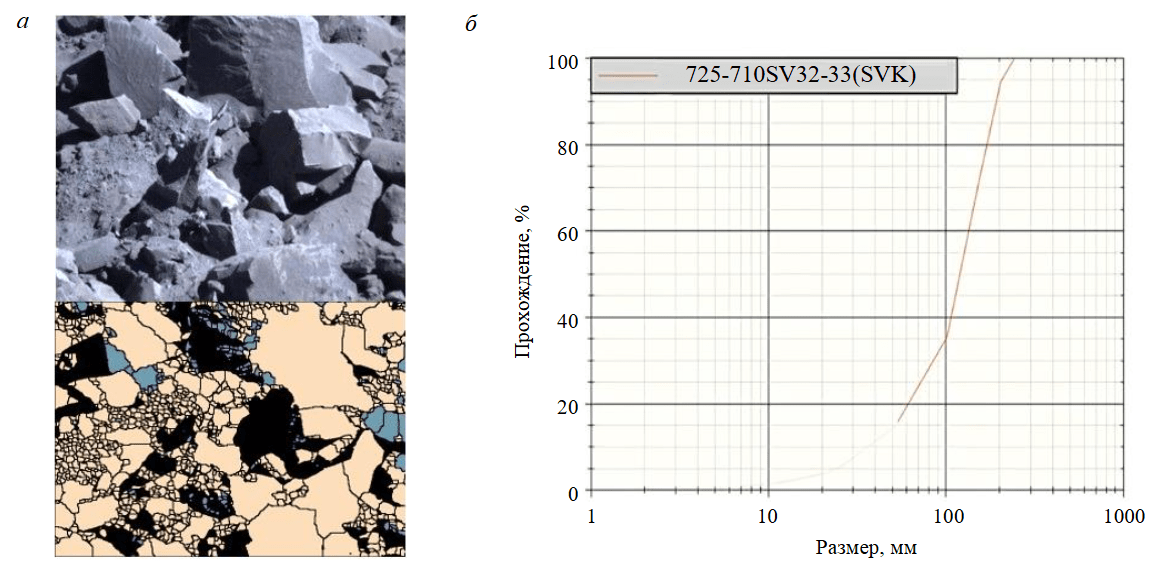
Рис.2. Изображение отбитой руды (а) и кривая распределения частиц по размерам из Split Desktop (б)
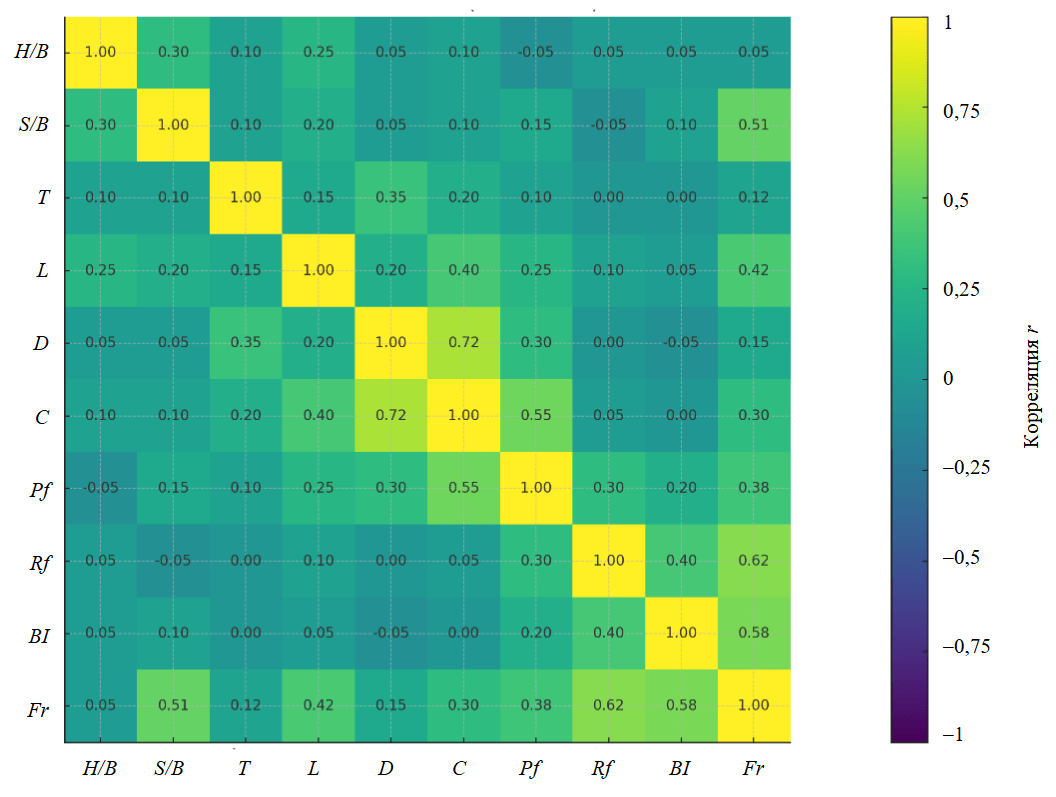
Рис.3. Корреляционная матрица
Корреляционная матрица (рис.3) дает линейное представление о том, как характеристики породы и параметры проектирования взрыва связаны с дроблением Fr. Наиболее сильные положительные связи наблюдаются с коэффициентом крепости породы Rf (r ≈ 0,62) и индексом взрываемости BI (r ≈ 0,58), что указывает на следующее: более благоприятные условия массива породы, как правило, обеспечивают более мелкое дробление при сопоставимых проектных параметрах. Геометрические параметры также имеют значения: коэффициент сближения скважин S/B (r ≈ 0,51) демонстрирует умеренно высокую корреляцию, что согласуется с улучшением рельефа ЛНС и взаимодействием трещин между рядами в пределах исследуемого диапазона. Параметры подачи энергии подтверждают эти тенденции – глубина скважины L (r ≈ 0,42) и расход взрывчатого вещества Pf (r ≈ 0,38) увеличиваются при использовании более мелкого продукта, что отражает увеличение продолжительности заряда колонны и повышение энергоемкости на единицу породы. В то же время коэффициент жесткости H/B (r ≈ 0,05) в этом диапазоне близок к нулю, а диаметр скважины D демонстрирует лишь слабую прямую связь с Fr. Это объясняется тем, что эффективная энергия в большей степени определяется зарядом C и Pf, а практика расчленения заряда или декирования ослабляет любое простое влияние диаметра.
Взаимосвязи между входными параметрами соответствуют практическим связям в проектировании работ. Наивысшая степень корреляции наблюдается между D и C (r ≈ 0,72), поскольку скважины большего диаметра вмещают большую массу заряда. Следом идет C и Pf (r ≈ 0,55), так как Pf зависит от массы заряда на единицу объема породы. Связь между T и D (r ≈ 0,35) отражает масштабирование забойки в соответствии с размером скважины для сохранения герметизации газов, в то время как H/B-S/B (r ≈ 0,30) изменяются совместно, поскольку оба коэффициента содержат параметр ЛНС. В целом матрица показывает, что характеристики породы (Rf, BI) задают базовый уровень дробления, в то время как геометрия (S/B) и энергонасыщенность (Pf, L через C) выступают основными управляемыми параметрами. Поскольку это линейный вид, нелинейные эффекты или пороговые значения, характерные для геометрии взрыва, могут быть представлены недостаточно полно. Поэтому данные корреляции следует рассматривать как наглядное руководство для отладки проектирования взрыва, а не как строгие причинно-следственные утверждения.
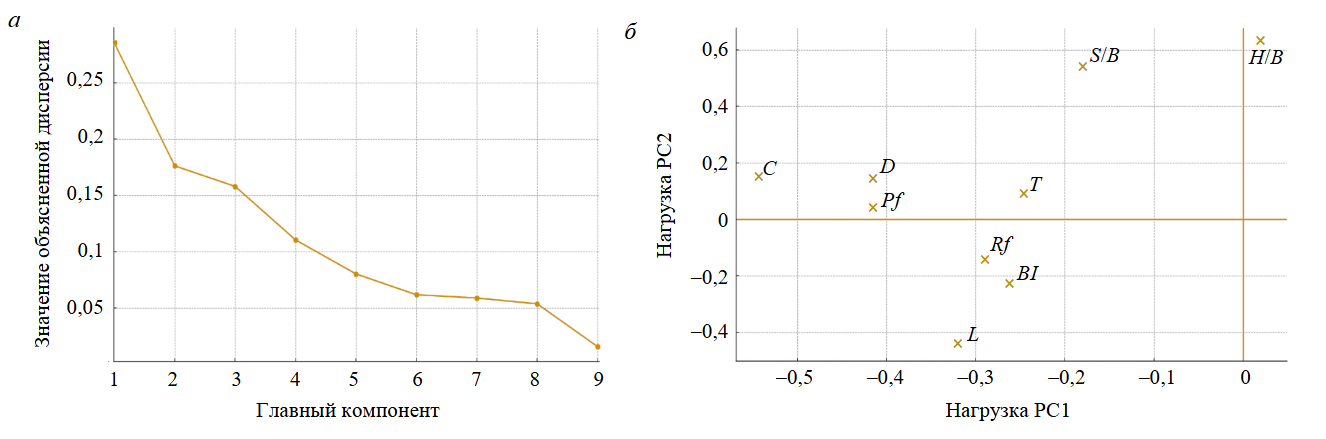
Рис.4. Анализ главных компонент: а – объясненная дисперсия компонент PCA; б – нагрузки PC1 и PC2
Метод главных компонент (PCA) был применен к девяти входным переменным для анализа мультиколлинеарности и выявления доминирующих факторов проектирования взрыва и крепости породы. Первые две компоненты охватили большую часть дисперсии входных данных, как показано на графике собственных значений (рис.4, а). На рис.4, б главная компонента PC1 определяется значительными нагрузками от C, D, Pf (в меньшей степени – T и L), представляя собой ось шкалы энергии (т.е. больший диаметр скважины, бо́льшие параметры заряда и увеличенная подаваемая энергия). Главная компонента PC2 противопоставляет коэффициенты рельефа (H/B, S/B) индексам взрываемости породы (Rf, BI, отрицательные значения), представляя собой ось «Рельеф породы». Это означает, что при одинаковом рельефе более крепкая порода требует большей энергии или корректировки проектирования взрыва для достижения одинакового уровня дробления Fr. Полученные результаты согласуются с корреляционной матрицей на рис.3, где доминируют переменные рельеф/коэффициент крепости породы (S/B, BI, Rf), а энергетические переменные (Pf, L, C, D) оказывают вторичное, управляемое влияние.
Методы искусственного интеллекта
Для прогнозирования дробления породы были использованы несколько передовых методов машинного обучения: ANN, PSO-ANN, ANFIS и GA-ANN. Анализ чувствительности проводился с использованием весов сети модели PSO-ANN, лучшей для определения относительного влияния входных параметров на результат. Метод Монте – Карло применялся для систематического исследования и оценки различных архитектур нейронных сетей путем изменения количества скрытых слоев (от одного до трех) и соответствующего количества нейронов в каждом слое. Этот метод вероятностной выборки позволил определить оптимальную архитектуру нейронной сети. Затем был применен градиентный спуск для навигации в пространстве решений и поиска оптимального значения дробления породы и соответствующих входных параметров. Для получения стабильной оценки времени обучения модели обучались многократно, n = 10000 циклов. В начале 10000 циклов фиксировалось время tstart, а в конце – tend. Среднее время цикла вычислялось как =(tend − tstart)/n. Все замеры времени проводились на ноутбуке HP ProBook 455 G8 (процессор Ryzen 7 5800U класса ПК, 8 ГБ оперативной памяти, встроенный графический процессор Radeon) под управлением Python 3.11/TensorFlow 2.19. Ускорение с помощью дискретного графического процессора не использовалось.
Итоговая очищенная выборка из n = 120 взрывов (2016-2024 гг.) соответствует целям исследования и размерности параметров (девять входных переменных). Она согласуется с предыдущими исследованиями моделирования буровзрывных работ, представленными в литературе (табл.2), где высокая точность прогнозирования достигалась на наборах данных аналогичного или меньшего размера. Для минимизации риска при конечном объеме выборки и систематической ошибке отбора мы обеспечили строгое разделение обучающей и тестовой выборок без утечки данных, используя шестикратную кросс-валидацию только в пределах обучающей выборки для выбора модели. На слепом тестовом наборе лучшая модель (PSO-ANN) достигает следующих показателей: R2 = 0,96; СКО = 0,17; САО = 0,30. Эти результаты соответствуют диапазону точности, заявленному для сопоставимых объемов выборок. В совокупности масштаб набора данных, соответствие литературной практике и контрольные показатели валидации/диагностики подтверждают, что данные достаточны и пригодны для моделирования заявленных требований.
Таблица 2
Показатели других исследований
|
Лучшая модель |
Другие модели |
Входные данные |
Набор данных |
R2 |
Источник |
|
PSO-ANFIS |
ANFIS; SVM; MNLR |
SC, T, S, B, MC |
72 |
0,89 |
[1] |
|
ANN |
|
D, L, B/S, T, Nr, Pf, RD, Tc |
250 |
0,98 |
[2] |
|
BPNN |
BPNN; RBFNN |
B, S, L, T, SC, SD |
103 |
0,90 |
[4] |
|
FIS |
FIS |
B, S, D, SHRN, DJ, Pf, T |
185 |
0,92 |
[15] |
|
FIS |
MVRA |
B, S, L, SD, T, MC, RD, Pf |
415 |
0,80 |
[16] |
|
ANN |
SVR; ANN; MVRA; Кузнецова |
S/B, L/B, B/D, T/B, Pf, E, Xb |
90 |
0,96 |
[17] |
|
ANN |
ABC |
B, S, L, T, Pf |
34 |
0,78 |
[18] |
|
RES |
MVRA |
B, MIC, SC, S/B, T/B, H/B, Nr, INCL, D, B/D |
52 |
0,86 |
[19] |
|
FFA-ANFIS |
GA-ANFIS; ANFIS; SVR; ANN |
B, S, T, Pf, MC, RMR |
88 |
0,98 |
[20] |
|
FFA-ANN |
FFA-ANN; FFA-ANFIS; SVM; GPR; SVM; KNN |
Pf, MC, S, T, B, H |
136 |
0,98 |
[2] |
|
GPR |
SVM; ANFIS; PSO-ANFIS |
B, S, Pf, T, E |
72 |
0,95 |
[21] |
|
ANN |
SVR; Кузнецова |
S/B, L/B, B/D, T/B, Pf, E, Xb |
102 |
0,87 |
[22] |
|
ANN |
MVRA |
D, Pf, TC, L, T, D, S/B |
180 |
0,99 |
[23] |
|
JSO-LGBM |
|
B, S, Pf, T, L, SD |
234 |
0,99 |
[24] |
|
ANN |
|
S, B, T, Pf, Lc, D, L |
70 |
0,88 |
[25] |
|
FFA-BGAM |
FFA-ANN; ANFIS; SVM; GPR; KNN |
Pf, MC, S |
136 |
0,98 |
[26] |
|
RES |
|
B, S/B, Pf, MH, H/B, HIL, HDVD, J/B, BI, IS, BHP, B/D |
64 |
0,93 |
[27] |
Примечание. BGAM – обобщенная аддитивная модель с усилением; BPNN – нейронная сеть с обратным распространением ошибки; MVRA – многомерная линейная регрессия; RES – система инжиниринга горных пород; JSO-LGBM – оптимизатор поиска на основе поведения медуз – облегченный градиентный бустинг; MIC – максимальная мгновенная масса заряда; INCL – угол наклона скважины; GPR – регрессия гауссовского процесса; B/D – отношение ЛНС к диаметру скважины; L/B – отношение глубины скважины к ЛНС; T/B – отношение забойки к ЛНС; Xb – размер блока в естественном состоянии; SC – удельная масса заряда; SD – подбуривание; RD – плотность породы; J – плотность трещин; SHRN – показатель отскока по Шмидту; Nr– количество рядов; PLI – коэффициент точечной нагрузки; Dr – интервал замедления между рядами; MC – максимальная масса заряда; TC – общая масса заряда на ступень замедления; E – модуль упругости; UCS – предел прочности на одноосное сжатие; MH – максимальное количество скважин на ступень замедления; HIL – угол наклона скважины; HDV – отклонение скважины; IS – последовательность подрыва; BHP – схема расположения скважин.
Наиболее эффективной моделью (табл.2) является оптимизатор поиска на основе поведения медуз – облегченная машина градиентного бустинга (JSO-LGBM) от М.Яри и соавторов [24]. Эта модель достигла значения R2 = 0,99 при использовании набора данных из 234 записей с шестью входными параметрами (B, S, Pf, T, L, SD). Превосходная производительность этой модели объясняется большим объемом набора данных, а также возможностями оптимизатора поиска на основе поведения медуз (JSO) в сочетании с GBM, что, вероятно, позволяет более эффективно улавливать нелинейные зависимости по сравнению с другими моделями. Наименее эффективная модель – искусственная нейронная сеть (ANN) Е.Эбрахими и соавторов [18], которая показала значение R2 = 0,78 при использовании набора данных из 34 записей с пятью входными параметрами (B, S, L, T, Pf). Ограниченный размер набора данных и менее сложная архитектура модели могли ограничить ее способность к обобщению и захвату вариативности данных, что привело к снижению точности прогнозирования.
Модель гауссовского процесса (GPR) В.Гао и соавторов [21] показала средний результат, достигнув значения R2 = 0,95 при использовании набора данных из 72 записей с пятью входными параметрами (B, S, Pf, T, E). Это стало возможным благодаря способности модели улавливать сложные нелинейные зависимости с помощью таких функций ядра, как радиальная базисная функция (RBF). Оценка неопределенности делает модель устойчивой к шумам, особенно в наборах данных малого и среднего размера, подобных использованным 72 записям. Сглаженные предсказания GPR, оптимизация гиперпараметров и гибкость в моделировании сложных зависимостей способствовали высокой эффективности модели.
При сравнении результатов модель авторов статьи PSO-ANN достигла значения R2 = 0,96 при использовании набора данных из 90 записей с семью входными параметрами. Она продемонстрировала хорошие показатели и была близка к другим высокоэффективным моделям, таким как ANN Л.Димитраки и соавторов [17] с R2 = 0,96 на выборке из 90 взрывных событий. Однако гибридные модели, использующие передовые методы и более крупные наборы данных, такие как FFA-ANN (R2 = 0,98, К.Фан и др. [2]) и ANN с большими наборами данных (R2 = 0,97, М.Яри и др. [24]), показывают несколько лучшие результаты по сравнению с нашей моделью. Эти результаты указывают на то, что точность и обобщающая способность модели могут быть улучшены за счет увеличения набора данных и добавления дополнительных входных параметров. Это позволит модели улавливать более сложные взаимодействия и улучшить обобщающую способность, как показывают наиболее эффективные модели.
Реализация ANN
Трехслойная прямая искусственная нейронная сеть (ИНС/ANN) была обучена с использованием метода стохастического градиентного спуска. Для определения оптимальной конфигурации сети был проведен поиск по сетке в сочетании с шестикратной кросс-валидацией. В ходе поиска по сетке исследовались следующие параметры: количество скрытых нейронов (от 5 до 50); скорость обучения (от 0,01 до 0,1); различные функции активации, включая выпрямленную линейную единицу (ReLU), сигмоидальную функцию и гиперболический тангенс. Среди всех протестированных функций ReLU стабильно демонстрировала лучшие результаты как по скорости сходимости, так и по точности прогнозирования. Как показано в табл.2, конфигурация с 15 нейронами и скоростью обучения 0,1 имела наименьшую СКО во всех проходах. Трехслойная ИНС достигла сходимости за 8 с при обучении на 100 эпохах. Ее основной компонент затрат имеет вид O(N·H), где N – количество обучающих выборок, обрабатываемых за эпоху; H – количество скрытых нейронов (т.е. обучаемых весов). Таким образом, время выполнения увеличивается с ростом N или H. При дообучении точная настройка с теплого старта на дополнительных 10 % новых данных завершилась примерно за 5 с.
Реализация ANFIS
ANFIS (адаптивная нейро-нечеткая система вывода) объединяет принципы нечеткой логики в нейронную сеть. Нейронная сеть формирует выражения типа if–then, выступая в роли эксперта по построению правил [28]. Для настройки параметров модели использовался поиск по сетке. Оптимизировались следующие параметры: количество функций принадлежности (от 2 до 7), тип функции принадлежности (гауссова, треугольная и обобщенная колоколообразная), скорость обучения (от 0,01 до 0,1), количество эпох обучения (от 50 до 150). Для точной настройки исходных параметров и следствий применялась гибридная стратегия оптимизации, сочетающая градиентный спуск с оценкой методом наименьших квадратов.
Как показано в табл.2, наилучшие результаты были достигнуты при использовании трех гауссовых функций принадлежности и скорости обучения 0,1 за 100 эпох. Обучение модели ANFIS завершилось за 75 с. Ее основной компонент затрат имеет вид O(N·R·M), где R – количество нечетких правил, созданных в процессе обучения; M – количество функций принадлежности, назначенных каждой входной переменной. Поскольку каждая выборка оценивается по отношению ко всем нечетким правилам, обучающим выборкам и функциям принадлежности, время обучения быстро возрастает при добавлении новых данных, правил или функций. При дообучении ANFIS не поддерживает быструю точную настройку, и любые новые данные требуют полного перестроения набора правил и повторного обучения модели.
Реализация GA-ANN
Согласно литературным данным, эффективность ИНС значительно повышается при использовании генетического алгоритма (GA) [29, 30]. Генетический алгоритм представляет собой стохастический метод поиска, способный избегать попадания в локальные минимумы – распространенный недостаток ИНС. Благодаря существенному преимуществу GА в проведении многонаправленного поиска, он способен находить глобальные минимумы и улучшать предсказательные возможности ИНС [31]. Поэтому веса и смещения нейронной сети обновлялись с помощью GА. Для преодоления проблем локальных минимумов, часто возникающих при обучении ИНС на основе обратного распространения ошибки, была реализована гибридная модель, объединяющая GА и ИНС.
При помощи комплексного поиска по сетке были исследованы ключевые параметры GА, такие как размер популяции (10-50), частота мутаций (1-10 %), количество поколений (50-150), стратегии кроссовера (одноточечный и равномерный). При кросс-валидации каждый набор параметров оценивался на основе среднего СКО для обеспечения надежности выбранной конфигурации. Как показано в табл.2, наименьшую ошибку и наивысшую точность обеспечили размер популяции 20, частота мутаций 5 % и 100 поколений.
Обучение модели GA-ANN заняло 115 с. Ее основной компонент затрат O(P·G·H) зависит от размера популяции генетического алгоритма P, количества поколений G и количества скрытых нейронов (весов) H в каждой сети. Таким образом, время выполнения значительно возрастает при увеличении размера популяции, количества поколений или расширении сети. При дообучении, поскольку генетический поиск исследует новый ландшафт отбора, обычно требуется полное переобучение при каждом изменении распределения данных.
Реализация PSO-ANN
Одним из недостатков ИНС является их склонность «застревать» в локальных минимумах [32]. Алгоритм метода роя частиц (PSO) способен осуществлять поиск в значительно большем пространстве и находить глобальные минимумы. В результате веса и смещения нейронной сети обновляются с использованием наилучших позиций, обнаруженных PSO.
Созданная трехслойная нейронная сеть с обратным распространением ошибки содержала десять нейронов в скрытом слое. Поиск по сетке применялся для исследования широкого диапазона гиперпараметров, включая размер роя (10-50 частиц), когнитивный коэффициент обучения C1 (1-2), социальный коэффициент обучения C2 (1,5-2), коэффициент инерции w (0,6-0,8), количество итераций (до 150). Архитектура ИНС включала один скрытый слой, причем количество нейронов в этом слое также варьировалось в процессе поиска. Как показано в табл.3, наилучшая конфигурация использовала 30 частиц, C1 = 1,3, C2 = 1,8, коэффициент инерции 0,8, итераций – 100.
Согласно табл.3, гибридные модели оптимизации стабильно превосходили отдельные модели ИНС и ANFIS по всем метрикам кросс-валидации (R2, СКО и САО). Наивысшую предсказательную точность с наименьшими значениями ошибок продемонстрировала модель PSO-ANN, за ней следовала модель GA-ANN, в то время как ANFIS показала умеренное улучшение по сравнению с базовой ИНС.
Таблица 3
Результаты кросс-валидации для всех моделей
|
Модель |
Лучшие параметры |
Среднее значение ± СО |
||
|
R2 |
СКО |
САО |
||
|
ANN |
Нейроны – 15; линейная регрессия – 0,01 |
0,87 ± 0,03 |
1,15 ± 0,28 |
1,67 ± 0,19 |
|
ANFIS |
Функции принадлежности – 3; эпохи – 200 |
0,89 ± 0,05 |
1,13 ± 0,32 |
1,34 ± 0,25 |
|
GA-ANN |
Нейроны – 15; поколения – 100; популяция – 20 |
0,93 ± 0,02 |
1,08 ± 0,21 |
1,12 ± 0,14 |
|
PSO-ANN |
Нейроны – 15; частицы – 30 |
0,95 ± 0,01 |
0,95 ± 0,17 |
0,85 ± 0,11 |
Все модели продемонстрировали низкие значения стандартного отклонения (СО) на разных этапах кросс-валидации, что указывает на стабильность и согласованность их работы независимо от способа разбиения данных. Такая стабильность в сочетании с постепенным улучшением, наблюдаемым в гибридных моделях, подчеркивает эффективность использования метаэвристической оптимизации для улучшения обобщающей способности моделей и снижения ошибок прогнозирования. Обучение модели PSO-ANN (рой – 30 частиц; итерации – 100) завершилось за 105 с. Ее основной компонент затрат O(S·I·H) очень быстро растет при увеличении размера роя S, количества итераций обновления позиции и скорости I, а также размера скрытого слоя H. При дообучении последние позиции роя могут быть использованы для теплого запуска, поэтому инкрементное обновление на новых данных происходит быстрее, чем первоначальный запуск. В табл.4 приведены сводные данные о сложности или основных компонентах затрат, а также измеренное время обучения и замечания, касающиеся дообучения.
Таблица 4
Вычислительный профиль оцениваемых моделей искусственного интеллекта: время выполнения, сложность и вопросы дообучения
|
Модель |
Время обучения |
Доминирующая стоимость |
Рекомендации к дообучению |
|
ANN |
8 с (100 эпох) |
O(N·H) |
Тонкая настройка на 10 % новых данных – 5 с |
|
ANFIS |
75 с |
O(N·R·M) |
Необходимо переобучение всех наборов правил |
|
GA-ANN |
115 с (поколения – 100; популяция – 20) |
O(P·G·H) |
Требуется переобучение при изменении распределения данных |
|
PSO-ANN |
105 с (рой – 30; итерации – 100) |
O(S·I·H) |
Возможно инкрементальное обновление с помощью теплого старта |
Анализ чувствительности
Для оценки влияния входных параметров на дробление породы был проведен анализ чувствительности с использованием весов сети наиболее эффективного алгоритма [33]:
где Ij указывает на относительную важность j-й входной переменной для выходной переменной в диапазоне 0-1; Ni, Nh – количество нейронов во входном и скрытом слоях соответственно; W – веса сети; верхние индексы i, h, o – входной, скрытый и выходной слои соответственно; нижние индексы k, m, n – номера нейронов во входном, скрытом и выходном слоях соответственно.
Оптимизация методом градиентного спуска
В данном исследовании применялась оптимизация методом градиентного спуска в сочетании с методом Монте – Карло для точной настройки архитектуры используемой PSO-ANN, целью которой является оптимизация модели с семью входными, одним выходным параметрами и двумя скрытыми слоями. В частности, определяется оптимальное количество нейронов – 50 в первом скрытом слое, 25 – во втором. Градиентный спуск – широко используемый итеративный алгоритм оптимизации в вычислительных приложениях и машинном обучении. Он применяется для эффективного поиска в пространстве решений для достижения максимального дробления породы и определения оптимальных параметров проектирования взрывных работ [34]. Основной принцип градиентного спуска заключается в итеративном обновлении параметров путем их перемещения в направлении, противоположном градиенту целевой функции, что постепенно приводит к оптимальному решению. В данном исследовании алгоритм градиентного спуска обновляет каждый входной параметр согласно следующему правилу:
где Pi – текущее значение оптимизируемого параметра; Poldi – значение параметра предыдущей итерации, позволяющее численно решить градиент через конечные разности; η – скорость обучения, представляет собой небольшое положительное значение, контролирующее величину каждого шага обновления, что влияет как на стабильность, так и на скорость сходимости; f – функция, представляет собой гибридную модель PSO-ANN, разработанную на основе оптимизированной методом PSO-ANN, которая прогнозирует дробление породы на основе параметров проектирования взрывных работ.
В исследовании была установлена скорость обучения η = 0,05 для обеспечения стабильной и достаточно быстрой сходимости. Итеративные обновления продолжались до тех пор, пока изменение прогнозируемого дробления между последовательными итерациями не становилось меньше 10–4; максимально допустимое количество итераций – 200 (для предотвращения бесконечных вычислений); случайное начальное значение – 42 (для обеспечения полной воспроизводимости процесса оптимизации).
Результаты и обсуждение
Для оценки эффективности каждой прогнозной модели использовались три ключевых показателя эффективности: СКО, САО и R2:
где n – количество наблюдений; yi – измеренное значение i-го наблюдения; y'i – предсказанное значение i-го наблюдения; – среднее значение.
В табл.5 представлены показатели эффективности лучших конфигураций каждой модели как на обучающей, так и на тестовой выборках. По всем метрикам результаты демонстрируют заметные различия в предсказательной способности в зависимости от выбранного подхода к моделированию и настройки гиперпараметров. Модель PSO-ANN показала наилучшие результаты, достигнув максимальных значений R2 (0,94 на обучающей выборке и 0,96 – на тестовой) и минимальных значений ошибки (СКО = 0,13 и 0,17; САО = 0,25 и 0,30 на обучающей и тестовой выборках соответственно). Это указывает на то, что алгоритм оптимизации роем частиц эффективно настроил параметры ИНС, позволив модели изучить сложные взаимосвязи входных и выходных параметров при сохранении отличной обобщающей способности на новых данных. Модель GA-ANN также продемонстрировала высокие результаты с показателями R2 = 0,93 как при обучении, так и при тестировании, а также сопоставимо низкие значения СКО и САО, что подтверждает преимущество использования генетических алгоритмов для оптимизации параметров.
Таблица 5
Показатели эффективности лучших моделей, рассчитанные на обучающей и тестовой выборках
|
Модель |
Параметр |
Обучающая выборка |
Тестовая выборка |
||||
|
R2 |
СКО |
САО |
R2 |
СКО |
САО |
||
|
ANN |
Нейроны – 15 |
0,87 |
0,45 |
0,50 |
0,85 |
1,75 |
1,57 |
|
GA-ANN |
Популяция – 10 |
0,93 |
0,15 |
0,80 |
0,93 |
0,80 |
0,47 |
|
PSO-ANN |
Размер частиц – 30 |
0,94 |
0,13 |
0,25 |
0,96 |
0,17 |
0,30 |
|
ANFIS |
Функция принадлежности – 3 |
0,91 |
0,42 |
0,50 |
0,87 |
1,36 |
1,08 |
Модель ANFIS, хотя и не показала лучшие результаты, достигла хороших показателей R2 = = 0,91 при обучении и R2 = 0,87 при тестировании. Это свидетельствует о том, что ее гибридный нейро-нечеткий подход способен эффективно выявлять нелинейные взаимосвязи в данных о взрывных работах даже без использования метаэвристической оптимизации. Напротив, модель ИНС продемонстрировала самую низкую предсказательную способность – R2 = 0,87 при обучении и R2 = 0,85 при тестировании и более высокими показателями ошибок. Это говорит о том, что базовая сеть испытывала трудности с захватом сложности данных по сравнению с гибридными подходами.
Все модели достигли высоких значений R2 при обучении, что указывает на хорошее выявление закономерностей в наборе данных. Производительность при тестировании также оставалась высокой, особенно для гибридных моделей (GA-ANN и PSO-ANN), что демонстрирует хорошую обобщающую способность и минимальное переобучение. Прогресс в результатах наглядно показывает влияние метаэвристической оптимизации на повышение точности и стабильности прогнозирования при моделировании взрывного дробления породы.
На рис.5, а показано, что прогнозы, сделанные моделью PSO-ANN, почти совпадают с фактическими измерениями дробления, что подчеркивает превосходство этой модели в прогнозировании дробления по сравнению с другими моделями. Модель PSO-ANN работает лучше, чем GA-ANN, ANFIS и ANN, благодаря эффективности PSO в исследовании пространства поиска и избегании локальных минимумов, способности динамически регулировать скорость и положение, а также вычислительной эффективности. Более простые механизмы обновления PSO позволяют находить оптимальные решения быстрее и точнее, чем GА, при этом минуя проблемы масштабируемости, характерных для ANFIS. Этот гибридный подход использует сильные стороны как PSO, так и ИНС, более эффективно оптимизируя веса нейронной сети и обеспечивая более высокую точность прогнозирования.
На рис.5, б-г показаны корреляции между наблюдаемым и расчетным дроблением для каждой модели. Большинство точек данных для всех моделей располагаются достаточно близко к линии наилучшего соответствия, что указывает на их потенциал в прогнозировании дробления. Среди всех моделей точки данных модели ИНС наиболее сильно отклоняются от линии наилучшего соответствия, поэтому она имеет самый низкий коэффициент детерминации R2. Это показывает, что алгоритмы оптимизации могут улучшить производительность модели ИНС, поскольку все оптимизированные модели (ANFIS, GA-ANN, PSO-ANN) работают лучше, чем автономная ИНС.
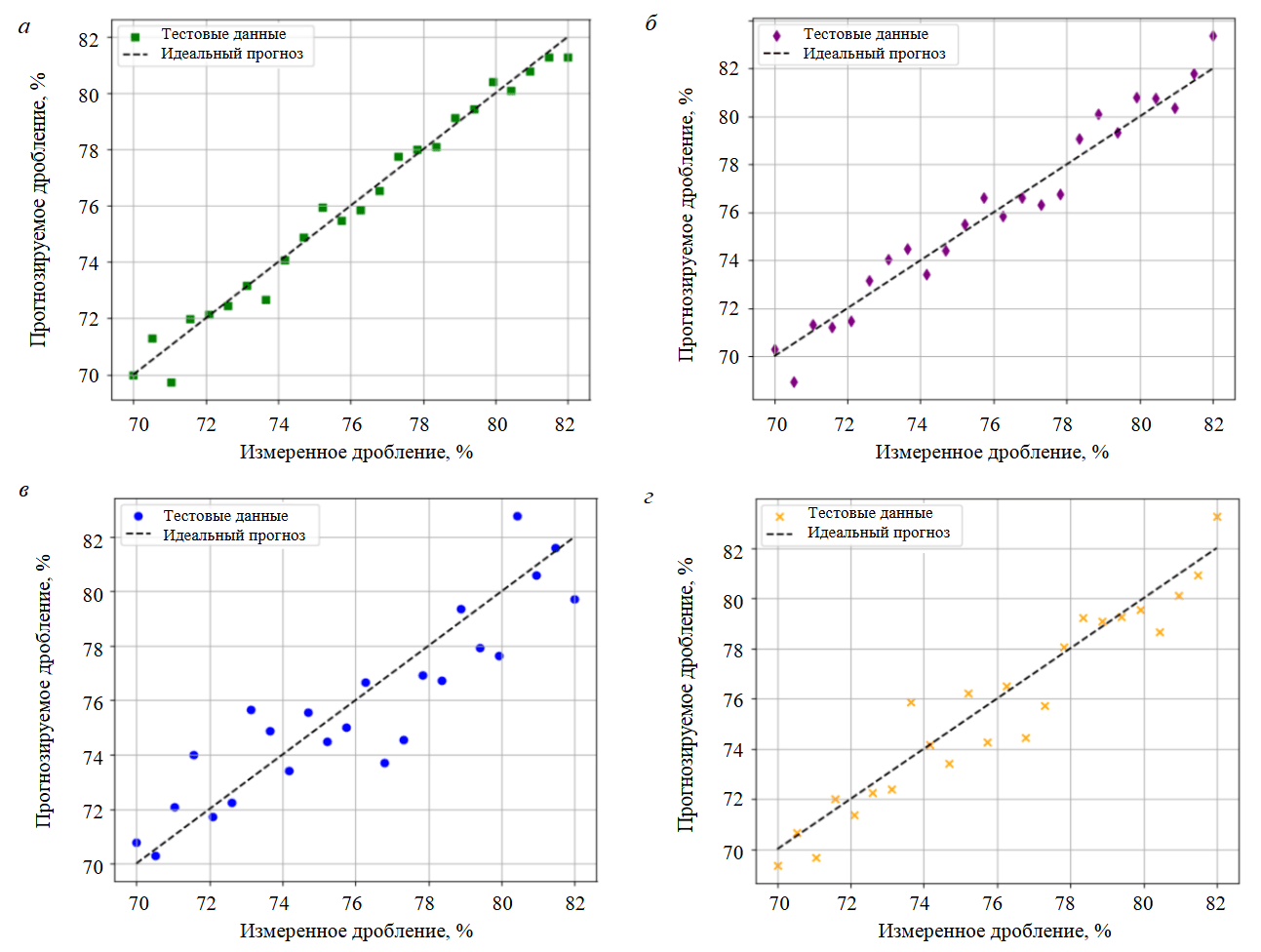
Рис.5. Диаграммы рассеяния для изучаемых моделей: а – PSO-ANN; б – GA-ANN; в – ANN; г – ANFIS
Анализ чувствительности
На рис.6, а представлена лепестковая диаграмма, где каждая ось соответствует одному из входных параметров (H/B, S/B, T, L, D, C, Pf, Rf, BI). Значения показателя прочности Ij нанесены вдоль этих осей. Область, ограниченная голубым многоугольником, отражает относительную чувствительность каждого параметра. Наиболее значимыми входными параметрами являются индекс взрываемости BI – 15,3 %, коэффициент крепости породы Rf – 14,7 % и коэффициент сближения скважин S/B – 14,7 %, на что указывает самый длинный выступ синего многоугольника. Наименее эффективным параметром является коэффициент жесткости H/B – 6,3 %, что подтверждается самым коротким выступом синего многоугольника. Анализ чувствительности подчеркивает решающую роль S/B в определении качества дробления [35-37]. Эти параметры следует рассматривать как приоритетные при проектировании взрывных работ. Высокая чувствительность BI, Rf и особенно S/B как контролируемого параметра, указывает на то, что даже незначительные корректировки могут привести к существенным изменениям в дроблении породы. Это дает инженерам мощный инструмент для управления результатами взрывания. С другой стороны, относительно низкая чувствительность H/B показывает, что его можно рассматривать как второстепенный фактор, позволяя инженерам сосредоточить усилия на более значимых параметрах. Полученные уровни чувствительности согласуются с корреляционным анализом, который также указывает на сильную положительную связь для BI, Rf и S/B и почти нулевую связь для H/B.
Рис.6, б демонстрирует средние абсолютные значения SHAP для дробления Fr, показывая средний вклад каждого входного параметра в прогноз модели. SHAP – это единая структура, основанная на теории кооперативных игр, которая объясняет отдельные прогнозы путем вычисления вклада каждого признака относительно базового ожидаемого значения [38]. Согласно представленному графику, наиболее значимым параметром является коэффициент крепости породы Rf, за которым следуют глубина скважины L; индекс взрываемости BI; расход взрывчатого вещества Pf. Другие параметры, такие как забойка T, коэффициент жесткости H/B и диаметр скважины D оказывают меньшее влияние на результат.
Эти результаты согласуются с анализом чувствительности (рис.6, а) и матрицей корреляций, что подтверждает надежность сделанных выводов. Соответствие результатов SHAP-анализа методу чувствительности повышает доверие к интерпретируемости модели и согласуется с известными физическими принципами взрывных работ, где свойства породы и параметры конструкции скважин определяют результаты дробления.
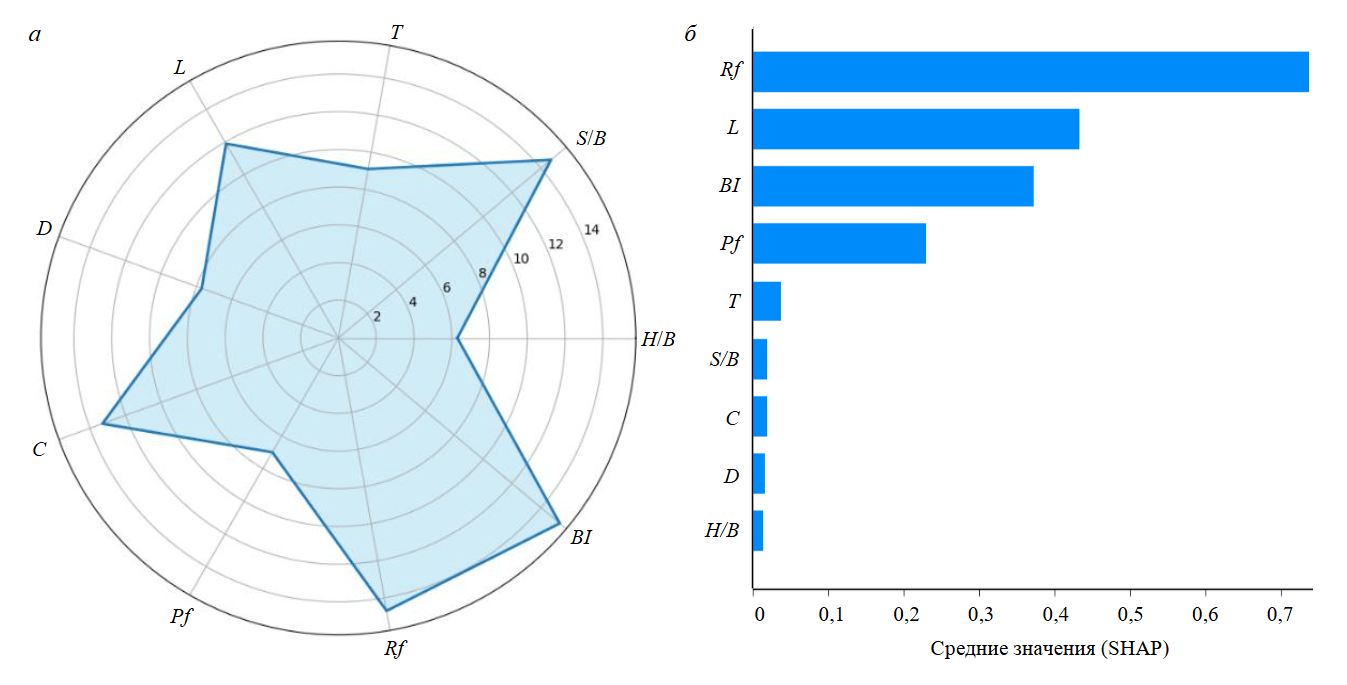
Рис.6. Анализ чувствительности (а) и средние абсолютные значения SHAP (показатели влияния на величину выходных данных модели) для дробления (б)
Оптимизация для максимизации дробления
На рис.7, а-г показаны результаты процесса оптимизации: начальные точки (семь) обозначены красным и выбраны случайным образом; оптимизированное значение показано синей точкой. В результате оптимизации достигнуто улучшение дробления примерно до 86 % при следующих уточненных входных параметрах: расход взрывчатого вещества Pf 0,56; заряд на интервал замедления С 374; коэффициент сближения скважин S/B 1,2; коэффициент жесткости H/B 2,5; забойка Т 4,6; глубина скважины L 15,5; диаметр D 191; коэффициент крепости Rf 8; индекс взрываемости BI 65.
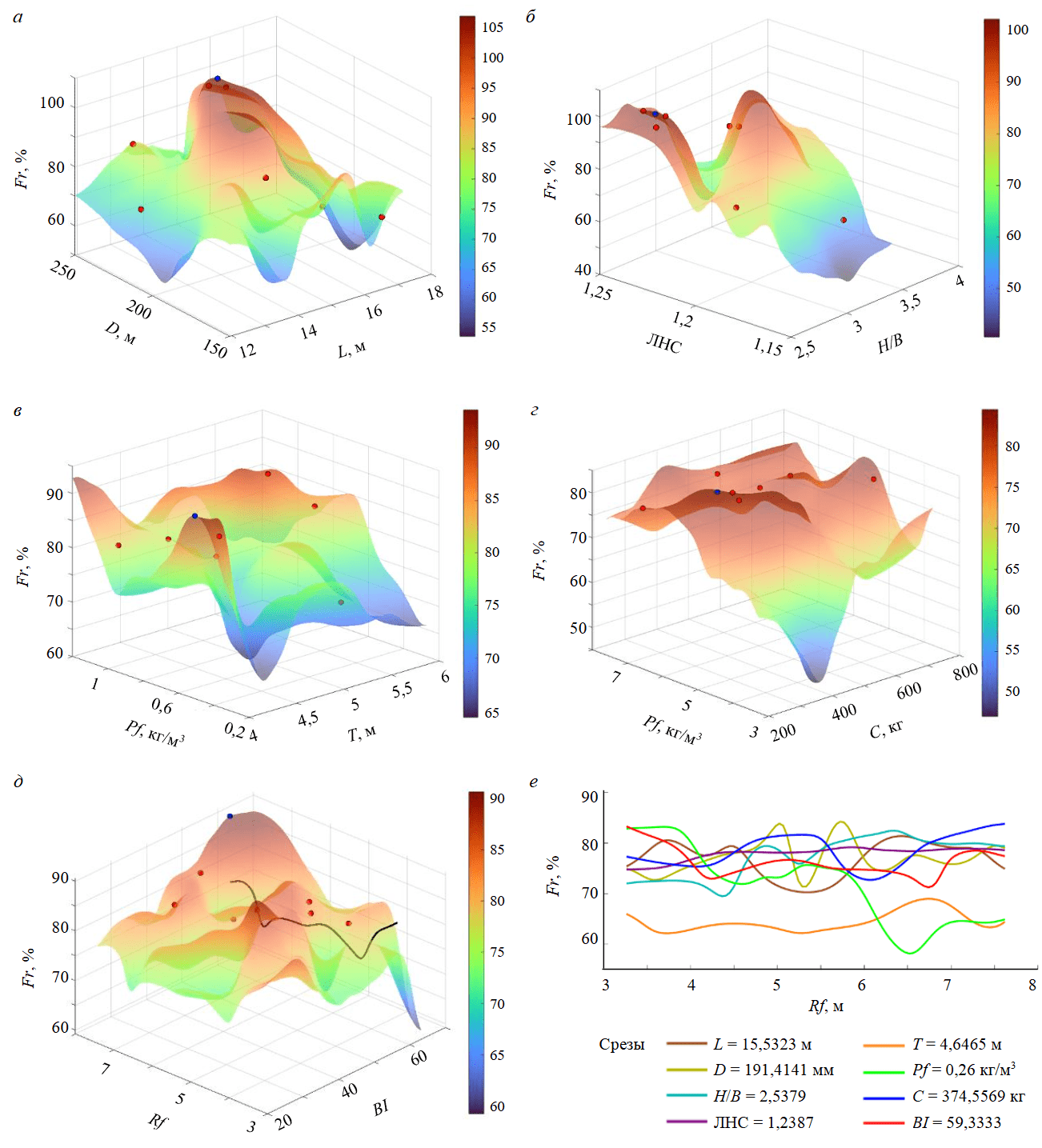
Рис.7. Пространство решений для дробления породы как выходного и входных параметров, взятых по два – зависимости диаметра и глубины отверстия от дробления Fr (а); соотношения расстояния к заряду и жесткости от Fr (б); коэффициента расхода взрывчатого вещества и забойки от Fr (в); коэффициента крепости породы и заряда на интервал замедления от Fr (г); коэффициента крепости породы и индекса взрываемости от Fr (д); совмещенный график для двумерных срезов (е)
Наивысшая точка на поверхности решений соответствует максимальному значению дробления породы, предсказанному моделью (около 86 %). Каждая точка на поверхности решений имеет десять компонент: девять компонент входных параметров и выходной компонент дробления породы. Поверхность решений позволяет выполнять прогнозирование, проводить оптимизацию, находить обратные решения, а также визуализировать взаимодействие различных параметров с выходным значением.
На трехмерном графике (рис.7, д) показано, что при увеличении коэффициента крепости породы (индекс взрываемости сохраняется постоянным вдоль отслеживаемой кривой, которая содержит синюю точку минимума) дробление постепенно снижается, а затем растет с колебаниями до достижения оптимального значения.
На рис.7, е представлена двумерная диаграмма зависимости дробления породы от коэффициента крепости породы – наиболее значимого входного параметра. При этом значения остальных девяти входных параметров в оптимальной точке остаются постоянными, а коэффициент крепости породы отображается во всем своем диапазоне.
Пространство решений подтверждает результаты проведенного анализа чувствительности. Диаграмма (рис.7, е) была создана путем изменения коэффициента крепости породы при фиксированных значениях всех остальных параметров. При этом был выполнен срез через наивысшую оптимизированную точку в пространстве решений. Индекс взрываемости и коэффициент сближения скважин являются вторыми по значимости входными параметрами после коэффициента крепости породы. Они демонстрируют резкие колебания в диапазоне значений. Это указывает на высокую чувствительность, поскольку изменения коэффициента сближения скважин существенно влияют на дробление. Коэффициент жесткости является наименее значимым параметром, что подтверждается плавными колебаниями, также указывающими на более низкую чувствительность.
Такая оптимизация дает несколько практических преимуществ: повышает эффективность за счет сокращения энергии и времени, необходимых для дробления и измельчения; снижает затраты на взрывные работы благодаря более эффективному использованию взрывчатых веществ; повышает безопасность за счет обеспечения стабильных условий взрывания; уменьшает воздействие на окружающую среду благодаря снижению вибраций; оптимизирует управление ресурсами путем точного применения буровых и взрывных материалов. Эти оптимизированные параметры значительно повышают эффективность, безопасность и рентабельность процесса взрывания.
Заключение
В данном исследовании представлена методика прогнозирования и оптимизации распределения частиц по размерам в отвалах горной массы, образующихся в результате взрывных работ на руднике Орапа в Ботсване, которым управляет компания Debswana. В исследовании были использованы различные методы искусственного интеллекта, включая ANN, GA-ANN, ANFIS и PSO-ANN. Эти модели были обучены с использованием данных о 120 взрывных работах. Для прогнозирования и оптимизации дробления было выбрано девять входных параметров.
Результаты показали, что модель PSO-ANN превзошла остальные, достигнув наивысшего значения R2, равного 0,96, и самых низких значений СКО и САО для тестового набора, равных 0,17 и 0,30 соответственно. Следовательно, наиболее подходящей для прогнозирования дробления оказалась гибридная модель PSO-ANN. Оптимизация дробления с помощью градиентного спуска с использованием метода Монте – Карло для поиска оптимальной архитектуры улучшила дробление примерно до 86 %. Оптимальная архитектура, полученная методом Монте – Карло – 7-65-30-1. Оптимальные входные параметры: расход взрывчатого вещества Pf – 0,56 кг/м3, заряд на интервал замедления С – 374 кг, коэффициент сближения скважин S/B – 1,2, коэффициент жесткости H/B – 2,5, забойка Т – 4,6 м, глубина скважины L – 15,5 м, диаметр D – 191 мм, коэффициент крепости породы Rf– 8 и индекс взрываемости BI – 65. Результаты анализа чувствительности показывают, что входными параметрами, оказывающими максимальное влияние на дробление, являются коэффициент крепости породы 15,3 %, индекс взрываемости 14,7 % и коэффициент сближения скважин 14,7 %. Напротив, коэффициент жесткости 6,3 % оказывает наименьшее влияние на дробление.
Модель, разработанная в этом исследовании, предназначена для масштабирования и адаптации к другим объектам добычи. Полученные результаты могут служить базовой моделью, которую затем можно усовершенствовать путем включения данных по конкретному объекту. С помощью итеративной перекалибровки и валидации параметры модели можно корректировать до тех пор, пока ошибки прогнозирования не будут сведены к минимуму. Это гарантирует, что адаптированная модель будет точно отражать условия нового объекта.
Литература
- Hasanipanah M., Amnieh H.B., Arab H., Zamzam M.S. Feasibility of PSO–ANFIS model to estimate rock fragmentation produced by mine blasting // Neural Computing and Applications. 2018. Vol. 30. Iss. 4. P. 1015-1024. DOI: 10.1007/s00521-016-2746-1
- Qiancheng Fang, Hoang Nguyen, Xuan-Nam Bui et al. Modeling of rock fragmentation by firefly optimization algorithm and boosted generalized additive model // Neural Computing and Applications. 2021. Vol. 33. Iss. 8. P. 3503-3519. DOI: 10.1007/s00521-020-05197-8
- Bakhtavar E., Khoshrou H., Badroddin M. Using dimensional-regression analysis to predict the mean particle size of fragmentation by blasting at the Sungun copper mine // Arabian Journal of Geosciences. 2015. Vol. 8. Iss. 4. P. 2111-2120. DOI: 10.1007/s12517-013-1261-2
- Zhi Yu, Xiuzhi Shi, Xianyang Qiu et al. Optimization of postblast ore boundary determination using a novel sine cosine algorithm-based random forest technique and Monte Carlo simulation // Engineering Optimization. 2021. Vol. 53. Iss. 9. P. 1467-1482. DOI: 10.1080/0305215X.2020.1801668
- Esmaeili M., Salimi A., Drebenstedt C. et al. Application of PCA, SVR, and ANFIS for modeling of rock fragmentation // Arabian Journal of Geosciences. 2015. Vol. 8. Iss. 9. P. 6881-6893. DOI: 10.1007/s12517-014-1677-3
- Dumakor-Dupey N.K., Arya S., Jha A. Advances in Blast-Induced Impact Prediction – A Review of Machine Learning Applications // Minerals. 2021. Vol. 11. Iss. 6. № 601. DOI: 10.3390/min11060601
- Jian Zhou, Yulin Zhang, Yingui Qiu. State-of-the-art review of machine learning and optimization algorithms applications in environmental effects of blasting // Artificial Intelligence Review. 2024. Vol. 57. Iss. 1. № 5. DOI: 10.1007/s10462-023-10636-8
- Kaklis K., Saubi O., Jamisola R., Agioutantis Z. Machine Learning Prediction of the Load Evolution in Three-Point Bending Tests of Marble // Mining, Metallurgy & Exploration. 2022. Vol. 39. Iss. 5. P. 2037-2045. DOI: 10.1007/s42461-022-00674-1
- Saadati G., Javankhoshdel S., Javad Mohebbi Najm Abad et al. AI-Powered Geotechnics: Enhancing Rock Mass Classification for Safer Engineering Practices // Rock Mechanics and Rock Engineering. 2024. P. 1-31. DOI: 10.1007/s00603-024-04189-7
- Kaklis K., Saubi O., Jamisola R., Agioutantis Z. A preliminary application of a machine learning model for the prediction of the load variation in three-point bending tests based on acoustic emission signals // Procedia Structural Integrity. 2021. Vol. 33. P. 251-258. DOI: 10.1016/j.prostr.2021.10.031
- Taihua Yang, Tian Wen, Xing Huang et al. Predicting Model of Dual-Mode Shield Tunneling Parameters in Complex Ground Using Recurrent Neural Networks and Multiple Optimization Algorithms // Applied Sciences. 2024. Vol. 14. Iss. 2. № 581. DOI: 10.3390/app14020581
- Zhiheng Ma, Jinguo Wang, Yanrong Zhao et al. Research on Multi-Objective Optimization Model of Foundation Pit Dewatering Based on NSGA-II Algorithm // Applied Sciences. 2023. Vol. 13. Iss. 19. № 10865. DOI: 10.3390/app131910865
- Lawal A.I. A new modification to the Kuz-Ram model using the fragment size predicted by image analysis // International Journal of Rock Mechanics and Mining Sciences. 2021. Vol. 138. № 104595. DOI: 10.1016/j.ijrmms.2020.104595
- Ghaeini N., Mousakhani M., Amnieh H.B., Jafari A. Prediction of blasting-induced fragmentation in Meydook copper mine using empirical, statistical, and mutual information models // Arabian Journal of Geosciences. 2017. Vol. 10. Iss. 18. № 409. DOI: 10.1007/s12517-017-3189-4
- Shams S., Monjezi M., Majd V.J., Armaghani D.J. Application of fuzzy inference system for prediction of rock fragmentation induced by blasting // Arabian Journal of Geosciences. 2015. Vol. 8. Iss. 12. P. 10819-10832. DOI: 10.1007/s12517-015-1952-y
- Asl P.F., Monjezi M., Hamidi J.K., Armaghani D.J. Optimization of flyrock and rock fragmentation in the Tajareh limestone mine using metaheuristics method of firefly algorithm // Engineering with Computers. 2018. Vol. 34. P. 241-251. DOI: 10.1007/s00366-017-0535-9
- Dimitraki L., Christaras B., Marinos V. et al. Predicting the average size of blasted rocks in aggregate quarries using artificial neural networks // Bulletin of Engineering Geology and the Environment. 2019. Vol. 78. Iss. 4. P. 2717-2729. DOI: 10.1007/s10064-018-1270-1
- Ebrahimi E., Monjezi M., Khalesi M.R., Armaghani D.J. Prediction and optimization of back-break and rock fragmentation using an artificial neural network and a bee colony algorithm // Bulletin of Engineering Geology and the Environment. 2016. Vol. 75. Iss. 1. P. 27-36. DOI: 10.1007/s10064-015-0720-2
- Hasanipanah M., Armaghani D.J., Monjezi M., Shams S. Risk assessment and prediction of rock fragmentation produced by blasting operation: a rock engineering system // Environmental Earth Sciences. 2016. Vol. 75. Iss. 9. № 808. DOI: 10.1007/s12665-016-5503-y
- Jian Zhou, Chuanqi Li, Arslan C.A. et al. Performance evaluation of hybrid FFA-ANFIS and GA-ANFIS models to predict particle size distribution of a muck-pile after blasting // Engineering with Computers. 2021. Vol. 37. Iss. 1. P. 265-274. DOI: 10.1007/s00366-019-00822-0
- Wei Gao, Karbasi M., Hasanipanah M. et al. Developing GPR model for forecasting the rock fragmentation in surface mines // Engineering with Computers. 2018. Vol. 34. Iss. 2. P. 339-345. DOI: 10.1007/s00366-017-0544-8
- Amoako R., Jha A., Shuo Zhong. Rock Fragmentation Prediction Using an Artificial Neural Network and Support Vector Regression Hybrid Approach // Mining. 2022. Vol. 2. Iss. 2. P. 233-247. DOI: 10.3390/mining2020013
- Tiile R.N. Artificial neural network approach to predict blast-induced ground vibration, airblast and rock fragmentation: A Thesis Presented to the Faculty of the Graduate School of the Missouri University of Science and Technology in Partial Fulfillment of the Requirements for the Degree Master of Science in Mining Engineering. Missouri, 2016. № 7571. 99 p.
- Yari M., He B., Armaghani D.J. et al. A novel ensemble machine learning model to predict mine blasting–induced rock fragmentation // Bulletin of Engineering Geology and the Environment. 2023. Vol. 82. Iss. 5. № 187. DOI: 10.1007/s10064-023-03138-y
- Koopialipoor M., Armaghani D.J., Haghighi M., Ghaleini E.N. A neuro-genetic predictive model to approximate overbreak induced by drilling and blasting operation in tunnels // Bulletin of Engineering Geology and the Environment. 2019. Vol. 78. Iss. 2. P. 981-990. DOI: 10.1007/s10064-017-1116-2
- Hosseini S., Poormirzaee R., Hajihassani M. An uncertainty hybrid model for risk assessment and prediction of blast-induced rock mass fragmentation // International Journal of Rock Mechanics and Mining Sciences. 2022. Vol. 160. № 105250. DOI: 10.1016/j.ijrmms.2022.105250
- Hosseini S., Mousavi A., Monjezi M., Khandelwal M. Mine-to-crusher policy: Planning of mine blasting patterns for environmentally friendly and optimum fragmentation using Monte Carlo simulation-based multi-objective grey wolf optimization approach // Resources Policy. 2022. Vol. 79. № 103087. DOI: 10.1016/j.resourpol.2022.103087
- Jelušič P., Ivanič A., Lubej S. Prediction of Blast-Induced Ground Vibration Using an Adaptive Network-Based Fuzzy Inference System // Applied Sciences. 2021. Vol. 11. Iss. 1. № 203. DOI: 10.3390/app11010203
- Mohamad E.T., Armaghani D.J., Hasanipanah M. et al. Estimation of air-overpressure produced by blasting operation through a neuro-genetic technique // Environmental Earth Sciences. 2016. Vol. 75. Iss. 2. № 174. DOI: 10.1007/s12665-015-4983-5
- Yilmaz A., Poli R. Successfully and efficiently training deep multi-layer perceptrons with logistic activation function simply requires initializing the weights with an appropriate negative mean // Neural Networks. 2022. Vol. 153. P. 87-103. DOI: 10.1016/j.neunet.2022.05.030
- Chen Z., Zhu L., Lu H. et al. Research on bearing fault diagnosis based on improved genetic algorithm and BP neural network // Scientific Reports. 2024. Vol. 14. № 15527. DOI: 10.1038/s41598-024-66318-0
- Temeng V.A., Ziggah Y.Y., Arthur C.K. A novel artificial intelligent model for predicting air overpressure using brain inspired emotional neural network. International Journal of Mining Science and Technology. 2020. Vol. 30. Iss. 5. P. 683-689. DOI: 10.1016/j.ijmst.2020.05.020
- Pizarroso J., Portela J., Muñoz A. NeuralSens: Sensitivity Analysis of Neural Networks // Journal of Statistical Software. 2022. Vol. 102. Iss. 7. 36 p. DOI: 10.18637/jss.v102.i07
- Armaghani D.J., Hasanipanah M., Mahdiyar A. et al. Airblast prediction through a hybrid genetic algorithm-ANN model // Neural Computing and Applications. 2018. Vol. 29. Iss. 9. P. 619-629. DOI: 10.1007/s00521-016-2598-8
- Hosseini M., Khandelwal M., Lotfi R., Eslahi M. Sensitivity analysis on blast design parameters to improve bench blasting outcomes using the Taguchi method // Geomechanics and Geophysics for Geo-Energy and Geo-Resources. 2023. Vol. 9. Iss. 1. № 9. DOI: 10.1007/s40948-023-00540-4
- Mboyo H.L., Bingjie Huo, Mulenga F. K. et al. Assessing the Impact of Surface Blast Design Parameters on the Performance of a Comminution Circuit Processing a Copper-Bearing Ore // Minerals. 2024. Vol. 14. Iss. 12. № 1226. DOI: 10.3390/min14121226
- Singh P.K., Roy M.P., Paswan R.K. et al. Rock fragmentation control in opencast blasting // Journal of Rock Mechanics and Geotechnical Engineering. 2016. Vol. 8. Iss. 2. P. 225-237. DOI: 10.1016/j.jrmge.2015.10.005
- Lundberg S.M., Su-In Lee. A Unified Approach to Interpreting Model Predictions // 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, December, 2017. 10 p. DOI: 10.48550/arXiv.1705.07874
