Разработка и применение новых методов оценки изменчивости качества полезных ископаемых на основе анализа больших данных для оперативного управления рудопотоком на горных предприятиях
- 1 — канд. техн. наук научный сотрудник Институт проблем комплексного освоения недр им. академика Н.В.Мельникова РАН ▪ Orcid
- 2 — канд. техн. наук заведующий лабораторией Институт проблем комплексного освоения недр им. академика Н.В.Мельникова РАН ▪ Orcid
- 3 — ведущий специалист ООО «Пиклема» ▪ Orcid
Аннотация
В статье проблема управления качеством рудопотоков на горнодобывающих предприятиях рассмотрена с точки зрения возможности применения больших данных для повышения эффективности качества полезных ископаемых. Отмечено, что оценка возможности сбора и обработки больших данных для управления качеством рудопотоков требует оптимального размера исчисляемой весовой характеристики, определяющей дискретность сбора данных и результативность их обработки. В настоящее время такой характеристикой является партия руды (или концентрата). Предложен научно-практический подход к определению размера партий на горнодобывающих предприятиях, основанный не на условиях бизнес-процессов, а на анализе распределения качественных параметров в массиве с учетом способов последующего транспортирования минерального сырья. Проведен анализ данных каждого из технологических процессов горно-технической системы и установлены принципы расчета минимально необходимых выборок данных для каждого из этапов технологического процесса. Рассмотрена возможность применения теоремы Котельникова для определения оптимального размера исчисляемой весовой характеристики партии минерального сырья в рамках контроля качества. Для получения качественной модели необходимый размер статистики работы карьера должен варьироваться от 16 до 52 мес. работы экскаватора в забое. Разброс зависит от значения коэффициента качественного распределения полезного ископаемого на горном предприятии. Также установлено, что для построения качественной модели должен учитываться упомянутый коэффициент, чем выше его значение, тем ниже должна быть частота дискретизации при сборе данных с технологических переделов.
Финансирование
Исследование выполнено за счет гранта Российского научного фонда № 22-17-00142.
Введение
Одним из ключевых процессов в горно-технической системе, определяющим эффективность ее функционирования, является управление качеством рудопотоков [1-3]. Исходя из этого, обоснование дискретности сбора данных должно производиться на базе данных о качественно-количественном распределении полезного ископаемого в природном массиве, а также с учетом анализа данных технологических процессов, которые связаны с перемещением горной массы после разрушения природного массива вплоть до ее транспортирования на переработку [4, 5].
По состоянию на 2024 г. примерно 55 % российских ИТ-компаний внедрили аналитику больших данных, а 31 % – планирует внедрение. Происходит изменение отношения к данным, в частности растет их ценность для бизнеса, так как с появлением инструментов их исследования появляются новые возможности оптимизации бизнес-модели. На основе больших данных о массиве горных пород, отражающих его качественные характеристики, можно обосновать параметры технологических процессов и рекомендаций по отбору и учету проб минерального сырья для отслеживания качественных параметров от выемки до получения готовой продукции на этапе обогащения [6, 7].
В горном деле достаточно хорошо регламентированы и подробно описаны методы отбора и подготовки проб для химического анализа и определения влажности (технологическое опробование) на стадиях складирования и обогащения полезных ископаемых. Например, ГОСТ 14180-80 является необходимым документом для организации опробования партий как руды, так и концентрата. Основная сложность привычного подхода связана с тем, что применяемый в расчетах исчисляемый весовой характеристикой термин «партия» не регламентируется. Определяющей формулировкой «партии» считается объем руды или концентрата, перемещенный за определенный период времени погрузки (разгрузки), размер которого устанавливается договорным соглашением. Это объясняется тем, что упомянутый стандарт ссылается на ГОСТ Р 50779.10 и ГОСТ Р 50779.11, где раскрывается система понятий и терминов в области теории вероятности и математической статистики. Размер партии в названном стандарте негласно трактуется как данность, полученная от условий приме-няемых процессов горно-технической системы. В нормативной документации понятие «партия» формулируется как количество единиц продукции, необходимое для удовлетворения спроса в течение определенного периода времени, или количество единиц продукции, производимое в рамках одного производственного цикла с учетом затрат на производство, хранение и логистику, что также указывает на составные атрибуты бизнес-процессов.
Однако подобные формулировки уместны для производства однотипных по качественным параметрам единиц товарной продукции. В горном же деле на размер партии влияет качественно-количественное распределение минерального компонента в массиве горных пород, а также применяемый способ и условия транспортирования горной массы, что обуславливает необходимость расчета оптимальной дискретности сбора информации по качественным параметрам [8]. В настоящее время на горнодобывающих предприятиях практикуются договорные соглашения об определении размера партии, от чего напрямую зависит частота опробования. Как правило, частота привязывается к «часовкам» внутри смены, что обусловлено удобством отслеживания.
Задача работы состоит в разработке научно обоснованной методики определения минимально необходимого размера партии транспортируемой горной массы с целью выявления оптимального количества данных для получения прогнозов качества подаваемого сырья [9]. Для решения поставленной задачи необходимо определить:
- минимальные размеры данных, частота сбора которых сможет характеризовать технологические процессы при освоении недр;
- количественные значения объема собираемых данных каждого из технологических процессов.
Поставленная научно-практическая задача является важнейшей при постановке требований и задач цифровизации горно-технической системы.
Методы
Как правило, для обоснования периода отбора проб применяют формулу
где М – масса опробуемой партии руды или концентрата, т; Q – производительность опробуемого потока, т/ч; N – число точечных проб:
V – коэффициент вариации, %.
Из применяемых в стандарте формул видно, что для вычисления периодичности отбора проб повсеместно учитывается весовая характеристика опробуемой партии минерального сырья. Причем ее размер будет зависеть от: производительности горно-технологического комплекса по доставке руды, дискретности движения составляющей единицы партии (например, самосвал), коэффициента вариации качества полезного ископаемого, регламентов усреднения сырья и т.д. Описанной методикой подтверждается, что на горнодобывающих предприятиях регламенты хотя и разрабатываются на основе коэффициента вариации качественных параметров, привязываются к «часовкам» внутри смены за счет договорного соглашения.
На основе классификации источников цифровых данных горно-технической системы по признаку объекта их получения определим, чем является массив горных пород с точки зрения «данных» и что на это влияет [4]. Качественные показатели минерального сырья в массиве связаны с [10-12]:
- геологической структурой (распределение сырья может зависеть от структуры месторождения, включая особенности образования и морфологии рудных тел, а также складки, разломы и другие элементы);
- петрографическим составом (качество сырья может изменяться в зависимости от характера взаиморасположения породообразующих и сопутствующих минералов, включая характер их преобразования и сростков, определяющий показатели извлечения при обогащении).
Распределение качества минерального сырья в массиве может быть представлено в виде различных моделей, таких как модель случайного распределения (предполагает, что качество сырья распределено случайным образом) и модель зонального распределения (качество сырья распределено зонально с выделением зон, характеризующихся разным качеством минерального сырья). Если в совокупности с моделью распределения учесть еще технологические особенности добычи и транспортирования горной массы, то распределение полезного компонента во времени будет представлять собой не что иное, как аналоговый сигнал с заданной максимальной амплитудой, а в случае зонального распределения и вовсе прогнозируемой амплитудой [13].
Для дискретизации аналогового сигнала в электронике с ХХ в. используют теорему Котельникова, также известную в западных странах под названием «теорема Найквиста – Шеннона», которая гласит, что любой непрерывный сигнал может быть восстановлен из его дискретных отсчетов, если частота дискретизации больше либо равна удвоенной максимальной частоте сигнала, или если требуется передать по каналу связи непрерывный сигнал с ограниченным спектром, то можно не передавать все его значения, а передать лишь мгновенные значения (отсчеты) через интервал [14, 15]. Регистрирующие устройства, как правило, фиксируют конечное число значений, поэтому мы получаем дискретные сигналы [16].
Математически теорему Котельникова можно записать следующим образом:
где f (t) – исходный сигнал; f (nT) – дискретные отсчеты сигнала; T – период дискретизации; sinc(x) – функция sinc (синусоидальная функция, нормализованная на единицу).
Применим теорему Котельникова к данным, формируемым при управлении горно-технической системой. Если надо передать некий сигнал, который возникает на этапе каждого из технологических процессов (буровзрывные работы, экскавация и транспортирование, складирование и обогащение твердых полезных ископаемых), не обязательно собирать и передавать все сигналы целиком. Можно передавать их мгновенные импульсы, опираясь на теорему Котельникова.
В методике по апробированию теоремы Котельникова использовались синтетические данные – объект, гибко изменяющийся в объемах по заранее выверенным закономерностям на основе обученной модели машинного обучения. Модель обучалась на реальных данных с датчиков автоматизированных систем двухмесячного объема, в частном случае применен алгоритм кластеризации k-means.
Разработанная методика состоит из этапов:
- генерация статистического распределения, имитирующая распределение качественных показателей полезного ископаемого в массиве;
- моделирование процессов буровзрывных работ, экскавации и транспортирования горной массы (для открытых горных работ);
- моделирование разгрузки автосамсвалов на породный склад или в бункер;
- моделирование работы ленточного конвейера с функционированием проборазделочной машины.
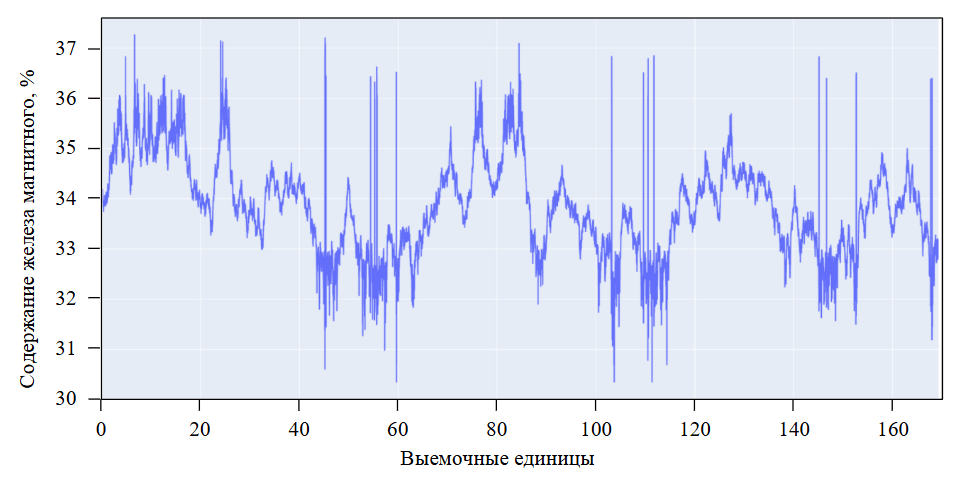
Рис.1. Первоначальное сгенерированное распределение качественных характеристик в объеме горных пород
Согласно методике, исследования имеют непосредственную связь с физическими процессами движения рудопотока горно-технической системы.
В качестве инструментов для работы с массивами данных в исследовании применены – библиотека NumPy для анализа и обработки сигналов, включая фильтрацию и преобразование Фурье; функция fftfreq библиотеки, которая возвращает массив частот, соответствующих индексам массива, полученного в результате применения быстрого преобразования Фурье [17].
В качестве основы создания алгоритма генерации статистического распределения качественных показателей полезного ископаемого в массиве взята референсная выборка из автоматизированной системы диспетчеризации за 2 мес. деятельности железорудного предприятия, ведущего добычу открытым способом [18-20]. В результате получено распределение (рис.1) качественных показателей полезного ископаемого в массиве горных пород для объема 17 тыс. экскаваторных ковшей [21, 22].
Полученное распределение разнесено по скважинам выемочных блоков случайным образом в соответствии с моделью зонального распределения [23]. Таким образом удалось определить множество блоков, имеющих отличное друг от друга качество с выдержанной зональностью внутри. Иными словами, один выемочный блок не мог иметь близрасположенные скважины с отличием по качеству более, чем на шаг в 10 ковшей (влево или вправо), соответствуя распределению (рис.1). Удалось сымитировать процесс, когда каждый загружаемый самосвал имеет выдержанное значение качественного параметра в кузове при выполнении процессов 1 и 2, согласно технологической цепочке горно-промышленных предприятий доставки руды с учетом качества (рис.2) [24-27]. Процессы 3 и 4 имитировались достаточно просто, поскольку являются линейными, за исключением этапа усреднения, где весь складируемый объем перемешивается из-за технологических особенностей горных предприятий в виде погрузки фронтальным погрузчиком или экскаватором [28, 29].
Для анализа данных проведем эксперимент, который включает несколько сценариев:
- Теорема Котельникова применена к первоначальному распределению (рис.1), где выемочной единицей является ковш экскаватора, т.е. допускается, что существует техническая возможность фиксирования на этапе 4 (рис.2) качества потока с дискретностью, равной каждому отгруженному ковшу. При этом сценарии не учитывается процесс усреднения, тем самым имитируется идеальный процесс добычи и транспортирования горной массы, состоящий из этапов 1, 2 и 4 (рис.2).
- Теорема Котельникова применена к средневзвешенному усредненному значению первоначального распределения, величина усреднения – кузов самосвала. При сценарии условно зафиксирована грузоподъемность самосвала в 7 ковшей с усреднением в данном объеме. На этапе 4 дискретность фиксации качества изменяется согласно объему усреднения – один самосвал или средневзвешенное на 14 ковшей. Итоговый сценарий, аналогично сценарию 1, состоит из этапов 1, 2 и 4 (рис.2).
- Теорема Котельникова применена к средневзвешенному усредненному значению первоначального распределения, величина усреднения – 3 кузова самосвала или 42 ковша. В данном случае производится имитация разгрузки самосвалов в приемный бункер при циклично-поточном способе транспортирования. Теорема применяется на этапе 4 транспортирования конвейером после питателя приемного бункера (рис.2).
- Теорема Котельникова применена к средневзвешенному усредненному значению первоначального распределения, величина усреднения – перегрузочный склад. При этом сценарии объем усреднения составил 10 самосвалов или 140 ковшей экскаватора, что имитирует небольшую секцию перегрузочного пункта. Теорема применяется аналогично предыдущим сценариям, фиксируемый объем – секция склада, а схема состоит из всех четырех этапов.
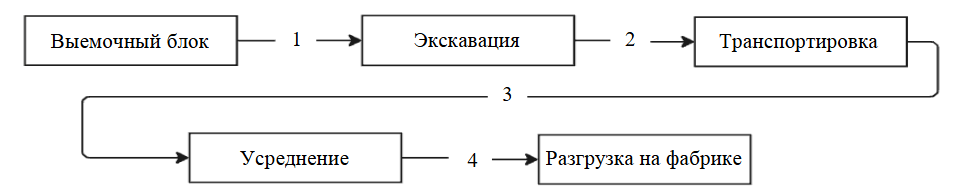
Рис.2. Общая имитируемая цепочка доставки руды с учетом качества
Стоит отметить, что усреднение большего объема для последующих сценариев не имеет значения, поскольку большинство современных горнодобывающих предприятий эксплуатирует автоматизированные системы диспетчеризации, которые позволяют делить склады большого объема на секции, производя районирование склада по качественному признаку. К тому же местом для восстановления исходного распределения до его дискретных отсчетов является ленточный конвейер, представляющий собой фрагментацию минерального сырья, привезенного автосамосвалом определенного объема. Основная задача всех сценариев – сравнить исходное качественное распределение с вновь полученным по теореме Котельникова и сделать для различных случаев выводы о применимости теоремы.
Перед началом эксперимента было принято решение проанализировать работу теоремы Котельникова на изменении величины распределения полезного ископаемого в массиве горных пород. Из референсной выборки данных, полученных с действующего железорудного месторождения, установлено, что коэффициент качественного распределения полезного ископаемого составляет 498 у.е. (spread = 498). В дальнейшем на основе выборки сгенерировано исходное распределение на spread = 1000 и 2000, имитирующее сложноструктурные, нарушенные блоки. Таким образом, эта часть эксперимента проводилась без учета технологии доставки горной массы, а теорема Котельникова применена в классическом виде – для воспроизведения исходного сигнала.
В качестве метрики, показывающей соответствие исходного распределения полученному по теореме, используется критерий согласия Колмогорова. Метод широко применяется на практике, поскольку предназначен для проверки гипотезы о принадлежности выборки некоторому закону распределения, т.е. для проверки соответствия эмпирического распределения предполагаемой модели.
Обсуждение результатов
На рис.3 показаны результаты восстановления исходного распределения в соответствии с описанной методикой (этап 1) для различного значения исходного распределения качества – 498, 1000 и 2000.
Результат работы теоремы Котельникова для применения в идеальных условиях горного предприятия вполне приемлем, поскольку удалось достаточно точно восстановить исходные распределения, оценочные коэффициенты показаны в табл.1.
Интерпретируя полученный результат, можно сделать ожидаемый вывод – чем выше исходное распределение, тем ниже должен быть интервал дискретизации. Для spread = 498 интервал должен составлять 104,95 с, т.е. при подобном распределении необходимо фиксировать каждый 105-й ковш для достижения сходимости, когда KS Statistic приближается к нулю, а P-value к единице. Для spread = 1000 и 2000 необходимо фиксировать каждый 43-й и 19-й ковш.
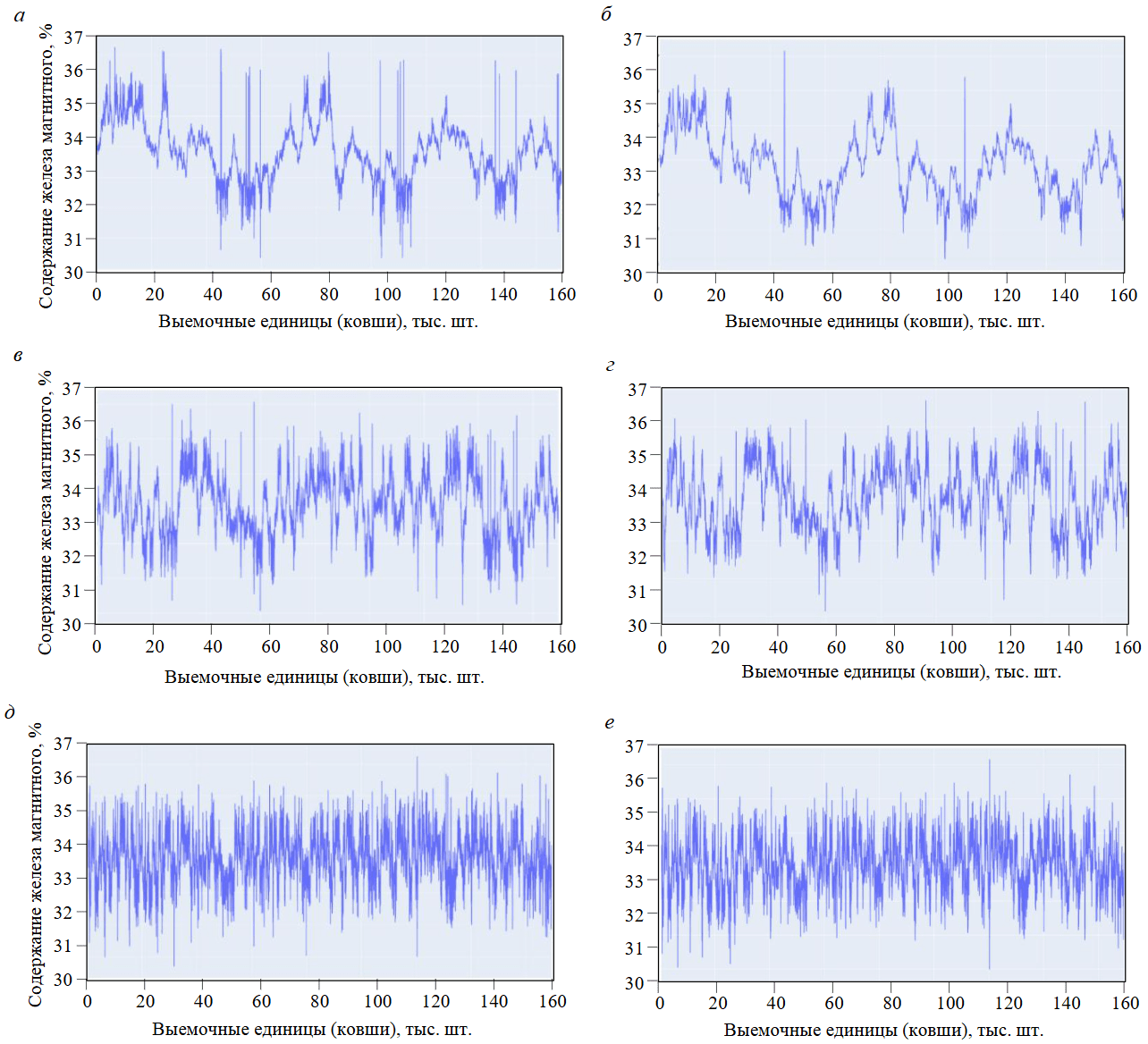
Рис.3. Исходные (а, в, д) и восстановленные по теореме Котельникова (б, г, е) распределения для spread = 498, 1000 и 2000
Таблица 1
Качество повторения исходного распределения на основе теоремы Котельникова для изменяющегося распределения
|
Распределение (spread) |
Тест Колмогорова – Смирнова |
Интервал дискретизации, с |
|
|
KS Statistic |
P-value |
||
|
498 |
0,0055 |
0,9999 |
104,950 |
|
1000 |
0,0076 |
0,9768 |
43,256 |
|
2000 |
0,0029 |
0,9999 |
19,329 |
Однако рассмотренная идеальная ситуация недостижима в условиях реального производства, поскольку существует множество ограничений и неопределенностей, одной из которых является усреднение полезного ископаемого в кузове самосвала и на перегрузочных усреднительных складах. Для оценки степени влияния объема усреднения на работу теоремы Котельникова смоделированы ситуации, где при транспортировании горной массы производится усреднение перевозимого сырья в объеме 1, 3 и 10 самосвалов (рис.4).
Исходя из рис.4, можно прийти к выводу, что чем выше объем усреднения, там хуже работает теорема Котельникова для воспроизведения исходного распределения. Например, в случае с усреднением в перегрузочном пункте (рис.4, д, е) теорема лишь определяет тренд [29]. Для повторения исходного распределения требуется более массивная выборка, о чем говорит табл.2.
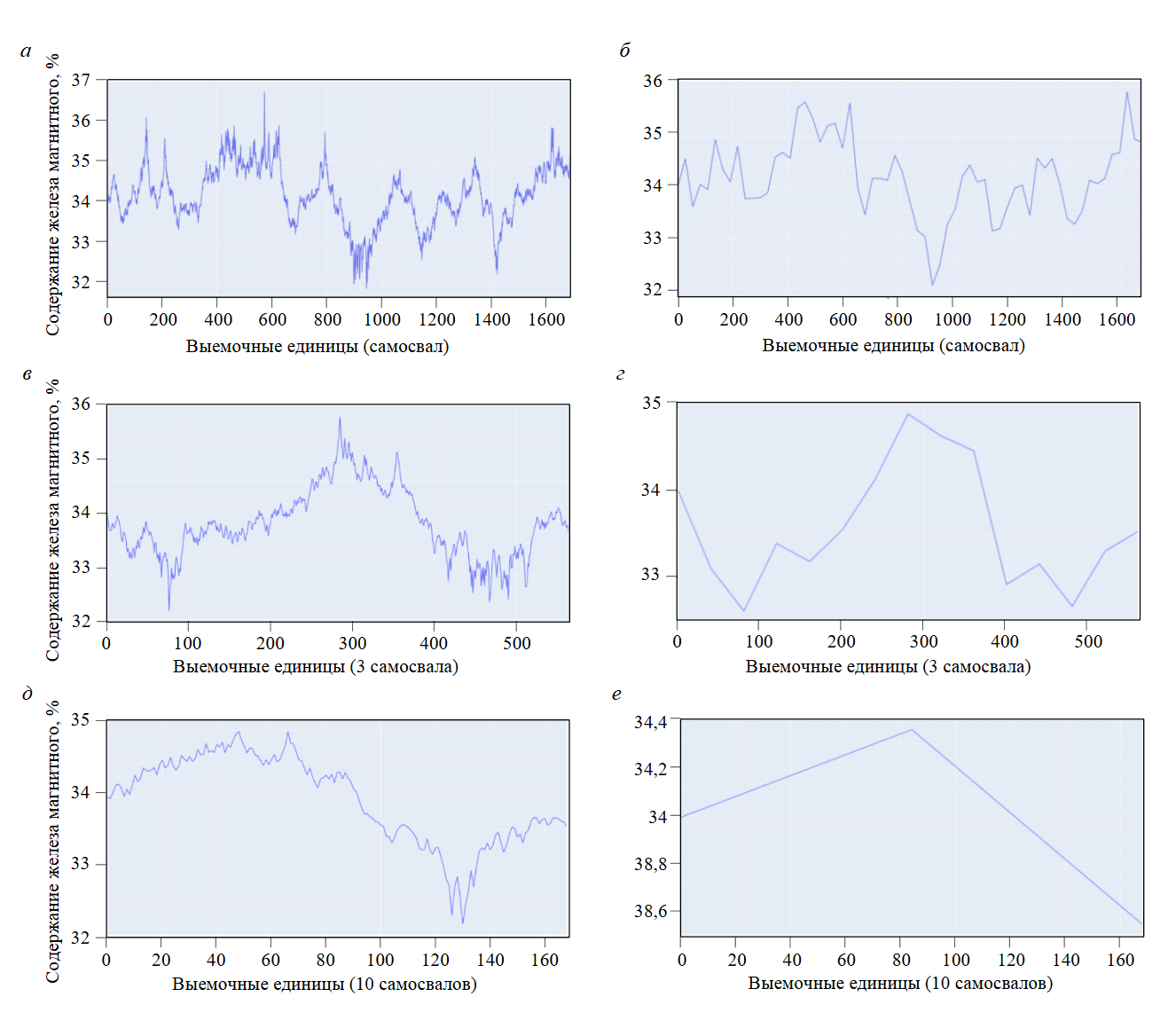
Рис.4. Исходные (а, в, д) и восстановленные по теореме Котельникова (б, г, е) распределения для объемов усреднения 1, 3 и 10 самосвалов
Таблица 2
Качество повторения исходного распределения на основе теоремы Котельникова для изменяющегося усреднения
|
Объем усреднения |
Тест Колмогорова – Смирнова |
Интервал дискретизации, с |
|
|
KS Statistic |
P-value |
||
|
1 самосвал |
0,0697 |
0,9092 |
27,323 |
|
3 самосвала |
0,1383 |
0,9064 |
40,286 |
|
10 самосвалов |
0,3669 |
0,6945 |
84,500 |
Из сравнения (табл.2) видно, что для случаев, когда мы рассматриваем фиксированный объем (блок, забой и др.), не всегда и не для любого объема усреднения возможно применить теорему Котельникова, что наиболее наглядно демонстрирует усреднение в 10 самосвалах. При этом качество воспроизведения исходного распределения весьма низкое [6].
Полученные результаты показывают, что применение теоремы Котельникова без глубокой оценки качества минерально-сырьевой базы нецелесообразно. Для обучения модели и построения качественных прогнозов качества добываемого сырья требуется большой объем статистических данных, которые необходимо собирать с горно-технической системы за счет внедрения цифровых решений [30, 31]. Новые ИТ-инструменты в области подходов к архивации данных и их быстрому восстановлению значительно снижают требования к носителям данных, что в свою очередь снижает стоимость хранения большого объема информации для последующего анализа.
Для оценки влияния характеристик полезного ископаемого на количество необходимых данных проведены сравнительные эксперименты, которые показывают, как spread влияет на интервал дискретизации и какой объем данных необходимо собрать для KS Statistic при разных схемах усреднения. Для эксперимента размер KS Statistic взят равным 0,07 как показатель сильно изменяющегося распределения (см. рис.3). При этом KS Statistic может быть абсолютно любым и зависит от условий и требований горного предприятия. Например, на показатель в разной степени будут влиять: грузоподъемность и количество самосвалов, производительность горно-технического комплекса, способ доставки минерального сырья, распределение полезных ископаемых в массиве, структура выемочных блоков, технологическая схема работы обогатительной фабрики и т.д. На рис.5 показано изменение частоты дискретизации от изменения параметра spread.
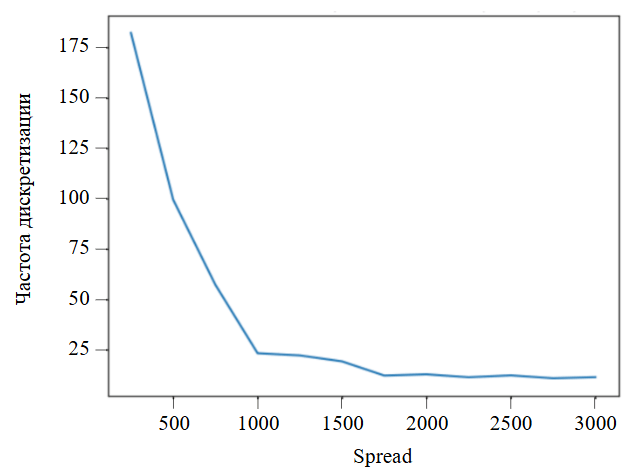
Рис.5. Зависимость частоты дискретизации от изменения параметра spread
Как видно на рис.5, чем выше spread, тем ниже должна быть частота, причем после spread = 1700 частота выходит на плато и не снижается. Это говорит о сниженной весовой характеристике каждого следующего фиксируемого значения при высоком spread, поэтому из-за снижения частоты дискретизации тренд графика менее подвержен резким изменениям.
Чтобы определить объем данных для разных схем усреднения, необходимый для достижения KS Statistic = 0,07, произведено построение графиков при усреднении в 10 и 100 самосвалах. Такая разница необходима для наглядной демонстрации влияния объема усреднения на необходимый объем исходных данных.
На рис.6 показано, что, несмотря на значительные объемы усреднения, всегда можно найти необходимый минимальный объем исходных данных, чтобы обучить модель. Так, для достижения KS Statistic = 0,07 при усреднении в объеме 10 автосамосвалов необходимо 50820 ковшей экскаватора, а для объема в 100 самосвалов – 203280 ковшей. Это эквивалентно 4,5 и 18 мес. работы предприятия (из расчета работы одного экскаватора) для каждого типа участка карьера с точки зрения распределения качества в массиве горных пород.
Однако стоит учитывать, что полученные цифры справедливы лишь для исходной выборки, которая показана на рис.6. Любое изменение исходных данных в корне может изменить картину, которая показана на рис.7.
Для получения качественной модели по теореме Котельникова при технологической цепочке доставки горной массы, например с усреднением в объеме 100 самосвалов, необходим размер статистики работы от 0,17 до 0,6 млн ковшей или от 16 до 52 мес. непрерывной работы экскаватора [32-34]. Такой разброс в значительной степени зависит от значения коэффициента качественного распределения полезного ископаемого.
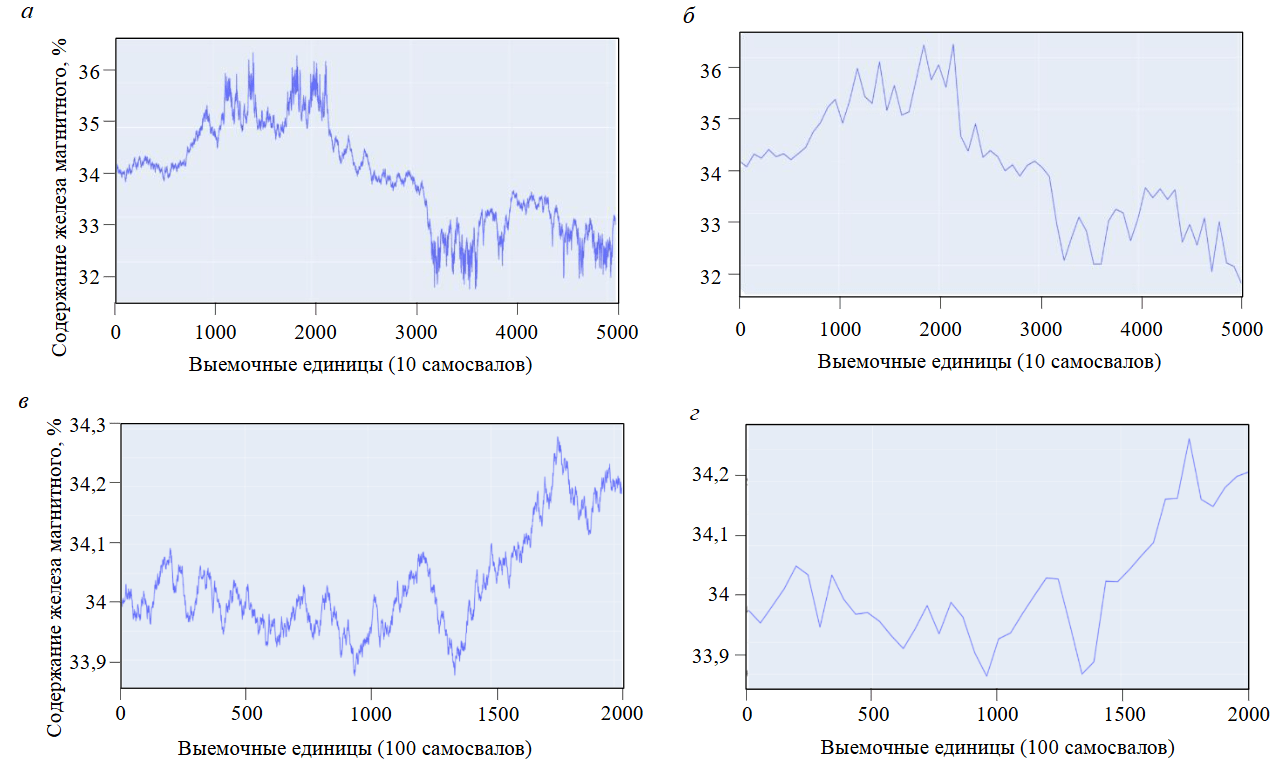
Рис.6. Исходные (а, в) и восстановленные по теореме Котельникова (б, г) распределения для объемов усреднения 10 и 100 самосвалов при KS Statistic = 0,07
Заключение
На основе проведенного по указанной методике исследования установлено, что теорему Котельникова можно применять для определения минимального размера партии транспортируемого минерального сырья с учетом производительности технологического оборудования – дискретности фиксации качественных параметров в процессе транспортирования горной массы. Также важным результатом применения теоремы Котельникова является обоснование минимально необходимого объема данных, которые описывают каждый из технологических процессов горно-технической системы. На основе этой информации можно однозначно определить необходимую частоту сбора данных для различных процессов при внедрении систем автоматизации.
Установлено, что минимальный объем данных и частота их фиксации, усреднения зависят от распределения качества минерального сырья в исходном природном массиве, структурных особенностей блоков, а также требований, предъявляемых к готовой продукции.
Фиксация и сбор данных должны выполняться для каждого технологического процесса согласно частоте видоизменения структурных свойств минерального сырья в его границах. Например, для этапа складирования горной массы фиксация качественных и количественных показателей должна осуществляться в момент отгрузки или наполнения склада.
Литература
- Каплунов Д.Р. Теоретические основы проектирования освоения недр: становление и развитие // Горный журнал. 2014. № 7. С. 49-51.
- Туртыгина Н.А., Мирошникова Л.К., Волков Н.А., Карпенко И.О. Перспективный метод прогнозирования и поиска сформировавшихся норильских месторождений с целью управления качеством добытых руд // Горный информационно-аналитический бюллетень. 2016. № 2. С. 313-319.
- Каплунов Д.Р., Рыльникова М.В., Юн А.Б., Терентьева И.В. Становление нового технологического уклада комплексного освоения недр при истощении балансовых запасов месторождений // Горный журнал. 2019. № 4. С. 11-14. DOI: 10.17580/gzh.2019.04.02
- Barnewold L., Lottermoser B.G. Identification of digital technologies and digitalisation trends in the mining industry // International Journal of Mining Science and Technology. 2020. Vol. 30. Iss. 6. P. 747-757. DOI: 10.1016/j.ijmst.2020.07.003
- Рыльникова М.В., Владимиров Д.Я., Пыталев И.А., Попова Т.М. Роботизированные геотехнологии как путь повышения эффективности и экологизации освоения недр // Физико-технические проблемы разработки полезных ископаемых. 2017. № 1. С. 92-101.
- Захаров В.Н., Каплунов Д.Р., Клебанов Д.А., Радченко Д.Н. Методические подходы к стандартизации сбора, хранения и анализа данных при управлении горнотехническими системами // Горный журнал. 2022. № 12. С. 55-61. DOI: 10.17580/gzh.2022.12.10
- Ломоносов Г.Г. Улучшение качества продукции горнодобывающего производства как фактор повышения эффективности российского горно-перерабатывающего комплекса // Рациональное освоение недр. 2015. № 2. С. 51-61.
- Sony M., Antony J., Douglas J.A. Essential ingredients for the implementation of Quality 4.0: A narrative review of literature and future directions for research // The TQM Journal. 2020. Vol. 32. Iss. 4. P. 779-793. DOI: 10.1108/TQM-12-2019-0275
- Zhang Qi, Jiao ShouTao, Lu XinXiang. Discussion on causality and correlation in geological research // Acta Petrologica Sinica. 2018. Vol. 34. № 2. P. 275-280.
- Туртыгина Н.А., Охрименко А.В., Ковальчук А.А., Калашников К.А. Планирование горных работ как организационный способ управления качеством минерального сырья в рудничной системе // Горный информационно-аналитический бюллетень. 2018. Спец. вып. 17. С. 3-11. DOI: 10.25018/0236-1493-2018-5-17-3-11
- Кантемиров В.Д., Яковлев А.М., Титов Р.С., Тимохин А.В. Совершенствование методов рудоподготовки минерального сырья при освоении сложноструктурных месторождений // Горная промышленность. 2022. № 1S. С. 63-70. DOI: 10.30686/1609-9192-2022-1S-63-70
- Ruihan Zhao, Liang Luo, Pengzhong Li, Jinguang Wang. An industrial heterogeneous data based quality management KPI visualization system for product quality control // Assembly Automation. 2022. Vol. 42. Iss. 6. P. 796-808. DOI: 10.1108/AA-05-2022-0139
- Roberts F.S., Sheremet I.A. Resilience in the Digital Age. Springer, 2021. 199 p. DOI: 10.1007/978-3-030-70370-7
- Xianming Liu, Guangyue Han. Information-Theoretic Extensions of the Shannon-Nyquist Sampling Theorem. ArXiv, 2018. 30 p. (Preprint). DOI: 10.48550/arXiv.1810.08089
- Юдин С.В. Теорема Котельникова и периодичность отбора выборок для карт Шухарта // Известия Тульского государственного университета. Технические науки. 2020. Вып. 10. С. 116-120.
- Zhexuan Zeng, Jun Liu, Ye Yuan. A Generalized Nyquist-Shannon Sampling Theorem Using the Koopman Operator // IEEE Transactions on Signal Processing. 2024. Vol. 72. P. 3595-3610. DOI: 10.1109/TSP.2024.3436610
- Шамбина C.В., Шамбин А.И. Научное программирование в Python // Труды ФОРА. 2023. № 28. С. 42-52.
- Ческидов В.В., Маневич А.И., Липина А.В. Получение и анализ больших данных в практике мониторинга состояния горнотехнических сооружений // Горная промышленность. 2019. № 2 (144). С. 86-88. DOI: 10.30686/1609-9192-2019-2-144-86-88
- Рыльникова М.В., Клебанов Д.А., Князькин Е.А. Анализ данных как основа повышения эффективности работы горнотранспортного оборудования при ведении открытых горных работ // Горная промышленность. 2023. № 1. С. 52-56. DOI: 10.30686/1609-9192-2023-1-52-56
- Куприянов В.В. Современные вопросы управления на основе системного подхода и теории информации // Горный информационно-аналитический бюллетень. 2014. № 2. С. 273-280.
- Ле Д.Х., Темкин И.О., До Т.Л., Агабубаев А.Т. Оптимизация управления режимами пуска скребкового конвейера на основе анализа результатов имитационного моделирования // Прикаспийский журнал: управление и высокие технологии. 2020. № 2 (50). С. 10-21. DOI: 10.21672/2074-1707.2020.50.2.010-021
- Туртыгина Н.А., Охрименко А.В., Цыганкова Д.Н. Систематизация факторов, влияющих на стабильность качества рудопотока // Научный вестник Арктики. 2022. № 13. С. 5-14. DOI: 10.52978/25421220_2022_13_5-14
- Швабенланд Е.Е., Лаптева М.И. Принципы управления качеством минерального сырья при комбинированной разработке сложноструктурных месторождений // Известия Тульского государственного университета. Науки о Земле. 2021. Вып. 3. С. 326-335. DOI: 10.46689/2218-5194-2021-3-1-320-329
- Рыльникова М.В., Власов А.В., Макеев М.А. Обоснование условий применения автоматизированных систем управления открытыми горными работами строительства комплекса циклично-поточной геотехнологии в карьере с помощью имитационного моделирования // Горная промышленность. 2021. № 4. С. 106-112. DOI: 10.30686/1609-9192-2021-4-106-112
- Teng Long, Zhangbing Zhou, Gerhard Hancke et al. A Review of Artificial Intelligence Technologies in Mineral Identification: Classification and Visualization // Journal of Sensor and Actuator Networks. 2022. Vol. 11. Iss. 3. № 50. DOI: 10.3390/jsan11030050
- Deryabin S.A., Temkin I.O., Zykov S.V. About some issues of developing Digital Twins for the intelligent process control in quarries // Procedia Computer Science. 2020. Vol. 176. P. 3210-3216. DOI: 10.1016/j.procs.2020.09.128
- Upadhyay S.P., Askari-Nasab H. Simulation and optimization approach for uncertainty-based short-term planning in open pit mines // International Journal of Mining Science and Technology. 2018. Vol. 28. Iss. 2. P. 153-166. DOI: 10.1016/j.ijmst.2017.12.003
- Wengang Zhang, Jianye Ching, Goh A.T.C., Leung A.Y.F. Big data and machine learning in geoscience and geoengineering: Introduction // Geoscience Frontiers. 2021. Vol. 12. Iss. 1. P. 327-329. DOI: 10.1016/j.gsf.2020.05.006
- Erkayaoglu M., Dessureault S. Improving mine-to-mill by data warehousing and data mining // International Journal of Mining, Reclamation and Environment. 2019. Vol. 33. Iss. 6. P. 409-424. DOI: 10.1080/17480930.2018.1496885
- Павлишина Д.Н., Шумилов П.А., Терещенко С.В. Разработка инструмента формирования эффективных технологических схем стабилизации качества рудопотока // Проблемы недропользования. 2017. № 1 (12). С. 48-54. DOI: 10.18454/2313-1586.2017.01.048
- Рыльникова М.В., Цупкина М.В., Кирков А.Е. Технологии сбора и обработки больших данных – основа повышения достоверности первичной информации о массивах горных пород при освоении месторождений полезных ископаемых и техногенных образований // Известия Тульского государственного университета. Науки о Земле. 2023. Вып. 1. С. 308-327. DOI: 10.46689/2218-5194-2023-1-1-308-327
- Chong-chong Qi. Big data management in the mining industry // International Journal of Minerals, Metallurgy and Materials. 2020. Vol. 27. Iss. 2. P. 131-139. DOI: 10.1007/s12613-019-1937-z
- Hui Yang, Yamei Luo, Xiaolei Ren et al. Risk Prediction of Diabetes: Big data mining with fusion of multifarious physical examination indicators // Information Fusion. 2021. Vol. 75. P. 140-149. DOI: 10.1016/j.inffus.2021.02.015
- Yijiu Zhao, Houjun Wang, Yanze Zheng et al. High sampling rate or high resolution in a sub-Nyquist sampling system // Measurement. 2020. Vol. 166. № 108175. DOI: 10.1016/j.measurement.2020.108175
