Моделирование напряженно-деформированного состояния блочного горного массива рудных месторождений при отработке системами разработки с обрушением
- 1 — д-р техн. наук заведующий кафедрой Санкт-Петербургский горный университет ▪ Orcid ▪ Elibrary ▪ Scopus
- 2 — канд. техн. наук доцент Санкт-Петербургский горный университет ▪ Orcid ▪ Elibrary
- 3 — аспирант Санкт-Петербургский горный университет ▪ Orcid
Аннотация
Статья посвящена анализу подходов к моделированию напряженно-деформированного состояния блочного горного массива в окрестности одиночной горной выработки и в зоне влияния породной консоли при разработке апатит-нефелиновых месторождений Хибин. Произведен анализ существующих в международной инженерной практике представлений о тектонических нарушениях как о геомеханическом элементе и опыта прогнозирования напряженно-деформированного состояния блочного горного массива. На основании анализа выполнена постановка базовых задач моделирования и приведены его основные результаты. Выработаны методологические рекомендации по решению аналогичных задач.
Финансирование
Работа выполнена при финансовой поддержке гранта Российского научного фонда (проект № 23-17-00144)
Введение
Мировой опыт разработки месторождений полезных ископаемых и строительства подземных горных выработок показывает, что определяющими устойчивость массива факторами являются параметры структурной нарушенности горного массива, его прочностные и деформационные свойства и параметры действующего в нем поля напряжений. Соотношения между количественными показателями указанных факторов определяют механизм деформирования системы отдельных блоков и характер потери ее устойчивости в целом. Самые распространенные на сегодняшний день методики прогноза устойчивости подземных горных выработок в явном виде не учитывают эти процессы и поэтому в отдельных случаях могут оказаться недостоверными. Существующий опыт предлагает применение рейтинговых подходов, которые в наибольшей мере учитывают описанные механизмы, но все классификации массива по трещиноватости и основанные на них методы оценки устойчивости (Дир, Бенявский, Лобшир, Хоек, Браун, Мэтьюз, Потвин, Бартон, Мавдесли) – это продукты статистической обработки данных об устойчивости породных обнажений горных выработок в различных горно-геологических условиях. В частных условиях разработки рудных месторождений могут возникать ситуации, когда эти методы не позволяют достоверно оценить и спрогнозировать устойчивость выработок и камер. На практике это приводит либо к завышению условий устойчивости, вследствие чего появляется необходимость постоянных перекреплений горных выработок и ликвидации различного рода аварий, либо к занижению условий устойчивости и, следовательно, к перерасходу материалов на крепление. В связи с этим актуальнейшим вопросом, стоящим перед фундаментальной геомеханикой, является формулирование методологии прогноза процессов, протекающих в трещиноватых горных массивах на разных масштабных уровнях.
Анализ состояния вопроса учета структурной нарушенности горного массива при выполнении обоснования параметров систем разработки рудных месторождений и существующих подходов к его решению позволяет выделить две основных группы методов – прямые и косвенные [1]. Прямые методы основаны на непосредственном использовании результатов лабораторных исследований фрагментов горного массива и натурных экспериментов, выполняемых в условиях шахт и рудников [2-4]. Косвенные методы базируются на применении моделей реального трещиноватого горного массива, построенных на некоторых изначальных предположениях о механическом поведении такого массива. Эти методы можно разделить на аналитические [5], эмпирические [6-8] и численные [9, 10]. Выбор методов учета структурной нарушенности горного массива в условиях конкретной геомеханической задачи обуславливается их достоинствами и недостатками [11, 12].
При определении деформационных и прочностных свойств горных пород в лабораторных условиях испытаниям подвергаются образцы, преимущественно полученные из керна [13, 14]. При таких испытаниях интегрально учитывается только структурная нарушенность с характерными размерами менее образца, что недостаточно для полноценного описания реального горного массива, так как он включает в себя иерархическую систему трещин и нарушений, в том числе с характерными размерами больше размеров породного образца [15, 16]. В качестве обоснованного дополнения к лабораторным исследованиям на образцах может выступать физическое моделирование структурно нарушенного горного массива с применением эквивалентных материалов, базирующееся на теории подобия [17]. Такой подход при корректной постановке задачи позволяет воспроизвести механизм деформирования и разрушения структурно нарушенного горного массива.
В практике проектирования геотехнических систем в качестве основного инженерного решения оценки структурной нарушенности горного массива выступают эмпирические методы [18, 19]. Они являются отражением накопленного опыта строительства подземных объектов в разных горнотехнических условиях в горных массивах с различной структурной нарушенностью [20-22]. Их широкая распространенность обуславливается возможностью количественного определения эквивалентных деформационных и прочностных свойств структурно нарушенного горного массива путем корректировки результатов лабораторных испытаний образцов горных пород на основании качественных оценок структурной нарушенности. Такая взаимосвязь свойств реализуется посредством эмпирически установленных закономерностей и, как правило, опирается на рейтинговые классификации массива горных пород [23-25]. Следует отметить, что за удобством применения эмпирических методов кроется очевидная привязанность используемых зависимостей деформационных и прочностных свойств в образце и в массиве к локализации места их установления [26, 27]. Вопрос корректности экстраполяции таких зависимостей на иные горные массивы может быть разрешен только после начала подземного строительства [28]. Использование представления структурно нарушенного горного массива в виде некоторой сплошной среды с эквивалентными прочностными и деформационными свойствами является существенным упрощением реального механизма его деформирования и разрушения.
В современных условиях для решения задач настоящей статьи применяются численные методы моделирования горного массива с трещиноватостью [29], основанные на положениях механики дискретных сред. Численное моделирование позволяет создавать цифровые двойники реальных структурно нарушенных горных массивов и при относительно малых затратах времени и труда осуществлять многовариантные эксперименты для оценки влияния структурной нарушенности на устойчивость геомеханических объектов. Очевидной проблемой такого подхода является то, что достоверность получаемых геомеханических оценок будет привязана к тому, насколько точно были определены исходные данные и граничные условия.
Развитие численных методов для решения задач прогноза напряженно-деформированного состояния трещиноватого горного массива требует разделить эту комплексную задачу на ряд более простых различных масштабных уровней. В этом случае решение задачи сводится к последовательному движению в массиве горных пород от мелкомасштабных задач (регионального уровня) в размерах целых месторождений полезных ископаемых или более мелких к более крупномасштабным в рамках повышения детализации отдельных расчетных областей внутри региональной модели. Очевидно, что в рамки такой последовательности хорошо вписывается известный метод субмоделирования [30, 31]. Настоящая публикация посвящена моделированию напряженно-деформированного состояния блочного горного массива в окрестности одиночных горных выработок и в зоне влияния породной консоли при разработке крутопадающих месторождений полезных ископаемых системами разработки с обрушением.
Постановка задач моделирования
Для анализа влияния способа задания тектонических нарушений на напряженно-деформированное состояние горного массива и на горные выработки было проведено многовариантное численное моделирование методом конечных элементов. Задача реализована в плоскодеформационной постановке.
Реализованы расчетные схемы двух видов:
- количество систем трещин n= 1, угол падения a = 60°, расстояние между нарушениями L = 200; 350; 500 м;
- количество систем трещин n= 2, углы падения a1 = 60° и a2 = 30°, расстояние между нарушениями L = 350 м.
Основной особенностью моделирования была реализация тектонических нарушений тремя разными способами: 1) неоднородность в рамках модели механики сплошной среды; 2) жесткий контакт трения; 3) когезионный контакт.
В первом способе тектоническое нарушение задавалось слоями: нарушенные породы – разрушенные породы – нарушенные породы с толщиной каждого слоя 5 м. Второй способ основан на задании попарных поверхностей контакта, соответствующих поверхностям нарушения; использован жесткий контакт с коэффициентом трения 0,4. Третий способ подразумевал создание на этапе разбиения сетки конечных элементов в зоне разлома прослойки когезионных элементов. Когезионная зона представляет собой слой конечной толщины, соответствующий мощности разрушенных пород 5 м. Такая зона служит для моделирования сцепления между поверхностями нарушения, при этом реализует возможность смещения двух поверхностей разлома без накопления значительных растягивающих напряжений.
Уровень напряжений в целиках между подготовительными выработками подконсольного пространства зависит от следующих горно-геологических условий: физико-механические свойства горного массива, геометрические параметры рудного тела, особенности распределения естественных напряжений, параметры очистных работ (глубина разработки, удаленность фронта работ, величины защитных углов). Защитные углы определяют величину опережения ведения работ на вышележащих горизонтах по отношению к нижележащим и зависят от прочностных свойств пород и параметров начального поля напряжений. В этой части исследования была предпринята попытка установить характер влияния на уровень напряженности массива в подконсольном пространстве глубины ведения работ.
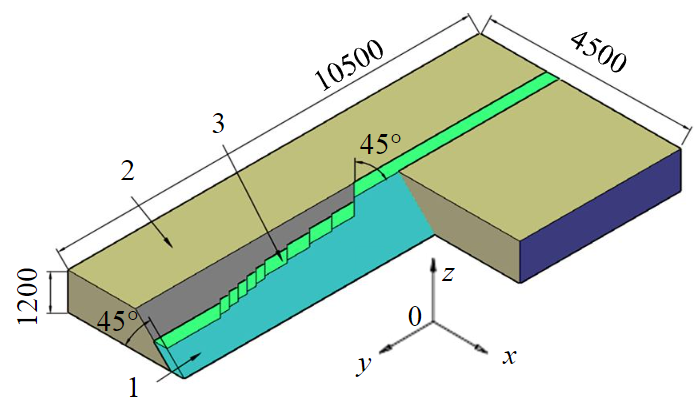
Рис.1. Геометрия пространственной численной модели для моделирования НДС в зоне влияния породной консоли 1 – рудное тело; 2 – вмещающий массив; 3 – моделируемые шаги отработки
Для решения задачи прогноза напряженно-деформированного состояния горного массива в зоне влияния породной консоли в программном комплексе Simulia Abaqus была разработана пространственная численная модель (рис.1). Для реализации многовариантного моделирования геометрия модели разрабатывалась идеализированной на основании месторождений Кукисвумчорр и Юкспор [32, 33]. Таким образом, истинная мощность рудного тела принята равной 200 м, угол падения – 45°. Отметка поверхности модели соответствует абсолютной отметке поверхности месторождения Кукисвумчорр +500 м. Для исключения влияния торцевого эффекта по оси 0y модель имеет буферные участки горного массива.
Расчетные шаги реализуются как последовательная ступенчатая выемка рудного тела. При этом извлекаемый фрагмент модели представляет собой четырехугольную призму. Форма призмы определяется в первую очередь отметкой горизонта, а во вторую – защитными углами отработки в горизонтальной плоскости. Отметки горизонтов модели приняты соответствующими реальным горизонтам месторождения Кукисвумчорр (+314, +296, +263, +236, +209, +183, +158, +133, +108, +75 м), а защитный угол соответствует среднему рекомендуемому значению для месторождений Кукисвумчорр и Юкспор и составляет 45°.
Размер шагов отработки принят переменным и увеличивается по направлению отработки. Длина шага отработки составляет 25; 50; 200; 500; 1000 м. Размер отрабатываемой части составляет 5475 м, а количество таких участков – 21.
Граничные условия модели реализованы следующим образом. На всех гранях модели за исключением верхней наложены запреты на перемещения по направлению нормалей. Поле напряжений модели генерировалось на основании данных о распределении компонент поля естественных напряжений на месторождении Кукисвумчорр и реализовано с кусочно-линейной зависимостью горизонтальных компонент напряжений от вертикальных для учета переменного коэффициента бокового распора.
Физико-механические свойства горного массива приняты соответствующими усредненным физико-механическим свойствам горных пород, характерных для горно-геологических условий апатит-нефелиновых месторождений Хибин, и представлены в табл.1. Для определения физико-механических свойств горного массива на участках тектонических нарушений авторами были использованы рекомендации монографии [34]. Параметры поля начальных напряжений приняты согласно табл.2.
Таблица 1
Физико-механические свойства массива
|
Материал |
Удельный вес, МН/м3 |
Коэффициент Пуассона |
Модуль упругости, МПа |
|
Вмещающие породы и руда |
0,028 |
0,25 |
16200 |
|
Разрушенный массив |
0,018 |
0,23 |
6350 |
|
Нарушенный массив |
0,018 |
0,023 |
635 |
Таблица 2
Параметры поля начальных напряжений
|
Абсолютная отметка, м |
Отметка модели, м |
Вертикальные напряжения sy, МПа |
Горизонтальные напряжения sx, МПа |
|
Горизонтальные напряжения sz, МПа |
|
|
+500 |
+1000 |
5,6 |
12,3 |
2,2 |
15,9 |
2,8 |
|
0 |
+500 |
19,6 |
43,1 |
48,6 |
||
|
–500 |
0 |
33,6 |
73,9 |
83,3 |
Результаты моделирования
Некоторые представительные результаты многовариантного численного моделирования формирования естественного напряженно-деформированного состояния горного массива блочной структуры и его перераспределения в окрестности одиночной горной выработки в постановке плоской деформации приведены на рис.2.
Результаты моделирования формирования напряженного состояния подконсольной области горного массива представлены в виде выявленных закономерностей распределения напряжений на отметке горных выработок в подконсольном пространстве (рис.3). Фактором, в наибольшей степени влияющим на напряженное состояние массива, является глубина ведения работ. Данные представлены для случая полного раскрытия текущего и вышележащего горизонтов.
Анализ и обсуждение результатов. Анализ полученных результатов численного моделирования формирования естественного напряженно-деформированного состояния горного массива блочной структуры и его перераспределения в окрестности одиночной горной выработки позволяет сделать следующие выводы. Модели неоднородности механики сплошной среды и когезионного контакта показывают идентичные результаты как при единственном тектоническом нарушении, так и при их системе. Модель твердого контакта трения в каждом случае дает несколько завышенные напряжения.
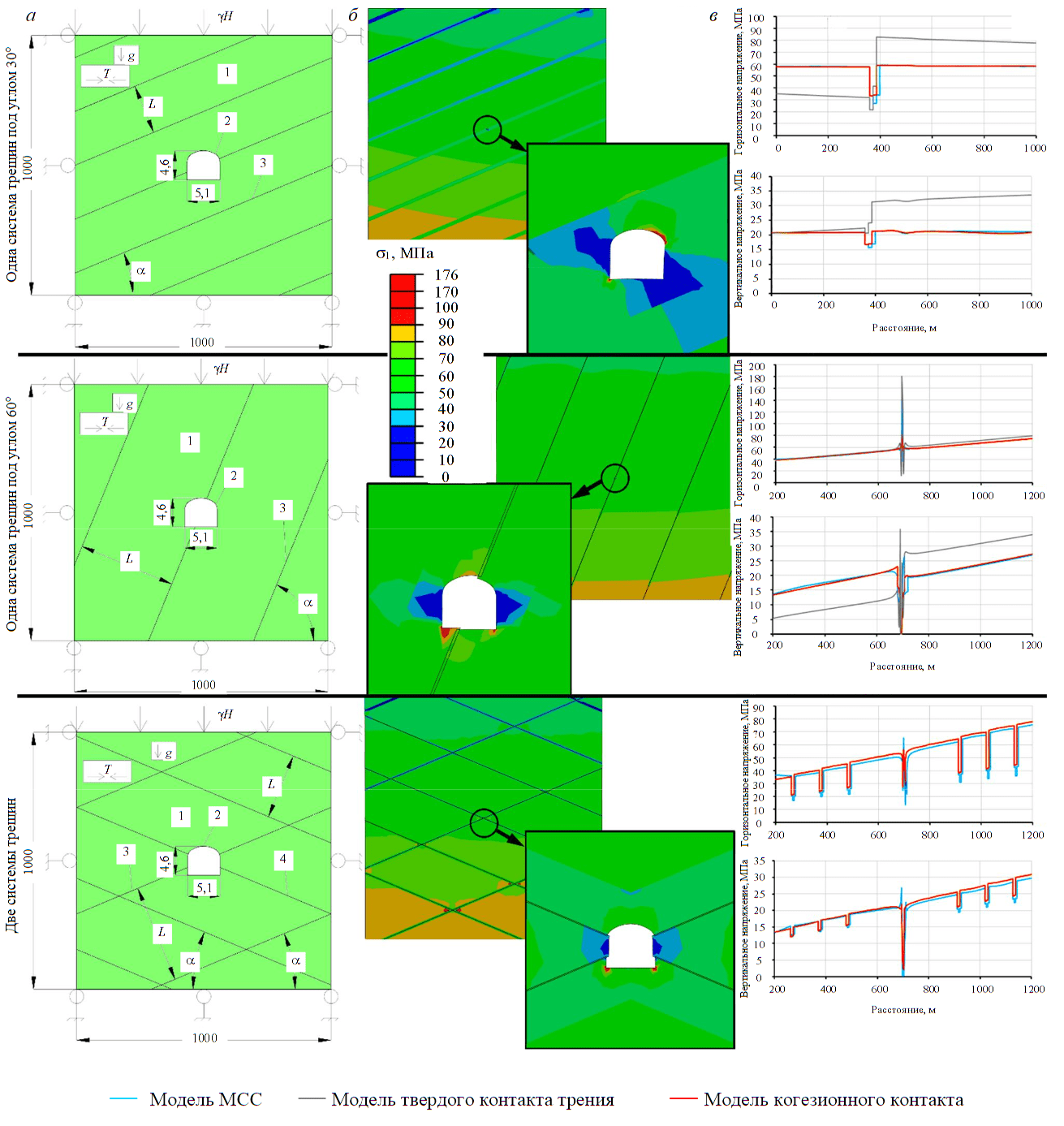
Рис.2. Расчетные схемы и основные результаты расчетов в постановке плоской деформации: а – расчетная схема; б – эпюра распределения главных напряжений; в – графики горизонтальных и вертикальных напряжений; L – расстояние между нарушениями в системе; a – угол падения нарушения 1 – массив горной породы; 2 – контур горной выработки; 3 – система тектонических нарушений № 1; 4 – система тектонических нарушений № 2
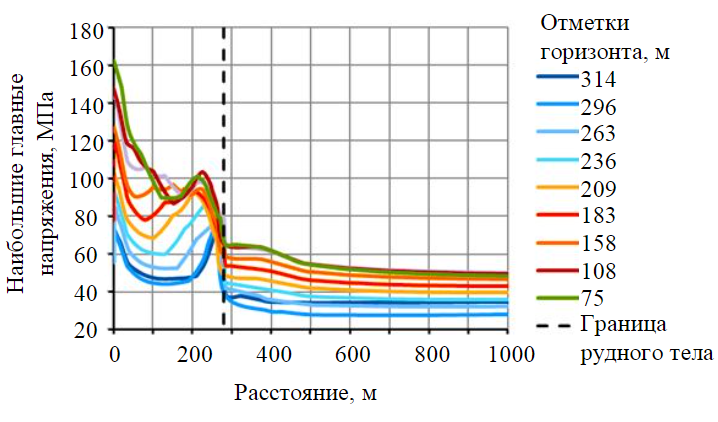
Рис.3. Кривые распределения наибольших главных напряжений в подконсольном пространстве при различной глубине ведения работ
Моделирование жесткого контакта трения оказывает влияние на напряженное состояние в окрестности тектонического нарушения, но размеры зоны такого влияния меньше, а растягивающих напряжений ввиду возможности сдвижения блоков не возникает. Однако такое сдвижение при достижении напряжениями прочности на сдвиг будет мгновенным, без возможности проникновения пород, слагающих контактные поверхности, друг в друга. В характерных точках выработки значения тангенциальных напряжений ниже, но в массиве в целом будут наблюдаться более высокие напряжения, чем при задании нарушений другими способами.
Наиболее подходящим для моделирования тектонических нарушений сдвижения представляется задание тектонического нарушения с помощью когезионных элементов, создающих слой конечной толщины с заданными физико-механическими свойствами. Уровень тангенциальных напряжений в пиковых точках превышает уровень начальных напряжений в два-три раза, что соответствует натурным данным. Такой способ моделирования тектонического нарушения показывает соответствие между уровнями напряжения при пересечении выработки одним нарушением вне зависимости от общего количества систем таких нарушений в массиве. Кроме того, когезионный контакт хорошо показывает себя при оценке совместного влияния нескольких разнонаправленных нарушений, пересекающихся с выработкой в одном месте.
Анализ полученных результатов численного моделирования формирования напряженного состояния подконсольной области горного массива позволяет сделать следующие выводы.
Распределение кривых по уровню напряжений соответствует распределению самих горизонтов по глубине. Зона опорного давления составляет порядка 100-120 м, далее уровень напряжений становится фоновым. Характер поведения кривых как в подконсольном пространстве (0-280 м), так и во вмещающем массиве одинаков. Поэтому для дальнейших исследований будет целесообразно аппроксимировать данные на участке, соответствующем расположению подготовительных выработок и целиков между ними.
Внешний вид кривых на обозначенном участке имеет полиномиальный вид. Была предпринята попытка описать их полиномиальными функциями второй степени вида , где – наибольшие главные напряжения, МПа; – расстояние, м; – коэффициенты квадратного уравнения (табл.3).
Таблица 3
Значения коэффициентов аппроксимации
|
Горизонт, м |
A |
B |
C |
Горизонт, м |
A |
B |
C |
|
314 |
0,0016 |
–0,4328 |
+72,534 |
183 |
0,0022 |
–0,5018 |
+110,06 |
|
296 |
0,0018 |
–0,4560 |
+70,32 |
158 |
0,0012 |
–0,3531 |
+116,59 |
|
263 |
0,0015 |
–0,4054 |
+79,493 |
133 |
0,0008 |
–0,3143 |
+124,83 |
|
236 |
0,0018 |
–0,4351 |
+86,862 |
108 |
0,0017 |
–0,5733 |
+139,66 |
|
209 |
0,0026 |
–0,5392 |
+97,771 |
75 |
0,0030 |
–0,9365 |
+162,27 |
На основании данных табл.3 можно определить зависимость наибольших главных напряжений от абсолютной отметки и положения точки измерения относительно подготовительного горизонта:
где – абсолютная отметка горизонта, м; – расстояние от проекции нижней границы рудного тела (лежачий бок), м.
В целом по месторождению Кукисвумчорр следует отметить гораздо большую неравномерность распределения напряжений в рудном теле по сравнению с месторождением Юкспор. Это можно объяснить большей неправильностью геометрии самого рудного тела, наличием участка выхода рудного тела на земную поверхность, значительными перепадами рельефа в зоне расположения рудного тела месторождения Кукисвумчорр, а также наличием в нем большего количества тектонических нарушений.
Наличие выхода на поверхность рудного тела вносит значительный вклад в формирование его напряженного состояния. В блоках рудного тела, которые имеют выход на поверхность, средний уровень напряжений выше по сравнению с блоками, не имеющими такого выхода. Это связано с тем, что топография земной поверхности, заложенная в конечно-элементную модель, имеет впадины, ориентированные наибольшим линейным размером перпендикулярно направлению действия наибольших гравитационно-тектонических естественных горизонтальных напряжений, и выступает их геометрическим концентратором.
Заключение
Авторами была предпринята попытка сформулировать основные положения методики численного моделирования напряженно-деформированного состояния блочных горных массивов при разработке наклонных и крутопадающих месторождений полезных ископаемых системами разработки с обрушением в окрестности одиночных горных выработок и в зоне влияния породной консоли. Основные положения методики являются результатом критического анализа информации, содержащейся в научных и нормативных источниках, а также многовариантного моделирования.
Моделирование в мелком масштабе не является конечной целью, анализ его результатов позволяет выявлять в блочном горном массиве месторождений наиболее высоконапряженные и опасные участки, в результате чего становится возможным корректно прогнозировать критическую глубину их удароопасности, а также заблаговременно планировать мероприятия по разгрузке горного массива, тем самым повысив безопасность горных работ.
Перспективным для дальнейших исследований в направлении моделирования напряженного состояния горного массива представляется изучение вопросов, связанных с использованием выходных данных численного моделирования в региональном масштабе в качестве исходных данных для выполнения численного моделирования блочного горного массива на более крупном масштабе, учитывающем наличие в нем трещин и нарушений более мелких размеров (т.е. с учетом иерархической структуры нарушений и трещин) с применением методики субмоделирования. Для изучения геомеханических процессов в горном массиве в зоне влияния породной консоли перспективным представляется установление влияния удаления фронта работ от исследуемой области, а также частичного и полного раскрытия вышележащего горизонта на напряженное состояние массива в подконсольном пространстве.
Литература
- Khani A., Baghbanan A., Norouzi S., Hashemolhosseini H. Effects of fracture geometry and stress on the strength of a fractured rock mass // International Journal of Rock Mechanics & Mining Sciences. 2013. Vol. 60. P. 345-352. DOI: 10.1016/j.ijrmms.2013.01.011
- Qibin Lin, Ping Cao, Jingjing Meng et al. Strength and failure characteristics of jointed rock mass with double circular holes under uniaxial compression: Insights from discrete element method modeling // Theoretical and Applied Fracture Mechanics. 2020. Vol. 109. № 102692. DOI: 10.1016/j.tafmec.2020.102692
- Peitao Wang, Meifeng Cai, Fenhua Ren. Anisotropy and directionality of tensile behaviors of a jointed rock mass subjected to numerical Brazilian tests // Tunnelling and Underground Space Technology. 2018. Vol. 73. P. 139-153. DOI: 10.1016/j.tust.2017.12.018
- Сохраби А., Надими А., Таловина И.В., Сафаи Х. Модель структуры и тектоническая эволюция системы разломов в южной части региона Хур, Центральный Иран // Записки Горного института. 2019. Т. 236. С. 142-152. DOI: 10.31897/PMI.2019.2.142
- Peitao Wang, Fenhua Ren, Shengjun Miao et al. Evaluation of the anisotropy and directionality of a jointed rock mass under numerical direct shear tests // Engineering Geology. 2017. Vol. 225. P. 29-41. DOI: 10.1016/j.enggeo.2017.03.004
- Hoek E., Carter T.G., Diederichs M.S. Quantification of the Geological Strength Index Chart // 47th US Rock Mechanics/Geomechanics Symposium, 23-26 June 2013, San Francisco, USA. OnePetro, 2013. 9 p. № ARMA-2013-672.
- Özkan I., Erdem B., Ceylanoğlu A. Characterization of jointed rock masses for geotechnical classifications utilized in mine shaft stability analyses // International Journal of Rock Mechanics and Mining Sciences. 2015. Vol. 73. P. 28-41. DOI: 10.1016/j.ijrmms.2014.10.001
- Meda A., Rinaldi Z., Spagnuolo S. et al. Hybrid precast tunnel segments in fiber reinforced concrete with glass fiber reinforced bars // Tunnelling and Underground Space Technology. 2019. Vol. 86. P. 100-112. DOI: 10.1016/j.tust.2019.01.016
- Peitao Wang, Fenhua Ren, Shengjun Miao et al. Evaluation of the anisotropy and directionality of a jointed rock mass under numerical direct shear tests // Engineering Geology. 2017. Vol. 225. P. 29-41. DOI: 10.1016/j.enggeo.2017.03.004
- Yang Jian Ping, Chen Wei Zhong, Yang Dian Sen, Yuan Jing Qiang. Numerical determination of strength and deformability of fractured rock mass by FEM modeling // Computers and Geotechnics. 2015. Vol. 64. P. 20-31. DOI: 10.1016/j.compgeo.2014.10.011
- Esfahani M.H., Hejazi F., Vaghei R. et al. Simplified Damage Plasticity Model for Concrete // Structural Engineering International. 2017. Vol. 27. Iss. 1. P. 68-78. DOI: 10.2749/101686616X1081
- Ivars D.M., Pierce M.E., Darcel C. et al. The synthetic rock mass approach for jointed rock mass modelling // International Journal of Rock Mechanics and Mining Sciences. 2011. Vol. 48. Iss. 2. P. 219-244. DOI: 10.1016/j.ijrmms.2010.11.014
- Козловский Е.Я., Журавков М.А. Определение и верификация параметров расчетной модели соляных пород с учетом разупрочнения и ползучести // Записки Горного института. 2021. Т. 247. С. 33-38. DOI: 10.31897/PMI.2021.1.4
- Myung Sagong, Duhee Park, Jaeho Yoo, Jun S. Lee. Experimental and numerical analyses of an opening in a jointed rock mass under biaxial compression // International Journal of Rock Mechanics and Mining Sciences. 2011. Vol. 48. Iss. 7. P. 1055-67. DOI: 10.1016/j.ijrmms.2011.09.001
- Kuranov A.D., Zuev B.Y., Istomin R.S. The forecast deformations of the ground surface during mining under protected objects // Innovation-Based Development of the Mineral Resources Sector: Challenges and Prospects. CRC Press, 2018. P. 39-50.
- Coli N., Berry P., Boldini D. In situ non-conventional shear tests for the mechanical characterization of a bimrock // International Journal of Rock Mechanics and Mining Sciences. 2011. № 48. Iss. 1. P. 95-102. DOI: 10.1016/j.ijrmms.2010.09.012
- Зуев Б.Ю. Методология моделирования нелинейных геомеханических процессов в блочных и слоистых горных массивах на моделях из эквивалентных материалов // Записки Горного института. 2021. Т. 250. С. 542-552. DOI: 10.31897/PMI.2021.4.7
- Qing-Xiang Meng, Huan-Ling Wang, Wei-Ya Xu, Yu-Long Chen. Numerical homogenization study on the effects of columnar jointed structure on the mechanical properties of rock mass // International Journal of Rock Mechanics and Mining Sciences. 2019. Vol. 124. № 104127. DOI: 10.1016/j.ijrmms.2019.104127
- Yingjie Xia, Chuanqing Zhang, Hui Zhou et al. Mechanical behavior of structurally reconstructed irregular columnar jointed rock mass using 3D printing // Engineering Geology. 2020. Vol. 268. № 105509. DOI: 10.1016/j.enggeo.2020.105509
- Subash Bastola, Ming Cai. Investigation of mechanical properties of jointed granite under compression using lattice-spring-based synthetic rock mass modeling approach // International Journal of Rock Mechanics and Mining Sciences. 2020. Vol. 126. № 104191. DOI: 10.1016/j.ijrmms.2019.104191
- Козырев А.А., Савченко С.Н., Панин В.И. и др. Геомеханические процессы в геологической среде горнотехнических систем и управление геодинамическими рисками. Апатиты: Кольский научный центр РАН, 2019. 431 с. DOI: 10.37614/978.5.91137.391.7
- Куранов А.Д. Применение численного моделирования для выбора безопасных параметров систем разработки рудных месторождений в высоконапряженных массивах // Записки Горного института. 2013. T. 206. C. 60-64.
- Protosenya A.G., Karasev M.A., Verbilo P.E. Research of the mechanical characteristics' anisotropy of apatite-nepheline ores block rock mass // International Journal of Mechanical Engineering and Technology. 2018. Vol. 9. № 11. P. 1962-1972.
- Verbilo P.E., Karasev M.A., Belyakov N.A., Iovlev G.A. Experimental and numerical research of jointed rock mass anisotropy in a three-dimensional stress field // Rudarsko-geološko-naftni zbornik. 2022. Vol. 37. № 2. P. 109-122. DOI: 10.17794/rgn.2022.2.10
- Козырев А.А., Панин В.И., Семенова И.Э. и др. Геомеханическое обеспечение технических решений при ведении горных работ в высконапряженных массивах // Физико-технические проблемы разработки полезных ископаемых. 2012. № 2. С. 46-55.
- Shabarov A.N., Kuranov A.D., Kiselev V.A. Assessing the zones of tectonic fault influence on dynamic rock pressure manifestation at Khibiny deposits of apatite-nepheline ores // Eurasian Mining. 2021. № 2. P. 3-7.
- Sánchez-Martín J., Galindo R., Arévalo C. et al. Optimized Design of Earth Dams: Analysis of Zoning and Heterogeneous Material in Its Core // Sustainability. 2020. Vol. 12. № 6667. DOI: 10.3390/su12166667
- Protosenya A.G., Vilner M.A. Assessment of excavation intersections’ stability in jointed rock masses using the discontinuum approach // Rudarsko-geološko-naftni zbornik. 2022. Vol. 37. № 2. P. 137-147. DOI: 10.17794/rgn.2022.2.12
- Mirenkov V.E. Deformation of Rock Mass in the Vicinity of Underground Opening at Great Depth // Journal of Mining Science. 2021. Vol. 57. Iss. 3. P. 380-385. DOI: 10.1134/S1062739121030030
- Chenyang Zhao, Lavasan A.A., Schanz T. Application of Submodeling Technique in Numerical Modeling of Mechanized Tunnel Excavation // International Journal of Civil Engineering. 2018. Vol. 17. Iss. 1. P. 75-89. DOI: 10.1007/s40999-018-0318-8
- Майборода-Хидирова Л.Р. Использование субмоделирования для численного решения задач геомеханики на разных масштабных уровнях // Проблемы разработки месторождений углеводородных и рудных полезных ископаемых. 2021. Т. 2. С. 60-65.
- Козырев А.А., Панин В.И., Семенова И.Э., Рыбин В.В. Геомеханическое обеспечение горных работ на горнодобывающих предприятиях Мурманской области // Горный журнал. 2019. № 6. С. 45-50. DOI: 10.17580/gzh.2019.06.05
- Козырев А.А., Панин В.И., Семенова И.Э. Опыт применения экспертных систем оценки напряженно-деформированного состояния массива горных пород для выбора безопасных способов отработки рудных месторождений // Записки Горного института. 2012. № 198. С.16-23.
- Кочарян Г.Г. Геомеханика разломов. М.: ГЕОС, 2016. 424 с.
