Modelling of the stress-strain state of block rock mass of ore deposits during development by caving mining systems
- 1 — Ph.D., Dr.Sci. Head of Department Saint Petersburg Mining University ▪ Orcid ▪ Elibrary ▪ Scopus
- 2 — Ph.D. Associate Professor Saint Petersburg Mining University ▪ Orcid ▪ Elibrary
- 3 — Postgraduate Student Saint Petersburg Mining University ▪ Orcid
Abstract
The article is devoted to the analysis of approaches to modeling the stress-strain state of a block rock mass in the vicinity of a single mine workings and in the area of rock cantilever influence during the development of the Khibiny apatite-nepheline deposits. The analysis of the existing in international engineering practice ideas about tectonic disturbances as a geomechanical element and the experience of predicting the stress-strain state of a block rock mass was carried out. On the basis of the analysis, the formulation of the basic modeling tasks is carried out and its main results are presented. Methodological recommendations for solving similar problems were developed.
Funding
The research was supported by a grant from the Russian Science Foundation (project N 23-17-00144)
Introduction
World experience in the development of mineral deposits and in the construction of underground mine workings shows that the factors determining the stability of the mass are the parameters of the structural disturbance of the rock mass, its strength and deformation properties, and the parameters of the in-situ stress field. The ratios between the quantitative indicators of these factors determine the mechanism of deformation of the system of individual blocks and the nature of the stability loss. The currently most common methods for predicting the stability of underground mine excavations do not explicitly take into account these processes and, therefore, in some cases may turn out to be unreliable. Existing experience suggests the use of rating approaches that take into account the described mechanisms to the greatest extent, but all classifications of the mass by fracturing and the stability assessment methods based on them (Dir, Benyavsky, Lobshir, Hoek, Brown, Matthews, Potwin, Barton, Mavdesli) are products of statistical processing of data on the stability of rock outcrops of mine workings in various mining and geological conditions. In the particular conditions of the development of ore deposits, situations may arise when these methods do not allow one to reliably assess and predict the stability of mine workings and chambers. In practice, this leads either to an overestimation of the stability conditions, as a result of which there is a need for constant reinforcing of mine workings and the elimination of various kinds of accidents, or to an underestimation of the stability conditions and, consequently, to an excessive consumption of materials for fastening. In this regard, the most urgent issue facing fundamental geomechanics is the formulation of a methodology for predicting processes occurring in fractured rock masses at different scale levels.
The analysis of the state of the issue of taking into account the structural disturbance of the rock mass when performing the justification of the parameters of the systems for the development of ore deposits and the existing approaches to its solution allows us to distinguish two main groups of methods – direct and indirect [1]. Direct methods are based on the direct use of the results of laboratory studies of rock mass fragments and field experiments performed in mines [2-4]. Indirect methods are based on the use of models of a real fractured rock mass built on some initial assumptions about the mechanical behavior of such a mass. These methods can be divided into analytical [5], empirical [6-8], and numerical [9, 10]. The choice of methods for taking into account the structural disturbance of the rock mass in the conditions of a specific geomechanical problem is determined by their advantages and disadvantages [11, 12].
When determining the deformation and strength properties of rocks in laboratory conditions, the samples mainly obtained from the core are tested [13, 14]. In such tests, only structural disturbance with characteristic dimensions less than the sample is integrally taken into account, which is not enough for a complete description of a real rock mass, since it includes a hierarchical system of cracks and disturbances, including those with characteristic dimensions larger than the rock mass sample [15, 16]. As a reasonable addition to laboratory studies on samples, physical modeling of a structurally disturbed rock mass using equivalent materials, based on the theory of similarity, can be used [17]. Such an approach, provided that the problem is correctly formulated, makes it possible to reproduce the mechanism of deformation and destruction of a structurally disturbed rock mass.
In the practice of designing geotechnical systems, empirical methods are used as the main engineering solution for assessing the structural disturbance of a rock mass [18, 19]. They reflect the accumulated experience in the construction of underground facilities in different mining conditions in rock mass with various structural disturbances [20-22]. Their wide distribution is due to the possibility of quantitative determination of the equivalent deformation and strength properties of a structurally disturbed rock mass by adjusting the results of laboratory tests of rock samples based on qualitative assessments of structural disturbance. Such a relationship of properties is realized through empirically established regularities and, as a rule, is based on the rating classifications of a rock mass [23-25]. It should be noted that applying empirical methods is convenient due to the fact that the used dependences of deformation and strength properties in the sample and in the rock mass are obviously attached to the localization of the place of their establishment [26, 27]. The question of the correctness of extrapolation of such dependencies to other rock mass can be resolved only after the start of underground construction [28]. Using the representation of a structurally disturbed rock mass in the form of some continuous medium with equivalent strength and deformation properties is a significant simplification of the real mechanism of its deformation and destruction.
In modern conditions, to solve the problems of this article, numerical methods for modeling a rock mass with fracturing [29], based on the principles of the mechanics of discrete media, are used. Numerical modeling makes it possible to create digital twins of real structurally disturbed rock masses and, with relatively little time and labor, to carry out multivariate experiments to assess the effect of structural disturbance on the stability of geomechanical objects. An obvious problem with this approach is that the reliability of the obtained geomechanical estimates will depend on the accuracy of the determined initial data and boundary conditions.
The development of numerical methods for solving the problems of predicting the stress-strain state of a fractured rock mass requires dividing this complex problem into a number of simpler different scale levels. In this case, the solution of the problem is reduced to sequential movement in the rock mass from small-scale problems (regional level) in the size of whole mineral deposits or smaller ones to larger-scale ones as part of increasing the specification of individual computational areas within the regional model. Obviously, the well-known submodeling method [30, 31] fits well into the framework of such a sequence. This publication is devoted to modeling the stress-strain state of a block rock mass in the vicinity of single mine workings and in the area of rock cantilever influence when developing steeply dipping mineral deposits with caving mining systems.
Statement of modelling problems
To analyze the influence of the method of simulating tectonic disturbances on the stress-strain state of the rock mass and mine workings, multivariate numerical modeling was carried out using the finite element method. The problem is implemented in a plane strain formulation.
Design schemes of two types are implemented:
- number of fracture systems n= 1, dip angle a = 60°, distances between fractures L = 200; 350; 500 м;
- number of fracture systems n= 2, dip angle a1 = 60° and a2 = 30°, distance between fractures L = 350 м.
The main feature of the modeling was the implementation of tectonic disturbances in three different ways: 1) inhomogeneity within the continuum mechanics model; 2) hard friction contact; 3) cohesive contact.
In the first method, the tectonic disturbance was specified in layers: disturbed rocks – destroyed rocks – disturbed rocks with a thickness of each layer of 5 m. The second method is based on specifying paired contact surfaces corresponding to the surfaces of the disturbance; a hard contact with a friction coefficient of 0.4 is used. The third method implied the creation of a layer of cohesive elements at the stage of splitting a mesh of finite elements in the fault zone. The cohesive zone is a layer of finite thickness corresponding to the thickness of the destroyed rocks of 5 m. Such a zone serves to model the adhesion between the surfaces of the disturbance, while realizing the possibility of displacement of two fault surfaces without the accumulation of significant tensile stresses.
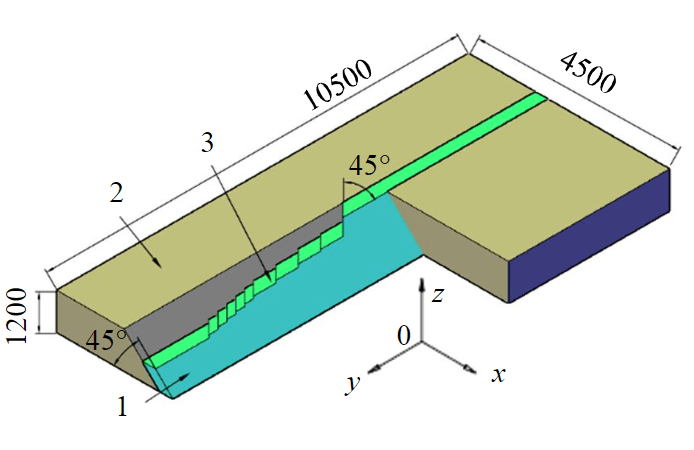
Fig.1. Geometry of 3D numerical model for modeling stress-strain state in the area of rock cantilever influence 1 – ore body; 2 – rock mass; 3 – simulated mining steps
The level of stresses in the pillars between the development workings of the under-cantilever area depends on the following mining and geological conditions: the physical and mechanical properties of the rock mass, the geometric parameters of the ore body, the features of the distribution of initial stresses, the parameters of mining operations (depth of development, remoteness of the work front, protective angles). Protective angles determine the value of advance work on the overlying horizons in relation to the underlying ones and depend on the strength properties of the rocks and the parameters of the initial stress field. In this part of the study, an attempt was made to establish the nature of the influence of the depth of work on the level of tension in the rock mass in the under-cantilever area.
To solve the problem of predicting the stress-strain state of a rock mass in the area of rock cantilever influence, a 3D numerical model was developed in the Simulia Abaqus software (Fig.1). To implement multivariate modeling, the geometry of the model was developed idealized based on the Kukisvumchorr and Yukspor fields [32, 33]. Thus, the true thickness of the ore body is assumed to be 200 m, the dip angle is 45°. The mark of the model surface corresponds to the absolute elevation of the surface of the Kukisvumchorr deposit +500 m. To exclude the influence of the end effect along the 0y axis, the model has buffer sections of the rock mass.
The design steps are implemented as a sequential stepwise excavation of the ore body. In this case, the extracted fragment of the model is a quadrangular prism. The shape of the prism is determined primarily by the horizon mark, and secondly by the protective angles of mining in the horizontal plane. The model horizons correspond to the real horizons of the Kukisvumchorr field (+314, +296, +263, +236, +209, +183, +158, +133, +108, +75 m), and the protective angle corresponds to the average recommended value for the Kukisvumchorr and Yukspor deposits and is 45°.
The size of mining steps is assumed variable and increases in the direction of mining. The length of the working step is 25; 50; 200; 500; 1000 m. The size of the mined part is 5475 m, and the number of such sections is 21.
The boundary conditions of the model are implemented as follows. On all the faces of the model, with the exception of the top one, prohibitions are imposed on movement in the direction of normals. The initial stress field of the model was generated based on data on the distribution of natural stress field components at the Kukisvumchorr field and implemented with a piecewise linear dependence of the horizontal stress components on the vertical ones to take into account the variable lateral thrust coefficient.
The physical and mechanical properties of the rock mass are taken to correspond to the averaged physical and mechanical properties of rocks characteristic of the mining and geological conditions of the Khibiny apatite-nepheline deposits, and are presented in Table 1. To determine the physical and mechanical properties of the rock mass in the areas of tectonic disturbances, the authors used the recommendations of the monograph [34]. The parameters of the initial stress field are taken according to Table 2.
Table 1
Mechanical properties of rock mass
|
Material |
Specific gravity, MN/m3 |
Poisson’s ratio |
Young modulus, MPa |
|
Rock mass and ore |
0.028 |
0.25 |
16200 |
|
Destroyed rock mass |
0.018 |
0.23 |
6350 |
|
Disturbed rock mass |
0.018 |
0.023 |
635 |
Table 2
Initial stress field parameters
|
Absolute mark, m |
Model mark, m |
Vertical stresses sy, MPa |
Horizontal stresses sx, MPa |
|
Horizontal stresses sz, MPa |
|
|
+500 |
+1000 |
5.6 |
12.3 |
2.2 |
15.9 |
2.8 |
|
0 |
+500 |
19.6 |
43.1 |
48.6 |
||
|
–500 |
0 |
33.6 |
73.9 |
83.3 |
Modelling results
Some representative results of multivariant numerical simulation of the formation of the natural stress-strain state of a block-structure rock mass and its redistribution in the vicinity of a single mine working in the formulation of plane strain are shown in Fig.2.
The results of modeling the formation of the stress state of the under-cantilever area of the rock mass are presented in the form of the revealed patterns of stress distribution at the level of mine workings in the under-cantilever area (Fig.3). The depth of work is the factor that most affects the stress state of the rock. The data are presented for the case of full disclosure of the current and overlying horizons.
Analysis and discussion of results. The analysis of the obtained results of numerical modeling of the formation of the natural stress-strain state of a rock mass with a block structure and its redistribution in the vicinity of a single mine working allows us to draw the following conclusions. Models of heterogeneity of continuum mechanics and cohesive contact show identical results both for a single tectonic disturbance and for their system. The model of hard friction contact in each case gives somewhat overestimated stresses.
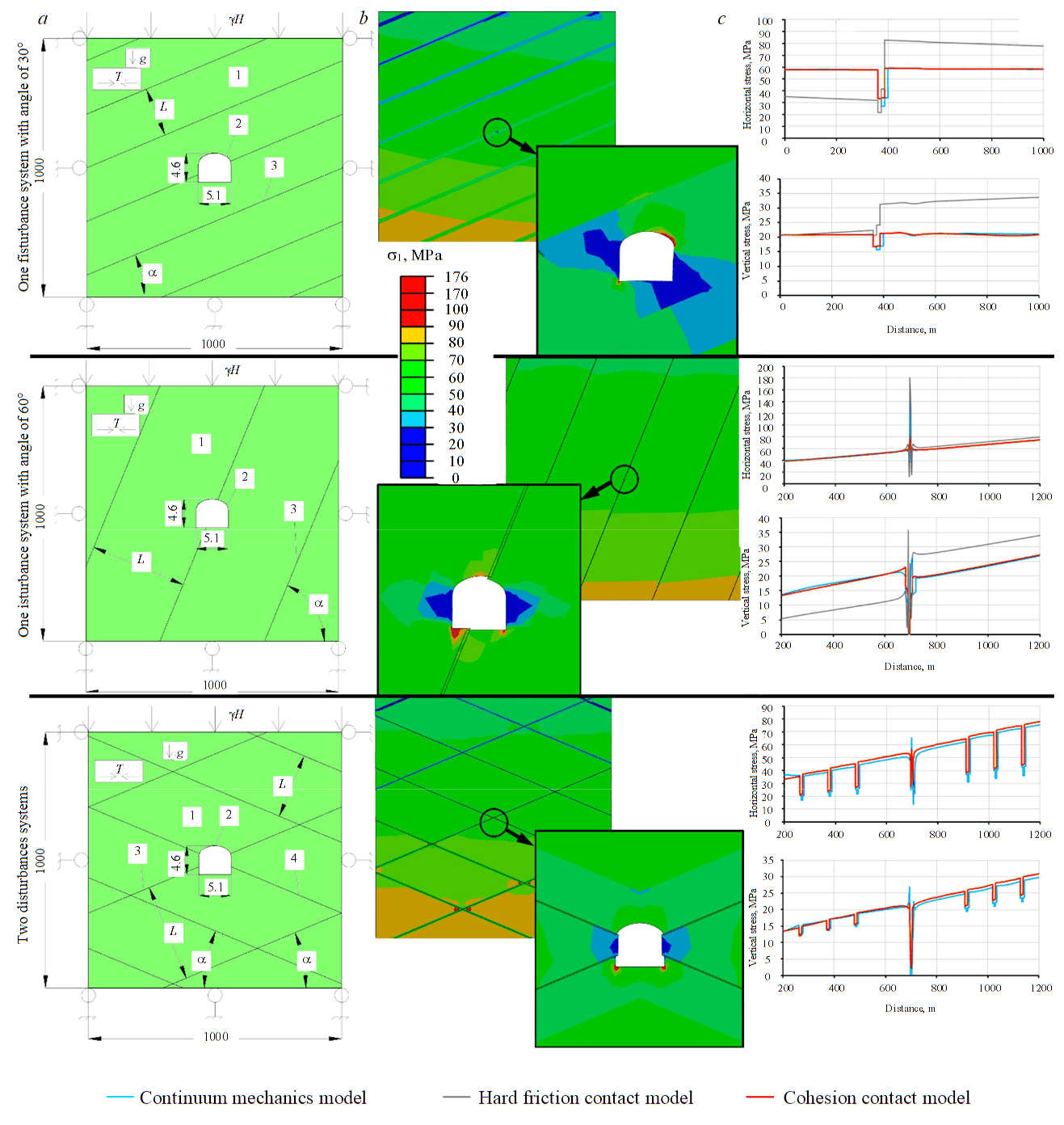
Fig.2. Design schemes and main results of modelling in the statement of plane strain: a – design scheme; b – principal stress distribution diagram; c – diagrams of horizontal and vertical stresses; L – distance between disturbances in the system; a – angle of disturbances 1 – rock mass; 2 – mine excavation; 3 – tectonic disturbances system N 1; 4 – tectonic disturbances system N 2
Modeling a tectonic disturbance in the form of an inhomogeneous medium within the framework of a continuum mechanics model does not allow explicit displacement of rock mass blocks relative to each other. As a result, tensile stresses appear in the block contact area, somewhat distorting the nature of the distribution of the stress field near the tectonic disturbance as a whole. Stress-strain state of a mass with the number of fracture systems n = 2 causes a higher stress level than in the case of n = 1, regardless of how many systems simultaneously intersect in the considered cross section of the working. At the same time, modeling of a tectonic disturbance in the form of an inhomogeneous medium with regard to continuum mechanics is the most efficient in terms of computational time and the most predictable and stable for mechanical behavior.
Modeling of a hard friction contact affects the stress state in the vicinity of a tectonic disturbance, but the size of the area of such influence is smaller, and tensile stresses do not arise due to the possibility of block displacement. However, such a shift, when the stresses reach the shear strength, will be instantaneous, without a possibility of penetration of the rocks that make up the contact surfaces into each other. At the characteristic points of the working, the values of tangential stresses are lower, but the mass as a whole will experience higher stresses than if the disturbances are specified in other ways.
The most suitable for modeling tectonic displacement disturbances is the task of a tectonic disturbance using cohesive elements that create a layer of finite thickness with specified physical and mechanical properties. The level of tangential stresses at peak points exceeds the level of initial stresses by two to three times, which corresponds to field data. This method of modeling a tectonic disturbance shows the correspondence between the stress levels at the intersection of a working with one disturbance, regardless of the total number of systems of such disturbances in the massif. In addition, the cohesive contact shows itself well in assessing the combined effect of several differently directed disturbances intersecting with the working in one place.
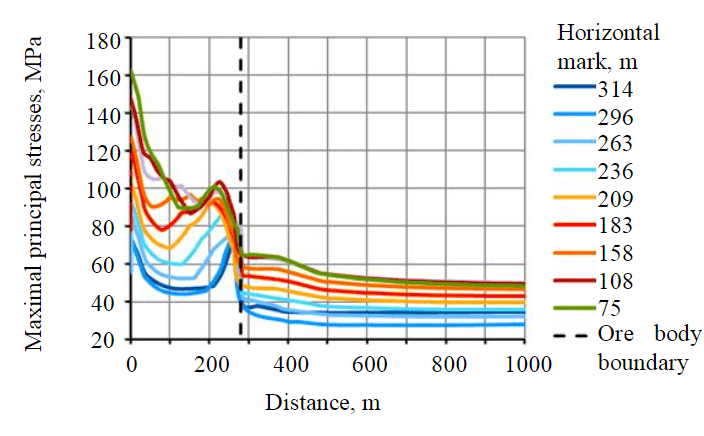
Fig.2. Design schemes and main results of modelling in the statement of plane strain: a – design scheme; b – principal stress distribution diagram; c – diagrams of horizontal and vertical stresses; L – distance between disturbances in the system; a – angle of disturbances 1 – rock mass; 2 – mine excavation; 3 – tectonic disturbances system N 1; 4 – tectonic disturbances system N 2
Analysis of the obtained results of numerical modeling of the formation of the stress state of the under-cantilever area of the rock mass allows us to draw the following conclusions.
The stress level distribution of the curves corresponds to the depth distribution of the horizons. The support pressure area is about 100-120 m, then the stress level becomes equal to the initial stress field. The behavior of the curves both in the under-cantilever space (0-280 m) and in the rock mass is the same. Therefore, for further research, it would be advisable to approximate the data in the area corresponding to the location of the development workings and pillars between them.
The appearance of the curves in the designated area has a polynomial form. An attempt was made to describe them by polynomial functions of the second degree in the form , where are the maximal principal stresses, MPa; – distance, m; are the ratios of the quadratic equation (Table 3).
Table 3
Approximation ratio values
|
Horizon mark, m |
A |
B |
C |
Horizon mark, m |
A |
B |
C |
|
314 |
0.0016 |
–0.4328 |
+72.534 |
183 |
0.0022 |
–0.5018 |
+110.06 |
|
296 |
0.0018 |
–0.4560 |
+70.32 |
158 |
0.0012 |
–0.3531 |
+116.59 |
|
263 |
0.0015 |
–0.4054 |
+79.493 |
133 |
0.0008 |
–0.3143 |
+124.83 |
|
236 |
0.0018 |
–0.4351 |
+86.862 |
108 |
0.0017 |
–0.5733 |
+139.66 |
|
209 |
0.0026 |
–0.5392 |
+97.771 |
75 |
0.0030 |
–0.9365 |
+162.27 |
Based on the data in Table 3, it is possible to determine the dependence of the maximal principal stresses on the absolute mark and the position of the measurement point relative to the preparation horizon:
where – absolute horizon mark, m; – distance from the projection of the lower boundary of the ore body (lying side), m.
In general, for the Kukisvumchorr deposit, it should be noted that the stress distribution in the ore body is much more uneven than for the Yukspor deposit. This can be explained by the greater irregularity of the geometry of the ore body itself, the presence of an outcrop of the ore body on the earth's surface, significant relief differences in the area of the ore body of the Kukisvumchorr deposit, as well as the presence of a large number of tectonic disturbances in it.
The presence of an exit to the surface of the ore body makes a significant contribution to the formation of its stress state. In blocks of the ore body that have an exit to the surface, the average stress level is higher compared to blocks that do not have such an exit. This is due to the fact that the topography of the earth's surface, embedded in the finite element model, has depressions oriented with the largest linear size perpendicular to the direction of action of the largest gravitational-tectonic natural horizontal stresses, and acts as their geometric concentrator.
Conclusion
The authors made an attempt to formulate the main provisions of the methodology for numerical modeling of the stress-strain state of block rock masses in the development of inclined and steeply dipping mineral deposits by mining systems with caving in the vicinity of single mine workings and in the area of influence of the rock cantilever. The main provisions of the methodology are the result of a critical analysis of information contained in scientific and regulatory sources, as well as multivariate modeling.
Modeling on a small scale is not the ultimate goal, the analysis of its results allows identifying the most highly stressed and dangerous areas in the block rock mass of deposits, as a result of which it becomes possible to correctly predict the critical depth of their rockburst hazard, as well as to plan in advance the measures to unload the rock mass thereby increasing the safety of mining operations.
For further research in the direction of modeling the stress state of a rock mass it seems promising to study the issues related to the use of the output data of numerical modeling on a regional scale as input data for numerical modeling of a block rock mass on a larger scale, taking into account the presence of fractures in it and smaller disturbances (i.e. taking into account the hierarchical structure of disturbances and fractures) using the sub-modeling technique. To study the geomechanical processes in the rock mass in the area of influence of the rock cantilever, it seems promising to establish the influence of the removal of the work front from the study area, as well as partial and complete opening of the overlying horizon, on the stress state of the mass in the under-cantilever area.
References
- Khani A., Baghbanan A., Norouzi S., Hashemolhosseini H. Effects of fracture geometry and stress on the strength of a fractured rock mass. International Journal of Rock Mechanics & Mining Sciences. 2013. Vol. 60, p. 345-352. DOI: 10.1016/j.ijrmms.2013.01.011
- Qibin Lin, Ping Cao, Jingjing Meng et al. Strength and failure characteristics of jointed rock mass with double circular holes under uniaxial compression: Insights from discrete element method modeling. Theoretical and Applied Fracture Mechanics. 2020. Vol. 109. N 102692. DOI: 10.1016/j.tafmec.2020.102692
- Peitao Wang, Meifeng Cai, Fenhua Ren. Anisotropy and directionality of tensile behaviors of a jointed rock mass subjected to numerical Brazilian tests. Tunnelling and Underground Space Technology. 2018. Vol. 73, p. 139-153. DOI: 10.1016/j.tust.2017.12.018
- Sohrabi A., Alireza N., Talovina I. V., Safaei H. Structural model and tectonic evolution of the fault system in the southern part of the Khur area, Central Iran. Journal of Mining Institute. 2019. Vol. 236, p. 142-152. DOI: 10.31897/PMI.2019.2.142
- Peitao Wang, Fenhua Ren, Shengjun Miao et al. Evaluation of the anisotropy and directionality of a jointed rock mass under numerical direct shear tests. Engineering Geology. 2017. Vol. 225, p. 29-41. DOI: 10.1016/j.enggeo.2017.03.004
- Hoek E., Carter T.G., Diederichs M.S. Quantification of the Geological Strength Index Chart. 47th US Rock Mechanics/Geomechanics Symposium, 23-26 June 2013, San Francisco, USA. OnePetro, 2013, p. 9. N ARMA-2013-672.
- Özkan I., Erdem B., Ceylanoğlu A. Characterization of jointed rock masses for geotechnical classifications utilized in mine shaft stability analyses. International Journal of Rock Mechanics and Mining Sciences. 2015. Vol. 73, p. 28-41. DOI: 10.1016/j.ijrmms.2014.10.001
- Meda A., Rinaldi Z., Spagnuolo S. et al. Hybrid precast tunnel segments in fiber reinforced concrete with glass fiber reinforced bars. Tunnelling and Underground Space Technology. 2019. Vol. 86, p. 100-112. DOI: 10.1016/j.tust.2019.01.016
- Peitao Wang, Fenhua Ren, Shengjun Miao et al. Evaluation of the anisotropy and directionality of a jointed rock mass under numerical direct shear tests. Engineering Geology. 2017. Vol. 225, p. 29-41. DOI: 10.1016/j.enggeo.2017.03.004
- Yang Jian Ping, Chen Wei Zhong, Yang Dian Sen, Yuan Jing Qiang. Numerical determination of strength and deformability of fractured rock mass by FEM modeling. Computers and Geotechnics. 2015. Vol. 64, p. 20-31. DOI: 10.1016/j.compgeo.2014.10.011
- Esfahani M.H., Hejazi F., Vaghei R. et al. Simplified Damage Plasticity Model for Concrete. Structural Engineering International. 2017. Vol. 27. Iss. 1, p. 68-78. DOI: 10.2749/101686616X1081
- Ivars D.M., Pierce M.E., Darcel C. et al. The synthetic rock mass approach for jointed rock mass modelling. International Journal of Rock Mechanics and Mining Sciences. 2011. Vol. 48. Iss. 2, p. 219-244. DOI: 10.1016/j.ijrmms.2010.11.014
- Kozlovskiy E.Ya., Zhuravkov M.A. Determination and verification of the calculated model parameters of salt rocks taking into account softening and plastic flow. Journal of Mining Institute. 2021. Vol. 247, p. 33-38. DOI: 10.31897/PMI.2021.1.4
- Myung Sagong, Duhee Park, Jaeho Yoo, Jun S. Lee. Experimental and numerical analyses of an opening in a jointed rock mass under biaxial compression. International Journal of Rock Mechanics and Mining Sciences. 2011. Vol. 48. Iss. 7, p. 1055-67. DOI: 10.1016/j.ijrmms.2011.09.001
- Kuranov A.D., Zuev B.Y., Istomin R.S. The forecast deformations of the ground surface during mining under protected objects. Innovation-Based Development of the Mineral Resources Sector: Challenges and Prospects. CRC Press, 2018, p. 39-50.
- Coli N., Berry P., Boldini D. In situ non-conventional shear tests for the mechanical characterization of a bimrock. International Journal of Rock Mechanics and Mining Sciences. 2011. N 48. Iss. 1, p. 95-102. DOI: 10.1016/j.ijrmms.2010.09.012
- Zuev B.Yu. Methodology of modeling nonlinear geomechanical processes in blocky and layered rock masses on models made of equivalent materials. Journal of Mining Institute. 2021. Vol. 250, p. 542-552. DOI: 10.31897/PMI.2021.4.7
- Qing-Xiang Meng, Huan-Ling Wang, Wei-Ya Xu, Yu-Long Chen. Numerical homogenization study on the effects of columnar jointed structure on the mechanical properties of rock mass. International Journal of Rock Mechanics and Mining Sciences. 2019. Vol. 124. N 104127. DOI: 10.1016/j.ijrmms.2019.104127
- Yingjie Xia, Chuanqing Zhang, Hui Zhou et al. Mechanical behavior of structurally reconstructed irregular columnar jointed rock mass using 3D printing. Engineering Geology. 2020. Vol. 268. N 105509. DOI: 10.1016/j.enggeo.2020.105509
- Subash Bastola, Ming Cai. Investigation of mechanical properties of jointed granite under compression using lattice-spring-based synthetic rock mass modeling approach. International Journal of Rock Mechanics and Mining Sciences. 2020. Vol. 126. N 104191. DOI: 10.1016/j.ijrmms.2019.104191
- Kozyrev A.A., Savchenko S.N., Panin V.I. et al. Geomechanical processes in the geological environment of mining systems and management of geodynamic risks. Apatity: Kolskii nauchnyi tsentr RAN, 2019, p. 431 (in Russian). DOI: 10.37614/978.5.91137.391.7
- Kuranov A.D. Application of numerical modeling for design of safety paramters of safety mining method in highly stressed masses. Journal of Mining Institute. 2013. Vol. 206, p. 60-64 (in Russian).
- Protosenya A.G., Karasev M.A., Verbilo P.E. Research of the mechanical characteristics' anisotropy of apatite-nepheline ores block rock mass. International Journal of Mechanical Engineering and Technology. 2018. Vol. 9. N 11, p. 1962-1972.
- Verbilo P.E., Karasev M.A., Belyakov N.A., Iovlev G.A. Experimental and numerical research of jointed rock mass anisotropy in a three-dimensional stress field. Rudarsko-geološko-naftni zbornik. 2022. Vol. 37. N 2, p. 109-122. DOI: 10.17794/rgn.2022.2.10
- Kozyrev A.A., Panin V.I., Semenova I.E. et al. Geomechanical Support of Geotechnical Solutions in High Stress Mining. Journal of Mining Science. 2012. Vol. 48. N 2, p. 241-248.
- Shabarov A.N., Kuranov A.D., Kiselev V.A. Assessing the zones of tectonic fault influence on dynamic rock pressure manifestation at Khibiny deposits of apatite-nepheline ores. Eurasian Mining. 2021. N 2, p. 3-7.
- Sánchez-Martín J., Galindo R., Arévalo C. et al. Optimized Design of Earth Dams: Analysis of Zoning and Heterogeneous Material in Its Core. Sustainability. 2020. Vol. 12. N 6667. DOI: 10.3390/su12166667
- Protosenya A.G., Vilner M.A. Assessment of excavation intersections’ stability in jointed rock masses using the discontinuum approach. Rudarsko-geološko-naftni zbornik. 2022. Vol. 37. N 2, p. 137-147. DOI: 10.17794/rgn.2022.2.12
- Mirenkov V.E. Deformation of Rock Mass in the Vicinity of Underground Opening at Great Depth. Journal of Mining Science. 2021. Vol. 57. Iss. 3, p. 380-385. DOI: 10.1134/S1062739121030030
- Chenyang Zhao, Lavasan A.A., Schanz T. Application of Submodeling Technique in Numerical Modeling of Mechanized Tunnel Excavation. International Journal of Civil Engineering. 2018. Vol. 17. Iss. 1, p. 75-89. DOI: 10.1007/s40999-018-0318-8
- Maiboroda-Khidirova L.R. Using Sub-Modeling for Numerical Solution of Geomechanics Problems at Different Scale Levels. Problemy razrabotki mestorozhdenii uglevodorodnykh i rudnykh poleznykh iskopaemykh. 2021. Vol. 2, p. 60-65 (in Russian).
- Kozyrev A.A., Panin V.I., Semenova I.E., Rybin V.V. Geomechanical support of mining operations in mines of the Murmansk Region. Gornyi zhurnal. 2019. N 6, p. 45-50 (in Russian). DOI: 10.17580/gzh.2019.06.05
- Kozyrev A.A., Panin V.I., Semenova I.E. Experience in expert systems application for estimation of stress-strain state of rock mass for selection of safe methods of ore deposits mining. Journal of Mining Institute. 2012. Vol. 198, p. 16-23 (in Russian).
- Kocharyan G.G. Geomechanics of Faults. Мoscow: GEOS, 2016, p. 424 (in Russian).
