Crystal morphology of spherical viruses
Abstract
The article discusses modern views on the structure of spherical virus capsids, which have the shape of icosahedrons (icosahedral viruses). Each face of icosahedron is composed of a single-layer closest packing of protein globules, which can have different orientation relative to the edges of icosahedron. If the lines of globules are parallel to the edges of icosahedron, then the capsid has a point symmetry group Ih (with symmetry planes), if they are not parallel – the symmetry group I (without planes). From a mathematical point of view, in both symmetry groups there are series that unite equally (up to similarity) arranged capsids. They are connected pairwise by transitions to dual forms (homologous series). A hypothesis is formulated that the largest spherical viruses can have even more diverse and complex capsid structures. Along with icosahedron, their basic forms can be any simple shapes, allowed in Ih and I symmetry groups (8 in total). A suggestion is made that transitions within similarity series and between homologous series have a phylogenetic significance. There are known spherical viruses of both symmetry groups. For example, the SARS-CoV-2 coronavirus has a symmetry group Ih and belongs to a well-known series. The crystallographic approach allows to construct a strict morphological classification of spherical viruses. This is important for their early recognition and separate examination. The article demonstrates practical application of crystal morphology in the study of viral systems – an urgent problem of geoecology and life protection.
Introduction
The SARS-CoV-2 coronavirus pandemic made representatives of different sciences talk about spherical viruses. Are they alive or not? What is their place in the structure and evolution of our world [6, 8]? These fundamental questions of natural science became secondary, and a comprehensive study of viral systems came to the forefront as the most important task of geoecology and life protection. Now it is necessary to unite the efforts in the study of these mechanisms that are destroying our biological species.
In viruses, everything is efficient – both genetic content (coiled DNA/RNA) and protective capsids (protein globular membranes). It is in the description of capsids that crystal morphology can have its say. Virus nomenclature and classification are considered complex areas of virology [3]. The grouping can be based on morphological and physiological criteria. The ideal that virologists strive for is a classification that reflects evolutionary and phylogenetic relationships of viruses and provides a convenient and reasonable nomenclature.
Why crystal morphology, after all viruses are not the subject of crystallography? Experiments on irradiation of spherical viruses with X-rays have shown that the shadow they casted was not round but rather polygonal. The required shape – an icosahedron – was identified using the modeling method [15, 16], and spherical viruses were named icosahedral. A relation to icosahedron and dodecahedron (they have the same symmetry as dual forms) has undergone a noticeable evolution in crystallography. R.-J.Haüy was the first to demonstrate that they cannot be crystalline polyhedra, because they contradict the law of rational ratios of intercepts, which bears his name today. It was an important discovery, because even J.Kepler and A.G.Werner considered these forms to be crystalline. Later, it was proved that fifth-order symmetry axes contradict the long-range translational order in crystals. Goniometric measurements by J.B.Romé de l'Isle showed that mineral dodecahedron and icosahedron, widely known from pyrite crystals, are not Platonic polyhedra but a pentagonal dodecahedron and its combination with an octahedron.
It would seem that the issue has been resolved. Nevertheless, crystallographers kept icosahedron and dodecahedron in sight. E.S.Fedorov [9], the founder of the Crystallography Department at Saint Petersburg Mining Institute, and V.V.Dolivo-Dobrovolsky [5], professor at the Department, examined them in the rank of dodecahedral-icosahedral system (precisely the system, to distinguish it fundamentally from crystallographic syngonies). From the complete group of symmetry elements 6L5 10L3 15L2 15PC, these forms have 3L2 and 4L3, as well as three more mutually perpendicular planes, located as in the cubic syngony [10]. Therefore, simple shapes of the dodecahedral-icosahedral system are at the same time combinations of certain special shapes of the cubic system, but only at specific angles between the faces, impossible in crystals. Required angular relations are hampered by lattice (i.e., translationally ordered) structure of the crystals.
Over the course of several decades, the range of crystallography objects has significantly expanded. Shechtmanites – alloys with a long-range but not translational order, admitting symmetry axes of fifth and other, previously forbidden, orders – have become full-fledged components. Active research is conducted on stable nanoscale fullerenes – carbon and metal-carbon polyhedral molecules (hollow and doped) with icosahedral symmetry [4], which do not have any long-range order at all (translational or non-translational). However, any real crystal is finite, only in theory its lattice is thought to be infinite. Finally, in the system of mineralogy there are organic minerals and mineraloids of globular structure. Considering palliative extensions of basic definitions, already made in crystallography and mineralogy, spherical viruses (at least their capsids) are obvious objects of these sciences that have a natural origin, because scientists are no longer confused by their organic composition, nanoscopic scale, lack of lattice and presence of fifth order axes [1], and the closest packing of globules on the faces of icosahedron directly refers to crystallography. Due to the importance of spherical viruses as an object of study, icosahedron and dodecahedron return to crystallography in the rank of dodecahedral-icosahedral syngony.
Spherical capsid geometry
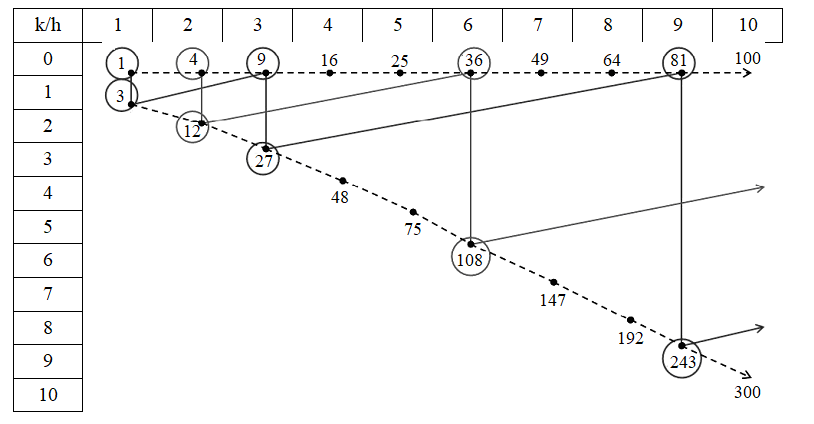
Capsid structure principles of spherical viruses and their classification are simple and concise [7]. Each capsid consists of 20 equilateral triangular mega-faces filled with protein globules according to the principle of single-layer closest packing of spheres. However, the edges of icosahedron may or may not coincide with the lines of globules. In the former case, the capsid has a point symmetry group (PSG) Ih (with symmetry planes), in the latter – I (without planes). There is a theorem indicating triangulation numbers allowed for capsids: Т = Рf2, where Р = h2 + hk + k2; 0 < h ≥ k ≥ 0 are any pairs of integers without common divisors; f = 1, 2, 3, ...; h, k are the coordinates of the end of mega-face basal edge in an oblique (60°) Cartesian coordinate system, aligned with the closest packing of globules; T is the capsid face area; f is the proportionality factor for identically oriented (similar in structure) faces.
T numbers are taken as a basis for capsid classification, they are quite informative. For example, capsids of two series have an Ih PSG: (h, k) = (f, 0); T = f2 (Table 1, first row) and (h, k) = (f, f), T = 3f2 (Table 1, diagonal). In the series (f, 0), it is always true that Т = (m – 1)2, where m is the number of globules on the mega-face edge. The number of globules in any capsid is 10Т + 2. They form morphological subunits: 12 pentamers and 10(Т – 1) hexamers. For any capsid, the number of elementary triangles, formed by three adjacent globules, is 20T.
Isomers, generators, homologous series
Analysis of the diversity of spherical viruses revealed isomers – capsids with the same T number (Table 1). For T = 49, they can be distinguished by symmetry: capsid (h, k) = (7, 0) has an Ih PSG, capsid (5, 3) – an I PSG. But for T = 91, both capsids (9, 1) and (6, 5) have an I PSG. Moreover, the structure of any capsid is uniquely identified by the symbols (h, k). It is these symbols that are proposed as a basis for the classification and nomenclature of icosahedral capsids.
Series (f, 0) and (f, f) with an Ih PSG are naturally related [2]. The simplest capsid in the (f, 0) series belongs to the φX174 bacteriophage (T = 1) and looks like a dodecahedron with 12 globules in the centers of the faces. The simplest capsid in the (f, f) series belongs to the turnip yellow mosaic virus (T = 3) and looks like a С60 fullerene with 32 globules in the centers of the faces; it is a truncated icosahedron, dual to the dodecahedron. A transition to the dual polyhedron with vertex truncation is performed according to the rule (h, k) → (h + 2k, h – k) and increases the T value by factor of three (Table 2).
Table 1
Triangulation numbers Т
|
k/h |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
|
1 |
3 |
7 |
13 |
21 |
31 |
43 |
57 |
73 |
91 |
111 |
|
2 |
|
12 |
19 |
28 |
39 |
52 |
67 |
84 |
103 |
124 |
|
3 |
|
|
27 |
37 |
49 |
63 |
79 |
97 |
117 |
139 |
|
4 |
|
|
|
48 |
61 |
76 |
93 |
112 |
133 |
156 |
|
5 |
|
|
|
|
75 |
91 |
109 |
129 |
151 |
175 |
|
6 |
|
|
|
|
|
108 |
127 |
148 |
171 |
196 |
|
7 |
|
|
|
|
|
|
147 |
169 |
193 |
219 |
|
8 |
|
|
|
|
|
|
|
192 |
217 |
244 |
|
9 |
|
|
|
|
|
|
|
|
243 |
271 |
|
10 |
|
|
|
|
|
|
|
|
|
300 |
Table 2
Dual transitions between homologous series (f, 0) and (f, f) with an Ih PSG
The indicated transitions are also allowed for capsids with an I PSG. Their variety also consists of homologous series (fh, fk), connected pairwise by dual transitions. At the beginning of the series there are capsids (h, k) that cannot be reduced to the indicated simpler transformations; they are called generators. Their criterion is that h and k are coprime integers, h – k is not divisible by 3. Isomers exist among generators too. These are the capsids (9, 1) and (6, 5) with T = 91, I PSG (Table 3). In paper [2], a general algebraic transformation of any capsid into any other was obtained.
Table 3
Triangulation numbers Т for capsid-generators [2]
|
k/h |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
7 |
13 |
|
31 |
43 |
|
73 |
91 |
|
|
2 |
|
|
19 |
|
|
|
67 |
|
103 |
|
|
3 |
|
|
|
37 |
49 |
|
79 |
97 |
|
139 |
|
4 |
|
|
|
|
61 |
|
|
|
133 |
|
|
5 |
|
|
|
|
|
91 |
109 |
|
151 |
|
|
6 |
|
|
|
|
|
|
127 |
|
|
|
|
7 |
|
|
|
|
|
|
|
169 |
193 |
|
|
8 |
|
|
|
|
|
|
|
|
217 |
|
|
9 |
|
|
|
|
|
|
|
|
|
271 |
|
10 |
|
|
|
|
|
|
|
|
|
|
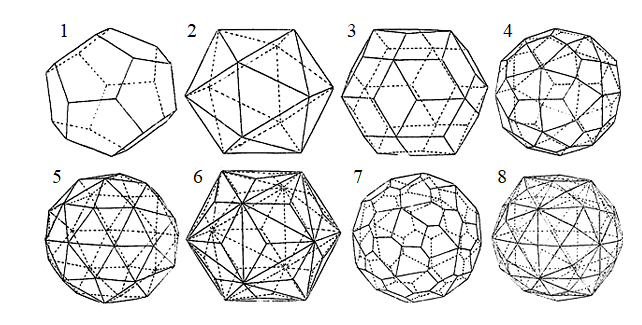
Simple shapes in Ih and I PSGs
1 – dodecahedron (12); 2 – icosahedron (20); 3 – triacontahedron (30); 4 – tetragontriicosahedron (60); 5 – trigonpentadodecahedron (60); 6 – trigontriicosahedron (60); 7 – pentagontriicosahedron (60), general shape in I PSG; 8 – hexaicosahedron (120), general shape in Ih PSG (value in brackets is the number of faces)
A crystallographic perspective suggests that everything can be even more diverse. Namely, icosahedron and its dual form dodecahedron, the presence of which becomes especially noticeable during dual transitions between homologous series, are only two simple shapes in icosahedral PSGs Ih and I. The icosahedral shape is used by the virus as a mega-form of the capsid, since at a given length of DNA/RNA chain, construction of an almost spherical shell requires a minimum amount of material (protein globules) and, possibly, time, and also because the mathematical coding for a highly-symmetric shape is easier than for a low-symmetric one (although we still poorly understand how this happens in the genome). And if viruses resort to such a trick as the reversal of the closest packing of protein globules relative to icosahedron edges, then why not assume that during capsid construction they use all the simple shapes, allowed in Ih and I PSGs? After all, some of them are a priori more spherical, and thus more optimal than the icosahedron, let alone dodecahedron (see Figure).
The icosahedral shape of spherical virus capsid was adopted basing on the fact that the contour of the shadow it casted when irradiated with X-rays was slightly polygonal. But other shapes (see Figure) also have polygonal outlines. It should also be noted that they can have different names. We follow the principles developed at the Fedorov Institute under the guidance of Professor A.K. Boldyrev.
Conclusion
The most reliable way to test the hypothesis that the largest spherical viruses can have a very diverse and complex capsid structure would be direct observation of crystallographically different capsids in a scanning electron microscope. It is to be expected that observation of the globular relief will be hampered by fibrillar projections. New types of capsids, more complex compared to ideal icosahedral ones, are most likely for the largest viruses, the size limits of which are currently unknown [11-14, 17]. As a result of collaboration between virologists and crystallographers, there is a possibility of discoveries at the intersection of sciences.
The proposed capsid classification (by simple shapes in Ih and I PSGs) and nomenclature (by (h, k) symbols) are mathematically rigorous and concise. With regard to their evolutionary and phylogenetic relationships, one can only assume that they are most likely within similarity series and between homologous series. The general algebraic transformation of any icosahedral capsid into any other one [2], found by the author, is of interest as a general mathematical formalism.
Expansion of the range of crystallography and mineralogy objects (quasicrystals, fullerenes, grapheme, etc.) leads to changes in corresponding fundamental definitions (crystal, mineral individual, mineral species, etc.). Active research on spherical viruses and isostructural fullerenes prompts a return of icosahedron and dodecahedron to crystallography in the rank of dodecahedral-icosahedral syngony with axial (I) and plane-axial (Ih) symmetry types.
