Кристалломорфология сферических вирусов
Аннотация
В статье рассмотрены современные взгляды на строение капсидов сферических вирусов, которые представляют собой икосаэдры (икосаэдрические вирусы). Каждая грань икосаэдра сложена однослойной плотнейшей упаковкой белковых глобул, которая может быть различно ориентирована относительно ребер икосаэдра. Если линии глобул расположены параллельно ребрам икосаэдра, то капсид имеет точечную группу симметрии Ih (с плоскостями симметрии), если не параллельны – группу симметрии I (без плоскостей). С математической точки зрения в обеих группах симметрии имеются серии, объединяющие одинаково (с точностью до подобия) устроенные капсиды. Они связаны попарно переходами к дуальным формам (гомологической серии). Сформулирована гипотеза о том, что у наиболее крупных сферических вирусов строение капсидов может быть еще разнообразнее и сложнее. Наряду с икосаэдром их базовыми формами могут быть любые простые формы, разрешенные в группах симметрии Ih и I (всего 8). Сделано предположение, что переходы в сериях подобия и между гомологическими сериями имеют филогенетическое значение. Известны сферические вирусы обеих групп симметрии. Например, коронавирус SARS-CoV-2 имеет группу симметрии Ih и принадлежит к хорошо известной серии. Кристаллографический подход позволяет построить строгую морфологическую классификацию сферических вирусов. Это важно для их раннего распознавания и раздельного исследования. Статья демонстрирует практическое применение кристалломорфологии в изучении вирусных систем – актуальной проблеме геоэкологии и охраны жизнедеятельности.
Введение
Пандемия коронавируса SARS-CoV-2 заставила заговорить о сферических вирусах представителей разных наук. Живые они или не живые? Каково их место в структуре и эволюции нашего мира [6, 8]? Эти фундаментальные вопросы естествознания стали второстепенными, на первый план в качестве важнейшей задачи геоэкологии и охраны жизнедеятельности вышло всестороннее изучение вирусных систем. Сейчас необходимо объединить усилия в исследовании этих механизмов, уничтожающих наш биологический вид.
В вирусах эффективно все – генетическое содержание (свернутые в клубки ДНК/РНК) и защитные капсиды (белковые глобулярные оболочки). Именно в описании капсидов кристалломорфология может сказать свое слово. Номенклатура и классификация вирусов считаются сложными областями вирусологии [3]. Группировка может быть основана на морфологических и физиологических критериях. Идеал, к которому стремятся вирусологи, – классификация, отражающая эволюционные и филогенетические взаимоотношения вирусов и обеспечивающая их удобную и рациональную номенклатуру.
Почему кристалломорфология, ведь вирусы – не предмет кристаллографии? Опыты по облучению сферических вирусов рентгеновскими лучами показали, что отбрасываемая ими тень не круглая, а скорее полигональная. Методом моделирования была подобрана нужная форма [15, 16] – икосаэдр, а сферические вирусы получили название икосаэдрических. Отношение к икосаэдру и додекаэдру (они имеют ту же симметрию как дуальные формы) претерпело в кристаллографии заметную эволюцию. Р.-Ж.Гаюи первый показал, что они не могут быть кристаллическими полиэдрами, ибо противоречат закону рационального двойного отношения параметров, носящему сегодня его имя. Это было важным открытием, ибо даже И.Кеплер и А.Г.Вернер считали эти формы кристаллическими. Позднее было доказано, что оси симметрии 5-го порядка противоречат дальнему трансляционному порядку в кристаллах. А гониометрические измерения Ж.Б.Ромэ-Делиля показали, что минеральные додекаэдр и икосаэдр, широко известные по кристаллам пирита, являются не платоновыми полиэдрами, а пентагондодекаэдром и его комбинацией с октаэдром.
Казалось бы, вопрос решен. Но кристаллографы держали икосаэдр и додекаэдр в поле зрения. В ранге додекаэдро-икосаэдрической системы (именно системы, чтобы принципиально отличать ее от кристаллографических сингоний) их рассматривали основатель кафедры кристаллографии Санкт-Петербургского горного института Е.С.Федоров [9] и профессор кафедры В.В.Доливо-Добровольский [5]. В полной группе элементов симметрии 6L5 10L3 15L2 15PC у этих форм есть 3L2 и 4L3, а еще три взаимно перпендикулярные плоскости, располагающиеся как и в кубической сингонии [10]. Поэтому простые формы додекаэдро-икосаэдрической системы являются в то же время комбинациями некоторых особых форм кубической системы, но лишь при особых, невозможных в кристаллах, величинах углов между гранями. Требуемым угловым отношениям мешает решетчатое (т.е. трансляционно упорядоченное) строение кристаллов.
За несколько десятилетий круг объектов кристаллографии заметно расширился. Полноправными составляющими стали шехтманиты – сплавы с дальним, но не трансляционным порядком, допускающие оси симметрии 5-го и других, ранее запрещенных, порядков. Активно изучаются наноразмерные стабильные фуллерены – углеродистые и металлоуглеродистые полиэдрические (полые и допированные) молекулы с икосаэдрической симметрией [4], которые вообще не обладают дальним (трансляционным и нетрансляционным) порядком. Однако любой реальный кристалл тоже конечен, лишь в теории его решетка мыслится бесконечной. Наконец, в системе минералогии есть органические минералы и минералоиды глобулярного строения. Ввиду уже сделанных в кристаллографии и минералогии паллиативных расширений базовых определений, сферические вирусы (по крайней мере их капсиды) являются очевидными объектами этих наук, имеющими естественное происхождение, ведь ученых уже не смущают их органический состав, наноразмерность, отсутствие решетки и наличие осей 5-го порядка [1], а плотнейшие упаковки глобул на гранях икосаэдра прямо обращают к кристаллографии. По причине важности сферических вирусов в качестве объекта изучения икосаэдр и додекаэдр возвращаются в кристаллографию в ранге додекаэдро-икосаэдрической сингонии.
Геометрия сферического капсида
Принципы строения капсидов сферических вирусов и их классификация просты и лаконичны [7]. Всякий капсид построен из 20 равносторонних треугольных мега-граней, заполненных белковыми глобулами по принципу однослойной плотнейшей шаровой упаковки. Однако ребра икосаэдра могут совпадать или не совпадать с линиями глобул. В первом случае капсид имеет точечную группу симметрии (т.г.с.) Ih (с плоскостями симметрии), во втором – I (без плоскостей). Существует теорема, указывающая разрешенные для капсидов триангуляционные числа: Т = Рf2, где Р = h2 + hk + k2; 0 < h ≥ k ≥ 0 – любые пары целых чисел без общих делителей; f = 1, 2, 3, ...; h, k – координаты конца базального ребра мега-грани в косоугольной (60°) декартовой системе координат, согласованной с плотнейшей упаковкой глобул; Т – площадь грани капсида; f – коэффициент пропорциональности для одинаково ориентированных (подобных по строению) граней.
В основу классификации капсидов положены числа Т, они достаточно информативны. Так, т.г.с. Ih имеют капсиды двух серий: (h, k) = (f, 0); T = f2 (табл.1, верхний ряд) и (h, k) = (f, f), T = 3f2 (табл.1, диагональ). В серии (f, 0) всегда Т = (m – 1)2, где m – число глобул на ребре мега-грани. Число глобул в любом капсиде 10Т + 2. Они образуют морфологические субъединицы: 12 пентамеров и 10(Т – 1) гексамеров. У любого капсида число элементарных треугольников, образованных тремя соседними глобулами, равно 20Т.
Изомеры, генераторы, гомологические серии
Анализ многообразия сферических вирусов обнаружил изомеры – капсиды с одинаковым числом Т (табл.1). Для Т = 49 их можно различить по симметрии: капсид (h, k) = (7, 0) имеет т.г.с. Ih, капсид (5, 3) – т.г.с. I. Но для Т = 91 оба капсида (9, 1) и (6, 5) имеют т.г.с. I. При этом символы (h, k) фиксируют строение любого капсида однозначно. Именно их предлагается положить в основу классификации и номенклатуры икосаэдрических капсидов.
Серии (f, 0) и (f, f) с т.г.с. Ih закономерно связаны [2]. Простейший капсид в серии (f, 0) принадлежит бактериофагу φX174 (Т = 1) и выглядит как додекаэдр с 12 глобулами в центрах граней. Простейший капсид в серии (f, f) принадлежит вирусу желтой мозаики турнепса (Т = 3) и выглядит как фуллерен С60 с 32 глобулами в центрах граней, это усеченный икосаэдр, который дуален додекаэдру. Переход к дуальному полиэдру с усечением вершин выполняется по правилу (h, k) → (h + 2k, h – k) и увеличивает Т втрое (табл.2).
Таблица 1
Триангуляционные числа Т
|
k/h |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
|
1 |
3 |
7 |
13 |
21 |
31 |
43 |
57 |
73 |
91 |
111 |
|
2 |
|
12 |
19 |
28 |
39 |
52 |
67 |
84 |
103 |
124 |
|
3 |
|
|
27 |
37 |
49 |
63 |
79 |
97 |
117 |
139 |
|
4 |
|
|
|
48 |
61 |
76 |
93 |
112 |
133 |
156 |
|
5 |
|
|
|
|
75 |
91 |
109 |
129 |
151 |
175 |
|
6 |
|
|
|
|
|
108 |
127 |
148 |
171 |
196 |
|
7 |
|
|
|
|
|
|
147 |
169 |
193 |
219 |
|
8 |
|
|
|
|
|
|
|
192 |
217 |
244 |
|
9 |
|
|
|
|
|
|
|
|
243 |
271 |
|
10 |
|
|
|
|
|
|
|
|
|
300 |
Таблица 2
Дуальные переходы между гомологическими сериями (f, 0) и (f, f) с т.г.с. Ih
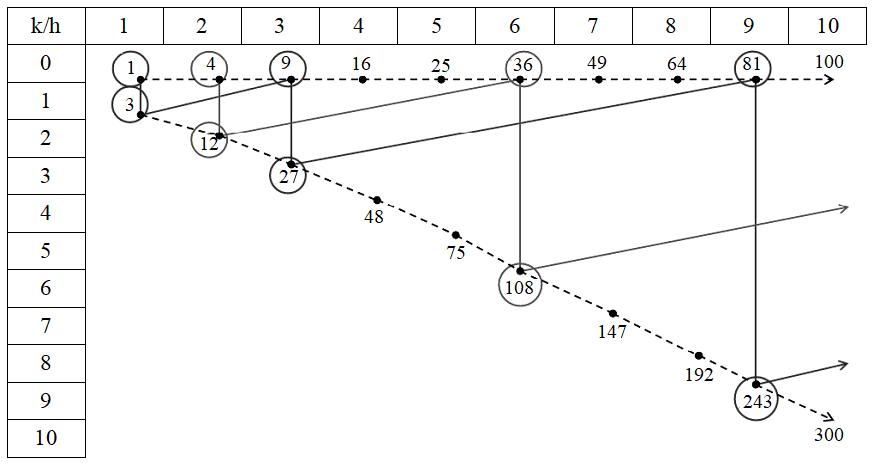
Указанные переходы разрешены и для капсидов с т.г.с. I. Их многообразие тоже состоит из гомологических серий (fh, fk), связанных попарно дуальными переходами. В начале серий находятся капсиды (h, k), не сводимые к более простым указанными преобразованиями, они названы генераторами. Их критерий: h и k взаимно просты, h – k не делится на 3. Изомеры существуют и среди генераторов. Таковы капсиды (9, 1) и (6, 5) с Т = 91, т.г.с. I (табл.3). В статье [2] получено общее алгебраическое преобразование любого капсида в любой другой.
Таблица 3
Триангуляционные числа Т для капсидов-генераторов [2]
|
k/h |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
7 |
13 |
|
31 |
43 |
|
73 |
91 |
|
|
2 |
|
|
19 |
|
|
|
67 |
|
103 |
|
|
3 |
|
|
|
37 |
49 |
|
79 |
97 |
|
139 |
|
4 |
|
|
|
|
61 |
|
|
|
133 |
|
|
5 |
|
|
|
|
|
91 |
109 |
|
151 |
|
|
6 |
|
|
|
|
|
|
127 |
|
|
|
|
7 |
|
|
|
|
|
|
|
169 |
193 |
|
|
8 |
|
|
|
|
|
|
|
|
217 |
|
|
9 |
|
|
|
|
|
|
|
|
|
271 |
|
10 |
|
|
|
|
|
|
|
|
|
|
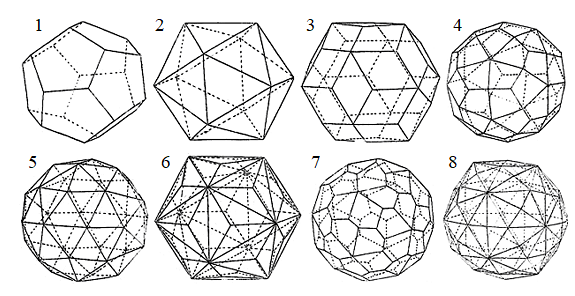
Простые формы в т.г.с. Ih и I
1 – додекаэдр (12); 2 – икосаэдр (20); 3 – триаконтаэдр (30); 4 – тетрагонтриикосаэдр (60); 5 – тригонпентадодекаэдр (60); 6 – тригонтриикосаэдр (60); 7 – пентагонтриикосаэдр (60), общая форма в т.г.с. I; 8 – гексаикосаэдр (120), общая форма в т.г.с. Ih (в скобках – число граней)
Кристаллографический взгляд позволяет предполагать, что все может быть еще разнообразнее. А именно, икосаэдр и дуальный к нему додекаэдр, присутствие которого особенно ощущается при дуальных переходах между гомологическими сериями, – лишь две простые формы в икосаэдрических т.г.с. Ih и I. Форма икосаэдра использована вирусом в качестве мега-формы капсида поскольку при данной длине цепочки ДНК/РНК для строительства почти сферической оболочки требуется минимальное количество материала (белковых глобул) и, возможно, времени, а также потому, что математическое кодирование высокосимметричной формы проще, чем формы низкосимметричной (хотя мы еще плохо понимаем, как это происходит в геноме). И уж если вирусы прибегают к такой уловке как разворот плотнейшей упаковки белковых глобул относительно ребер икосаэдра, то почему не предположить, что при строительстве капсида они используют все простые формы, разрешенные в т.г.с. Ih и I? Ведь некоторые из них заведомо сферичнее, и тем самым оптимальнее, чем икосаэдр и, тем более, додекаэдр (рисунок).
Икосаэдрическая форма капсида сферического вируса была принята на том основании, что контур тени, отбрасываемой им при облучении рентгеновскими лучами, был слегка полигональным. Но и другие формы (рисунок) имеют полигональные контуры. Заметим также, что они могут называться по-разному. Мы следуем принципам, разработанным в Федоровском институте под руководством профессора А.К.Болдырева.
Заключение
Самым надежным способом проверки высказанной гипотезы о том, что у наиболее крупных сферических вирусов строение капсида может быть весьма разнообразным и сложным, было бы прямое наблюдение кристаллографически различных капсидов в сканирующем электронном микроскопе. Следует ожидать, что наблюдение глобулярного рельефа будет затруднено фибриллярными отростками. Новые типы капсидов, усложненные по сравнению с идеальными икосаэдрическими, наиболее вероятны для самых крупных вирусов, предельные размеры которых сегодня неизвестны [11-14, 17]. В результате сотрудничества вирусологов и кристаллографов на стыке наук возможны открытия.
Предлагаемые классификация (по простым формам в т.г.с. Ih и I) и номенклатура (по символам (h, k)) капсидов математически строги и лаконичны. Относительно их эволюционных и филогенетических взаимоотношений можно лишь предполагать, что они наиболее вероятны в сериях подобия и между гомологическими сериями. Найденное автором общее алгебраическое преобразование любого икосаэдрического капсида в любой другой [2] интересно как общий математический формализм.
Расширение круга объектов кристаллографии и минералогии (квази-кристаллы, фуллерены, графены и других) приводит к изменениям соответствующих фундаментальных определений (кристалла, минерального индивида, минерального вида и т.д.). Активное изучение сферических вирусов и изоструктурных им фуллеренов побуждает к возвращению икосаэдра и додекаэдра в кристаллографию в ранге додекаэдро-икосаэдрической сингонии с аксиальным (I) и планаксиальным (Ih) видами симметрии.
Литература
- Atabekov I.G. The Use of Viral Structures as Nanotechnology Tools. Rossiiskie nanotekhnologii. 2008. Vol. 3. N 1-2, p. 132-141 (in Russian).
- Voytekhovsky Yu.L. From teaching experience. III. Crystallography of icosahedral viruses. Vestnik of Geosciences. 2020. N 4, p. 40-44. DOI: 10.19110/geov.2020.4.6 (in Russian).
- Gnutova R.V. Modern trends in taxonomy and nomenclature of viruses. Uspehi sovremennoj biologii. 2011. Vol. 131. N 6, p. 563-577 (in Russian).
- Deffeis K., Deffeis S. Amazing Nanostructures. Moscow: Binom. Laboratoriya znanii, 2011, p. 206 (in Russian).
- Dolivo-Dobrovolskii V.V. A Study of Dodecahedral-Icosahedral System. Zapiski Rossiiskogo mineralogicheskogo obshchestva. 1924. N 1, p. 169-181 (in Russian).
- Zhdanov V.M., Lvov D.K., Zaberezhny A.D. The place of viruses in the biosphere. Problems of Virology. 2012. N 1, p. 21-32 (in Russian).
- Kostyuchenko V.A., Mesyanzhinov V.V. Architecture of Spherical Viruses. Uspekhi biologicheskoi khimii. 2002. Vol. 42, p. 177-192 (in Russian).
- Urusov V.S. Symmetry and Dissymmetry in the Evolution of the World: Monograph. Moscow: Librokom, 2013, p. 266 (in Russian).
- Fedorov E.S. Practical Course on the Main Branches of Crystallography. Petrograd: Ekonomicheskaya tipo-litografiya, 1915, p. 20 (in Russian).
- Chuprunov E.V. Symmetry and Pseudo-Symmetry of Crystals. Nizhnii Novgorod: Izdatelstvo Nizhegorodskogo gosuniversiteta, 2015, p. 658 (in Russian).
- Xiao C., Chipman P.R., Battisti A.J. et al. Cryo-electron microscopy of the giant Mimivirus. Journal of Molecular Biology. 2005. Vol. 353. Iss. 3, p. 493-496. DOI: 10.1016/j.jmb.2005.08.060
- Forterre P., Gaïa M. Giant viruses and the origin of modern eukaryotes. Current Opinion in Microbiology. 2016. Vol. 31, p. 44-49. DOI: 10.1016/j.mib.2016.02.001
- Claverie J., Ogata H., Audic S. et al. Mimivirus and the emerging concept of the “giant” virus. Virus Research. 2006. Vol. 117. Iss. 1, p. 133-144. DOI: 10.1016/j.virusres.2006.01.008
- Raoult D., LaScola B., Birtles R. The discovery and characterization of Mimivirus, the largest known virus and puta-tive pneumonia agent. Clinic Infection Diseases. 2007. Vol. 45. Iss. 1, p. 95-102. DOI: 10.1086/518608
- Rux J., Kuser P., Burnett R. Structural and phylogenetic analysis of Adenovirus hexons by use of high-resolution X-ray crystallographic, molecular modeling, and sequence-based methods. Journal of Virology. 2003. Vol. 77. Iss. 17, p. 9553-9566. DOI: 10.1128/JVI.77.17.9553-9566.2003
- Simpson A.A., Nandhagopal N., Van Etten J.L., Rossmann M.G. Structural analyses of Phycodnaviridae and Iri-doviridae. Acta Crystallographica. 2003. Vol. D59. Iss. 12, p. 2053-2059.
- Van Etten J.L. Giant viruses. American Scientist. 2011. Vol. 99. Iss. 4, p. 304-311. DOI: 10.1511/2011.91.304
