Численное моделирование двустенного шарового резервуара
- 1 — д-р техн. наук профессор Уфимский государственный нефтяной технический университет
- 2 — инженер ЗАО «Нефтемонтаждиагностика»
Аннотация
Обширным и важным классом многослойных конструкций оболочек являются трехслойные конструкции. В трехслойной конструкции важную роль играет жесткий заполнитель, за счет которого разнесены несущие слои, что придает пакету слоев высокую жесткость и прочность при относительно малом весе. Комбинируя толщины несущих слоев и заполнителя, можно добиться необходимых свойств трехслойной конструкции оболочки. По сравнению с традиционными одностенными трехслойная конструкция обладает повышенной жесткостью и прочностью, что позволяет уменьшить толщину и массу оболочек. С целью снижения металлоемкости конструкции шарового резервуара для хранения сжиженных газов в настоящей работе рассмотрена конструкция двустенного резервуара, в котором межстенное пространство заполнено армированным пенополиуретаном. Численное моделирование позволило определить параметры напряженно-деформированного состояния конструкции с погрешностью не более 5 %. Установлено на примере резервуара объемом 4000 м3, что пространственная конструкция стенки шарового резервуара позволяет снизить металлоемкость до 19 %. Областью применения результатов исследования может быть оценка напряженно-деформированного состояния шаровых резервуаров при их проектировании. Разработана методика построения конструкции двустенного шарового резервуара в программном комплексе SCAD, позволяющая произвести расчет напряженно-деформированного состояния (НДС) методом конечных элементов. Разработана численная модель двустенного шарового резервуара. Установлено, что для получения результатов расчета с погрешностью P ≤ 5 % размер конечного элемента не должен превышать 300×300×δ мм. В результате исследования конструкции двустенного шарового резервуара установлены конструктивные параметры, позволяющие обеспечить эксплуатационную надежность сооружения при снижении металлоемкости по сравнению с одностенным резервуаром на 19 %
Введение. Основные подходы к изучению ортотропных оболочек были рассмотрены В.З.Власовым [12]. В работе [4] А.И.Голованов с соавторами рассмотрели проблемы построения моделей трехслойных оболочек методом конечных элементов (МКЭ). Разработали квадратичный конечный элемент, который распространяется на класс физически и геометрически нелинейных задач. Использован метод пошагового нагружения в форме модифицированной лагранжевой постановки.
В своей работе [9] Р.З.Киселева предложила алгоритм формирования матриц жесткости объемных конечных элементов (КЭ) с узловыми неизвестными в виде перемещений и их первых производных и алгоритм преобразования матриц жесткости и векторов узловых нагрузок КЭ, примыкающих к границе раздела слоев оболочек вращения с различными физико-механи¬ческими свойствами.
Ежегодно количество работ, исследующих трехслойные конструкции, увеличивается. Однако большая часть из них посвящена рассмотрению пластин для прямолинейной плоскости. Многие научные публикации посвящены многослойным оболочкам для плоских покрытий с различными характеристиками жесткости слоев [5, 15].
Наибольшее распространение в практических расчетах нашли дифференциальные теории: теория упругопластических процессов А.А.Ильюшина и теории пластического течения при комбинированном упрочнении, базирующиеся на концепции микронапряжений В.В.Новожилова.
В настоящее время существует множество вариантов моделей упругопластического деформирования металла, основанных на теории течения при его упрочнении. Предполагается, что металл однороден и начально изотропен. В процессе упругопластического деформирования в нем может возникнуть только деформационная анизотропия. В работе [1] представлен обзор работ, основанных на теории течения. Под научным руководством академика РАЕН В.С.Бондаря выполнена работа [11], в которой приведен вариант математической модели неупругого деформирования и накопления повреждений конструкционных материалов. Разработан программный комплекс оценки и прогнозирования ресурса конструкционных материалов, состоящий из модуля определения материальных функций по результатам базового эксперимента и модуля расчета кинетики напряженно-деформированного состояния и процесса накопления повреждений. В работе [14] предложен прикладной вариант теории упругопластических процессов и накопления повреждений материалов, основанный на теории В.С.Бондаря. Автор апробировал вариант теории на ряде конструкционных материалов, указал, что ошибка результатов расчета не превышает 10 % от результатов экспериментов, однако данную теорию можно применять только при малых деформациях. В теории оболочек под малыми деформациями понимают деформации, не превышающие толщины стенки.
Т.Р.Ищанов [8] анализировал напряженно-деформированное состояние тонких оболочек с учетом поперечного сдвига при различных вариантах аппроксимации угловых перемещений. На основе соотношений В.В.Новожилова разработан алгоритм исследования НДС при использовании скалярной и векторной интерполяционных процедур. В работе [3] приведен обзор работ, посвященных исследованию методов сведения трехмерной задачи теории упругости к двумерной теории пластин и оболочек. Н.А.Гуреева [6] выполнила сравнительный анализ эффективности использования конечных элементов треугольной и четырехугольной форм расчета оболочек вращения. Показано, что расчеты, выполненные с использованием треугольных КЭ, обладают существенно большей погрешностью по сравнению с конечно-элементными решениями, полученными на основе использования четырехугольных КЭ. Работа [10] посвящена качественному анализу метода конечных суперэлементов (МКСЭ) Федоренко. Получены априорные оценки погрешностей МКСЭ в шкале пространств Соболева на примере задачи Дирихле.
В химической, нефтехимической, нефтеперерабатывающей и других отраслях промышленности России для хранения жидкостей и газов широко применяют шаровые резервуары. За последние годы наблюдается увеличение производственных объемов промышленных предприятий, а с этим возрастает площадь территорий объектов. Но размеры промышленных территорий ограничены в своих параметрах, следовательно, необходимо увеличить единичную емкость шаровых резервуаров, что повлечет за собой уменьшение площади резервуарных парков, снижение металлоемкости на единицу объема хранимого продукта, снижение затрат на монтажные работы, на установку контрольно-измерительных приборов, сооружение технологических трубопроводов, а также повлияет на снижение потерь продукта от испарения.
Стенка резервуара является важной частью резервуарной конструкции. На оболочку резервуара действуют значительные нагрузки и воздействия. От выбора стали и параметров стенки зависит состояние резервуара в процессе строительства и дальнейшей эксплуатации. С увеличением вместимости резервуара для обеспечения прочности и устойчивости стенки необходимо либо применять сталь с улучшенными характеристиками, либо увеличивать толщину стенки, при этом учитывая экономическую выгоду.
В настоящее время при проектировании шаровых резервуаров в России руководствуются нормативными документами – ГОСТами* и сводами правил**, расчет внешних нагрузок производят по своду правил***. Актуальность данной работы заключается в том, что вопрос работоспособности шаровых резервуаров для хранения углеводородного сырья с учетом ортотропности физических свойств оболочек изучен недостаточно.
Конструкция двустенного шарового резервуара. В настоящей работе рассмотрен вариант двустенной конструкции (рис.1), состоящей из внешних слоев малой толщины и системы ферм, играющей роль слоя-заполнителя.

Внутренний слой резервуара представляет собой оболочку, собранную из отдельных стальных листов, раскроенных на заводе из прокатных листов, а затем деформированных для придания сферической кривизны. Радиус кривизны листов равен радиусу оболочки. Внутренний слой выполнен из стали ОН9 с 9 %-м содержанием никеля, отличающейся высокой упругостью, необходимой для хранения криогенных жидкостей, с временным сопротивлением σв = 640 МПа и пределом текучести σT = 595 МПа.
Заполнитель представляет собой систему ферм, которая при выпучивании пластинок остается несгибаемой и создает для них дополнительные опорные закрепления. Деформации стенки внутри каждого такого поля рассматривают как самостоятельные. Ферменный заполнитель прикреплен к внешнему и внутреннему слою уголками, которые привариваются к оболочке в местах сварки листов внутренней оболочки.
Внешний слой шарового резервуара собирают из стальных листов длиной 6 и шириной 2 м так, чтобы место стыка стальных листов приходилось на балку жесткости, представляющую собой уголок. Таким образом, создано сварное соединение для односторонней сварки на подкладке, где подкладкой служит полка уголка. Внешняя оболочка резервуара опирается на опоры из труб, соединенные между собой связями. Внешний слой шарового резервуара изготовлен из стали класса прочности С345 марки 09Г2С. Особенностью этой марки стали является низкий порог хладноломкости, хорошая свариваемость и необходимая прочность.
Геометрические параметры внутреннего, наружного и срединного слоя стенки резервуара определяются расчетом в зависимости от заданных нагрузок [2].
Создание численной модели в программном комплексе SCAD [7]. Модели стенок резервуара разбили на конечные элементы – призмы размером 0,3×0,3×δi, где толщина листов стенки резервуара δi = 14 мм. Срединный слой принимали как стержневые элементы длиной конечного элемента l = 0,42 м. Опорные стойки приняли как стержни наружным диаметром 0,3 м с толщиной стенки 0,02 м.
Опорные столики, соединяющие стенку резервуара с опорными стойками, приняли как листовые элементы с дискретизацией на КЭ размером 0,1×0,1×0,02. В нижние части опорных стоек ввели связи по осям X, Y, Z ортогональной системы координат.
Сбор нагрузок и воздействий. Первыми шагами расчета трехслойного шарового резервуара является определение внешних нагрузок, построение расчетной схемы, а также установление характера (формы) эпюры приложения этих нагрузок. Можно выделить нагрузки, действующие на трехслойный шаровой резервуар: собственный вес металлоконструкции трехслойного шарового резервуара; снеговая нагрузка, рассматриваемая в трех вариантах; ветровая нагрузка; температурные климатические воздействия; нагрузка от избыточного давления; нагрузка от гидростатического давления. Расчет вариантов сочетания нагрузок* показал, что максимальная нагрузка, действующая на шаровой резервуар, составляет 232,5 кПа.
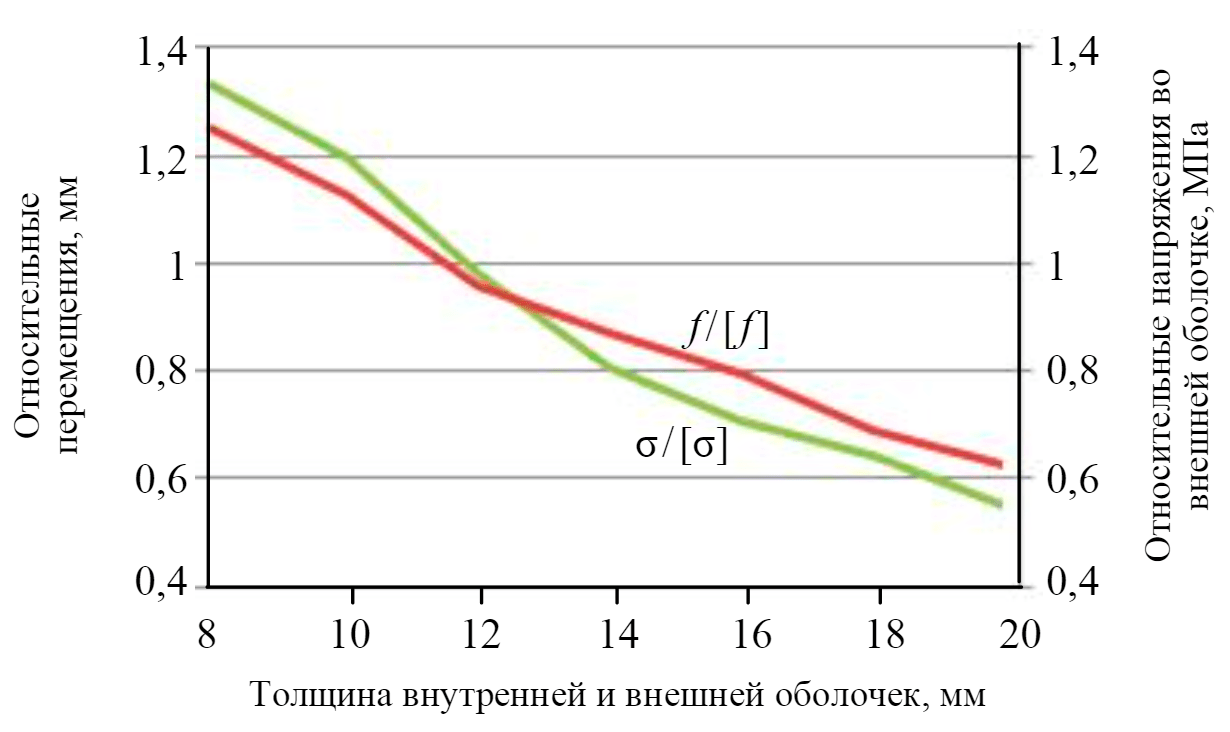

Для исследования применялись безразмерные величины: относительная величина напряжений σ/[σ], возникающая в сечении элемента под воздействием нагрузок и воздействий, где [σ] –допустимые напряжения, равные: для стали марки 09Г2С 190 МПа, для стали марки ОН9 – 315 МПа [11]
В модели резервуара принято, что внутренняя и наружная стенки имеют равные толщины. Исследование влияния толщины стенок на величины перемещений и напряжений показано на рис.2. По зависимостям σ/[σ] = F (δ) и f/[f] = F (δ) видно, что обе функции практически линейно убывающие. Исследуя поведение двух функций, приходим к выводу, что оптимальной толщиной оболочек с учетом запаса на коррозию δ = 14 мм.
В связи с тем, что в резервуаре будет храниться продукт с температурой Т = –160 oС, необходимо обеспечить теплоизоляцию. В качестве теплоизоляции принят слой пенополиуретана толщиной В = 400 мм с характеристиками: плотность ρ = 150 кг/м3, коэффициент теплопроводности λ = 0,3∙106 Вт/м∙К. Для исключения мостиков холода связи в фермах выполнены из стеклопластика марки ВПС-30 с характеристиками: плотность ρ = 1800 кг/м3, модуль упругости Е = 55∙103 МПа, коэффициент линейного расширения \(\ \alpha_t=8,3\cdot106{^oC^{-1}} \). На рис.3, а представлены зависимости прочности и устойчивости стержней ферменного заполнителя от их параметров. По зависимости можно сделать вывод об уменьшении относительных напряжений в ферменном заполнителе в связи с увеличением диаметра стрежня ферменного заполнителя. Исследуя поведение зависимости, приходим к выводу, что оптимальным параметром стрежня ферменного заполнителя будет являться 120×12 мм.
Из конструктивных соображений – рационального очертания фермы и удобства прикрепления – желателен угол, равный 45°. При малых углах ферма становится слишком вытянутой, при больших – высокой, что делает их громоздкими и неэкономичными. Исследуя зависимость относительных напряжений от угла между стенкой и стержнем ферменного заполнителя, можно утверждать, что угол, равный 45°, оптимален для ферменного заполнителя.
Размер шага, с каким следует устанавливать фермы, можно вывести согласно зависимости относительных напряжений и устойчивости стержней от шага расстановки ферм (рис.3, б). Можно утверждать, что оптимальным шагом будет являться расстояние не более 400 мм.
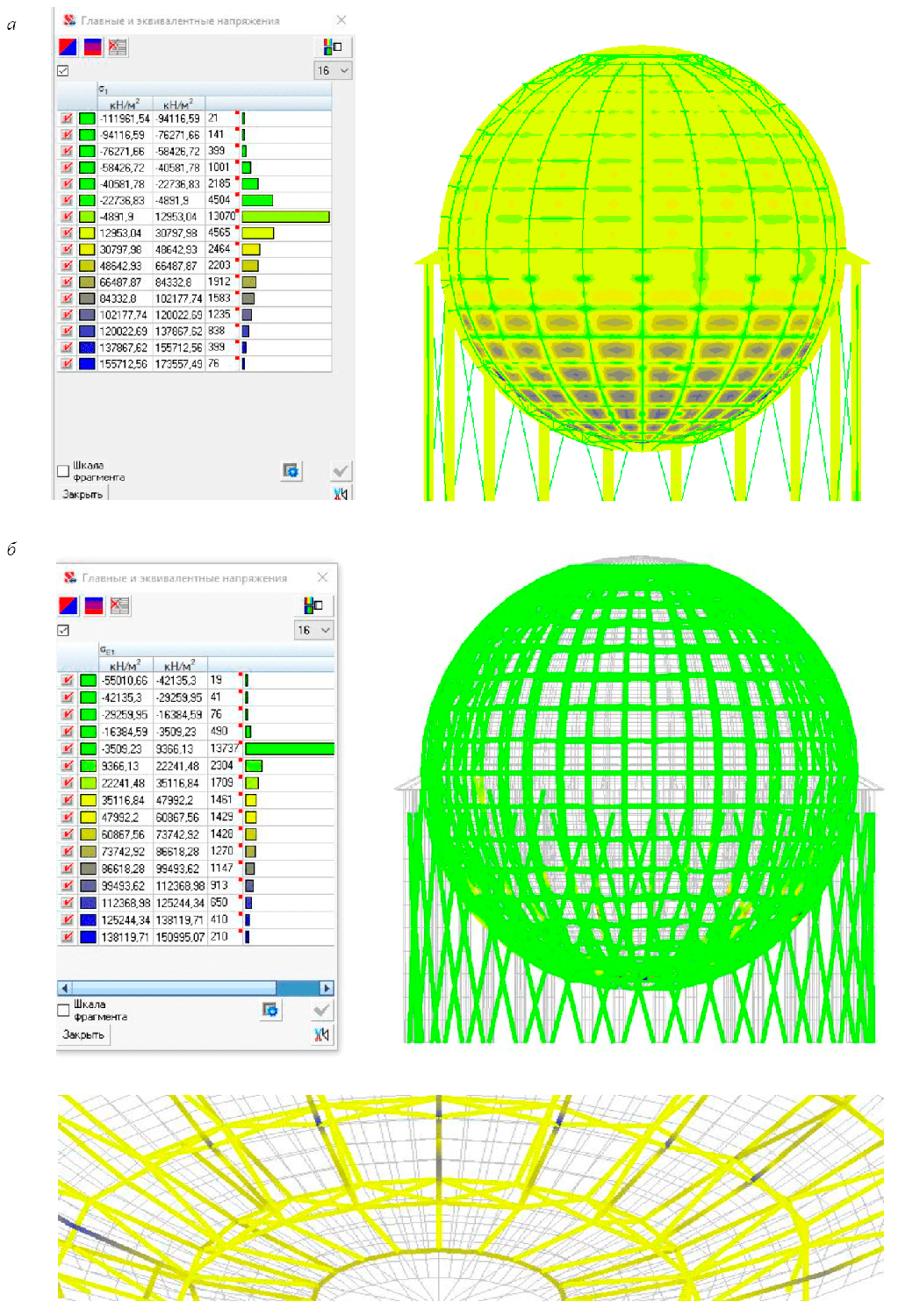
Обсуждение результатов. Результатом расчета являются цветовые схемы распределения перемещений внешней стенки, усилий и напряжений в двустенном шаровом резервуаре. Результаты расчета представлены на рис.4, 5. На рис.4 видно, что максимальные перемещения во внешней стенке шарового резервуара не превышают 90 мм.
Предельно допустимые перемещения для стальных конструкций пролетом до 30 м, согласно своду правил*: D/200 = 20000/200 = 100 мм, где D – диаметр двустенного шарового резервуара, равный 20000 мм. Согласно расчету двустенного шарового резервуара, перемещения конструкции меньше 100 мм, что является допустимым.
Распределение главных и эквивалентных напряжений во внутреннем слое резервуара представлено на рис.5, а. Из рис.5, а видно, что в пластинах оболочки напряжения сжатия достигают 111,9 МПа, а в ребрах жесткости напряжения растяжения равны 173,5 МПа.
На рис.5, б представлено распределение главных и эквивалентных напряжений в срединном слое резервуара. Максимальные напряжения растяжения в срединном слое достигают 150,9 МПа, а максимальные напряжения сжатия 55,01 МПа. Причем преимущественно напряжения растяжения наблюдаются в нижнем поясе срединного слоя, где стержни примыкают к днищу оболочки.
В таблице представлены сравнительные результаты расчетов, полученные МКЭ с аналитическим методом расчета. Видно, что погрешность между результатами расчетов, полученных численным (МКЭ) и аналитическим методами, не превышают 4,35 %.
Сравнение полученных результатов
| Аналитический расчет | Численный расчет | Погрешность, % |
| Максимальные перемещения общей конструкции, мм | ||
| 93,1 | 89,58 | 4,07 |
| Максимальные эквивалентные напряжения внутреннего слоя, МПа | ||
| 180,78 | 173,56 | 4,16 |
| Аналитический расчет | Численный расчет | Погрешность, % |
| Максимальные эквивалентные напряжения срединного слоя, кПа | ||
| 150,9 | 157,46 | 4,35 |
| Максимальные эквивалентные напряжения внешнего слоя, МПа | ||
| 164,00 | 157,5 | 4,13 |
Для исследования металлоемкости трехслойного шарового резервуара необходим сравнительный объект – однослойный шаровой резервуар с идентичным объемом. Масса оболочки трехслойного шарового резервуара с рассчитанными параметрами равна 110 т, а масса оболочки однослойного шарового резервуара с толщиной стенки 40 мм, изготовленного в АО «Уралхиммаш», составляет 136 т. При сравнении масс двустенного и одностенного шаровых резервуаров масса разработанной конструкции меньше на 19 %.
Заключение. Представленные исследования проведены в рамках линейной постановки задачи. По предложенной методике расчета можно определить оптимальные сечения внутренней и наружной оболочки, сечения связей между оболочками, т.е. решить задачу в первом приближении. Результаты исследования показали перспективность многослойных конструкций в резервуаростроении.
Однако на практике невозможно изготовить оболочку с идеальной геометрией. Так в шаровом резервуаре для хранения углеводородного сырья имеет место конструктивная нелинейность, вызванная наличием врезок патрубков, люков, опорных элементов. Геометрическую нелинейность характеризуют остаточные сварочные деформации и ошибки монтажников при сборке резервуара из отдельных листов. В настоящее время существует методика лазерного сканирования крупных резервуаров [13], позволяющая оценить отклонения стенки от проектного положения с высокой разрешающей способностью. Физическая нелинейность в стенке резервуара вызвана формообразованием листовых оболочечных элементов и сваркой их между собой. Таким образом, научный и практический интерес вызывает вопрос оценки напряженно-деформированного состояния оболочек в условиях нелинейности при упруго-пластичном состоянии металла. Это станет следующим объектом наших исследований.
Выводы. Разработана методика построения конструкции двустенного шарового резервуара в программном комплексе SCAD, позволяющая произвести расчет НДС методом конечных элементов.
Разработана численная модель двустенного шарового резервуара. Установлено, что для получения результатов расчета с погрешностью P ≤ 5 % размер конечного элемента не должен превышать 300×300×δ мм.
Исследована конструкция двустенного шарового резервуара. Установлены конструктивные параметры, позволяющие обеспечить эксплуатационную надежность сооружения при снижении металлоемкости по сравнению с одностенным резервуаром на 19 %.
Литература
- Abashev D.R. Development of the model of elastoplastic deformation, fatigue criteria and methods for identifying material parameters of construction alloys: Avtoref. dis. … kand. fiz.-mat. nauk. Korolev: Tsentralnyi nauchno-issledovatelskii institut mashinostroeniya, 2016, p. 21 (in Russian).
- Abdullin I.N. Modeling a girder filler in a three-layer structure. Poisk effektivnykh reshenii v protsesse sozdaniya i realizatsii nauchnykh razrabotok v rossiiskoi aviatsionnoi i raketnokosmicheskoi promyshlennosti: Mezhdunarodnaya nauchno-prakticheskaya konferentsiya “Poisk effektivnykh reshenii v protsesse sozdaniya i realizatsii nauchnykh razrabotok v rossiiskoi aviatsionnoi i raketnokosmicheskoi promyshlennosti”, Kazan, 5-8 avgusta 2014, p. 307-312 (in Russian).
- Annin B.D., Volchkov Yu.M. Non-classical models for the theory of plates and shells. Prikladnaya mekhanika i tekhnicheskaya fizika. 2016. Vol. 57. N 5, p. 5-14. DOI: 10.15372/PMTF20160501 (in Russian).
- Golovanov A.I., Tyuleneva O.N., Shigabutdinov A.F. Finite element method in statics and dynamics of thin-walled structures. Moscow: Fizmatlit, 2006, p. 392 (in Russian).
- Gorshkov A.G., Starovoitov E.I., Yarovaya A.V. Mechanics of layered viscoelastoplastic structural elements. Moscow: Fizmatlit, 2003, p. 577 (in Russian).
- Gureeva N.A. Comparative analysis for the efficiency of using finite elements of triangular and quadrangular shapes in the calculations of shells. Avtoref. dis. … kand. tekhn. nauk. Volgograd: Volgogradskaya gosudarstvennaya selskokhozyaistvennaya akademiya, 2004, p. 28 (in Russian).
- Zelivyanskii E., Karpilovskii V., Kriksunov E. Transition from an architectural solution to a design scheme. SCADmaster. 2000. N 5, p. 40-43 (in Russian).
- Ishchanov T.R. Finite element analysis of the stress-strain state of thin shells taking into account the transverse shear for var-ious options of approximation of angular displacements: Avtoref. dis. … kand. tekhn. nauk. Volgograd: Volgogradskii gosudarstvennyi agrarnyi universitet. 2018, p. 21 (in Russian).
- Kiseleva R.Z. Calculation of layered plates and revolution shells based on three-dimensional finite elements without the as-sumption of normal deformation: Avtoref. dis. ... kand. tekhn. nauk. Volgograd: Volgogradskaya gosudarstvennaya selskokhozyaistvennaya akademiya, 2010, p. 20 (in Russian).
- Lazareva S.A. Approximation properties of the Fedorenko finite superelement method. Vychislitelnye tekhnologii. 2008. Vol. 13. Spetsialnyi vypusk 4, p. 75-81 (in Russian).
- Makarov D.A. Mathematical modeling of the processes of non-isothermal inelastic deformation and damage accumulation in structural materials. Avtoref. dis. … kand. fiz.-mat. nauk. Moscow, Moskovskii avtomekhanicheskii institut, 2005, p. 21 (in Russian).
- Kabrits S.A., Mikhailovskii E.I., Tovstik P.E., Chernykh K.F., Shamina V.A. General non-linear theory of elastic shells. St Petersburg: Izd-vo Sankt-Peterburgskogo universiteta, 2002, p. 388 (in Russian).
- Salnikov A.P Assessment of the stress-strain state of reservoirs by the state of ground-based laser scanning. Avtoref. dis. … kand. fiz.-mat. nauk. Moscow: Rossiiskii gosudarstvennyi universitet nefti i gaza im. I.M.Gubkina, 2016, p. 22 (in Russian).
- Semenov P.V Applied version of the theory of elastoplastic processes and the accumulation of material damage. Avtoref. dis. … kand. fiz.-mat. nauk. Moscow: Moskovskii avtomekhanicheskii institut, 2013, p. 21 (in Russian).
- Abot J.L., Daniel I.M., Gdoutos E.E. Contact Law for Composite Sandwich Beams. Journal of Sandwich Structures and Materials. 2002. Vol. 4. N 2, p. 157-173. DOI: 10.1177/1099636202004002705

