Применение машинного обучения при моделировании параметров бурового раствора реологической модели Гершеля – Балкли для оптимизации промывки скважины
- 1 — канд. техн. наук научный руководитель лаборатории Санкт-Петербургский горный университет императрицы Екатерины II ▪ Orcid ▪ Scopus ▪ ResearcherID
- 2 — д-р техн. наук научный руководитель научного центра, заведующий кафедрой Санкт-Петербургский горный университет императрицы Екатерины II ▪ Orcid ▪ Scopus
- 3 — канд. техн. наук исполнительный директор научного центра Санкт-Петербургский горный университет императрицы Екатерины II ▪ Orcid ▪ Scopus ▪ ResearcherID
- 4 — ведущий инженер лаборатории Санкт-Петербургский горный университет императрицы Екатерины II ▪ Orcid
Аннотация
Буровые промывочные жидкости на водной и углеводородной основах представляют собой полидисперсные нелинейно-вязкие системы, напряженное состояние которых качественно описывается реологической моделью Гершеля – Балкли. В данной работе выдвинута гипотеза о том, что повышение качества выноса шлама может быть достигнуто путем выбора наиболее эффективной комбинации трех параметров реологической модели при проектировании свойств бурового раствора – начального напряжения сдвига, коэффициента консистенции и показателя нелинейности модели. Определение эффективной комбинации реологических параметров модели Гершеля – Балкли для обеспечения равномерного профиля скоростей осуществлялось методами корреляционного и регрессионного анализов и методом машинного обучения. Расчетная часть работы проведена в пакете символьных вычислений Wolfram Mathematica. Определены детерминированные участки зависимости количественного показателя равномерности профиля скоростей от реологических коэффициентов. Для удобства инженерных расчетов построена линейная математическая модель, отражающая связь модифицированного коэффициента эксцесса от коэффициентов трехпараметрического реологического уравнения Гершеля – Балкли. Предложенную методику можно рекомендовать для проектирования новых буровых промывочных систем и тестирования существующих для заданных технологических параметров промывки скважины.
Введение
Одной из важнейших функций буровых промывочных жидкостей является вынос частиц выбуренной породы из скважины. Качество выноса достигается за счет скорости потока в кольцевом пространстве скважины, плотности раствора и его реологических характеристик. Правильный выбор реологических характеристик буровых растворов способствует повышению механической скорости проходки [1]. Управление реологическими характеристиками технологических жидкостей для строительства скважин достигается путем выбора реагентов и их концентраций [2, 3]. Вид профиля скоростей промывочной жидкости значительно влияет на качество выноса шлама [4]. При достижении плоского распределения скоростей в кольцевом пространстве скважины частицам передается наиболее равномерный импульс в направлении потока. При движении жидкостей в трубах профиль скоростей имеет симметричное распределение с максимальной скоростью в центре потока [5]. При движении в затрубном пространстве максимальная скорость смещается к оси труб, что приводит к неравномерному выносу шлама и образованию его скоплений у стенок скважины [6, 7], что подтверждается графиками аналитических и численных решений уравнений движения [8, 9]. Неравномерность профиля скоростей при движении в трубах и кольцевых каналах подтверждается экспериментально [10]. В исследовании [11] показана достаточно высокая сходимость результатов численного эксперимента по моделированию потоков жидкости с частицами шлама с результатами стендового эксперимента. Аналогичные решения можно получить с использованием методов контрольного объема в программных комплексах Ansys или OpenFOAM [12, 13]. Также расчетные пакеты позволяют моделировать очистку ствола скважины от шлама с учетом скорости вращения бурильной колонны [14] и тепловых эффектов [15]. Учет температурных факторов имеет особую значимость при строительстве и освоении скважин в Арктической зоне [16, 17]. В исследовании [18] рассматривается вопрос моделирования выноса шлама в наклонно-направленных и горизонтальных скважинах в условиях высоких температур и давлений. Также в настоящее время значительное внимание уделяется потерям бурового раствора. Расчет скоростей и давлений для конкретных скважинных условий способствует совершенствованию технологии промывки при поглощении бурового раствора [19].
При моделировании потоков технологических жидкостей важнейшую роль играет выбор реологической модели. Доказано, что реологические свойства современных буровых промывочных жидкостей наиболее качественно отражает модель Гершеля – Балкли [20-22]. Она подходит как для растворов, содержащих в рецептуре твердую фазу, так и без нее [23]. Наиболее точным методом определения коэффициентов реологической модели является метод наименьших квадратов, который применяется к аппроксимации экспериментальной зависимости касательных напряжений от скоростей сдвига [24]. Математическая постановка задачи движения технологической жидкости в кольцевом пространстве включает уравнение движения, реологическую модель жидкости и граничные условия. Важную роль играет выбор реологической модели раствора, так как путем управления ее коэффициентами можно влиять на распределение скоростей и давлений. Математическая модель движения бурового раствора в кольцевом пространстве скважины взята из исследования [24], где представлен способ нахождения численного решения распределения скоростей нелинейно-вязкой жидкости реологической модели Гершеля – Балкли в кольцевом пространстве скважины. В отличие от модели Оствальда – де Ваале она содержит три коэффициента:
где τ0 – начальное напряжение сдвига; γ – скорость сдвига; K – коэффициент консистенции; n – показатель нелинейности.
Стационарное модифицированное дифференциальное уравнение движения Навье – Стокса для нахождения поля скоростей:
где ρ – плотность жидкости; r – радиальная координата; g – ускорение свободного падения; ∂p/∂z – градиент давлений на расстоянии L.
Для граничных условий кольцевого пространства:
где w – скорость слоя жидкости; R1 – внешний радиус бурильной трубы; R2 – радиус скважины.
Допущениями являются несжимаемость жидкости ρ = const и предположение одномерности и стационарности потока:
В исследовании [24] сравнивались решения в приближении ньютоновской среды с аналитическим решением для течения Пуазейля в кольцевом зазоре. Доказана физическая адекватность численного решения при варьировании входных параметров. Численное решение получено с использованием языка Wolfram Language в виде интерполирующей функции, позволяющей отобразить значение скорости в зависимости от координаты. Также введен числовой показатель равномерности профиля скоростей, именуемый модифицированным коэффициентом эксцесса:
где μ1, μ2 – центральные моменты, примененные к распределению скоростей в потоке.
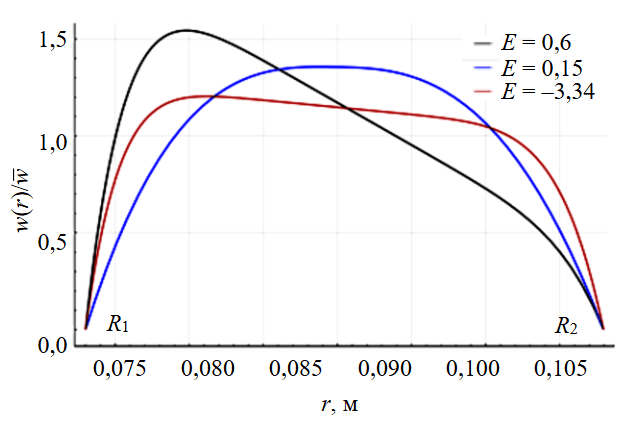
Рис.1. Наиболее плоские и вытянутые профили скоростей
Минимальность данного параметра свидетельствует о наличии наиболее равномерного профиля скоростей потока. Использование программного кода позволяет получать численное решение для профиля скоростей и соответствующего ему модифицированного коэффициента эксцесса, показывающего равномерность профиля скоростей. Для наиболее качественной визуальной оценки распределения скоростей отображают графически в безразмерном виде, представляющем собой отношение скорости в точке к средней скорости потока – w(r)/w¯. Область построения расположена между стенками бурильной трубы R1 и скважины R2. Примеры распределения скоростей и соответствующие значения коэффициента эксцесса изображены на графике (рис.1). Наиболее вытянутый и смещенный профиль соответствует наибольшему значению параметра E.
Известно, что в модели Шведова – Бингама на равномерность распределения скоростей влияет значение начального напряжения сдвига, а на среднюю скорость потока – пластическая вязкость. В степенной модели Оствальда – де Ваале снижение показателя n приводит к образованию плоского профиля скоростей, недостатком приближения данной модели можно считать отсутствие учета начальных напряжений сдвига бурового раствора τ0. Реологическое уравнение степенной среды имеет вид:
В исследовании [24] показано, что в модели явной корреляции между параметрами Гершеля – Балкли τ0, K, n и модифицированным коэффициентом эксцесса E не наблюдается. Это подтверждает невозможность управления распределением скоростей жидкости при помощи параметров τ0 ,K, n независимо друг от друга. Управление отдельно показателем нелинейности n, как в степенной модели, не имеет положительного результата [4, 8]. С учетом обнаруженных недостатков целью работы является разработка способа определения связей между тремя реологическими параметрами модели Гершеля – Балкли с тенденцией к образованию равномерного профиля скоростей, численную оценку которого можно провести с использованием модифицированного коэффициента эксцесса.
Методы
Для определения влияния комбинации параметров модели Гершеля – Балкли (1) на равномерность профиля скоростей потока необходимо найти зависимость модифицированного коэффициента эксцесса E от коэффициентов τ0, K, n. Так как E зависит от вида распределения скоростей, полученного численным решением уравнения движения с заданными геометрическими условиями, перепадов давлений и параметров жидкости, задача сводится к нахождению зависимости между числовыми параметрами, при этом предполагается нелинейный вид зависимости:
Для нахождения зависимости данного вида необходимо составить таблицу значений параметров E, τ0, K, n, соответствующую физическим и технологическим параметрам процесса промывки скважины. В качестве ограничений τ0, K, n при предварительной подготовке таблицы значений предлагается использовать широкие диапазоны параметров, соответствующие параметрам бурового раствора [25]: начальное напряжение сдвига 0,1≤τ0≤5 Па; коэффициент консистенции 2≤K≤15 Па·сn; показатель нелинейности 0,15≤n≤1. Для работы с наиболее перспективными жидкостями предполагается использование реологических параметров, обеспечивающих высокое качество выноса шлама в ламинарном режиме, рассчитать которые можно по методикам источника [26]. При ламинарном режиме движения динамические давления ниже, чем при турбулентном, что снижает вероятность гидроразрыва пласта при промывке, поэтому рассчитывается критическая скорость бурового раствора, свыше которой режим движения переходит в турбулентный [27].
Далее вычисляется индекс качества выноса шлама для критической скорости бурового раствора, методика вычисления включает расчет скорости транспорта шлама на основании разницы скорости потока и скорости оседания частицы. Необходимо учитывать касательные напряжения и режим обтекания в окрестностях частицы, который может быть ламинарным или турбулентным. Для коэффициентов τ0, K, n, соответствующих высоким показателям индекса очистки, рассчитывается профиль скоростей при давлениях, соответствующих критической скорости бурового раствора. Рассчитанный модифицированный коэффициент эксцесса E заносится в таблицу, подлежащую дальнейшей обработке.
Трехфакторная зависимость E=f(τ0, K, n) может иметь выраженный нелинейный характер. Дальнейшая задача включает в себя нахождение детерминированных участков зависимости вида (2) с возможностью определения линейных участков, после чего возможно построение линейной многофакторной регрессионной зависимости:
где ai – коэффициенты регрессии.
Преимущество выделения линейных участков заключается в возможности перехода к аналитическому виду зависимости, которую предпочитают использовать проектировщики гидравлической программы бурения для оценки равномерности профиля скоростей при выборе промывочной жидкости.
Для описания многофакторных нелинейных зависимостей успешно применяются методы машинного обучения. Например, в работе [28] описывается опыт использования нейронной сети для оценки эквивалентной циркуляционной плотности на основе большого массива данных. В статье [29] применялся метод нейронных сетей для прогнозирования пластической и эффективной вязкостей буровых растворов на углеводородной основе. В исследовании [30] использовалась модель Гауссовского процесса для прогнозирования реологических свойств раствора по шести факторам: вязкости по воронке Марша, плотности, объемном содержании воды, нефти и твердых веществ, температуре. Коэффициент детерминации превышал 0,9, что указывает на высокую точность прогнозирования. Авторы работы [31] используют гибридное машинное обучение для быстрого прогнозирования реологических и фильтрационных свойств буровых растворов на водной основе. В рамках исследования [32] метод машинного обучения задействован для прогнозирования пористости и проницаемости при бурении. В статье [33] предложен способ обучения нейронных сетей (язык программирования Python) прогнозированию свойств буровых растворов в условиях высокого давления и температуры. Результаты прогнозирования сравниваются с реологическими моделями Гершеля – Балкли и степенного закона. Значения напряжения сдвига были спрогнозированы с помощью трех входных параметров: скорости сдвига, давления и температуры. Авторы исследования [34] для применения логарифмической линейной (L-L) математической модели разработали скрипт на языке Wolfram Language. С помощью данного кода была реализована математическая модель для анализа реологических свойств бурового раствора, основанная на нелинейной зависимости измеренных значений напряжения сдвига и скорости сдвига бурового раствора, используемого в процессе бурения нефтяных и геотермальных скважин. Методы машинного обучения хорошо зарекомендовали себя в решении задач прогнозирования осложнений при эксплуатации скважин [35, 36]. Такие подходы применимы для обработки промысловых данных с высоким количеством шумов, которые возможны при наличии высокого уровня воздействия случайных факторов.
Исходя из целей данного исследования, язык Wolfram Language выбран для полного цикла расчетов, в том числе численного решения уравнения движения относительно профиля скорости и нахождения детерминированных участков зависимости (3). С использованием функции Predict выбирается метод машинного обучения – «Случайный лес», «Ближайшие соседи», «Дерево решений» и др. [37]. Недостатком предиктивных моделей является отсутствие возможности построения зависимости аналитического вида. Определение линейных участков зависимости позволяет осуществить переход к модели линейной многофакторной регрессии. Опция LinearRegression в функции Predict позволяет строить многофакторные линейные зависимости вида (4). Для выбора наиболее эффективного метода функции Predict при обработке первично составленной таблицы данных используется заранее написанный шаблон по применению каждого и сравнения коэффициента детерминации R2. Для поиска детерминированных участков, потенциально подходящих для построения аналитической формы (4), используется метод с наивысшим значением R2. Наличие же детерминированных участков легко определить путем анализа графиков ComparisonPlot и ResidualPlot, показывающих отклонение между фактическим и прогнозируемым значениями и величину отклонения на разных участках прогнозируемого значения.
Разработана методика определения наиболее эффективных комбинаций параметров модели Гершеля – Балкли для обеспечения высокого качества очистки ствола скважины, в том числе путем формирования наиболее равномерного профиля скоростей, которую определяют следующие этапы:
- Используя методику расчета коэффициента эффективности выноса шлама, необходимо определить первичные требования к реологическим характеристикам бурового раствора в приближении степенного реологического закона при обеспечении ламинарного режима движения.
- Определить вид профиля скоростей с расчетом модифицированного коэффициента эксцесса для жидкости Гершеля – Балкли с показателями K и n, удовлетворяющими первичным требованиям.
- Определить комбинации τ0, K, n, удовлетворяющие требованию высоких значений коэффициента эффективности выноса шлама, а также равномерный профиль скоростей с наименьшим показателем модифицированного коэффициента эксцесса E.
- С использованием методов машинного обучения определить связь τ0, K, n с количественным показателем равномерности профиля скоростей потока – модифицированным коэффициентом эксцесса E.
- При определении участков, подлежащих построению аналитической формы линейной многофакторной регрессии, рассчитать коэффициенты модели.
- Разработать методические рекомендации по проектированию буровых промывочных жидкостей с эффективной комбинацией реологических коэффициентов τ0, K, n для обеспечения высокого качества выноса шлама в ламинарном режиме при наличии равномерного профиля скоростей потока.
Обсуждение результатов
С использованием языка Wolfram Language сгенерировано 9235 комбинаций параметров τ0, K, n в следующих границах варьирования и шагом Δ:
Выполнен расчет коэффициента эффективности выноса шлама для критической скорости бурового раствора – скорости, свыше которой раствор начинает движение в турбулентном режиме. Такой выбор обоснован ограничением безопасных показателей бурения при ламинарном режиме, имеющем значительно меньшие гидродинамические давления. Общими входными параметрами расчетов являются плотность бурового раствора 1200 кг/м3; плотность шлама 2300 кг/м3; диаметр сферической модели крупного шлама 7,6 мм; диаметр скважины 215,9 мм; внешний диаметр бурильной трубы 146 мм.
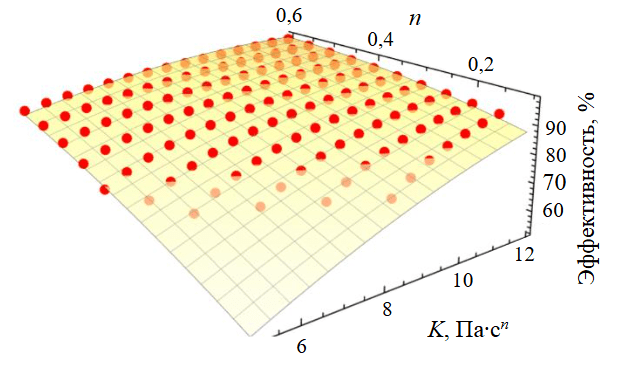
Рис.2. Зависимости коэффициента эффективности выноса шлама от коэффициентов K и n реологической модели степенной жидкости
Количество комбинаций 7980 дает эффективность выноса более 70 %, 7582 комбинации – более 80 %. Наибольшая эффективность при n = 1, но современные растворы для бурения наклонно-направленных и горизонтальных скважин обладают выраженными псевдопластичными свойствами, и часто параметр n << 1 [38]. График, характеризующий тенденцию изменения коэффициента эффективности выноса шлама от реологических коэффициентов K и n, представлен на рис.2. С ростом коэффициентов консистенции K и нелинейности n скорость оседания частиц снижается, поскольку коэффициент консистенции в степенной реологической модели является аналогом вязкости, следовательно повышение вязкости снижает скорость оседания частиц за счет повышения удерживающей способности потоком жидкости частиц во взвешенном состоянии. Данный вывод соответствует теории числа Стокса за счет вязкостных характеристик жидкости [39].
Коэффициент нелинейности в степенной реологической модели показывает неньютоновское поведение среды – с ростом скорости сдвига снижается вязкость при низких значениях показателя степени. Следовательно, при n → 1 вязкость имеет меньшую тенденцию к убыванию, при n = 1 вязкость постоянна, при росте n > 1 жидкость можно считать дилатантной, но такие жидкости не применяются при бурении. Увеличение вязкости повышает удерживающую способность, поэтому ее снижение, отражаемое снижением коэффициента n, не желательно в задаче выноса шлама. С ростом данных коэффициентов критическая скорость бурового раствора растет. Турбулентный режим наступает при более высоких скоростях, что благоприятно для процесса бурения, так как можно повышать скорость потока путем увеличения расхода, избегая перехода в турбулентный режим с высоким давлением [40].
На наличие турбулентных потоков влияет гидравлический диаметр кольцевого пространства, реологические характеристики промывочной жидкости и ее плотность. Наиболее оперативным методом предупреждения возникновения турбулентного режима является снижение расхода промывочной жидкости и поддержание ее параметров в диапазоне проектируемой гидравлической программы бурения. В проектах строительства скважин также проводят контроль давлений в терминах эквивалентной циркуляционной плотности [41].
Рассчитаны значения модифицированного коэффициента эксцесса для каждого распределения скоростей при варьировании коэффициентов τ0, K, n в условиях перепада давлений соответствующего критической скорости потока. По статистическому правилу двух сигм определены профили с наиболее равномерным распределением скоростей с вероятностью 95 %. Количество 4845 элементов с эффективностью выноса более 70 % и n ≤ 0,8 соответствует актуальным в настоящее время рецептурам буровых промывочных жидкостей. Для них вычислены значения показателя равномерности профиля скоростей. Тест был проведен для жидкостей с эффективностью выноса более 70 % и n ≤ 0,8. Следующим шагом являлось определение зависимости вида (3) модифицированного коэффициента эксцесса от параметров реологической модели. Основываясь на результатах исследования [24], можно предположить, что искомая связь является нелинейной. Ввиду многофакторности задачи аппроксимации был использован шаблон подбора метода машинного обучения. Данные делились случайным образом на тренировочную и тестовую выборки в пропорции 80/20 соответственно. Входными параметрами являлись τ0, K, n выходным – модифицированный коэффициент эксцесса E. По коэффициенту детерминации определено, что метод «Нейронная сеть» языка Wolfram Language является наиболее эффективным в данной задаче, R2 = 0,996 (рис.3). Распределение отклонений (рис.3, б) также свидетельствует о высоком качестве аппроксимации. Анализ графиков показал, что детерминированные последовательности определены для модифицированного коэффициента эксцесса, начиная с 0,9. Дальнейшее рассмотрение задачи продолжается исключительно на данном участке.
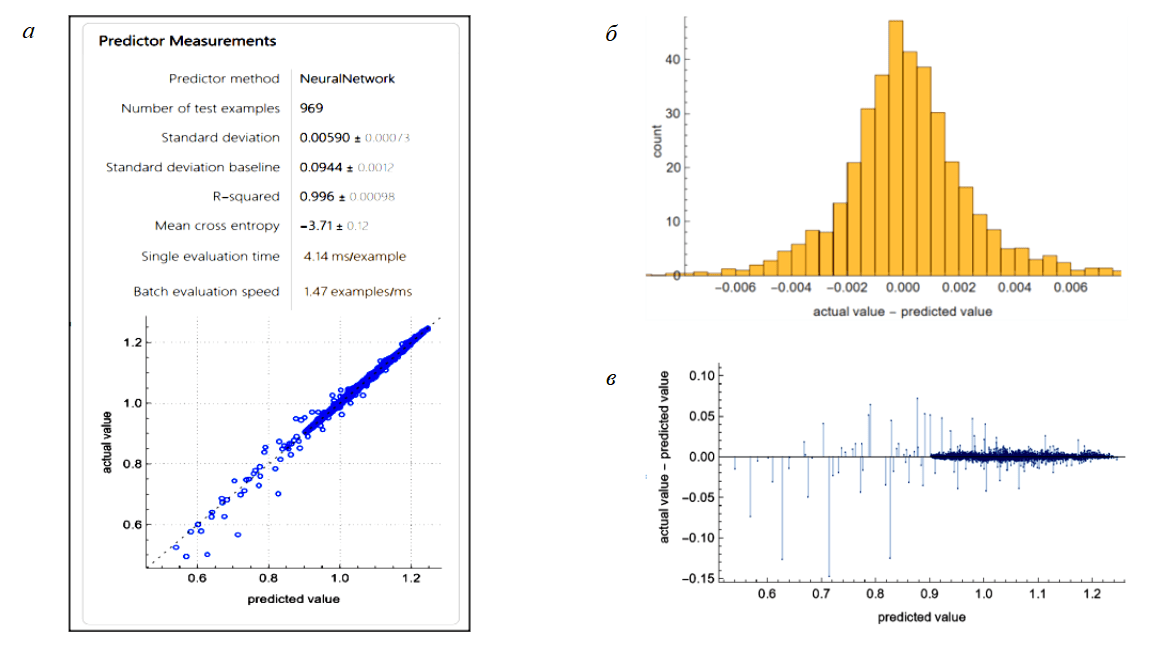
Рис.3. Характеристики нейросетевого метода: а – диалоговое окно характеристик метода; б – гистограмма отклонений ResidualHistogram; в – распределение отклонений по областям ResidualPlot
Наиболее равномерным профилем скоростей из детерминированных значений является 0,9 ≤ Е ≤ 0,95. Ограничение параметров (5) ужесточается из-за требований соответствия высоким показателям выноса шлама:
Согласно исследованию [24], управление данными параметрами независимо друг от друга в приближении реологической модели Гершеля – Балкли для достижения равномерного профиля скоростей невозможно. Анализ комбинаций параметров реологической модели, эффективных для выноса шлама в ламинарном режиме с наличием наиболее равномерных профилей скорости, показал необходимость выполнения условий для параметров n и τ0 в зависимости от K:
Таким образом установлено, что при использовании долота и бурильных труб с диаметрами 215,9 и 146 мм соответственно наиболее равномерным распределениям скоростей жидкостей реологической модели Гершеля – Балкли соответствуют значения расчетного параметра диапазона 0,9 ≤ 𝐸 ≤ 0,95. Для достижения данных показателей определены границы допустимых значений реологических параметров (6) и (7).
Изложенная последовательность расчетов требует достаточно высоких инженерных навыков и специализированного программного обеспечения для обработки данных, что затруднительно для производственной сферы. Исходя из этого, для конечного пользователя, например инженера по буровым растворам, была бы полезна конечная расчетная формула и рекомендации к ее применению.
На детерминированном участке значений (6) в диапазоне 0,9 ≤ 𝐸 ≤ 0,95 предлагается построить модель линейной многофакторной регрессии вида (4), по которой можно рассчитать модифицированный коэффициент эксцесса и сделать прогноз вида профиля скоростей при тестировании рецептур буровых растворов. Для значений, удовлетворяющих (6), (7), с использованием языка Wolfram Language применены функции линейной многофакторной регрессии – LinearModelFit. Значение коэффициента детерминации R2 = 0,83, наибольшее количество отклонений зафиксировано около 0. Для прогнозирования равномерности профиля скоростей с целью повышения качества выноса шлама подтверждается возможность применения построенного регрессионного уравнения:
На графиках (рис.4) показаны проекции четырехмерной модели (8) на трехмерное пространство при фиксированных значениях реологических параметров. Поверхности отклика обеспечивают аппроксимацию исходных данных на рассматриваемых участках. Низкие значения отклонений и значение R2 = 0,83 объясняются незначительным проявлением нелинейности в окрестности поверхности отклика. Пренебрегая невысокой нелинейностью, можно использовать формулу (8) для достаточно простого вычисления. Для наиболее равномерного профиля значения E будут принимать наименьшие значения при соблюдении условий (6)-(7).
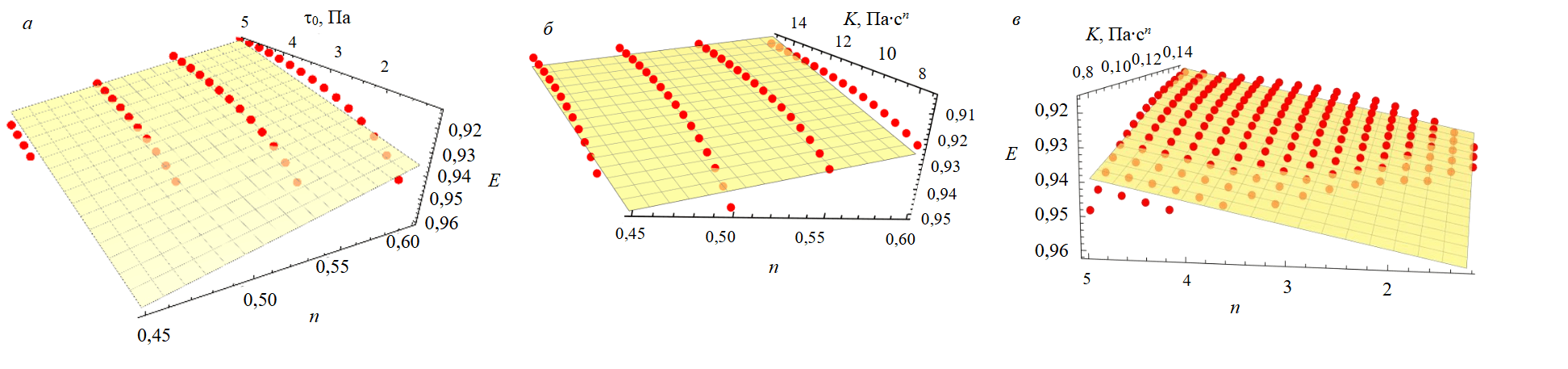
Рис.4. Трехмерные проекции линейной регрессии: а – τ0, n, E при K = 8 Па∙сn; б – K,n, E при τ0 = 3 Па; в – K, τ0, E при n = 0,45
Для проверки представленного метода моделирования сравним два набора параметров реологической модели при моделировании распределения скоростей численным решением и с использованием метода контрольного объема пакета Ansys Fluent. Преимуществом программ CDF является высокая точность расчетов, учитывающих различные факторы [42]. Условия расчета: диаметр скважины 215,9 мм; внешний диаметр трубы 146 мм; плотность раствора 1200 кг/м3. Для модели Гершеля – Балкли тестируется два набора параметров:
1) τ0= 3,5 Па, n = 0,6, K = 7, удовлетворяющие условиям (6), (7);
2) τ0= 2 Па, n = 0,4, K = 7, не удовлетворяющие условиям (6), (7).
При расчете модифицированного коэффициента эксцесса по приближенной формуле (8) для набора параметров 1 E = 0,928, набора параметров 2 E = 0,967. Установлено, что для набора параметров 1 профиль скоростей более равномерный по сравнению с набором параметров 2. Анализ графиков (рис.5) показывает соответствие решений, полученных численным методом, решениям, полученным с использованием метода контрольного объема. Незначительное отклонение может быть обосновано различием расчетных алгоритмов Wolfram Language с построением интерполирующей функции численного решения и решателя пакета Ansys Fluent. При этом видно, что гипотеза о наличии более плоского профиля скоростей для набора параметров 1 подтверждается при расчете обоими методами.
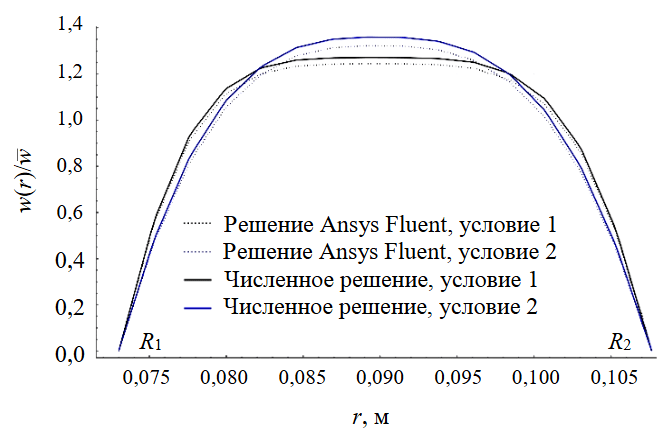
Рис.5. Сравнение распределений скоростей, полученных с использованием численного решения и с помощью пакета Ansys Fluent
Заключение
В работе представлен способ определения связи между параметрами модели Гершеля – Балкли и модифицированным коэффициентом эксцесса для обеспечения равномерного профиля скоростей бурового раствора в кольцевом пространстве скважины. Научная новизна работы заключается в одновременном учете трех параметров реологической модели Гершеля – Балкли и выводе условий совместимости для них. Проанализирована гипотеза о возможности управления распределением скоростей нелинейно-вязкой жидкости в кольцевом пространстве скважины при помощи выбора комбинаций параметров реологической модели. Повышение качества выноса шлама может достигаться путем поддержания наиболее эффективной комбинации параметров модели Гершеля – Балкли при проектировании свойств бурового раствора для обеспечения наиболее равномерного профиля скоростей.
Анализ влияния коэффициентов модели Гершеля – Балкли на равномерность профиля скоростей показал качественно новый характер, в отличие от использования упрощенных реологических моделей. В то время как для модели Шведова – Бингама равномерность профиля скоростей достигается управлением начального напряжения сдвига, для степенной модели Оствальда – де Ваале – показателем n, для модели Гершеля – Балкли установлено одновременное влияние τ0, K, n, что приводит к необходимости установления связи между ними.
В работе показан метод определения взаимосвязи трех параметров реологической модели с показателем равномерности профиля скоростей. В качестве примера рассмотрены комбинации наиболее предпочтительных реологических параметров для промывки кольцевого пространства между трубой и скважиной диметрами 146 и 215,9 мм соответственно. Определены условия совместимости для коэффициентов τ0, n с коэффициентом консистенции K. Построена линейная математическая модель E=f(τ0, K, n), отражающая связь количественного параметра, используемого для оценки зависимости равномерного профиля скоростей, с коэффициентами трехпараметрического реологического уравнения Гершеля – Балкли.
Выполнение данных рекомендаций по проектированию параметров промывочной жидкости может привести к образованию равномерного профиля скоростей, что улучшит вынос шлама. Использование построенной модели позволит сравнивать равномерность профиля скоростей числовым путем для тестирования потенциально рекомендуемых к применению жидкостей, для сравнения результатов расчетов использовался пакет Ansys Fluent.
С помощью описанной методологии можно провести анализ изменения профиля скоростей для наиболее распространенных комбинаций геометрических параметров кольцевого пространства. Наличие шлама в буровом растворе приводит к изменению его плотности и реологических характеристик. Замер параметров бурового раствора со шламом при температурных диапазонах месторождения позволяет моделировать процесс для условий, приближенных к скважинным. Также эти данные могут быть получены с использованием системы непрерывного анализа бурового раствора на буровой установке. Перспективным является построение номограмм для реологических параметров модели Гершеля – Балкли в зависимости от отношения диаметров. Наличие функциональных зависимостей дает возможность наиболее эффективно выбрать параметры раствора для обеспечения равномерного профиля скоростей в кольцевом пространстве скважины.
Литература
- Jalakani R., Tabatabaee Moradi S.S., Morenov V. Reliability Analysis of a Drilling Bit Penetration Model in Oil and Gas Wells: A Case Study // International Journal of Engineering – Transactions B: Applications. 2024. Vol. 37. Iss. 11. P. 2213-2222. DOI: 10.5829/ije.2024.37.11b.08
- Raupov I., Rogachev M., Sytnik J. Design of a Polymer Composition for the Conformance Control in Heterogeneous Reservoirs // Energies. 2023. Vol. 16. Iss. 1. № 515. DOI: 10.3390/en16010515
- Zubkova O.S., Kuchin V.N., Toropchina M.A., Ivkin A.S. Potential Application of Saponite Clay for Production of Drilling Fluids // International Journal of Engineering – Transactions B: Applications. 2024. Vol. 37. Iss. 11. Р. 2142-2149. DOI: 10.5829/ije.2024.37.11b.01
- Ferroudji H., Rahman M.A., Hadjadj A. et al. 3D numerical and experimental modelling of multiphase flow through an annular geometry applied for cuttings transport // International Journal of Multiphase Flow. 2022. Vol. 151. № 104044. DOI: 10.1016/j.ijmultiphaseflow.2022.104044
- Ashena R., Badrouchi F., Elmgerbi A. et al. Stepwise mathematical derivation of the Herschel–Bulkley laminar fluid flow equations – in pipes // Journal of Petroleum Exploration and Production Technology. 2023. Vol. 13. Iss. 2. P. 625-643. DOI: 10.1007/s13202-022-01566-2
- Belimane Z., Hadjadj A., Ferroudji H. et al. Modeling surge pressures during tripping operations in eccentric annuli // Journal of Natural Gas Science and Engineering. 2021. Vol. 96. № 104233. DOI: 10.1016/j.jngse.2021.104233
- Chandrasekhar S.V. Annular Couette–Poiseuille flow and heat transfer of a power-law fluid – analytical solutions // Journal of Non-Newtonian Fluid Mechanics. 2020. Vol. 286. № 104402. DOI: 10.1016/j.jnnfm.2020.104402
- Xiaofeng Sun, Kebo Zhang, Ye Chen et al. Study on the settling velocity of drilling cuttings in the power law fluid // Powder Technology. 2020. Vol. 362. P. 278-287. DOI: 10.1016/j.powtec.2019.11.025
- Roberts T.G., Cox S.J. An analytic velocity profile for pressure-driven flow of a Bingham fluid in a curved channel // Journal of Non-Newtonian Fluid Mechanics. 2020. Vol. 280. № 104278. DOI: 10.1016/j.jnnfm.2020.104278
- Lin Zhang, Yigang Wang, Dake Chen, Cheng Chen. Prediction and correction of scaling effects on velocity profile in hydraulic laboratory experiments // Desalination and Water Treatment. 2019. Vol. 149. 2019. P. 31-42. DOI: 10.5004/dwt.2019.23848
- Sirui Tong, Bin Miao, Mengsong Shen et al. Experimental and numerical analysis of granular phase flow behavior in a rotary bed reactor: Velocity profile study // Powder Technology. 2024. Vol. 444. № 119992. DOI: 10.1016/j.powtec.2024.119992
- Харламов С.Н., Джанхорбани М., Брыксин М.Р. Аспекты компьютерного моделирования процессов транспорта и очистки от шлама горизонтальных участков скважин // Математическое моделирование. 2022. Т. 34. № 11. С. 77-106. DOI: 10.20948/mm-2022-11-06
- Muangput B., Zin T., Namchanthra S. et al. CFD elucidation of high-pressure subcooled boiling flow towards effects of variable refrigerant properties using OpenFOAM empirical closures // Applications in Engineering Science. 2024. Vol. 19. № 100187. DOI: 10.1016/j.apples.2024.100187
- Alade O., Mahmoud M., Al-Nakhli A. Rheological studies and numerical investigation of barite sag potential of drilling fluids with thermochemical fluid additive using computational fluid dynamics (CFD) // Journal of Petroleum Science and Engineering. 2023. Vol. 220. Part A. № 111179. DOI: 10.1016/j.petrol.2022.111179
- Gulraiz S., Gray K.E. A model for investigating wellbore hydraulics of thermo-thixotropic drilling fluids // Geothermics. 2021. Vol. 96. № 102214. DOI: 10.1016/j.geothermics.2021.102214
- Litvinenko V.S., Dvoynikov M.V., Trushko V.L. Elaboration of a conceptual solution for the development of the Arctic shelf from seasonally flooded coastal areas // International Journal of Mining Science and Technology. 2021. Vol. 32. Iss. 1. P. 113-119. DOI: 10.1016/j.ijmst.2021.09.010
- Leusheva E., Morenov V. Effect of Temperature Conditions in Arctic Offshore Oil Fields on the Rheological Properties of Various Based Drilling Muds // Energies. 2022. Vol. 15. Iss. 5. № 5750. DOI: 10.3390/en15155750
- Al-Shargabi M., Davoodi S., Wood D.A. et al. Hole-cleaning performance in non-vertical wellbores: A review of influences, models, drilling fluid types, and real-time applications // Geoenergy Science and Engineering. 2024. Vol. 233. № 212551. DOI: 10.1016/j.geoen.2023.212551
- Buslaev G.V., Belkin A.S. Development and Field Testing of the Downhole Multi-Purpose Thrusting Device for Drilling of Deep Vertical and Directional Wells // SPE Russian Petroleum Technology Conference, 26-28 October 2015, Moscow, Russia. OnePetro, 2015. № SPE-176539-MS. DOI: 10.2118/176539-MS
- Abdullah A.H., Ridha S., Mohshim D.F., Maoinser M.A. An experimental investigation into the rheological behavior and filtration loss properties of water-based drilling fluid enhanced with a polyethyleneimine-grafted graphene oxide nanocomposite // RSC Advances. 2024. Vol. 14. Iss. 15. P. 10431-10444. DOI: 10.1039/D3RA07874D
- Saasen A., Ytrehus J.D. Viscosity Models for Drilling Fluids – Herschel-Bulkley Parameters and Their Use // Energies. 2020. Vol. 13. Iss. 20. № 5271. DOI: 10.3390/en13205271
- Bavoh C.B, Ofei T.N., Lai B. et al. Assessing the impact of an ionic liquid on NaCl/KCl/polymer water-based mud (WBM) for drilling gas hydrate-bearing sediments // Journal of Molecular Liquids. 2019. Vol. 294. № 111643. DOI: 10.1016/j.molliq.2019.111643
- Leusheva E., Brovkina N., Morenov V. Investigation of Non-Linear Rheological Characteristics of Barite-Free Drilling Fluids // Fluids. 2021. Vol. 6. Iss. 9. № 327. DOI: 10.3390/fluids6090327
- Никитин В.И. Анализ решения задачи о нахождении распределения скоростей при ламинарном движении нелинейно-вязкой промывочной жидкости в кольцевом пространстве скважины // Записки Горного института. 2022. Т. 258. С. 964-975. DOI: 10.31897/PMI.2022.93
- Heidari M., Shahbazi Kh., Fattahi M. Experimental study of rheological properties of aphron based drilling Fluids and their effects on formation damage // Scientia Iranica. Transactions C: Chemistry and Chemical Engineering. 2017. Vol. 24. Iss. 3. P. 1241-1252. DOI: 10.24200/sci.2017.4108
- Табатабаи Моради С.Ш. Вероятностное исследование оптимизации промывки скважины // Записки Горного института. 2022. Т. 258. С. 956-963. DOI: 10.31897/PMI.2022.67
- Nikolaev A., Goluntsov A., Breff A.T. Determination of the coefficient of hydraulic resistance when using anti-turbulence additives // Reliability: Theory & Applications. 2024. Vol. 19. Special Issue 6 (81). P. 107-124. DOI: 10.24412/1932-2321-2024-681-107-124
- Alkinani H.H., Al-Hameedi A.T.T., Dunn-Norman S., Lian D. Application of artificial neural networks in the drilling processes: Can equivalent circulation density be estimated prior to drilling? // Egyptian Journal of Petroleum. 2020. Vol. 29. Iss. 2. P. 121-126. DOI: 10.1016/j.ejpe.2019.12.003
- Alsabaa A., Gamal H., Elkatatny S., Abdelraouf Y. Machine Learning Model for Monitoring Rheological Properties of Synthetic Oil-Based Mud // ACS Omega. 2022. Vol. 7. Iss. 18. P. 15603-15614. DOI: 10.1021/acsomega.2c00404
- Song Deng, Bingzhao Huo, Shoukun Xu et al. Prediction of water-in-oil emulsion drilling fluids rheological properties based on GPR-Bagging ensemble learning // Colloids and Surfaces A: Physicochemical and Engineering Aspects. 2024. Vol. 686. № 133336. DOI: 10.1016/j.colsurfa.2024.133336
- Davoodi S., Mehrad M., Wood D.A. et al. Hybridized machine-learning for prompt prediction of rheology and filtration properties of water-based drilling fluids // Engineering Applications of Artificial Intelligence. 2023. Vol. 123. Part C. № 106459. DOI: 10.1016/j.engappai.2023.106459
- Jian Sun, Rongjun Zhang, Mingqiang Chen et al. Identification of Porosity and Permeability While Drilling Based on Machine Learning // Arabian Journal for Science and Engineering. 2021. Vol. 46. Iss. 7. P. 7031-7045. DOI: 10.1007/s13369-021-05432-x
- Quitian-Ardila L.H., Garcia-Blanco Y.J., Rivera A. De J. et al. Developing a machine learning-based methodology for optimal hyperparameter determination – A mathematical modeling of high-pressure and high-temperature drilling fluid behavior // Chemical Engineering Journal Advances. 2024. Vol. 20. № 100663. DOI: 10.1016/j.ceja.2024.100663
- Andaverde J.A., Wong-Loya J.A., Vargas-Tabares Y., Robles M. A practical method for determining the rheology of drilling fluid // Journal of Petroleum Science and Engineering. 2019. Vol. 180. P. 150-158. DOI: 10.1016/j.petrol.2019.05.039
- Tananykhin D.S., Struchkov I.A., Khormali A., Roschin P.V. Investigation of the influences of asphaltene deposition on oilfield development using reservoir simulation // Petroleum Exploration and Development. 2022. Vol. 49. Iss. 5. P. 1138-1149. DOI: 10.1016/S1876-3804(22)60338-0
- Podoprigora D.G., Byazrov R.R., Lagutina M.A. et al. A novel integrated methodology for screening, assessment and ranking of promising oilfields for polymer floods // Advances in Geo-Energy Research. 2024. Vol. 12. № 1. P. 8-21. DOI: 10.46690/ager.2024.04.02
- Villalobos Alva J. Beginning Mathematica and Wolfram for Data Science. Apress, 2021. 416 p. DOI: 10.1007/978-1-4842-6594-9
- Misbah B., Elgaddafi R., Malhas R.N. et al. Exploring the rheology characteristics of Flowzan and Xanthan polymers in drilling water based fluids at high-temperature and high-shear rates // Geoenergy Science and Engineering. 2024. Vol. 243. № 213309. DOI: 10.1016/j.geoen.2024.213309
- Phirommark P., Namchanthra S., Chaiyanupong J. et al. CFD elucidation of microscopic particles in a low-volumetric classifier towards effects of Stokes number and density ratio // International Journal of Thermofluids. 2023. Vol. 20. № 100497. DOI: 10.1016/j.ijft.2023.100497
- Singh R., Ahmed R., Karami H. et al. CFD Analysis of Turbulent Flow of Power-Law Fluid in a Partially Blocked Eccentric Annulus // Energies. 2021. Vol. 14. Iss. 3. № 731. DOI: 10.3390/en14030731
- Badrouchi F., Rasouli V., Badrouchi N. Impact of hole cleaning and drilling performance on the equivalent circulating density // Journal of Petroleum Science and Engineering. 2022. Vol. 211. № 110150. DOI: 10.1016/j.petrol.2022.110150
- Tananykhin D.S. Scientific and Methodological Support of Sand Management During Operation of Horizontal Wells // International Journal of Engineering – Transactions A: Basics. 2024. Vol. 37. Iss. 7. P. 1395-1407. DOI: 10.5829/ije.2024.37.07a.17
