Применение методов цифрового моделирования для прогнозирования параметров развала взорванной горной массы
- канд. техн. наук доцент Санкт-Петербургский горный университет императрицы Екатерины II ▪ Orcid
Аннотация
Рассмотрены особенности моделирования развала взорванной горной массы. Описаны различные применяемые подходы и алгоритмы. Приведены рассуждения о дальнейшем развитии отечественных цифровых технологий в горной отрасли. Описаны основные проблемы моделирования взрывного воздействия на массив горных пород. Показано, что в связи с большой сложностью математического описания горного массива и процессов взрывного разрушения при моделировании используют различные допущения, которые, безусловно, влияют на качество моделирования с точки зрения его соответствия реальным процессам. Сравниваются результаты классического решения разлета кусков горной массы на основе законов Ньютона и решения с допущением, что взорванная горная масса в начальный момент времени перемещается как единый неделимый объем и разрушается только в момент соприкосновения с поверхностью. Показано, что при одном и том же взрывном воздействии и разном представлении горного массива (2D-модель с кусками разных размеров и плотности) сформированные развалы отличаются. Наиболее близкие по форме развалы (для двух вариантов расчета) получаются для горной массы, смоделированной кусками размером 50 и 100 мм. Полученные результаты позволяют сделать вывод, что при определенных условиях формирование развала допустимо проводить по упрощенной (альтернативной) методике – рассматривать перемещение горной породы после взрывного воздействия как единого куска с последующим рассыпанием на фрагменты в момент приземления.
Введение
Внедрение различных цифровых решений в горной отрасли происходит по всем направлениям, используемым в процессе добычи полезных ископаемых [1, 2], начиная с оцифровки месторождений [3], моделирования процессов [4-6], расчета рисков [7, 8], организации устойчивой и безопасной связи [9], применения методов искусственного интеллекта [10, 11], создания цифровых двойников, ввода цифровых помощников, разработки систем автоматизации [12, 13], диагностики состояния оборудования [14, 15] и заканчивая разработкой полноценных программных комплексов, в которых хранится вся информация о месторождении и этапах его отработки с полным или частичным использованием инструментов Индустрии 4.0 [16, 17].
Вычислительные мощности современных компьютеров позволяют вернуться к различным задачам горного производства, которые были поставлены исследователями в середине XX в., на заре эры компьютерных технологий, но на тот момент не могли быть решены.
Одна из таких глобальных задач – прогнозирование формирования развала взорванной горной массы, которая со временем трансформировалась в более конкретную задачу – прогнозирование местоположения каждой точки взрываемого блока в развале взорванной горной массы. Тем самым изначальная задача определения геометрических параметров развала (ширины, длины и высоты) переросла в полноценное моделирование движения горной массы при взрыве с определением местоположения любой точки блока в любой момент времени. На протяжении последних 50-60 лет четко прослеживается усложнение как в постановке задачи, так и в применяемых решениях. На первых порах начинали с определения двухмерной или трехмерной геометрии формы развала и примерной карты распределения содержания полезного компонента [18] с заданием эмпирических коэффициентов (значения которых определялись для каждого объекта индивидуально), учитывающих влияние параметров буровзрывных работ и характеристик горного массива. На сегодняшний день производится полное моделирование всех процессов разрушения (детонация взрывчатого вещества, распространение волн напряжений, взрывное разрушение горного массива и формирование развала) [19-21] с получением полного профиля развала и подробного распределения в нем полезного компонента [22]. Массив горных пород при этом моделировали в виде матрицы кругов (шаров) или квадратов (кубов) [23, 24], представляя его как отдельные блоки (шаблоны), динамика которых рассчитывалась заранее [21, 25, 26]. Таким образом, вводили различные упрощения для представления структуры реального горного массива, рассматривая его как изотропную среду и т.д. [27, 28]. Проведенный анализ показал, что механизм передачи энергии взрыва окружающей среде, особенности ее возникновения [29, 30] и распределения по видам работ во многом и определяют формирование развала взорванной горной массы.
Методы
В математическом моделировании развала взорванной горной массы необходимо учитывать много аспектов, но в настоящей статье рассмотрены самые главные, без которых моделирование вообще не имеет смысла. Это математические описания объекта исследования и моделируемого процесса, которые должны максимально реалистично описывать поведение объекта в реальном мире, иначе результаты моделирования можно будет использовать только в игровой компьютерной индустрии или в презентационных целях (красивые картинки).
Для рассматриваемой задачи объект исследования – это массив горных пород, подготовленный к взрыву (взрываемый блок или его часть); процесс – это перемещение взорванной горной массы (движение каждого куска). Как известно, взрывное разрушение происходит в несколько стадий [31-33]. В связи с этим необходимо моделировать каждый этап (стадию) взрыва. При этом возникают следующие проблемы:
- При моделировании каждого этапа используются разные подходы и по времени этапы накладываются друг на друга (не идут последовательно).
- Моделирование объекта исследования. В настоящий момент с точки зрения моделирования практически ничего не известно о горном массиве. Для качественного моделирования необходимо знать структуру горного массива (трещиноватость или начальную кусковатость), физико-механические характеристики каждого исходного куска горного массива (отдельности) и его положение в пространстве.
- Математическое описание горного массива после взрывного воздействия (до начала перемещения).
Если вторую проблему еще можно попытаться решить путем использования современных технических средств (прозвучивание и т.д.), то состояние горного массива на момент перемещения вряд ли удастся определить экспериментальным путем. Выполнить полное моделирование взрыва и его воздействия на горный массив пытались многие ученые, но с учетом отмеченных сложностей задача до сих пор не решена. Поэтому при моделировании исследователи прибегают к большим допущениям, которые хоть и позволяют выполнить расчеты в приемлемое время, но не всегда отражают реальную картину. Например, представляют горный массив в виде частиц кубической формы размерами 1x1x1 или 2x2x2 м и моделируют формирование развала. В реальных условиях трудно представить, что развал формируется именно такими частицами взорванной горной массы.
Представление горного массива в виде частиц одинакового размера рассматривается как самый распространенный подход к моделированию, который используется многими исследователями (компании Геомикс, Blast Maker и др). Моделирование образования продуктов детонации (воздействие на исследуемый объект – горную породу), распространения волн напряжений и связанного с ними взрывного разрушения горных пород требует отдельного описания и в настоящей статье не представлено. Нами использован только конечный результат этих исследований. Взрывное воздействие может по-разному задаваться (моделироваться) в разных программах, поэтому оно в статье не указывается, как и используемые параметры БВР.
Процесс перемещения горной массы напрямую связан с механизмом передачи энергии взрыва горному массиву, т.е. разлет взорванной горной массы происходит за счет давления, оказываемого на горный массив продуктами детонации (газами). При условно известном взрывном воздействии на массив горных пород (давление продуктов взрыва) и условно известном состоянии горного массива в начальный момент перемещения (исходная кусковатость) можно смоделировать движение каждого куска взорванной горной массы. С этой целью используются различные библиотеки (физические движки, LS-DYNA, SIMULIA Abaqus, Rocky DEM), активно применяемые в научной и игровой компьютерной индустриях, при помощи которых движение объектов происходит строго по законам классической механики Ньютона [34] и выглядит вполне реалистично. При правильной настройке входных параметров можно добиться хорошей сходимости с экспериментальными данными.
Моделирование взрываемого блока
Основные элементы, которые используются для построения модели горного массива, подготовленного к взрыву:
- Частица (тело) – прочный объект, расстояние между любыми двумя точками которого всегда постоянная величина. Тела могут отражать поверхность земли, нетронутый горный массив (статические тела) и объекты, которые могут перемещаться (динамические объекты), например раздробленные куски горной массы.
- Фигура – некий геометрический объект, повторяющий контур тела, необходимый для задания свойств объектам (например, упругость, плотность и т.д.) и проверки взаимодействия тел (столкновений).
- Специальные ограничения, необходимые, например, для моделирования трения между телами и предотвращения взаимного проникновения тел друг в друга, что допустимо в моделировании и недопустимо в реальной жизни.
- Расчетный модуль, определяющий в соответствии со всеми ограничениями перемещение тела во времени с использованием дискретных временных шагов.
При разрешении одного ограничения мы нарушаем другие, поэтому для получения приемлемого решения необходимо несколько раз перебрать все ограничения (самая ресурсозатратная задача). Для упрощения модели горный массив, подготовленный к взрыву, обычно создается из динамических объектов одинакового размера (квадрат при решении плоской задачи, куб при решении объемной). Каждый объект размещается геометрически так, чтобы он описывал контур взрываемого блока или его части. Размер объектов может быть различным, но надо учитывать тот факт, что при уменьшении размеров увеличивается сложность и время расчетов. Поэтому чаще всего размеры объектов делают со стороной, равной 1 или 0,5 м. В нашем случае смоделируем исследуемый объект в программном комплексе Rocky (в других программных комплексах результат будет точно такой же, т.к. все они используют законы классической механики).
Исследовалась модель, построенная как часть взрываемого блока, ограниченная уступом и первым рядом взрываемых скважин. Высота уступа составляла 10 м, угол откоса – 70°, линия сопротивления по подошве – 5,6 м, расстояние от первого ряда до бровки уступа – 2 м. Влияние горно-геологических условий и параметров БВР, интервалов замедления в настоящей статье не представлено.
Модель формировалась всегда из одинаковых частиц разного размера – от 0,5 до 0,05 м (рис.1). В связи с тем, что в используемой программе частицы в виде куба не предусмотрены, они создавались во внешней программе (графическом редакторе Space Сlaim) с последующим внедрением в программу Rocky. Исследовалось поведение частиц с двумя значениями плотности 1800 и 2500 кг/м3; модуль упругости 1 ГПа; коэффициент Пуассона 0,24; коэффициент трения 0,8; динамический коэффициент трения 0,7. Координаты частиц задавались через CSV-файлы, в которых прописывались координаты, указывалось время появления частицы в моделировании (рис.2). Итоговое графическое представление моделей показано на рис.3.
Рис.1. Моделируемая частица размером 0,3 м
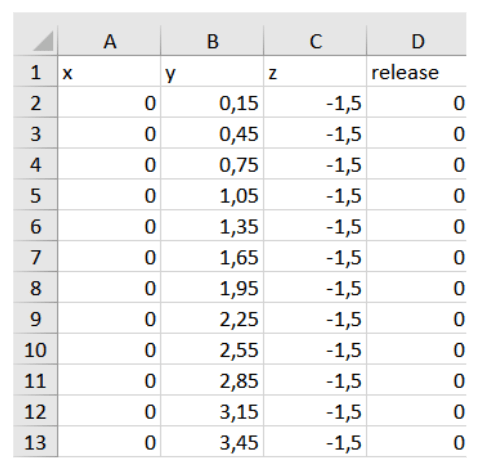
Рис.2. Фрагмент CSV-файла с информацией о координатах частиц
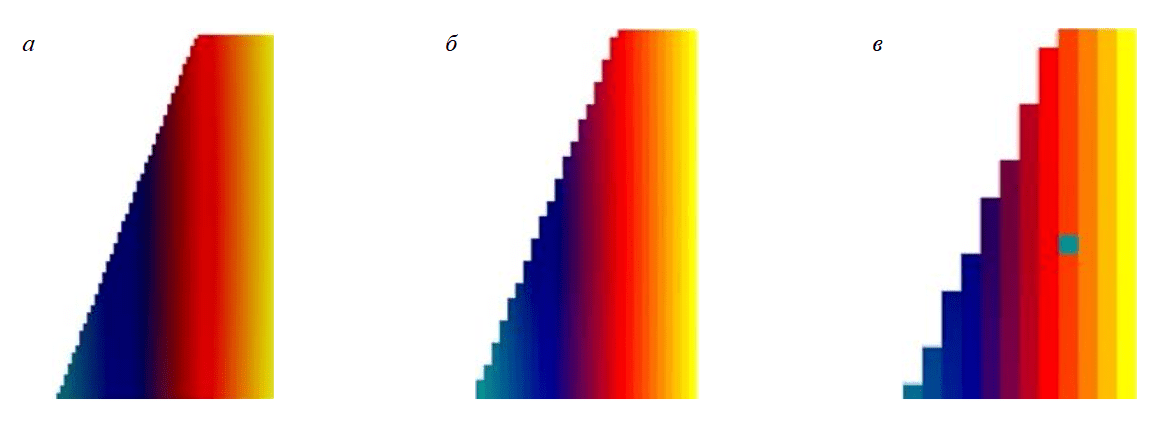
Рис.3. Модели, сформированные из частиц различных размеров: а – 0,1 м; б – 0,2 м; в – 0,3 м
В данном случае цветовая гамма не несет какой-то смысловой нагрузки и представлена сугубо в презентационных целях, но для отслеживания перемещения отдельных частей горной массы такая возможность представлена во всех аналогичных программах. Несмотря на то, что частицы задавались в виде объемных тел, в конкретном случае решалась плоская задача. Для исключения перемещения частиц в третьем измерении в модель искусственно были добавлены две прозрачные стенки с нулевым коэффициентом трения, между которыми шло перемещение частиц. Моделируется уже разрушенный взрывом горный массив, поэтому тот факт, что взрывные скважины бурятся с «перебуром» и взрывному воздействию подвержены горные породы ниже подошвы уступа, игнорируется.
Моделирование разлета
После формирования модели горного массива необходимо сымитировать взрывное воздействие. Для этого в применяемом физическом движке (в остальных все аналогично) предусмотрены следующие возможности: задание силы, момента и импульса. Полноценное моделирование разлета кусков взорванной горной массы и формирования развала – довольно трудная задача. В данном исследовании сравнивается моделирование развала, выполненное двумя способами, – классическим и с допущениями (альтернативным):
- Разлет частиц по баллистическим траекториям с определением координат частицы в любой момент времени (классическая задача).
- Первоначальное перемещение горной массы как единого куска с последующим рассыпанием в момент приземления (упрощенная задача).
В нашем исследовании проверяется гипотеза о формировании развала как перемещения всего объема отбиваемой горной массы на определенное расстояние с последующим рассыпанием кусков горной массы при ударе о поверхность. Данное предположение основывалось на анализе видеосъемки взрывов, сделанных на высокоскоростную камеру при проведении научно-исследовательских работ на одном из месторождений Якутии.
Эксперименты
Разлет частиц по баллистическим траекториям с определением координат частицы в любой момент времени. В классическом случае взрывное воздействие на частицы (приведение горных пород в движение) задавалось через функцию Motion Frames. После начала движения для предотвращения рассыпания частиц вправо, в сторону ненарушенного массива горных пород, создавался специальный ограничитель. Представлены начальное состояние модели (до начала движения) (рис.4, а), момент разлета частиц (рис.4, б), конечное состояние (развал) (рис.4, в).
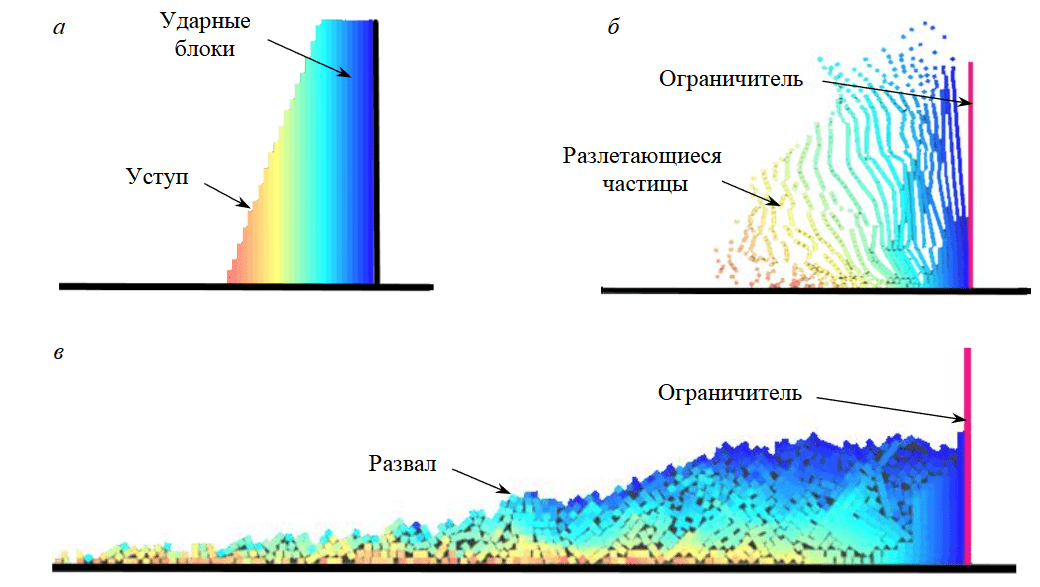
Рис.4. Этапы моделирования по классическому варианту [35]
Первоначальное перемещение горной массы как одного куска с последующим рассыпанием в момент приземления. В данной, альтернативной, задаче рассматривается перемещение блока как одного куска. При этом блок после взрывного воздействия движется как единый кусок, а разрушение блока на части происходит только в момент его соприкосновения с поверхностью. Движение горным породам задается при помощи платформы, осуществляющей перемещение центра тяжести блока под углом 45° со скоростью 2 м/с по вертикальной и горизонтальной осям (рис.5, а). Через 0,05 с воздействие прекращалось, блок продолжал двигаться под действием сил инерции и при соприкосновении с поверхностью рассыпался. Как и в первом случае, для предотвращения рассыпания частиц вправо, в сторону ненарушенного массива горных пород, создавался специальный ограничитель (рис.5, б). На рис.5, в представлено конечное состояние горных пород.
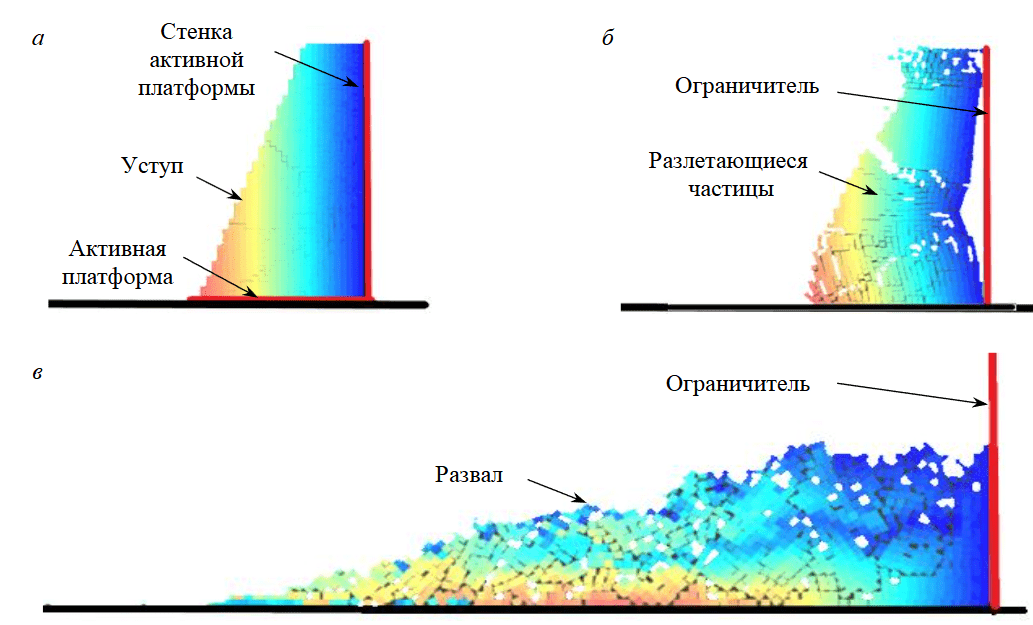
Рис.5. Этапы моделирования по альтернативному варианту [35]
Результаты исследования
При сравнении развалов, полученных разными способами, в качестве критериев были выбраны следующие параметры: ширина, высота и угол развала, расстояние до центра масс развала, разница между центрами масс, а также время, необходимое для моделирования. Координаты центра тяжести развалов определялись при помощи программы Space Claim, контур полученных развалов обводился в AutoCAD. Полученные таким способом параметры развалов представлены на рис.6. Цифрами на рисунках показана разница в метрах между центрами масс развалов, полученных разными способами, например разница центров масс развалов для частиц размером 100 мм и плотностью 2500 кг/м3 составляет 0,5 м (рис.6, а). Для частиц размером 0,05 м развалы моделировались только при условии, что их плотность 1800 кг/м3 (рис.7). Результаты расхождения параметров развала, полученных разными способами, для частиц одинакового размера и плотности представлены в таблице.
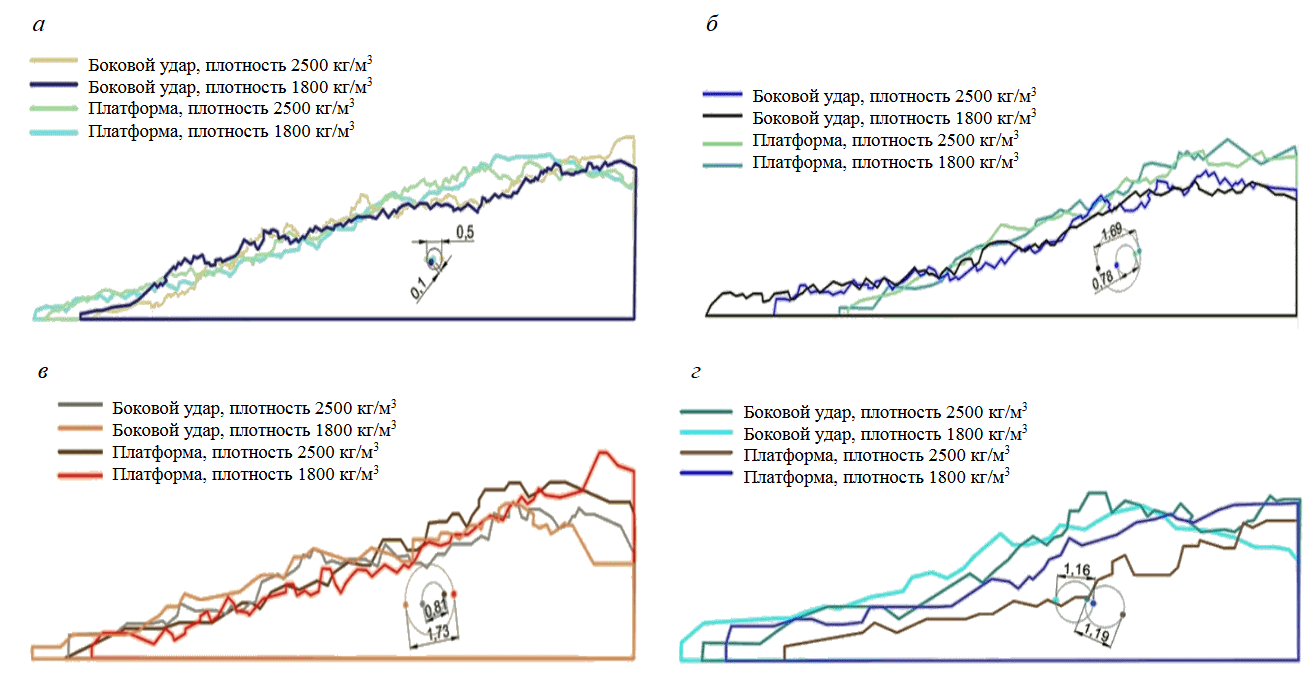
Рис.6. Сопоставление контуров развала и центров масс [35] для частиц: а – 0,1 м; б – 0,2 м; в – 0,3 м; г – 0,5 м
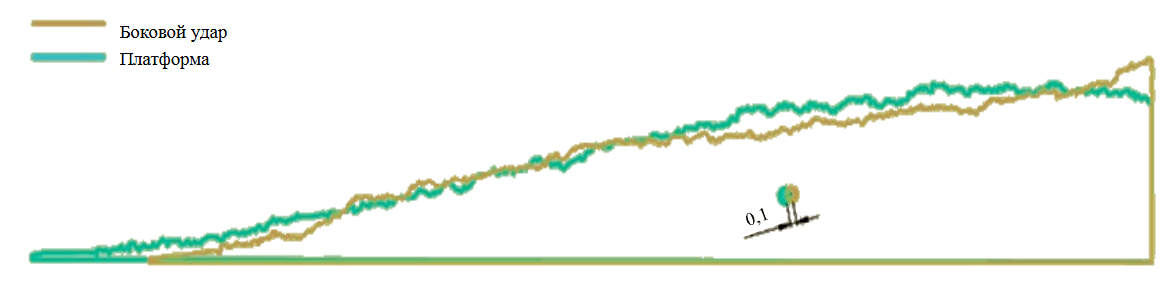
Рис.7. Сопоставление контуров развала и центров масс [35]
Результаты моделирования
|
Размер частиц, м |
Плотность, кг/м3 |
Разница между центрами масс, м |
Разница в высоте развала, м |
Разница в ширине развала, м |
Разница в высоте развала, % |
Разница в ширине развала, % |
|
0,5 |
1800 |
1,16 |
0,06 |
1,39 |
1,36 |
7,29 |
|
0,5 |
2500 |
1,19 |
0,79 |
2,57 |
16,53 |
13,92 |
|
0,3 |
1800 |
1,73 |
0,37 |
2,10 |
9,76 |
9,86 |
|
0,3 |
2500 |
0,81 |
0,52 |
0,15 |
13,72 |
0,75 |
|
0,2 |
1800 |
1,69 |
0,81 |
5,49 |
22,50 |
23,71 |
|
0,2 |
2500 |
0,78 |
0,84 |
2,58 |
21,71 |
12,54 |
|
0,1 |
1800 |
0,10 |
0,02 |
1,14 |
0,53 |
6,08 |
|
0,1 |
2500 |
0,50 |
0,05 |
1,85 |
1,28 |
10,05 |
|
0,05 |
1800 |
0,10 |
0,01 |
1,15 |
0,32 |
5,24 |
Обсуждение результатов
Итоги моделирования сильно зависят от заданных граничных условий. Например, при одинаковых условиях, высота развала для частиц размером 0,5x0,5 м составляет 4,41-4,47 м, а для частиц размером 0,1x0,1 м – 3,9-3,95 м. Результат моделирования формирования развала по различным подходам показал, что с уменьшением размера куска и плотности уменьшается разница между центрами масс развалов, сформированных по первой и второй задачам. Наименьшее отклонение 0,1 м наблюдается для плотности частиц 1800 кг/м3 и размеров частиц 0,05 и 0,1 м. Остальные параметры для данных частиц отличаются не более чем на 5 %.
Все это позволило сделать вывод, что при определенных условиях формирование развала допустимо проводить по упрощенной методике – рассматривать перемещение горной массы как одного куска с последующим рассыпанием в момент приземления. Данный подход реализован в разработанном программном обеспечении [36]. В первом приближении задача решалась в плоской постановке, а это очень существенное допущение [37]. Современные компьютерные мощности позволяют выполнить данное исследование в 3D-постановке. В настоящее время эти работы активно проводятся на базе Центра цифровых технологий Горного университета.
В связи с уходом из России зарубежных компаний наметился переход на программные комплексы, разработанные российскими специалистами. Самый простой и быстрый путь – это копирование всех существующих решений. При этом в программные комплексы копируются как решения, так и термины, принятые в оригинальном продукте. Отметим, что в России законодательно запрещено применение зарубежных слов при наличии в русском языке аналога.
Простая замена зарубежного программного продукта на аналогичную российскую разработку (копирующую зарубежный продукт) не повысит эффективность предприятия. Необходимо создавать новые программные продукты с решениями, опережающими существующие зарубежные разработки. Технологический и научный прорыв произойдет при объединении усилий всех разработчиков (хотя бы в рамках стандартизации и обмена данными), без этого невозможно создать передовой программный комплекс с функционалом, перекрывающим потребности всей горной отрасли. Для грамотного использования сложных программных комплексов необходимо реально разбираться во всех тонкостях процессов горного производства, что невозможно без получения хорошего специализированного образования [38].
Цифровые технологии активно входят в нашу жизнь, но это всего лишь инструмент, который помогает решать поставленные перед нами задачи. Совсем недавно горная наука относилась к разряду искусства [39], в ней очень много неопределенностей, которые сложно описать математическим языком, зачастую, по мнению автора, необходимо просто прислушаться к своей интуиции, к людям, которые непосредственно работают на производстве и знают все тонкости работы. Представляется, что окончательная настройка используемого программного комплекса вместе с такими людьми – правильное управленческое решение для руководителей.
Заключение
С научной точки зрения наиболее правильное решение для моделирования развала (конечный этап взрывного разрушения) – это расчет движения каждого отдельного куска взорванной горной массы на основе классической механики Ньютона, но на это требуются большие вычислительные мощности, и куски горной массы должны быть разных размеров и формы. Использование альтернативных подходов, например представленных в настоящей статье, требует, во-первых, научного обоснования, во-вторых, описания границ использования (может не подходить для всех условий) и обязательного промышленного подтверждения.
Формирование развала взорванной горной массы – сложная и до сих пор не решенная задача. В настоящее время существуют лишь некие упрощения решения классической задачи. При неправильном задании граничных условий исследователи получат результат, отличный от реальности. Упрощение задачи должно делаться на основе знаний [38] о процессах взрывного разрушения, иначе исследователи пойдут по неверному пути. При реализации какого-либо решения программными средствами до потенциальных пользователей должны быть донесены все используемые упрощения и допущения.
Литература
- Маховиков А.Б., Филясова Ю.А. Цифровые технологии при добыче твердых полезных ископаемых в Арктике // Устойчивое развитие горных территорий. 2024. Т. 16. № 3. С. 1110-1117. DOI: 10.21177/1998-4502-2024-16-3-1110-1117
- Фомин С.И., Говоров А.С. Стратегия формирования рабочей зоны карьеров на основе управления бортовым со-держанием полезных компонентов в руде // Горный информационно-аналитический бюллетень. 2024. № 11. С. 165-179. DOI: 10.25018/0236_1493_2024_11_0_165
- Егоров А.С., Калинин Д.Ф., Секерина Д.Д. Геотектоническая модель глубинного строения Змеиногорского рудного района Рудного Алтая по данным геологической интерпретации комплекса геофизических съемок // Известия Томского политехнического университета. Инжиниринг георесурсов. 2024. Т. 335. № 8. С. 148-160. DOI: 10.18799/24131830/2024/8/4431
- Багаутдинов И.И., Беляков Н.А., Севрюков В.В., Рассказов М.И. Применение модели упрочняющегося грунта для прогноза зоны пластических деформаций массива слабоустойчивых пород Яковлевского железорудного месторождения // Горный журнал. 2022. № 12. С. 16-21. DOI: 10.17580/gzh.2022.12.03
- Жуковский Ю.Л., Сусликов П.К. Оценка потенциального эффекта применения технологии управления спросом на горных предприятиях // Устойчивое развитие горных территорий. 2024. Т. 16. № 3. С. 895-908. DOI: 10.21177/1998-4502-2024-16-3-895-908
- Галимьянов А.А., Казарина Е.Н. Уточнение актуальности скважинной забойки // Вестник Кузбасского государственного технического университета. 2025. № 2 (168). С. 94-100. DOI: 10.26730/1999-4125-2025-2-94-100
- Shojaee Barjoee S., Rodionov V. Mathematical modeling and optimization of workplace illumination in ceramic industries (Iran) using DIALux evo // Journal of Infrastructure, Policy and Development. 2024. Vol. 8. № 15. № 5918. DOI: 10.24294/jipd5918
- Shojaee Barjoee S., Rodionov V.A. Respirable Dust in Ceramic Industries (Iran) and its Health Risk Assessment using De-terministic and Probabilistic Approaches // Pollution. 2024. Vol. 10. Iss. 4. P. 1206-1226. DOI: 10.22059/POLL.2024.376043.2360
- Маховиков А.Б., Крыльцов С.Б., Матрохина К.В., Трофимец В.Я. Система защищенной корпоративной связи для металлургического предприятия // Цветные металлы. 2023. № 4. С. 5-13. DOI: 10.17580/tsm.2023.04.01
- Секерина Д.Д., Саитгалеев М.М., Сенчина Н.П. и др. Роль сдвиговых дислокаций и грабен-рифтов в контроле нефтегазоносности глубинных горизонтов Русско-Часельского вала (Западно-Сибирская провинция) // Горные науки и тех-нологии. 2025. Т. 10. № 2. С. 109-117. DOI: 10.17073/2500-0632-2025-02-399
- Зайцева Е.В., Кочнева А.А., Катунцов Е.В., Киба М.Р. Подходы к цифровой обработке изображений в горной промышленности // XXI век: итоги прошлого и проблемы настоящего плюс. 2024. Т. 13. № 1 (65). С. 62-67.
- Ромашев А.О., Николаева Н.В., Гатиатуллин Б.Л. Формирование адаптивного подхода с применением технологии машинного зрения для определения параметров осаждения продуктов обогащения // Записки Горного института. 2022. Т. 256. С. 677-685. DOI: 10.31897/PMI.2022.77
- Рассказов И.Ю., Федотова Ю.В., Аникин П.А. и др. Совершенствование автоматизированной системы геомеханического мониторинга и раннего предупреждения опасных геодинамических явлений // Горный информационно-аналитический бюллетень. 2022. № 12-1. С. 106-121. DOI: 10.25018/0236_1493_2022_121_0_106
- Koteleva N., Korolev N. A Diagnostic Curve for Online Fault Detection in AC Drives // Energies. 2024. Vol. 17. Iss. 5. № 1234. DOI: 10.3390/en17051234
- Koteleva N., Valnev V. Automatic Detection of Maintenance Scenarios for Equipment and Control Systems in Industry // Applied Sciences. 2023. Vol. 13. Iss. 24. № 12997. DOI: 10.3390/app132412997
- Клебанов А.Ф., Бондаренко А.В., Жуковский Ю.Л., Клебанов Д.А. Организация удаленных центров управления горным предприятием: стратегические предпосылки и этапы реализации // Горная промышленность. 2024. № 4. С. 174-183. DOI: 10.30686/1609-9192-2024-4-174-183
- Лукичев С.В., Наговицын О.В. Цифровая трансформация и технологическая независимость горнодобывающей отрасли // Горная промышленность. 2022. № 5. С. 74-78. DOI: 10.30686/1609-9192-2022-5-74-78
- Yang R.L., Kavetsky A. A three dimensional model of muckpile formation and grade boundary movement in open pit blasting // International Journal of Mining and Geological Engineering. 1990. Vol. 8. Iss. 1. P. 13-34. DOI: 10.1007/BF00881125
- Zhi Yu, Xiu-Zhi Shi, Zong-Xian Zhang et al. Numerical Investigation of Blast-Induced Rock Movement Characteristics in Open-Pit Bench Blasting Using Bonded-Particle Method // Rock Mechanics and Rock Engineering. 2022. Vol. 55. Iss. 6. P. 3599-3619. DOI: 10.1007/s00603-022-02831-w
- Wei Fu, Furtney J., Valencia J. Blast Movement Simulation Through a Hybrid Approach of Continuum, Discontinuum, and Machine Learning Modeling // 57th U.S. Rock Mechanics/Geomechanics Symposium, 25-28 June 2023, Atlanta, GA, USA. OnePetro, 2023. № ARMA-2023-0831. DOI: 10.56952/ARMA-2023-0831
- Zhixian Hong, Ming Tao, Mingsheng Zhao et al. Numerical modelling of rock fragmentation under high in-situ stresses and short-delay blast loading // Engineering Fracture Mechanics. 2023. Vol. 293. № 109727. DOI: 10.1016/j.engfracmech.2023.109727
- Яницкий Е.Б., Кабелко С.Г., Дунаев В.А., Рахманов Р.А. Компьютерное моделирование смещения горной массы и оценка разубоживания руды в результате массового взрыва при открытой разработке месторождений // Взрывное дело. 2018. № 120/77. С. 94-108.
- Kucewicz M., Łukasz M., Baranowski P. et al. Numerical modeling of blast-induced rock fragmentation in deep mining with 3D and 2D FEM method approaches // Journal of Rock Mechanics and Geotechnical Engineering. 2024. Vol. 16. Iss. 11. P. 4532-4553. DOI: 10.1016/j.jrmge.2024.01.017
- Sellers E., Furtney J., Onederra I., Chitombo G. Improved understanding of explosive–rock interactions using the hybrid stress blasting model // The Journal of The Southern African Institute of Mining and Metallurgy. 2012. Vol. 112. Iss. 8. P. 721-728.
- Vasylchuk Y.V., Deutsch C.V. Approximate blast movement modelling for improved grade control // Mining Technology. 2019. Vol. 128. Iss. 3. P. 152-161. DOI: 10.1080/25726668.2019.1583843
- Cundall P.A., Strack O.D.L. A discrete numerical model for granular assemblies // Géotechnique. 1979. Vol. 29. Iss. 1. P. 47-65. DOI: 10.1680/geot.1979.29.1.47
- Hosseini S., Poormirzaee R., Hajihassani M. An uncertainty hybrid model for risk assessment and prediction of blast-induced rock mass fragmentation // International Journal of Rock Mechanics and Mining Sciences. 2022. Vol. 160. № 105250. DOI: 10.1016/j.ijrmms.2022.105250
- Жариков И.Ф., Захаров В.Н., Норель Б.К. Паспорт прочности и уравнение связи между инвариантами напряжений и деформаций для неоднородных горных пород в объемном напряженном состоянии // Известия Российской академии наук. Механика твердого тела. 2015. № 6. С. 49-60.
- Молдован Д.В., Чернобай В.И., Ястребова К.Н. Влияние композитного материала в конструкции забойки на ее работоспособность // Горный информационно-аналитический бюллетень. 2023. № 9-1. С. 110-121. DOI: 10.25018/0236_1493_2023_91_0_110
- Молдован Д.В., Чернобай В.И., Соколов С.Т., Баженова А.В. Конструктивные решения запирания продуктов взрыва во взрывной полости // Горный информационно-аналитический бюллетень. 2022. № 6-2. С. 5-17. DOI: 10.25018/0236_1493_2022_62_0_5
- Казаков Н.Н., Викторов С.Д., Шляпин А.В., Лапиков И.Н. Дробление горных пород взрывом в карьерах. М.: Российская академия наук, 2020. 520 с.
- Куринной В.П. Теоретические основы взрывного разрушения горных пород. Днепр, 2018. 280 с.
- Peng Xu, Renshu Yang, Jinjing Zuo et al. Research progress of the fundamental theory and technology of rock blasting // International Journal of Minerals, Metallurgy and Materials. 2022. Vol. 29. Iss. 4. P. 705-716. DOI: 10.1007/s12613-022-2464-x
- Verbilo P., Karasev M., Belyakov N., Iovlev G. Experimental and numerical research of jointed rock mass anisotropy in a three-dimensional stress field // Rudarsko-geološko-naftni zbornik. 2022. Vol. 37. № 2. P. 109-122. DOI: 10.17794/rgn.2022.2.10
- Баженова А.В. Прогнозирование смещения рудных контуров при формировании развала взорванной горной массы на карьерах: Автореф. канд. дис. … техн. наук. СПб: Санкт-Петербургский горный университет, 2023. 20 с.
- Свидетельство о государственной регистрации программы для ЭВМ № 2024660948 РФ. Программа для определения смещения рудных контуров при формировании развала взорванной горной массы / Н.И.Котелева, С.В.Хохлов, А.В.Баженова. Опубл. 14.05.2024. Бюл. № 5.
- Engmann E., Ako S., Bisiaux B. et al. Measurement and Modelling of Blast Movement to Reduce Ore Losses and Dilution at Ahafo Gold Mine in Ghana // Ghana Mining Journal. 2013. Vol. 14. P. 27-36.
- Litvinenko V.S. Digital Economy as a Factor in the Technological Development of the Mineral Sector // Natural Resources Research. 2020. Vol. 29. Iss. 3. P. 1521-1541. DOI: 10.1007/s11053-019-09568-4
- Рудник С.Н., Афанасьев В.Г., Самыловская Е.А. 250 лет на службе Отечеству: Санкт-Петербургский горный университет императрицы Екатерины II в цифрах и фактах // Записки Горного института. 2023. Т. 263. С. 810-830.
