Особенности и информативные возможности раннерадиального режима на КВД в горизонтальных скважинах с близко расположенными трещинами МГРП
- 1 — аспирант Институт проблем нефти и газа РАН ▪ Orcid
- 2 — д-р техн. наук главный научный сотрудник Институт проблем нефти и газа РАН ▪ Orcid
Аннотация
Бурение горизонтальных скважин (ГС) с многостадийным гидроразрывом пласта (МГРП) является одним из наиболее частых решений при разработке низкопроницаемых нефтяных и газовых коллекторов. При этом осложнена оценка параметров системы пласт – скважина по данным гидродинамических исследований (ГДИ) ввиду нереалистичных времен получения отклика на радиальный режим течения. Устранить эту неопределенность возможно, используя данные раннерадиального режима, возникающего на начальном этапе записи кривой восстановления давления (КВД). Однако для его проявления необходимо, чтобы расстояние между трещинами вдоль горизонтального ствола было достаточно большим по сравнению с полудлинами трещин. На практике это условие обычно не выполняется, что делает невозможным такой способ оценки гидропроводности пласта. В то же время ГС с МГРП характеризуются сложным характером КВД, что связано с особенностью взаимодействия трещин. Поведение КВД на раннем периоде замера зависит от длительности отработки скважины перед остановкой, подобно КВД в скважине вблизи непроницаемой границы пласта. Впервые выявлено, что для достаточно коротких времен отработки на раннем этапе КВД может проявляться радиально подобный режим, вызванный формированием эллиптического течения вокруг трещин. Доказана устойчивость данного режима и взаимосвязь положения графика производной давления с параметрами формируемого эллиптического течения. Получена эмпирическая формула, обеспечивающая оценку коэффициента гидропроводности пласта по данному режиму с достаточной точностью для часто встречающегося на практике диапазона параметров геометрии ГС с МГРП. Результаты работы расширяют возможности достоверной оценки параметров системы пласт – скважина для ГС с МГРП в низкопроницаемых коллекторах по данным ГДИ, включая исследования новых скважин в процессе освоения или при запуске после длительного простоя.
Финансирование
Работа подготовлена в рамках выполнения Государственного задания ИПНГ РАН по теме «Создание новых технологий эффективного экологически чистого извлечения углеводородов в сложных горно-геологических условиях на основе системного подхода к изучению и моделированию полного жизненного цикла нефтегазовых месторождений» (125020501405-1).
Введение
Бурение горизонтальных скважин (ГС) с многостадийным гидроразрывом пласта (МГРП) на сегодняшний день – один из основных способов вскрытия пласта при разработке низкопроницаемых нефтяных и газовых объектов [1, 2]. Оценка параметров системы пласт – скважина для ГС с МГРП при проведении различных промысловых исследований осложнена рядом причин:
- Снижение достоверности оценки фильтрационно-емкостных свойств (ФЕС) пласта при проведении геофизических исследований (ГИС) в горизонтальном стволе и необходимость привлечения дорогостоящего комплекса исследований для уточненной оценки ФЕС [3, 4].
- Наличие неопределенности по дренируемым толщинам:
– отсутствие прямой оценки по ГИС, так как скважины с ГС зачастую не пересекают подошву пласта;
– при вскрытии расчлененных коллекторов – неясность по охвату дренированием толщин, вскрытых трещинами ГРП, в связи с косвенными оценками закрепленной высоты трещины.
- Неравномерность распределения добычи по работающим портам МГРП – по данным промыслово-геофизических исследований преимущественная доля добычи (>60 %) зачастую приходится на один-два порта, в то время как часть портов показывает долю от 5 % и менее [5, 6].
- Длительные сроки выхода на радиальный (позднерадиальный) режим при проведении гидродинамического исследования (ГДИ) [7, 8].
При интерпретации данных ГДИ первично определяемым параметром является гидропроводность пласта kh/µ, по значению которой при известной вязкости флюида µ и работающей толщине h определяется проницаемость пласта k. По значению проницаемости пласта рассчитываются остальные параметры системы пласт – скважина: геометрические характеристики скважины (полудлина трещины Xf, проводимость трещины Fc, длина ГС и др.) и различные составляющие скин-фактора (полный, геометрический, механический), расстояние до границ и др.
Наличие значительного числа влияющих параметров осложняет их независимую оценку и требует комплексирования ГДИ с промыслово-геофизическими исследованиями [9-11]. Авторы работ [12, 13] вводят понятие инвариантов – комплексных параметров, определяющих поведение давления при определенном режиме течения. В исследованиях [14, 15] предложено использовать «фильтрационную и емкостную составляющие потока». Чтобы разделить влияние различных параметров пласта и скважины и выполнить их индивидуальную оценку, необходима достоверная оценка гидропроводности (и связанной с ней проницаемости) пласта. В статье [16] представлен анализ поведения давления ГС с кластерным ГРП, отмечающимся более сложным характером отклика.
С точки зрения гидродинамических исследований ГС с МГРП являются не единственными сложными системами пласт – скважина. Длительными сроками выхода на радиальный режим могут характеризоваться и вертикальные скважины (ВС) со сверхдлинными трещинами ГРП, эксплуатирующиеся в коллекторах со сверхнизкой проницаемостью. Оценка свойств системы в таком случае может успешно решаться за счет применения алгоритмов деконволюции [17] или анализа динамики добычи (АДД) [18]. Не менее сложным является и случай трещиноватых карбонатных коллекторов, особенно в условиях их вскрытия горизонтальными стволами или ВС с ГРП. Оценка фильтрационных параметров таких коллекторов осуществляется как за счет комплексирования ГДИ с микросейсмикой [19], так и использования многомерных статистических моделей [20].
Таким образом, проблема определения истинной гидропроводности является критически важной с точки зрения достоверности получаемых результатов ГДИ и их дальнейшего применения при проектировании и мониторинге разработки месторождения.
Методы
Широко используются такие методы, как деконволюция и АДД, разработка которых направлена на решение проблемы недостаточной длительности КВД. Применение таких методов на ГС с МГРП в большинстве случаев не решает задачу получения отклика на позднерадиальный режим, так как для этого все равно требуется значительное время, также недостижимое и при использовании указанных методов. Рассмотрим данную проблему более подробно.
Режимы течений, характерные для скважин с МГРП. Длительные сроки выхода на радиальный режим для скважин с МГРП обусловлены наличием комплекса различного вида течений, возникающих на соответствующих этапах ГДИ [10, 21, 22]:
- билинейный с наклоном (тангенсом угла наклона) производной давления i= 1/4;
- ранний линейный к трещине с i= 1/2;
- раннерадиальный вокруг трещин с горизонтальным участком производной;
- поздний линейный к стволу ГС с i= 1/2;
- позднерадиальный, формирующийся вокруг ствола ГС на позднем этапе записи кривых стабилизации давления (КСД).
Выход на позднерадиальный режим может характеризоваться длительными сроками (до нескольких десятков лет), что определяет невозможность его получения на практике [8]. Время достижения позднерадиального режима зависит от параметров, определяющих пьезопроводность пласта и конструкцию скважины. Но для типично эксплуатируемых ГС с МГРП низкопроницаемых пластов описанный порядок является характерным. Невозможность достижения позднерадиального режима вносит значительную неопределенность в результаты интерпретации исследований таких скважин.
Оценка гидропроводности пласта возможна и по данным раннерадиального режима. Вертикальное положение горизонтального участка («полки») производной для него обратно пропорционально произведению Nkh/µ, где N – количество трещин [22, 23]. Однако для возникновения раннерадиального режима должен выполняться критерий отсутствия интерференции между трещинами на соответствующем временном интервале, что достижимо при относительно малых полудлинах трещин Xf и больших расстояниях между трещинами L с соотношением не менее L/Xf от 3 до 5 [23]. С учетом тенденции к увеличению числа стадий МГРП и полудлин трещин, на залежах с трудноизвлекаемыми запасами критерий проявления раннерадиального режима часто не выполняется.
При плотном расположении трещин после раннего линейного режима может проявляться другое характерное течение, контролируемое сильной интерференцией трещин с псевдоустановившимся распределением давления между ними [24]. Такое поведение схоже с псевдостационарным режимом в ограниченном пласте. Отличие в том, что нестационарное возмущение давления продолжает распространяться за пределами ограниченного трещинами объема. В литературе не встречается однозначного названия для данного вида течения. Однако наиболее подходящим, на наш взгляд, является термин «псевдоограниченное течение» [25]. Его характерный признак на диагностическом графике КСД – проявление наклона, близкого к 1, аналогично «классическому» псевдостационарному течению.
На рис.1 сопоставлены диагностические графики синтетических КСД с параметрами, представленными в табл.1, с вариацией длины горизонтального ствола hw. Расчеты выполнены в программном пакете планирования и интерпретации ГДИ Kappa Saphir с использованием аналитической модели ГС с МГРП. Для варианта с hw = 400 м (с соотношением L/Xf = 2) выхода на ранне-радиальный режим не происходит, вместо него наблюдается переходный режим между ранним и поздним линейными течениями в интервале 2-30 ч. Для вариантов с длиной ГС 25 и 100 м, характеризующихся близким расположением трещин, отмечается упомянутый рост производной давления с наклоном i = 1, соответствующий псевдоограниченному течению, с последующим выходом на поздний линейный режим. При этом для варианта с hw = 25 м выход на псевдоограниченный режим наблюдается сразу после билинейного течения, без проявления раннего линейного режима.
Таблица 1
Параметры скважины с МГРП
|
Параметр |
Значение |
Параметр |
Значение |
|
Проницаемость k, мД |
1 |
Пластовое давление Pi, бар |
300 |
|
Пористость m, д.ед. |
0,1 |
Количество трещин N |
3 |
|
Толщина h, м |
30 |
Полудлина трещин Xf, м |
50 |
|
Полная сжимаемость сt ·10–5, бар–1 |
3,6 |
Проводимость трещин Fc, мД·м |
300 |
|
Вязкость µ, мПа·с |
1 |
Дебит скважины q, м3/сут |
10 |
|
Объемный коэффициент B |
1 |
Скин-фактор S |
0,3 |
|
Радиус скважины, мм |
99,4 |
|
|
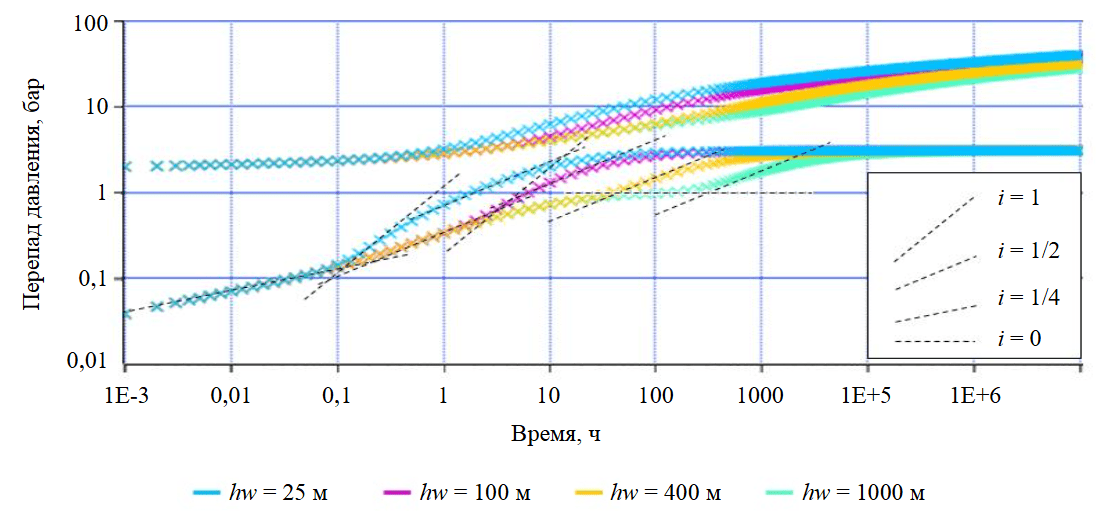
Рис.1. Пример проявления псевдоограниченного течения для скважины с МГРП
Особенности проявления режимов на КВД. Наличие комплекса режимов течения, а также режимов, аналогичных работе скважины в ограниченном пласте, вызывают зависимость поведения КВД в ГС с МГРП от длительности ее отработки перед закрытием. Такие процессы также отмечаются при исследовании скважин в областях с наличием незамкнутых границ пласта. В случае кратковременной отработки этих скважин, при последующей записи КВД в начальный период реакции на границу наблюдается отличный от КСД характер поведения производной. Такое поведение обусловлено особенностями суперпозиции реакций давления на непроницаемую границу, возникших при отработке и последующем закрытии [24, 26]. Аналогичным образом ведут себя производные давления для примеров, представленных на рис.1, причем наиболее сильному «искажению» подвержены варианты с проявлением псевдоограниченного течения. Изменение поведения происходит в определенном диапазоне длительности отработки Tотр, индивидуальном в зависимости от представленных значений параметров системы пласт – скважина.
Такие особенности поведения производной характеризуются одним интересным явлением, возникающим для значений Tотр из определенного интервала, при котором отмечается отличие формы КВД от КСД. На рис.2 показано сопоставление КСД и КВД для представленных ранее вариантов hw, где КВД построены для разных значений Tотр и hw. Для всех четырех вариантов hw на производной КВД отмечается формирование горизонтального участка с последующим незначительным «провалом». При этом наблюдается близость между «полкой» раннерадиального режима КСД и формирующейся «полкой» КВД при кратковременной отработке (рис.2, г). Можно предположить, что и для остальных вариантов проявление горизонтального участка на КВД после кратковременной отработки может являться характерным признаком, позволяющим оценивать гидропроводность пласта без достижения позднерадиального режима.
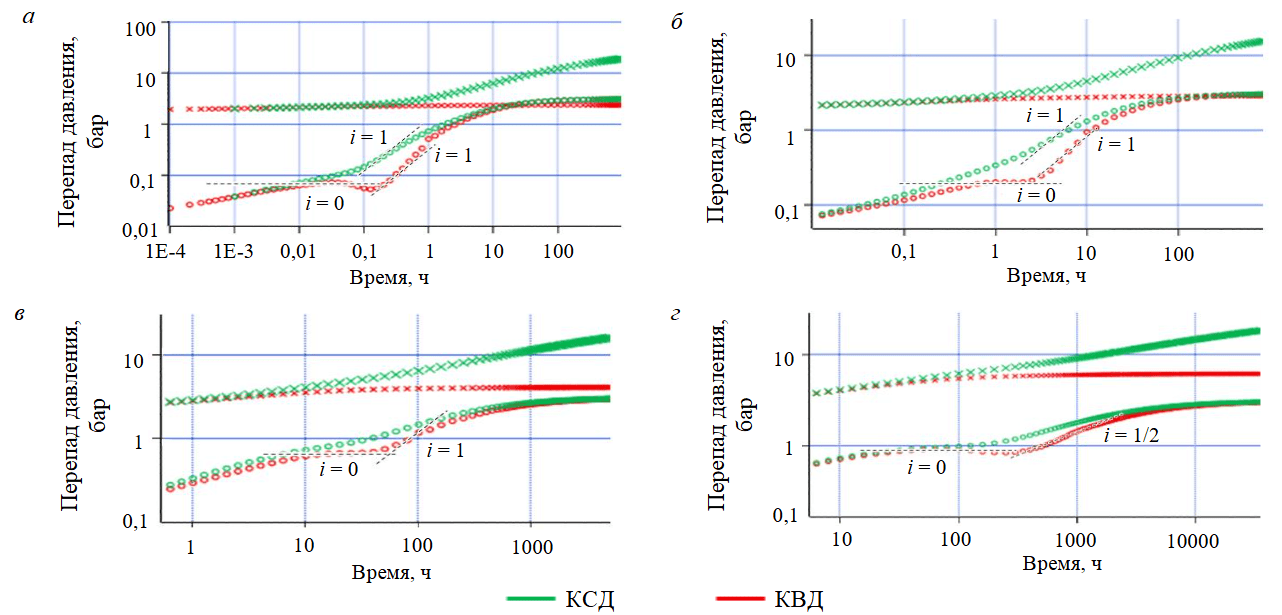
Рис.2. Увеличенный масштаб периода формирования горизонтального участка при кратковременной отработке для различных вариантов длины ГС: а – hw = 25 м, Tотр = 0,1 ч; б – hw = 100 м, Tотр = 1 ч; в – hw = 400 м, Tотр = 10 ч; г – hw = 1000 м, Tотр = 100 ч
В табл.2 сопоставлены значения кажущейся проводимости khT, определенной по горизонтальному участку производной КВД после кратковременной отработки, с исходной проводимостью пласта khисх. Из таблицы видно, что соотношения khT/khисх не характеризуются однозначной зависимостью. Только для варианта hw = 1000 м с наличием раннерадиального участка на КСД это соотношение приближается к ожидаемой величине – количеству трещин N = 3, хотя и превышает его более чем на 10 %. В остальных вариантах значения существенно выше, что указывает на иной характер течения, формирующего «полку» на производной КВД. В отличие от классического раннерадиального режима, такая «полка» формируется и при малых значениях L/Xf, но только на КВД после кратковременной отработки.
Таблица 2
Сопоставление кажущейся проводимости с исходной величиной
|
hw,м |
khT, мД·м |
khисх, мД·м |
khT/khисх |
|
25 |
1283,7 |
30,0 |
42,8 |
|
100 |
459,4 |
30,0 |
15,3 |
|
400 |
140,3 |
30,0 |
4,7 |
|
1000 |
101,9 |
30,0 |
3,4 |
Зависимость формирующегося горизонтального участка на КВД от продолжительности переходных режимов. Если выявленная «полка» на КВД действительно связана с проявлением радиально подобного режима течения, а не возникает из-за наложения переходных режимов, то ее вертикальное положение не должно зависеть от таких параметров, как время отработки Tотр и сжимаемость системы ct. Для анализа влияния Tотр построено семейство синтетических КВД для значений Tотр от 1 до 1000 ч с параметрами системы пласт – скважина, представленными в табл.3 (рис.3, а). Как видно, КВД демонстрируют выявленную ранее зависимость формы производной от длительности отработки. При этом наблюдается явное формирование горизонтального участка на одном и том же вертикальном уровне. Признаки образования горизонтального участка наблюдаются при Tотр = 5 ч и прекращаются при Tотр = 500 ч. Можно отметить одинаковое время начала выхода на горизонтальный участок. Изменение Tотр влияет на продолжительность доминирования горизонтального участка.
Таблица 3
Параметры скважины с МГРП для оценки режима кратковременной отработки
|
Параметр |
Значение |
Параметр |
Значение |
|
Проницаемость k, мД |
1 |
Пластовое давление Pi, бар |
112 |
|
Пористость m, д.ед. |
0,25 |
Количество трещин N |
3 |
|
Толщина h, м |
25 |
Расстояние между краевыми трещинами (длина ГС) hw, м |
450 |
|
Полная сжимаемость сt ·10–5, бар–1 |
4,3 |
Полудлина трещин Xf, м |
200 |
|
Вязкость µ, мПа·с |
1 |
Проводимость трещин Fc, мД·м |
500 |
|
Объемный коэффициент B |
1 |
Дебит скважины q, м3/сут |
10 |
|
Радиус скважины, мм |
70 |
Скин-фактор S |
0,1 |
Для оценки влияния сжимаемости системы ct в качестве базового принят вариант с параметрами согласно табл.3 при длительности отработки Tотр = 100 ч. Вариация сжимаемости при построении синтетических кривых производилась до полного прекращения признаков проявления горизонтального участка. Охваченный диапазон значений составил 1∙10–6-3∙10–3 бар–1 (рис.3, б). Как и в случае с длительностью отработки, изменение сжимаемости не оказывает влияния на вертикальное положение горизонтального участка, формирование которого наблюдается на одном и том же уровне. Вариация ct влияет на все временные характеристики КВД, поэтому изменяется не только продолжительность горизонтального участка, но и время начала выхода на него.
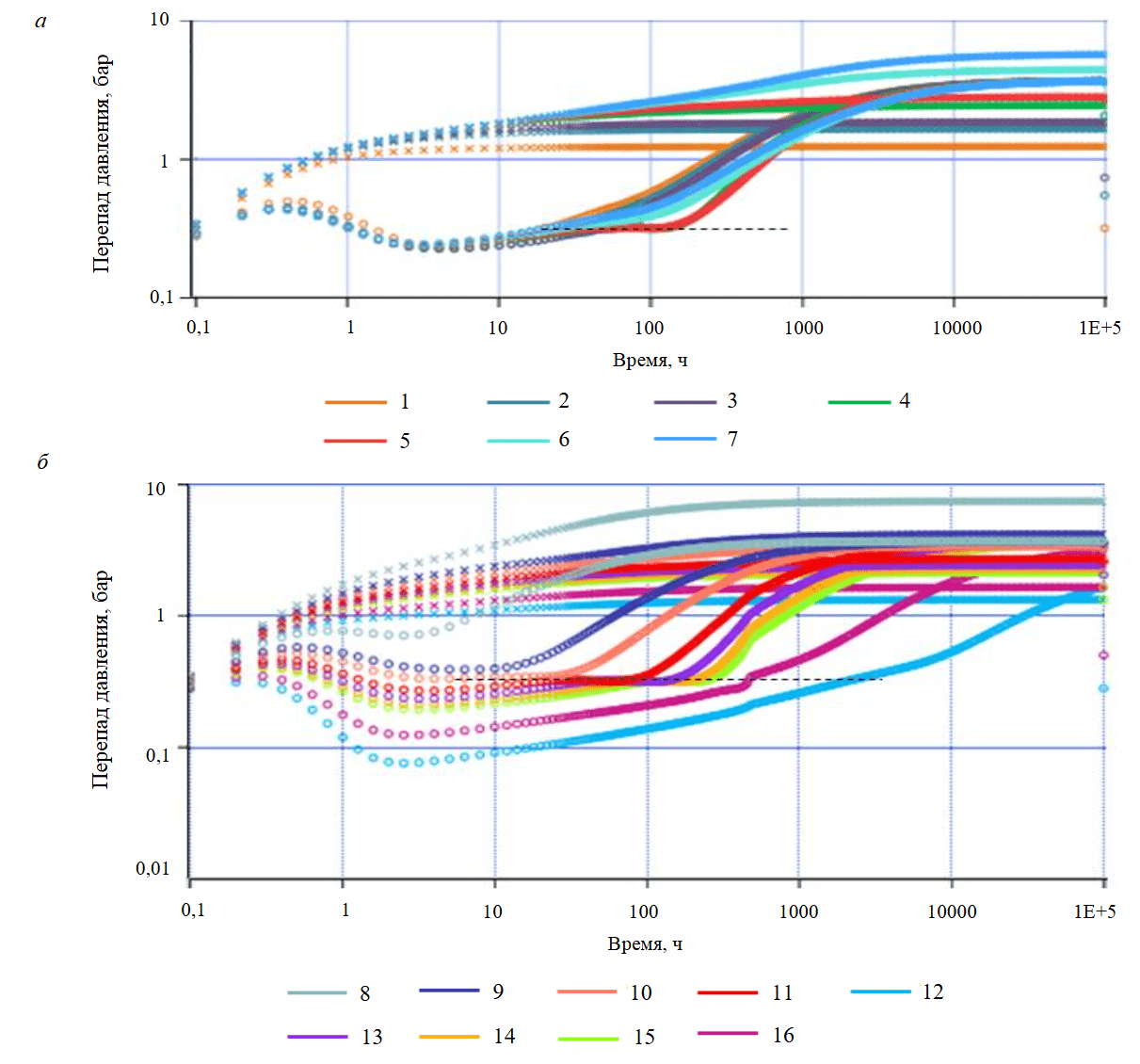
Рис.3. Семейство КВД для различных значений Tотр (а) и ct (б)
1 – Tотр = 1 ч; 2 – Tотр = 5 ч; 3 – Tотр = 10 ч; 4 – Tотр = 50 ч; 5 – Tотр = 100 ч; 6 – Tотр = 500 ч; 7 – Tотр = 1000 ч; 8 – ct = 1·10–6 бар–1; 9 – ct = 5·10–6 бар–1; 10 – ct = 1·10–5 бар–1; 11 – ct = 2,5·10–5 бар–1; 12 – ct = 3·10–3 бар–1; 13 – ct = 4,3·10–5 бар–1; 14 – ct = 6,5·10–5 бар–1; 15 – ct = 9·10–5 бар–1; 16 – ct = 5·10–4 бар–1
Таким образом, одинаковое вертикальное положение горизонтального участка на КВД при различных значениях Tотр и ct указывает на то, что формируемая «полка» характеризует определенный радиально подобный режим течения, для которого следует найти соответствующие зависимости от параметров пласта и скважины.
Анализ формирующихся режимов течения по данным численного моделирования. Для выявления особенностей режима течения, связанного с формирующейся «полкой» на графике производной КВД после кратковременной отработки, рассмотрим характер изменения распределений пластового давления (формирования областей дренирования) по данным численного моделирования КВД. С этой целью выполнен расчет с использованием 2D-численной модели в Kappa Saphir для параметров скважины с МГРП, представленных в табл.3, при отработке длительностью Tотр = 100 ч. С целью выявления возможных различий в поведении КВД расчет производился для трещин с бесконечной и конечной проводимостями.
На диагностическом графике смоделированной КВД (рис.4) выявляются следующие характерные режимы:
- Замеры для трещины бесконечной проводимости – линейное течение с наклоном производной i= 1/2, для трещины конечной проводимости – билинейное течение с i = 1/4 (1 ч).
- Переходный режим (20 ч).
- Ранний горизонтальный участок, i= 0 (60 ч).
- Незначительный прогиб производной (120 ч).
- Псевдоограниченное течение, i= 1 (500 ч).
- Позднее линейное течение, i= 1/2 (2000 ч).
- Позднее радиальное течение, i= 0 (6∙104 ч).
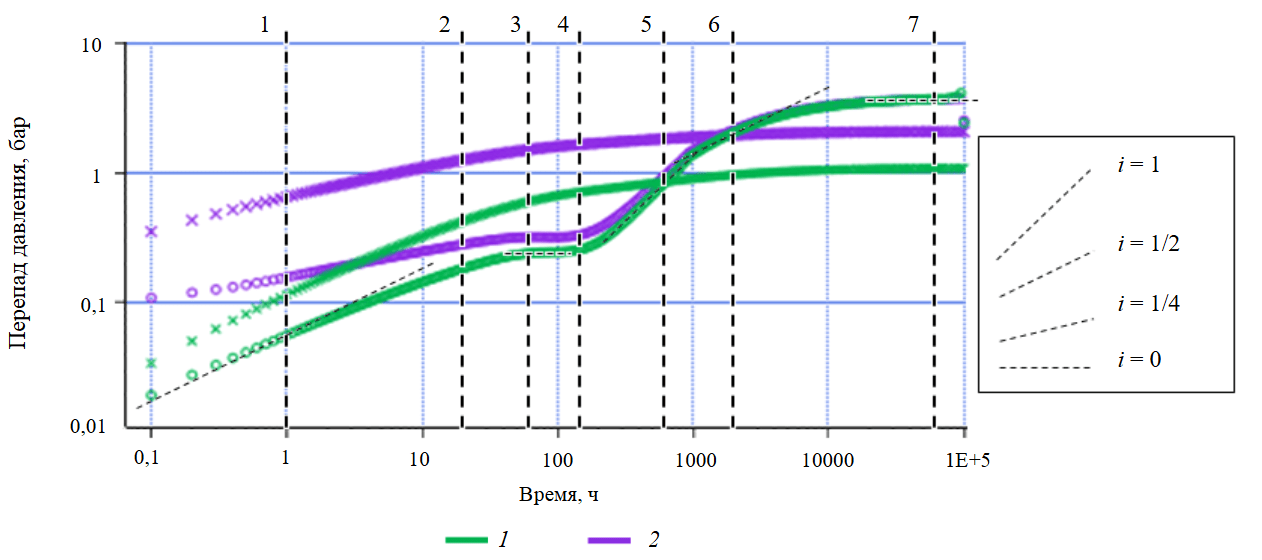
Рис.4. Диагностический график КВД при кратковременной отработке скважины с МГРП по данным табл.3.
Трещины бесконечной (1) и конечной (2) проводимости
Как видно, за исключением периода 1, представленные периоды КВД для обоих вариантов проводимости трещин характеризуются аналогичными режимами течения. При этом для трещин бесконечной проводимости ранний горизонтальный участок на графике производной располагается ниже, чем для трещин конечной проводимости. С момента начала доминирования псевдоограниченного режима 5 наблюдается тенденция к сближению кривых производных давления, которые полностью совпадают по окончании позднего линейного режима.
В рассматриваемом случае по окончании билинейного режима для трещины конечной проводимости не происходит формирование раннего линейного течения, а наблюдается переходный период и образование горизонтального участка. Отсутствие линейного течения объясняется значением безразмерного коэффициента проводимости CfD = Fc /(kXf ) = 2,5. Известно, что при значениях СfD, близких к 1,6, наблюдается наибольшая длительность билинейного режима [26]. Это объясняет получение длительно доминирующего билинейного режима в представленном примере, маскирующего участок линейного течения перед формированием раннего горизонтального участка.
На рис.5 представлены распределения давления в окрестности скважины, полученные по результатам расчета КВД для трещин бесконечной проводимости, на характерные моменты времени, отмеченные цифрами на рис.4:
- в период доминирования линейного течения наблюдается формирование областей сниженного давления вокруг трещин;
- во время переходного периода отмечаются признаки слабой интерференции между трещинами;
- при формировании раннего горизонтального участка наблюдается образование эллипсов вокруг трещин;
- в период провала производной происходит смыкание эллипсов, образованных вокруг соседних трещин (сильная интерференция);
- этап доминирования псевдоограниченного течения характеризуется распространением областей интерференции до концов трещин;
- в период проявления поздних линейного (6) и радиального (7) режимов наблюдается формирование соответствующих прямоугольных и круглых областей дренирования вокруг ГС.
На рис.6 представлены аналогичные распределения давления для трещин конечной проводимости. В период проявления раннего горизонтального участка 3 вокруг трещин также наблюдается формирование эллипсов с последующим их смыканием в интервале времени 4. При этом для трещин конечной проводимости происходит формирование более сжатых по вертикали эллипсов, частично охватывающих поверхность трещины. Причиной этому является формирование областей сниженного давления вокруг центральной части трещин в момент доминирования билинейного режима 1, что обусловлено наличием градиента давления внутри трещины конечной проводимости. Последующее развитие эллипса на этапе 3 происходит напрямую из области сниженного давления, образованной в период доминирования билинейного режима 1, поэтому его геометрия связана с проводимостью трещины.
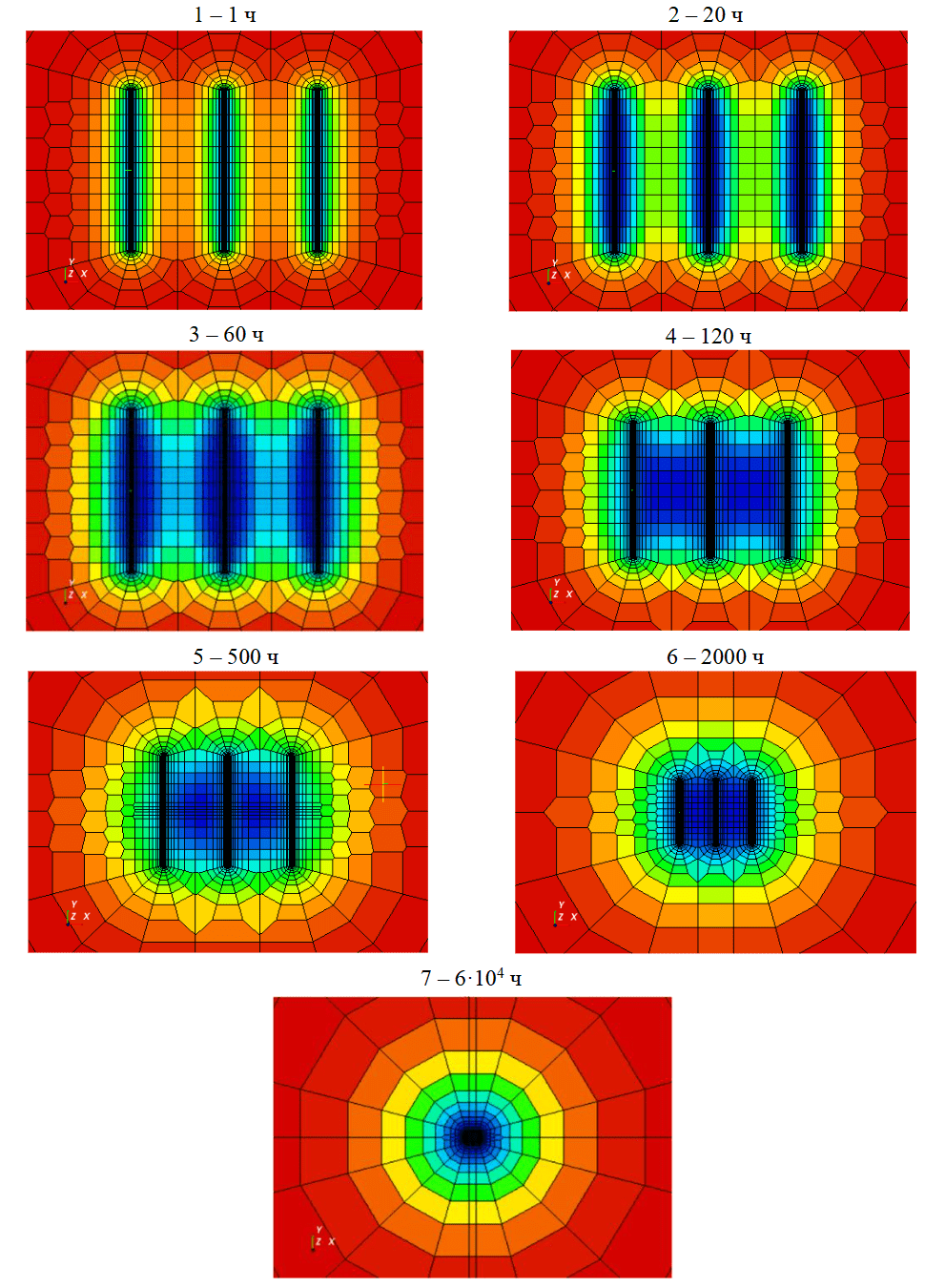
Рис.5. Распределения давления на моменты доминирования характерных режимов. Трещины бесконечной проводимости.
Синий цвет соответствует областям минимального давления, красный – максимального
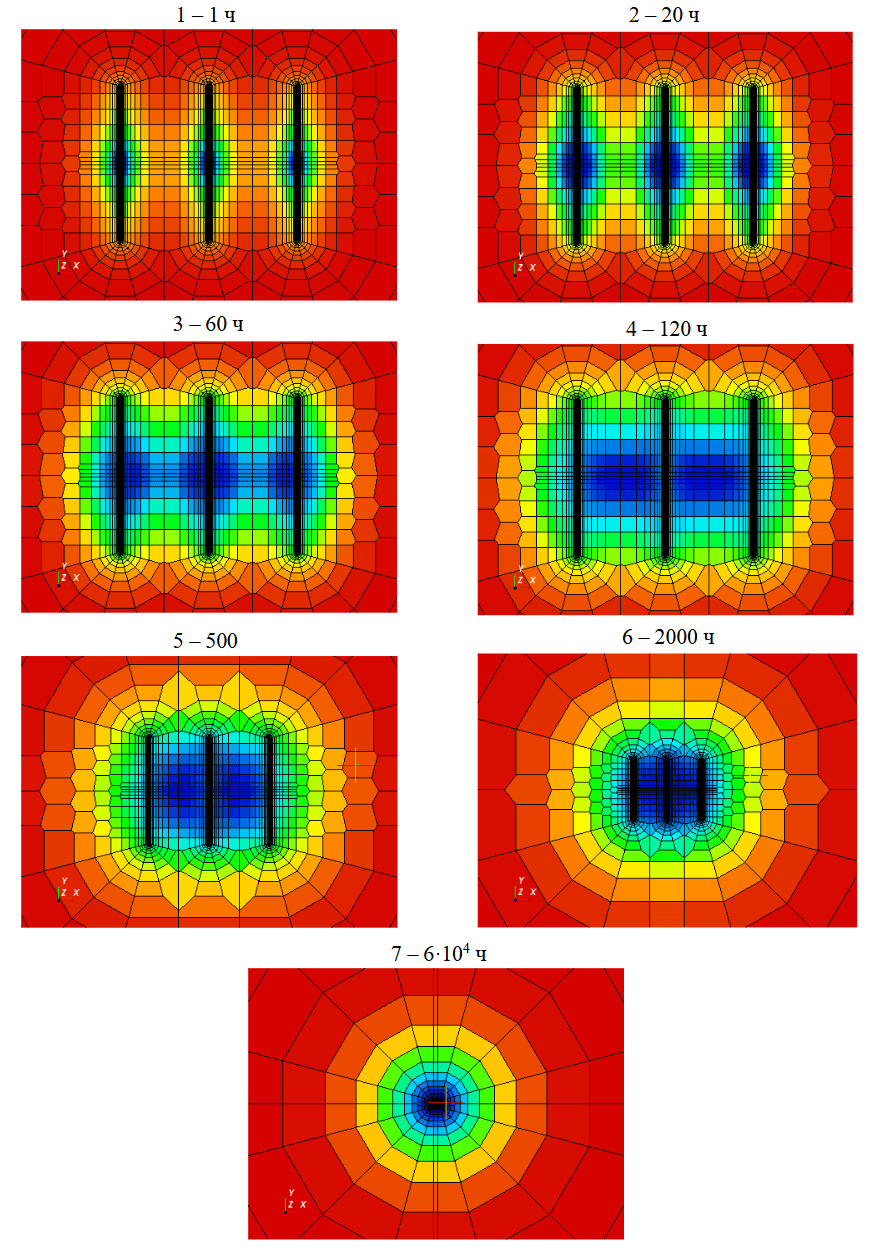
Рис.6. Распределения давления на моменты доминирования характерных режимов. Трещины конечной проводимости
Условные обозначения см. на рис.5
Таким образом, расхождение в поведении КВД между моделями трещин конечной и бесконечной проводимостей в периоды 1-4 обусловлено различием в охваченной дренированием площади. Последующие временные интервалы характеризуются идентичной динамикой охвата дренированием. В целом представленные численные расчеты позволяют сделать вывод о том, что для скважин с МГРП проявление раннего горизонтального участка на КВД после кратковременной отработки связано с формированием псевдорадиального (эллиптического) режима течения вокруг отдельных трещин. Из-за отличия в геометрии этих областей от строго круговых зон для классического раннерадиального режима следует ожидать и иную связь положения «полки» производной с истинной гидропроводностью пласта.
Различие в поведении графиков производной КВД между случаями трещин бесконечной и конечной проводимости требует более подробного исследования. С этой целью были выполнены расчеты синтетических КВД для двух типов проводимости трещин при ранее рассмотренных вариантах длины ГС hw и параметрах системы пласт – скважина (см. табл.1).
На рис.7 сопоставлены диагностические графики синтетических КВД на среднем периоде времени для трещин бесконечной и конечной проводимости для четырех значений hw, где цифрами отмечены следующие характерные режимы:
- Ранний горизонтальный участок.
- Снижение производной.
- Минимум производной («провал»).
- Период псевдоограниченного течения.
При наиболее плотном размещении трещин (рис.7, а) наблюдается максимальное расхождение между графиками для трещин бесконечной и конечной проводимости. Как и на рис.4, производная для трещин бесконечной проводимости проходит ниже. Расхождение также отмечается и по времени проявления режимов: участок1 для трещин бесконечной проводимости проявляется позднее. По мере увеличения расстояния между трещинами (hw) в остальных вариантах наблюдается визуальное сближение между кривыми, однако в абсолютных значениях расхождение в положении «полки» горизонтального участка 1 остается в пределах одного порядка в диапазоне 0,0175-0,046 бар (табл.4). При этом наблюдаются практически одинаковые временные интервалы доминирования режимов.
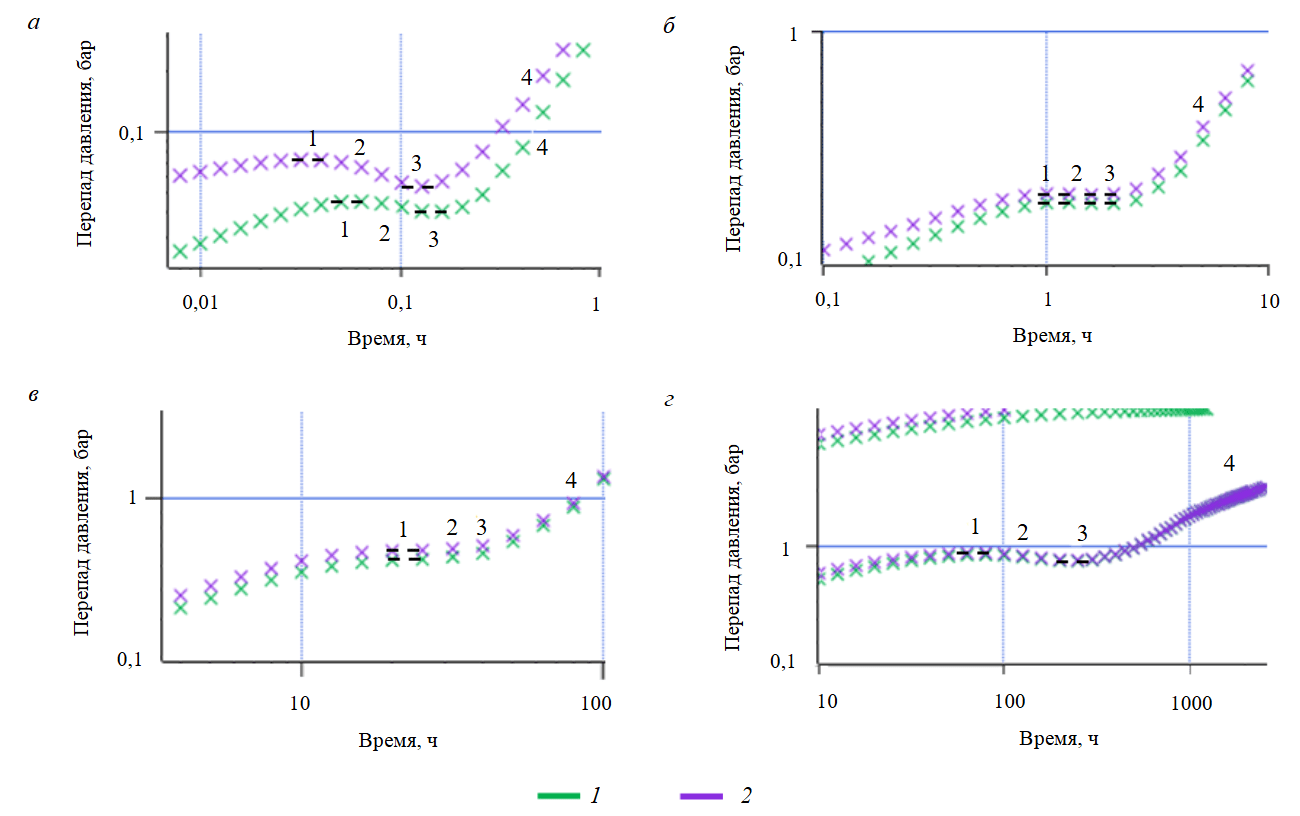
Рис.7. Сопоставление диагностических графиков КВД для трещин бесконечной (1) и конечной (2) проводимости на среднем периоде времени: а – hw = 25 м, Tотр = 0,1 ч; б – hw = 100 м, Tотр = 1 ч; в – hw = 400 м, Tотр = 10 ч; г – hw = 1000 м, Tотр = 100 ч
Отдельный интерес представляет изменяющийся характер «провала» производной для различных значений hw. Он является максимальным для hw = 25 м, для hw = 100 м в периоды 1-3 наблюдается формирование единой полки, для hw = 400 м в периоды 2-3 происходит незначительный рост производной, а для hw = 1000 м снова наблюдается снижение производной и ее минимум.
Таблица 4
Сопоставление положения «полки» горизонтального участка 1 для трещин бесконечной и конечной проводимости
|
Проводимость трещины |
Положение горизонтального участка |
|||||||
|
hw = 25 м |
hw = 100 м |
hw = 400 м |
hw = 1000 м |
|||||
|
i, бар |
Δ, бар |
i, бар |
Δ, бар |
i, бар |
Δ, бар |
i, бар |
Δ, бар |
|
|
Бесконечная |
0,0452 |
0,0277 |
0,186 |
0,0175 |
0,626 |
0,046 |
0,896 |
0,022 |
|
Конечная |
0,0729 |
0,2035 |
0,672 |
0,918 |
||||
В табл.5 сведены значения времени t для середин четырех рассматриваемых периодов, по значениям которых с помощью опции оценки радиуса исследования в Kappa Saphir определены условные радиусы исследования Rиссл. Расчет радиусов производится согласно известному соотношению через коэффициент пьезопроводности [24, 27]. Отметим, что хотя константа в формуле для Rиссл может быть выбрана различным способом [28, 29], в Kappa Saphir используется наиболее распространенное выражение, впервые обоснованное van Poolen в 1964 г. [24]. За исключением варианта hw = 25 м, а также участка 1 для варианта hw = 100 м, времена характерных периодов для трещин конечной и бесконечной проводимости не различаются. При этом выявляются следующие закономерности:
- период проявления раннего горизонтального участка на производной КВД соответствует времени, когда дренированием охвачена зона с горизонтальным размером меньше половины расстояния между трещинами L/2;
- по мере расширения области дренирования и приближения ее горизонтального размера к L/2 начинаются процессы интерференции между трещинами, обуславливающие снижение производной;
- в зоне минимума («провала») производной радиус исследования (области дренирования) соответствует половине расстояния между трещинами Rиссл≈ L/2;
- в период псевдоограниченного течения Rиссл превышает L/2 примерно в 1,5-2 раза.
Таблица 5
Средние значения времени и радиуса исследования на четырех участках при трещинах бесконечной и конечной проводимости
|
Проводимость трещины |
Середина интервала доминирования режима |
|||||||
|
Участок 1 |
Участок 2 |
Участок 3 |
Участок 4 |
|||||
|
t, ч |
Rиссл, м |
t, ч |
Rиссл, м |
t, ч |
Rиссл, м |
t, ч |
Rиссл, м |
|
|
hw = 25 м (L/2 = 6,25 м) |
||||||||
|
Бесконечная |
0,0634 |
4,5 |
0,1005 |
5,6 |
0,159 |
7,1 |
0,5036 |
12,6 |
|
Конечная |
0,0320 |
3,2 |
0,0798 |
5,0 |
0,127 |
6,3 |
0,318 |
10,0 |
|
hw = 100 м (L/2 = 25 м) |
||||||||
|
Бесконечная |
1,265 |
19,9 |
1,592 |
22,4 |
2,0475 |
25,4 |
5,0357 |
39,8 |
|
Конечная |
1,0475 |
18,1 |
1,592 |
22,4 |
2,0475 |
25,4 |
5,0357 |
39,8 |
|
hw = 400 м (L/2 = 100 м) |
||||||||
|
Бесконечная |
20,0 |
79,4 |
25,2 |
89,0 |
40,0 |
112,1 |
79,8 |
158,3 |
|
Конечная |
20,0 |
79,4 |
25,2 |
89,0 |
40,0 |
112,1 |
79,8 |
158,3 |
|
hw = 1000 м (L/2 = 250 м) |
||||||||
|
Бесконечная |
79,8 |
158,3 |
159,2 |
223,7 |
250,5 |
280,5 |
600,5 |
434,3 |
|
Конечная |
79,8 |
158,3 |
159,2 |
223,7 |
250,5 |
280,5 |
600,5 |
434,3 |
Выявленные закономерности подтверждаются при анализе распределений давления на рассматриваемых периодах времени для рассчитанных вариантов. Соответствующие рисунки аналогичны рис.5 и 6 и не приводятся для сокращения объема статьи. Для всех вариантов без исключения наблюдается явная корреляция с результатами оценки Rиссл:
- в период проявления на производной КВД горизонтального участка наблюдается формирование эллипсов в ближайшей к трещинам зоне;
- в период снижения производной отмечается смыкание эллипсов между трещинами;
- на момент «провала» (минимума) производной формируется единая область сниженного давления в пространстве, ограниченном соседними трещинами;
- в период псевдоограниченного течения происходит расширение этой области вдоль направления, параллельного трещинам.
Из данных выводов также ясны причины наибольшего различия в поведении КВД между случаями трещин бесконечной и конечной проводимости при hw = 25. Они обусловлены наибольшими расхождениями в геометрии соответствующих эллипсов из-за наиболее вытянутой формы областей между трещинами. При этом для hw = 25 м различия в геометрии эллипсов наблюдаются на протяжении всего среднего этапа и ожидаемо исчезнут только при выходе области дренирования за пределы трещин на позднем линейном течении. Также для этого варианта при трещинах конечной проводимости область дренирования в пространстве между трещинами на всех четырех режимах существенно меньше, что и обуславливает более высокое расположение «полки» производной относительно случая трещин бесконечной проводимости. Для hw = 100 м различия не являются столь существенными, особенно на участках 3 и 4. Это определяет близость производных давления между двумя вариантам проводимости трещин. Для hw = 400 м и hw = 1000 м визуальных отличий не наблюдается.
По данным визуальной оценки отсутствие «провала» производной для hw = 100 м объясняется тем, что даже при смыкании эллипсов на протяжении периодов 2 и 3, для обоих вариантов проводимости наблюдается сохранение структуры эллиптического потока. Аналогичным образом объясняется начало роста производной с периода 2 для hw = 400 м: с момента смыкания эллипсов область начинает формировать структуру, которая визуально не отличается от образующейся в период 4. Для вариантов hw = 25 м и hw = 1000 м каждый из отмеченных этапов характеризуется формированием структуры потока, отличающейся от предыдущего этапа.
Таким образом, результаты численных расчетов показывают, что возникновение раннего горизонтального участка производной на КВД после кратковременной отработки связано с формированием эллиптического режима течения вокруг трещин ГРП. При этом наблюдаются различия в геометрических параметрах образующихся эллипсов, обусловленные типом проводимости и плотностью расположения трещин, влияющие на положение «полки» горизонтального участка.
Обсуждение результатов
Анализ возможности оценки свойств пласта по бирадиальному режиму. В общепринятой практике и теории ГДИ для радиально подобного вида течения, характерного на определенных периодах времени для скважин с горизонтальным окончанием или с вертикальной трещиной гидроразрыва, используется термин «псевдорадиальный режим» [24, 30, 31]. Считается, что псевдорадиальный режим полностью тождественен «обычному» радиальному режиму по своим диагностическим признакам в виде горизонтального участка на билогарифмическом графике и методике оценки фильтрационных свойств пласта по его вертикальному положению. Таким образом, при псевдорадиальном режиме линии постоянного давления являются окружностями (а область дренирования – круговой), с учетом масштабирования по координатным осям в анизотропном случае.
Вместе с тем ряд авторов выделяет еще один характерный радиально подобный вид течения, обычно возникающий как переходный между линейным и псевдорадиальным режимами. Он может быть связан с упомянутыми типами заканчивания: вертикальными скважинами с ГРП [32-34], ГС с МГРП [35-37], ГС в естественно-трещиноватых пластах [38, 39]. Его возникновение также возможно в случае притока в анизотропных по латерали пластах [32]. Форма линий постоянного давления (и области дренирования) при подобном режиме является эллиптической. Такое название иногда применяется и для самого режима. В зависимости от причин формирования линии постоянного давления могут описываться как подобными эллипсами с эквивалентным масштабированием в псевдорадиальную конфигурацию, так и софокусными эллипсами с другой геометрией течения. В некоторых публикациях для такого течения используется синонимичный термин «бирадиальный режим», название которого, по всей видимости, обусловлено соответствующим характером симметрии потока.
Впервые диагностический признак эллиптического (бирадиального) режима описал в 1993 г. D.Tiab в работе [40]. В дальнейшем другие авторы развили предложенный им метод [37, 41]. На основании регрессионного анализа построенных им кривых для трещины бесконечной проводимости D.Tiab вывел следующую зависимость для производной давления по времени:
где Xe – половина длины стороны замкнутой прямоугольной области, в которой рассматривается течение; tDA – безразмерное время,
A – площадь области; PD – безразмерное давление,
В размерном виде уравнение (1) будет иметь вид:
Здесь произведение в левой части соответствует логарифмической производной изменения давления по времени (производной Бурде). Площадь A определяется произведением длин сторон прямоугольной области дренирования 2Xe и 2Ye, при этом направление Xe параллельно трещине.
Рассмотрим возможность применения метода D.Tiab к выявленному выше эллиптическому течению на КВД после кратковременной отработки. Исходя из рис.5 и 6 и оценок времени проявления характерных режимов, можно предположить, что ограничивающая эллипсы зона дренирования формируется в пределах области распространения трещин и половины расстояния между ними, поэтому Xe = Xf, Ye = L/2.
Из предложенной D.Tiab зависимости (2) очевидно, что в период доминирования бирадиального режима график логарифмической производной должен быть представлен прямолинейным участком с наклоном 0,36. Действительно, при проверке наличие такого режима проявляется для примеров, представленных на рис.7 для обоих вариантов проводимости трещин.
Исходя из наличия характерного диагностического признака и соответствующей зависимости, для бирадиального режима можно выполнить аналогичную раннерадиальному режиму предварительную оценку гидропроводности пласта. Согласно формуле (2), оценка должна производиться путем определения значения производной давления (tΔP′) на соответствующий данному режиму момент времени t:
Для скважины с МГРП аналогично раннерадиальному режиму следует ожидать, что соотношение полученного кажущегося и исходного значений гидропроводности должно соответствовать количеству трещин N. Отметим, что в правой части выражения (3) присутствует коэффициент пьезо-проводности k/(mμct), в величину которого входит проницаемость k. Следовательно, для оценки гидропроводности в реальных условиях требуется более сложный расчет. Однако для верификации метода можно принять, что пьезопроводность является известной величиной.
В табл.6 представлены результаты определения гидропроводности по формуле (3) на участке с наклоном i =0,36 для вариантов, показанных на рис.7. В последнем столбце приведено соотношение полученной кажущейся и исходной гидропроводности. Как видно из таблицы, наиболее близкое значение соотношения к количеству трещинN = 3 наблюдается для варианта hw = 25 м c трещиной конечной проводимости. Однако данный факт является скорее совпадением, так как в целом видна тенденция по снижению соотношения по мере увеличения длины ГС, и значения меняются в широком диапазоне. Также видно, что при hw = 25 м и hw = 100 м бо́льшая величина соотношения характерна для трещины бесконечной проводимости.
Таблица 6
Сопоставление кажущейся гидропроводности с исходным значением
|
Вариант |
Длина ГС hw, м |
Fc, мД·м |
(kh/μ)исх, мД·м/мПа·с |
t, ч |
tΔP′, бар |
(kh/μ)бирад, мД·м/мПа·с |
(kh/μ)бирад /(kh/μ)исх |
|
1 |
25 |
Бесконечная |
30 |
0,005 |
0,0213 |
267,8 |
8,9 |
|
25 |
300 |
0,0556 |
102,6 |
3,4 |
|||
|
2 |
100 |
Бесконечная |
0,03 |
0,0553 |
62,6 |
2,1 |
|
|
100 |
300 |
0,0891 |
38,9 |
1,3 |
|||
|
3 |
400 |
Бесконечная |
4 |
0,479 |
48,7 |
1,6 |
|
|
400 |
300 |
||||||
|
4 |
1000 |
Бесконечная |
0,551 |
30,4 |
1,0 |
||
|
1000 |
300 |
Таким образом, для выявленного эллиптического режима на КВД скважины с МГРП после кратковременной отработки не применимы критерий бирадиального течения с наклоном производнойi =0,36 и эмпирическая формула D.Tiab. Дальнейшая работа должна быть связана с анализом течения в период проявления горизонтального участка производной и зависимости положения «полки» от параметров системы пласт – скважина.
Эмпирическая формула для оценки гидропроводности по горизонтальному участку эллиптического режима. Из представленного выше анализа следуют выводы:
- горизонтальный участок на графике производной КВД после кратковременной отработки соответствует эллиптическому режиму течения;
- положение «полки» производной должно иметь связь с фильтрационными параметрами пласта (гидропроводностью) и геометрическими характеристиками эллиптического течения, формируемого в системе пласт – трещины МГРП.
С целью поиска зависимости для положения «полки» горизонтального участка производной было выполнено 40 расчетов синтетических КВД с вариацией следующих параметров системы пласт – скважина:
- Дебит q.
- Проницаемость k.
- Толщина пласта h.
- Вязкость µ.
- Полудлина трещины Xf.
- Длина ГС hw.
Указанные параметры были выбраны как непосредственно определяющие «полку» горизонтального участка на позднем (истинном) радиальном режиме (q, k, h, µ), так и те, от которых зависит проявление горизонтального участка и геометрия соответствующего эллиптического течения (Xf, hw). Подбор значений параметров производился случайным способом при условии проявления горизонтального участка эллиптического режима на производной КВД для времени отработки T = 100 ч. При этом на данном этапе исследований рассматривался только случай трещин бесконечной проводимости, с целью снижения количества факторов, влияющих на положение горизонтального участка.
Значения параметров по вариантам и результаты расчетов приведены в табл.7. В столбце 12 для сравнения представлены оценки гидропроводности по участку с наклоном i = 0,36. Несмотря на ранее выявленное отсутствие зависимости между истинной гидропроводностью, ее расчетным значением по участку с i = 0,36 и количеством трещин, при выполнении текущих оценок в формуле (3) количество трещин учитывалось из теоретических соображений, аналогично раннерадиальному режиму:
Таблица 7
Исходные параметры и результаты оценки гидропроводности для синтетических вариантов
|
Вариант |
q, м3/сут |
k, мД |
h, м |
µ, мПа·с |
(kh/μ)исх, мД·м/мПа·с |
Xf, м |
Длина ГС hw, м |
Количество трещин N |
Расстояние между трещинами L, м |
Участок i = 0,36 (4) |
Участок i = 0 (5) |
||||
|
tΔP′ при t = 1 ч, бар |
kh/μ, мД·м/мПа·с |
δ, % |
tΔР′, бар |
kh/μ, мД·м/мПа·с |
δ, % |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
1 |
10 |
0,7 |
15 |
6 |
1,8 |
100 |
1000 |
7 |
167 |
0,615 |
1,2 |
–33 |
2,143 |
1,8 |
3 |
|
2 |
20 |
0,7 |
23 |
15 |
1,1 |
60 |
300 |
5 |
75 |
1,267 |
3,0 |
182 |
7,818 |
1,0 |
–3 |
|
3 |
5 |
1 |
10 |
30 |
0,3 |
150 |
1000 |
10 |
111 |
1,520 |
0,2 |
–48 |
1,754 |
0,3 |
3 |
|
4 |
11 |
1 |
20 |
1 |
20,0 |
70 |
400 |
3 |
200 |
0,224 |
31,5 |
57 |
0,836 |
20,4 |
2 |
|
5 |
17 |
0,3 |
10 |
1 |
3,0 |
100 |
800 |
8 |
114 |
0,349 |
8,2 |
172 |
1,308 |
3,0 |
1 |
|
6 |
8 |
0,4 |
5 |
3 |
0,7 |
80 |
1200 |
9 |
150 |
0,520 |
1,7 |
152 |
4,050 |
0,7 |
1 |
|
7 |
26 |
2 |
30 |
25 |
2,4 |
130 |
300 |
4 |
100 |
0,477 |
10,8 |
352 |
3,485 |
2,3 |
–3 |
|
8 |
6 |
0,8 |
23 |
12 |
1,5 |
60 |
700 |
7 |
117 |
0,543 |
1,5 |
–4 |
1,712 |
1,6 |
3 |
|
9 |
14 |
0,8 |
14 |
3 |
3,7 |
80 |
200 |
3 |
100 |
0,672 |
10,2 |
172 |
2,687 |
3,5 |
–5 |
|
10 |
18 |
0,2 |
22 |
14 |
0,3 |
130 |
500 |
8 |
71 |
0,575 |
1,9 |
501 |
5,959 |
0,3 |
7 |
|
11 |
16 |
1,3 |
18 |
7 |
3,3 |
120 |
1000 |
10 |
111 |
0,151 |
11,3 |
239 |
0,702 |
3,4 |
3 |
|
12 |
27 |
1,7 |
24 |
5 |
8,2 |
120 |
550 |
4 |
183 |
0,324 |
23,1 |
183 |
2,056 |
8,2 |
0 |
|
13 |
8 |
0,9 |
26 |
9 |
2,6 |
150 |
200 |
3 |
100 |
0,202 |
10,8 |
315 |
1,153 |
2,5 |
–3 |
|
14 |
13 |
0,7 |
19 |
13 |
1,0 |
120 |
900 |
9 |
113 |
0,266 |
3,7 |
261 |
2,085 |
1,1 |
3 |
|
15 |
21 |
1,7 |
17 |
9 |
3,2 |
70 |
1100 |
10 |
122 |
0,358 |
7,4 |
130 |
1,784 |
3,3 |
4 |
|
16 |
19 |
2 |
10 |
18 |
1,1 |
80 |
500 |
5 |
125 |
1,297 |
2,9 |
159 |
8,586 |
1,1 |
1 |
|
17 |
17 |
0,7 |
16 |
4 |
2,8 |
120 |
400 |
4 |
133 |
0,489 |
8,5 |
203 |
2,774 |
2,8 |
–1 |
|
18 |
15 |
1,1 |
19 |
11 |
1,9 |
60 |
800 |
9 |
100 |
0,392 |
4,8 |
155 |
2,303 |
2,0 |
3 |
|
19 |
13 |
1,7 |
23 |
6 |
6,5 |
130 |
400 |
5 |
100 |
0,128 |
25,6 |
292 |
0,485 |
6,7 |
3 |
|
20 |
24 |
1,3 |
35 |
23 |
2,0 |
100 |
1000 |
9 |
125 |
0,285 |
6,7 |
237 |
2,612 |
2,1 |
5 |
|
21 |
70 |
2 |
21 |
8 |
5,3 |
70 |
700 |
4 |
233 |
2,025 |
9,5 |
82 |
16,399 |
5,8 |
10 |
|
22 |
15 |
1 |
6 |
16 |
0,4 |
97 |
800 |
7 |
133 |
1,365 |
1,1 |
205 |
12,211 |
0,4 |
5 |
|
23 |
15 |
0,5 |
18 |
25 |
0,4 |
108 |
700 |
8 |
100 |
0,605 |
1,6 |
345 |
7,034 |
0,4 |
12 |
|
24 |
55 |
1,3 |
10 |
7 |
1,9 |
119 |
500 |
7 |
83 |
1,290 |
7,2 |
289 |
4,566 |
2,0 |
6 |
|
25 |
10 |
1,2 |
12 |
10 |
1,4 |
98 |
700 |
7 |
117 |
0,304 |
4,5 |
215 |
1,891 |
1,5 |
2 |
|
26 |
29 |
0,3 |
18 |
11 |
0,5 |
75 |
500 |
9 |
63 |
1,197 |
2,1 |
327 |
8,797 |
0,5 |
1 |
|
27 |
45 |
1,5 |
34 |
8 |
6,4 |
140 |
500 |
3 |
250 |
0,649 |
17,5 |
174 |
6,609 |
6,6 |
4 |
|
28 |
53 |
0,7 |
26 |
11 |
1,7 |
132 |
700 |
10 |
78 |
0,541 |
7,8 |
372 |
2,982 |
1,7 |
3 |
|
29 |
15 |
1,7 |
6 |
21 |
0,5 |
130 |
900 |
9 |
113 |
0,668 |
1,9 |
293 |
4,775 |
0,5 |
1 |
|
30 |
9 |
0,8 |
24 |
15 |
1,3 |
141 |
600 |
5 |
150 |
0,209 |
5,0 |
289 |
2,270 |
1,4 |
7 |
|
31 |
12 |
0,6 |
14 |
24 |
0,4 |
87 |
500 |
9 |
63 |
0,617 |
1,5 |
342 |
4,409 |
0,4 |
1 |
|
32 |
32 |
1,5 |
16 |
23 |
1,0 |
137 |
1200 |
8 |
171 |
0,584 |
4,1 |
292 |
7,217 |
1,1 |
8 |
|
33 |
67 |
1 |
25 |
8 |
3,1 |
98 |
500 |
5 |
125 |
1,399 |
9,1 |
192 |
8,855 |
3,1 |
1 |
|
34 |
12 |
1,6 |
8 |
27 |
0,5 |
120 |
900 |
6 |
180 |
0,752 |
1,6 |
234 |
9,332 |
0,5 |
10 |
|
35 |
60 |
1,1 |
24 |
1 |
26,4 |
145 |
1200 |
6 |
240 |
0,226 |
63,3 |
140 |
0,988 |
27,3 |
3 |
|
36 |
37 |
0,8 |
33 |
26 |
1,0 |
69 |
1000 |
9 |
125 |
0,926 |
2,9 |
186 |
10,706 |
1,1 |
12 |
|
37 |
18 |
0,7 |
11 |
22 |
0,4 |
91 |
500 |
5 |
125 |
1,959 |
1,1 |
214 |
21,820 |
0,4 |
5 |
|
38 |
54 |
1,9 |
19 |
28 |
1,3 |
132 |
1100 |
7 |
183 |
1,070 |
4,3 |
235 |
12,250 |
1,4 |
10 |
|
39 |
14 |
1,7 |
26 |
23 |
1,9 |
145 |
800 |
7 |
133 |
0,194 |
6,9 |
260 |
1,514 |
2,0 |
3 |
|
40 |
8 |
1,5 |
15 |
4 |
5,6 |
148 |
1000 |
6 |
200 |
0,081 |
17,0 |
201 |
0,514 |
5,7 |
1 |
Как видно из столбца 13, приемлемая погрешность оценки гидропроводности по формуле (4) (4 %) наблюдается только для варианта 8. В целом по вариантам среднее значение погрешности по модулю составляет δ = 218 %, что еще раз подтверждает нерелевантность оценки параметров пласта по участку с наклономi = 0,36.
Эмпирическая зависимость для оценки гидропроводности по «полке» горизонтального участка эллиптического режима отыскивалась с учетом следующих соображений. Для классического радиального режима вклад осесимметричной геометрии течения в зависимость между дебитом и гидропроводностью определяется граничным условием на стенке скважины, вытекающим из закона Дарси:
где h2πr соответствует площади стенки скважины (2πr – ее периметру), через которую осуществляется приток; – градиенту давления.
Скважина приближенно считается точечным источником с радиусом rc → 0, что приводит к присутствию в итоговом решении только множителя 2π в качестве комплексного вклада периметра стенки скважины и расстояния, влияющего на действующий градиент давления.
В случае эллиптического притока к трещине бесконечной проводимости в роли источника выступает поверхность трещины с ненулевым периметром 4Xf (площадью 4Xfh), а градиент давления должен иметь связь с половиной расстояния между трещинами L/2. Включив обе указанные величины в соответствующие части формулы для положения «полки» производной и подбирая недостающий множитель, удалось выявить следующую эмпирическую зависимость:
или
Результаты оценки гидропроводности по «полке» горизонтального участка эллиптического режима с использованием формулы (5) представлены в столбце 15 табл.7. В столбце 16 приведены соответствующие значения погрешностей. Ошибка в оценке значения гидропроводности не превышает 12 % и по большинству вариантов находится в пределах 5-6 %, составляя в среднем 4,05 %.
Обозначив левую часть формулы (6) как PD, можно дополнительно оценить точность полученной эмпирической зависимости, сравнив ее значение с 1 для всех рассмотренных вариантов. По результатам оценки среднее значение PD по вариантам отличается от 1, но характеризуется близкой величиной – 0,969. При этом ни в одном из вариантов погрешность не превышает критичный с точки зрения устоявшейся практики ГДИ порог в 15 %.
Таким образом, несмотря на то, что эмпирическая зависимость (5) на рассмотренной выборке вариантов дает небольшое смещение оценок, полученные результаты указывают на ее практическую применимость, в отличие от оценок по участку с наклоном i = 0,36. Отметим, что исходя из характера распределений давления на рис.5 и 6, зависимость (5) может иметь обобщение и на случай трещин конечной проводимости. При этом потребуется замена величины Xf на эквивалентную протяженность области внутри трещин, охваченной перераспределением давления к моменту развития эллиптического режима.
Несмотря на полученные оптимистичные результаты, область применимости эмпирической формулы (5) требует дальнейшего исследования. Для достаточно больших расстояний между трещинами «полка» эллиптического режима на КВД начинает совпадать с появляющейся «полкой» раннерадиального режима на КСД. Следовательно, формула (5) должна переходить в классическую формулу оценки гидропроводности для радиального режима с поправкой на число трещин.
В частности, расстояние между трещинами по вариантам в табл.7 находится в диапазоне 63-250 м при среднем значении 132 м. Представляет интерес проверка вариантов, находящихся вне этого диапазона. Для этого вернемся к ранее рассмотренным четырем вариантам длины горизонтального ствола hw при N = 3 – 25, 100, 400 и 1000 м. Значения PD для них соответственно составляют 0,994, 1,023, 0,865 и 0,493. Как видно, для вариантов hw = 25 м и hw = 100 м, значение L для которых (12,5 и 50 м) ниже минимальной величины из указанного выше диапазона, величина PD даже ближе к единице, чем в большинстве ранее рассмотренных вариантов. Для hw = 400 м (L = 200 м) отклонение PD от единицы существенно выше, но также укладывается в 15 %-ный коридор. Значительное (более 50 %) отклонение наблюдается только для варианта hw = 1000 м (L = 500 м) с явно проявляющимся раннерадиальным течением на КСД. Подтверждается вывод, что зависимость (5) для трещин бесконечной проводимости перестает работать при значительном увеличении расстояния между трещинами (по отношению к их полудлине Xf).
Возможности использования эллиптического режима на практике. С учетом того, что для возникновения эллиптического режима требуется кратковременная отработка, наиболее очевидной возможностью его получения на практике является исследование новых скважин, запускающихся в эксплуатацию непосредственно после бурения. Такое исследование предполагает кратковременную отработку скважины в процессе освоения, после которой должна последовать остановка скважины на КВД. При этом необходимая длительность периодов отработки и остановки должна оцениваться с помощью расчета синтетических кривых (дизайна) исследования, основывающихся на конструкции скважин (количество трещин и расстояние между ними) и прогнозируемых параметрах системы пласт – скважина. Расчет дизайна включает анализ чувствительности с учетом неопределенности исходных данных. По завершении записи КВД производится повторный запуск скважины с целью доосвоения, проведения исследований для оценки продуктивности (индикаторной диаграммы) или непосредственно эксплуатации в нефтегазосборный коллектор.
Другой вариант практического использования – эксплуатирующиеся скважины после их длительного простоя вследствие различных технологических причин. В таком случае также должен составляться дизайн исследования, по которому оценивается как сама возможность получения эллиптического режима (достаточность времени остановки), так и необходимая длительность отработки и последующего закрытия на КВД.
Заключение
Достоверная оценка параметров системы пласт – скважина при интерпретации ГДИ ГС с МГРП в низкопроницаемых коллекторах связана со значительными трудностями из-за практически недостижимого времени выхода на позднерадиальный режим и, как следствие, высокой неопределенности в оценке коэффициента гидропроводности пласта. Альтернативным решением является оценка гидропроводности по данным раннерадиального режима. Однако соответствующий горизонтальный участок проявляется на билогарифмическом графике производной давления только при достаточно больших расстояниях между трещинами по сравнению с их полудлиной.
Представленные и проанализированные в настоящей статье аналитические и численные расчеты значительного числа синтетических вариантов показывают, что при достаточно коротком времени отработки скважины перед остановкой возможно проявление на КВД иного вида радиально подобного режима. Он также характеризуется формированием горизонтальной «полки» производной с возможным последующим «провалом» и переходом к режиму псевдоограниченного течения в области между трещинами с единичным наклоном графика производной. Выявленный радиально подобный режим характеризуется эллиптической формой зон дренирования в области между трещинами и прекращается при их смыкании после возникновения сильной межтрещинной интерференции. Вертикальное положение «полки» производной устойчиво по отношению к времени отработки и общей сжимаемости системы и связано с гидропроводностью пласта и параметрами трещин (число трещин, их полудлина, проводимость, расстояние между ними).
Применение к обнаруженному эллиптическому режиму известного эмпирического метода D.Tiab на основе участка графика производной с наклоном 0,36 (бирадиальный режим) приводит к кратным ошибкам в оценке гидропроводности и не имеет перспектив с практической точки зрения. С учетом наблюдаемой геометрии формируемого эллиптического течения предложена эмпирическая формула для оценки гидропроводности по «полке» производной в случае трещин бесконечной проводимости. Она показала достаточную точность для практического применения (ошибка не более 12 %, в среднем около 4 %) при относительно малых расстояниях между трещинами. По мере их увеличения точность оценки снижается.
Выполненные исследования расширяют возможности проведения информативных ГДИ ГС с МГРП в низкопроницаемых коллекторах с достоверной оценкой параметров системы пласт – скважина за счет комбинации короткой отработки, например после запуска скважины с последующей остановкой на КВД. Определение эффективного дизайна таких исследований в зависимости от особенностей пласта и конструкции скважины является предметом дальнейших исследований.
Необходимо изучение области применимости предложенной эмпирической формулы и/или ее уточнение для корректной оценки гидропроводности по мере перехода от обнаруженного эллиптического к известному раннерадиальному режиму при больших расстояниях между трещинами. Также представляет практический интерес ее обобщение на случай трещин конечной проводимости.
Литература
- Аржиловский А.В., Грищенко А.С., Смирнов Д.С. и др. Опыт применения горизонтальных скважин с многостадийным гидроразрывом пласта в условиях низкопроницаемых отложений тюменской свиты месторождений ООО «РН-Уватнефтегаз» // Нефтяное хозяйство. 2021. № 2. С. 74-76. DOI: 10.24887/0028-2448-2021-2-74-76
- Walker L. Technology Focus: Unconventional and Tight Reservoirs (July 2024) // Journal of Petroleum Technology. 2024. Vol. 76. Iss. 7. P. 88-89. DOI: 10.2118/0724-0088-JPT
- Manuaba I.B.G.H., Aljishi M., Van Steene M., Dolan J. Logging-While-Drilling Laterolog vs. Electromagnetic Propagation Measurements: Which Is Telling the True Resistivity? // SPE Journal. 2024. Vol. 29. Iss. 8. P. 4000-4013. DOI: 10.2118/219772-PA
- Carpenter C. Holistic Approach Uses Electromagnetic Tools, LWD Data To Improve Reservoir Understanding // Journal of Petroleum Technology. 2024. Vol. 76. Iss. 1. P. 95-97. DOI: 10.2118/0124-0095-JPT
- Белова А.А., Овчинников К.Н., Буянов А.В. и др. Долговременный мониторинг профиля притока газовой горизон-тальной скважины после проведения МГРП посредством маркерных полимерных технологий // Газовая промышленность. 2020. № 9 (806). С. 86-94.
- Асмандияров Р.Н., Ипатов А.И., Язьков А.В. и др. Опыт «Газпром нефти» в тестировании коммерческих систем маркерного мониторинга работы нефтяных скважин и оценке их надежности // Нефтяное хозяйство. 2023. № 12. С. 53-57. DOI: 10.24887/0028-2448-2023-12-53-57
- Zhenzhen Wang, Chen Li, King M.J. Applications of Asymptotic Solutions of the Diffusivity Equation to Infinite Acting Pressure Transient Analysis // SPE Journal. 2024. Vol. 29. Iss. 8. P. 4069-4093. DOI: 10.2118/180149-PA
- Кременецкий М.И., Ипатов А.И. Применение промыслово-геофизического контроля для оптимизации разработки месторождений нефти и газа. В 2 т. Т. 1. Основы гидродинамико-геофизического контроля разработки и мониторинга добычи. М.; Ижевск: ИКИ, 2020. 660 с.
- Ипатов А.И., Кременецкий М.И. Проблемы промыслово-геофизического контроля в условиях «новой экономиче-ской политики» // Актуальные проблемы нефти и газа. 2022. Вып. 2 (37). С. 87-99. DOI: 10.29222/ipng.2078-5712.2022-37.art6
- Гришина Е.И., Кременецкий М.И., Буянов А.В. Прогноз выработки неоднородного пласта в горизонтальных сква-жинах с многостадийным гидроразрывом пласта по результатам комплексных геофизических и гидродинамических иссле-дований // Нефтепромысловое дело. 2020. № 5 (617). С. 38-43. DOI: 10.30713/0207-2351-2020-5(617)-38-43
- Ипатов А.И., Кременецкий М.И., Гуляев Д.Н. и др. Гидродинамический и геофизический мониторинг разработки сложнопостроенных месторождений углеводородов // Нефтяное хозяйство. 2015. № 9. С. 68-72.
- Grishina E. Using Well Testing and Production Logging Methods to Estimate Individual Frature's Parametres and Perfor-mance in a Fractured Horizontal // SPE Russian Petroleum Technology Conference, 15-17 October 2018, Moscow, Russia. OnePetro, 2018. № SPE-191563-18RPTC-MS. DOI: 10.2118/191563-18RPTC-MS
- Kremenetskiy M., Kokurina V., Morozovskiy N., Grishina E. PI Evaluation by Well Tests in Case of Low Permeability Formations Exposed by Complex Geometry Fracs // SPE Russian Petroleum Technology Conference, 16-18 October 2017, Moscow, Russia. OnePetro, 2017. № SPE-187766-MS. DOI: 10.2118/187766-MS
- Коваленко И.В. Инвариант связи фильтрационных и емкостных параметров на неустановившемся режиме фильт-рации к скважинам с многостадийным гидроразрывом пласта как инструмент интерпретации данных гидродинамических исследований // Нефтепромысловое дело. 2022. № 8 (644). С. 13-20. DOI: 10.33285/0207-2351-2022-8(644)-13-20
- Коваленко И.В. Прогнозирование продуктивности горизонтальных скважин с многостадийным гидроразрывом пласта: Автореф. дис. … д-р техн. наук. Тюмень: Тюменский индустриальный университет, 2021. 38 с.
- Никонорова А.Н., Ворон К.А., Кременецкий М.И. и др. Оценка динамики добычных возможностей нефтегазовых горизонтальных скважин с многостадийным ГРП по результатам гидродинамических исследований на основе диагностики ранних режимов течения // Экспозиция Нефть Газ. 2024. № 6 (107). С. 50-56. DOI: 10.24412/2076-6785-2024-6-50-56
- Туленков С.В., Туленкова С.В., Мамонов Д.М. и др. Апробация деконволюции при интерпретации данных гидроди-намических исследований скважин с гидравлическим разрывом газонасыщенных низкопроницаемых ачимовских отложений // Научный журнал Российского газового общества. 2024. № 3 (45). С. 102-109.
- Асалхузина Г.Ф., Давлетбаев А.Я., Абдуллин Р.И. и др. Гидродинамические методы исследования скважин в рядной системе разработки на месторождении с низкопроницаемым коллектором // Нефтегазовое дело. 2021. Т. 19. № 3. С. 49-58. DOI: 10.17122/ngdelo-2021-3-49-58
- Martyushev D.A., Yongfei Yang, Kazemzadeh Y. et al. Understanding the Mechanism of Hydraulic Fracturing in Naturally Fractured Carbonate Reservoirs: Microseismic Monitoring and Well Testing // Arabian Journal for Science and Engineering. 2024. Vol. 49. Iss. 6. P. 8573-8586. DOI: 10.1007/s13369-023-08513-1
- Галкин В.И., Мартюшев Д.А., Пономарева И.Н., Черных И.А. Особенности формирования призабойных зон про-дуктивных пластов на месторождениях с высокой газонасыщенностью пластовой нефти // Записки Горного института. 2021. T. 249. C. 386-392. DOI: 10.31897/PMI.2021.3.7
- Сальникова О.Л., Черных И.А., Мартюшев Д.А., Пономарева И.Н. Особенности определения фильтрационных пара-метров сложнопостроенных карбонатных коллекторов при их эксплуатации горизонтальными скважинами // Известия Томско-го политехнического университета. Инжиниринг георесурсов. 2023. Т. 334. № 5. С. 138-147. DOI: 10.18799/24131830/2023/5/3970
- Гришина Е.И. Геофизический и гидродинамический контроль эксплуатации неоднородных коллекторов на основе инвариантных параметров в скважинах с высокотехнологичным заканчиванием: Автореф. дис. … канд. техн. наук. М.: Рос-сийский государственный университет нефти и газа (национальный исследовательский университет) имени И.М. Губкина, 2021. 24 с.
- Кременецкий М.И., Ипатов А.И. Применение промыслово-геофизического контроля для оптимизации разработки месторождений нефти и газа. В 2 т. Т. 2. Роль гидродинамико-геофизического мониторинга в управлении разработкой. М.; Ижевск: ИКИ, 2020. 756 с.
- Houzé O., Viturat D., Fjaere O.S. et al. Dynamic Data Analysis, v5.42. Kappa, 1988-2021. 776 p.
- Wentao Zhou, Raj Banerjee, Poe B. et al. Semianalytical Production Simulation of Complex Hydraulic-Fracture Networks // SPE Journal. 2014. Vol. 19. Iss. 1. P. 6-18. DOI: 10.2118/157367-PA
- Transient Well Testing / Ed. by M.M. Kamal. Society of Petroleum Engineers, 2009. 860 p.
- Horne R.N. Modern Well Test Analysis: A Computer-Aided Approach. Petroway, 1995. 257 p.
- Hossain M.E., Tamim M., Rahman N.M.A. Effects of Criterion Values on Estimation of the Radius of Drainage and Stabili-zation Time // Journal of Canadian Petroleum Technology. 2007. Vol. 46. Iss. 3. P. 24-30. DOI: 10.2118/07-03-01
- Ramakrishnan T.S., Prange M.D., Kuchuk F.J. Radius of Investigation in Pressure Transient Testing // Transport in Porous Media. 2020. Vol. 131. Iss. 3. P. 783-804. DOI: 10.1007/s11242-019-01367-y
- Мажар В.А., Ридель А.А., Колесников М.В. и др. Опыт гидродинамических исследований в скважинах со сложной конструкцией // Актуальные проблемы нефти и газа. 2022. Вып. 2 (37). С. 127-138. DOI: 10.29222/ipng.2078-5712.2022-37.art9
- Сергеев В.Л., Донг Ван Хоанг. Адаптивная интерпретация гидродинамических исследований горизонтальных скважин с идентификацией псевдорадиального потока // Известия Томского политехнического университета. Инжиниринг георесурсов. 2017. Т. 328. № 10. С. 67-73.
- Kuchuk F., Bringham W.E. Transient Flow in Elliptical Systems // Society of Petroleum Engineers Journal. 1979. Vol. 19. Iss. 6. P. 401-410. DOI: 10.2118/7488-PA
- Escobar F.-H., Montealegre M.M., Cantillo J.-H. Conventional analysis for characterization of bi-radial (elliptical) flow in infinite-conductivity vertical fractured wells // CT&F – Ciencia, Tecnología y Futuro. 2006. Vol. 3. № 2. P. 141-147.
- Amini S., Ilk D., Blasingame T.A. Evaluation of the Elliptical Flow Period for Hydraulically-Fractured Wells in Tight Gas Sands – Theoretical Aspects and Practical Considerations // SPE Hydraulic Fracturing Technology Conference, 29-31 January 2007, College Station, TX, USA. OnePetro, 2007. № SPE-106308-MS. DOI: 10.2118/106308-MS
- Badazhkov D., Ovsyannikov D., Kovalenko A. Analysis of Production Data with Elliptical Flow Regime in Tight Gas Res-ervoirs // SPE Russian Oil and Gas Technical Conference and Exhibition, 28-30 October 2008, Moscow, Russia. OnePetro, 2008. № SPE-117023-MS. DOI: 10.2118/117023-MS
- Weiyao Zhu, Yunfeng Liu, Zhongxing Li et al. Study on Pressure Propagation in Tight Oil Reservoirs with Stimulated Res-ervoir Volume Development // ACS Omega. 2021. Vol. 6. Iss. 4. P. 2589-2600. DOI: 10.1021/acsomega.0c04661
- Apte S.S., Lee W.J. Elliptical Flow Regimes in Horizontal Wells with Multiple Hydraulic Fractures // SPE Hydraulic Fractur-ing Technology Conference and Exhibition, 24-26 January 2017, The Woodlands, TX, USA. OnePetro, 2017. № SPE-184856-MS. DOI: 10.2118/184856-MS
- Escobar F.H., Ghisays-Ruiz A., Bonilla L.F. New model for elliptical flow regime in hydraulically-fractured vertical wells in homogeneous and naturally-fractured systems // ARPN Journal of Engineering and Applied Sciences. 2014. Vol. 9. № 9. P. 1629-1636.
- Zhiming Chen, Xinwei Liao, Wei Yu, Sepehrnoori K. Pressure-Transient Behaviors of Wells in Fractured Reservoirs With Natural- and Hydraulic-Fracture Networks // SPE Journal. 2019. Vol. 24. Iss. 1. P. 375-394. DOI: 10.2118/194013-PA
- Tiab D. Analysis of Pressure and Pressure Derivative without Type-Curve Matching – III. Vertically Fractured Wells in Closed Systems // SPE Western Regional Meeting, 26-28 May 1993, Anchorage, AK, USA. OnePetro, 1993. № SPE-26138-MS. DOI: 10.2118/26138-MS
- Malallah A., Nashawi I.S., Algharaib M. A comprehensive analysis of transient rate and rate derivative data of an oil well intercepted by infinite-conductivity hydraulic fracture in closed systems // Journal of Petroleum Exploration and Production Technology. 2024. Vol. 14. Iss. 3. P. 805-822. DOI: 10.1007/s13202-023-01732-0
