Гранулометрия в рамках кинематической теории преобразования открытых систем
- д-р геол.-минерал. наук профессор Томский политехнический университет ▪ Orcid
Аннотация
Образование полимодальных распределений частоты встречаемости размеров песчаных фракций обусловлено изменением кинетической энергии водной среды в процессе отложения осадков в открытых системах-фациях. Повышение релевантности информации о палеоусловиях осадконакопления имеет большое значение в интерпретации результатов гранулометрического анализа. В качестве материалов исследований были взяты результаты гранулометрического анализа песчано-алевритовых отложений различных пластов в скважинах, находящихся на территориях нефтегазовых месторождений п-ва Ямал. На основе кинематической теории преобразования открытых систем определено уравнение зависимости размеров отложенных фракций от их кинематических параметров – периода времени и расстояния отложения. Это позволяет вычислить их в исследуемой фациальной системе по данным размеров и процентного содержания фракций в диапазоне диаметров 0,001-1 мм. Целью работы является представление результатов выявления фаций на основе вычислений кинематических параметров потока зерен песка и мелкодисперсных частиц с использованием уравнения интенсивности процессов преобразования открытых систем в рамках универсальной кинематической теории. Параметром, обладающим наибольшей информативностью, является расстояние переноса частиц при отложении, которое контролируется размером осаждающихся зерен. Изменение величины данного параметра зависит от перемены угла наклона поверхности дна, размеров частиц, глубины отложения. Сопоставляя величину вычисленного параметра с диаметром фракций, можно провести идентификацию исследуемой зоны с ее фациальной принадлежностью.
Финансирование
Работа подготовлена в рамках программы развития Томского политехнического университета.
Введение
Любая открытая система структурируется/деструктурируется под внешним динамическим воздействием, обмениваясь веществом и энергией с внешней средой. Внешнее воздействие передает энергию, импульс элементам открытой системы, тем самым меняя их состояния. Но меняется не только состояние среды, сами элементы систем могут преобразоваться в качественно иные элементы, предполагая проявление нелинейного диссипативного процесса преобразования [1, 2]. Если в результате трансформации систем происходит некая структуризация среды (являющаяся аттрактором в фазовом пространстве), то данный процесс преобразования «несет в себе информацию» о закономерностях изменений состояний структурных элементов, т.е. происходит воплощение состояния самого процесса-аттрактора [3].
Согласно универсальной кинематической теории процесса преобразования открытых систем, каждое состояние процесса преобразования дискретно и связано с константой – «золотой» пропорцией [3]. Формы статистических распределений интенсивностей процессов преобразования различных (геологических, геохимических, географических, геофизических, биологических и др.) открытых динамических систем почти всегда полимодальны [4-6]. Проведенные исследования показали, что величины мод плотностей распределений интенсивностей не только геохимических [3, 5], но и речных (стоки расхода воды) [4] систем подчиняются уравнениям данной универсальной кинематической теории. Очевидно, что полимодальность плотностей статистических распределений различных систем будет являться маркером их открытости к внешним влияниям с различными режимами.
Еще с середины ХХ в. определены причины возникновения полимодальных распределений размеров осадка в различных фациях [7-9]. Исследования показали, что виды переноса песка (взвесь, сальтация и волочение) и унаследования результатов динамической эрозии обломочных материалов являются причинами формирования двух- либо трехмодальных статистических плотностей распределения размеров песчаных гранул.
В работе [10] экспериментальные исследования динамических характеристик оборудования грануляции микрокристаллической целлюлозы и моногидрата α-лактозы выявили, что степень грануляции и размеры гранул сильно зависят от отношения скорости подачи порошка (сырья) к скорости крутящего момента шнека. Увеличение мод в распределении размеров гранул происходит при уменьшении скорости подачи порошка, что является косвенным подтверждением зависимости появления мод от режимов воздействия.
В статье [11] авторы подтвердили, что формы гистограмм большинства выборок плотности вероятностей распределения размеров зерен осадочной породы в системе река – озеро полимодальны – с тремя модами, обусловленными внешним водо-климатическим воздействием. В свою очередь проведенное исследование гранулометрического состава песка (на о-ве Фишер) выявило его бимодальное распределение размеров, а именно крупного и среднего диаметра песчинок [12]. Размер песка соответствовал фациям, т.е. условиям осадконакопления.
Как правило, в разведке и добыче нефти и газа гранулометрический анализ песчаников проводится с целью определения фаций для выявления пластов с наилучшими коллекторскими свойствами. Образование полимодальных гистограмм распределений размеров гранул песка связывают с изменениями кинетической энергии транспортирующей водной среды и процессов осадконакопления [13, 14]. Чем меньше размер (масса) гранул, тем значительней транспортирующее расстояние от места их генезиса [15]. В работе [16] проведен гранулометрический анализ фаций песчаников формации Исе. Песчинки имеют низкую сферичность и варьируются от угловатых до субкруглых. Гистограммы распределений размеров зерен демонстрируют как унимодальные, так и бимодальные формы. Плотности вероятностей распределений размеров частиц (фракций) в основном асимметричны, с различным модами, проявления которых также обусловлены изменением скорости потока транспортирующей среды.
Согласно приведенным работам, образование полимодальных распределений песчаных фракций обусловлено изменением кинетической энергии водной среды в процессе отложения осадков. В этом случае плотность вероятности фракционирования (содержания размеров гранул) будет эквивалентна интенсивности процессов отложения на исследуемой территории. В кинематической теории преобразования открытых систем определено уравнение интенсивности процессов трансформации, которое есть функция отношения временных периодов внутренней трансформации к внешнему воздействию [3]. Преобразуя данное уравнение определенным образом, можно получить зависимость размеров (диаметра) гранул от их кинематических параметров (скорости отложения гранул, периода времени отложения), являющихся следствием внешнего воздействия. Таким образом, определив гранулометрический состав песчано-пелитовой фракции и вычислив кинематические параметры каждой усредненной фракции, можно использовать их в качестве дополнительных факторов при анализе фаций. Данные величины параметров будут отражать последний условный этап палеоотложений, зафиксированный в керне.
Целью данной работы является иллюстрирование результатов выявления динамики среды осадконакопления на основе вычислений кинематических параметров потока зерен песка и мелкодисперсных частиц с использованием уравнения интенсивности процессов преобразования открытых систем в рамках универсальной кинематической теории. Выявление фаций (обстановок осадконакопления) на основе кинематических параметров возможно только при условии однородности источников осадочного вещества и при условии, что все фракции подвергаются переносу.
Методы
В качестве материалов исследований были взяты результаты гранулометрического анализа песчано-алевритовых отложений различных пластов в скважинах, находящихся на территориях нефтегазовых месторождений п-ва Ямал – участки Тамбейского, Малыгинского и Тасийского месторождений (см. таблицу). Для гранулометрического изучения осадочного материала применили метод лазерной дифрактометрии, основанный на рассеянии света с целью определения размеров исследуемых зерен.
Содержание фракций песчаных пород в пластах нефтегазовых участков п-ва Ямал, %
|
Участок отбора керна |
Пласт |
Размер частиц, мм* |
||||||||||||
|
Песчаная фракция |
Алеврит |
Пелит |
|
|||||||||||
|
0,8-0,5 (0,65) |
0,5-0,4 (0,45) |
0,4-0,315 (0,357) |
0,315-0,25 (0,28) |
0,25-0,2 (0,22) |
0,2-0,16 (0,18) |
0,16-0,1 (0,13) |
0,1-0,05 (0,075) |
0,05-0,01 (0,03) |
0,01-0,005 (0,0075) |
0,005-0,001 (0,003) |
<0,001 (0,001) |
|
||
|
Тасийский |
ТП22 |
1,02 |
1,27 |
2,5 |
3,8 |
6,1 |
19,8 |
27,1 |
18,7 |
7,3 |
1,3 |
2,5 |
2,3 |
|
|
Западно-Тамбейский |
ТП22 |
0 |
0 |
0 |
0 |
1 |
1,5 |
13,8 |
52,2 |
17,2 |
1 |
3,45 |
6,9 |
|
|
Западно-Тамбейский |
ТП1 |
0 |
0 |
1,24 |
7,13 |
10,0 |
36,7 |
22,9 |
11,2 |
5,2 |
3,4 |
2,2 |
0 |
|
|
Малыгинский |
ТП15 |
0 |
0 |
0 |
1 |
2,73 |
11,4 |
30,5 |
28,7 |
14,3 |
2,2 |
4,7 |
3 |
|
* В скобках указаны средние величины частиц.
Согласно универсальной кинематической теории преобразования открытых систем, интенсивность преобразования эквивалентна процентному (долевому) содержанию преобразованных элементов данной системы. Это могут быть содержания вторичных минералов либо химических элементов во флюидопроницаемых породах, пласты которых представляют собой открытые геологические системы [3, 5], расход воды в стоках речных систем [4] и т.д. В нашем случае фациальная обстановка, определяемая локальным условием гранулярной седиментации, будет представлять собой открытую систему с внешним гидродинамическим воздействием. Процентное, долевое содержание гранул соответствует интенсивности процесса гранулярного отложения осадков. Поэтому, используя основное уравнение кинематической теории с дальнейшим его преобразованием, можно вывести зависимости таких кинематических параметров, как скорость и период гранулярных отложений, характеризующие степени влияния внешних факторов на размеры зерен.
Интенсивность процесса преобразования определяется согласно уравнению [3]
где q – коэффициент пропорциональности; Δτ – период потенциального преобразования элементов систем, являющийся внутренней характеристикой данных элементов, Δτ = ±(τ – τ0); Δt – период внешнего влияния, при котором элементы систем успевают начать свое преобразование, Δt = ±(t – t0); τ0, t0 – начальные временные параметры.
В данной работе вместо процесса преобразования анализируется процесс отложения зерен в рамках кинематической модели.
При изучении динамики осадконакопления в береговой зоне (на основе гранулометрического исследования поверхностных отложений и экстраполяции различных гранулометрических индексов) выявляется соответствие между распределением энергии волн и эволюцией береговой линии, где сочетание полученных результатов и гранулометрического анализа объясняет закономерности распределения классов осадочных пород [17]. Исследования других авторов показали, что осадки, собранные вдоль береговой линии, как правило, являются крупно- и среднезернистыми песками, а осадки, собранные вблизи бордюра субаквальных дюн – средне- и мелкозернистые [18]. Для объяснения гранулометрических явлений были разработаны различные модели на основе действующих на частицу сил, таких как сопротивление, турбулентность, кажущаяся гравитация, силы Ван-дер-Ваальса и подъемная сила, с целью прогнозирования переходов между движущимися/стационарными дюнами и движущимся/неподвижным дном [19].
Также представлены уравнения для прогнозирования скорости песчаной эрозии и скорости осаждения песка [20], построены модели критических значений скоростей транспортировки песка, на основании которых устойчивое состояние возможно при условии, когда размытый с верхней части пласта песок, заменяется новым песком, добытым вверх по течению. При более высоких скоростях песчаная дюна (вал) начинает распадаться на серию медленно движущихся дюн, при этом частицы песка переносятся от верхней по течению части дюны к нижней. По мере дальнейшего увеличения скорости потока дюны полностью разрушаются, и песок образует движущийся слой вдоль дна [21]. Направление эволюции наносов в открытых донных системах (на глубинах до 2,5 м) в первую очередь связано с изменением скорости волновой переработки и направления течений [22, 23].
Результаты исследований показали, что устойчивые состояния процессов отложения мелкодисперсных фракций могут реализоваться и при внешнем гидродинамическом воздействии, но с определенной кинетической энергией, соответствующей массам и размерам гранул. При введении условия постоянной и одинаковой плотности исследуемых гранул с соответствующим эквивалентом размера частиц их массе можно рассмотреть модель воздействия потока воды на частицы на основе использования кинематических зависимостей.
Из таблицы известны параметры размеров фракций и их процентная доля. В уравнении (1) размер фракции очевидно связан с транспортировкой, т.е. с одним из временных параметров. Для определения данной связи исследуем возможности стандартного приема. Используя уравнение Стокса для погружения частиц в спокойной воде, в рамках кинематической концепции получим зависимость скорости погружения от размера частиц d:
где g – ускорение свободного падения, м/с2; µ – кинематическая вязкость воды, м2/с.
Для определения палеоусловий осадконакопления применить формулу (2) не представляется возможным, поскольку необходимо не только знать вязкость воды, зависящую от температуры среды, но и, самое главное, необходимо учесть влияние скорости внешнего потока на частицы с различным типом переноса – взвесь алевро-пелитов и сальтация песка. От этого зависит и высота подъема гранул в толще воды.
В случае исследования внешнего гидродинамического влияния при окончательном периоде отложения начальное время отложения осадка необходимо заменить на интервал времени последнего переноса от места размыва до верхней точки «зависания». Величина этого параметра зависит от глубины водоема (т.е. от средней высоты зависания относительно дна), динамических характеристик потока и диаметра частиц. В рамках кинематической модели осаждения для определенной по размеру группы частиц данный параметр может являться усредненной постоянной величиной. В уравнении (1) для гранулометрического распределения временной параметр t интерпретируется как время течения потока воды при его воздействии на зерна. Причем основным фактором влияния на процесс отложения частиц будет гидродинамическое воздействие, где расстояние переноса фракций в последнем периоде транспортировки до их отложения как для водного потока, так и для частиц будут равны. В этом случае время течения водного потока будет меньше времени переноса гранул вследствие большей скорости воды относительно скоростей переноса песчано-пелитовых фракций.
Процесс окончательной седиментации частиц в большей степени зависит от внешних факторов. Поэтому вероятность (интенсивность) накопления фракций обусловлена влиянием только внешнего потока при условии τ = 0. В первом приближении для исследуемых фракций в уравнении (1) введем постоянный параметр, характеризующий интенсивность начального процесса накопления, . Тогда интенсивность отложения частиц (прямо пропорциональная вероятности) трансформируется в следующую зависимость:
Введем следующие кинематические параметры: среднюю скорость течения воды v; скорость отложения υ; окончательный период времени отложения гранул tот. Основное условие отложения – L= υtот = vt. Тогда после преобразования зависимости (3) и применения основного условия отложения получим связь скорости течения воды с временем переноса гранул при транспортировке гранул до их отложения:
Известно, что размер переносимой песчано-алевритовой фракции связан со скоростью потока воды, причем с увеличением скорости воды повышается и критическая величина размера переносимых частиц. Производная d (размер/диаметр фракций) относительно времени переноса частиц будет соответствовать скорости течения воды как функции времени переноса гранул:
Возьмем неопределенный интеграл от функции v(tот) по времени переноса зерен и определим диаметр фракции:
Скорость и период отложения частиц зависят от их размера (диаметра). На основании известных экспериментальных данных, представленных в работе [24], зависимости отложения осадка от скорости течения воды и размера отложенных частиц (рис.1) была определена полиномиальная зависимость граничной скорости процесса отложения частиц (по модулю) от их размера:
При установлении постоянной величины параметра t0 и использовании данных размеров фракций (см. таблицу), а также уже полученной зависимости скорости отложения частиц от диаметра гранул (5) (рис.1) можно по формуле (4) вычислить период отложения.
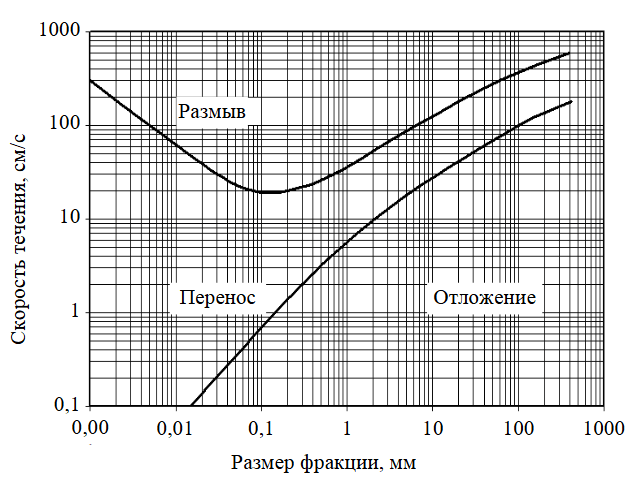
Рис.1. Зависимости Ф.Хьюльстрема, показывающие связи процессов переноса, размыва, отложения с размерами фракций и скоростями течения водного потока
Определим начальный параметр t0, являющийся усредненным периодом времени последнего переноса от отрыва до верхней точки «зависания» в процессе последнего периода отложения фракций при условии a = 1. Следовательно данный параметр должен быть связан со средней начальной скоростью отрыва гранул ⟨υкр⟩ и средним путем переноса от места отрыва до верхней точки L0. Средняя скорость переноса водой для каждой фракции от места отрыва до отложения частицы – величина постоянная.
Анализ таблицы указывает на то, что средний диаметр фракций с наибольшим содержанием (четыре усредненных значения с общей долей более 70 %) 0,1 мм, что совпадает с критической скоростью срыва Хьюльстрема. Средняя критическая величина скорости отрыва (размыва) этих фракций ≈ 0,1-0,15 м/с. В свою очередь, согласно зависимости Г.И.Шамова, средняя скорость размыва пропорциональна средней глубине потока [25]:
На рис.2 показана условная схема отрыва и переноса пелитово-песчаных фракций, где максимальная высота подъема частиц соответствует средней глубине потока. На основании формулы Г.И.Шамова средняя высота подъема частиц относительно максимальной и минимальной критических величин скоростей отрыва рассчитывается: ⟨h⟩=1/2(hmin+hmax)≈0,1 м. Согласно экспериментальным данным, в состоянии покоя воды и при температуре 15-20 °C средняя скорость ⟨υh⟩ падения частиц (d ~ 0,1 мм) в неподвижной воде приблизительно равна 0,007 м/с [9]. В этом случае, определив sin α (рис.2) как отношение векторов скоростей падения частиц к минимальному значению критической величины sin α= υh/υкр=0,07, можно вычислить среднюю величину постоянной пути отложения: L0= ⟨h⟩/sin α=1,43 м. Далее вычисляем постоянную величину параметра времени начального гидродинамического влияния: t0=L0/⟨υкр⟩≈14,3.
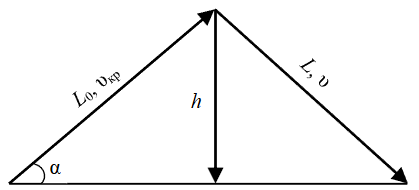
Рис.2. Условная схема последнего периода переноса и отложения гранул в результате сальтации и взвеси в водной среде
При значительном отличии диаметров исследуемых частиц от 0,1 мм величина постоянной начального времени будет отличаться от заданной t0.
Рассмотрим еще две константы. Постоянная Q должна быть меньше интенсивности I, поэтому при минимальной величине Imin = 0,01 д.ед. с точки зрения 5 %-ного отклонения устанавливаем константу Q = 0,0095 д.ед. Константа c в уравнении (4) должна быть меньше минимального диаметра исследуемых фракций. По таблице выбираем наименьшее значение (⇐ 0,001 мм) и с 5 %-ным отклонением определяем константу с = 0,00095 мм.
Таким образом, выявленные величины констант уравнения (4) релевантны изучаемым выборкам таблицы, следовательно их использование позволит определять время последнего этапа отложения осадков. Очевидно, что использование вычисленных констант ограничено диаметром фракций от 0,001 до 1 мм, а уравнение (4) можно применять только для водной среды при переносе зерен в результате сальтации и взвеси.
В данном случае возникает необходимость в подтверждении валидности вычисленного временного параметра. Она определяется «правильными» зависимостями – соответствием тренда полученных при сопоставлении эмпирических данных уравнения (размер фракции и их долевое содержание) вычисленным параметрам. Достоверность уравнения (4) подтверждается в следующих регрессиях. Во-первых, противоположными трендами для песчаной и пелитовой фракций в зависимостях скорости и времени осаждения (в последнем периоде) от размера частиц. Это показано в работах [26, 27], где экспериментально и теоретически подтверждено, что с увеличением скорости течения смеси мелкая фракция перемещается вверх в виде взвеси, а более крупная (песок) оседает, перемещаясь в нижних слоях, что и приводит к противоположным зависимостям. Во-вторых, с увеличением времени осаждения гранул должно пропорционально увеличиваться их долевое содержание, но с различным трендом в зависимости от размера фракции. При соблюдении указанных пунктов валидность уравнения (4) можно считать доказанной.
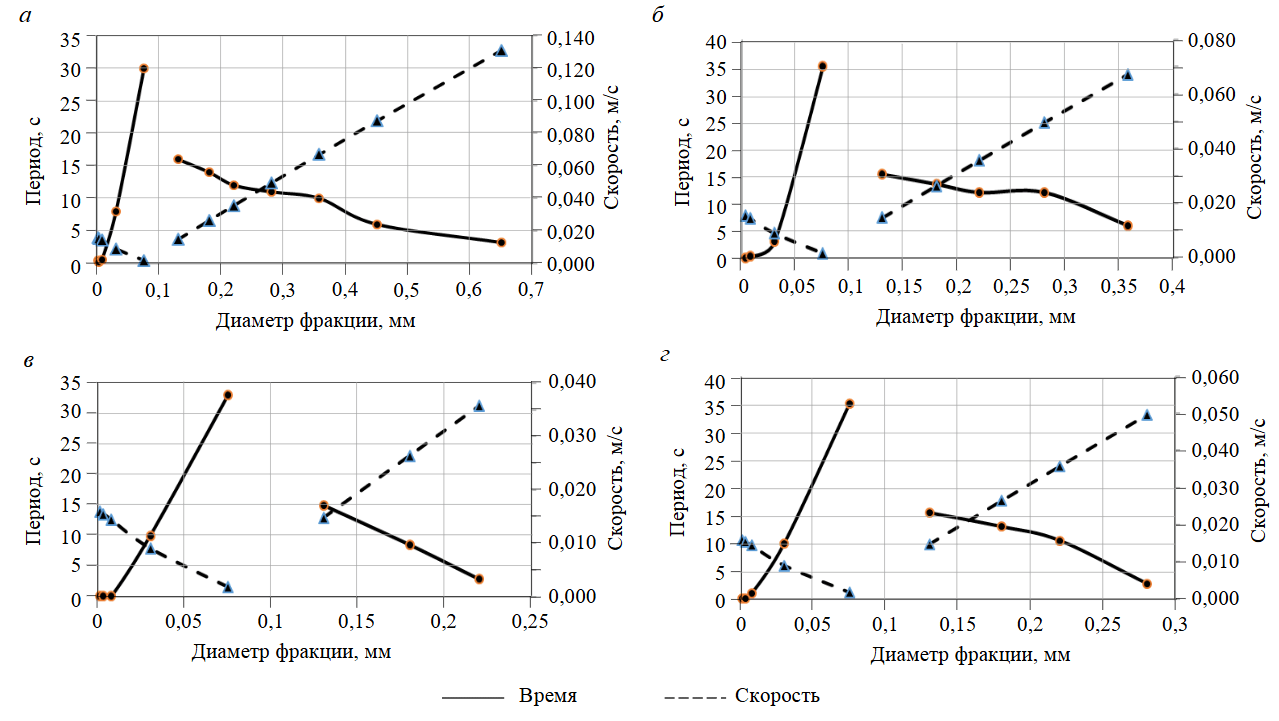
Рис.3. Зависимости скорости и времени осаждения частиц от усредненных диаметров фракций исследуемых участков: Тасийский – ТП22 (а); Западно-Тамбейский – ТП1 (б); Западно-Тамбейский – ТП22 (в); Малыгинский – ТП15 (г)
С практической точки зрения уравнение (4) можно использовать для гранулометрического фациального анализа в качестве дополнительного источника информации. В таблице представлены результаты исследования керна в пластах, в которых был проведен традиционный фациальный анализ, для которого применялась стандартная методика фациальной интерпретации отложений по данным стандартного каротажа, разработанная В.С.Муромцевым [28]. Каротажные кривые «привязываются» к интервалам отбора керна и проводится корреляция между физическими характеристиками разреза и литогенетическими типами отложений. Определяются формы каротажных кривых, устанавливается последовательность их смены по разрезу, осуществляется сравнение каротажных характеристик выбранных интервалов разреза с электрометрическими моделями известных фаций [29-31]. Проводится анализ керна различными методами – литолого-петрографическими, геохимическими и палеонтологическими. При сопоставлении полученной информации устанавливаются условия осадконакопления. В этом случае появляется возможность сравнения полученных данных между собой и их сопоставления с результатами исследований предложенной кинематической теории.
Результаты
Кинематические параметры нелинейно зависят от размеров оседающих частиц. Применение уравнений (4) и (5) позволяет вычислить периоды осаждения частиц и сопоставить их величины с размером фракций (рис.3); тренды периодов отложения и их скорости обратно пропорциональны, и, главное, для алеврито-пелитовой и песчаной фракций данные параметры имеют противоположные направления трендов.
С точки зрения динамических процессов алеврито-пелитовая фракция подчиняется мезодинамике – на скорость осаждения частиц влияет площадь их поверхности, т.е. чем больше площадь (размер), тем значительней сила сопротивления молекул воды. Для песчаной фракции более значимую роль играет сила гравитации, т.е. скорость осаждения зерен пропорциональна их массе – размеру с учетом влияния классических сил гидродинамики. В рамках кинематической модели уравнения (4) данные фракционные различия динамических функций формируют правильно подобранные константы – Q,a,c.
На рис.4 (Тасийский участок) отображены три прямо пропорциональные зависимости долевого содержания фракций от времени. Каждая регрессия представляет собой группу фракций определенных размеров, где группа песчаных гранул ⇐ 0,13-0,28 мм выделяется наибольшим углом наклона к оси абсцисс (~78,5°). Остальные зависимости трех исследуемых выборок, не приведенных на рис.4 (ТП1, ТП22, ТП15), формируют по две положительные регрессии – для пелитовых и песчаных фракций.
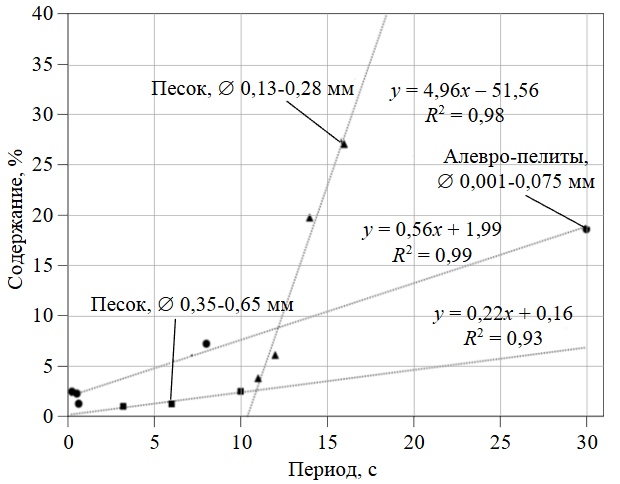
Рис.4. Зависимости долевого содержания частиц от периодов времени их осаждения для фракций с различными групповыми размерами (Тасийский участок – ТП22)
Очевидно, что мелкодисперсный песок (диаметром до 0,3 мм) пласта ТП22 Тасийского участка осаждается с большой вероятностью в границах особого режима отложения tот = 11-20 с, что возможно связано со снижением гидродинамической активности.
Рассмотрим фациальную принадлежность изучаемых зон на основе краткого изложения результатов традиционных исследований.
Изучаемая зона пласта ТП22 скважины Тасийского участка относится к фации погруженных частей регрессивного бара. В качестве обоснования приведем итоги литологического описания керна. В фациальном анализе используют параметр α-диаграммы каротажа собственной поляризации: αПС = (Umax – U)/(Umax – Umin), где U – измеряемое напряжение, мВ. Песчаники мелкозернистые и алевролиты с разной сортировкой (αПС = 0,5-0,6). Развита тонкая и редкая мелкая пологонаклонная, горизонтальная и пологоволнистая слоистость. Породы содержат мелкий растительный детрит, редкие следы зарывающихся организмов. Для этой фации характерно устойчивое снижение гидродинамической активности до среднего уровня.
Зона пласта ТП1 Западно-Тамбейской скважины относится к фации песчано-алевритовых осадков подножий баров прибрежной полосы моря. Пласт подстилается однородными аргиллитами с прослоями песчаника, на отдельных участках до их неравномерного переслаивания. Формирование отложений осуществлялось в условиях от средней, снижающейся с течением времени, до низкой и очень низкой динамики водной среды, возможно, обусловленной возрастанием глубины бассейна седиментации.
Зона пласта ТП22 Западно-Тамбейской скважины относится к фации алевритов и мелкозернистых песков склоновых частей подводных баров прибрежной полосы моря. Разрез представлен переслаиванием черных алевролитов и светло-серых мелкозернистых песчаников с тонкими горизонтальными прослойками алевролитов. Алевролиты плотные, с включениями растительного детрита. Стабильность обстановок осадконакопления проявилась в литологической выдержанности накопившихся осадков, их толщин и значительной песчанистости разрезов. Волновой характер движения водной среды устанавливается преимущественно по волнистым типам слоистости, особенно по наличию разнонаправленной косоволнистой слоистости, а также по зигзагообразным формам аномалий диаграмм каротажа собственной поляризации (ПС), отражающим частую смену гидродинамической активности вод, в которых осаждались осадки. Накопление отложений пласта ТП22 осуществлялось в мелководном морском бассейне на фоне регрессии моря. На морской режим осадкообразования указывает наличие ихнофоссилий.
Зона пласта ТП15 Малыгинской скважины относится кфации песчаных осадков стрежневых частей русел ограниченно меандрирующих рек аллювиально-озерной равнины. Песчаные осадки формировались в водной среде с очень высокой гидродинамической активностью, что выразилось в высоких значениях αПС (0,8-1). Аномалии ПС располагаются в зоне отрицательных отклонений, имеют форму четырехугольника с осложненной и сильно осложненной зубчатостью боковой стороной, отражающей непостоянный водный режим – неоднократный спад и усиление гидродинамической активности, характерный для русел рек меандрирующего типа.
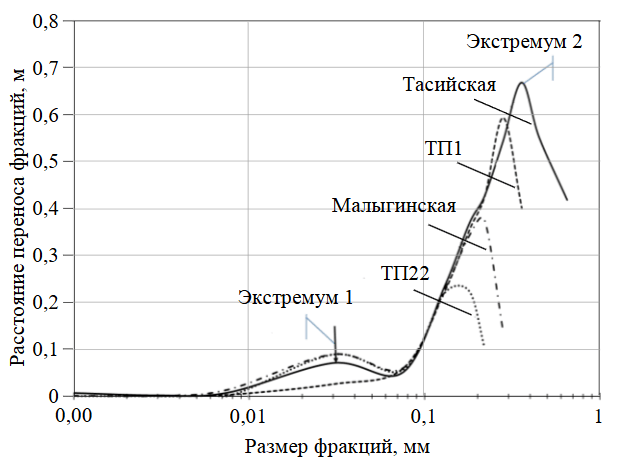
Рис.5. Зависимость расстояния переноса частиц при их отложении от логарифма диаметра зерен
Одним из кинематических параметров является расстояние переноса при окончательном отложении частиц L. Следует отметить, что данный параметр переноса выражает не весь путь движения, а только его часть – последний – окончательный этап отложения. На рис.5 показаны зависимости данного параметра от средних размеров осаждающих фракций в каждой исследуемой зоне. Согласно полученным результатам можно сделать два вывода:
- величины экстремумов точек перегиба (экстремум 2) для каждой изучаемой зоны отличаются и зависят от размеров фракций и исследуемых фаций;
- для исследуемой зоны ТП1 отсутствует экстремум 1, в других зонах данный экстремум контролируется фракцией одного диаметра – 0,03 мм.
Обсуждение результатов
Повышение степени соответствия действительности при определении палеоусловий осадконакопления, как правило, основано на комплексировании различных методов анализа, где гранулометрия (диаграммы Р.Пассега, Г.Ф.Рожкова) в сочетании с другими методами фациального анализа способствует получению более достоверных фациальных реконструкций [32, 33]. В этом случае (в фациальном анализе) развитие возможностей гранулометрического метода должно повысить информативность и точность установления условий седиментаций. Например, для вычисления расхода влекомых наносов используют отдельные из восьми альтернативных групп формул в зависимости от типа доминирующего влияния динамики воды [34].
Анализ полученных зависимостей (см. рис.3, 4), выполненных на основании применения уравнений (4), (5), позволяет удостовериться в релевантности использования данных формул в гранулометрии. Основная практическая значимость полученных уравнений и констант заключена в возможности их применения для анализа фаций в пределах диаметров гранул 0,001-1 мм.
В работе [9] указаны три базовые причины зависимостей размеров осаждающих гранул от пространственной морфологии прибрежно-морских фаций. Во-первых, крупность наносов определяется уклоном дна, т.е. с увеличением угла наклона поверхности дна диаметр осаждающих фракций увеличивается. Во-вторых, при удалении от уреза в любую сторону увеличивается размер осаждающих частиц. В-третьих, размер фракций песчаного вала распределяется от максимума на гребне к уменьшению диаметра частиц вниз по склону. Перечисленные утверждения (основанные на эмпирических знаниях) можно использовать для анализа полученных зависимостей рис.5.
Если под углом наклона дна (гипотенузы прямоугольного треугольника) понимать угол α между нормалями к береговой линии, лежащими параллельно поверхности воды и дну (рис.6), а прилежащий к углу катет треугольника направлен в сторону моря, то гипотенуза прямоугольного треугольника будет соответствовать расстоянию переноса гранул в процессе отложений в результате сальтации [25]. С увеличением угла наклона дна α при неизменном месте начала процесса переноса относительно береговой линии будут увеличиваться расстояние переноса при отложении (относительно косинуса угла) и размер осаждающих фракций. На рис.5 данное явление представлено в диапазоне фракций диаметром от 0,075 мм до точки экстремума 2 различных диаметров частиц в зависимости от фаций. Дальнейшее уменьшение расстояния при увеличении размера частиц (т.е. увеличении α) может быть обусловлено уменьшением глубины осаждения (регрессия, образование песчаного бара).
В свою очередь, мелкодисперсная фракция (взвесь) оседает в более спокойных условиях и, начиная с размера частиц 0,03 мм происходит резкое увеличение долевого содержания отложений до размера 0,13-0,18 мм (см. таблицу). Отправная точка ⇐ 0,03 мм на рис.5 выделяется экстремумом 1 только у трех фаций. Возможно, это связано с началом массового вертикального отложения частиц, когда кроме основной вертикальной компоненты еще присутствует незначительная величина горизонтальной компоненты скорости, и время осаждения увеличено в сравнении с временем осаждения частиц в условиях более глубоководной фации (с одной вертикальной компонентой), например пласта ТП1.
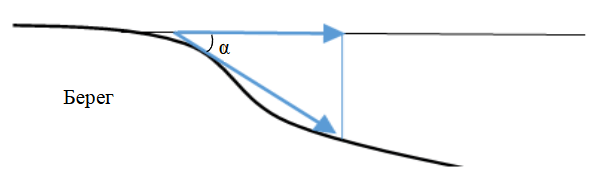
Рис.6. Схема угла наклона дна моря возле береговой линии
Заключение
Полученные кинематические зависимости позволяют сделать следующие выводы:
- Участок Тасийской скважины пласта ТП22 формировался в условиях периодического гидродинамического воздействия при значительном наклоне поверхности морского дна с образованием песчаного вала типа бара. Наибольший экстремум 2 – расстояния переноса при отложении наибольшей фракции (в сравнении с двумя исследуемыми морскими отложениями) – свидетельствует о сильном гидродинамическом влиянии.
- Участок Западно-Тамбейской скважины пласта ТП1 формировался в морских условиях в наиболее глубоководной зоне (подножий бара со стороны моря), что подтверждается отсутствием экстремума 1 и относительно значимой величиной экстремума 2.
- Участок Малыгинской скважины пласта ТП15 формировался в водной среде при периодическом гидродинамическом воздействии. Определив альтернативно-традиционными методами то, что формирование среды происходило в континентальных условиях, можно отнести данную фацию к стрежневой части русел, потому что проявляется сильная фракционная периодичность со средней величиной экстремума 2 (см. рис.5), и наличие экстремума 1 подтверждает сезонное изменение глубины.
- Участок Западно-Тамбейской скважины пласта ТП22 формировался в прибрежно-морских условиях недалеко от береговой линии (наименьшая величина экстремума 2) при волновом воздействии с дальнейшим образованием бара.
Расстояние переноса зерен при их отложении в диапазоне 0,1-0,5 мм является индикатором интенсивности гидродинамического влияния, а диапазон 0,03-0,04 мм отражает присутствие/отсутствие горизонтальной компоненты вектора скорости, косвенно обусловленного глубиной отложения.
Таким образом, вычисляемые кинематические параметры зерен при их отложении на качественном уровне позволяют уточнять и дополнять палеообстановку осадконакоплений, уже определенную традиционным способом.
Применение полученных уравнений (4) и (5) при фациальном анализе песчано-алевритовых отложений позволяет определять такие кинематические параметры как скорость, период времени и расстояние перемещения при отложении частиц. Вычисление данных параметров исследуемых фаций даже не в абсолютных, а в условных единицах может послужить дополнительным, уточняющим, источником информации гидродинамических палеоусловий седиментации. В этом случае наибольшей информативностью обладает параметр «расстояние переноса частиц при отложении», который контролируется размером осаждающихся гранул. Изменение его величины зависит от перемены угла наклона поверхности дна, размеров частиц, глубины отложения. Сопоставляя величину вычисленного параметра с диаметром фракций, можно провести идентификацию исследуемой зоны с ее фациальной принадлежностью.
Литература
- Васильев Ю.С., Волкова В.Н., Козлов В.Н. Концепция открытой системы: история, состояние, перспективы развития // Системный анализ в проектировании и управлении: Сборник научных трудов XXII Международной научно-практической конференции, 10-11 июня 2019. Политех-Пресс, 2019. Ч. 1. С. 5-17.
- Haddad W.M., Somers L. Partial stability of nonlinear dissipative feedback systems // International Journal of Control. 2024. Vol. 97. Iss. 6. P. 1432-1443. DOI: 10.1080/00207179.2023.2208690
- Мельник И.А. Полимодальность распределения вторичных каолинитов в открытых системах песчаных коллекторов // Известия Томского политехнического университета. Инжиниринг георесурсов. 2023. Т. 334. № 8. С. 17-29. DOI: 10.18799/24131830/2023/8/4163
- Мельник И.А. Полимодальное распределение вероятности расхода воды в речных системах // Известия Томского политехнического университета. Инжиниринг георесурсов. 2024. Т. 335. № 1. С. 46-56. DOI: 10.18799/24131830/2024/1/4411
- Мельник И.А., Недоливко Н.М. Экстремумы дискретного распределения содержания бора как показатели гидродинамики осадконакопления // Нефтяное хозяйство. 2022. № 10. С. 14-18. DOI: 10.24887/0028-2448-2022-10-14-18
- Суханов В.В., Иванов О.А. О полимодальном распределении Курильского эпипелагического нектона по массе тела особей // Известия Тихоокеанского научно-исследовательского рыбохозяйственного центра. 2001. Т. 128. С. 390-408.
- Weltje G.J., Prins M.A. Muddled or mixed? Inferring palaeoclimate from size distributions of deep-sea clastics // Sedimentary Geology. 2003. Vol. 162. Iss. 1-2. P. 39-62. DOI: 10.1016/S0037-0738(03)00235-5
- Doeglas D.J. Interpretation of the results of mechanical analyses // Journal of Sedimentary Petrology. 1946. Vol. 16. № 1. P. 19-40. DOI: 10.1306/D426924C-2B26-11D7-8648000102C1865D
- Котельников Б.Н. Реконструкция генезиса песков. Гранулометрический состав и анализ эмпирических полигонов распределения. Л.: Изд-во Ленинградского университета, 1989. 132 с.
- Mendez Torrecillas C., Halbert G.W., Lamprou D.A. A novel methodology to study polymodal particle size distributions produced during continuous wet granulation // International Journal of Pharmaceutics. 2017. Vol. 519. Iss. 1-2. P. 230-239. DOI: 10.1016/j.ijpharm.2017.01.023
- Ashley G.M. Interpretation of Polymodal Sediments // The Journal of Geology. 1978. Vol. 86. № 4. P. 411-421. DOI: 10.1086/649710
- Asthana R., Shrivastava P.K., Srivastava H.B. et al. Hydrochemistry and sediment characteristics of polar periglacial lacustrine environments on Fisher Island and Broknes Peninsula, East Antarctica // Advances in Polar Science. 2013. Vol. 24. № 4. P. 281-295. DOI: 10.3724/SP.J.1085.2013.00281
- Myo Min Htun, Sugeng Sapto Surjono, Jarot Setyowiyoto. Granulometry analysis of Ngrayong sandstone, Tempuran Area, Rembang Zone, North East Java Basin // IOP Conference Series: Earth and Environmental Science. 2020. Vol. 451. № 012082. DOI: 10.1088/1755-1315/451/1/012082
- San Yee Khaing, Yuichi Sugai, Myo Min Tun et al. Textural Characteristics and Depositional Environment of Ngrayong Sandstone (Middle Miocene) from Rembang Area, Northeast Java, Indonesia // Open Journal of Geology. 2022. Vol. 12. № 12. P. 1102-1119. DOI: 10.4236/ojg.2022.1212052
- Ikhane P.R., Akintola A.I., Bankole S.I. et al. Granulometric analysis and heavy mineral studies of the sandstone facies exposed near Igbile, southwestern Nigeria // International Research Journal of Geology and Mining. 2013. Vol. 3. № 4. P. 158-178.
- Madukwe H.Y. Granulometric Analysis Of The Sandstone Facies Of The Ise Formation, Southwestern Nigeria // Journal of Multidisciplinary Engineering Science and Technology. 2016. Vol. 3. Iss. 2. P. 3909-3919.
- Remmache K., Nour El Islam Bachari, Nacef L., Houma F. Granulometric Indices Mapping in Relation to Hydrodynamic Factors for Beach Characterization and Monitoring with Very High Spatial Resolution // Data Science and Application. 2020. Vol. 3. № 1. P. 5-12.
- Das G.K. Granulometry of Beach Sands // Coastal Environments of India. Springer, 2022. P. 79-94. DOI: 10.1007/978-3-031-18846-6_5
- Dabirian R., Mohan R.S., Shoham O. Mechanistic modeling of critical sand deposition velocity in gas-liquid stratified flow // Journal of Petroleum Science and Engineering. 2017. Vol. 156. P. 721-731. DOI: 10.1016/j.petrol.2017.06.006
- Salama M.M. Sand Production Management // Journal of Energy Resources Technology. 2000. Vol. 122. Iss. 1. P. 29-33. DOI: 10.1115/1.483158
- Danielson T.J. Sand Transport Modeling in Multiphase Pipelines // Offshore Technology Conference, 30 April – 3 May 2007, Houston, TX, USA. OnePetro, 2007. № OTC-18691-MS. DOI: 10.4043/18691-MS
- Чечко В.А., Топчая В.Ю. Многолетние данные гранулометрических параметров донных осадков как индикатор устойчивости обстановки осадконакопления // Успехи современного естествознания. 2021. № 3. С. 86-91. DOI: 10.17513/use.37598
- Крыленко М.В., Крыленко В.В. Исследование гранулометрического состава пляжевых и донных отложений Бакальской косы // Экологическая безопасность прибрежной и шельфовой зон моря. 2018. № 4. С. 40-49. DOI: 10.22449/2413-5577-2018-4-40-49
- Hjulström F. Transportation of Detritus by Moving Water // Recent Marine Sediments. A Symposium. The American Association of Petroleum Geologists, 1955. Special Publication № 4. P. 5-31. DOI: 10.2110/pec.55.04.0005
- Белолипецкий В.М., Генова С.Н. Вычислительный алгоритм для определения динамики взвешенных и донных наносов в речном русле // Вычислительные технологии. 2004. Т. 9. № 2. С. 9-25.
- Сальников С.Н., Карандаев Г.З. Анализ распределения концентрации песка по фракциям, их средневзвешенной крупности и скорости течения гидросмеси по высоте сечения гидротранспортной трубы // Вестник Южно-Уральского государственного университета. Серия «Строительство и архитектура». 2016. Т. 16. № 1. С. 26-34.
- Иванов В.А., Дыкман В.З., Ефремов О.И. Кинетика взвесей в прибрежной области моря // Морской гидрофизический журнал. 2006. № 4. С. 49-61.
- Муромцев В.С. Электрометрическая геология песчаных тел – литологических ловушек нефти и газа. Л.: Недра, 1984. 260 с.
- Чудинова Д.Ю., Чибисов А.В., Махныткин Е.М., Минниахметова Р.М. Оценка влияния литолого-фациальных особенностей отложений на эффективность выработки запасов нефти // Вестник Евразийской науки. 2022. Т. 14. № 6. № 45NZVN622.
- Белозеров Б.В. Роль седиментационных моделей в электрофациальном анализе терригенных отложений // Известия Томского политехнического университета. 2011. Т. 319. № 1. С. 116-123.
- Кислухин И.В. Особенности геологического строения и нефтегазоносность юрско-неокомских отложений полуострова Ямал. Тюмень: Тюменский государственный нефтегазовый университет, 2012. 116 с.
- Хуснуллина Г.Р., Биркле Е.А., Лебедев А.И. Гранулометрический анализ песчаников викуловской свиты (апт, нижний мел) Красноленинского месторождения (Западная Сибирь) // Литосфера. 2012. № 6. С. 90-99.
- Вакуленко Л.Г., Предтеченская Е.А., Чернова Л.С. Опыт применения гранулометрического анализа для реконструкции условий формирования песчаников продуктивных пластов васюганского горизонта (Западная Сибирь) // Литосфера. 2003. № 3. С. 99-108.
- Поздняков Ш.Р., Шмакова М.В. Расчет расхода влекомых наносов на реках с крупнофракционными донными отложениями // Ученые записки Российского государственного гидрометеорогического университета. 2016. № 45. С. 20-27.
