Оценка влияния функции определения расстояния на результаты оптимизации географического размещения генерации на основе возобновляемых источников энергии с применением метаэвристического алгоритма
- 1 — Младший научный сотрудник Уральский федеральный университет имени первого Президента России Б.Н.Ельцина ▪ Orcid ▪ ResearcherID
- 2 — канд. техн. наук Доцент Уральский федеральный университет имени первого Президента России Б.Н.Ельцина ▪ Orcid ▪ ResearcherID
Аннотация
Обеспечение электроснабжения труднодоступных и удаленных территорий Российской Федерации является актуальной проблемой с тех пор, как появилась единая электроэнергетическая система. С учетом положений доктрины энергетической безопасности РФ, трендов по декарбонизации экономики и снижения стоимости оборудования для реализации электроустановок на базе возобновляемых источников энергии электроснабжение удаленных территорий при помощи такой генерации является прямой альтернативой установке дизельной генерации. Геологоразведочные работы преимущественно проводятся на удаленных территориях, где отсутствует возможность централизованного электроснабжения. В связи с развитием промышленных комплексов по добыче сырья, а также сопутствующей бытовой нагрузки актуальной задачей является размещение крупных объектов возобновляемой генерации в районах проведения геологоразведочных работ. Для решения задачи оптимального размещения возобновляемой генерации активно используются метаэвристические методы оптимизации, на результаты которых влияет корректная настройка их внутренних параметров, совместно с большими объемами метеорологических и климатических данных. В статье приводятся результаты исследования влияния функций, определяющих расстояние между агентами метаэвристического алгоритма оптимизации, на результаты оптимизации географического размещения фотоэлектрических и ветровых электростанций. Для сравнения влияния на итоговые результаты в качестве функций расстояния рассмотрены функция евклидова расстояния и функция гаверсинуса. Оценка результатов оптимизации проводилась для солнечных и ветровых электростанций – мощности 45 и 25 МВт на территории Вагайского района Тюменской обл. и Тунгокоченского района Забайкальского края. Полученные результаты показывают низкую степень влияния изменения функции определения расстояния между географическими точками, но обуславливают необходимость ее корректного выбора при оптимизации размещения ветровых электростанций для исключения пропуска локальных оптимумов.
Финансирование
Исследование выполнено при финансовой поддержке Министерства науки и высшего образования Российской Федерации в рамках Программы развития Уральского федерального университета имени первого Президента России Б.Н.Ельцина в соответствии с программой стратегического академического лидерства «Приоритет-2030».
Введение
Российская Федерация имеет богатый минерально-ресурсный потенциал, представленный комплексом полезных ископаемых, распределенных по огромной территории. В минерально-сырьевую базу входят нефть, газ, металлические руды, минеральное сырье, используемое в строительстве, и т.д. Разработка месторождений и добыча сырья проводятся практически по всей обширной территории страны от Кавказа до Дальнего Востока. Для подтверждения потенциала территорий предварительно проводятся геологоразведочные экспедиции. Территории, где проводится геологоразведка, являются труднодоступными и удаленными от централизованного электроснабжения [1, 2]. Для обеспечения электрической энергией в таких условиях используются мобильные установки на базе нескольких дизельных генераторов малой мощности или быстросборных установок на базе одного дизельного генератора повышенной мощности [3, 4]. Данный способ электроснабжения является простым в эксплуатации техническим решением, но имеет ряд особенностей, связанных с необходимостью доставки топлива к месту конечного потребления, а также с негативным влиянием генерации такого типа на экологическую обстановку (выбросы оксидов азота и углерода) [5-7].
Образованные в случае успешного завершения геологоразведочных работ на перспективных территориях промышленные предприятия по разработке месторождений и добыче сырья, а также вахтовые поселки в дальнейшем требуют строительства протяженных линий электропередачи, либо создания локальной электростанции для электроснабжения потребителей. В доктрине энергетической безопасности РФ говорится о снижении доли используемой генерации на основе неэкономичного и неэкологичного дизельного топлива и замещении ее установками, использующими локальные энергетические ресурсы. В соответствии с этими положениями размещение электростанций на основе возобновляемых источников энергии (ВИЭ) является прямой альтернативой дизельным установкам.
Современный курс на декарбонизацию всех отраслей экономики предполагает переход на более экологичные виды генерации, в том числе и при электроснабжении удаленных и труднодоступных территорий. В рамках развития экономики РФ существуют программы поддержки декарбонизации и развития зеленой энергетики [8]. При рассмотрении перспективных территорий для проведения продолжительных геологоразведочных работ [9-11] и экологического состояния этих территорий [12-14] имеет смысл проведение оценки потенциала территорий с точки зрения установки генерации на базе возобновляемых источников энергии [15]. Даже при наличии большого потенциала для реализации генерации на базе ВИЭ на территории РФ (большие площади, разнообразные метеорологические и климатические условия) для успешного использования генерации такого типа необходимо производить оптимизацию географического размещения энергообъектов. Целью оптимизации в первую очередь является повышение объемов вырабатываемой электроэнергии, выраженное в коэффициенте использования установленной мощности (КИУМ). КИУМ является одним из контролируемых параметров вводимых объектов генерации ВИЭ, необходимых для отбора проектов для участия в программе государственной поддержки ДПМ ВИЭ 2.0. Согласно конкурсной документации необходимым минимумом для фотоэлектрических станций (ФЭС) является значение КИУМ 0,14 о.е., а для ветровых электростанций (ВЭС) – 0,27.
Для проведения оптимизации такого типа требуется использование метеорологических данных, системы прогнозирования КИУМ, а также оптимизационных методов, способных показывать высокие результаты при работе с неоднородными, сложными формами целевых функций. Существует множество факторов, влияющих на результаты оптимизации, одним из которых является определение расстояния между географическими точками, определяющими различные потенциальные положения планируемого энергообъекта.
В качестве эффективных инструментов для решения задачи оптимизации в условиях сложных, уникальных форм целевых функций широко применяются метаэвристические методы оптимизации [16-18], такие как алгоритм светлячков [19, 20], алгоритм стаи серых волков [21-23] и т.д. Метаэвристические методы оптимизации основаны на наблюдении естественного поведения различных живых организмов во время выполнения естественных процессов, необходимых для их функционирования (поиска пищи, охоты и т.д.). Математически описанное поведение животных и насекомых находит применение практически во всех отраслях экономики: инжиниринге, строительстве, логистике, энергетике. Такие оптимизационные методы имеют ряд преимуществ перед классическими методами оптимизации, основанными на градиентном спуске или обобщенном методе Ньютона, которые также применяются в технических задачах.
К основным преимуществам метаэвристических методов перед методами нелинейного математического программирования можно отнести:
- универсальность (метаэвристические методы подходят как для простых моноэкстремальных функций, так и для сложных функций уникальной формы с множеством экстремумов);
- меньшую вероятность «зависания» алгоритма в области локального оптимума или на плато целевой функции;
- меньшую зависимость результата от выбранного начального приближения (расположения агентов алгоритма).
Одним из главных недостатков метаэвристических методов является необходимость настройки внутренних параметров алгоритмов, значение которых может изменяться в зависимости от рассматриваемой задачи, целевой функции и системы ограничений.
Часто оптимизационные задачи, решаемые при помощи метаэвристических методов (в том числе методов роевого интеллекта) имеют целочисленную или дискретную постановку – перемещение агентов алгоритма выполняется по заранее определенным узлам сетки пространства решений. В такой постановке задачи наиболее распространенной функцией выступает евклидово расстояние [24, 25] и большее внимание в исследованиях направлено на тонкую настройку других внутренних параметров алгоритмов. При решении задачи оптимизации с использованием сетки географических координат, допускающих нецелочисленные значения, целесообразно использование функции гаверсинуса, применяемой в алгоритмах для определения географического положения в транспортных системах [26, 27].
В статье проводится исследование влияния функции определения расстояния, используемой внутри алгоритмов оптимизации, на итоговые результаты оптимизации расположения генерации на базе ВИЭ. Целью исследования является проверка гипотезы о влиянии выбора функции определения расстояния между точками, определяющими географическое положение электростанции, внутри алгоритма оптимизации. Научная новизна исследования выражена в применении оптимизационного метода, основанного на метаэвристическом алгоритме, и определения степени влияния внутренних параметров этого алгоритма на итоговые результаты оптимизации географического расположения электростанций на базе ВИЭ различных типов и установленной мощности.
Для проверки гипотезы были выбраны территории, перспективные для проведения геологоразведочных работ, в двух регионах – Урал [28-31] и Забайкальский край [32].
Методы
Задача определения оптимального расположения электростанций, функционирующих на основе ВИЭ, с целью достижения максимального значения КИУМ этих станций, относится к задачам оптимизации с уникальными целевыми функциями сложной формы. Целевая функция задачи является зависимостью величины КИУМ от электротехнических параметров (вид источника первичной энергии, установленная мощность электростанции), географических параметров (расположение энергообъекта) и климатических параметров (температура воздуха, влажность, скорость и порывистость ветра, величина солнечной инсоляции, альбедо поверхности и т.д.). Данную зависимость невозможно определить с использованием комбинаций математических и тригонометрических функций таким образом, чтобы выражение являлось интерпретируемым.
Для оценки энергетического потенциала территорий и прогнозирования генерации электрической энергии от ВИЭ активно применяются методы искусственного интеллекта и, в частности, регрессионные модели машинного обучения [33-35]. Использование таких методов позволяет описать зависимости между метеорологическими и климатическими параметрами, имеющими стохастический характер, и генерацией электростанций на основе ВИЭ с высокой точностью по сравнению с подходами, основанными на использовании вероятностных распределений [36-38].
Для расчета целевой функции, использующейся в поставленной задаче, применяется разработанная авторами [39] модель машинного обучения для оценки КИУМ электростанций на базе ВИЭ. В основе модели лежит ансамблевый алгоритм машинного обучения – алгоритм случайного леса. Разработанная модель принимает в качестве входных параметров следующие данные: тип источника первичной энергии; установленную мощность энергообъекта; географическое положение энергообъекта; метеорологические параметры (отличающиеся в зависимости от типа источника первичной энергии).
Разработанная модель обучена на данных, содержащих информацию о географическом положении энергообъектов, объемах генерации в течение календарного года, метеорологических параметрах на территории расположения энергообъектов за последние пять лет. Данные для обучения модели получены в ходе анализа информации о выдаче и погашении сертификатов, подтверждающих объем производства электрической энергии, и перечня квалифицированных генерирующих объектов, функционирующих на основе ВИЭ.
Для решения задачи оптимального размещения электростанций на основе ВИЭ применяется метаэвристический алгоритм светлячков, адаптированный под поставленную задачу. Выбор алгоритма светлячков обоснован его эффективностью в рамках оптимизации географического расположения ВИЭ, показанной в исследовании [39] при сравнении различных алгоритмов оптимизации, в частности алгоритмов случайного поиска, роя частиц, светлячков и стаи серых волков.
Процесс решения задачи оптимизации с использованием предложенного алгоритма можно разделить на четыре этапа:
- подготовка – выбор исследуемой географической территории и формирование ограничений на расположение энергообъектов (границы территории);
- формирование начальной популяции – агенты размещаются на случайных позициях внутри определенных границ территории;
- поиск оптимального расположения – итерационный процесс перемещения агентов в соответствии с их значениями целевой функции и заданными параметрами алгоритма;
- заключительный – отчет по результатам проведенной оптимизации (статистические расчеты и визуализация результатов).
Математическое описание перемещения агентов алгоритма:
где xi, xj – положения агентов (географические широта и долгота); xbi – положение агента с наилучшим значением целевой функции; α – масштабирующий коэффициент, определяющий величину случайного перемещения агентов; β – функция притяжения между агентами (зависит от значения целевой функции и расстояния между агентами); сrand – случайное число в интервале от нуля до единицы.
Функция притяжения определяется следующим образом:
где γ – мера прозрачности среды, в которой передвигаются агенты; d – расстояние между двумя агентами; β0 – величина привлечения агента на расстоянии d = 0.
Для корректной работы алгоритма необходимо настроить внутренние параметры:
– α – коэффициент, определяющий величину шага агента в случайном направлении (задается в относительных единицах в соответствии с размерами рассматриваемой области оптимизации). Может быть константой на протяжении всего процесса оптимизации, изменяться по заданному закону относительно текущей итерации расчета. Коэффициент α разумно уменьшать по ходу оптимизации для обеспечения сходимости всех агентов к одной точке;
– β0 – коэффициент, определяющий степень притяжения между агентами при минимальном расстоянии. Является компонентой для расчета функции притяжения β. Может быть задан константой или изменяться в ходе оптимизации. Необходимо начинать с меньших значений на старте оптимизации, а затем увеличивать коэффициент до единицы для того, чтобы усилить исследовательскую способность на начальных итерациях, а на последних – ускорить сходимость;
– γ – коэффициент, который определяет степень прозрачности среды и влияет на величину перемещения агентов с меньшим значением целевой функции к агентам с большим значением целевой функции. Может изменяться от 0 до 1. При значении γ = 0 среда считается полностью прозрачной, в результате чего алгоритм превращается в случайный поиск. При значении γ = 1 среда считается полностью непрозрачной;
– d – функция расстояния между двумя агентами алгоритма. При изменении функции может изменяться поведение алгоритма. Так как в данной постановке задачи оптимизация производится в рамках географических координат, то наиболее подходящими функциями расчета могут выступать евклидово расстояние и расстояние по гаверсинусу.
Ранее [40] уже были определены интервалы оптимальных значений для параметров α, β0 и γ. Не рассматривалось влияние функции, используемой для расчета расстояния между агентами алгоритма на результат оптимизации. В рамках данного исследования рассматривается влияние функции для расчета расстояния между двумя географическими точками.
Так как для расчетов используются географические координаты потенциального расположения энергообъектов, сформулирована гипотеза о некорректности использования евклидова расстояния в качестве функции для расчета расстояния в данной постановке задачи оптимизации. Для улучшения результатов оптимизации предлагается использовать функцию гаверсинуса, применяемую в навигационных расчетах, и имеющую физическую и географическую обоснованность.
Евклидово расстояние между двумя точками в географических координатах определяется в соответствии с выражением
где φ1, φ2 – координаты широты первой и второй точек, рад; λ1, λ2 – координаты долготы первой и второй точек, рад.
Формула гаверсинуса для определения расстояния между двумя точками в географических координатах:
где r– радиус большого круга сферы, км.
Евклидово расстояние применяется для вычисления расстояния между точками на плоскости и представляет собой длину отрезка, соединяющего две точки. Формула гаверсинуса является редко используемой тригонометрической формулой и применяется в основном в навигации для определения кратчайших расстояний между точками маршрута.
При сравнительно небольших изменениях географического положения точек (смещение порядка 1 км) кривизна поверхности сегмента сферы довольно точно аппроксимируется плоскостью. Разница между расстояниями, определяемыми в евклидовом плане и по формуле гаверсинуса, при таких смещениях составляет около 0,1 % [41]. При расположении точек на больших расстояниях (разница в несколько географических градусов) точность аппроксимации кривизны сферы плоским планом значительно снижается и различия в расстояниях, определяемых двумя способами, становятся значительными. Из-за искажения проекции меркатора отрезок прямой, соединяющей две точки (евклидово расстояние), не является кратчайшим расстоянием между ними. Вместо этого кратчайшим расстоянием является кривая – проекция дуги на сфере (гаверсинус).
Обсуждение результатов
Для верификации выдвинутой гипотезы о некорректности использования евклидова расстояния в качестве функции для расчета расстояния в задаче оптимального размещения электростанций на базе ВИЭ были проведены расчеты для двух районов России, где по данным Единого фонда геологической информации о недрах и Росгеологии активно ведутся геологоразведочные работы. Сравнение результатов производилось для двух территорий и электростанций. Были рассмотрены районы (рис.1), в которых проводятся геологоразведочные экспедиции: Тунгокоченский муниципальный округ, Забайкальский край (месторождения россыпного золота); Вагайский район, Тюменская обл. (торфяные месторождения).
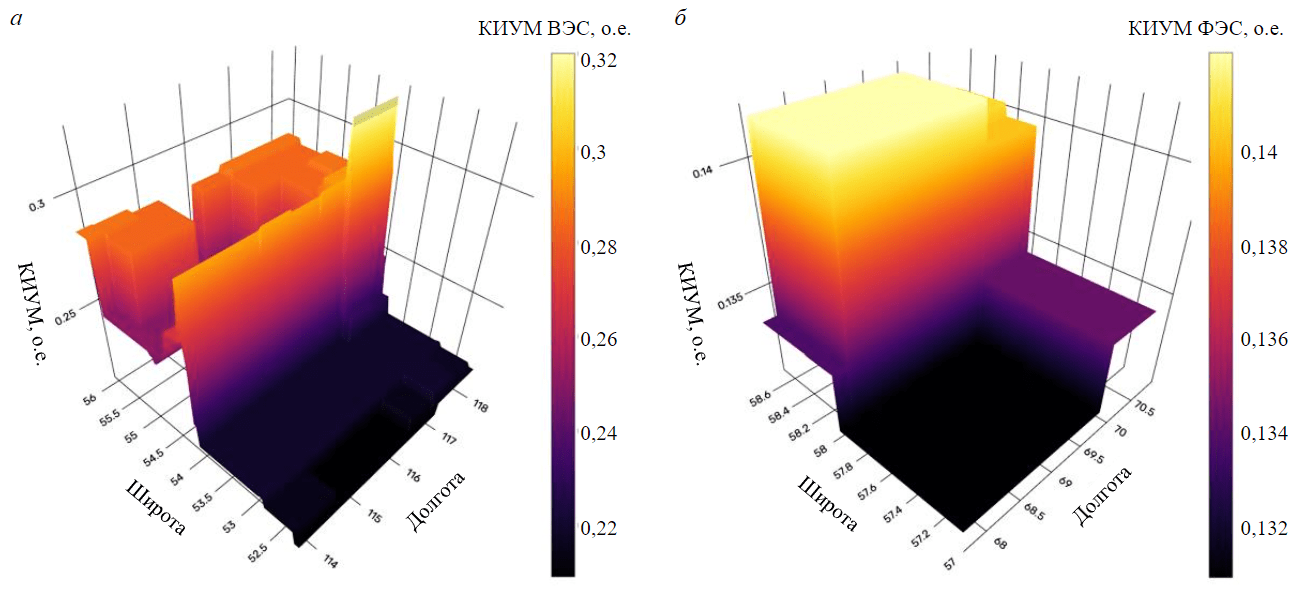
Рис.1. Примеры формы целевой функции исследуемой задачи оптимизации: а – для Тунгокоченского района; б – для Вагайского района
Для определения ошибки результатов вычисления расстояний двумя методами с разницей в координатах более одного географического градуса были использованы результаты расположения агентов на этапе формирования начальной популяции алгоритма (рис.2). Результаты сравнения расчетов расстояния двумя методами сведены в таблицу. В таблице представлена абсолютная ошибка евклидова расстояния по сравнению с гаверсинусом:
где dhav – расстояние по гаверсинусу, км; deuc – расстояние по Евклиду, км.
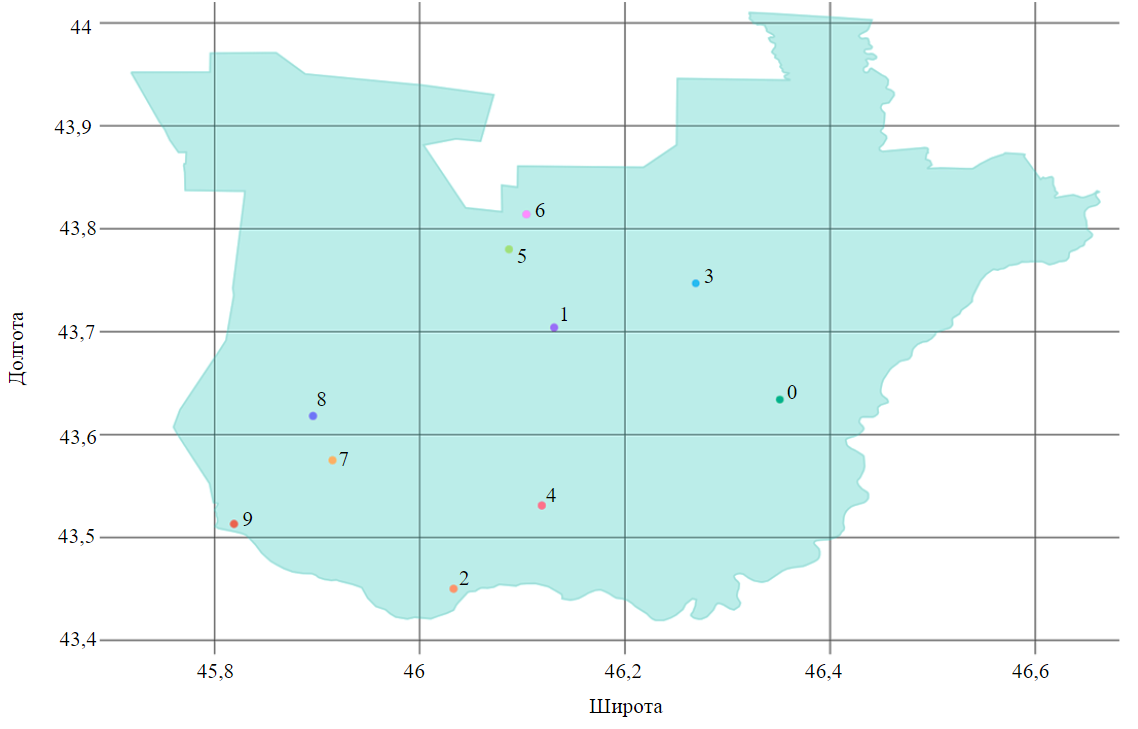
Рис.2. Расположение агентов на начальной популяции
Ошибка вычисления расстояния между агентами при использовании евклидова расстояния, км
|
Агент |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
0 |
–6,329 |
–8,043 |
–1,333 |
–6,297 |
–6,815 |
–5,786 |
–13,186 |
–13,935 |
–15,719 |
|
1 |
–6,329 |
0 |
–0,945 |
–3,989 |
–0,022 |
–0,604 |
–0,172 |
–5,429 |
–6,628 |
–7,768 |
|
2 |
–8,043 |
–0,945 |
0 |
–4,072 |
–1,764 |
–0,231 |
–0,361 |
–2,266 |
–2,399 |
–6,162 |
|
3 |
–1,333 |
–3,989 |
–4,072 |
0 |
–2,357 |
–5,489 |
–4,596 |
–9,444 |
–10,619 |
–11,783 |
|
4 |
–6,298 |
–0,022 |
–1,764 |
–2,357 |
0 |
–0,108 |
–0,021 |
–6,042 |
–6,202 |
–9,131 |
|
5 |
–6,815 |
–0,604 |
–0,231 |
–5,489 |
–0,108 |
0 |
–0,207 |
–3,087 |
–4,172 |
–5,362 |
|
6 |
–5,786 |
–0,172 |
–0,361 |
–4,596 |
–0,021 |
–0,207 |
0 |
–3,262 |
–4,305 |
–5,515 |
|
7 |
–13,186 |
–5,429 |
–2,266 |
–9,444 |
–6,042 |
–3,087 |
–3,262 |
0 |
–0,207 |
–2,340 |
|
8 |
–13,935 |
–6,629 |
–2,399 |
–10,619 |
–6,202 |
–4,172 |
–4,305 |
–0,207 |
0 |
–1,255 |
|
9 |
–15,719 |
–7,769 |
–6,162 |
–11,783 |
–9,131 |
–5,362 |
–5,515 |
–2,340 |
–1,255 |
0 |
На основании данных об ошибках определения расстояния между агентами из таблицы можно сделать вывод, что аппроксимации земной поверхности плоскостью и расчет расстояния в евклидовом пространстве в рамках данной задачи неприменимы. Ошибка определения расстояния имеет нелинейный характер, связанный с неоднородным изменением кривизны земной поверхности в широтном и долготном направлениях. Несмотря на нелинейность, прослеживается увеличение погрешности при увеличении расстояния между рассматриваемыми точками. Ошибка в расчетах расстояния в рассматриваемом примере достигает 15-16 км (0,14 град) на расстояниях между точками, равным 56 км (0,5 град долготы).
Анализируя ошибки определения расстояния (см. таблицу) и форму целевых функции (см. рис.1), можно заметить, что погрешность в 16 км (0,14 град) является довольно серьезной в рамках рассматриваемой задачи. На интервале в 0,1 град широты/долготы может произойти изменение значения КИУМ (для более платообразных поверхностей) или пропущена область глобального оптимума (для поверхностей с узкими областями глобального оптимума). Реальные размеры энергообъектов: 2-3 км – расстояние между крайними точками занимаемой фотоэлектрическими панелями Оренбургской СЭС-5, 6-8 км – расстояние между крайними ветрогенераторами Каменской ВЭС. Погрешность, превышающая габариты энергообъектов в 2-5 раз, неприемлема с точки зрения определения географической точки для их размещения, но, учитывая выбор места размещения генерации на основе ВИЭ с возможностью введения новых очередей (увеличения установленной мощности, расширения занимаемой территории), может быть допустима.
Ниже представлены результаты сравнения оптимизации размещения электростанций на базе ВИЭ с использованием функций евклидова расстояния и гаверсинуса для расчета расстояния между агентами алгоритма.
При рассмотрении территории Тунгокоченского муниципального округа проводилась оптимизация расположения ВЭС с установленной мощностью 25 МВт. В результате была определена целевая функция изменения КИУМ (см. рис.1, а) с явно выраженной зоной глобального оптимума, расположенной на 54-й широте. Результаты оптимизации при использовании двух функций для вычисления расстояния представлены на рис.3 На рис.3, а приведены графики плотности распределения лучших значений КИУМ, найденных в ходе 100 запусков алгоритма оптимизации. На рис.3, б представлено географическое расположение лучших решений алгоритма на карте района в ходе 100 запусков алгоритма оптимизации, зеленым цветом показаны результаты при использовании евклидова расстояния, синим – гаверсинуса, заштрихованные области – участки геологоразведочных работ.
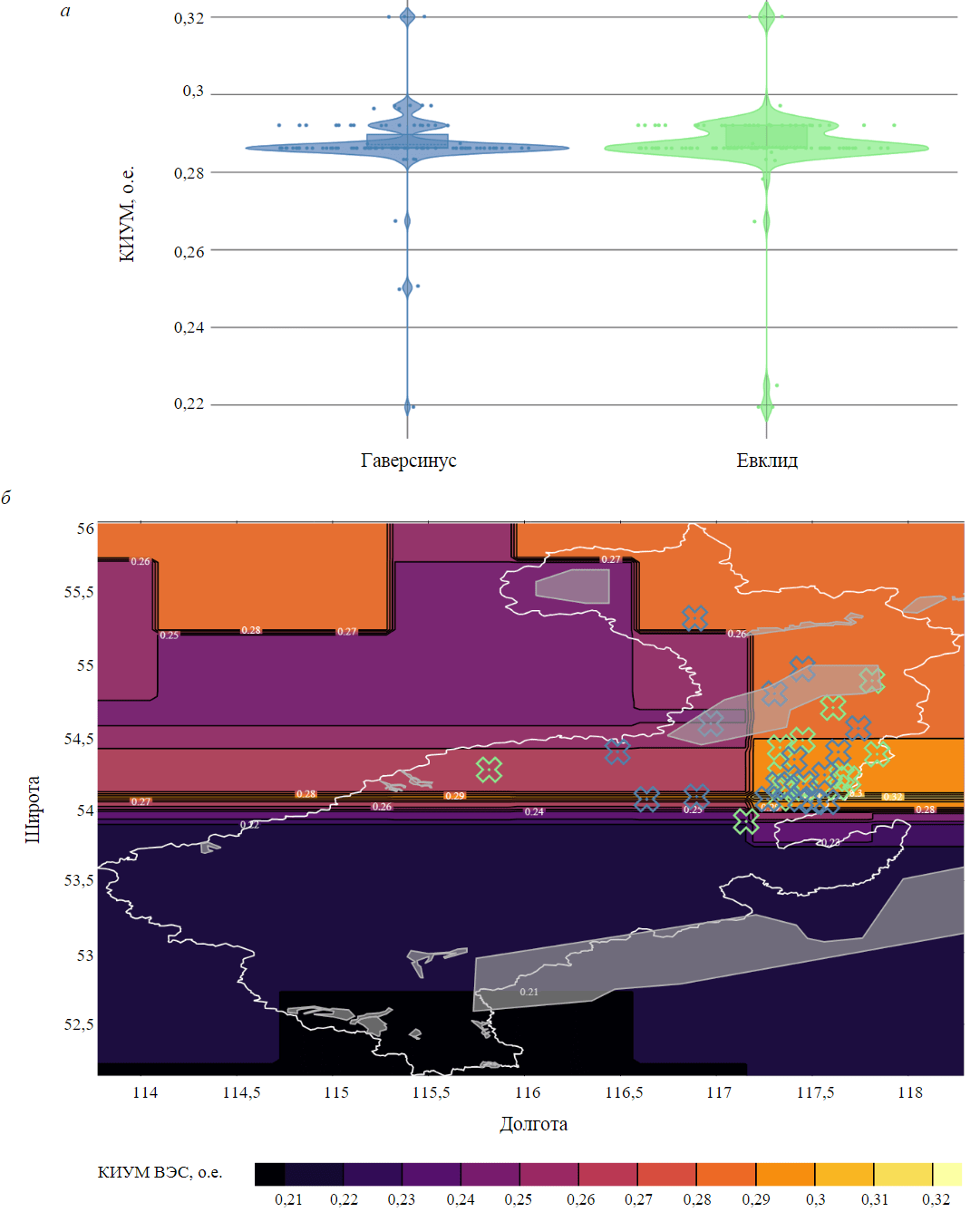
Рис.3. Распределение значений КИУМ, определенных в ходе оптимизации расположения ВЭС 25 МВт на территории Тунгокоченского муниципального округа: а – скрипичные диаграммы распределения значений КИУМ; б – географическое распределение оптимальных точек размещения
Для удобства восприятия результатов на карты (рис.3, б; 4, б) наложены целевые функции (см. рис.1) в форме линий равного уровня, демонстрирующие изменение КИУМ электростанции на рассматриваемых территориях.
На основании полученных результатов для Тунгокоченского района были сформулированы следующие выводы:
- Распределения результатов оптимизации для двух функций расчета расстояния имеют схожую форму. Распределение результатов для функции гаверсинуса имеет более четкую форму, чем для функции евклидова расстояния. При использовании функции гаверсинуса алгоритм более четко определяет области локальных оптимумов.
- Географическое расположение результатов оптимизации на рис.3, б демонстрирует, что найденные решения более равномерно распределены между областью глобального (54 широта) и локального (56 широта) оптимумов.
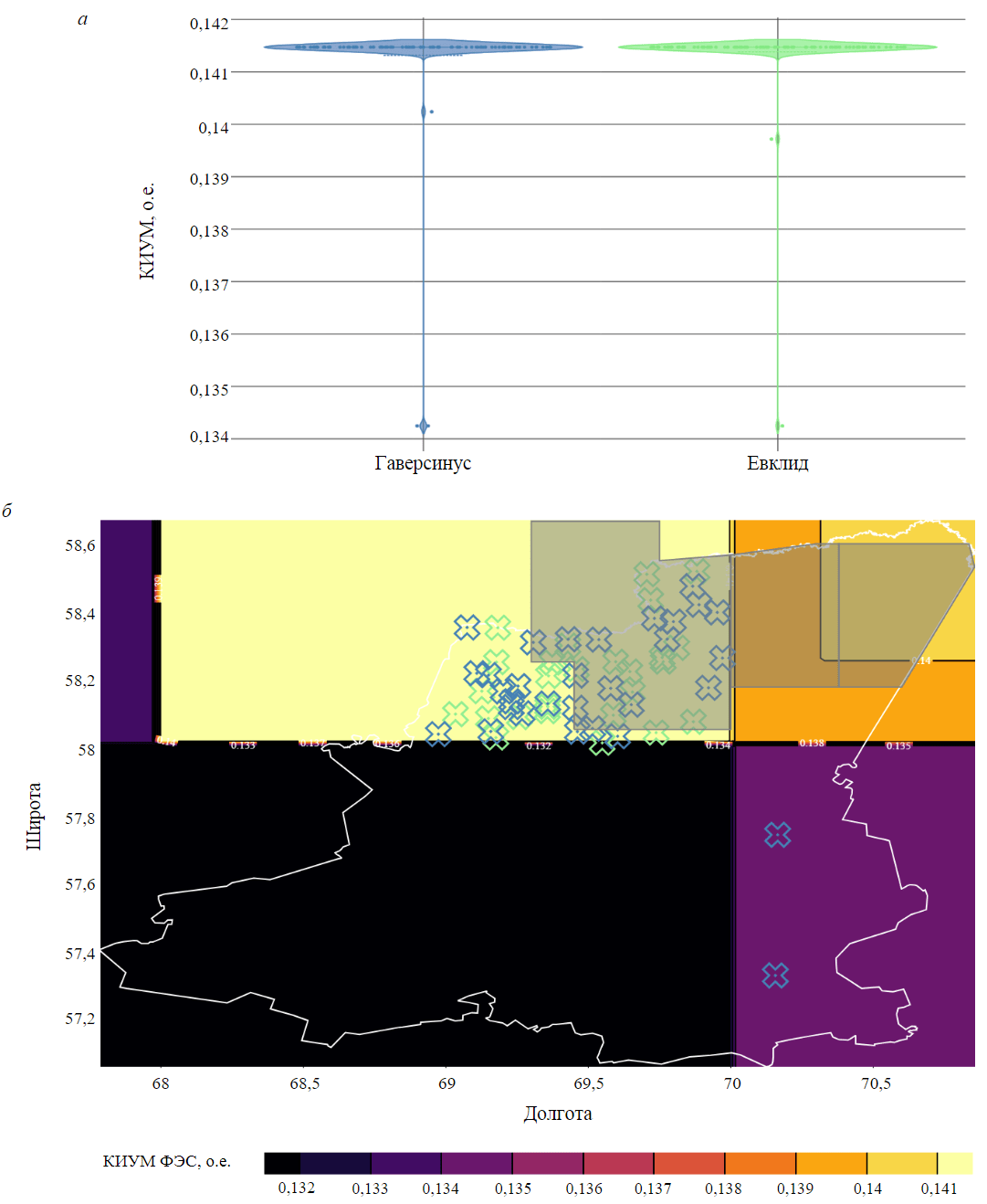
Рис.4. Распределение значений КИУМ, определенных в ходе оптимизации расположения ФЭС 45 МВт на территории Вагайского района: а – скрипичные диаграммы распределения значений КИУМ; б – географическое распределение оптимальных точек размещения
При рассмотрении территории Вагайского района была проведена оптимизация расположения ФЭС с установленной мощностью 45 МВт. Функция зависимости значений КИУМ от географического положения (см. рис.1, б) имеет платообразную форму со слабовыраженной зоной глобального оптимума (разница между минимумом и максимумом порядка 0,01 о.е.). По результатам оптимизации были получены распределения результатов работы алгоритма в ходе 100 запусков при разных функциях расстояния (рис.4, а) и географическое отображение координат лучших решений алгоритма в ходе 100 запусков (рис.4, б), зеленым цветом показаны результаты при использовании евклидова расстояния, синим – гаверсинуса, заштрихованные области – участки геологоразведочных работ.
Для территории Вагайского района получены следующие результаты:
- Так как поверхность целевой функции имеет платообразную форму, большинство найденных алгоритмом решений располагаются в одной зоне.
- В связи с тем, что зона глобального оптимума слабо выражена (разница между минимальным и максимальным значениями КИУМ составляет 0,01 о.е), более 90 % найденных решений соответствуют зоне глобального оптимума.
- Распределения результатов оптимизации (рис.4, а) практически идентичны по форме, а единичные отклонения обусловлены природой оптимизационного алгоритма.
В рамках оптимизации расположения ФЭС функция зависимости КИУМ от координатного положения изменяется преимущественно в широтном направлении (что объясняется физикой процесса распределения солнечного излучения в атмосфере Земли) и имеет платообразную ступенчатую форму. Для небольших территорий (район, муниципальный округ) такие особенности функции изменения КУИМ приводят к отсутствию локальных оптимумов. В результате выбор функции для определения расстояния между агентами алгоритма практически не оказывает влияния на результаты оптимизации. Данное влияние может проявляться при рассмотрении больших территорий в рамках страны или региона.
В рамках оптимизации расположения ВЭС функция зависимости КИУМ от координатного положения имеет более неоднородный характер распределения, в меньшей степени зависящий от широтного положения (более важным критерием является ландшафт местности), и явно выраженные локальные оптимумы. В таких условиях выбор функции для определения расстояния между агентами оптимизационного алгоритма оказывает заметное влияние на результаты оптимизации. Влияние выражается в более четких границах распределения результатов (при использовании функции гаверсинуса) и пропуске локальных оптимумов (при использовании функции евклидова расстояния), но по-прежнему мало отражается на поиске глобального оптимума целевой функции.
На основании проведенного анализа результатов оптимизации расположения электростанций на базе ВИЭ различных типов и установленной мощности для районов, на территории которых активно проводятся геологоразведочные работы, можно сделать вывод о влиянии функции расчета расстояния между агентами алгоритма на результаты оптимизации. Влияние выбранной функции для расчета расстояния между агентами алгоритма проявляется в большей степени для целевых функций с большим количеством явно выраженных зон локальных оптимумов (Тунгокоченский муниципальный округ, ВЭС), чем для платообразных функций со сравнительно небольшим изменением значений КИУМ или явно выраженной зоной глобального оптимума (Вагайский район, ФЭС).
Заключение
Исследования позволили сформулировать гипотезу о влиянии используемой функции для определения расстояния между агентами метаэвристического алгоритма светлячков на результаты оптимизации географического расположения электростанций на базе ВИЭ с целью увеличения КИУМ. Для проверки гипотезы использованы две функции определения расстояния между географическими точками – евклидова расстояния и гаверсинуса. При прямом сравнении результатов вычисления расстояния двумя функциями было установлено, что ошибка в расчетах расстояния достигает 0,14 географических градусов (15-16 км) на расстояниях между рассматриваемыми точками равным приблизительно 0,5 град долготы (что соответствует расстоянию порядка 56 км). Данные результаты соответствуют физической теории о геометрических параметрах земного шара и вычислению кратчайшего пути между двумя точками на земной поверхности. Установлено, что при наблюдаемых ошибках вычисления расстояния в ходе реализации алгоритма оптимизации может быть пропущена зона глобального/локального оптимума для функций изменения КИУМ с явно выраженными локальными оптимумами, а для функций платообразных форм может наблюдаться недостижение зоны глобального оптимума.
В ходе проведения расчетных экспериментов – оптимизации географического расположения объектов ВИЭ-генерации на территории Тунгокоченского и Вагайского районов РФ были сделаны следующие выводы относительно сформулированной гипотезы:
- В задачах оптимизации географического расположения ФЭС (Вагайский район) целевая функция (зависимость КИУМ от географических координат) имеет платообразную форму. Изменение функции определения расстояния между агентами оптимизационного алгоритма не оказало существенного влияния на результаты оптимизации. Распределение результатов при использовании функции евклидова расстояния и гаверсинуса оказались идентичными.
- В задачах оптимизации географического расположения ВЭС (Тунгокоченский район) целевая функция (зависимость КИУМ от географических координат) имеет более неоднородную форму с явно выраженными областями локальных оптимумов. Изменение функции определения расстояния между агентами оптимизационного алгоритма оказывает влияние на результаты оптимизации, но практически не влияет на нахождение глобального оптимума. Влияние выражено более четким определением зон локальных оптимумов целевой функции (при использовании функции гаверсинуса).
Расчетные эксперименты частично подтвердили сформулированную в начале исследования гипотезу. Одновременно определены необходимые корректировки, отражающие результаты экспериментов. Выбор функции для определения расстояния между агентами метаэвристического оптимизационного алгоритма в действительности имеет ограниченное влияние на результаты оптимизации географического размещения электростанций на базе ВИЭ с целью повышения КИУМ.
При решении задачи оптимизации размещения ФЭС на сравнительно небольших территориях с использованием метаэвристических алгоритмов выбор функции определения расстояния между агентами практически не влияет на результат. При выборе оптимального местоположения ВЭС при помощи метаэвристических алгоритмов выбор функции для оценки расстояния между агентами алгоритма может привести к пропуску важных с точки зрения расположения реального объекта локальных оптимумов.
Результаты исследования могут быть использованы при определении технологически целесообразных и энергоэффективных локаций расположения генерации на базе ВИЭ, в том числе для электроснабжения районов, в которых активно проводятся геологоразведочные работы, труднодоступных и удаленных от централизованного электроснабжения территорий.
Литература
- Яковлева Э.В. Электротехнический комплекс для электроснабжения геологоразведочных работ с использованием солнечной электростанции: Автореф. дис. … канд. техн. наук. СПб: Национальный минерально-сырьевой университет «Горный», 2013. 22 с.
- Яковлева Э.В. Электроснабжение геологоразведочных работ с использованием гибридных электростанций // Горное оборудование и электромеханика. 2013. № 3. С. 19-22.
- Лимитовский А.М., Башкуров А.Ю. Электростанции собственных нужд как альтернатива когенерационного энергообеспечения объектов минерально-сырьевого комплекса // Разведка и охрана недр. 2019. № 9. С. 35-37.
- Башкуров А.Ю. Оптимизация энергообеспечения потребителей геологоразведочных работ при централизованном и локальном электроснабжении объектов // Горный информационно-аналитический бюллетень. 2015. № 2. С. 386-391.
- Титов С.В. Методы и способы снижения выбросов судовыми дизельными энергетическими установками: Автореф. дис. … д-ра техн. наук. Новосибирск: Сибирский государственный университет водного транспорта, 2022. 35 с.
- Heikkila J., Ingo S. Измерения выбросов твердых частиц и отдельных компонентов отработавших газов – методы и задачи на будущее // Двигателестроение. 2017. № 4 (270). С. 46-52.
- Ntziachristos L., Saukko E., Ronkko T. et al. Влияние условий и методики пробоотбора на результаты измерений твердых частиц судовым дизелем // Двигателестроение. 2017. № 4 (270). С. 53-61.
- Максимов А. ВИЭ 2.0: Новая программа развития «зеленой» энергетики в России // Энергетическая политика. 2020. № 11 (153). С. 22-27. DOI: 10.46920/2409-5516_2020_11153_22
- Ахметшин А.И. Эффективность экологической политики нефтегазодобывающих регионов Севера России / Управление региональным развитием: проблемы, возможности, перспективы развития: Сборник научных статей по материалам Международной научно-практической конференции с международным участием, 28 ноября 2018, Чебоксары, Россия. Чебоксары: Чувашский государственный педагогический университет им. И.Я.Яковлева, 2018. С. 462-469.
- Липина С.А. Экономическая интеграция Северо-Кавказского региона // Современные производительные силы. 2013. № 3. С. 67-75.
- Сенкевич В.С. Особенности и результаты бурения глубинных геохимических поисков на флангах Мулинской впадины (Забайкальский край) / Научно-методические основы прогноза, поисков, оценки месторождений алмазов, благородных и цветных металлов: Сборник тезисов докладов IХ Международной научно-практической конференции, 17-19 апреля 2019, Москва, Россия. М.: Центральный научно-исследовательский геологоразведочный институт цветных и благородных металлов, 2019. С. 195-196.
- Забураева Х.Ш. Геоэкологические основы повышения эффективности использования сельскохозяйственных земель (на примере Чеченской Республики) // Теоретическая и прикладная экология. 2012. № 2. С. 79-84.
- Носкова Е.В. Статистические характеристики скорости ветра и их динамика в Забайкальском крае // Записки Забайкальского отделения Русского географического общества. 2014. Вып. 133. Т. 1. С. 131-138.
- Ерофеева А.А. Природно-ресурсные факторы формирования социально-экономических связей Тобольского, Уватского и Вагайского районов // Региональные геосистемы. 2021. Т. 45. № 3. С. 316-327. DOI: 10.52575/2712-7443-2021-45-3-316-327
- Косьянов В.А., Лимитовский А.М., Меркулов М.В., Головин С.В. Повышение эффективности комплексного энерго-обеспечения децентрализованных геолого-разведочных объектов в условиях Заполярья и Крайнего Севера // Известия высших учебных заведений. Геология и разведка. 2014. № 4. С. 81-85.
- Yanpu Zhao, Changsheng Huang, Mengjie Zhang, Yang Cui. AOBLMOA: A Hybrid Biomimetic Optimization Algorithm for Numerical Optimization and Engineering Design Problems // Biomimetics. 2023. Vol. 8. Iss. 4. № 381. DOI: 10.3390/biomimetics8040381
- Rahman C.M., Rashid T.A., Alsadoon A. et al. A Survey on Dragonfly Algorithm and its Applications in Engineering // Evolutionary Intelligence. 2023. Vol. 16. Iss. 1. P. 1-21. DOI: 10.1007/s12065-021-00659-x
- Shukla N.K., Srivastava R., Mirjalili S. A Hybrid Dragonfly Algorithm for Efficiency Optimization of Induction Motors // Sensors. 2022. Vol. 22. Iss. 7. № 2594. DOI: 10.3390/s22072594
- Güven A.F., Yörükeren N., Tag-Eldin E., Samy M.M. Multi-Objective Optimization of an Islanded Green Energy System Utilizing Sophisticated Hybrid Metaheuristic Approach // IEEE Access. 2023. Vol. 11. P. 103044-103068. DOI: 10.1109/ACCESS.2023.3296589
- Ali S., Rehman A.U., Wadud Z. et al. Demand Response Program for Efficient Demand-Side Management in Smart Grid Considering Renewable Energy Sources // IEEE Access. 2022. Vol. 10. P. 53832-53853. DOI: 10.1109/ACCESS.2022.3174586
- Xingyu Jiang, Jiazhen Li, Yitao Lu, Guangdong Tia. Design of Reverse Logistics Network for Remanufacturing Waste Machine Tools Based on Multi-Objective Gray Wolf Optimization Algorithm // IEEE Access. 2020. Vol. 8. P. 141046-141056. DOI: 10.1109/ACCESS.2020.3011509
- Wei Zhang, Sai Zhang, Fengyan Wu, Yagang Wang. Path Planning of UAV Based on Improved Adaptive Grey Wolf Op-timization Algorithm // IEEE Access. 2021. Vol. 9. P. 89400-89411. DOI: 10.3390/s22145232
- Guo M.W., Wang J.S., Zhu L.F., Guo S.S., Xie W. An Improved Grey Wolf Optimizer Based on Tracking and Seeking Modes to Solve Function Optimization Problems // IEEE Access. 2020. Vol. 8. P. 69861-69893. DOI: 10.1109/ACCESS.2020.2984321
- Shyh-Jier Huang, Xian-Zong Liu, Wei-Fu Su, Shu-Hsuan Yang. Application of Hybrid Firefly Algorithm for Sheath Loss Reduction of Underground Transmission Systems // IEEE Transactions on Power Delivery. 2013. Vol. 28. № 4. P. 2085-2092. DOI: 10.1109/TPWRD.2013.2265913
- Srinivasan B., Venkatesan R., Aljafari B. et al. A Novel Multicriteria Optimization Technique for VLSI Floorplanning Based on Hybridized Firefly and Ant Colony Systems // IEEE Access. 2023. Vol. 11. P. 14677-14692. DOI: 10.1109/ACCESS.2023.3244346
- Anbalagan A., Sundarsingh E.F., Ramalingam V.S. et al. Smart Dynamic Position Tracking Wearable for Geofencing in Marine Environment // IEEE Transactions on Instrumentation and Measurement. 2023. Vol. 72. № 8005109. DOI: 10.1109/TIM.2023.3311076
- Jimoh O.D., Ajao L.A., Adeleke O.O., Kolo S.S. A Vehicle Tracking System Using Greedy Forwarding Algorithms for Public Transportation in Urban Arterial // IEEE Access. 2020. Vol. 8. P. 191706-191725. DOI: 10.1109/ACCESS.2020.3031488
- Керимов И.А., Бачаева Т.Х., Висмурадов А.В., Даукаев А.А. Распределение твердых нерудных полезных ископаемых на территории Чеченской Республики // Вестник академии наук Чеченской Республики. 2015. № 3 (28). С. 103-112.
- Асхабова Х.Н., Оздыханов М.С., Солтамурадов Г.Д. Оценка экологического состояния окружающей среды на территории Чеченской Республики в 2017 г. // Успехи современного естествознания. 2019. № 1. С. 7-12.
- Солодовников А.Ю. География Тюменской области: полезные ископаемые и их использование. Тюмень: ТюмГУ-Press, 2023. 352 с.
- Солодовников А.Ю. Минерально-сырьевые ресурсы Вагайского района и их использование // Горные ведомости. 2017. № 3 (151). С. 68-77.
- Барабашева Е.Е., Брылева М.С. К вопросу о формах нахождения и механизмах концентрирования золота углями на примере Забайкальских угольных месторождений // Горный информационно-аналитический бюллетень. 2016. № 9. С. 194-203.
- Ahmed R., Sreeram V., Mishra Y., Arif M.D. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization // Renewable and Sustainable Energy Reviews. 2020. Vol. 124. № 109792. DOI: 10.1016/j.rser.2020.109792
- Сергеев Н.Н., Матренин П.В. Обзор международного опыта в прогнозировании генерации возобновляемых источников энергии с помощью методов машинного обучения // iPolytech Journal. 2023. Т. 27. № 2. С. 354-369. DOI: 10.21285/1814-3520-2023-2-354-369
- Nespoli A., Ogliari E., Leva S. et al. Day-Ahead Photovoltaic Forecasting: A Comparison of the Most Effective Techniques // Energies. 2019. Vol. 12. Iss. 9. № 1621. DOI: 10.3390/en12091621
- Wais P. Two and three-parameter Weibull distribution in available wind power analysis // Renewable Energy. 2017. Vol. 103. P. 15-29. DOI: 10.1016/j.renene.2016.10.041
- Wannakam K., Jiriwibhakorn S. Evaluation of Wind Energy Production Using Weibull Distribution and Artificial Neural Networks / 2018 International Conference on Engineering, Applied Sciences, and Technology, 4-7 July 2018, Phuket, Thailand. IEEE, 2018. 4 p. DOI: 10.1109/iceast.2018.8434474
- Simeng Cheng, Yimiao Xie, Zhan Shu et al. Effect of Different Solar Irradiance Parameters on Reliability Evaluation of the Grid // IOP Conference Series: Earth and Environmental Science. 2019. Vol. 300. Iss. 4. № 042115. DOI: 10.1088/1755-1315/300/4/042115
- Bramm A.M., Eroshenko S.A., Khalyasmaa A.I., Matrenin P.V. Grey Wolf Optimizer for RES Capacity Factor Maximization at the Placement Planning Stage // Mathematics. 2023. Vol. 11. Iss. 11. № 2545. DOI: 10.3390/math11112545
- Bramm A.M., Mazunina M.V. Effects of the Firefly Optimization Algorithm Hyperparameters on the Optimal Placement Problem Results of Renewables-Based Power Plants / 2023 Belarusian-Ural-Siberian Smart Energy Conference, 25-29 September 2023, Ekaterinburg, Russia. IEEE, 2023. P. 48-53. DOI: 10.1109/BUSSEC59406.2023.10296466
- Maria E., Budiman E., Haviliddin, Taruk M. Measure distance locating nearest public facilities using Haversine and Euclidean Methods // Journal of Physics: Conference Series. 2020. Vol. 1450. № 012080. DOI: 10.1088/1742-6596/1450/1/012080
