Evaluation of the impact of the distance determination function on the results of optimization of the geographical placement of renewable energy sources-based generation using a metaheuristic algorithm
- 1 — Junior Researcher Ural Federal University named after the first President of Russia B.N.Yeltsin ▪ Orcid ▪ ResearcherID
- 2 — Ph.D. Associate Professor Ural Federal University named after the first President of Russia B.N.Yeltsin ▪ Orcid ▪ ResearcherID
Abstract
Since the United Power System was created electrical supply of remote and hard-to-reach areas remains one of the topical issues for the power industry of Russia. Nowadays, usage of various renewable energy sources to supply electricity at remote areas has become feasible alternative to usage of diesel-based generation. It becomes more suitable with world decarbonization trends, the doctrine of energy security of Russia directives, and equipment cost decreasing for renewable energy sources-based power plants construction. Geological exploration is usually conducted at remote territories, where the centralized electrical supply can not be realized. Placement of large capacity renewable energy sources-based generation at the areas of geological expeditions looks perspective due to development of industrial clusters and residential consumers of electrical energy at those territories later on. Various metaheuristic methods are used to solve the task of optimal renewable energy sources-based generation geographical placement. The efficiency of metaheuristics depends on proper tuning of that methods hyperparameters, and high quality of big amount of meteorological and climatic data. The research of the effects of the calculation methods defining distance between agents of the algorithm on the optimization of renewable generation placement results is presented in this article. Two methods were studied: Euclidean distance and haversine distance. There were two cases considered to evaluate the effects of distance calculation method change. The first one was for a photovoltaic power plant with installed capacity of 45 MW placement at the Vagaiskii district of the Tyumen region. The second one was for a wind power plant with installed capacity of 25 MW at the Tungokochenskii district of the Trans-Baikal territory. The obtained results show low effects of distance calculation method change at average but the importance of its proper choose in case of wind power optimal placement, especially for local optima’s identification.
Funding
The research funding from the Ministry of Science and Higher Education of the Russian Federation (Ural Federal University named after the first President of Russia B.N.Yeltsin within the Priority-2030 Program) is gratefully acknowledged.
Introduction
The Russian Federation has a huge potential in terms of mineral resources and fossil fuels represented by complex of minerals distributed over a vast territory. This mineral complex consists of oil, natural gas, coal, metallic ores, raw mineral materials which are used in building industry, etc. The development of raw materials deposits and their extraction are carried out throughout the vast territory of the country from the Caucasus to the Far East. Geological exploration expeditions play an important role in confirming the mining potential of the territories. These expeditions are usually carried out in remote areas, where the centralized electrical supply can not be realized [1, 2]. Mobile generation systems, based on small-capacity diesel generators, or fast-built installations, based on one large-capacity diesel generator, are used to provide electricity in these conditions [3, 4]. The use of diesel generators is the simple way to establish a local electrical supply. However, there are some specific aspects of exploitation, related to fuel transportation and the negative ecological impact (emissions of nitrogen and carbon oxides) [5-7].
Mining and industrial clusters and working settlements are developed in the area if geological exploration succeeds. These new consumers of electricity require the construction of long overhead power transmission lines or a local power plant for electrical supply. Decreasing the share of diesel-based generation and replacing it with local energy sources-based generation is one of the keynotes of the Russian Energy Security Doctrine. Developing renewable energy sources-based power generation (RES) in areas of geological exploration is a major alternative for non-environmentally friendly diesel generation with low efficiency considering these keynotes.
Decarbonization trends of all sections of the economy suggest the integration of more environmentally friendly energy sources into the economy, including electrical supply to remote and hard-to-reach areas. The government's economic development plan for the Russian Federation includes programs to support decarbonization and the development of green power generation [8]. It is reasonable to evaluate the potential for locating RES-based power plants at geological exploration sites [9-11], considering both their environmental impact [12-14] and mining prospects in these territories [15]. Optimization of the geographical location of RES-based generation is essential for efficient use, particularly in large countries such as the Russian Federation, which have various climatic zones with diverse meteorological conditions. The goal of this optimization is to maximize electricity generation, represented by the capacity utilization factor (CF), of power plants. CF is one of the parameters used as indicators for new project selection within governmental support programs such as PSA RES 2.0. The minimum requirements for CF for photovoltaic power plants (PVPP) and wind power plants (WPP) in Russia are 0.14 and 0.27 p.u., respectively, according to official tender documentation.
Meteorological data, a CF forecasting system, and appropriate mathematical optimization methods capable of showing high results when working with heterogeneous, complex objective function forms are required for optimization of this type. There are many factors affecting the optimization results. One of these factors is the determination of the distance between geographical points that determine the various potential positions of the planned power generation unit. Not all methods are suitable for this task, and some show good results when dealing with uneven and complex objective functions.
Different metaheuristic [16-18] optimization methods such as the Firefly algorithm [19, 20], Grey Wolfs Pack [21-23], etc. are effective tools for optimizing in complex and unique situations.
Metaheuristics is based on the natural behavior of animals and insects during vital processes, such as food search and hunting. Mathematical descriptions of animal and insect behavior are used in many economic fields, including engineering, construction, logistics, and the power industry. Metaheuristic algorithms have advantages over traditional optimization methods based on gradient descent or generalized Newton's method, which are also used for technical tasks.
The main advantages of metaheuristics include:
- universality: optimization algorithms can be used for both simple single-extremum problems and unique multiple-extremums;
- smaller probability of getting stuck in a local extremum or plain space;
- smaller influence of initial evaluation on final results of the optimization (algorithm’s agents first placement).
One of the main drawbacks of metaheuristic optimization algorithms is the need to tune their hyperparameters. The efficient values of these parameters may vary depending on the task being considered, the objective function, or the restriction system.
There are various factors that affect the results of RES-based power generation optimization. One of these factors is the distance calculation function used in the algorithm. Metaheuristic methods are often applied to optimization tasks involving integer-valued or discrete parameters. In these cases, the agents of the algorithm move to predefined grid nodes in the solution space, and Euclidean distance [24, 25] is typically used by default. A significant part of research focuses on accurately tuning the hyperparameters of the algorithm, while working on optimization tasks that use geographical coordinates as parameters. When working with optimization tasks where there are not only integer values but also infinite fractional values, haversine distances, which are used in transport logistics and navigation [26, 27] could be used as an alternative to Euclidean distance.
This research presents the effects of the distance function used in optimization algorithms on RES-based generation placement optimization results. The main objective is to confirm the hypothesis that selection of the distance functions affects the optimization results. Application of optimization methods based on metaheuristic algorithms for geographical placement of different types and capacities of RES-generation, and evaluation of various distance functions' influence on results represent the scientific novelty of this study.
To confirm the hypothesis, two areas were considered for geological exploration: the Urals [28-31] and the Trans-Baikal territory [32].
Methodology
The objective function of the optimization task has a unique form and contains many local maximum areas, considering the geographical placement of RES-based generation to maximize its CF. The objective function shows how CF changes depending on electrical parameters (energy source type and installed capacity), geographical parameters (location of power plant) and climatic/meteorological parameters (air temperature, humidity, wind speed, solar irradiation, albedo, etc.) This function cannot be defined using interpretable combinations of mathematical and trigonometric functions.
Models, based on artificial intelligence (AI), especially forecasting models [33-35], are widely used to evaluate the potential and efficiency of RES-based power plant placement in areas. AI-model are able to describe the correlations between stochastic climatic and meteorological parameters and electricity production of RES-based power generation. The results of these models are highly accurate compared to traditional approaches based on probability distributions [36-38].
The machine learning forecasting model for RES-based generation CF values forecasting proposed by the authors in [39] which is based on an ensemble algorithm named “random forest”, was used to determine the objective function for this research. The initial data for this model include the type of energy source, installed capacity of the power plant, geographical location, and a number of meteorological variables (which may vary depending on the type of energy source).
The developed model was trained using data on the geographical positions of RES-based power plants, electricity generation throughout the year and averaged meteorological parameters for the area of the power plants for five years. The data used to train the model was extracted from certificates confirming the origin of electricity consumed for qualified RES-generation.
The adapted firefly's optimization algorithm was applied to the task of optimal RES-based geographical placement of generation. This algorithm was chosen because of its efficiency in this task, which has been demonstrated in comparison with random search, particle swarm optimization, fireflies, and grey wolf pack optimization algorithms in [39].
The optimization task solution process using the proposed algorithm can be divided into four stages, as follows:
- preparation – choosing the area under consideration and forming restrictions on the power plant's placement (borders of the area);
- initial population creation – creating agents and randomly distributing them within the borders of the considered area;
- optimal placement search – an iterative process of moving agents according to their objective function values and algorithm parameters;
- final – end of optimization and creation of a report on results (statistical metrics and visualization of results).
Mathematical description of the agent's movement process:
where xi, xj are the agent’s positions (geographical latitude and longitude); xbi is the position of the agent with the highest objective function score; α is the coefficient determines random move of agents; β is the agents attraction function (depends on the agent’s values of the objective function and the distance between them); сrand is the random value in range from zero to one.
The agent's attraction function is defined as follows:
where γ is the transparency coefficient; d is the distance between two agents; β 0 – attractionforce of the agent at the distance of d = 0.
It is required to tune the hyperparameters to provide correct work of the proposed metaheuristic algorithm:
– α is the coefficient defining the step length of the agent in the random direction (measures in p.u. according to the size of the considered optimization area). This coefficient may remain constant during the optimization process, or it may change according to the chosen pattern. The reasonable change of α is to decrease it during the optimization process to provide the convergence of the agents to one area;
– β0 is the coefficient defining the strength of attractiveness between agents on the minimal distance. This coefficient is used to define the attractiveness function β. This could remain constant or change according to the pattern. It is necessary to use a smaller values of β0 at the beginning, and then gradually increase β0 till the value of 1.0 to strengthen the exploration ability at the start of the algorithm and to accelerate the convergence of the algorithm at the final iterations;
– γ is the coefficient which defines the transparency of the environment and affects the movement of the agents with the smaller values of the objective function to the agents with the higher values of the objective function. This coefficient could change in the range from zero to one. If γ = 0, then the environment is assumed as fully transparent, which leads to the algorithm transforming into a random search. If γ = 1, then the environment is assumed as fully non-transparent;
– d is a function of the distance between agents of the algorithm. The behavior of the algorithm may change if the distance function is changed. In the stated problem, the position of agents refers to the actual values of geographical latitude and longitude, so the most suitable distance functions may be Euclidean distance and haversine distance.
Optimal values for the parameters α, β0 и γ listed above were defined in the previous research [40]. Effects of the agent’s distance function selection on the optimization results have not been studied in the previous research. Different distance functions are considered to calculate the distance between two geographical points in the frame of the current research.
Since the geographical coordinates of the potential location of power plants are used for calculations, a hypothesis about the incorrectness of using the Euclidean position as a function for calculating the distance in this formulation of the optimization problem was formulated.
It is proposed to use the haversine function, which is used in navigation calculations and has physical and geographical validity to improve the optimization results.
The Euclidean distance between two geographical points is defined as follows:
where φ1, φ2 are latitude coordinates of two points, rad; λ1, λ2 are longitude coordinates of two points, rad.
The haversine distance between two geographical points is defined as follows:
where r is the major sphere’s circle radius, km.
Euclidean distance is applicable to calculating the distance between two points on the same plane, and it equals the length of a straight line connecting these points. The haversine equation is rarely used trigonometric function and mainly uses in the field of navigation to calculate the shortest distance between any two route points.
The curvature of the Earth's surface can be accurately approximated by the plane when considering small distances between two points (about 1 km). The difference between Euclidean and Haversine distance functions in these cases is about 0.1 % [41]. The accuracy of the plane approximation decreases with increasing distance between the points. When the distance is near to a few geographical degrees, the difference between the two distance functions becomes noticeable. These differences are due to Mercator projection distortions. Therefore, the shortest distance between any two points on Earth's curved surface is measured by the Haversine formula, not by a straight line (Euclidean).
Results and discussion
The calculations were provided to confirm the proposed hypothesis. Two territories of the Russian Federation were chosen for these calculations. Geological exploration expeditions are actively performed in these territories in accordance with the Unified Fund of Geological Information about the Subsoil of the Russian Federation and Rosgeo data. The obtained results of comparison for two types of RES-based power generation were provided. Figure 1 shows the form of the objective functions for the two considered territories: Tungokochenskii district of Trans-Baikal region, where placer gold deposits are being explored, and Vagaiskii district of Tumen region where peat deposits are being investigated.
The results of the agent's placement at the initial population creation stage are presented in Fig.2. These results were used to evaluate the difference between two methods for calculating distance when the distance between two points is greater than one degree. The Table shows the absolute error of the Euclidean distance compared to the haversine:
where dhav is the distance according to the haversine method, km; deuc is the distance according to the Euclidean method, km.
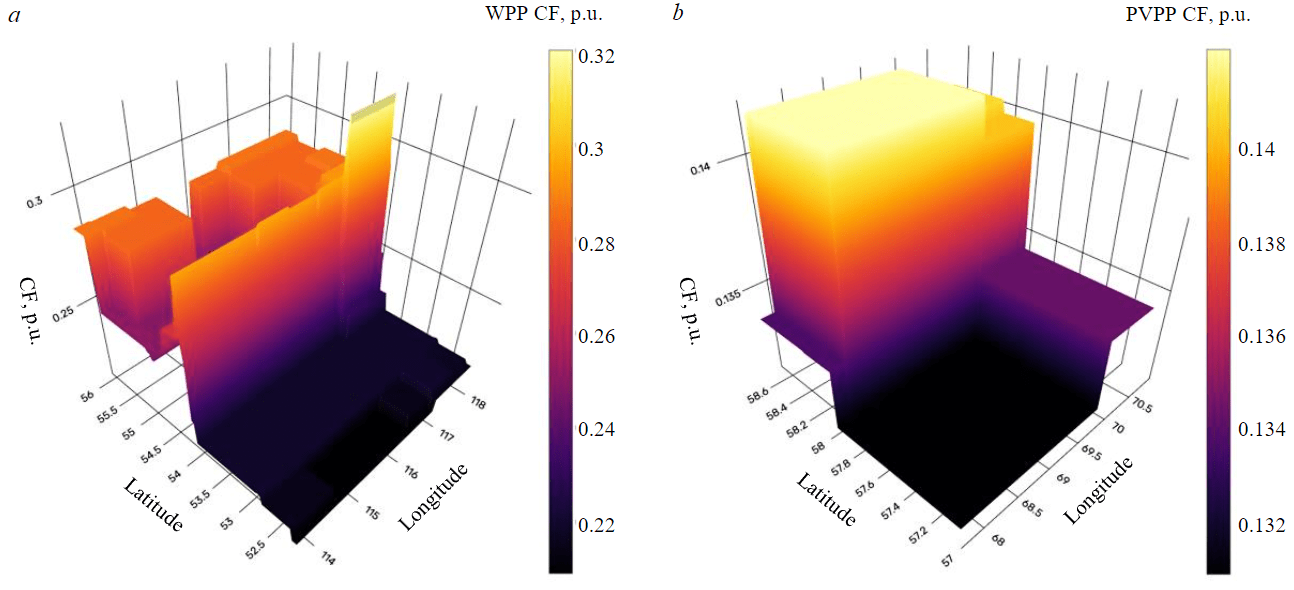
Fig.1. The objective function examples of the optimization task under study: а – WPP placed in the Tungokochenskii district; b – PP placed in the Vagaiskii district
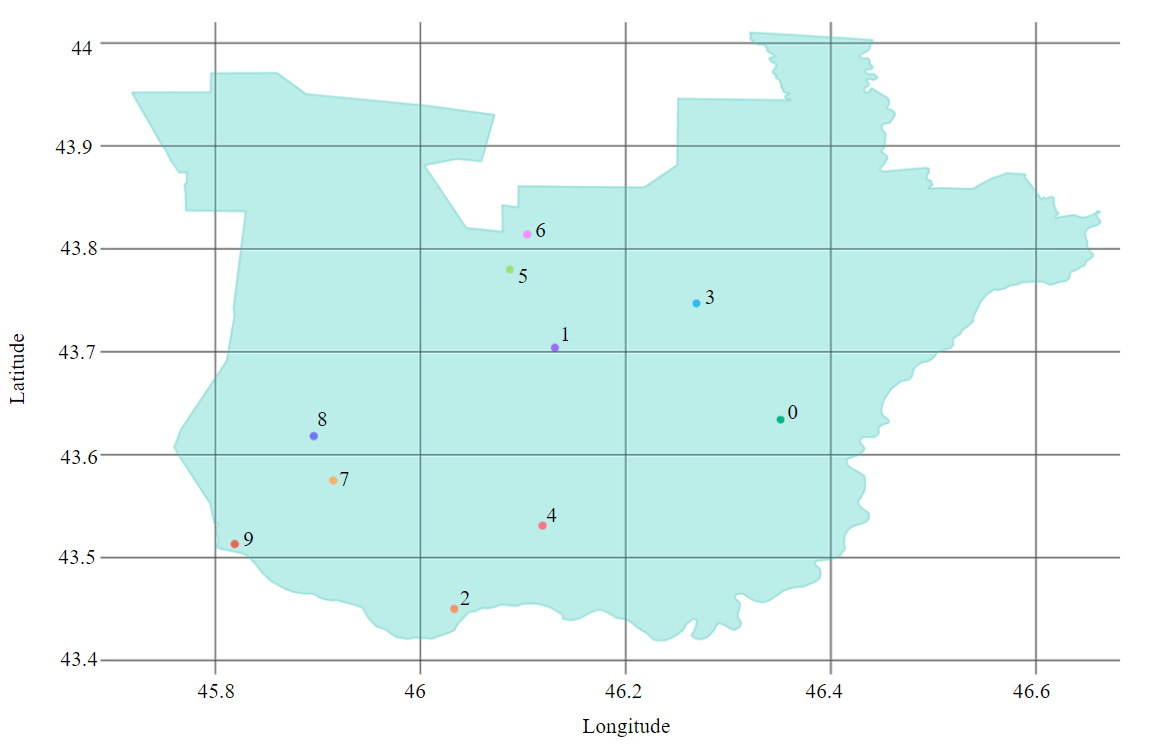
Fig.2. Initial population agent’s placement
The difference of Euclidean distance and haversine for initial population agent’s distance calculation, km
|
Agent |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
0 |
–6.329 |
–8.043 |
–1.333 |
–6.297 |
–6.815 |
–5.786 |
–13.186 |
–13.935 |
–15.719 |
|
1 |
–6.329 |
0 |
–0.945 |
–3.989 |
–0.022 |
–0.604 |
–0.172 |
–5.429 |
–6.628 |
–7.768 |
|
2 |
–8.043 |
–0.945 |
0 |
–4.072 |
–1.764 |
–0.231 |
–0.361 |
–2.266 |
–2.399 |
–6.162 |
|
3 |
–1.333 |
–3.989 |
–4.072 |
0 |
–2.357 |
–5.489 |
–4.596 |
–9.444 |
–10.619 |
–11.783 |
|
4 |
–6.298 |
–0.022 |
–1.764 |
–2.357 |
0 |
–0.108 |
–0.021 |
–6.042 |
–6.202 |
–9.131 |
|
5 |
–6.815 |
–0.604 |
–0.231 |
–5.489 |
–0.108 |
0 |
–0.207 |
–3.087 |
–4.172 |
–5.362 |
|
6 |
–5.786 |
–0.172 |
–0.361 |
–4.596 |
–0.021 |
–0.207 |
0 |
–3.262 |
–4.305 |
–5.515 |
|
7 |
–13.186 |
–5.429 |
–2.266 |
–9.444 |
–6.042 |
–3.087 |
–3.262 |
0 |
–0.207 |
–2.340 |
|
8 |
–13.935 |
–6.629 |
–2.399 |
–10.619 |
–6.202 |
–4.172 |
–4.305 |
–0.207 |
0 |
–1.255 |
|
9 |
–15.719 |
–7.769 |
–6.162 |
–11.783 |
–9.131 |
–5.362 |
–5.515 |
–2.340 |
–1.255 |
0 |
Based on the data in Table, it can be concluded that the plane approximation and Euclidean distance calculations are not applicable to this task. The error distribution in distance calculation is nonlinear, which could be due to the uneven curvature of the Earth's surface across latitude and longitude. Even though the error in distance calculation may be nonlinear, there is a positive correlation between the error values and the distance between two points. In the example presented, the maximum error reached 15-16 km (0.14 degrees) when the distance between the two points was 56 km (half a degree).
Such errors (Table) are significant for the studied optimization task, considering the objective function's form (Fig.1). A drastic change in the CF value may occur within an interval of 0.1 degrees of longitude or latitude for flat surfaces, or the optimal area may be missed for surfaces with a peaked shape. The size of a RES-based power plant is equal to 2-3 km for one of the Orenburg PVPPs or 6-8 km for Kamenskaya WPP, which is the distance between two end wind generators. An error that is 2-5 times larger than the size of the object under consideration is unacceptable, but it may be tolerable if installations of new units (capacity increase, territory expansion) for this power plant are considered later.
The comparison of the results of optimizing the placement of RES-based power plants placement using two different distance functions (Euclidean and haversine) presented below.
The 25 MW WPP placement optimization was considered for the Tungokochenskii district area. The objective function for this area (see Fig.1, a) is characterized by a global optimum area clearly localized at 54 degrees latitude. Figure 3 shows the results of comparing two distance functions for calculating agent distances. Figure 3, a shows distribution density curves of the best CF values found by the optimization algorithm after 100 iterations, and Fig.3, b shows the geographical location of the best results on the district map, projected onto the objective function plane. In both figures, green colors represent results obtained using the Euclidean distance function, while blue colors represent haversine results, and gray areas represent territory exploration expeditions.
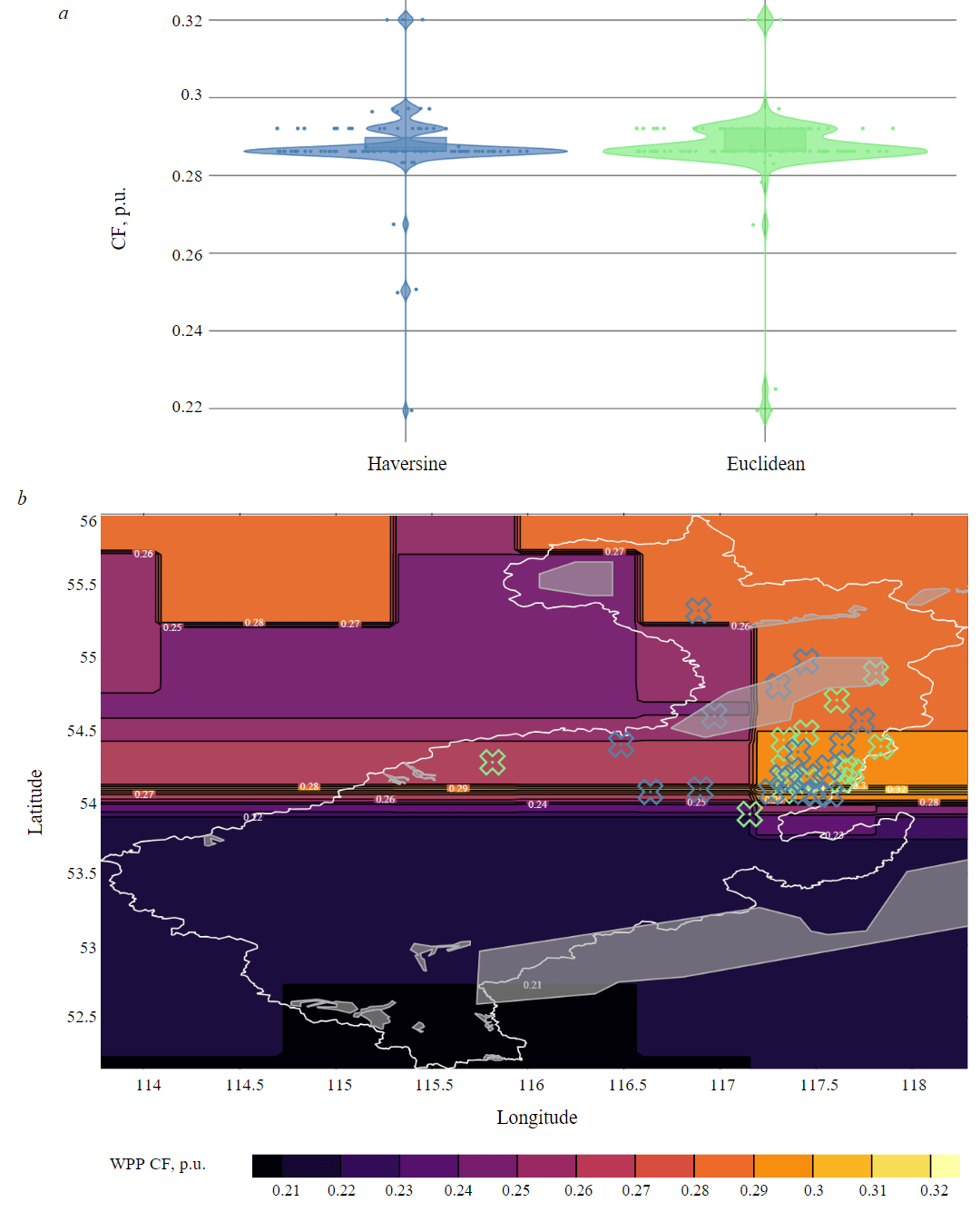
Fig.3. Distribution of the optimal CF values which were defined during the 25 MW WPP placement optimization in the Tungokochenskii district: a – violin plots for CF values of the optimal placement results; b – geographical distribution of the optimal placement results
For the convenience of perceiving the results geographical maps of the considered districts (Fig.3, b and 4, b) were combined with the objective functions (see Fig.1) in the form of a contour plots which demonstrate changes in the CF values of the power plant at the considered territories.
The following conclusions were formulated based on the obtained results for the Tungokochenskii district:
- The violin distribution plots have a similar shape for both distance functions. The haversine results distribution plot is more clearly defined than the Euclidean distance results. The optimization algorithm more accurately identifies global optimum areas when using the haversine distance function.
- The geographical distribution of the optimization results (Fig.3, b) shows that most of the results fall between 54th and 56th latitudes, which are the global optimum and local optimal areas, respectively.
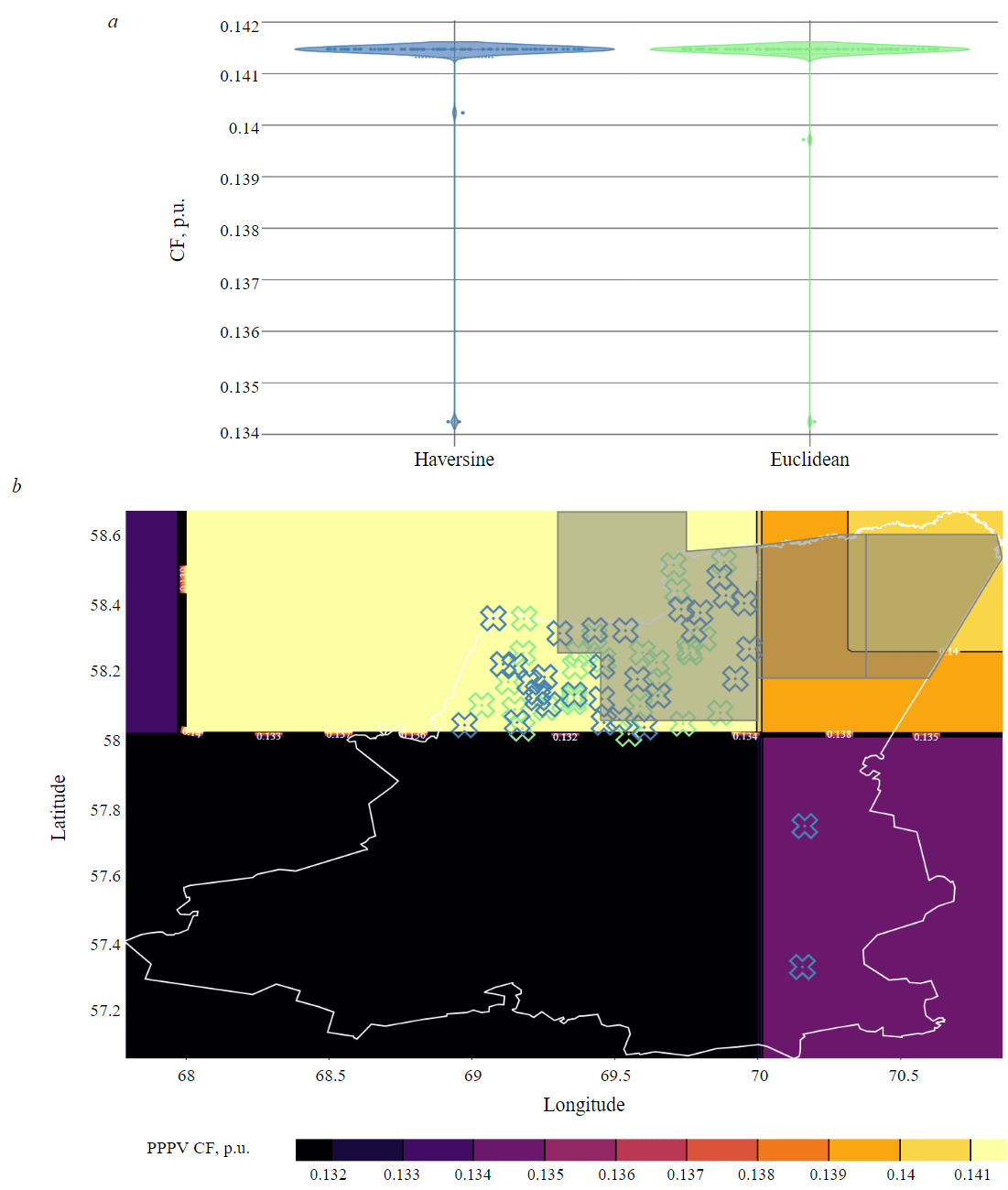
Fig.4. Distribution of the optimal CF values which were defined during the 45 MW PVPP placement optimization in the Vagaiskii district: a – violin plots for CF values of the optimal placement results; b – geographical distribution of the optimal placement results
The 45 MW PVPP placement optimization was considered for the Vagaiskii district area. The objective function for this area (see Fig.1, b) is flat and has a poorly expressed global optimum (the difference between the minimum and maximum values is 0.01 p.u.). Figure 4, a shows the distribution density curves of the best CF values found by the optimization algorithm after 100 iterations. Figure 4, b shows the geographical location of these results projected onto the district map in the plane of the objective function. In both figures, green represents the results obtained using the Euclidean distance function, and blue represents haversine results. Grey areas represent the territories of geological exploration expeditions.
The following conclusions were formulated based on the obtained results for the Vagaiskii district:
- The majority of the solutions found are located in the same area due to the flat form of the objective function.
- More than 90 % of the results correspond to the global optimum area, due to the flat form of the objective function (the difference between minimum and maximum values of CF is 0.01 p.u.).
- Violin distribution plots are nearly identical for both distance functions used (Fig.4, a), with only minor deviations explained by the stochastic nature of the optimization algorithm.
The objective function of the CF values changes mainly in the latitude direction and has a flattened, stepwise form, which can be explained by the physics of solar irradiation spreading. This leads to the absence of a local optimal area for small territories (district, municipal district), so the choice of distance function does not affect the optimization results. However, the effect of the distance function may become noticeable when considering larger territories such as an entire region or country.
The objective function of the CF values has a more stochastic distribution than that of PVPP, and it clearly has localized sub-optimal areas. The latitude dependency plays a smaller role, and the landscape specifics are more significant. The choice of the distance function significantly affects the optimization results, considering these conditions. These effects are evident in the more distinct borders of the distribution plot (when using the haversine function), and local optimal areas are exceeded (when using Euclidean distance). However, the change in the distance function still has minor effects on the overall results.
There is an influence of the selected distance calculation function on the optimization algorithm, when considering tasks for RES-based power generation optimization in territories where geological exploration is actively conducted. This influence has a major impact on tasks where the objective function has narrow optimal and suboptimal areas (Tungokochenskii district and WPP placement). A minor impact was observed in the task with a flat objective function and one optimal area (Vagaiskii district and PVPP placement).
Conclusion
The hypothesis about selecting a function for distance calculation in the firefly's metaheuristic optimization algorithm has an impact on the results of optimization when optimizing the placement of RES-based power generation using CF values as an objective function. Two functions for calculating the distance between two geographic points were used to validate the proposed hypothesis: Euclidean distance and haversine distance. When these two functions were compared directly, the maximum error was 0.14 degrees of geography (15-16 km), and the distance between the two points corresponded to a maximum error of 0.5 degrees of geography (which corresponds to the distance of about 56 km). These comparison results confirmed the physical theory of Earth's surface geometry and the shortest path between two points on a sphere.
It was noted that with the observed errors in calculating the distance during the implementation of the optimization algorithm, the zone of global/local optimum can be skipped for the functions of the CF change with clearly expressed local optima, and for functions of flat shapes there may be a failure to reach the global optimum zone.
The following conclusions about the initial hypothesis were formulated based on the results of the experiments on the RES-based generation placement optimization in the territories of the Tungokochenskii and Vagaiskii districts:
- The objective function (dependency of CF values from geographical coordinates) has a flat form for the tasks of PVPP placement optimization (Vagaiskii district). Changing the distance calculation function has a minor impact on the placement optimization results for 45 MW PVPP in the Vagaiskii district. The distribution of results is almost identical for both the Euclidean and haversine distances.
- The objective function has a more uneven and peaked shape with clearly defined optimal regions for WPP placement (Tungokochenskii district) optimization. Changing the calculation method for distance has a notable impact, but barely affects the reachability of the global optimum. This effect is mainly expressed in a more distinct detection of local optimal areas when using the haversine method.
The initial hypothesis was partially confirmed by the results obtained during the experiments. Also, several adjustments to the initial hypothesis were made based on the results. The selection of the distance calculation function had a limited impact on the results of RES-based geographical placement optimization to increase the CF of the power plant.
The distance function selection does not affect the optimization results when PVPP placement optimization is considered on relatively small territories. However, the distance function may lead to the skipping of important local optimal areas when considering WPP placement optimization.
The results of the research could be used to find a technically reasonable and energy-efficient location for the placement of RES-based power plants. These results also could also be useful for electricity supply in remote areas, hard-to-reach areas, or areas where geological exploration is taking place.
References
- Yakovleva E.V. Electrotechnical complex with photovoltaic power plant for electricity supply of the geological exploration expedition: Avtoref. dis. … kand. tekhn. nauk. St. Petersburg: Natsionalnyi mineralno-syrevoi universitet “Gornyi”, 2013, p. 22 (in Rus-sian).
- Yakovleva E.V. Electrosupply of Prospecting Works with Use of Hybrid Power Stations. Mining Equipment and Electromechanics. 2013. N 3, p. 19-22 (in Russian).
- Limitovskiy A.M., Bashkurov A.Yu. Auxiliary power plants as an alternative energy cogeneration facilities mineral complex. Prospect and protection of mineral resources. 2019. N 9, p. 35-37 (in Russian).
- Bashkurov A.Yu. Optimization of centralized and localized energy supply of mineral exploration services customers. Mining Informational and Analytical Bulletin. 2015. N 2, p. 386-391 (in Russian).
- Titov S.V. Methods and techniques for reducing emissions from marine diesel power plants. Avtoref. dis. … d-ra tekhn. nauk. Novosibirsk: Sibirskii gosudarstvennyi universitet vodnogo transporta, 2022, p. 35 (in Russian).
- Heikkila J., Ingo S. Izmereniya vybrosov tverdykh chastits i otdelnykh komponentov otrabotavshikh gazov – metody i zadachi na budushchee. Dvigatelestroenie. 2017. N 4 (270), p. 46-52 (in Russian).
- Ntziachristos L., Saukko E., Ronkko T. et al. Vliyanie uslovii i metodiki probootbora na rezul'taty izmerenii tverdykh chastits sudovym dizelem. Dvigatelestroenie. 2017. N 4 (270), p. 53-61 (in Russian).
- Maksimov A. RES 2.0: New program for the development of “green” energy in Russia. Energy Policy. 2020. N 11 (153), p. 22-27 (in Russian). DOI: 10.46920/2409-5516_2020_11153_22
- Akhmetshin A.I. Ecological problems of Russian regions with oil&gas-oriented industry. Regional development management: problems, opportunities, and prospectives: Proceedings of the International scientific-practical conference with international attendance, 28 November 2018, Cheboksary, Russia. Cheboksary: Chuvashskii gosudarstvennyi pedagogicheskii universitet im. I.Ya.Yakovleva, 2018, p. 462-469 (in Russian).
- Lipina S.A. North-Caucasian region economic integration. Sovremennye proizvoditelnye sily. 2013. N 3, p. 67-75 (in Russian).
- Senkevich V.S. Features and results of drilling deep geochemical searches on the flanks of the Mulinskaya Depression (Trans-Baikal territory). Scientific and methodological foundations of forecasting, prospecting, and evaluation of deposits of diamonds, precious and non-ferrous metals: Collection of abstracts of the IX International Scientific and Practical Conference, April 17-19, 2019, Moscow, Russia. Moscow: Tsentralnyi nauchno-issledovatelskii geologorazvedochnyi institut tsvetnykh i blagorodnykh metallov, 2019, p. 195-196 (in Russian).
- Zaburayeva Kh.Sh. Geoecological basis of increasing efficiency of agricultural lands use (by the example of Chechen Republic). Theoretical and Applied Ecology. 2012. N 2, p. 79-84 (in Russian).
- Noskova E.V. Statistical features of wind speed dynamics in the Trans-Baikal territory. Zapiski Zabaikalskogo otdeleniya Russkogo geograficheskogo obshchestva. 2014. Iss. 133. Vol. 1, p. 131-138 (in Russian).
- Erofeeva A.A. Analysis natural systems Tobolsk, Uvatsky and Vagaysky districts as the reasons for the formation socio-economic relations. Regional Geosystems. 2021. Vol. 45. N 3, p. 316-327 (in Russian). DOI: 10.52575/2712-7443-2021-45-3-316-327
- Kosyanov V.A., Limitovsky A.M., Merkulov M.V., Golovin S.V. Increasing of effectiveness in combination energy-supply of decentralized geological objects in Arctic and utmost North environment. Proceedings of higher educational establishments. Geology and Exploration. 2014. N 4, p. 81-85 (in Russian).
- Yanpu Zhao, Changsheng Huang, Mengjie Zhang, Yang Cui. AOBLMOA: A Hybrid Biomimetic Optimization Algorithm for Numerical Optimization and Engineering Design Problems. Biomimetics. 2023. Vol. 8. Iss. 4. N 381. DOI: 10.3390/biomimetics8040381
- Rahman C.M., Rashid T.A., Alsadoon A. et al. A Survey on Dragonfly Algorithm and its Applications in Engineering. Evolutionary Intelligence. 2023. Vol. 16. Iss. 1, p. 1-21. DOI: 10.1007/s12065-021-00659-x
- Shukla N.K., Srivastava R., Mirjalili S. A Hybrid Dragonfly Algorithm for Efficiency Optimization of Induction Motors. Sensors. 2022. Vol. 22. Iss. 7. N 2594. DOI: 10.3390/s22072594
- Güven A.F., Yörükeren N., Tag-Eldin E., Samy M.M. Multi-Objective Optimization of an Islanded Green Energy System Utilizing Sophisticated Hybrid Metaheuristic Approach. IEEE Access. 2023. Vol. 11, p. 103044-103068. DOI: 10.1109/ACCESS.2023.3296589
- Ali S., Rehman A.U., Wadud Z. et al. Demand Response Program for Efficient Demand-Side Management in Smart Grid Considering Renewable Energy Sources. IEEE Access. 2022. Vol. 10, p. 53832-53853. DOI: 10.1109/ACCESS.2022.3174586
- Xingyu Jiang, Jiazhen Li, Yitao Lu, Guangdong Tia. Design of Reverse Logistics Network for Remanufacturing Waste Machine Tools Based on Multi-Objective Gray Wolf Optimization Algorithm. IEEE Access. 2020. Vol. 8, p. 141046-141056. DOI: 10.1109/ACCESS.2020.3011509
- Wei Zhang, Sai Zhang, Fengyan Wu, Yagang Wang. Path Planning of UAV Based on Improved Adaptive Grey Wolf Optimization Algorithm. IEEE Access. 2021. Vol. 9, p. 89400-89411. DOI: 10.3390/s22145232
- Guo M.W., Wang J.S., Zhu L.F., Guo S.S., Xie W. An Improved Grey Wolf Optimizer Based on Tracking and Seeking Modes to Solve Function Optimization Problems. IEEE Access. 2020. Vol. 8, p. 69861-69893. DOI: 10.1109/ACCESS.2020.2984321
- Shyh-Jier Huang, Xian-Zong Liu, Wei-Fu Su, Shu-Hsuan Yang. Application of Hybrid Firefly Algorithm for Sheath Loss Reduction of Underground Transmission Systems. IEEE Transactions on Power Delivery. 2013. Vol. 28. N 4, p. 2085-2092. DOI: 10.1109/TPWRD.2013.2265913
- Srinivasan B., Venkatesan R., Aljafari B. et al. A Novel Multicriteria Optimization Technique for VLSI Floorplanning Based on Hybridized Firefly and Ant Colony Systems. IEEE Access. 2023. Vol. 11, p. 14677-14692. DOI: 10.1109/ACCESS.2023.3244346
- Anbalagan A., Sundarsingh E.F., Ramalingam V.S. et al. Smart Dynamic Position Tracking Wearable for Geofencing in Marine Environment. IEEE Transactions on Instrumentation and Measurement. 2023. Vol. 72. N 8005109. DOI: 10.1109/TIM.2023.3311076
- Jimoh O.D., Ajao L.A., Adeleke O.O., Kolo S.S. A Vehicle Tracking System Using Greedy Forwarding Algorithms for Public Transportation in Urban Arterial. IEEE Access. 2020. Vol. 8, p. 191706-191725. DOI: 10.1109/ACCESS.2020.3031488
- Kerimov I.A., Bachaeva T.Kh., Vismuradov A.V., Daukaev A.A. Solid non-metallic minerals spreading on the Chechen Republic territory. Vestnik akademii nauk Chechenskoi Respubliki. 2015. N 3 (28), p. 103-112 (in Russian).
- Askhabova Kh.N., Ozdykhanov M.S., Soltamuradov G.D. Evaluation of the ecological state of the environment in the terri-tory of the Chechen Republic in 2017. Advances in Current Natural Sciences. 2019. N 1, p. 7-12 (in Russian).
- Solodovnikov A.Yu. Tyumen region geography: minerals and their use. Tyumen: TyumGU-Press, 2023, p. 352 (in Russian).
- Solodovnikov A.Yu. Mineral resources of the Vagaiskii district and their use. Gornye vedomosti. 2017. N 3 (151), p. 68-77 (in Russian).
- Barabasheva E.E., Bryljova M.S. On the question of forms concentrating of gold coals for example Transbaikal coalfields. Mining Informational and Analytical Bulletin. 2016. N 9, p. 194-203 (in Russian).
- Ahmed R., Sreeram V., Mishra Y., Arif M.D. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renewable and Sustainable Energy Reviews. 2020. Vol. 124. N 109792. DOI: 10.1016/j.rser.2020.109792
- Sergeev N.N., Matrenin P.V. A review of international experience in forecasting renewable energy generation using machine learning methods. iPolytech Journal. 2023. Vol. 27. N 2, p. 354-369 (in Russian). DOI: 10.21285/1814-3520-2023-2-354-369
- Nespoli A., Ogliari E., Leva S. et al. Day-Ahead Photovoltaic Forecasting: A Comparison of the Most Effective Techniques. Energies. 2019. Vol. 12. Iss. 9. N 1621. DOI: 10.3390/en12091621
- Wais P. Two and three-parameter Weibull distribution in available wind power analysis. Renewable Energy. 2017. Vol. 103, p. 15-29. DOI: 10.1016/j.renene.2016.10.041
- Wannakam K., Jiriwibhakorn S. Evaluation of Wind Energy Production Using Weibull Distribution and Artificial Neural Networks. 2018 International Conference on Engineering, Applied Sciences, and Technology, 4-7 July 2018, Phuket, Thailand. IEEE, 2018, p. 4. DOI: 10.1109/iceast.2018.8434474
- Simeng Cheng, Yimiao Xie, Zhan Shu et al. Effect of Different Solar Irradiance Parameters on Reliability Evaluation of the Grid. IOP Conference Series: Earth and Environmental Science. 2019. Vol. 300. Iss. 4. N 042115. DOI: 10.1088/1755-1315/300/4/042115
- Bramm A.M., Eroshenko S.A., Khalyasmaa A.I., Matrenin P.V. Grey Wolf Optimizer for RES Capacity Factor Maximiza-tion at the Placement Planning Stage. Mathematics. 2023. Vol. 11. Iss. 11. N 2545. DOI: 10.3390/math11112545
- Bramm A.M., Mazunina M.V. Effects of the Firefly Optimization Algorithm Hyperparameters on the Optimal Placement Problem Results of Renewables-Based Power Plants. 2023 Belarusian-Ural-Siberian Smart Energy Conference, 25-29 September 2023, Ekaterinburg, Russia. IEEE, 2023, p. 48-53. DOI: 10.1109/BUSSEC59406.2023.10296466
- Maria E., Budiman E., Haviliddin, Taruk M. Measure distance locating nearest public facilities using Haversine and Euclidean Methods. Journal of Physics: Conference Series. 2020. Vol. 1450. N 012080. DOI: 10.1088/1742-6596/1450/1/012080
