Методика определения погрешностей сегментированных GRID моделей открытых горных выработок, построенных по результатам аэрофотосъемки с беспилотного воздушного судна
Аннотация
Предложена методика построения цифровой модели рельефа по результатам аэрофотосъемки с беспилотного воздушного судна, основанная на разделении исходного облака точек на равные сегменты. Это позволяет, сделав допущение о линейном характере изменения высоты точек в отдельном сегменте, аппроксимировать их отдельными плоскостями. По рассеиванию точек относительно аппроксимирующих поверхностей были рассчитаны среднеквадратические погрешности моделей относительно исходных данных, что позволило выявить зависимость погрешности построения модели относительно размеров составляющих их сегментов, а также предложить метод фильтрации ячеек, содержащих выбросы относительно ожидаемой погрешности модели. Предлагаемая методика была апробирована на моделях трех горных объектов – известнякового карьера, отвала фосфогипса и торфяного разреза. Результаты эксперимента показали кратное уменьшение погрешности модели относительно стандартных DEM моделей, что обеспечивает требуемую точность, предъявляемую к горно-графической документации.
Введение
Разработка месторождений полезных ископаемых неразрывно связана с маркшейдерским обеспечением [1], которое включает инженерное сопровождение горных работ [2], наблюдение за геомеханическими процессами [3, 4], учет движения объемов полезного ископаемого [5], сбор, хранение и обобщение информации о пространственно-временных изменениях, происходящих как на земной поверхности, так и под землей [6]. Объединяет эти задачи понятие маркшейдерской съемки, включающее процессы инструментальных измерений, их математической обработки, и представление полученных данных в удобной для последующей работы форме [7, 8]. Последовательность выполняемых операций на каждом этапе должна обеспечивать строгий контроль качества получаемых, используемых и выдаваемых данных с возможностью локализации и фильтрации содержащих недопустимые погрешности (выбросы) [9].
Эмпирическое определение погрешностей основано на статистической оценке закономерностей рассеивания измерений. Необходимым условием при этом является наличие избыточных измерений, общее количество которых обеспечивает надежность формируемых таким образом оценок. Избыточные измерения формируются при определенных геометрических условиях, таких как равенство повторных измерений между собой или равенство нулю сумм приращений координат или высот в замкнутых полигонах [10]. При отсутствии избыточных измерений оценка точности становится возможна лишь в виде предположения, основывающегося на экстраполяции погрешностей измерений на результат, что позволяет получить лишь ожидаемые погрешности, а не найти фактические.
Большинство инженерных маркшейдерских съемок, которые направлены на геометрическое обеспечение горных работ, связанных с решением задач определения объемов добытой горной массы, построением маркшейдерской горно-графической документации, выносом проектных координат в натуру и т.д., не формируют достаточного объема избыточных измерений. В таком случае контроль качества работ требует дополнительных выборочных съемок, что, в свою очередь, допускает риск получения ложных выводов за счет экстраполяции результатов локальной проверки на всю работу в целом. Современные средства маркшейдерских измерений, примерами которых могут служить наземные и воздушные лазерно-сканирующие системы, беспилотные фотограмметрические системы, получили повсеместное внедрение [11, 12], поскольку позволяют минимизировать время выполнения полевых работ. Однако при всех своих преимуществах (скорости и полноте собираемых данных, безопасности выполнения работ) вопросы обработки получаемых данных, оценки их точности, сопоставления разновременных моделей и решение с их помощью инженерных горно-геологических задач до сих пор не найдены [13, 14].
Постановка проблемы
Высокая скорость съемки и полнота данных, получаемых средствами лазерно-сканирующих и фотограмметрических съемок, достигаются за счет автоматизации процесса измерений, которая может быть получена только при полном отсутствии априорного выбора конкретных объектов съемки, другими словами, пользователь может заранее указать лишь общую область съемки, а не отдельные интересующие его объекты. В результате формируемые этими системами массивы данных «облака точек» представляют собой набор координат, нерегулярно и случайно покрывающий объект съемки [15, 16].
Случайность данных дистанционного зондирования не позволяет выполнить прямое сравнение нескольких разновременных съемок, так как каждый раз точки будут по-новому размещаться на снимаемом объекте, не позволяя заранее однозначно предсказать фактическое содержание модели и требуя сбора избыточной информации для гарантии результата, поэтому объем данных может превышать десятки и сотни миллионов точек. Показательно, что такой объем информации лишь уменьшает случайность и дискретность модели, не решая проблему, подменяя ее трудностями с хранением, обработкой и передачей больших данных [17].
Если проблема случайности модели может быть экстенсивно снижена увеличением плотности точек, то проблема дискретности – нет. Какова бы ни была плотность сформированного облака, дискретные точки не в состоянии полностью заполнить все пространство модели. В свою очередь, одно из основных требований, предъявляемых к горно-графической документации, – возможность получения информации в любой точке, для чего необходимо интерполировать содержащиеся в облаке точки [18].
Данная задача решается путем построения цифровых моделей местности (ЦММ), вопросам создания которых посвящены научные работы [2, 11]. ЦММ в горном деле использовались при решении задач планирования и оценки запасов полезных ископаемых, моделирования геомеханических процессов [19] методами конечных элементов, оценки рисков экологических аварий [20].
Стандартным способом построения ЦММ для решения инженерных задач является интерполяция пространства между точками треугольными полигонами, вершины которых определяются по алгоритму Делоне или подобным ему. Такой алгоритм построения ЦММ эффективно работает для съемок, результат которых состоит из набора характерных точек местности, выбранных маркшейдером при проведения съемочных работ, исходя из его личного опыта и представления о форме рельефа. Выбранные специалистом точки образуют массив характерных точек рельефа, позволяющих выбрать структурные линии, формирующие модель, адекватную снимаемому рельефу [21].
Применение подобной процедуры к облакам точек высокой плотности не показывает высокой эффективности, поскольку объем получаемой полигональной модели удваивается относительно исходной из-за того, что она должна содержать в себе сведения не только о точках, но и об их связях между собой. Сама же модель останется нерегулярной и примет все погрешности исходных данных, не обладая при этом инструментами явной оценки точности составляющих ее полигонов и требуя дополнительных ресурсов для последующей работы [22]. Снижение требований к ресурсам, необходимым для обработки таких моделей, достигается в основном путем предварительного разряжения исходного облака точек, что в результате уменьшает и плотность результирующей модели. При этом, очевидно, снижаются подробность и информативность модели, а также обесценивается предварительно выполненная работа по определению положения удаленных из обработки точек [23].
Потенциальным способом нивелирования недостатков полигональных моделей является использование сегментированных GRID моделей, состоящих из набора равных по типу и размерам территориально сопряженных ячеек, упорядоченных в виде матрицы [24]. Регулярность получаемой модели делает ее более устойчивой к случайности распределения исходных точек в плане за счет того, что положение границ составляющих модель сегментов определяется размером ячейки и положением единственной начальной точки [25]. Весомым преимуществом такого подхода является также инвариантность итогового объема данных модели относительно исходного облака точек, которая достигается благодаря наполнению модели информацией путем создания в каждой ячейке атрибутов, обобщающих необходимые свойства попавших в ее границы точек [26].
Благодаря указанным преимуществам сегментированные модели нашли широкое применение в задачах по геодезии и картографии, а вопросы их создания и совершенствования не теряют актуальности и решаются учеными всего мира [27-29].
GRID модели используются в задачах по картографии [30], таксации лесов [31, 32] и общей связи с ГИС-системами. Однако, несмотря на многие явные преимущества сегментированных моделей, вопросы их использования для решения задач горного и маркшейдерского дела остаются не решенными [5]. Одним из фундаментальных препятствий к их внедрению в повседневную практику является отсутствие инструментов оценки их точности [33]. Оценка точности сегментированных моделей выполняется путем дополнительных измерений геодезическими средствами для выборочного контроля качества выполненных работ, но требует дополнительных затрат времени и средств [34].
Цель данной работы заключается в описании разработанного авторами метода оценки точности сегментированных моделей по их внутреннему наполнению, выявлении основных зависимостей формирования погрешностей сегментированных моделей и определении их оптимальных параметров применительно к решению задач в горном деле.
Методы
Стандартной формой хранения сегментированных ЦММ является DEM (Digital elevation model) формат, представляющий собой геопривязанное растровое изображение, в котором значения пикселей определяют среднюю высотную отметку в каждой ячейке [35]. Так как ни сам формат, ни программы, его создающие, не дают информации о качестве определения результирующих высотных отметок, авторским коллективом была разработана собственная программа, позволяющая рассчитывать сегментированные модели из облаков точек с сохранением информации о погрешностях аппроксимации точек в отдельных ячейках, а также рассчитывать на их основании общую среднеквадратическую погрешность всей модели в целом.
В качестве аппроксимирующих функций были рассмотрены два варианта:
- средняя отметка всех точек в ячейке (стандартная DEM модель);
- плоскость, задаваемая функцией вида Z= Ax + By + C; параметры A, B и C определялись по методу наименьших квадратов (авторская PLANE модель):
Среднеквадратическая погрешность аппроксимации точек в k-й ячейке может быть найдена по формуле
где – отметка, вычисленная по аппроксимирующей функции k-й ячейки в точке (xi, yi); zi– высотная отметка точки (xi, yi); nk – количество точек в k-й ячейке; rk–количество степеней свободы в k-й ячейке,определяемое в зависимостиот типа аппроксимирующей поверхности (rk = nk – 1 для средней отметки; rk = nk – 3 для плоскости).

Рис.1. Облака точек, исследуемых в работе объектов: а – известняковый карьер; б – отвал фосфогипса; в – торфяное месторождение
Общая среднеквадратическая погрешность модели может быть вычислена на основе среднеквадратических погрешностей аппроксимации отдельных ячеек (2) с учетом количества степеней свободы, участвующих в их определении:
где mk – среднеквадратическая погрешность аппроксимации в k-й ячейке; N – количество присутствующих в модели ячеек.
В качестве исследуемых выбраны три горных объекта, модели которых были получены фотограмметрическим способом, расчет облаков точек выполнялся в программе Agisoft Metashape (рис.1, таблица).
Основные характеристики исследуемых объектов
|
Параметр |
Известняковый карьер |
Отвал фосфогипса |
Торфяное месторождение |
|
Площадь, га |
41 |
159 |
28 |
|
Перепад высот, м |
132 |
112 |
23 |
|
Количество точек в исходной модели, тыс. точек |
11823 |
16242 |
5331 |
|
Объем модели (формат .asci), Мб |
956 |
529 |
365 |
|
Используемый БЛА |
DJI Phantom 3 PRO |
Autel Robotics EVO II Pro |
DJI Phantom 4 PRO |
|
Высота съемки, м |
100 |
150 |
150 |
|
Количество снимков, шт. |
127 |
1800 |
536 |
|
Размер матрицы, inch CMOS |
1/2,3 |
1 |
1 |
|
Разрешение снимков, Mpixels |
12,4 |
20 |
20 |
По каждому облаку точек были построены сегментированные модели с размером ячейки 1; 1,5; 2; 2,5; 5; 10; 15; 20; 25; 50 м, рассчитаны СКП (среднеквадратические погрешности) каждой ячейки (при положительном значении rk), найдены общие СКП моделей, а также построены карты распределения СКП внутри каждой модели.
Обсуждение результатов
Рассчитанные для каждого случая по формуле (3) среднеквадратические погрешности моделей представлены на графиках (рис.2).
При анализе полученных зависимостей видно, что погрешности DEM моделей одинаково ведут себя во всех рассматриваемых объектах, пропорционально уменьшаясь вместе с размером ячейки в модели. При этом для равных значений размеров ячеек в разных моделях достигаются разные значения СКП, возрастающие прямо пропорционально увеличению общего перепада высот в модели, приведенного в таблице. Средняя высотная отметка, использующаяся при построении DEM модели, не позволяет дать состоятельную оценку точкам в аппроксимируемой площади при наличии в ней негоризонтальных участков, погрешность результирующей высоты в ячейке прямо связана с величиной перепада высот внутри нее. Уменьшение размера ячейки снижает шанс большого перепада высоты, тем самым уменьшая погрешность модели в целом.
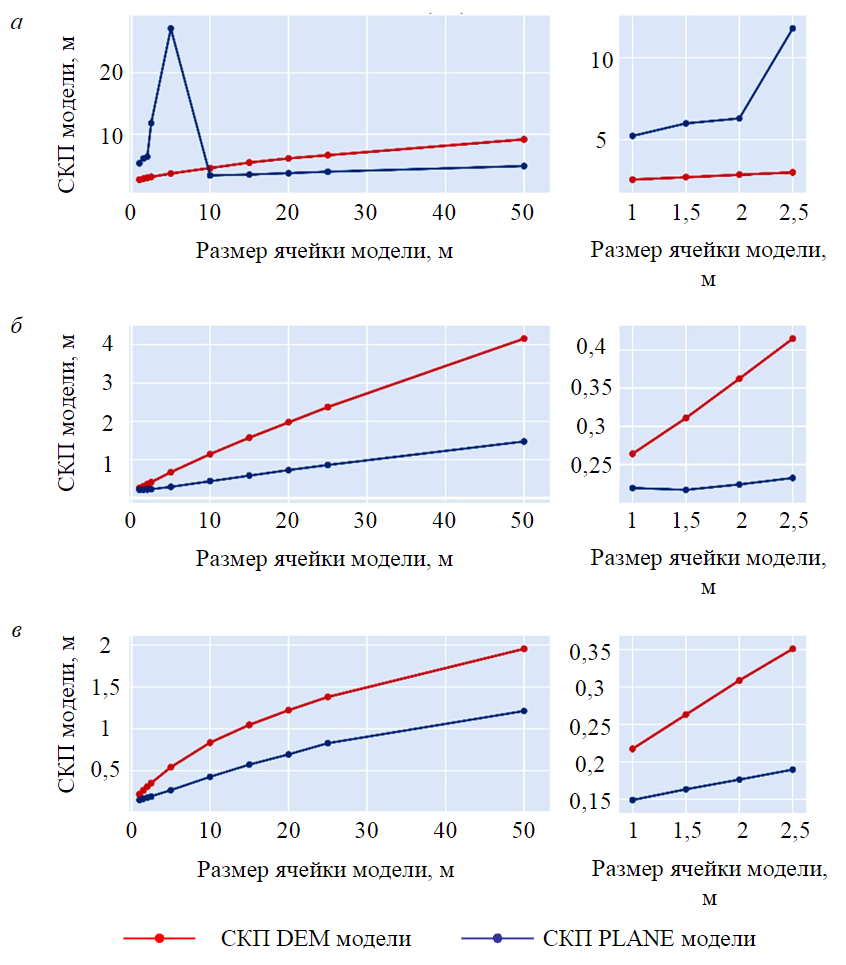
Рис.2. Зависимость СКП сегментированных моделей от размера ячейки модели для объектов: а – известняковый карьер; б – отвал фосфогипса; в – торфяное месторождение
Однако полученные для минимальных из рассмотренных размеров ячеек в один метр погрешности превышают значения, допустимые для маркшейдерских съемок. Формально, экстраполировав линейный характер погрешности модели, можно определить необходимый размер ячейки для каждого случая. Но в силу того, что количество ячеек в модели увеличивается относительно размера ячейки квадратично, такое решение приведет к лавинообразному увеличению объема общей модели, что повлечет за собой как проблемы с наполнением сформированных ячеек информацией, так и трудности с хранением, передачей и обработкой модели в целом.
Использование в качестве аппроксимирующей поверхности плоскости снижает влияние характера распределения высот внутри ячейки на погрешность модели в целом. Такой эффект достигается за счет того, что PLANE модель будет качественно повторять исходный набор данных в случае равномерного изменения высоты в рамках отдельной ячейки. При сопоставлении зависимости погрешности PLANE и DEM моделей видно, что, за исключением моделей известнякового карьера с размерами ячеек 1-5 м, выдвинутое предположение соответствует результатам эксперимента.
Выделенная аномалия выявляет основной недостаток PLANE модели – в случае аппроксимации рельефа, содержащего вертикальные участки, функция (1) может дать неопределенное значение, высотой отметки стремящееся к ±∞. Среднеквадратическая погрешность, рассчитываемая по формулам (2) и (3), в силу возведения в квадрат отклонений между отметками модели и точками облака чувствительна к наличию в исходных данных грубых результатов, поэтому может дать завышенное значение. На рис.3 представлены зависимости погрешностей модели с распределением погрешности отдельных ячеек в ней.
При анализе распределения погрешностей ячеек внутри модели видно, что выбросы в значениях погрешности PLANE модели с малыми размерами ячеек вызваны присутствием в выборке малочисленных ячеек с грубыми ошибками, превышающими в отдельных случаях сотни метров, что физически невозможно, исходя из фактического перепада высот внутри модели (см. таблицу). Ячеек с таким значением СКП при больших размерах ячеек нет, поскольку большая аппроксимируемая площадь внутри ячейки содержит помимо вертикально распределенных точек участки местности с более плоским рельефом, «выполаживающим» результирующую поверхность. Максимальная погрешность аппроксимации точек в ячейке при этом совпадает с максимальной погрешностью DEM модели. Постоянство результирующей отметки внутри ячейки DEM модели не позволяет ее СКП превысить некоторое пороговое значение, инвариантное к размеру ячейки модели и определяемое перепадом высот в самом исходном облаке точек.
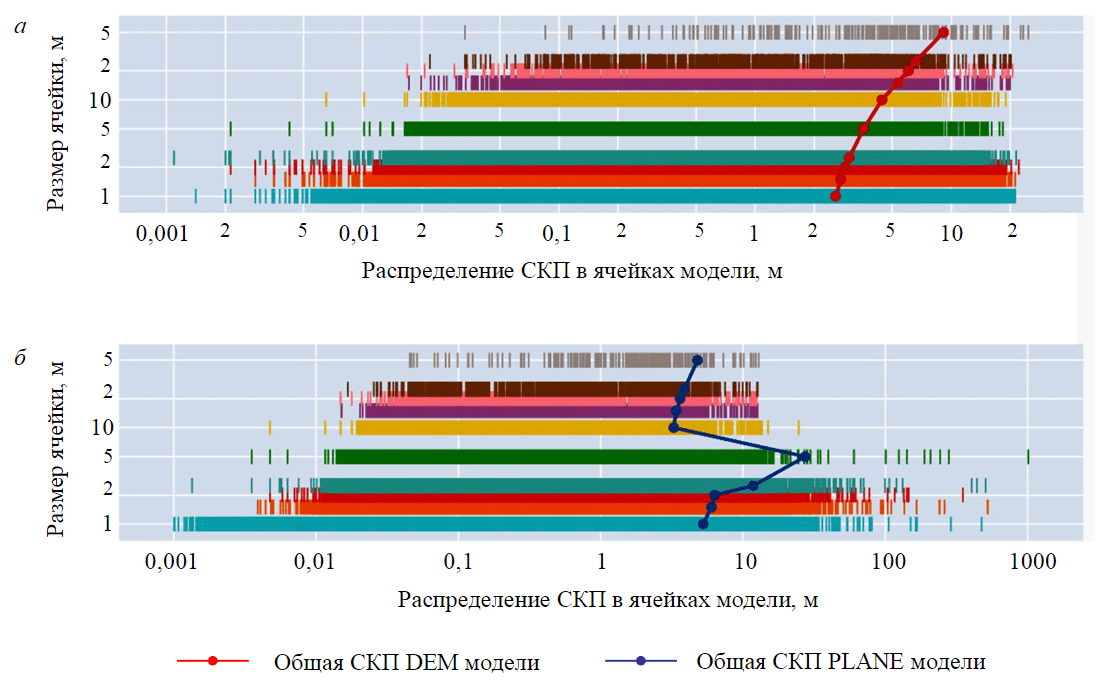
Рис.3. Распределение СКП отдельных ячеек внутри моделей: а – DEM модели; б – PLANE модели
Во всех рассматриваемых случаях как для DEM, так и для PLANE модели рассчитанное значение общей СКП модели смещено от медианного значения распределения погрешности отдельных, составляющих ее ячеек в большую сторону, что также является следствием грубых неустраненных погрешностей в отдельных ячейках модели.
Для исправления выявленного смещения были отфильтрованы ячейки, которые содержат значения СКП, выходящие за верхний предел статистически значимой выборки рассматриваемой модели:
где IQR – межквартильный размах (разница между квартилями выборки Q3 и Q1– значениями, разделяющими в упорядоченном ряду СКП ячеек модели первые 75 и 25 % от общего количества значений соответственно).
Выбор в пользу формулы (4) для определения допустимого значения СКП и отказ от других статистических критериев нахождения выбросов был сделан исходя из того, что общее распределение погрешностей отдельных сегментов внутри модели имеет существенную левостороннюю асимметрию, что видно на диаграммах рассеивания (рис.3). Применение формулы (4) дает большую устойчивость результатов в случае ненормального распределения случайной величины.
Значения общих СКП моделей после фильтрации представлены на рис.4. Графики показывают, что после фильтрации ячеек, содержащих выбросы, вид зависимости изменения СКП модели во всех случаях принимает плавный характер. При этом вид зависимости для каждого из рассмотренных объектов имеет некоторые характерные особенности, объяснимые индивидуальным распределением рельефа внутри сетки сегментированной модели. Следует обратить внимание на подобие формы кривых распределения погрешностей DEM и PLANE моделей в рамках каждого из рассмотренных объектов, а также на то, что СКП PLANE модели в 1,5-10 раз меньше относительно аналогичной DEM модели.
На рис.5 изображена карта распределения погрешности PLANE модели объекта «Известняковый карьер» после фильтрации. При визуальном анализе видно, что, даже несмотря на большой размер ячейки, доминирующая площадь модели определена с погрешностями, не превышающими 10 см, что отвечает требованиям, предъявляемым к горно-графической документации. Редкие значения, превышающие порог в 0,1 м, локализованы в участках рельефа, содержащих не типичные для основной модели объекты, например негабариты, обозначающие берму безопасности, вывалы на откосах, растительность, постройки в северной части карьера и т.д.
Заключение
Качество каждой модели, наравне с ее наполнением, является уникальным для каждого случая съемки. Общая погрешность модели складывается из набора отдельных слабо коррелирующих между собой факторов, определяющих качество внутреннего и внешнего ориентирования модели и погрешность измерений при съемке. Сложность определения и управления этими факторами на практике часто приводит к результатам непредсказуемого и неудовлетворительного качества, отчего возможность апостериорной оценки точности результирующей модели приобретает дополнительную ценность [17].
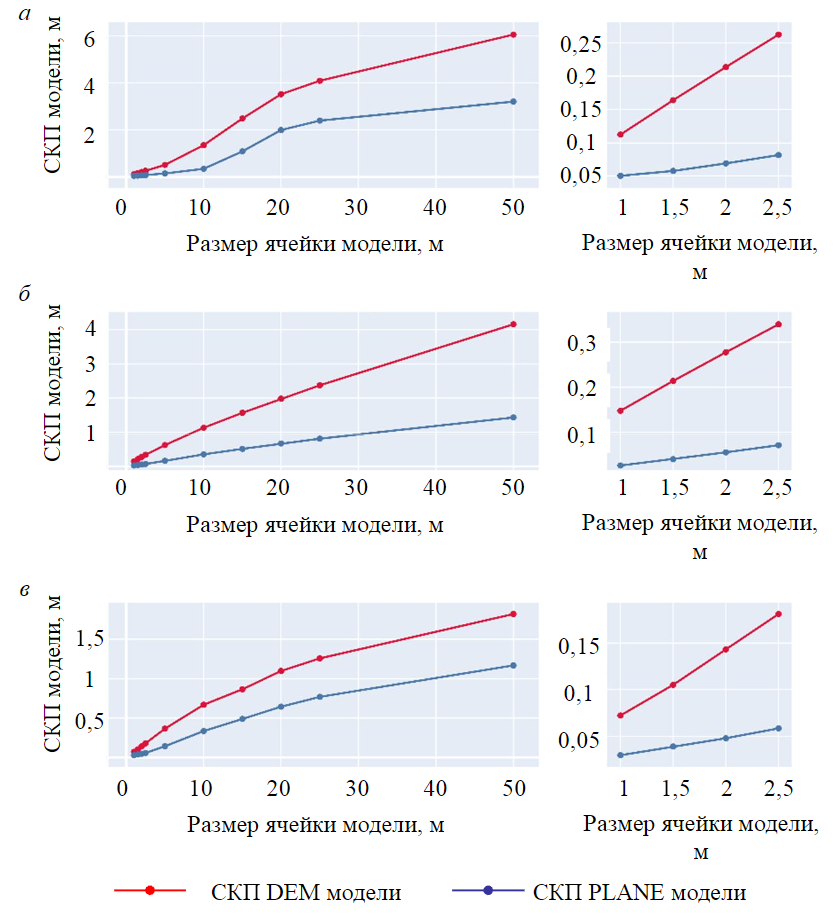
Рис.4. Зависимость СКП сегментированных моделей от размера ячейки модели после фильтрации для объектов: а – известняковый карьер; б – отвал фосфогипса; в – торфяное месторождение
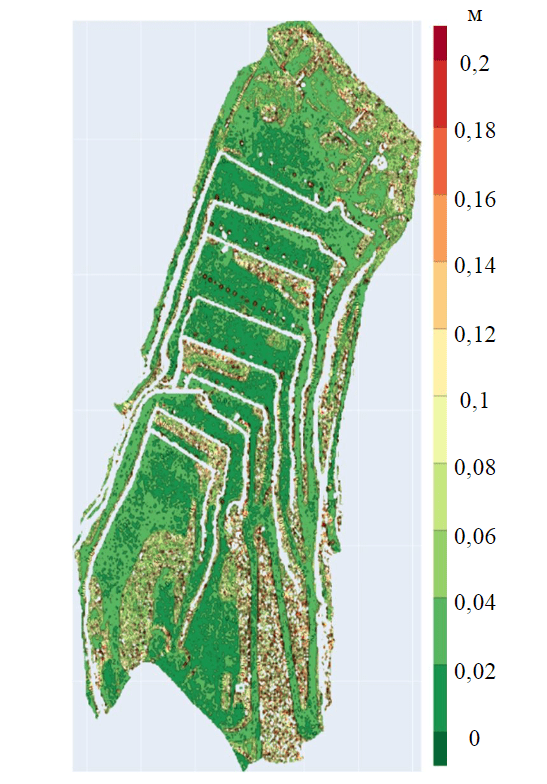
Рис.5. Распределение СКП ячеек внутри PLANE модели известнякового карьера при размере ячейки 2,5 м
Предлагаемый метод моделирования позволяет сопоставить каждый элемент с мерой его точности. Полученные в результате PLANE модели соответствуют по своей точности требованиям, предъявляемым к горно-графической документации, а порядок выполненного эксперимента и обработки его результатов можно рассматривать как инструмент комплексного анализа качества получаемых облаков точек.
Несмотря на то что полученные результаты исследования решают сформулированные во вводной части задачи, описанные подходы являются скорее инструментом, предоставляющим широкие возможности решения различных горно-технических задач. Объем данных в результате аппроксимации исходных облаков точек кратно уменьшился относительно исходного облака (в 100-300 раз для модели с размером ячейки в один метр и еще больших значений для ячеек большего размера). Все это позволяет в перспективе использовать получаемые модели не только для решения инженерных задач, но и для глубокого обучения нейронных сетей при прогнозе геодинамических проявлений, компьютерного зрения при беспилотном управлении горной техники и множества других задач.
Литература
- Цыгляну П.П., Ромашева Н.В., Фадеева М.Л., Петров И.В. Инжиниринговые проекты в топливно-энергетическом комплексе России: актуальные проблемы, факторы и рекомендации по развитию // Уголь. 2023. № 3. С. 45-51. DOI: 10.18796/0041-5790-2023-3-45-51
- Borisov M., Simić R., Petrović V.M., Milinčić M. Analiza kvaliteta 3D modela zasnovanih na digitalnoj fotogrametriji // Geodetski glasnik. 2021. Vol. 52. P. 5-26.
- Уразбаев Г.М., Алтаева А.А., Кожаев Ж.Т., Мустафин М.Г. Геодезический мониторинг за деформациями инженерных сооружений // Комплексное использование минерального сырья. 2021. Т. 317. № 2. С. 69-77. DOI: 10.31643/2021/6445.20
- Саблин М.В., Боргер Е.Б., Кутепов Ю.И. и др. Геомеханическое обоснование отработки свиты угольных пластов на шахте им. А.Д. Рубана под гидроотвалом открытых горных работ // Горный информационно-аналитический бюллетень. 2019. № 6. С. 124-135. DOI: 10.25018/0236-1493-2019-06-0-124-135
- Пономаренко М.Р., Кутепов Ю.И., Шабаров А.Н. Информационно-аналитическое обеспечение мониторинга состояния объектов открытых горных работ на базе технологий веб-картографии // Горный информационно-аналитический бюллетень. 2022. № 8. С. 56-70. DOI: 10.25018/0236_1493_2022_8_0_56
- Шокер Х.М., Мустафин М.Г. Геодезическое обеспечение использования технологии лазерного сканирования для фиксации памятников культурного наследия // Геодезия и картография. 2020. Т. 82. № 2. С. 2-10. DOI: 10.22389/0016-7126-2021-968-2-2-10
- Ferrero A.M., Migliazza M., Roncella R., Rabbi E. Rock slopes risk assessment based on advanced geostructural survey techniques // Landslides. 2011. Vol. 8. P. 221-231. DOI: 10.1007/s10346-010-0246-4
- Abellan A., Derron M.H., Jaboyedoff M. “Use of 3D Point Clouds in Geohazards” Special Issue: Current Challenges and Future Trends // Remote Sensing. 2016. Vol. 8. Iss. 2. № 130. DOI: 10.3390/rs8020130
- Мустафин М.Г., Нгуен В.Х. Оценка вертикальных смещений оснований зданий и сооружений на основе анализа элементов деформационной сети // Геодезия и картография. 2019. Т. 80. № 3. С. 11-19. DOI: 10.22389/0016-7126-2019-945-3-11-19
- Brigadnov I., Lutonin A., Bogdanova K. Error State Extended Kalman Filter Localization for Underground Mining Environments // Symmetry. 2023. Vol. 15. Iss. 2. № 344. DOI: 10.3390/sym15020344
- Кротенок А.Ю., Шурыгин Д.Н., Литовченко Т.В. и др. Фотограмметрическая обработка изображений на основе беспилотных летательных аппаратов и наземного лазерного сканирования при проектировании открытых горных работ // Горный информационно-аналитический бюллетень. 2017. № 12. С. 50-55. DOI: 10.25018/0236-1493-2017-12-0-50-55
- Бударова В.А., Мартынова Н.Г., Шереметинский А.В., Привалов А.В. Наземное лазерное сканирование объектов промышленных площадок на территории нефтегазовых месторождений // Московский экономический журнал. 2019. № 6. С. 8-14. DOI: 10.24411/2413-046X-2019-16004
- Пономаренко М.Р., Кутепов Ю.И., Волков М.А., Гринюк А.П. Космические методы в составе комплексного деформационного мониторинга земной поверхности горного предприятия // Горный информационно-аналитический бюллетень. 2020. № 12. С. 103-113. DOI: 10.25018/0236-1493-2020-12-0-103-113
- Samylovskaya E., Makhovikov A., Lutonin A. et al. Digital Technologies in Arctic Oil and Gas Resources Extraction: Global Trends and Russian Experience // Resources. 2022. Vol. 11. Iss. 3. № 29. DOI: 10.3390/resources11030029
- Чибуничев А.Г., Михайлов А.П., Старшов В.В. Автоматическое построение плотного облака точек по множеству снимков на основе полуглобального метода отождествления соответственных точек // Известия высших учебных заведений. Геодезия и аэрофотосъемка. 2015. № 2. С. 14-18.
- Rosnell T., Honkavaara E. Point Cloud Generation from Aerial Image Data Acquired by a Quadrocopter Type Micro Unmanned Aerial Vehicle and a Digital Still Camera // Sensors. 2012. Vol. 12. Iss. 1. P. 453-480. DOI: 10.3390/s120100453
- Гусев В.Н., Блищенко А.А., Санникова А.П. Исследование комплекса факторов, оказывающих влияние на погрешность реализации маркшейдерской съемки горных объектов с применением геодезического квадрокоптера // Записки Горного института. 2022. Т. 254. С. 173-179. DOI: 10.31897/PMI.2022.35
- Martino S., Mazzanti P. Integrating geomechanical surveys and remote sensing for sea cliff slope stability analysis: the Mt. Pucci case study (Italy) // Natural Hazards and Earth System Sciences. 2014. Vol. 14. Iss. 4. P. 831-848. DOI: 10.5194/nhess-14-831-2014
- Novozhenin S.U., Bogdanova K.A., Kempler A.K. Comparative analysis of modelling methods of the tunnel construction harmful effect // Journal of Physics: Conference Series. 2019. Vol. 1333. Iss. 3. № 032059. DOI: 10.1088/1742-6596/1333/3/032059
- Бригида В.С. Анализ данных для формирования пространственных геоэкологических моделей // Экология. Экономика. Информатика. Серия: Системный анализ и моделирование экономических и экологических систем. 2022. Т. 1. № 7. С. 108-114. DOI: 10.23885/2500-395X-2022-1-7-108-114
- Ghadi Y. 3D Modelling of Earth Kinematics in Palestine for GNSS and Geodetic Time-Dependent Positioning // International Journal of Recent Technology and Engineering. 2019. Vol. 8. Iss. 3. P. 6034-6039. DOI: 10.35940/ijrte.C5577.098319
- Riquelme A.J., Tomás R., Abellán A. Characterization of rock slopes through slope mass rating using 3D point clouds // International Journal of Rock Mechanics and Mining Sciences. 2016. Vol. 84. P. 165-176. DOI: 10.1016/j.ijrmms.2015.12.008
- Юнусов А.Г., Дждид А.Д., Бегляров Н.С., Елшеви М.А. Оценка влияния изменения плотности облака точек на точность автоматической сегментации // Геодезия и картография. 2020. Т. 81. № 7. С. 47-55. DOI: 10.22389/0016-7126-2020-961-7-47-55
- Chenlei Lv, Weisi Lin, Baoquan Zhao. Approximate Intrinsic Voxel Structure for Point Cloud Simplification // IEEE Transactions on Image Processing. 2021. Vol. 30. P. 7241-7255. DOI: 10.1109/TIP.2021.3104174
- Gezawa A.S., Bello Z.A., Qicong Wang, Lei Yunqi. A voxelized point clouds representation for object classification and segmentation on 3D data // Journal of Supercomputing. 2022. Vol. 78. P. 1479-1500. DOI: 10.1007/s11227-021-03899-x
- Li Pengfei, Zhang Xiaochen, Yan Lu et al. Comparison of interpolation algorithms for DEMs in topographically complex areas using airborne LiDAR point clouds // Transactions of the Chinese Society of Agricultural Engineering. 2021. Vol. 37. № 15. P. 146-153. DOI: 10.11975/j.issn.1002-6819.2021.15.018
- Вальков В.А., Виноградов К.П., Валькова Е.О., Мустафин М.Г. Создание растров высокой информативности по данным лазерного сканирования и аэрофотосъемки // Геодезия и картография. 2022. Т. 83. № 11. С. 40-49. DOI: 10.22389/0016-7126-989-11-40-49
- Donnellan A., Parker J., Heflin M. et al. Improving access to geodetic imaging crustal deformation data using GeoGateway // Earth Science Informatics. 2022. Vol. 15. Iss. 3. P. 1513-1525. DOI: 10.1007/s12145-020-00561-7
- Liang He, Junru Zhang, Suozhong Chen et al. Three-dimensional hydrogeological modeling method and application based on TIN-GTP-TEN // Earth Science Informatics. 2022. Vol. 15. Iss. 1. P. 337-350. DOI: 10.1007/s12145-021-00727-x
- Yong Li, Yinzheng Luo, Xia Gu et al. Point Cloud Classification Algorithm Based on the Fusion of the Local Binary Pattern Features and Structural Features of Voxels // Remote Sensing. 2021. Vol. 13. Iss. 16. № 3156. DOI: 10.3390/rs13163156
- Lingchen Lin, Kunyong Yu, Xiong Yao et al. UAV Based Estimation of Forest Leaf Area Index (LAI) through Oblique Photogrammetry // Remote Sensing. 2021. Vol. 13. Iss. 4. № 803. DOI: 10.3390/rs13040803
- Блищенко А.А., Санникова А.П. Применение беспилотных летательных аппаратов при маркшейдерском обеспечении съемки лесного фонда // Вестник СГУГиТ. 2022. Т. 27. № 1. С. 42-51. DOI: 10.33764/2411-1759-2022-27-1-42-51
- Санникова А.П., Добрянский И.А., Волошина Е.А. Проблемы современного маркшейдерско-геодезического обеспечения открытых горных работ // Естественные и технические науки. 2022. № 4 (167). С. 91-94. DOI: 10.25633/ETN.2022.04.10
- Курков В.М., Киселева А.С., Чибуничев А.Г. Исследование точности цифровой модели рельефа, построенной по материалам беспилотной аэрофотосъемки и воздушного лазерного сканирования // Производственные системы будущего: опыт внедрения Lean и экологических решений: Материалы международной научно-практической конференции, 13-14 апреля 2022, Кемерово, Россия. Кемерово: Кузбасский государственный технический университет имени Т.Ф.Горбачева, 2022. С. 309.1-309.9.
- Boliang Guan, Shujin Lin, Ruomei Wang et al. Voxel-based quadrilateral mesh generation from point cloud // Multimedia Tools and Applications. 2020. Vol. 79. Iss. 29-30. P. 20561-20578. DOI: 10.1007/s11042-020-08923-5
