Комплексная модель регулируемого электропривода ротора буровой установки
- 1 — д-р техн. наук профессор РГУ нефти и газа (НИУ) имени И.М.Губкина ▪ Orcid
- 2 — канд. техн. наук заведующий кафедрой РГУ нефти и газа (НИУ) имени И.М.Губкина ▪ Orcid
- 3 — студент РГУ нефти и газа (НИУ) имени И.М.Губкина ▪ Orcid
Аннотация
Рассмотрена и реализована модифицированная математическая модель асинхронный электропривод ротора – колонна бурильных труб – долото – горная порода, развивающая и обобщающая результаты ранее выполненных исследований. Модель включает следующие подсистемы: модель асинхронного привода с векторным управлением; модель формирования момента сопротивления на забое долота, учитывающую особенности взаимодействия долота и породы; модель многомассовой механической части, учитывающую деформацию колонны бурильных труб; подсистему формирования энерготехнологических параметров буровой установки. Комплексная модель позволяет рассчитать и оценить выбранные режимы бурения с учетом их электромеханической, энергетической и технологической эффективности и динамики процессов бурения. Выполненное компьютерное моделирование режимов бурения подтвердило возможность возникновения stick-slip-эффекта, сопровождаемого высокочастотными вибрациями при остановках долота, при которых возможно изменение направления вращения долота, его ускоренный износ и отвинчивание бурового инструмента. Длительные остановки долота приводят к существенному снижению средней скорости вращения долота, чем можно объяснить снижение механической скорости бурения и повышение энергозатрат при бурении в зоне неустойчивого вращения долота. Модель может быть использована как базовая для дальнейшего совершенствования систем управления роторным бурением.
Введение
Электропривод ротора буровой установки отличается сложной механической частью (рис.1). Вращение ротора двигателя через передаточное устройство передается на ротор буровой установки и через колонку бурильных труб (КБТ) – на долото. Под действием момента ротора буровой установки, приложенного к верху колонны, и момента сопротивления долота, приложенного к низу колонны, бурильные трубы деформируются и закручиваются на некоторый угол, значение которого зависит от длины, диаметра и упругих свойств колонны и может достигать десятков оборотов. В процессе бурения угол закручивания может оставаться практически неизменным, при этом осуществляется равномерное вращение долота. При изменении в процессе бурения угла закручивания возникает неравномерное неустойчивое вращение долота (stick-slip-эффект) с длительными остановками, погружениями в породу и срывами долота, а также появлением крутильных и продольных автоколебаний бурового инструмента [1]. Особенно часто (более 50 % времени бурения) такой режим возникает при работе с PDC-долотами режуще-истирающего типа. Режимы неустойчивого вращения долота могут превалировать в процессе бурения скважин [2, 3], снижая энергетическую эффективность бурения и ускоряя износ бурового инструмента [4, 5]. Задача данной работы заключается в создании комплексной модели буровой установки асинхронный электропривод ротора – колонна бурильных труб – долото – горная порода, имитирующей основные процессы электроприводного роторного бурения, с набором характеристик для анализа электромеханической, энергетической и технологической эффективностей режимов бурения. Итоги работы развивают результаты ранее выполненных исследований [6-8].
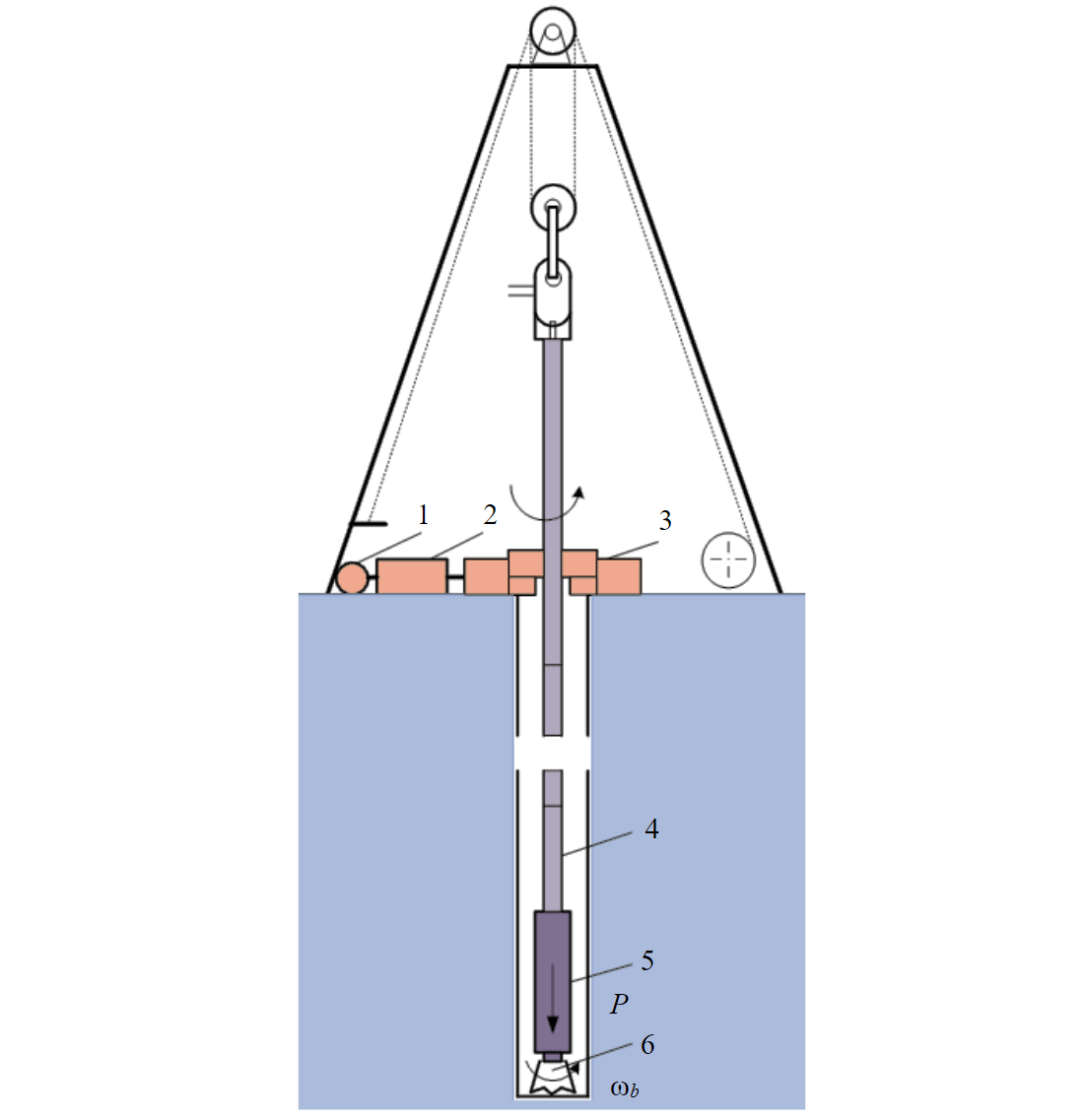
Рис.1. Схема буровой установки 1 – привод ротора; 2 – передаточные устройства, 3 – ротор буровой установки; 4 – колонна бурильных труб; 5 – компоновка низа колонны; 6 – долото
Методология
Моделирование асинхронного электропривода буровой установки осуществлялось в среде Matlab Simulink. Структурная схема базовой модели представлена на рис.2. Модель включает следующие основные подсистемы: IM-Sub-system – модель асинхронного двигателя с векторной системой управления на базе PI регуляторов потокосцепления, скорости и тока; Meh-Subsystem – модель механической части электропривода, включающая ротор двигателя, ротор буровой установки, механизмы передачи и колонну бурильных труб; двухмассовая модель механической части привода ротора БУ представлена на рис.3; Tb0-Subsystem, Tb1-Subsystem, Tb-Sub-system – подсистемы модели момента сопротивления на долоте; ETP-Subsystem – подсистема формирования энерготехнологических параметров бурения.
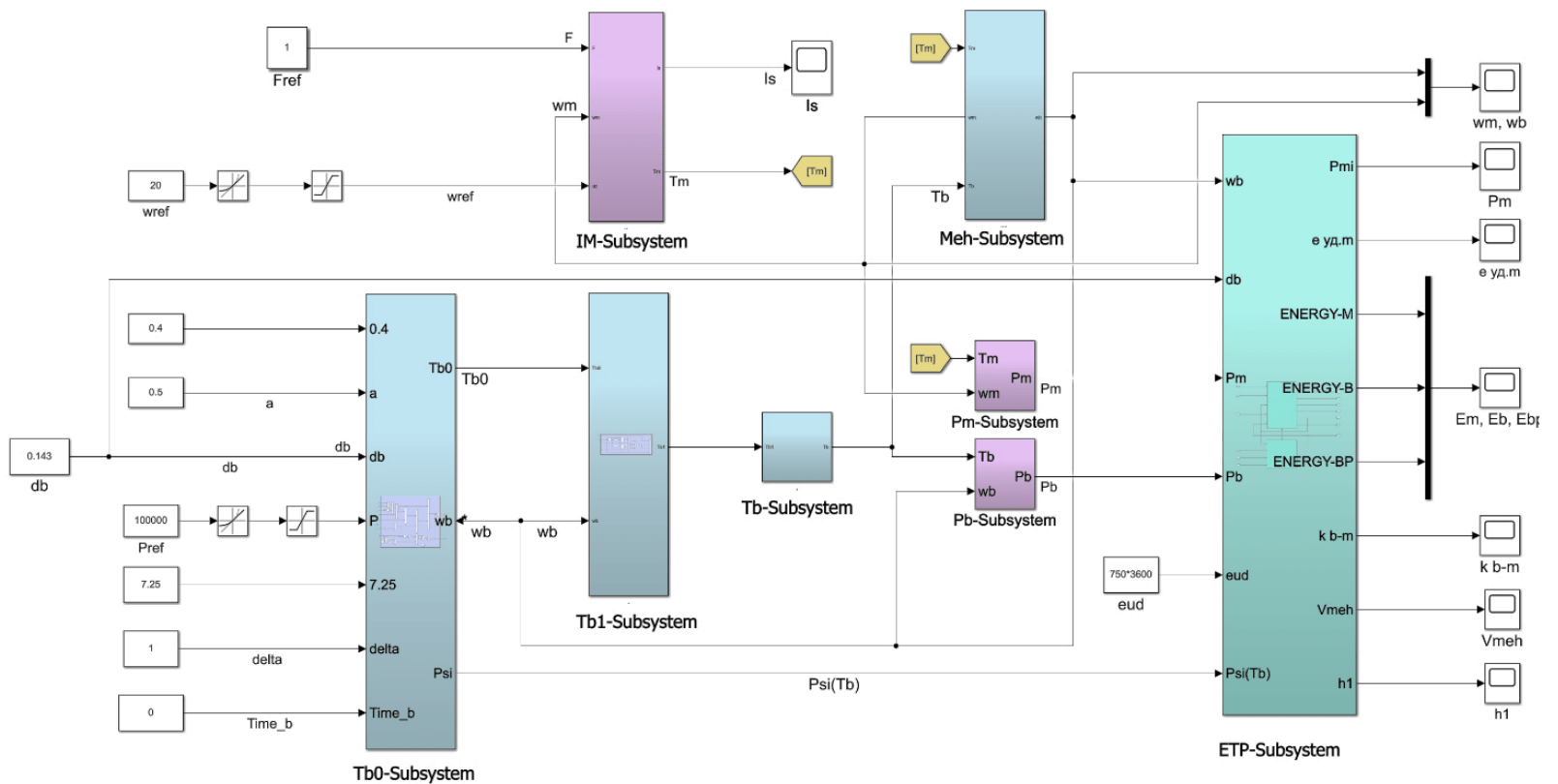
Рис.2. Структурная схема асинхронного привода ротора буровой установки

Рис.3. Двухмассовая модель механической части привода ротора
Основные номинальные параметры асинхронного двигателя привода ротора серии AFD составляют следующие: мощность 1000 кВт; напряжение 660 В; ток 1075 А; момент 9620 Н·м; частота вращения 993 об/мин.
«Моделирование двигателя осуществлялось в координатах (х, у), скорость вращения которых равна скорости вращения поля статора (ωк = ω1), с базовым вектором напряжения (uSx = U1; uSy = 0)» [7].Математическая модель двигателя представлена следующей системой уравнений в операторном виде*:
где ω1 = 104,7 c–1 – синхронная скорость; p = 3 – число пар полюсов ; ωm – скорость вала двигателя; ψRx, ψRy – потокосцепления ротора по осям x, y; ψSx, ψSy – потокосцепления статора по осям x, y; iRx, iRy – токи ротора по осям x, y; iSx, iSy – токи статора по осям x, y; Tm – момент двигателя; s – оператор; RR, RS – активные сопротивления ротора и статора; Lm, LR, LS – взаимная и собственные индуктивности ротора и статора; TR = LR/RR – постоянная времени ротора; T'S=L'S/r – постоянная времени статора; r = RS + k2rRR; kr = Lm/LR; L'S= LS –Lm2/LR.
Параметры, входящие в уравнения системы (1), следующие: RR = 0,00267 Ом; r = 0,939 Ом; kr = 0,939; L'S= 0,00034 Гн; T'S= 0,068 с; ТR = 1,064 с.
Определение параметров двигателя – активных сопротивлений, индуктивностей и постоянных времени, а также параметров PI-регуляторов – осуществлялось по следующим методикам [8-10]. При параллельной форме записи выражения передаточной функции параметры PI-регулятора потокосцепления составили Рψ = 410, Iψ = 14. Параметры PI-регуляторов скорости и тока,настроенные на технический оптимум, составили: Рω = 166, Iω = 16,5 (для регулятора скорости) и PI = 3, II = 10 (для регулятора тока).
Механическая часть электропривода реализована в виде многомассовых (от двух до четырех масс) эквивалентных систем в блоке Meh-Subsystem. Исходные данные для моделирования соответствуют буровой установке типа БУ-5000/320. Длина колонны бурильных труб принята равной 3000 м, диаметр труб dt = 0,127 (толщина стенки 0,09 м), компоновка низа КБТ выполнена из труб УБТ 203×80 (90 м), диаметр долота dt = 0,295 м (PDC долото 295,3FD257M-A27). Математическая модель двухмассовой механической системы в операторном виде представлена следующей системой уравнений:
где ωb(t) – скорость вращения долота, рад/с; Tr1 – момент сопротивления первой массы, Н·м; Tb – момент сопротивления, приложенный ко второй массе (момент на долоте), Н·м; Tr1 – момент сопротивления первой массы, определяющийся произведением коэффициента внешнего вязкого трения a на скорость вращения двигателя ωm.
Расчетные моменты инерции элементов двухмассовой системы: J1 = 66,5, J2 = 12,5 кг·м2; коэффициент жесткости с12 = 22,8 Н·м/рад; коэффициент вязкого трения β12 = 0,06 Н·м·с/рад; коэффициент внешнего вязкого трения α = 0,5 Н·м·с/рад.
Составление операторных уравнений трех- и четырехмассовой системы также не вызывает трудностей. Расчетные моменты инерции элементов трехмассовой системы: J1 = 55, J2 = 17, J3 = 7 кг·м2; коэффициенты жесткости с12 = 25, с23 = 263 Н·м/рад; коэффициенты вязкого трения: β12 = β23 = 0,03 Н·м·с/рад. Расчетные моменты инерции элементов четырехмассовой системы: J1 = 55, J2 = 8,5, J3 = 8,5 кг·м2; коэффициенты жесткости с12 = 50, с23 = 50, с34 = 263 Н·м/рад; коэффициенты вязкого трения β12 = β23 = β34 = 0,02 Н·м·с/рад. Все параметры механической системы приведены к скорости вращения двигателя.
Определение момента Tb реализовано в трех блоках: Tb0-Subsystem; Tb1-Subsystem и Tb-Subsystem. Моделирование момента сопротивления долота осуществляется в блоке Tb0-Subsystem по следующему выражению [1]:
где a – эмпирический коэффициент; P – осевая нагрузка на долото, Н; ωb(t) – скорость вращения долота, рад/с; δ0 = 1 – поправка, рад/с; ψ(tb) – функция, учитывающая изменение момента в процессе бурения по мере износа долота за время наработки tb, ч.
Определение параметров осуществлялось с учетом сопротивления горных пород разрушению при бурении скважин [11, 12].
Согласно источнику [1], функция ψ(tb) может быть представлена следующей зависимостью:
Максимальная осевая нагрузка на долото при моделировании может достигать P = 200 кН; значение эмпирического коэффициента для мягких пород а = 1, для твердых пород а = 0,5; максимальная скорость вращения долота ωb = 21 рад/с (200 об/мин).
Переход от статического момента сопротивления Tb0(t) к моменту Tb(t), учитывающему фрикционные изменения момента при переходе через ноль, осуществляется в блоке Tb1-Subsystem (согласно модели Штрибека [13, 14]):
где r = 1signωb; |ωb| > 0,001; r = 1,1signωb, |ωb| £ 0,001.
В подсистеме Tb-Subsystem учитывается наличие в колонне бурильных труб не только крутильных, но и продольных колебаний, изменяющих в процессе бурения осевую нагрузку на долото; моделирование таких колебаний осуществлялось по гармоническому закону [15]. Формула для определения результирующего момента сопротивления на долоте имеет вид [8]
где h – коэффициент, принимающий значение от 0 до 1; v – угловая частота продольных колебаний, соответствующих значениям от 0,5 до 3 Гц; ξ(t) – функция белого шума для учета продольных случайных колебаний с амплитудным значением 3 кН·м.
Вычисление мгновенной (в момент времени t) мощности на валу двигателя Pm(t) и мощности на долоте Pb(t) осуществляется, исходя из значений моментов Tm(t), Tb(t) и скоростей ωm(t), ωb(t) в блоках Pm-Subsystem и Pb-Subsystem:
В блоке ETP-Subsystem вычисляются энергетические и технологические параметры буровой установки. Общий расход энергии электропривода и энергия на долоте за время бурения T определяются следующими выражениями:
Отношение затрат энергии на долоте и на двигателе определяет коэффициент эффективности использования электроэнергии привода
Энергетические и технологические характеристики связаны через показатели удельной энергоемкости различных пород – Mechanical specific energy (MSE) [16, 17]. Согласно данным энергокаротажа, которые могут входить в современные геолого-технологические исследования, значения удельного энергопотребления на разрушение горной породы (табл.1) в зависимости от класса энергоемкости породы могут изменяться от нескольких единиц до нескольких тысяч кВт·ч/м3 [18]. Данные по удельным еуд (MSE) и общим Еb(t) затратам энергии на долоте позволяют определить механическую скорость бурения Rate of penetration (ROP)
где Fb – площадь долота, м2; среднее значение мощности на долоте (интегральная оценка за время T), кВт.
Таблица 1
Показатели энергоемкости бурения [18]
|
Класс породы |
Энергоемкость |
Удельное энергопотреблениееуд, кВт·ч/м3 |
|
IIIIII |
Низкая |
До 15,615,6-31,231,2-62,5 |
|
IVV |
Малая |
62,5-125125-250 |
|
VIVII |
Средняя |
250-500500-1000 |
|
VIIIIX |
Повышенная |
1000-20002000-4000 |
|
Х |
Высокая |
Свыше 4000 |
Значение механической скорости бурения позволяет определить другой характерный показатель роторного бурения – углубку за один оборот долота
где k = π/1800 – коэффициент размерности.
В бурении используется и величина, обратная h1, называемая Rate of penetration index (RPI).
Наряду с удельными энергозатратами на долоте, необходимыми для разрушения породы, предлагается ввести показатель общих удельных затрат электропривода ротора
где среднее значение мощности электропривода (интегральная оценка за время T), кВт.
Энергия электропривода включает энергию на долоте, а также энергию, затрачиваемую на холостое вращение КБТ, и потери энергии на трение, в том числе на трение колонны о стенки скважины. Поэтому общие удельные затраты электроэнергии на бурение значительно превышают удельные энергозатраты на разрушение породы еуд.m? еуд. При этом параметр еуд.m проще определить на практике в процессе бурения.
Таким образом предложена модифицированная комплексная модель асинхронный электропривод ротора – колонна бурильных труб – долото – горная порода. Модель представляет собой нелинейную систему с обратными связями, что обусловливает возможность появления автоколебаний в системе [19, 20]. Основными входными параметрами модели являются нагрузка на долото Pref (Weight on bit – WOB) и скорость вращения nref , об/мин (Revolution per minute – RPM) [21-24], а выходными – электромеханические параметры привода (скорости, моменты, токи, мощности), а также энергетические и технологические характеристики буровой установки [18, 25-28]. Сочетание параметров (WOB×RPM) определяет режимы бурения, а выходные параметры позволяют оценить выбранные режимы бурения с позиций их электромеханической, энергетической и технологической эффективности и с учетом динамики процессов бурения [29-31].
Обсуждение результатов
Некоторые результаты моделирования для указанной буровой установки, исходные данные и режимы бурения представлены в табл.2.
Таблица 2
Результаты моделирования режимов электроприводного роторного бурения
|
Номеррежима |
Параметры |
||||||
|
WOB×RPM,кН·об/мин |
Pm, кВт |
Pb, кВт |
Kb – m |
vmeh, м/ч |
h1, мм/об |
еуд.m, кВт·ч/м3 |
|
|
1 |
20×20 |
30,2 |
2,3 |
0,078 |
0,07 |
0,10 |
6237 |
|
2 |
40×30 |
59,8 |
5,5 |
0,096 |
0,17 |
0,14 |
5073 |
|
3 |
80×50 |
143,1 |
15,3 |
0,108 |
0,45 |
0,21 |
4491 |
|
4 |
120×70 |
255,1 |
29,8 |
0,117 |
1,25 |
0,27 |
4116 |
|
5 |
160×90 |
374,4 |
45,8 |
0,123 |
1,33 |
0,30 |
3933 |
|
6 |
200×110 |
523,2 |
65,3 |
0,125 |
1,90 |
0,34 |
3857 |
|
7 |
20×70 |
103,3 |
12,7 |
0,123 |
0,38 |
0,08 |
3919 |
|
8 |
60×90 |
198,1 |
26,3 |
0,133 |
0,77 |
0,14 |
3625 |
|
9 |
100×110 |
313,6 |
42,9 |
0,137 |
1,26 |
0,18 |
3525 |
|
10 |
120×130 |
450,4 |
62,4 |
0,139 |
1,83 |
0,23 |
3474 |
|
11 |
180×150 |
603,0 |
84,8 |
0,141 |
2,49 |
0,27 |
3426 |
|
12 |
20×120 |
202,4 |
21,6 |
0,107 |
0,63 |
0,08 |
4521 |
|
13 |
40×130 |
265,3 |
30,4 |
0,115 |
0,89 |
0,10 |
4199 |
|
14 |
80×150 |
396,0 |
50,1 |
0,127 |
1,47 |
0,15 |
3805 |
|
15 |
120×170 |
547,0 |
72,6 |
0,133 |
2,13 |
0,19 |
3621 |
|
16 |
120×30 |
82,0 |
5,1 |
0,062 |
0,14 |
0,21 |
7816 |
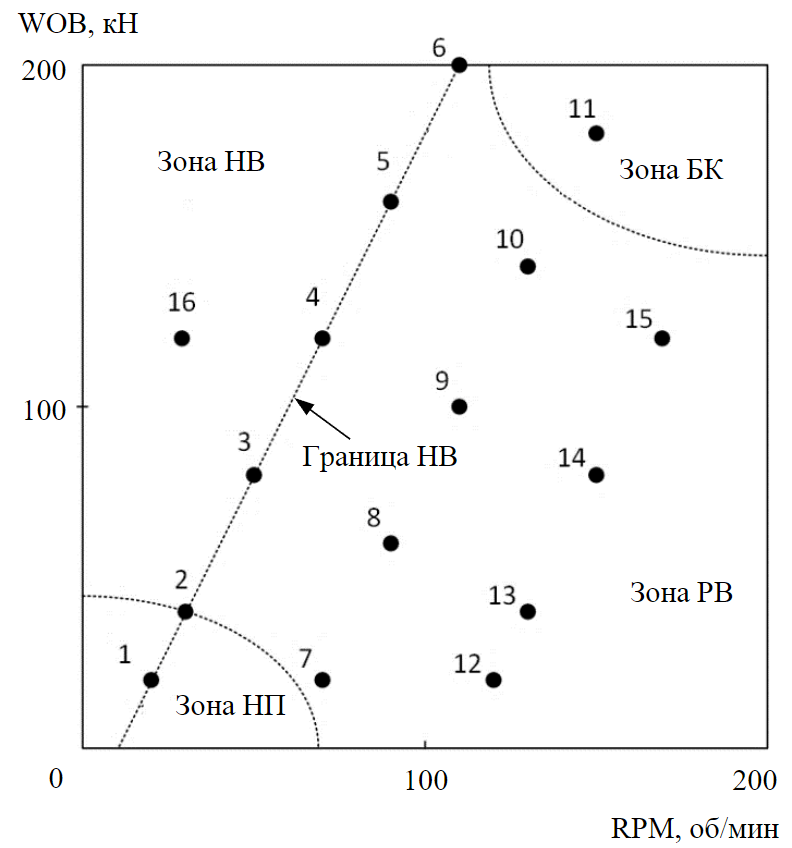
Рис.4. Режимы роторного бурения НВ – неравномерное вращение долота; РВ – равномерное вращение долота; НП – недостаточные параметры; БК – боковые кручения

Рис.5. Графики скорости ротора (1) и долота (2) в режиме 16 неравномерного вращения долота с длительными остановками (а) и в режиме 9 равномерного вращения (б)
Одной из основных задач при выполнении буровых работ является анализ режимов бурения в координатах (WOB×RPM) [32-35]. Первые шесть режимов относятся к режимам неустойчивого вращения долота и, как показано на рис.4, в координатах (WOB×RPM) отделяют зону равномерного вращения долота от зоны неравномерного вращения с длительными остановками. В рассмотренных режимах отмечается невысокий уровень механической скорости бурения, что объясняется большим диаметром долота и достаточно высокой энергоемкостью породы VII класса (принято 750 кВт·ч/м3). Для долота диаметром 0,128 м при бурении пород II-III классов энергоемкости механическая скорость бурения достигает нескольких десятков метров в час. Приведенные значения углубки долота достаточно большие, в литературе можно встретить более низкие значения ограничения углубки, но при этом расчет ведут на оборот ротора двигателя, а не долота, отношение которых определяется передаточным отношением.
На основании анализа режимов (1-15) можно заключить, что по энерготехнологическим характеристикам трудно выделить режимы неравномерного вращения (НВ) долота, если они близки к зоне равномерного вращения (РВ). Так, по всем характеристикам режимы 4 (на границе зон) и 9 (внутри зоны РВ) близки. Чем больше удален режим НВ от зоны РВ, например, режим 16, тем легче по приведенным характеристикам установить факт неустойчивого вращения долота. Для режимов внутри зоны НВ характерно явное снижение механической скорости бурения ROP и повышение уровня энергозатрат. Графики скорости долота и ротора буровой установки для режима 16 представлены на рис.5, а. Для сравнения на рис.5, б приведены графики скорости долота и ротора для режима равномерного вращения долота в точке 9, в котором колебания скорости долота значительно меньше и отсутствуют остановки долота. Отметим, что в обоих случаях пуск двигателя привода осуществлялся без нагрузки, при отключенной муфте между двигателем и ротором буровой установки и с плавным нарастанием заданной скорости. Длительные остановки долота приводят к существенному снижению средней скорости долота, чем можно объяснить снижение механической скорости бурения и повышение энергозатрат при бурении в зоне НВ. В процессе бурения происходит износ долота, что, согласно уравнению (2), влияет на момент сопротивления долота, при этом граница зоны неравномерного вращения долота перемещается вправо, увеличивая площадь зоны НВ долота. С другой стороны, на величину зоны неравномерного вращения влияет и диаметр долота, при его уменьшении граница зоны неравномерного вращения долота смещается влево, уменьшая площадь зоны НВ долота.
Наряду с зонами равномерного и неравномерного вращения долота на рис.4 выделена зона недостаточных параметров бурения НП (insufficient parameters) [20], при работе в которой бурение неэффективно из-за низкого ROP. Зона РВ также может быть разделена, в верхней ее части (режим 11) механическая скорость бурения максимальна, но при этом происходит ускоренный износ долота и возникает режим ударов колонны по стенке скважины – боковые колебания (backward whirl) [21].
В режимах неустойчивого неравномерного вращения долота, как видно из рис.5, а, имеют место остановки долота длительностью в несколько секунд. В режимах 1-6 на границе неравномерного вращения остановки минимальны и увеличиваются по мере удаления рабочей точки вглубь зоны НВ, достигая десятка секунд. При увеличении масштаба рисунка видно, что на интервалах остановки процесс изменения скорости затухает [9]. Как показано на рис.6, а скорость «замирает» от небольших положительных и отрицательных начальных значений, стремясь к нулю. Имеют место высокочастотные колебания (до 3000 Гц) – крутильная вибрация, снижающая ресурс долота. Пересчет высокочастотных колебаний скорости в ускорения позволил получить кривую вибрации в принятых в бурении единицах измерения – шоках. Расчетный график вибрации долота, представленный на рис.6, б, подтверждает на практике возможность возникновения опасных вибраций, достигающих несколько десятков шоков [25, 34].
Установлено, что в интервалах замирания на долото воздействует положительный и отрицательный моменты, превышающие 80 кН·м, которым соответствуют силы, воздействующие на резцы (зубки) долота до 15-20 кН, что согласовывается с критическим усилием, при котором может происходить скол армирующей пластинки зубка [26, 27]. Кроме того, достигаемое значение момента, воздействующего на долото, превышает рекомендуемое развинчивающее усилие резьбового соединения долота. Для резьбового соединения долота 185,7 мм оно составляет 21,7 кН·м, что значительно меньше достигаемых на долоте значений момента. Это подтверждает возможность ускоренного износа и потери (отвинчивания) долота и нецелесообразность работы долота в stick-slip-режимах [27, 32]. Особенно быстрый износ долота при высокочастотных крутильных колебаниях обусловлен изменением направления вращения долота, при котором сила реакции породы направлена не навстречу зубков долота, а по касательной к ним, вызывая сколы армирующих зубки пластин и вырывание зубков из гнезд корпуса долота [33, 34]. Учитывая конструкцию PDC долот, моделирование фрикционных изменений момента на долоте Тb(t) при переходе скорости через ноль более обоснованно осуществлять по модели, отличающейся от модели (3) смещением вверх по оси ординат. Возможный вариант такой модели представлен в работе [35]. Расчеты показали, что такое смещение приводит к увеличению риска возникновения stick-slip эффекта.
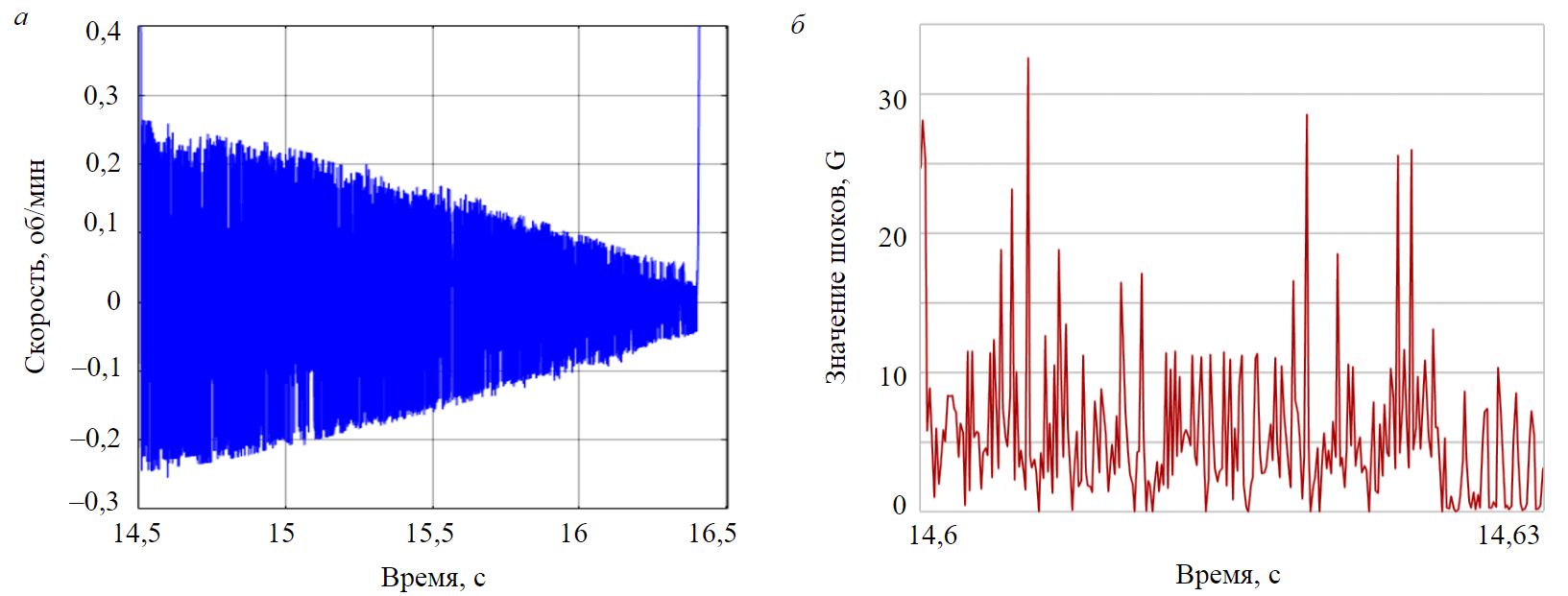
Рис.6. Высокочастотные колебания (а) и вибрация (б) долота при остановке и в stick-slip-режиме
Заключение
Предложена модификация комплексной модели асинхронный электропривод ротора – колонна бурильных труб – долото – горная порода, позволяющая рассчитать и оценить выбранные режимы бурения с учетом их электромеханической, энергетической и технологической эффективности [36-38] и динамики процессов бурения [29, 30, 39]. Результаты моделирования соответствуют практике роторного бурения [40-42]. Выполненное компьютерное моделирование режимов бурения подтвердило возможность возникновения stick-slip-эффекта, сопровождаемого высокочастотными вибрациями при остановках долота, при которых возможно изменение направления вращения долота, его ускоренный износ и отвинчивание бурового инструмента. Модель может быть использована в качестве базовой для дальнейшего совершенствования управления роторным [43-45] и другими [46-48] способами бурения.
Литература
- Юнин Е.К. Автоколебания в глубоком бурении. М.: Либроком, 2013. 264 с.
- Guangjian Dong, Ping Chen. A Review of the Evaluation, Control, and Application Technologies for Drill String Vibrations and Shocks in Oil and Gas Well // Shock and Vibration. 2016. № 7418635. 34 p. DOI: 10.1155/2016/7418635
- Saldivar Márquez M.B., Boussaada I., H.Mounier, Niculescu S.-I. Analysis and Control of Oilwell Drilling Vibrations.
- A Time-Delay Systems Approach. Springer International Publishing Switzerland, 2015. 282 p. DOI: 10.1007/978-3-319-15747-4
- Yang Liu, Wei Lin, Chávez J.P., De Sa R. Torsional stick-slip vibrations and multistability in drill-strings // Applied Mathematical Modelling. 2019. Vol. 76. P. 545-557. DOI: 10.1016/j.apm.2019.06.012
- Liping Tang, Xiaohua Zhu, Xudong Qian, Changshuai Shi. Effects of weight on bit on torsional stick-slip vibration of oil well drill string // Journal of Mechanical Science and Technology. 2017. Vol. 31. № 10. P. 4589-4597. DOI: 10.1007/s12206-017-0905-7
- Ершов М.С., Балицкий В.П., Мелик-Шахназарова И.А. Исследование работы привода постоянного тока ротора буровой установки в режиме неустойчивого вращения долота // Горный информационно-аналитический бюллетень. 2020. № 11.
- C. 166-179. DOI: 10.25018/0236-1493-2020-11-0-166-179
- Ершов М.С., Комков А.Н., Феоктистов Е.А. Работа электроприводов постоянного и переменного тока ротора буровой установки в режиме неустойчивого вращения долота // Горный информационно-аналитический бюллетень. 2021. № 6. С. 153-167. DOI: 10.25018/0236_1493_2021_6_0_153
- Ершов М.С., Феоктистов Е.А. Влияние режима неустойчивого вращения долота на энергоэффективность электропривода ротора буровой установки // Горный информационно-аналитический бюллетень. 2022. № 1. С. 148-161. DOI: 10.25018/0236_1493_2022_1_0_148
- Dardan Klimenta, Antti Hannukainen, Antero Arkkio. Estimating the parameters of induction motors in different operating regimes from a set of data containing the rotor cage temperature // Electrical Engineering. 2018. № 100. P. 139-150.
- DOI: 10.1007/s00202-016-0497-8
- Vaziri V., Oladunjoye I.O., Kapitaniak M. et al. Parametric analysis of a sliding-mode controller to suppress drill-string stick-slip vibration // Meccanica. 2020. № 55. P. 2475-2492. DOI: 10.1007/s11012-020-01264-5
- Двойников М.В. Исследования технико-технологических параметров бурения наклонных скважин // Записки Горного института. 2017. Т. 223. С. 86-92. DOI: 10.18454/PMI.2017.1.86
- Долгий И.Е., Николаев Н.И. Сопротивление горных пород разрушению при бурении скважин // Записки Горного института. 2016. Т. 221. С. 655-660. DOI: 10.18454/PMI.2016.5.655
- Saldivar B., Mondié S., Ávila Vilchis J.C. The control of drilling vibrations: A coupled PDE-ODE modeling approach // International Journal of Applied Mathematics and Computer Science. 2016. Vol. 26. № 2. P. 335-349. DOI: 10.1515/amcs-2016-0024
- Погорелов Д.Ю., Лысиков Н.Н. Силы взаимодействия долота с породой при компьютерном моделировании динамики бурильной колонны // Нефтегазовое дело. 2019. № 3. С. 211-236.
- Коронатов В.А. Основы математической строгой теории глубокого бурения // Системы. Методы. Технологии. 2020. № 2 (46). С. 23-29. DOI: 10.18324/2077-5415-2020-2-23-29
- Kunshin A., Dvoynikov M., Timashev E., Starikov V. Development of Monitoring and Forecasting Technology Energy Efficiency of Well Drilling Using Mechanical Specific Energy // Energies. 2022. Vol. 15 (19). DOI: 10.3390/en15197408
- Kadochnikov V.G., Dvoynikov M.V. Development of Technology for Hydromechanical Breakdown of Mud Plugs and Improvement of Well Cleaning by Controlled Buckling of the Drill String // Applied Sciences. 2022. Vol. 12 (13). DOI: 10.3390/app12136460
- Лукьянов Э.Е., Кудашева С.В. Методические рекомендации по интерпретации данных ГТИ. Новосибирск: Историческое наследие Сибири, 2016. 512 с.
- Vromen T.G.M., Dai C.H., Van de Wouw N. et al. Mitigation of torsional vibrations in drilling systems: a robust control approach // IEEE Transactions on Control Systems Technology. 2019. Vol. 27. Iss. 1. № 8094252. P. 249-265. DOI: 10.1109/TCST.2017.2762645
- Tengesdal N.K., Hovda S., Holden C. A Discussion on the Decoupling Assumption of Axial and Torsional Dynamics in Bit-rock Models // Journal of Petroleum Science and Engineering. 2021. Vol. 202. № 108070. DOI: 10.1016/j.petrol.2020.108070
- Amorim Jr.D.S., Santos O.L.A., Azevedo R.C. New industry standards to increase the reliability of drilling operations // Holos. 2019. Vol. 6. P. 1-14. DOI: 10.15628/Holos.2019.9009
- Нескоромных В.В., Попова М.С., Головченко А.Е.и др. Методика управления процессом бурения и экспериментальные исследования сил сопротивления при бурении долотами с резцами PDC // Записки Горного института. 2020. Т. 245. С. 539-546. DOI: 10.31897/PMI.2020.5.5
- Нескоромных В.В., Чихоткин А.В. Аналитическое исследование механики разрушения горных пород резцами PDC c учетом динамических процессов резания-скалывания горной породы и сопротивления среды // Горный информационно-аналитический бюллетень. 2020. № 4. С. 127-136. DOI: 10.25018/0236-1493-2020-4- 0-127-136
- Нескоромных В.В., Попова М.С., Зотов З.Г., Лиу Баочанг. Алгоритм управления системой алмазного бурения // Известия Томского политехнического университета. Инжиниринг георесурсов. 2022. Т. 333. № 2. С. 81-89. DOI: 10.18799/24131830/2022/2/3562
- Abdul Rani A.M., Khairiyah I., Ab Adzis A.H. et al. Investigation on the effect of changing rotary speed and weight bit on PCD cutter wear // Journal of Petroleum Exploration and Production Technology. 2020. Vol. 10. P. 1063-1068. DOI: 10.1007/s13202-019-00795-2
- Третьяк А.А., Литкевич Ю.Ф., Борисов К.А. Влияние крутильных и продольных колебаний на скорость бурения
- и образование поломок режущих элементов буровых долот, армированных PDC // Известия Томского политехнического университета. Инжиниринг георесурсов. 2019. Т. 330. № 12. C. 135-141. DOI: 10.18799/24131830/2019/12/2410
- Борисов К.А., Третьяк А.А., Сидорова Е.В. Влияние вибраций на прочностные свойства буровых долот // Разведка
- и охрана недр. 2019. № 12. С. 33-37.
- Третьяк А.Я., Сидорова Е.В., Литкевич Ю.Ф. и др. Контроль ресурса PDC-пластин бурового долота // Известия Томского политехнического университета. Инжиниринг георесурсов. 2021. Т. 332. № 8. C. 28-35. DOI: 10.18799/24131830/2021/8/3302
- Литвиненко В.С., Двойников М.В. Методика определения параметров режима бурения наклонно прямолинейных участков скважины винтовыми забойными двигателями // Записки Горного института. 2020. Т. 241. С. 105-112. DOI: 10.31897/PMI.2020.1.105
- Нескоромных В.В., Попова М.С. Разработка методики управления процессом бурения на основе комплексного анализа критериев // Записки Горного института. 2019. Т. 240. С. 701-710. DOI: 10.31897/PMI.2019.6.701
- Козярук А.Е. Опыт создания и перспективы развития электромеханических комплексов – технологических, движения и позиционирования технических средств освоения шельфа // Записки Горного института. 2016. Т. 221. С. 701-705. DOI: 10.18454/PMI.2016.5.701
- Zhiqiang Huang, Yachao Ma, Qin Li, Dou Xie. Geometry and force modeling, and mechanical properties study of polycrystalline diamond compact bit under wearing condition based on numerical analysis // Advances in Mechanical Engineering. 2017.
- Vol. 9 (6). P. 1-15. DOI: 10.1177/1687814017702080
- Guohui Zhang, Xiwen Zhang, Rong Chen et al. Pediction method of rock stratum anti-diamond characteristics of carbonate rocks used in Qinghai YingXi block // 2018 3rd International Conference on Advances in Energy and Environment Research (ICAEER 2018), September 2018, Guilin, China. E3S Web of Conferences. 2018. Vol. 53 (12). № 03002. Р. 1-5. DOI: 10.1051/e3sconf/20185303002
- Заляев М.Ф. Исследование вибрации при бурении скважин на Термокарстовом газоконденсатном месторождении // Нефтегазовое дело. 2015. № 4. Т. 13. С. 36-40.
- Леонов Г.А., Киселева М.А. Устойчивость электромеханических моделей буровых установок при резкопеременных нагрузках // Доклады Академии наук. 2012. T. 444. № 2. C. 160-164.
- Dvoynikov M.V., Nutskova M.V., Blinov P.A. Developments Made in the Field of Drilling Fluids by Saint Petersburg Mining University // International Journal of Engineering, Transactions A: Basics. 2020. Vol. 33. Iss. 4. P. 702-711. DOI: 10.5829/IJE.2020.33.04A.22
- Litvinenko V.S., Dvoynikov M.V. Monitoring and control of the drilling string and bottomhole motor work dynamics // Topical Issues of Rational use of Natural Resources. 2019. Vol. 2. P. 804-809. DOI: 10.1201/9781003014638-42
- Guanggjian Dong, Ping Chen. A Review of the Evaluation, Control, and Application Technologies for Drill String Vibrations and Shoks in Oil and Gas Well // Shock and Vibration. 2016. № 7418635. 34 p. DOI: 10.1155/2016/7418635
- Ritto T.G., Ghandchi-Tehrani M. Active control of stick-slip torsional vibrations in drill-strings // Journal of Vibration and Control. 2018. Vol. 25. Iss.1. P. 1-9. DOI: 10.1177/1077546318774240
- Pérez-Aracil J., Camacho-Gómez C., Pereira E. et al. Eliminating Stick-Slip Vibrations in Drill-Strings with a Dual-Loop Control Strategy Optimised by the CRO-SL Algorithm // Mathematics 2021. Vol. 9. № 1526. DOI: 10.3390/math9131526
- Pavković D., Šprljan P., Cipek M., Krznar M. Cross-axis control system design for borehole drilling based on damping optimum criterion and utilization of proportional-integral controllers // Optimization and Engineering. 2021. Vol. 22. P. 51-81. DOI: 10.1007/s11081-020-09566-z
- Wei Lin, Paez Chavez J., Yang Liu et al. Stick-slip suppression and speed tuning for a drill-string system via proportional-derivative control // Applied Mathematical Modelling. 2020. Vol. 82. P. 487-502. DOI: 10.1016/j.apm.2020.01.055
- Vaziri V., Kapitaniak M., Wiercigroch M. Suppression of drill-string stick–slip vibration by sliding mode control:
- Numerical and experimental studies // European Journal of Applied Mathematics. 2018. Vol. 29. Iss. 5. P. 805-825. DOI: 10.1017/S0956792518000232
- Литвиненко В.С., Двойников М.В. Обоснование выбора параметров режима бурения скважин роторными управляемыми системами // Записки Горного института. 2019. Т. 235. C. 24-29. DOI: 10.31897/PMI.2019.1.24
- MacLean J.D.J., Vaziri V., Aphalec S.S., Wiercigrochd M. Feedback control method to suppress stick-slip in drill-strings featuring delay and actuation constraints // The European Physical Journal Special Topics. 2021. Vol. 230. P. 3627-3642.
- DOI: 10.1140/epjs/s11734-021-00228-4
- Симонянц С.Л., Аль Тии М. Стимулирование процесса бурения верхним силовым приводом с использованием винтового забойного двигателя // Записки Горного института. 2019. Т. 238. С. 438-442. DOI: 10.31897/PMI.2019.4.438
- Dvoynikov M.V., Sidorkin D.I., Kunshin A.A., Kovalev D.A. Development of hydraulic turbodrills for deep well drilling // Applied Sciences (Switzerland). 2021. Vol. 11. Iss. 16. DOI: 10.3390/app11167517
- Dvoynikov M., Kunshin A., Blinov P., Morozov V. Development of Mathematical Model for Controlling Drilling Parameters with Screw Downhole Motor // International Journal of Engineering, Transactions A: Basics. 2020. Vol. 33. Iss.7. P. 1423-1430. DOI: 10.5829/IJE.2020.33.07A.30
- Podoliak A.V., Blinov P.A. The technology of directional drilling in ice via drills on carrying cable // International Journal of Applied Engineering Research. 2016. Vol. 11 (9). P. 6411-6417.
