Оценка сдвиговой прочности горных пород по трещинам на основе результатов испытаний образцов сферическими инденторами
- 1 — канд. техн. наук ведущий научный сотрудник Санкт-Петербургский горный университет ▪ Orcid
- 2 — канд. техн. наук заведующий лабораторией Санкт-Петербургский горный университет ▪ Orcid
- 3 — инженер Санкт-Петербургский горный университет ▪ Orcid
Аннотация
Представлены экспериментальные данные о связи остаточной сдвиговой прочности горных пород по сомкнутым трещинам с функциональными характеристиками ненарушенных пород – растягивающей и сжимающей составляющими сцепления, шероховатостью поверхностей трещин и уровнем нормальных напряжений. Разработан единый комплексный подход к определению сдвиговой прочности ненарушенных и разрушенных пород, остаточной сдвиговой прочности по сомкнутым шероховатым трещинам. Подход предусматривает выделение интервалов напряжений, соответствующих различным видам разрушения, для каждого из которых предлагается критерий прочности, выражаемый через функциональные характеристики ненарушенной породы. Разработан экспресс-метод оценки остаточной сдвиговой прочности пород по трещинам с шероховатой поверхностью, при котором в качестве базового метода испытаний применяется усовершенствованный метод нагружения образцов сферическими инденторами. Экспресс-метод реализует переход от данных механических испытаний образцов сферическими инденторами к показателям сдвиговой прочности по трещинам в массиве горных пород с учетом уровня нормальных напряжений и шероховатости поверхностей трещин, измеряемых в натурных условиях. При этом применяется шкала шероховатости, разработанная Бартоном. Экспресс-метод информативен и доступен в полевых условиях.
Введение
Разрушение горных пород в массиве в процессе эксплуатации месторождения происходит в условиях неоднородного напряженного состояния в режиме перераспределения напряжений при ведении горных работ и имеет вероятностный характер [1, 2]. Поэтому для геомеханического подобия процессам, встречающимся в горной практике [3, 4], при лабораторных механических испытаниях пород и их поверхностей ослабления (трещин) особое внимание следует уделять представительности испытаний в отношении вида напряженного состояния и механизма разрушения, характерных для реальных условий в массиве. Указанным требованиям отвечают методы раскалывания образцов сосредоточенными нагрузками [5] – метод нагружения образцов сферическими инденторами [6] и его аналог point-load strength test [7]. Эти методы испытаний реализуют сложный механизм разрушения образцов, включающий локальные разрушения ненарушенной породы путем отрыва и среза, а также деформирование разрушенной породы при высоких сжимающих напряжениях. Учитывая техническую простоту и доступность для массового применения, усовершенствованный метод нагружения образцов сферическими инденторами применяется в качестве базового метода испытаний при упрощенной оценке показателей паспортов предельной и остаточной прочности горной породы [8, 9].
Для массива характерно существенное различие прочностных свойств слагающих пород и поверхностей ослабления (трещин) [10-12]. Сопротивление сдвигу по трещинам в массиве горных пород чаще оценивается на основе лабораторных испытаний малогабаритных образцов по сомкнутым (закрытым) трещинам и описанию природных трещин в полевых условиях [13-15]. На практике для описания природных трещин применяют как шкалу стандартных профилей шероховатости, разработанную Бартоном [16], так и оценку шероховатости в первом приближении, основанную на выделении ровного, волнистого или ступенчатого морфологических типов закрытых трещин согласно отечественной классификации [17]. При этом определение сдвиговой прочности (СП) по трещинам в лабораторных условиях нередко затрудняется отсутствием необходимого объема проб, разбросом характеристик трещин, несоответствием геометрических размеров трещин и параметров их шероховатости в образце и массиве. К тому же повреждения поверхностей природных трещин при отборе проб и подготовке к испытаниям образцов дополнительно искажают экспериментальные данные. Из-за сложности отбора представительных проб актуальной является разработка доступных в полевых условиях ускоренных методов определения сдвиговой прочности пород по трещинам по данным технически простых испытаний малогабаритных образцов.
Представлены результаты исследований, направленных на разработку нового подхода к оценке сдвиговой прочности горных пород по трещинам на основе данных испытаний ненарушенных образцов сферическими инденторами. Подход учитывает уровень напряжений и шероховатость трещин в реальных условиях, предназначен для получения исходных данных о СП массива горных пород по поверхностям ослабления.
Методы
Для оценки предельного напряженного состояния трещиноватого массива в качестве эмпирического критерия разрушения широко используются данные построения огибающей предельных кругов напряжений Мора (паспорта прочности). При этом сдвиговую прочность массива горных пород принято оценивать на основе определения свойств ненарушенных пород и интегральной оценки влияния на них поверхностей ослабления (трещин) [18-20].
Одни и те же горные породы в различных напряженных состояниях могут хрупко разрушаться и пластически деформироваться [21, 22]. При этом переход от одного вида разрушения к другому при изменении напряженного состояния происходит постепенно [23], с определенной вероятностью его реализации [24]. На диаграмме Мора это проявляется в том, что сдвиговая прочность породных образцов, как ненарушенных, так и разрушенных при трехосном сжатии либо ослабленных трещинами, характеризуется подобными по форме огибающими предельных кругов напряжений [16, 23]. Огибающие кривые прочности как ненарушенной, так и структурно ослабленной породы при переходе из интервала растягивающих напряжений в интервал сжимающих напряжений выполаживаются и имеют тенденцию к слиянию при высоком уровне напряжений [25, 26].
Построение огибающих кругов напряжений Мора, соответствующих предельной и остаточной прочности пород, по данным лабораторных испытаний цилиндрических образцов, связано с проведением многочисленных испытаний в широком диапазоне напряжений на сложном оборудовании. Учитывая сложность и трудоемкость этого подхода, широкое распространение получили упрощенные расчетные методы построения огибающих предельной и остаточной прочности, основанные на эмпирических зависимостях сдвиговой прочности от нормальных напряжений с учетом особенностей конкретных пород [25, 27, 28]. В качестве основных параметров эмпирических зависимостей (критериев разрушения) обычно используют значения механических показателей, характеризующих различные виды разрушения (сдвиг и отрыв), и которые определяются технически простыми и доступными способами [29, 30]. Наиболее распространены два подхода к представлению эмпирических зависимостей (критериев разрушения).
Первый подход заключается в использовании математических формул, описывающих единую зависимость для всего диапазона возможных значений нормальных напряжений [16, 29, 31]. Недостатком подобных эмпирических критериев разрушения обычно является ограниченность их области применения особенностями конкретных пород, видом разрушения или диапазоном напряжений [32]. Например, расчетный метод построения паспорта прочности по данным определения пределов прочности при одноосном сжатии и растяжении (ГОСТ 21153.8) не рекомендуется применять в диапазоне нормальных напряжений, превышающем значения 1,5 предела прочности при одноосном сжатии.
Второй (комплексный) подход предусматривает условное выделение интервалов нормальных напряжений, соответствующих различным видам разрушения, для каждого из которых предлагается отдельный критерий прочности. При построении зависимостей в выделенных интервалах напряжений предпочтение отдается простым эмпирическим формулам. Например, при описании прочности на сдвиг по шероховатой трещине в соответствии с критерием Паттона и при определении предельной и остаточной прочности горных пород при трехосном сжатии в соответствии со стандартом ISRM используется билинейная аппроксимация предельных огибающих. А в соответствии с модифицированным критерием прочности Мора – Кулона прямолинейная предельная огибающая в интервале растягивающих напряжений заменяется дугой окружности [30].
Сопротивление сдвигу по трещинам различного типа в осадочных, магматических и метаморфических породах может быть описано общими зависимостями, учитывающими для сомкнутых трещин углы наклона неровностей поверхности, прочностные свойства стенок трещин и уровень нормальных напряжений. При этом сопротивление сдвигу существенно различается для трещин ровного, волнистого и ступенчатого морфологических типов [33-35]. С учетом этого предложен нелинейный эмпирический критерий СП по трещинам в массиве горных пород (критерий Бартона – Бандиса), который учитывает шероховатость и прочность породных стенок трещин [36]:
где σn – эффективное нормальное напряжение; JRC – коэффициент шероховатости трещин, изменяется от 0° для гладких поверхностей скольжения до 20° для ступенчатых шероховатых поверхностей; JCS – предел прочности поверхности трещины при сжатии; φr – остаточный угол трения (около 30°).
Эмпирическая формула Бартона – Бандиса позволяет учитывать особенности изменения параметров предельных огибающих прочности по трещинам в массиве горных пород. Анализ данного подхода показал, что при нормальном напряжении σn, превышающем прочность поверхности трещин JCS, либо низком напряжении σn, соответствующем величине угла трения более 70°, уравнение (1) перестает работать. Учитывая это, в работе [37] отмечено, что при проектировании бортов карьеров критерий Бартона – Бандиса следует использовать с осторожностью. Опубликовано большое количество исследований, направленных на совершенствование этого критерия [38-40].
Аналогичный комплексный подход предложен и для построения паспорта прочности горной породы по результатам испытаний на раскалывание образцов сферическими инденторами усовершенствованным методом, разработанным в Санкт-Петербургском горном университете [41, 42]. Суть этого метода испытаний заключается в осевом сжатии образца двумя сферическими инденторами, фиксации разрушающей силы P и измерении в разрушенном образце площади поверхности отрыва S и зон разрушенной срезом породы вблизи инденторов F1 и F2, из которых учитывают большую F (рис.1, а). Таким образом, в рамках известного подхода предложено существенное уточнение – помимо определения растягивающей составляющей напряжений σt в образце дополнительно оценивается сжимающая составляющая напряжений p при локальном разрушении срезом. Это позволяет, в отличие от стандартного метода испытаний (ГОСТ 24941), учитывать сложный характер разрушения образца, включающий деформирование разрушенной породы на контактах с инденторами и разрушение породы путем отрыва внутри образца и среза на границе разрушенных зон.
При вычислении параметров паспорта прочности в качестве функциональных характеристик, определяющих разрушение горной породы, приняты растягивающая и сжимающая составляющие предельного сопротивления срезу (сцепления):
Для удобства расчетов формулы могут выражаться при помощи показателя хрупкости K (K = p/σt) или коэффициента хрупкости Kf, равного отношению пределов прочности при одноосном сжатии и растяжении (Kf = σc/σT). При этом установлена взаимосвязь σt и p с пределами прочности:
На диаграмме Мора огибающую предельных кругов напряжений породы аппроксимировали комплексом взаимосвязанных отрезков – прямолинейными отрезками, соответствующими устойчивым видам макроразрушения (отрывом, срезом и квазипластическим деформированием), и дугами окружностей предельных кругов напряжений Мора, для которых вид разрушения носит вероятностный характер (рис.1, б). При этом вероятностному разрушению отрывом или сдвигом соответствовало сцепление C0, которое аппроксимировали отрезком дуги круга Мора {–σt; p} в интервале нормальных напряжений от 0 до (p – σt)/2, а вероятностному разрушению срезом или квазипластическому деформированию соответствовало максимальное сопротивление срезу τmax, которое аппроксимировали отрезком дуги круга Мора {σ3М; σ1М }:
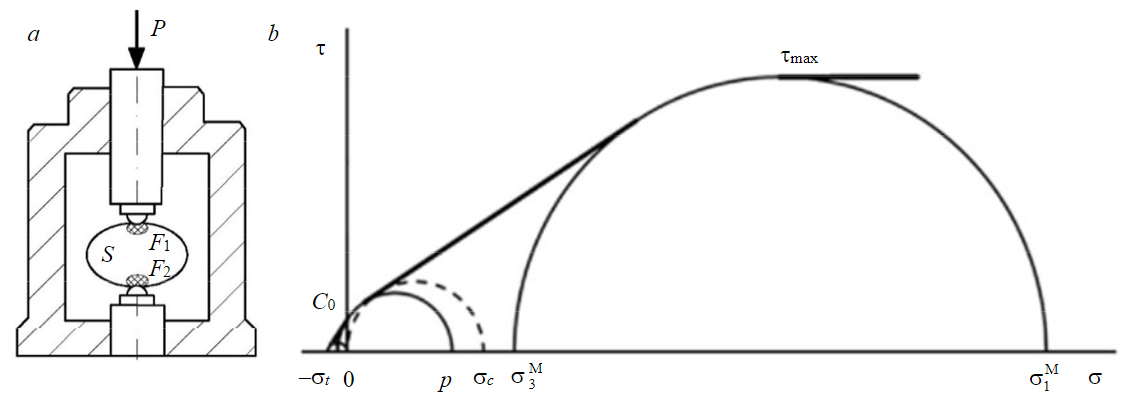
Рис. 1. Построение паспорта прочности ненарушенного образца горной породы [5]: а – схема испытания образца сферическими инденторами; б – построение паспорта прочности образца в системе координат Мора
В интервалах нормальных напряжений, соответствующих устойчивым видам макроразрушения, огибающую предельных кругов напряжений предложено аппроксимировать касательными к кругам вероятностного разрушения. При этом необходимо отметить, что прямолинейный отрезок огибающей, соответствующий разрушению срезом, аппроксимируется единой касательной к кругам Мора, соответствующим условной величине прочности при «чистом» сдвиге (при главных нормальных напряжениях {–C0; C0}) и максимальному сопротивлению срезу τmax (при напряжениях {σ3М; σ1М }).
Результаты сопоставления экспериментальных и расчетных данных свидетельствуют о том, что комплексный подход применим и для упрощенной оценки остаточной прочности разрушенных пород [9] и сдвиговой прочности по сомкнутым трещинам [43]. При этом установлены зависимости [43], связывающие параметры остаточной СП с функциональными характеристиками ненарушенной породы σt и p без учета особенностей шероховатости поверхностей трещин. Принимая во внимание предварительный характер таких результатов, в Санкт-Петербургском горном университете выполнены комплексные исследования, направленные на разработку экспресс-метода оценки сдвиговой прочности горных пород по шероховатым трещинам на основе результатов испытаний малогабаритных образцов сферическими инденторами.
Под остаточной прочностью понимается «запредельная» прочность разрушенного образца при деформациях, которые могут быть разумно получены в трехосных испытаниях [5]. В ходе исследований изучены следующие вопросы:
- основные закономерности изменения остаточной СП разрушенной при трехосном сжатии породы и шероховатых трещин в зависимости от уровня нормальных напряжений (общий вид огибающих предельной и остаточной прочности на диаграмме Мора, интервалы возможных значений сдвиговой прочности, зависимость параметров огибающих предельных кругов напряжений Мора от вида макроразрушения);
- влияние шероховатости и относительной прочности поверхности стенок трещин, хрупкости породы на прочность при сдвиге;
- связь параметров остаточной СП разрушенной породы и шероховатых трещин с параметрами прочности ненарушенной породы.
Для обеспечения представительности испытаний в отношении вида напряженного состояния и механизма разрушения выполнены сопоставительные испытания широкого круга твердых горных пород от слабых и пластичных до прочных и хрупких (кембрийская глина, мрамор, известняк, аргиллит, алевролит, уголь, хромит и т.д.) на раскалывание образцов сферическими инденторами [9, 43], на одноосное и трехосное сжатие в режиме регулируемой осевой деформации образцов. Предел прочности пород σc изменялся от 2,55 до 179,34 МПа, а коэффициент хрупкости Kf от 5,8 до 13,9. При этом испытаниям на сжатие подвергнуты как монолитные, так и содержащие естественные и искусственные трещины образцы.
Испытания на сжатие проведены в соответствии с требованиями стандартных методов Российской Федерации (ГОСТ 21153.2 и 21153.8) и международного общества ISRM в жестком нагрузочном устройстве БВ-21, которое установлено на прессе, рассчитанном на создание сжимающего усилия до 1000 кН, и укомплектовано насосной станцией, рассчитанной на давление рабочей жидкости до 60 МПа. Испытания образцов пород сферическими инденторами проведены в нагрузочном устройстве БУ-11 (Россия), которое установлено в универсальной испытательной машине Insight 50 (USA), рассчитанной на создание сжимающего усилия до 50 кН. Приложение нагрузок к образцам осуществляли в соответствии с ГОСТ 24941 через стальные инденторы диаметром 15 мм с твердостью по Роквеллу HRC 60-65 единиц. Испытаниям подвергали образцы толщиной 20-50 мм с ожидаемой площадью поверхности разрыва 5-20 см2.
Обсуждение результатов
По результатам комплексных исследований механических свойств горных пород получены новые экспериментальные данные о связи остаточной сдвиговой прочности горных пород по сомкнутым трещинам с функциональными характеристиками ненарушенных пород σt и p, шероховатостью поверхностей трещин и уровнем нормальных напряжений.
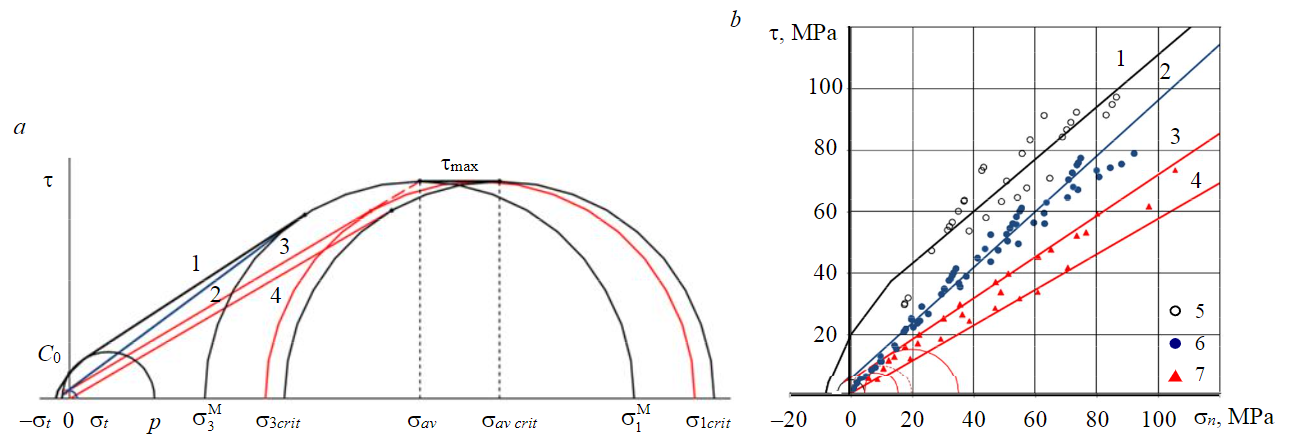
Рис.2. Построение огибающих СП горной породы и трещин (а); экспериментальные данные сопоставительных испытаний мрамора (б) 1, 2 – предельная и остаточная прочность породы; 3, 4 – остаточная СП по трещинам (JRC = 20; JRC = 0); 5, 6 – предельная и остаточная прочность разрушенной при трехосном сжатии породы; 7 – остаточная прочность при срезе со сжатием по трещинам
Принято считать, что на диаграмме Мора предельное «критическое» состояние, соответствующее максимальному сопротивлению срезу τmax, характеризуется отношением минимального и максимального главных нормальных напряжений, равным 1/3 [25, 33]. Учитывая это, компоненты предельного критического напряженного состояния (σ3crit и σ1crit) приняты в качестве характеристики СП вдоль наиболее ослабленных поверхностей. Критическое состояние {σ = σav crit; τ = τmax} рассматривалось как переходное предельное напряженное состояние, соответствующее вероятностному характеру разрушения при сдвиге вдоль плоских трещин.
Сделанные допущения позволили построить огибающую остаточной СП по плоским трещинам на основе результатов испытаний монолитного образца инденторами. На диаграмме Мора огибающая остаточной прочности при сдвиге по плоской трещине аппроксимируется комплексом взаимосвязанных отрезков – дугой окружности предельного круга напряжений Мора {σ3crit = τmax; σ1crit = 3τmax)}, для которого вид разрушения носит вероятностный характер, и двумя прямолинейными отрезками, касательными к этому кругу, и соответствующими устойчивым видам макроразрушения (рис.2, а, огибающая 4). Один из отрезков проходит через начало координат под углом остаточного трения φr, равным 30°, и касается круга в точке с координатами {σ = (2 – sinφr)τmax; τ = cosφrτmax}, а горизонтальный отрезок касается круга в точке с координатами {σ = 2τmax; τ = τmax}.
На диаграмме Мора обоснованность такой аппроксимации подтверждает совпадение нижней границы области значений остаточной СП по ровным трещинам в мраморе, установленной при трехосных испытаниях, с расчетной огибающей остаточной СП по плоской ровной трещине (рис.2, б).
В интервале средних нормальных напряжений, соответствующих устойчивому макроразрушению образцов срезом, огибающая остаточной прочности разрушенной породы аппроксимируется отрезком единой касательной к кругам Мора, соответствующим максимальному сопротивлению срезу и условной прочности чистого сдвига разрушенной породы [9, 37]. Установлено, что в интервале средних нормальных напряжений, превышающих условные пределы прочности при одноосном сжатии, огибающие остаточной СП как разрушенной породы (рис.2, а, огибающая 2), так и остаточной СП по шероховатой трещине с JRC = 20 (рис.2, а, огибающая 3) достоверно аппроксимируются отрезками общих касательных к кругам Мора. Они соответствуют условной прочности при чистом сдвиге разрушенной породы (при главных нормальных напряжениях {–σt; σt}) и максимальному сопротивлению срезу τmax. При этом остаточной прочности разрушенной породы соответствует отрезок касательной к кругу Мора, общему для ненарушенной и разрушенной породы, а остаточной СП по шероховатой трещине соответствует отрезок касательной к кругу Мора, направленный в условную точку с координатами {σ = σav; τ = τmax}.
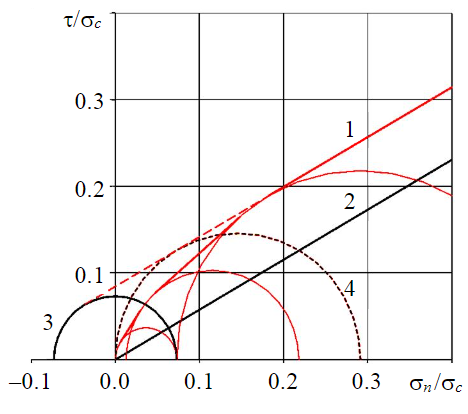
Рис.3. Построение расчетной огибающей относительной остаточной СП по трещинам в интервале низких нормальных напряжений для Kf = 7,5 1 – JRC= 20; 2 – JRC= 0; 3 – разрушенная порода при чистом сдвиге; 4 – JRC= 20 (прочность стенок трещины)
На диаграмме Мора обоснованность предлагаемой аппроксимации для огибающей сдвиговой прочности по трещинам с шероховатыми поверхностями стенок подтверждает совпадение верхней границы области значений остаточной СП по шероховатым трещинам в мраморе, установленной при трехосных испытаниях, с расчетной огибающей остаточной прочности при сдвиге (рис.2, б, огибающая 3).
При низких нормальных напряжениях огибающая остаточной прочности разрушенной породы имеет нелинейный вид и касается круга Мора, соответствующего остаточной прочности при одноосном сжатии (рис.3) [9]. Для уточнения вида предельных огибающих остаточной прочности разрушенной породы и остаточной сдвиговой прочности по трещинам в этом интервале нормальных напряжений проведены дополнительные лабораторные испытания.
Экспериментально установлено, что при нормальных напряжениях, не превышающих условные пределы прочности при одноосном сжатии, определяющими параметрами паспортов остаточной сдвиговой прочности разрушенной породы и трещин с шероховатой поверхностью (JRC = 20) являются: абсолютная величина растягивающей составляющей сцепления σt, условные пределы прочности при одноосном сжатии, которые подобны параметрам паспорта прочности ненарушенной породы – сцеплению C0 и пределу прочности при одноосном сжатии σc:
где φr – условный угол трения по шероховатой трещине с JRC = 20.
Для интервала нормальных напряжений (меньших σ0r) характерными являются два предельных напряженных состояния поверхностей трещин, описываемые дугами окружностей кругов Мора и {σ3 = 0; σ1 = σt}, аналогичные предельным напряженным состояниям ненарушенной породы – переходному состоянию от разрушения срезом к разрушению отрывом {σ3 = –σt ; σ1 = p} и разрушению отрывом при напряжениях . Промежутки между ними аппроксимируются прямолинейными отрезками, образованными общими касательными к окружностям (рис.3, огибающая 1).
По результатам исследований установлено, что отклонение от прямолинейного вида огибающей остаточной сдвиговой прочности по трещинам с шероховатой поверхностью (JRC = 20) происходит при среднем нормальном напряжении, меньшем условного предела прочности при одноосном сжатии σ0r. Этому напряженному состоянию соответствует круг Мора с минимальным главным нормальным напряжением, равным σt (рис.4). Радиус этого предельного круга Мора соответствует аналогу сжимающей составляющей сцепления p, численно равному разности между условным пределом прочности при одноосном сжатии и аналогом сцепления (σ0r – σt).
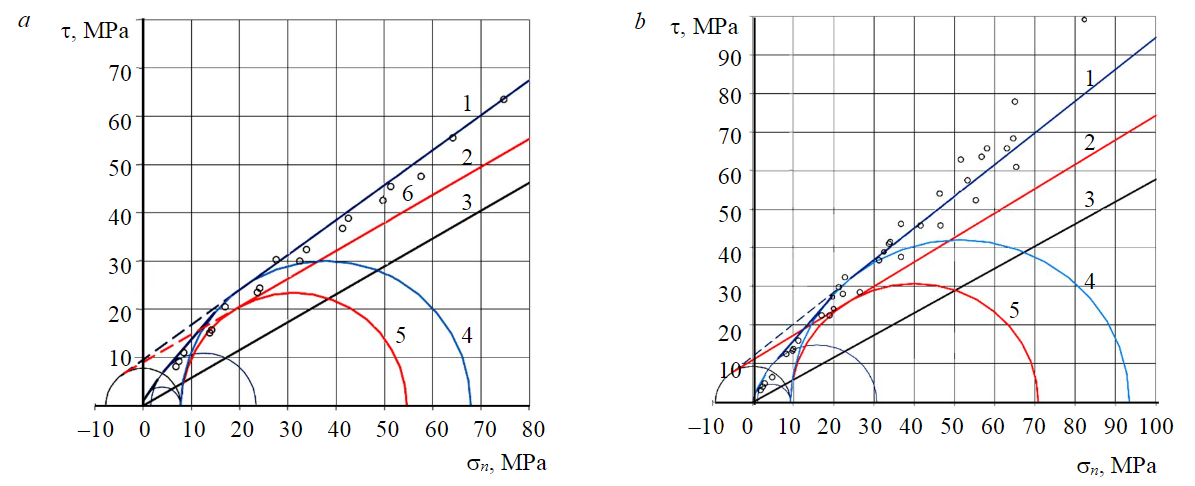
Рис.4. Построение расчетных огибающих остаточной СП в алевролите (а) и песчанике (б) 1 – разрушенная порода; 2, 3 – трещина (JRC = 20 и JRC= 0); 4, 5 – прочность при σ3 = σt разрушенной породы и стенок трещины (JRC = 20); 6 – остаточная прочность разрушенной при трехосном сжатии породы
На диаграмме Мора огибающую остаточной прочности разрушенной породы при низких нормальных напряжениях в первом приближении допустимо аппроксимировать отрезком, параллельным аналогичному отрезку огибающей предельной прочности [9]. Уточняется вид кривой в области низких напряжений в соответствии с комплексным подходом. Экспериментально установлено, что огибающие остаточной прочности породы, разрушенной при сжатии и срезе по сомкнутым шероховатым трещинам (JRC = 20), практически не отличаются в интервале нормальных напряжений, не превышающем σt. Этому интервалу соответствуют круги Мора со значениями σ3 не более .
Учитывая, что вероятностному состоянию, переходному к устойчивому разрушению образцов срезом, соответствует круг Мора со значением σ3, равным σt, предельную огибающую в интервале, который характеризуется значениями σ3 от 2 до σt, допустимо аппроксимировать общей касательной к соответствующим кругам Мора, соответствующим срезу по сомкнутым шероховатым трещинам. Параметры кругов Мора, характеризующих подобные напряженные состояния при сдвиге по ненарушенной и разрушенной породе и сомкнутым шероховатым трещинам при низких нормальных напряжениях, представлены в табл.1.
Таблица 1
Соответствие параметров кругов Мора для характерных предельных напряженных состояний ненарушенных и разрушенных сжатием пород и их трещин
|
Описание предельного напряженного состояния ненарушенной породы |
Описание поверхности сдвига |
|||||
|
Ненарушенная порода, МПа |
Разрушенная при сжатии порода, МПа |
Ступенчатая сомкнутая поверхность, МПа |
||||
|
σ3 |
σ1 |
σ3 |
σ1 |
σ3 |
σ1 |
|
|
Разрушение отрывом при растяжении со сжатием |
|
C0 |
0 |
σt |
0 |
σt |
|
Вероятное разрушение отрывом или срезом при растяжении со сжатием |
–σt |
p=σc-C0 |
|
σ0r-σt |
|
σ0r-σt |
|
Разрушение срезом при неравномерном сжатии |
C0 |
2σc-C0 |
σt |
2σ0R-σt |
σt |
2σ0r-σt |
Разработан единый комплексный подход к определению предельной и остаточной сдвиговой прочности горных пород и остаточной сдвиговой прочности по сомкнутым шероховатым трещинам. В соответствии с этим на диаграмме Мора предельная огибающая остаточной СП по шероховатым трещинам имеет криволинейный вид при низких нормальных напряжениях, прямолинейный при среднем уровне нормальных напряжений и выполаживается при высоком уровне напряжений.
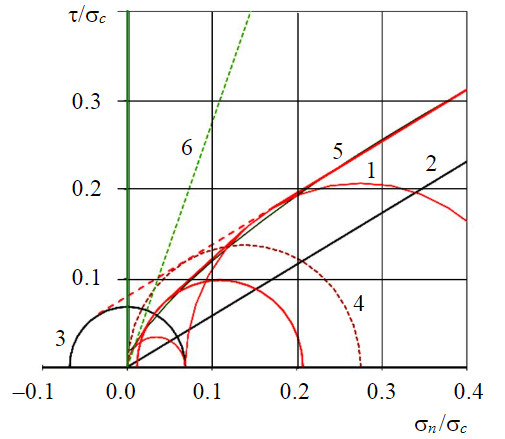
Рис.5. Построение расчетной огибающей относительной остаточной СП по шероховатой (JRC = 20) трещине в интервале низких нормальных напряжений для Kf = 8 См. условные обозначения 1-4 на рис.3; 5 – по критерию Бартона – Бандиса; 6 – граница области применения критерия Бартона – Бандиса
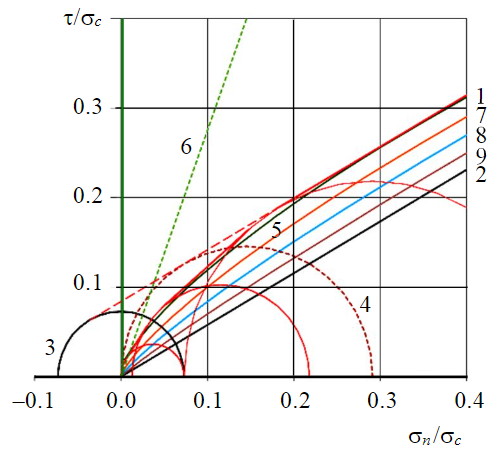
Рис.6. Построение огибающих относительной остаточной СП по трещинам различного морфологического типа в интервале низких нормальных напряжений для Kf = 7,5 1 – JRC= 20; 2 – JRC = 0; 3 – разрушенная порода при чистом сдвиге; 4 – JRC = 20 (прочность стенок трещины); 5 – JRC= 20 (по критерию Бартона – Бандиса); 6 – граница области применения критерия Бартона – Бандиса; 7 – JRC= 15; 8 – JRC= 10; 9 – JRC= 5
Для обоснования предлагаемого комплексного подхода проведены сравнительные расчеты сдвиговой прочности по трещинам с использованием критерия прочности Бартона – Бандиса по формуле (1) для заданных значений остаточного угла трения φr = 30° и коэффициента шероховатости трещин JRC (0; 5; 10; 15; 20°). Также расчетные данные сопоставлены с экспериментальными данными запредельных испытаний при одноосном и трехосном сжатии монолитных и содержащих естественные и искусственные трещины образцов.
Установлено, что при низких нормальных напряжениях отклонение расчетных значений сдвиговой прочности по шероховатым трещинам, вычисленных по результатам испытаний сферическими инденторами, от аналогичных значений, вычисленных в соответствии с критерием прочности Бартона – Бандиса для значения коэффициента JRC = 20°, варьирует в зависимости от величины нормального напряжения и хрупкости породы и для Kf = 5-10 составляет около 5 % (рис.5). Отклонение расчетных значений сдвиговой прочности по шероховатым трещинам в интервале средних нормальных напряжений, превышающих условные пределы прочности при одноосном сжатии, увеличивается от 3-6 % в интервале σ ≈ 0,2-0,6σc до 6-9 % при σ = 0,7σc и достигает 10-18 % при σ = σc.
Сравнение расчетных показателей сдвиговой прочности, выполненное в относительных (в долях от σc) величинах нормального напряжения, показало, что при низких нормальных напряжениях для большинства осадочных пород (аргиллитов, мергелей, алевролитов, известняков, глинистых и карбонатных песчаников), которым соответствуют значения коэффициента хрупкости пород Kf от 6,5 до 8,5, интервалы возможных значений сдвиговой прочности (от минимальных, соответствующих плоским трещинам, до максимальных, соответствующих ступенчатым шероховатым трещинам) практически совпадают. Для более хрупких пород (Kf ≥ 10) интервал возможных значений прочности при оценке прочности с применением предлагаемого комплексного подхода уже, а для более пластичных пород (5 ≤ Kf ≤ 6) шире.
Установлено, что в интервале нормальных напряжений 0,01-0,7σc огибающие сдвиговой прочности по плоским ровным и ступенчатым шероховатым трещинам, построенные в соответствии с предлагаемым комплексным подходом, тесно согласуются с семейством предельных огибающих остаточной СП для значений коэффициента JRC от 0 до 20°, построенных в соответствии с критерием Бартона – Бандиса (рис.6). Принимая это во внимание при построении предельных огибающих для учета влияния шероховатости в интервалах низких и средних нормальных напряжений, рекомендуется придерживаться пропорциональной зависимости изменения СП от коэффициента шероховатости, аналогичной формуле (1).
Разработан экспресс-метод оценки остаточной сдвиговой прочности пород по шероховатым сомкнутым трещинам, при котором в качестве базового метода испытаний применяется усовершенствованный метод нагружения образца сферическими инденторами. Экспресс-метод реализует переход от данных механических испытаний ненарушенных образцов сферическими инденторами к показателям СП по трещинам в породном массиве на основе единого подхода к оценке показателей сдвиговой прочности горных пород по сомкнутым трещинам с учетом уровня нормальных напряжений и шероховатости трещин, измеряемых в природных условиях. При этом для описания шероховатости трещин допускается применение как шкалы шероховатости, разработанной Бартоном [16], так и оценка шероховатости в первом приближении, основанная на морфологическом типе трещин [34].
Экспресс-метод включает следующие этапы:
- Оценка шероховатости стенок трещин и нормальных напряжений в полевых условиях.
- Проведение испытаний на раскалывание ненарушенных малогабаритных образцов породы нагружением сферическими инденторами в лабораторных или полевых условиях; построение паспорта прочности и определение параметров СП ненарушенной породы по результатам испытаний образцов сферическими инденторами в соответствии с методикой (см. рис.1, б).
- Построение на диаграмме Мора огибающих остаточной прочности и определение параметров остаточной СП по ступенчатым шероховатым (JRC= 20) и плоским ровным трещинам (JRC = 0). При построении огибающей остаточной СП по ступенчатой шероховатой трещине в качестве исходных данных принимаются предельные напряженные состояния. Они описываются дугами окружностей кругов Мора {σ3 = 0; σ1 = σt}, , {σ3 = σt; σ1 = (2σ0r – σt)} и условной точкой достижения ненарушенной породой максимального сопротивления срезу τmax при высоких нормальных напряжениях с координатами {σ = σav; τ = τmax} (рис.2, огибающая 3). При этом промежутки между дугами аппроксимируются прямолинейными отрезками, образованными общими касательными к окружностям (рис.3).
- Построение на диаграмме Мора огибающей остаточной СП по трещине с учетом шероховатости и уровня нормальных напряжений в природных условиях и определение параметров остаточной СП по трещине. Для этого на диаграмме Мора проводятся отрезки, соединяющие точки на огибающих остаточной СП для ступенчатых шероховатых и плоских ровных трещин и соответствующие одинаковым характерным значениям σ3, равным 0, , σt и условной точке с координатами {σ = σav; τ = τmax} (рис.2, а, огибающая 3). Отрезки разбиваются на интервалы точками, которые соотносятся с заданными значениями JRC относительно JRC= 20 (рис.7). Затем через семейство этих точек проводятся огибающие остаточной прочности при сдвиге, соответствующие заданной шероховатости стенок трещин. Расчетные параметры огибающей остаточной прочности (условное остаточное сцепление Cr и угол остаточного трения φr) вычисляются для заданных интервалов нормальных напряжений.
В качестве примера использования экспресс-метода на рис.7 показано построение огибающих относительной остаточной СП по сомкнутым трещинам ровного, волнистого и ступенчатого морфологических типов горной породы согласно отечественной классификации [34]. Им соответствуют оценочные величины коэффициента шероховатости для вычислений по формуле (1): для гладких плоских трещин JRC = 0-5; гладких волнистых тектонических трещин JRC = 8-12; шероховатых волнистых трещин JRC = 15-20 [34]. В качестве исходных данных о шероховатости трещин приняты средние для типов значения. Заданное значение Kf = 8 характерно для осадочных пород типа алевролитов и известняков [8].
Результаты расчета средних значений параметров огибающих относительной остаточной сдвиговой прочности (относительного Cr/σc и φr) по сомкнутым (закрытым) трещинам различных морфологических типов для заданных интервалов нормальных напряжений, соответствующих низкому, среднему и высокому уровням нормальных напряжений, представлены в табл.2.
Предлагаемый экспресс-метод определения остаточной сдвиговой прочности по сомкнутым трещинам может быть реализован также по данным определения двух других прочностных характеристик ненарушенной породы – пределов прочности при одноосном сжатии σc и растяжении σT. В этом случае необходимые для расчетов значения растягивающей σt и сжимающей p составляющих сцепления С0 предварительно вычисляются алгебраически по приведенным формулам (4)-(6).
Таблица 2
Расчетные значения параметров Cr/σc и φr огибающих остаточной СП породы по сомкнутым трещинам различных морфологических типов (Kf = 8)
|
Морфологический тип трещин |
Интервал 1 |
Интервал 2 |
Интервал 3 |
||||||
|
σ/σc, МПа |
Cr/σc |
jr, град |
σ/σc, МПа |
Cr/σc |
jr, град |
σ/σc, МПа |
Cr/σc |
jr, град |
|
|
Ровные |
0,0006-0,017 |
0,002 |
39 |
0,017-0,110 |
0,004 |
32 |
0,110-2,773 |
0,007 |
31 |
|
Волнистые |
0,0025-0,029 |
0,006 |
50 |
0,029-0,136 |
0,019 |
36 |
0,136-2,838 |
0,040 |
30 |
|
Ступенчатые |
0,0044-0,041 |
0,007 |
54 |
0,041-0,162 |
0,040 |
39 |
0,162-2,904 |
0,074 |
30 |
Заключение
Представлены новые экспериментальные данные о связи остаточной сдвиговой прочности горных пород по сомкнутым трещинам с функциональными характеристиками ненарушенных пород – растягивающей σt и сжимающей p составляющими предельного сопротивления срезу без нормальных напряжений (сцепления) С0, шероховатостью поверхностей трещин и уровнем нормальных напряжений.
Установлено, что на диаграмме Мора предельная огибающая остаточной СП по шероховатым трещинам имеет криволинейный вид при «низких» нормальных напряжениях, прямолинейный при среднем уровне нормальных напряжений и выполаживается при высоком уровне. При этом в диапазоне низких нормальных напряжений определяющими параметрами паспортов остаточной сдвиговой прочности породы и трещин со ступенчатой шероховатой поверхностью являются абсолютная величина растягивающей составляющей σt сцепления C0 и условные пределы прочности при одноосном сжатии σ0R и σ0r, которые подобны параметрам паспорта прочности ненарушенной породы – сцеплению C0 и пределу прочности при одноосном сжатии σc. В диапазоне средних нормальных напряжений огибающие остаточной прочности аппроксимируются прямолинейными отрезками общих касательных к окружностям кругов Мора, соответствующих предельным состояниям разрушенной породы при чистом сдвиге и квазипластическом деформировании.
Разработан единый комплексный подход к определению сдвиговой прочности ненарушенных и разрушенных пород и остаточной сдвиговой прочности по сомкнутым шероховатым трещинам, основанный на оценке предельных напряжений, при которых вид разрушения имеет вероятностный характер. Подход предусматривает выделение интервалов напряжений, соответствующих различным видам разрушения, для каждого из которых предлагается критерий прочности, выражаемый через функциональные характеристики ненарушенной породы σt и p.
Результаты сопоставительных механических испытаний горных пород и сравнительных расчетов прочности по трещинам, согласно комплексному подходу и в соответствии с критерием прочности Бартона – Бандиса, свидетельствуют об обоснованности предлагаемого подхода. Установлено, что в интервале нормальных напряжений 0,01-0,7σc огибающие сдвиговой прочности по ровным плоским и ступенчатым шероховатым трещинам, построенные в соответствии с разработанным комплексным подходом, тесно согласуются с семейством предельных огибающих остаточной СП для значений коэффициента JRC от 0 до 20°, построенных в соответствии с критерием Бартона – Бандиса.
Разработан экспресс-метод оценки остаточной сдвиговой прочности пород по трещинам с шероховатой поверхностью, при котором в качестве базового метода испытаний применяется усовершенствованный метод нагружения образцов сферическими инденторами. Экспресс-метод реализует переход от данных механических испытаний образцов сферическими инденторами к показателям СП по трещинам в массиве горных пород с учетом уровня нормальных напряжений и шероховатости поверхностей трещин, измеряемых в натурных условиях. При этом применяется шкала шероховатости, разработанная Бартоном. Экспресс-метод информативен и доступен в полевых условиях при помощи технически простых нагрузочных устройств. Допускается испытание малогабаритных образцов неправильной формы.
Литература
- Трушко В.Л., Протосеня А.Г. Перспективы развития геомеханики в условиях нового технологического уклада // Записки Горного института. 2019. Т. 236. 2019. С. 162-166. DOI: 10.31897/PMI.2019.2.162
- Trushko V.L., Sergeev I.B., Shabarov A.N. The Development of Geomechanical Engineering in Mining // ISRM European Rock Mechanics Symposium – EUROCK 2018, 22-26 May 2018, Saint-Petersburg, Russia. 2018. OnePetro, 2018. Vol. 1. P. 95-104. № ISRM-EUROCK-2018-009.
- Зуев Б.Ю. Методология моделирования нелинейных геомеханических процессов в блочных и слоистых горных массивах на моделях из эквивалентных материалов // Записки Горного института. 2021. Т. 250. С. 542-552. DOI: 10.31897/PMI.2021.4.7
- Shabarov A.N., Zuev B.Y., Krotov N.V. Prospects of the physical model-based study of geomechanical processes // ISRM European Rock Mechanics Symposium – EUROCK 2018, 22-26 May 2018, Saint Petersburg, Russia. 2018. OnePetro, 2018. Vol. 1. P. 423-430. № ISRM-EUROCK-2018-052.
- Протодьяконов М.М., Вобликов В.С., Ильницкая Е.И. Методика определения прочности горных пород на образцах неправильной формы. М.: Изд-во Института горного дела им. А.А.Скочинского, 1961. 8 с.
- Карташов Ю.М., Матвеев Б.В., Михеев Г.В., Фадеев А.Б. Прочность и деформируемость горных пород. М.: Недра, 1979. 269 с.
- Franklin J.A. Suggested Methods for Determining Points Load Strength // International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1985. Vol. 22. Iss. 2. P. 51-60. DOI: 10.1016/0148-9062(85)92327-7
- Коршунов В.А., Карташов Ю.М. Новый способ определения предела прочности при растяжении горных пород // Записки Горного института. 2011. Т. 190. С. 202-206.
- Korshunov V.A., Solomoichenko D.A., Bazhukov A.A. Strength Estimation of Fractured Rock Using Compression – A Specimen with Spherical Indenters // ISRM European Rock Mechanics Symposium – EUROCK 2018, 22-26 May 2018, Saint Petersburg, Russia. 2018. OnePetro, 2018. Vol. 1. P. 299-305. № ISRM-EUROCK-2018-034.
- Фисенко Г.Л. Прочностные характеристики массива горных пород. Механика горных пород и маркшейдерское дело. М.: Углетехиздат, 1959. С. 91-100.
- Ismail M.K.A., Mohd-Nordin M.M., Hasan A.S.Md. et al. Shear strength behaviour of rock joint material influenced by different weathering grade // Journal of Physics: Conference Series. 2019. Vol. 1349. Iss. 1. № 012069. DOI: 10.1088/1742-6596/1349/1/012069
- Li Y., Oh J., Mitra R., Canbulat I. A Fractal Model for the Shear Behaviour of Large-Scale Opened Rock Joints // Rock Mechanics and Rock Engineering. 2017. Vol. 50. Iss. 1. P. 67-79. DOI: 10.1007/s00603-016-1088-8
- Фисенко Г.Л. Методы количественной оценки структурных ослаблений массива горных пород в связи с анализом их устойчивости // Современные проблемы механики горных пород. Л.: Наука, 1972. С. 21-29.
- Stigsson M., Mas Ivars D. A Novel Conceptual Approach to Objectively Determine JRC Using Fractal Dimension and Asperity Distribution of Mapped Fracture Traces // Rock Mechanics and Rock Engineering. 2019. Vol. 52. P. 1041-1054. DOI: 10.1007/s00603-018-1651-6
- Ríos-Bayona F., Johansson F., Mas-Ivars D. Prediction of Peak Shear Strength of Natural, Unfilled Rock Joints Accounting for Matedness Based on Measured Aperture // Rock Mechanics and Rock Engineering. 2021. Vol. 54. Iss. 3. P. 1533-1550. DOI: 10.1007/s00603-020-02340-8
- Barton N. Shear strength criteria for rock, rock joints, rockfill and rock masses: Problems and some solutions // Journal of Rock Mechanics and Geotechnical Engineering. 2013. Vol. 5. Iss. 4. P. 249-261. DOI: 10.1016/j.jrmge.2013.05.008
- Patton F.D. Multiple Modes of Shear Failure in Rock // 1st ISRM Congress, 25 September – 1 October 1966, Lisbon, Portugal. OnePetro, 1966. Vol. 1. P. 509-513. № ISRM-1CONGRESS-1966-087.
- Гудман Р. Механика скальных пород. М.: Стройиздат, 1987. 232 с.
- Латышев О.Г., Франц В.В., Прищепа Д.В. Моделирование и прогноз прочности при сдвиге горных пород по трещине // Известия вузов. Горный журнал. 2017. № 2. С. 50-56.
- Протосеня А.Г., Вербило П.Э. Изучение прочности на сжатие трещиноватого горного массива // Записки Горного института. 2017. Т. 223. С. 51-57. DOI: 10.18454/PMI.2017.1.51
- Протосеня А.Г., Иовлев Г.А. Прогноз пространственного напряженно-деформированного состояния физически нелинейного грунтового массива в призабойной зоне тоннеля // Горный информационно-аналитический бюллетень. 2020. № 5. C. 128-139. DOI: 10.25018/0236-1493-2020-5-0-128-139
- Protosenya A., Vilner M. Assessment of Excavation Intersections’ Stability in Jointed Rock Masses Using the Discontinuum Approach // Rudarsko-geološko-naftni zbornik. 2022. Vol. 37. Iss. 2. P. 137-147. DOI: 10.17794/rgn.2022.2.12
- Мюллер Л. Инженерная геология. Механика скальных массивов. М.: Мир, 1971. 240 с.
- Кузнецов Г.Н. Механические свойства горных пород. Задачи и методы их изучения в связи с вопросами управления горным давлением. М.: Углетехиздат, 1947. 180 с.
- Тарасов Б.Г. Закономерности деформирования и разрушения горных пород при высоких давлениях: Автореф. дис. ... д-ра техн. наук. СПб: ЛГИ, 1991. 46 с.
- Ladanyi B., Archambault G. Simulation of the Shear Behavior of a Jointed Rock Mass // The 11th U.S. Symposium on Rock Mechanics (USRMS), 16-19 June 1970, Berkeley, California. OnePetro, 1970. P. 105-125. № ARMA-69-0105.
- Bieniawski Z.T. Estimating the strength of rock materials // Journal of the South African Institute of Mining and Metallurgy. 1974. Vol. 74. № 8. P. 312-320.
- Eberhardt E. The Hoek-Brown Failure Criterion // Rock Mechanics and Rock Engineering. 2012. Vol. 45. P. 981-988. DOI: 10.1007/s00603-012-0276-4
- Протодьяконов М.М. Обобщенное уравнение огибающих к предельным кругам напряжений Мора // Исследование физико-механических свойств горных пород применительно к задачам управления горным давлением. М.: Изд-во Академии наук СССР, 1962. С. 82-89.
- Labus J.F., Zang A. Mohr-Coulomb Failure Criterion // Rock Mechanics and Rock Engineering. 2012. Vol. 45. P. 975-979. DOI: 10.1007/s00603-012-0281-7
- Singh H.K., Basu A. Evaluation of existing criteria in estimating shear strength of natural rock discontinuities // Engineering Geology. 2018. Vol. 232. P. 171-181. DOI: 10.1016/j.enggeo.2017.11.023
- Thirukumaran S., Indraratna B. A review of shear strength models for rock joints subjected to constant normal stiffness // Journal of Rock Mechanics and Geotechnical Engineering. 2016. Vol. 8. Iss. 3. P. 405-414. DOI: 10.1016/j.jrmge.2015.10.006
- Quansheng Liu, Yongchao Tian, Dongfeng Liu, Yalong Jiang. Updates to JRC-JCS model for estimating the peak shear strength of rock joints based on quantified surface description // Engineering Geology. 2017. Vol. 228. P. 282-300. DOI: 10.1016/j.enggeo.2017.08.020
- Могилевская С.Е. Экспресс-метод ВНИИГ определения параметров сопротивления сдвигу по трещинам в скальных породах. Опыт и перспективы использования // Геотехника. Оценка состояния оснований и сооружений: Труды международной конференции, 13-16 июня 2001, Санкт-Петербург, Россия. 2001. Т. 1. С. 41-49.
- Liren Ban, Weisheng Du, Tianwei Jin et al. A roughness parameter considering joint material properties and peak shear strength model for rock joints // International Journal of Mining Science and Technology. 2021. Vol. 31. Iss. 3. P. 413-420. DOI: 10.1016/j.ijmst.2021.03.007
- Barton N.R. Shear Strength of Rock, Rock Joints and Rock Masses // The 11th U.S. Symposium on Rock Mechanics (USRMS), 16-19 June 1969, Berkeley, California. OnePetro, 1969. P. 3-16. № ARMA-69-0105.
- Read J., Stacey P. Guidelines for Open Pit Slope Design. Clayton: CSIRO Publishing, 2009. 496 p. DOI: 10.1071/9780643101104
- Jie Yang, Guan Rong, Di Hou et al. Experimental study on peak shear strength criterion for rock joints // Rock Mechanics and Rock Engineering. 2016. Vol. 49. P. 821-835. DOI: 10.1007/s00603-015-0791-1
- Zhi Cheng Tang, Louis Ngai Yuen Wong. New Criterion for Evaluating the Peak Shear Strength of Rock Joints Under Different Contact States // Rock Mechanics and Rock Engineering. 2016. Vol. 49. Iss. 4. P. 1191-1199. DOI: 10.1007/s00603-015-0811-1
- Rihong Cao, Hang Lin, Ping Cao. Strength and failure characteristics of brittle jointed rock-like specimens under uniaxial compression: Digital speckle technology and a particle mechanics approach // International Journal of Mining Science and Technology. 2018. Vol. 28. Iss. 4. P. 669-677. DOI: 10.1016/j.ijmst.2018.02.002
- Коршунов В.А., Карташов Ю.М., Козлов В.А. Определение показателей паспорта прочности горных пород методом разрушения образцов сферическими инденторами // Записки Горного института. 2010. Т. 185. С. 41-45.
- Korshunov V.A., Tsirel S.V., Melnikov N.Ya., Bazhukov A.A. Geomechanical Substantiation of Calculate Indentors of the Rock Mass Strength for Slopes Stability Analysis of Open Pit // ISRM European Rock Mechanics Symposium – EUROCK 2018, 22-26 May 2018, Saint Petersburg, Russia. OnePetro, 2018. Vol. 2. P. 1053-1058. № ISRM-EUROCK-2018-149
- Павлович А.А., Коршунов В.А., Бажуков А.А., Мельников Н.Я. Оценка прочности массива горных пород при разработке месторождений открытым способом // Записки Горного института. 2019. Т. 239. С. 502-509. DOI: 10.31897/PMI.2019.5.502
