Анализ решения задачи о нахождении распределения скоростей при ламинарном движении нелинейно-вязкой промывочной жидкости в кольцевом пространстве скважины
- канд. техн. наук доцент Самарский государственный технический университет ▪ Orcid
Аннотация
Современные буровые промывочные жидкости являются нелинейно-вязкими средами, обладающими начальным напряжением сдвига. В классических научных работах по гидромеханическому моделированию движения буровых растворов в трубах и кольцевых каналах использовали приближения Шведова – Бингама и степенную модель Оствальда – де Ваале, которые не в полной мере учитывали поведение технологических жидкостей в широком диапазоне скоростей сдвига. В статье представлено численное решение математической модели движения буровой промывочной жидкости трехпараметрической реологической модели Гершеля – Балкли в кольцевом пространстве скважины. Модель Гершеля – Балкли в реологическом уравнении учитывает наличие начального напряжения сдвига и тенденцию к изменению вязкости при изменении скорости сдвига, что отличает ее от моделей Оствальда – де Ваале и Шведова – Бингама. Целевой функцией при решении уравнения движения является распределение скоростей в радиальном направлении восходящего потока промывочной жидкости. Анализ полученного решения основан на теории влияния вида профиля скоростей на качество выноса шлама при очистке ствола скважины. В связи с особенностью математической постановки задачи, предполагающей необходимость решения дифференциального уравнения движения, в качестве расчетного инструмента был использован пакет символьных вычислений Wolfram Mathematica. Проведенный анализ численного решения позволил сделать выводы о возможности его применения в оценке вида профиля скоростей при движении буровой промывочной жидкости в кольцевом пространстве скважины. Обоснована возможность использования модифицированного коэффициента эксцесса как относительного количественного параметра для оценки равномерности профиля скоростей.
Введение
Применение буровых промывочных жидкостей необходимо при бурении нефтяных скважин. Множество функций, выполняемых промывочными системами, позволяют обеспечивать безопасное и безаварийное ведение буровых работ. Буровые промывочные жидкости являются полидисперсными системами, обладающими тиксотропными свойствами. Необходимо учитывать особенности их описания и проектирования. Моделирование рецептур буровых промывочных жидкостей – важная, но не простая задача из-за математического учета химических взаимодействий реагентов. Разнообразие производителей материалов для буровых растворов осложняет данный процесс. В общем случае эта задача не имеет решения. При описании воздействия входного параметра рецептуры на выходной параметр при фиксированных значениях остальных пользуются упрощениями, в том числе с применением многофакторного анализа [1]. В результате проектирования буровых промывочных жидкостей могут быть получены качественные полидисперсные системы, удовлетворяющие важным требованиям – проектная плотность, низкий показатель фильтрации, учет требований химического состава для бурения неустойчивых отложений, значения вязкостных характеристик, в том числе в зависимости от температурного фактора [2].
Существуют важные технологические параметры, такие как полное скважинное давление, имеющее аналог в терминах эквивалентной циркуляционной плотности, или индекс очистки скважины на основании скорости восходящего потока и скорости оседания частиц, которые рассчитываются для скважинных условий, исходя из выбора реологической модели буровой промывочной жидкости [3-5]. Одним из возможных гидродинамических расчетов является определение вида профиля скоростей потока, который влияет на качество выноса частиц выбуренной породы [6]. Такое физическое явление интерпретируется тем, что при наличии плоского профиля скоростей частицам выбуренной породы передается импульс более равномерно. Это способствует повышению качества их выноса из скважины. При вытянутом профиле скоростей частицы шлама имеют тенденцию смещаться из центра потока к стенкам скважины, что вызывает их циркуляцию в потоке жидкости и снижает качество очистки ствола скважины [7-9]. При анализе качества выноса в зависимости от вида профиля скоростей важно указывать реологическую модель жидкости, относительно которой делаются выводы. Особенность заключается в том, что жидкости, описываемые различными реологическими моделями, имеют значительное различие в распределении скоростей в восходящем потоке [10-12].
Вопросам построения профиля скоростей технологических жидкостей посвящено достаточно много исследований. Фундаментальные исследования [13] анализируют движение ньютоновских сред, а также сред реологических моделей Шведова – Бингама и Оствальда – де Ваале. Анализ влияния реологических характеристик на распределения скоростей показал следующие закономерности: при движении ньютоновских сред единственным значимым реологическим параметром является динамическая вязкость. Ее рост снижает среднюю скорость потока, при ламинарном режиме профиль скоростей имеет более вытянутый вид, чем при турбулентном. Решение для сред Шведова – Бингама имеет принципиальное отличие от ньютоновской и степенной модели – оно отдельно рассматривается для ядра потока и периферийных областей. Под понятием ядра потока предполагается наличие в центре потока области, в которой слои жидкости имеют одинаковую скорость. В данной модели два реологических параметра оказывают влияние на вид профиля скоростей. Рост динамического напряжения сдвига увеличивает ядро потока, а увеличение пластической вязкости снижает среднюю скорость. Для степенной реологической модели установлены зависимости распределения скоростей от индекса консистенции K, являющегося аналогом пластической вязкости, и показателя нелинейности n, отражающего тенденцию к изменению вязкости при изменении скорости сдвига. Для жидкостей модели Оствальда – де Ваале наличие ядра потока, как отдельной рассматриваемой области, не предполагается. Анализ имеющегося аналитического решения показал характерное снижение средней скорости потока при повышении индекса реологической модели K и образование более плоского профиля скоростей при снижении коэффициента n. Общая закономерность при движении
неньютоновских сред – при турбулентном режиме профиль скоростей имеет более вытянутую форму, чем при ламинарном. Это объясняется наличием тиксотропной структуры в отличие от ньютоновских сред.
Применимость описанных реологических моделей к описанию современных буровых промывочных жидкостей имеет ряд ограничений. Ньютоновская модель недопустима при моделировании реологических свойств буровых систем, так как не учитывает начальных напряжений сдвига и возможность изменения вязкости при движении. Реологическое уравнение Шведова – Бингама не берет в расчет изменение вязкости при изменении скорости сдвига. Степенная модель Оствальда – де Ваале учитывает изменение вязкости, но не предусматривает начальное напряжение сдвига. Так как современные промывочные жидкости имеют начальное напряжение сдвига и тенденцию к изменению вязкости при изменении скорости сдвига, то возникает необходимость использования модифицированного степенного закона Гершеля – Балкли, учитывающего оба признака неньютоновской среды [14-16]. Исследования при моделировании движения жидкостей ограничиваются моделями Шведова – Бингама и Оствальда – де Ваале, что в недостаточной точности учитывает реальные параметры среды [12, 17]. При поиске решения уравнения движения для трехпараметрической модели жидкости Гершеля – Балкли возрастает математическая сложность задачи и результат расчета приближается к реальным технологическим условиям.
Известны теоретические и экспериментальные исследования, цель которых – влияние эксцентриситета и вращения бурильной колонны на скважинное давление и очистку ствола скважины [18-20]. Для моделирования динамических давлений и многофазных потоков часто используют метод контрольного объема программы ANSYS или его аналоги [21-23]. В работе [24] методом контрольного объема моделируют потоки в случае отрицательного эксцентрического, концентрического и положительного эксцентрического расположения бурильной колонны в скважине. В исследовании [25] с использованием CFD-DEM моделирования производится оценка влияния формы бурильной трубы на возникновение вторичных потоков и качество выноса шлама. Задачи, связанные с выносом шлама, также решают экспериментальным путем [26-28]. В статье [29] доказывается существование слабого решения начально-краевой задачи с условием прилипания на границе для математической модели движения жидкости Гершеля – Балкли. При описании решения задачи течения жидкости Гершеля – Балкли в кольцевом канале авторы работы [30] обсуждают упрощенное решение для распределения скоростей потока в интегральном виде, предполагая наличие ядра потока и двух периферийных областей с дальнейшим их моделированием в пакете симуляции гидравлических процессов CFD программного комплекса ANSYS. Данное предположение является упрощением и не позволяет оценить влияние реологических параметров жидкости на образование равномерного распределения скоростей, так как предполагается наличие ядра потока для жидкости модели Гершеля – Балкли с любой комбинацией коэффициентов. Если рассматривать модифицированный степенной закон как совокупность модели Шведова – Бингама и Оствальда – де Ваале, для первой из которых наличие ядра потока – стандартное допущение, то для классического степенного закона данное упрощение не принято вводить, и образование равномерного распределения скоростей рассматривается в зависимости от показателя нелинейности. Поэтому при формулировке задачи об оценке вида профиля скорости, оказывающего влияние на качество выноса шлама, упрощение о наличии ядра потока как обязательно присутствующей части является некорректным и ее решение не может привести к правильному анализу технологического процесса промывки. Практическим применением методов математического моделирования потоков в скважине является возможность оценки влияния реологических параметров жидкости на эффективность выноса шлама. Отличие постановки задачи от известных ранее исследований – нахождение решения для распределения скоростей с учетом трех параметров реологической модели, наиболее качественно отражающей реальные свойства бурового раствора. Результат исследований может быть применен для определения оптимальных диапазонов реологических параметров промывочных жидкостей с целью разработки новых, наиболее качественных рецептур.
Исходя из проведенных исследований, посвященных движению неньютоновских сред в трубах и кольцевых каналах, поставлена задача нахождения и анализа численного решения уравнений движения жидкости Гершеля – Балкли в кольцевом пространстве скважины при ламинарном
режиме. Выбор такого режима обоснован наличием более равномерного профиля скоростей у неньютоновских сред по сравнению с турбулентным и меньшей потерей давлений в кольцевом пространстве. При ламинарном режиме движения наименьшие потери давлений позволяют минимизировать фильтрацию жидкой фазы в пласт, что также является актуальной задачей при промывке скважин [31-33]. Математическая постановка задачи о ламинарном движении жидкости Гершеля – Балкли в кольцевом пространстве скважины позволяет произвести нахождение численного решения для профиля скоростей как функции от радиальной координаты без применения методов конечного элемента.
Методология
Представленная стационарная одномерная модель движения жидкости Гершеля – Балкли не реализует все стороны физического поведения течения неньютоновской жидкости в кольцевом пространстве, но может показывать определенную тенденцию. Это позволяет моделировать движение буровых промывочных жидкостей с некоторыми допущениями.
Для рассматриваемого плоского течения справедливы допущения:
- жидкость несжимаемая, изотропная, нелинейно-вязкая;
- движение стационарное;
- движение плоскопараллельное, т.е. все характеристики не зависят от оси z, поток ламинарный;
- частицы жидкости движутся только благодаря наличию градиента давления;
- кольцевой канал считается вертикальным и концентрическим.
Математическая постановка задачи о нахождении распределения скоростей при ламинарном режиме движения жидкости Гершеля – Балкли в кольцевом пространстве скважины заключается в решении стационарного модифицированного дифференциального уравнения движения Навье – Стокса [34, 35]
где ρ – плотность жидкости; r – радиальная координата; g – ускорение свободного падения.
Касательные напряжения τ, входящие в уравнение (1), зависят от скорости w. В качестве параметра τ, входящего в уравнение движения (1), выступает уравнение реологической модели Гершеля – Балкли, являющееся определяющим соотношением, отражающим связь сдвиговых напряжений от скорости сдвига,
где t0 – начальное напряжение сдвига; $\dot{γ}$ – скорость сдвига.
Функция (2) определена во всей области изменения скоростей сдвига $\dot{γ}$ Знак «+» берется при $\dot{γ}$ > 0 «–» при $\dot{γ}$ < 0, с учетом $\dot{γ}$ = 0 при |τ| ≤ τ0 [13].
Распределение скоростей в радиальном направлении находится из связи скорости сдвига с градиентом скорости:
где w – компонента скорости вдоль координаты z, соноправленной с осью трубы; t – время.
Уравнение движения (1) дополняется условием несжимаемости
Из предположения одномерности потока и уравнения неразрывности накладывается условие для распределения скоростей
с соответствующими граничными условиями для кольцевого пространства:
где R1 – внешний радиус бурильных труб; R2 – радиус скважины; din, dex – соответствующие диаметры; L – длина рассматриваемого участка скважины.
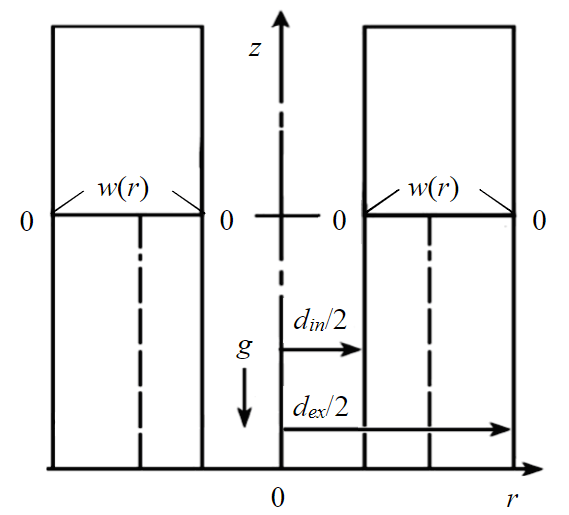
Рис.1. Схема кольцевого пространства скважины с граничными условиями для поля скоростей
Эти условия отражают условия прилипания на стенке бурильной трубы и скважины и для градиента давлений, входящего в уравнение (1). Схема кольцевого пространства скважины с граничными условиями для поля скоростей представлена на рис.1. В задаче моделирования выноса шлама из кольцевого пространства вертикальной скважины считается, что поток промывочной жидкости движется в направлении оси z. Ускорение свободного падения действует в противоположном направлении.
В такой постановке задачи распределение скоростей является симметричным относительно оси z. Следовательно, поиск решения будет производиться для плоского вида движения в области R1<r<R2.
Поставленная задача решается с помощью программного средства Wolfram Mathematica, позволяющего при использовании функции численного решения дифференциальных уравнений NDSolve найти искомую функцию распределения скоростей w(r) в виде структуры интерполирующей функции (Interpolating Function). Interpolating Function – объект, который представляет собой таблицу значений функции w(ri) в различных точках из отрезка [R1,R2] и позволяет найти значение функции в любой точке этого отрезка путем интерполяции расчетных данных. Предполагается, что в промежутках между заданными точками функция является гладкой. С интерполяционной функцией можно обращаться так же, как с любой встроенной, т.е. дифференцировать, интегрировать, строить ее график. При построении графиков распределений скоростей используется безразмерная скорость, представляющая собой для каждой жидкости отношение распределения скоростей в радиальном направлении к средней скорости потока $w(r)/\overline{w}$. Анализ распределений скоростей в масштабе безразмерных переменных позволяет качественно оценить наличие тенденции к образованию плоского профиля.
Для тестирования расчетных методов, реализованных в среде Wolfram Mathematica, произведено сравнение аналитического решения для задачи ламинарного движения ньютоновской жидкости в кольцевом зазоре с решением, полученным численным путем. Ламинарное установившееся течение вязкой жидкости, происходящее под действием продольного градиента давления, также называется течением Пуазейля [13]. Аналитическое решение для профиля скоростей имеет вид:
В качестве входных параметров реологической модели (2) использована комбинация τ0 = 0, n = 1, K = 0,001 Па·с. Такой набор параметров соответствует характеристикам воды при 20 °С. Модель Гершеля – Балкли принимает вид модели ньютоновской среды, и индекс консистенции соответствует параметру динамической вязкости. В качестве геометрических параметров для расчетов взят зазор 50 мм между стенкой скважины и внешней стенкой бурильной трубы с радиусами R2 = 107,15 и R1 = 57,15 мм соответственно. Градиент давлений, вычисленный согласно методике [13], равен 0,09239 Па/м. Данный градиент давлений соответствует расходу 0,0005 м3/с через сечение кольцевого канала с указанными геометрическими параметрами. Число Рейнольдса – Re = 1937, вычисленное для движения ньютоновской среды в кольцевом канале со скоростью 0,01937 м/с, подтверждает наличие ламинарного режима движения. Сопоставление профилей скоростей доказывает состоятельность расчетного метода, так как результат численного расчета совпадает с известным аналитическим решением. На основании данного сравнения предполагается возможность применения описанного расчетного метода к решению задачи о движении жидкости реологической модели Гершеля – Балкли в кольцевом пространстве.
Для количественной оценки образования плоского профиля скоростей при сравнении нескольких жидкостей предложено использовать модифицированный коэффициент эксцесса
где μ2 и μ4 – центральные моменты.
Такой модифицированный коэффициент эксцесса, вычисляемый с использованием центральных эмпирических моментов второго и четвертого порядков, является относительной величиной, применяемой при количественной оценке равномерности распределения скоростей жидкостей, отличающихся реологическими коэффициентами модели Гершеля – Балкли и движущихся при одинаковых скважинных условиях. Аргументами центральных моментов по аналогии с выборочным методом из математической статистики выступают значения безразмерной скорости, рассчитанные численным методом вдоль радиальной компоненты. Минимальность данного параметра является критерием наличия наиболее равномерного распределения скоростей вдоль радиального направления потока в рамках производимого сравнительного анализа. Использование такого количественного параметра может позволить определить зависимость вида профиля скоростей от реологических характеристик промывочных жидкостей.
Входными данными для расчетов являлись параметры 22-х промывочных жидкостей из исследования [36]. Представленные параметры жидкостей полностью подходят для численного моделирования потоков и содержат реологические параметры модели Гершеля – Балкли τ0, K, n. Эти параметры были определены с использованием цифрового электронного реометра компании Fann модели 286. В качестве параметра τ0 для расчета профилей скоростей берется указанное значение статического напряжения сдвига за 10 с. Реологические показатели буровых промывочных жидкостей из исследования [36] представлены в табл.1. В качестве геометрических параметров для расчетов взят зазор 50 мм между стенкой скважины и внешней стенкой бурильной трубы с диаметрами 214,3 и 114,3 мм соответственно. При расчетах использовались фиксированные модельные параметры плотности жидкости 1200 кг/м3 и градиента давлений 500 Па/м, соответствующего ламинарному режиму движения промывочных жидкостей в кольцевом пространстве [13].
Таблица 1
Реологические показатели буровых растворов в зависимости от механизма растворения реагентов в воде
|
Номер |
Структурообразователь |
C, % |
Статическое |
Индекс |
Показатель |
|
|
10 с |
10 мин |
|||||
|
1 |
CMC HV + PAC R |
0,1 + 0,15 |
3,5 |
4,5 |
14,80 |
0,18 |
|
2 |
CMC LV + PAC L |
0,15 + 0,15 |
1,2 |
3,7 |
12,70 |
0,17 |
|
3 |
Barazan + PAC R |
0,05 + 0,15 |
3,3 |
4,1 |
12,31 |
0,18 |
|
4 |
Barazan + CMC HV |
0,05 + 0,20 |
3,4 |
3,5 |
7,51 |
0,22 |
|
5 |
Barazan + CMC LV |
0,05 + 0,35 |
3,4 |
3,5 |
13,11 |
0,22 |
|
6 |
Barazan + PAC L |
0,05 + 0,3 |
2,9 |
3,3 |
7,17 |
0,22 |
|
7 |
КССБ-2 + РАС R |
1,0 + 0,15 |
2,0 |
2,9 |
7,02 |
0,24 |
|
8 |
КССБ-2 + СМС HV |
1,0 + 0,20 |
2,0 |
2,2 |
6,21 |
0,24 |
|
9 |
Глицерин + РАС R |
3,0 + 0,15 |
2,8 |
3,5 |
10,76 |
0,24 |
|
10 |
Глицерин + СМС HV |
3,0 + 0,2 |
4,0 |
5,1 |
7,04 |
0,24 |
|
11 |
Глицерин + СМС LV |
3,0 + 0,35 |
1,5 |
2,3 |
3,97 |
0,24 |
|
12 |
Глицерин + ИКПАН SL |
3,0 + 0,4 |
3,1 |
3,3 |
20,35 |
0,24 |
|
13 |
Глицерин + ИКПАН R |
3,0 + 0,4 |
1,9 |
2,1 |
12,47 |
0,25 |
|
14 |
Глицерин + РАС L |
3,0 + 0,35 |
1,2 |
2,1 |
2,98 |
0,30 |
|
15 |
НТФ + РАС R |
0,15 + 0,15 |
3,5 |
3,9 |
14,12 |
0,18 |
|
16 |
НТФ + СМСНУ |
0,15 + 0,20 |
3,5 |
3,9 |
5,70 |
0,30 |
|
17 |
РАС L + EZ MUD |
0,35 + 0,05 |
1,1 |
1,7 |
5,62 |
0,31 |
|
18 |
CMC LV + ИКПАН SL |
0,2 + 0,4 |
1,7 |
2,3 |
4,01 |
0,33 |
|
19 |
РАС L + ИКПАН SL |
0,2 + 0,4 |
1,8 |
2,4 |
3,81 |
0,35 |
|
20 |
CMC LV + EZ MUD |
0,35 + 0,05 |
1,1 |
1,2 |
2,39 |
0,36 |
|
21 |
НТФ + ИКПАН SL |
0,15 + 0,4 |
0,9 |
2,2 |
2,20 |
0,53 |
|
22 |
НТФ + ИКПАН R |
0,15 + 0,4 |
0,2 |
1,0 |
3,60 |
0,55 |
Обсуждение
В результате численного эксперимента для заданных скважинных условий были получены распределения скоростей для 22-х промывочных жидкостей с псевдопластичной реологической структурой, описываемой моделью Гершеля – Балкли (2). Решение уравнения движения (1) в вычислительном пакете Wolfram Mathematica с учетом (3)-(5) и граничных условий для кольцевого пространства скважины (6) представляет собой структуру интерполирующей функции с областью определения в пределах R1≤r≤R2. Область значений интерполирующей функции содержит распределение безразмерной скорости в зависимости от радиальной координаты. Графические изображения распределений скоростей представлены на рис.2. Соответствующие им значения модифицированного коэффициента эксцесса приведены в виде столбчатого графика на рис.3, а. Анализ значений рассчитанного модифицированного коэффициента эксцесса (8) показал, что наименьшие достигнуты у жидкостей 11, 14, 20. Следовательно, согласно его назначению, данные жидкости имеют наиболее плоские профили скоростей, способствующие более качественному выносу шлама, чем, например, у жидкостей 1, 2, 3 с наибольшим показателем эксцесса. Такой вывод подтверждается графическим анализом распределений скоростей на рис.2, б, где представлены наиболее вытянутые и плоские профили.
В дополнение к графикам профилей скоростей на рис.3, б отражены значения средней скорости потока для каждой жидкости. Значимым является наблюдение, что наибольшую среднюю скорость имеют жидкости 11, 14, 20. Высокие значения средней скорости потока также делают их наиболее предпочтительными. Скорость восходящего потока должна превышать скорость оседания шлама. Плоский вид профиля скоростей предупреждает возникновение скопления твердых частиц выбуренной породы у стенок скважины и их дальнейшую циркуляцию в потоке [6].
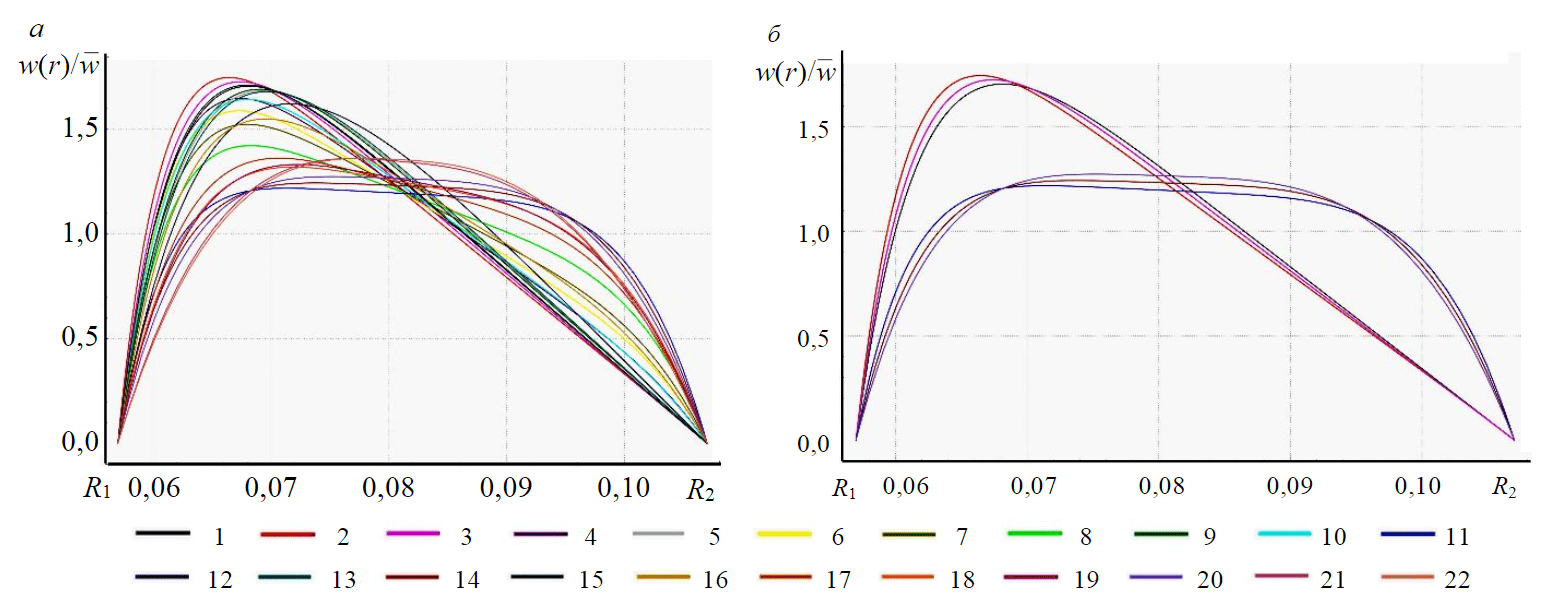
Рис.2. Распределения скоростей в кольцевом пространстве для 22-х тестируемых промывочных жидкостей (а); наиболее плоские и островершинные профили скоростей промывочных жидкостей (б) 1-22 – номера жидкостей (табл.1)
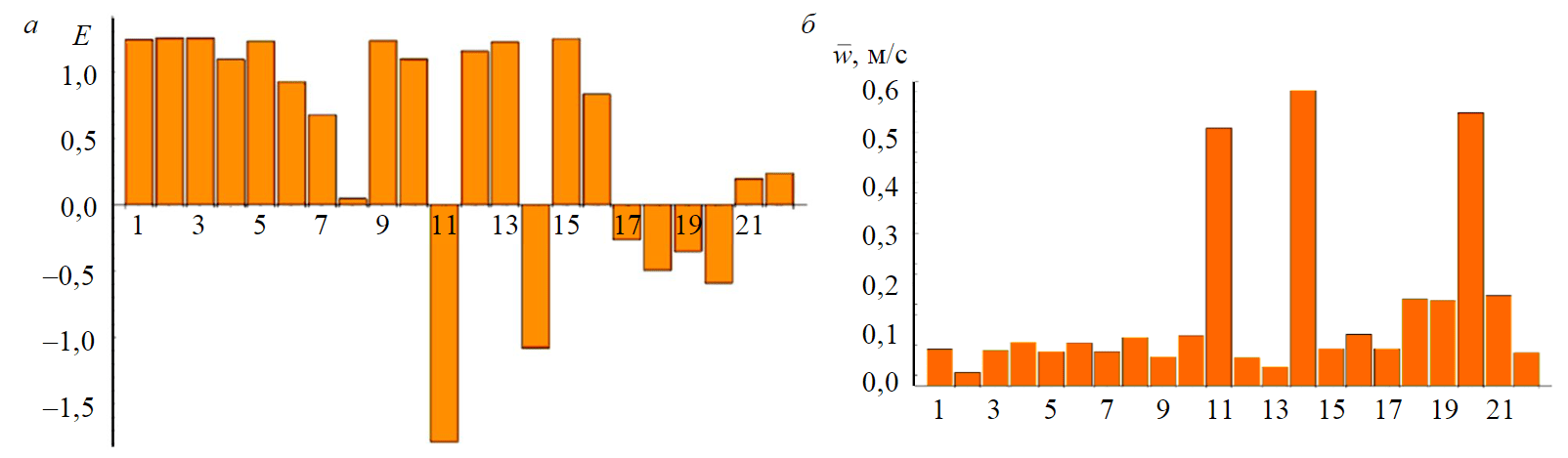
Рис.3. Характеристики распределений скоростей: модифицированный коэффициент эксцесса (а); средняя скорость (б) 1-22 – номера жидкостей (табл.1)
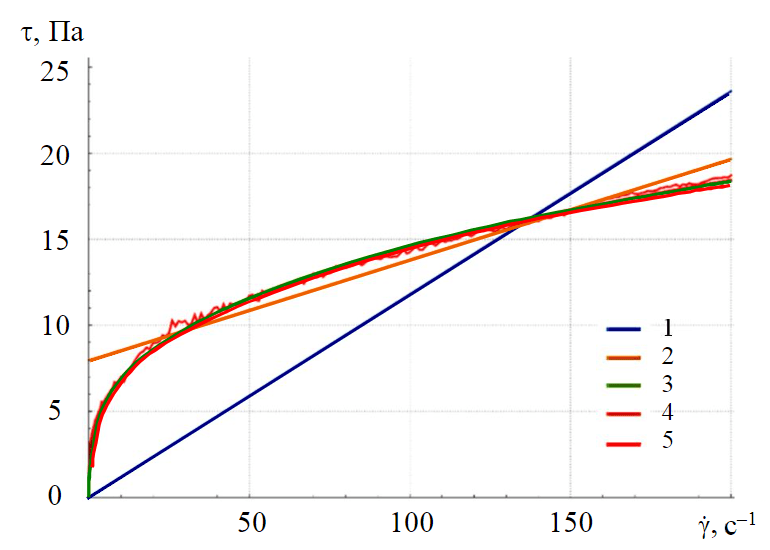
Рис.4. Аппроксимация экспериментальной зависимости реологическими моделями 1 – Ньютона (0,118084 $\dot{γ}$); 2 – Шведова – Бингама (0,0585243 $\dot{γ}$ + 7,96111); 3 – Оствальда – де Ваале (3,17628 $\dot{γ}$0,331203); 4 – Гершеля – Балкли (2,33712 $\dot{γ}$0,375308 + 1,39014); 5 – эксперимент
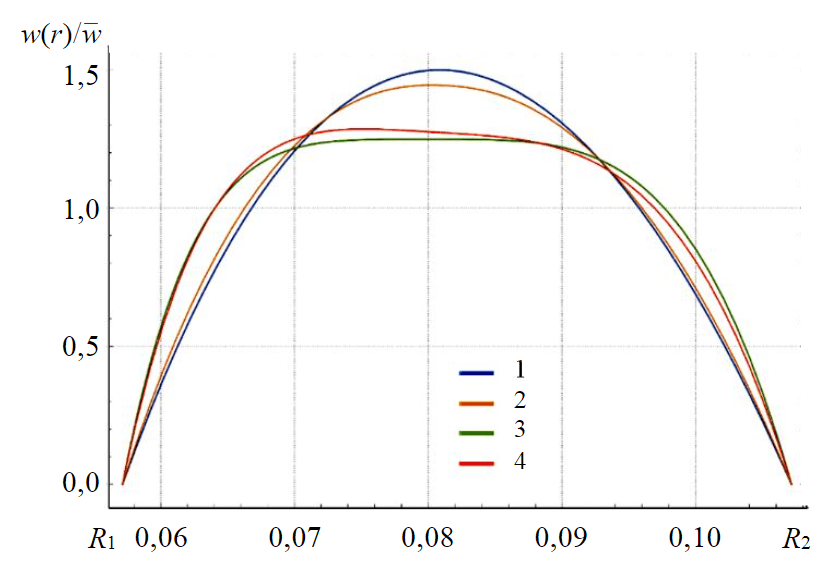
Рис.5. Распределения скоростей в кольцевом пространстве для различных реологических моделей 1 – Ньютона; 2 – Шведова – Бингама; 3 – Оствальда – де Ваале; 4 – Гершеля – Балкли
Отметим, что полученный вид графиков (см. рис.2) имеет тенденцию к смещению потока к оси бурильных труб. Данная тенденция соответствует результатам, представленным в работах [13, 37] для моделей ньютоновской, бингамовской, степенной жидкости. Значительным отличием полученного решения для модели Гершеля – Балкли от классической степенной модели является зависимость профиля скорости от показателей τ0, K, n, а не только от n и K. Для степенной модели установлено, что снижение n приводит к наличию плоского профиля скоростей, в то время как для модели Гершеля – Балкли данное утверждение не является истиной. Бингамовская модель учитывает показатели τ0 и K, что является значительным упрощением. Для бингамовской модели установлено, что снижение пластической вязкости, т.е. K при , уменьшает среднюю скорость потока, а увеличение τ0 приводит к образованию более широкого ядра потока, а именно области в профиле скоростей, движущейся с равномерной скоростью. На графиках рис.2 видно, что для некоторых жидкостей установлена тенденция к образованию ядра потока (жидкости 11, 14, 20), в отличие от других (жидкости 1, 2, 3).
В ряде задач буровые промывочные жидкости подлежат описанию более простыми реологическими уравнениями, чем модель Гершеля – Балкли. Рассмотрим различие видов профилей скоростей в зависимости от выбранной реологической модели. Воспользуемся экспериментальными данными, полученными при тестировании полимер-глинистой промывочной жидкости с использованием реометра Anton Paar Physica MCR52. Аппроксимация экспериментальной зависимости τ(γ) проводилась методом наименьших квадратов. Построенные реологические кривые изображены на рис.4. Очевидно, что наиболее качественная аппроксимация соответствует модели Гершеля – Балкли. Рассмотрим разницу между профилями скоростей для каждой реологической модели. Для этого воспользуемся наборами параметров τ0, K, n соответствующих уравнений. Данные параметры представлены в табл.2. Профили скоростей в кольцевом пространстве для моделей Ньютона, Шведова – Бингама, Оствальда – де Ваале и Гершеля – Балкли представлены на рис.5. В качестве входных параметров движения использовались те же условия, что и для 22-х тестируемых ранее жидкостей. В отличие от классических работ по гидромеханике, в которых для жидкости Шведова – Бингама наличие ядра потока является допущением и аналитическое решение строится в кусочном виде, численное решение этого не предполагает и профили скоростей для ньютоновской среды и среды Шведова – Бингама для данной промывочной жидкости схожи. Для среды Шведова – Бингама наблюдается незначительное отклонение потока к стенке трубы и менее вытянутый профиль. Для степенных моделей присутствует характерное смещение центра потока к стенке трубы. При этом наиболее плоское распределение наблюдается у модели Оствальда – де Ваале, о чем свидетельствует наименьшее значение модифицированного коэффициента эксцесса. Реологическая модель Оствальда – де Ваале пренебрегает наличием начального напряжения сдвига τ0, которое присутствует у буровых промывочных жидкостей. Этот факт также подтверждается на графиках рис.4. и данными табл.2.
Таблица 2
Параметры реологических моделей полимер-глинистой промывочной жидкости
|
Реологическая модель |
τ0, Па |
Индекс |
Показатель |
|
Ньютона |
0 |
0,118 |
1 |
|
Шведова – Бингама |
7,961 |
0,059 |
1 |
|
Оствальда – де Ваале |
0 |
3,176 |
0,331 |
|
Гершеля – Балкли |
1,39 |
2,337 |
0,375 |
Целесообразным является установление зависимости между реологическими параметрами модели Гершеля – Балкли и наличием плоского профиля скорости. Для этого методами корреляционного анализа построены зависимости параметров жидкостей τ0, K, n и Е. Парные корреляционные поля изображены на рис.6.
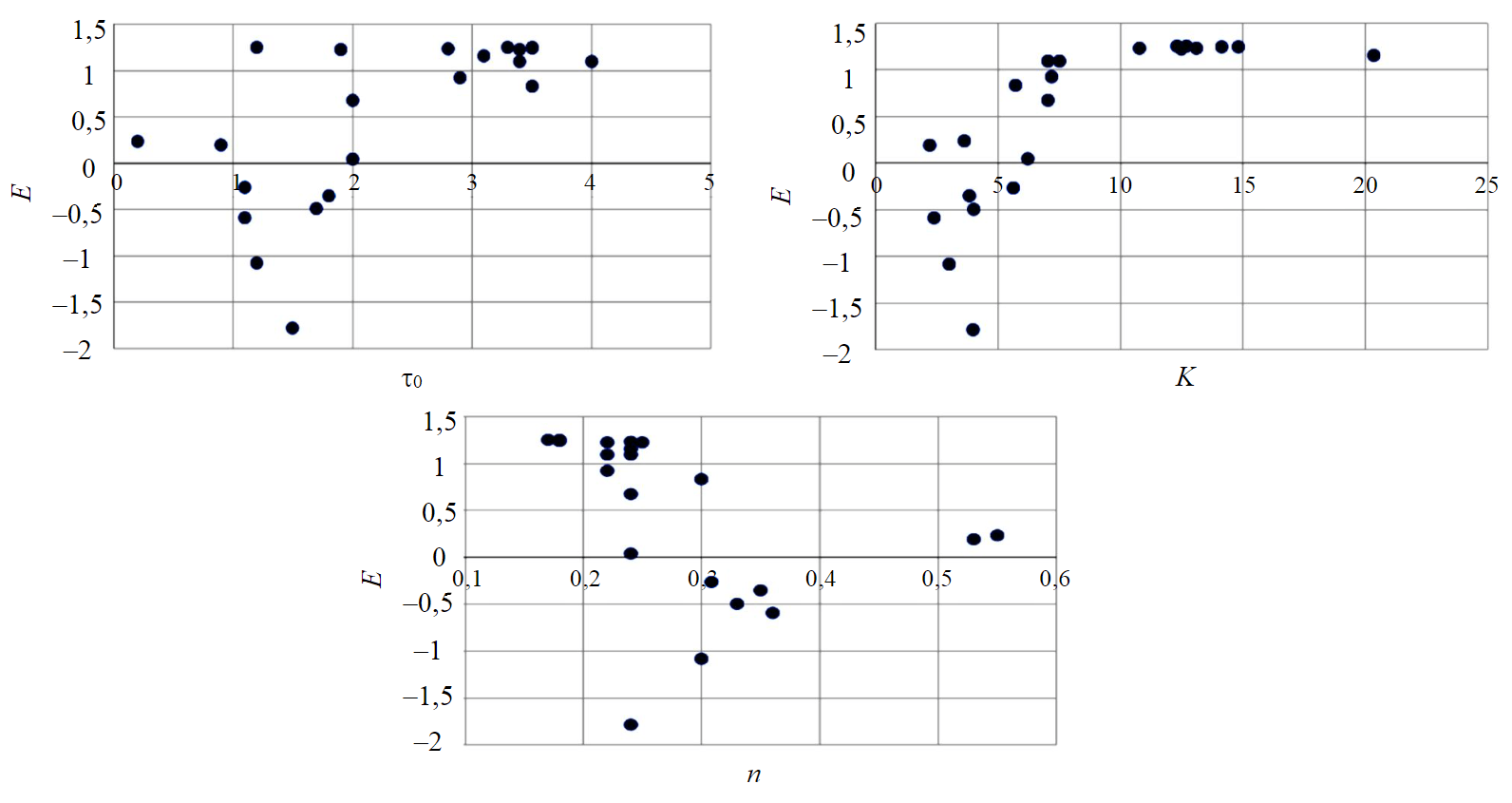
Рис.6. Корреляционные поля зависимости показателя E от коэффициентов реологической модели Гершеля – Балкли
Визуальная оценка этих связей и значения коэффициента корреляции не позволяют определить наилучшую комбинацию показателей τ0, K, nдля создания наиболее плоского профиля скорости. Абсолютное значение коэффициента корреляции, рассчитанного для каждой парной зависимости, не превышает 0,6, что также указывает на отсутствие детерминированных связей или нелинейный характер. Возможно, эта задача может быть решена с использованием методов многофакторного анализа, в том числе с применением нейросетевых технологий [37, 38], так как метод парной корреляции не дает успешных результатов. Этот факт обосновывается тем, что при решении уравнения движения для данного типа жидкостей вклад вносят все три параметра реологической модели τ0, K, n и плоский профиль скоростей достижим лишь при их определенных комбинациях. Таким образом, показано, что влияние на профиль скоростей только при помощи показателя нелинейности невозможно, как это предполагается в случае степенной модели [13]. С технологической точки зрения интересно определение связей между реологическими параметрами модели Гершеля – Балкли, обеспечивающими наиболее равномерный вынос шлама в потоке. Разработка новых составов, обеспечивающих прохождение осложненных интервалов, способных обеспечить высокое качество выноса шлама, является приоритетной задачей, включающей подбор рецептур для вскрытия продуктивных пластов [39-41]. Перспективная задача – изучение вязкоупругих свойств некоторых типов промывочных жидкостей, оказывающих влияние на вынос шлама [42].
Выводы
Определение вида профиля скорости в кольцевом пространстве скважины может быть произведено с использованием методов математического моделирования. Анализ литературных источников по теме математического моделирования гидродинамических процессов показал наличие значительных упрощений в выборе реологических моделей для описания реальных свойств буровых промывочных жидкостей. Представлена и обоснована математическая модель движения промывочной жидкости в скважине. Показан способ нахождения профиля скоростей для реологической модели типа Гершеля – Балкли. Эта реологическая модель является наиболее универсальной и предпочтительной для описания современных буровых промывочных жидкостей. Решение уравнения движения с граничными условиями для кольцевого пространства скважины жидкости Гершеля – Балкли реализовано на языке символьных вычислений Wolfram Mathematica. Анализ полученного численного решения показал соответствие вида профилей скоростей принципам гидравлики при сравнении с решениями для более простых реологических моделей. Разработанный подход можно использовать для численного тестирования параметров движения буровых промывочных жидкостей с целью оценки качества выноса шлама по профилю скоростей. По результатам исследований можно выбирать жидкость с наиболее плоским профилем скоростей. Введен модифицированный коэффициент эксцесса в качестве количественного показателя равномерности профиля скоростей потока. Проанализированы корреляционные поля зависимостей реологических параметров технологических жидкостей и показателя эксцесса. Установлено, что приближение классической степенной модели Оствальда – де Ваале с требованием снизить показатель нелинейности для более равномерного профиля скоростей для промывочных жидкостей не вполне корректно, так как данная связь не подтверждается реологической моделью Гершеля – Балкли, которая наиболее качественно аппроксимирует экспериментальные реологические кривые. Задача по определению оптимальных диапазонов реологических параметров промывочных систем, обеспечивающих наиболее качественный вынос шлама, в том числе с установлением равномерного распределения скоростей, требует дополнительного численного и экспериментального исследования. Для проведения численного эксперимента может быть рекомендован подход, описанный в настоящей работе. Результаты исследования, с учетом принятых допущений, могут быть использованы для разработки научных основ обоснования и оптимизации рецептур буровых промывочных жидкостей с применением методов математического моделирования.
Литература
- Ali I. Maqsood A., Ganat T. Experimental Study of Bentonite-Free Water Based Mud Reinforced with Carboxymethylated Tapioca Starch: Rheological Modeling and Optimization Using Response Surface Methodology (RSM) // Polymers. Vol.13. Iss. 19. № 3320. DOI: 10.3390/polym13193320
- Табатабаи Моради С.Ш., Николаев Н.И., Николаева Т.Н. Разработка составов буферных жидкостей и тампонажных растворов для крепления скважин в условиях высоких температур // Записки Горного института. Т. С. 174-178. DOI: 10.31897/PMI.2020.2.174
- Salehnezhad L., Heydari A., Fattahi M. Experimental investigation and rheological behaviors of water-based drilling mud contained starch-ZnO nanofluids through response surface methodology // Journal of Molecular Liquids. 2019. Vol. 276. P. 417-430. DOI: 10.1016/j.molliq.2018.11.142
- Vipulanandan C., Mohammed A.S. Hyperbolic rheological model with shear stress limit for acryla-mide polymer modified bentonite drilling muds // Journal of Petroleum Science and Engineering. 2014. Vol. 122. P. 38-47. DOI: 10.1016/j.petrol.2014.08.004
- Winiowski R., Skrzypaszek K., Maachowski T. Selection of a Suitable Rheological Model for Drilling Fluid Using Applied Numerical Methods // Energies. 2020. Vol. 13. Iss. 12. № DOI: 10.3390/en13123192
- Mitchell J. Trouble-Free Drilling. Volume 1: Stuck Pipe Prevention. Conroe: Drilbert Engineering, 2002. 295 p.
- Karimi M., Holt C., Moellendick T.E. Trouble Free Drilling with Casing Drilling; a Process Focused on Preventing the Drilling Problems // International Petroleum Technology Conference, 15-17 November 2011, Bangkok, Thailand. OnePetro, 2011. № IPTC-14866-MS. DOI: 10.2523/IPTC-14866-MS
- Ming Tang, Taiheng Zhang, Shiming He et al. Modeling of laminar flow in an eccentric elliptical annulus for YPL fluid // Journal of Natural Gas Science and Engineering. 2019. Vol. 64. P. 118-132. DOI: 10.1016/j.jngse.2019.02.001
- Bridges S., Robinson L. A Practical Handbook for Drilling Fluids Processing. Gulf Drilling Guides. 2020. 594p. DOI: 1016/B978-0-12-821341-4.00001-4
- Рыльцев И.А., Рыльцева К.Е., Шрагер Г.Р. Кинематика течения степенной жидкости в трубе переменного сечения // Вестник Томского государственного университета. Математика и Механика. 2020. Т. С. 125-138. DOI: 10.17223/19988621/63/11
- Epelle E.I., Obande W., Okolie J.A., Wilberforce T. CFD modelling and simulation of drill cuttings transport efficiency in annular bends: Effect of particle size polydispersity // Journal of Petroleum Science and Engineering. 2022. Vol. 208. P. 992-1004. DOI: 10.1016/j.petrol.2021.109795
- Roberts T.G., Roberts T.G., Cox S.J. An analytic velocity profile for pressure-driven flow of a Bingham fluid in a curved channel // Journal of Non-Newtonian Fluid Mechanics. 2020. Vol. 280. № 104278. DOI: 10.1016/j.jnnfm.2020.104278
- Leonov E.G., Isaev V.I. Applied Hydro-Aeromechanics in Oil and Gas Drilling. New York: John Wiley & Sons, 2010. 427 p. DOI: 10.1002/9780470542392
- Heidari M., Shahbazi K., Fattahi M. Experimental study of rheological properties of aphron based drilling Fluids and their effects on formation damage // Transactions on Chemistry and Chemical Engineering. 2017. Vol. 24. Iss. 3. P. 1241-1252. DOI: 10.24200/SCI.2017.4108
- Jimoh M.O., Salawudeen T.O., Arinkoola A.O., Daramola M.O. Rheological study of a new water-based drilling fluid using Ubakala clay in the presence of natural polymers // Chemical Engineering Communications. 2021. Vol. 208. Iss. 9. P. 1335- DOI: 10.1080/00986445.2020.1774374
- Khalil M., Jan B.M. Herschel-Bulkley rheological parameters of a novel environmentally friendly lightweight biopolymer drilling fluid from xanthan gum and starch // Journal of Applied Polymer Science. 2012. Vol. 124. Iss. 1. P. 595-606. DOI: 10.1002/APP.35004
- Chandrasekhar S.V. Annular Couette-Poiseuille flow and heat transfer of a power-law fluid – analytical solutions // Journal of Non-Newtonian Fluid Mechanics. 2020. Vol. 286. № 104402. DOI: 10.1016/j.jnnfm.2020.104402
- Добик Ю.А. Влияние вращения бурильной колонны на транспорт шлама в горизонтальной скважине // Строительство нефтяных и газовых скважин на суше и на море. 2019. № 3. С. 25-29. DOI: 10.30713/0130-3872-2019-3-25-29
- Харламов С.Н., Джангхорбани М. Процессы транспорта шлама при очистке скважин с произвольной ориентацией буровых труб, содержащих эксцентрично расположенное круглое ядро с подвижной стенкой: проблемы, результаты, перспективы (обзор) // Известия Томского политехнического университета. Инжиниринг георесурсов. 2020. Т.331. № 7. C. 131-149. DOI: 10.18799/24131830/2020/7/2725
- Mohammadsalehi M., Malekzadah N. Application of New Hole Cleaning Optimization Method within All Ranges of Hole Inclinations // International Petroleum Technology Conference, 7-9 February 2012, Bangkok, Thailand. European Association of Geoscientists & Engineers, 2012. DOI: 10.2523/IPTC-14154-MS
- Ferroudji H., Rahman M.A., Hadjadj A. et al. 3D numerical and experimental modelling of multiphase flow through an annular geometry applied for cuttings transport // International Journal of Multiphase Flow. 2022. Vol. 151. № 104044. DOI: 10.1016/j.ijmultiphaseflow.2022.104044
- Tong T.A., Mengjiao Yu, Ozbayoglu E., Takach N. Numerical simulation of non-Newtonian fluid flow in partially blocked eccentric annuli // Journal of Petroleum Science and Engineering. 2020. Vol. 193. № 107368. DOI: 10.1016/j.petrol.2020.107368
- Yeo L., Feng Y., Seibi A., Temani A. Optimization of hole cleaning in horizontal and inclined wellbores: A study with computational fluid dynamics // Journal of Petroleum Science and Engineering. 2021. Vol. 205. № 108993. DOI: 10.1016/j.petrol.2021.108993
- Busch A., Johansen S.T. Cuttings transport: On the effect of drill pipe rotation and lateral motion on the cuttings bed // Journal of Petroleum Science and Engineering. 2020. Vol. 191. № 107136. DOI: 10.1016/j.petrol.2020.107136
- Tie Yan, Jingyu Qu, Xiaofeng Sun et al. Numerical investigation on horizontal wellbore hole cleaning with a four-lobed drill pipe using CFD-DEM method // Powder Technology. 2020. Vol. 375. P. 249-261. DOI: 10.1016/j.powtec.2020.07.103
- Heshamudin N.S., Katende A., Rashid H.A., Ismail I. Experimental investigation of the effect of drill pipe rotation on improving hole cleaning using water-based mud enriched with polypropylene beads in vertical and horizontal wellbores // Journal of Petroleum Science and Engineering. 2019. Vol. 179. P. 1173-1185. DOI: 10.1016/j.petrol.2019.04.086
- Liu T., Leusheva E., Morenov V. et al. Influence of Polymer Reagents in the Drilling Fluids on the Efficiency of Deviated and Horizontal Wells Drilling // Energies. 2020. Vol. 13. № 4704. DOI: 10.3390/en13184704
- Mamane Kondo Issoufou, Xianzhi Song, Zhaopeng Zhu et al. Predicting cuttings settling velocity in drilling muds and in rising-bubbles-containing muds // Journal of Petroleum Science and Engineering. 2021. Vol. 204. № 108766. DOI: 1016/j.petrol.2021.108766
- Турбин М.В. Исследование начально-краевой задачи для модели движения жидкости Гершель-Балкли // Вестник Воронежского государственного университета. Серия: Физика. Математика. 2013. № 2. С. 247-258.
- Ming Tang, Lanfeng Yuan, Shiming He, Tao Fu. Simplified modeling of YPL fluid flow through a concentric elliptical annular pipe // Journal of Petroleum Science and Engineering. 2018. Vol. 162. P. 225-232. DOI: 10.1016/j.petrol.2017.12.030
- Nikitin V.I., Zhivaeva V.V., Nechaeva O.A., Kamaeva E.A. Influence of capillary pressure on the restoration of the bottomhole zone permeability at the filtrate-oil interfacial phase // Topical Issues of Rational Use of Natural Resources. 2019. P. 558- DOI: 10.1201/9781003014638-12
- Nikitin V.I., Nechaeva O.A., Mozgovoi G.S. Analysis of the results of the experiment to determine the saturation of the filtrate of drilling fluid of the core sample // AIP Conference Proceedings. 2021. Vol. 2410. 1. № 020014. DOI: 10.1063/5.0067566
- Nikitin V.I., Zhivaeva V.V., Mozgovoy G.S. Calculation of Saturation and Depth of Filtrate Penetration in the Primary Opening // Proceedings of the International Conference Engineering Innovations and Sustainable Development. Cham: Springer, 2022. Vol. 210. DOI: 10.1007/978-3-030-90843-0_30
- Никитин В.И., Живаева В.В., Казазян М.Г. Нахождение профиля скоростей буровых промывочных жидкостей реологической модели Гершеля – Балкли в кольцевом пространстве скважины // Строительство нефтяных и газовых скважин на суше и на море. 2021. № 11. С. 22-25. DOI: 33285/0130-3872-2021-11(347)-22-25
- Vajravelu K., Sreenadh S., Devaki P., Prasad K.V. Mathematical model for a Herschel-Bulkley fluid flow in an elastic tube // Central European Journal of Physics. Vol. 9. Iss. 5. P. 1357-1365. DOI: 10.2478/s11534-011-0034-3
- Шарафутдинов З.З., Шарафутдинова Р.З. Буровые растворы на водной основе и управление их реологическими параметрами // Нефтегазовое дело. 2004. № 1. 2 c.
- Belimanea Z., Hadjadj A., Ferroudj H. et al. Modeling surge pressures during tripping operations in eccentric annuli // Journal of Natural Gas Science and Engineering. 2021. Vol. 96. № 104233 DOI: 10.1016/j.jngse.2021.104233
- Alkinani H.H., Al-Hameedi A.T.T., Norman S.D., Lian D. Application of artificial neural networks in the drilling processes: Can equivalent circulation density be estimated prior to drilling? // Egyptian Journal of Petroleum. Vol. 29. Iss. 2. P. 121-126. DOI: 10.1016/j.ejpe.2019.12.003
- Двойников М.В., Кучин В.Н., Минцаев М.Ш. Разработка вязкоупругих систем и технологии изоляции водоносных горизонтов с аномальными пластовыми давлениями при бурении нефтегазовых скважин // Записки Горного института. 2021. Т. 247. С. 57-65. DOI: 31897/PMI.2021.1.7
- Blinov P.A., Dvoynikov M.V. Rheological and filtration parameters of the polymer salt drilling fluids based on xanthan gum // Journal of Engineering and Applied Sciences. Vol. 13. Iss. 14. P. 5661-5664. DOI: 10.3923/jeasci.2018.5661.5664
- Уляшева Н.М., Леушева Е.Л., Галишин Р.Н. Разработка композиции бурового раствора для проводки наклонно направленного ствола скважины с учетом реологических параметров жидкости // Записки Горного института. Т. 244. С. 454- 461 DOI: 10.31897/PMI.2020.4.8
- Wernera B., Myrseth V., Saasenc A. Viscoelastic properties of drilling fluids and their influence on cuttings transport // Journal of Petroleum Science and Engineering. 2017. Vol. 156. P. 845-851. DOI: 10.1016/j.petrol.2017.06.063
