Problem solution analysis on finding the velocity distribution for laminar flow of a non-linear viscous flushing fluid in the annular space of a well
- Ph.D. Associate Professor Samara State Technical University ▪ Orcid
Abstract
Modern drilling fluids are non-linear viscous media with an initial shear stress. In classical scientific works on hydromechanical modeling of drilling fluids motion in pipes and annular channels the Shvedov – Bingham approximation and Ostwald – de Waale power-law model were used, which did not fully account for behavior of technological fluids in a wide range of shear rates. This article presents a numerical solution for a mathematical model of drilling fluid motion of the three-parameter Herschel – Bulkley rheological model in the annular space of the well. The Herschel – Bulkley model in the rheological equation takes into account the presence of initial shear stress and a tendency for viscosity to change with shear rate, which distinguishes it from the Ostwald – de Waale and Shvedov – Bingham models. The target function in solving the equation of motion is the velocity distribution in the radial direction of the upward flow of the flushing fluid. The analysis of obtained solution is based on the theory of velocity profile influence on quality of cuttings removal during wellbore cleaning. Due to peculiarities of mathematical statement of the task, which supposes necessity of differential equation of motion solution, Wolfram Mathematica computational software has been used as a calculation tool. The analysis of numerical solution allowed to draw conclusions about the possibility of its application in evaluation of velocity profile when drilling fluid moves in annular space of the well. The possibility for application of modified excess coefficient as a relative quantitative parameter for evaluation of velocity profile uniformity was substantiated.
Introduction
The use of drilling fluids is mandatory when drilling oil wells. Many functions performed by flushing systems ensure safe and accident-free drilling operations. Drilling fluids are polydisperse systems with thixotropic properties. Their characterization and design must be taken into account. Simulation of drilling fluid formulations is an important but not easy task due to mathematical consideration of chemical interactions between the reagents. The variety in manufacturers of drilling fluid materials complicates this process. In general, this problem has no solution. When describing the impact of an input parameter of a formulation on an output parameter with fixed values of the others, simplifications are used, including the use of multivariate analysis [1]. As a result of designing the drilling fluids, high-quality polydisperse systems satisfying important requirements – design density, low filtration index, consideration of chemical composition requirements for drilling unstable sediments, values of viscosity characteristics, including those depending on temperature factor, can be obtained [2].
There are important technological parameters, such as total well pressure, which has an analogue in terms of equivalent circulation density, or well cleaning index based on upward flow rate and particle sedimentation rate that are calculated for well conditions, based on the choice of rheological model of the drilling fluid [3-5]. One possible hydrodynamic calculation is determining the type of flow velocity profile that affects the quality of the cuttings removal [6]. This physical phenomenon is interpreted in a way that a flat velocity profile results in a more uniform impulse transfer to the drilled rock particles. This improves the quality of their removal from the well. With an elongated velocity profile, cuttings tend to move away from the centre of the flow towards the well walls, causing them to circulate in the fluid flow and reducing the quality of wellbore cleaning [7-9]. When analyzing the quality of the transportation, depending on the type of velocity profile, it is important to specify the rheological model of the fluid, against which conclusions are drawn. The peculiarity is that fluids described by different rheological models have a significant difference in upstream velocity distribution [10-12].
Quite a number of works have been devoted to velocity profile construction of technological fluids. Fundamental research [13] analyzes the motion of Newtonian media, as well as media described by rheological models of Shvedov – Bingham and Ostwald – de Waale. Analysis of the rheological characteristics influence on velocity distributions showed the following patterns: in the motion of Newtonian media, the only significant rheological parameter is the dynamic viscosity. Its growth reduces the average flow rate. In laminar mode velocity profile is more elongated than in turbulent mode. The Shvedov – Bingham solution has a fundamental difference from Newtonian and power-law models – it is considered separately for the core of the flow and peripheral areas. The notion of a flow core implies a region in the centre of the flow, where fluid layers have the same velocity. In this model, two rheological parameters affect the shape of the velocity profile. An increase in dynamic shear stress increases the flow core, whereas an increase in plastic viscosity lowers the average velocity. The dependencies of velocity distribution on consistency index K, which is an analogue of plastic viscosity, and the non-linearity index n, reflecting the tendency of viscosity to change with a change in shear rate, are determined for a power-law rheological model. For Ostwald – de Waale model fluids, the presence of a flow core as a separate considered region is not assumed. Analysis of the available analytical solution shows a characteristic reduction in the average flow velocity when the rheological model index K increases and a flatter velocity profile when the coefficient n decreases. The general pattern for non-Newtonian media is that in turbulent mode the velocity profile is more elongated than in laminar mode. This is explained by the presence of a thixotropic structure in contrast to Newtonian media.
The applicability of the described rheological models to the description of modern drilling fluids has a number of limitations. The Newtonian model is unsuitable for simulating rheological properties of drilling systems, as it does not account for initial shear stress and the possibility of viscosity changing with motion. The Shvedov – Bingham rheological equation does not take into account the viscosity change with shear rate. The Ostwald – de Waale power-law model takes viscosity change into account, but does not include an initial shear stress. Since modern flushing fluids have an initial shear stress and tend to change viscosity with changes in shear rate, it becomes necessary to use a modified Herschel – Bulkley power law that considers both features of a non-Newtonian medium [14-16]. Research in simulation of fluid motion is limited to the Shvedov – Bingham and Ostwald – de Waale models, which do not take into account real parameters of the medium in sufficient accuracy [12, 17]. When searching for solution of motion equation for three-parameter Herschel – Bulkley fluid model, mathematical complexity of the problem increases and calculation result is closer to real technological conditions.
Theoretical and experimental investigations are known, the purpose of which is the effect of eccentricity and drill string rotation on well pressure and wellbore cleaning [18-20]. For simulation of dynamic pressure and multiphase flows, the ANSYS control volume method or its analogues are often used [21-23]. In [24] the control volume method simulates flows in the case of negative eccentric, concentric and positive eccentric drill string location in the wellbore. In [25] the influence of drill pipe shape on secondary flows and cuttings removal is evaluated using CFD-DEM simulation. Cuttings removal problems are also solved experimentally [26-28]. In [29] it has been proved that there is a weak solution of initial-boundary value problem with interface sticking condition for mathemati-cal model of Herschel – Bulkley fluid flow. In describing the solution for Herschel – Bulkley annular fluid flow problem, the authors of [30] discuss a simplified solution for velocity distribution in integ-ral form, assuming the flow core and two peripheral areas with their further simulation in the hydraulic simulation package CFD of the ANSYS software. This assumption is a simplification and does not allow evaluating the influence of rheological parameters of the fluid on the formation of a uniform velocity distribution, as it is supposed that there is the presence of the flow core for the Herschel – Bulkley model fluid with any combination of coefficients. If the modified power law is considered as a combination of Shvedov – Bingham and Ostwald – de Waale models, for the former of which the presence of the flow core is a standard assumption, then for the classical power law this simplification is not accepted, and the formation of a uniform velocity distribution is considered as a function of the non-linearity index. Therefore, when formulating the problem of velocity profile evaluation, influencing the cuttings removal quality, the simplification concerning the presence of flow core as a mandatory part is incorrect and its solution cannot lead to the proper analysis of the flushing technological process. The practical application of mathematical modeling methods of flows in a well is the possibility to estimate the influence of rheological parameters of the fluid on the efficiency of cuttings removal. The difference of problem statement from known investigations is a solution for velocity distribution taking into account three parameters of rheological model, which most qualitatively reflects real properties of drilling mud. The result of research can be applied to determination of optimum ranges for rheological parameters of flushing fluids for the development of new, most quality formulations.
Based on the conducted research on the motion of non-Newtonian media in pipes and annular channels, the task of finding and analyzing numerical solution of Herschel – Bulkley fluid motion equations in the annular space of a well in laminar mode has been set. The choice of such mode is justified by the presence of more uniform velocity profile of non-Newtonian media in comparison with turbulent one and less pressure loss in annular space. In laminar mode, the lowest pressure loss allows to minimize filtration of liquid phase into the formation, which is also an urgent task in well flushing [31-33]. Mathematical formulation of the laminar Herschel – Bulkley problem in the annular space of the well allows to find a numerical solution for the velocity profile as a function of radial coordinate without using finite element methods.
Methodology
The presented stationary one-dimensional Herschel – Bulkley model of fluid motion does not represent all aspects of the physical behaviour of non-Newtonian fluid flow in an annular space, but it can show a certain trend. This allows to simulate the movement of drilling fluids with some assumptions.
For the considered plane flow, the following assumptions are valid:
- fluid is incompressible, isotropic, non-linearly viscous;
- motion is stationary;
- motion is plane-parallel, i.e. all characteristics are independent of the z-axis, flow is laminar;
- fluid particles move only because of the pressure gradient;
- the circular channel is considered vertical and concentric.
The mathematical formulation of the problem on finding the velocity distribution in laminar mode of Herschel – Bulkley fluid motion in the annular space of the well consists in solving the stationary modified Navier – Stokes differential equation of motion [34, 35]
where ρ – fluid density; r – radial coordinate; g – acceleration of gravity.
The tangential stresses included in equation (1) depend on the velocity w. The parameter included in equation of motion (1), is the Herschel – Bulkley rheological model equation, which is the defining ratio reflecting the relationship between shear stresses and shear rate,
where τ0 – initial shear stress; $\dot{γ}$ – shear rate.
Function (2) is defined in the entire range of shear rate $\dot{γ}$ Sign “+” is taken at $\dot{γ}$ > 0, “–” at $\dot{γ}$< 0, and = 0 at |τ| ≤ τ0 [13].
The velocity distribution in the radial direction is found from the relationship between the shear rate and the velocity gradient:
where w – velocity component along the coordinate z, aligned with the pipe axis; t – time.
The equation of motion (1) is supplemented by the incompressibility condition
From the assumption of one-dimensional flow and the continuity equation a condition for the velocity distribution is imposed
with appropriate boundary conditions for the annular space:
where R1 – external radius of drill pipes; R2 – well radius; din, dex – corresponding diameters; L – the length of the considered well section.
These conditions reflect sticking conditions on drill pipe and well wall and for pressure gradient included in equation (1). The well annular space scheme with boundary conditions for velocity field is shown in Fig.1. In the modeling problem of cuttings removal from the annular space of vertical well, it is assumed that the flow of flushing fluid moves in the direction of z-axis. Free fall acceleration acts in opposite direction.
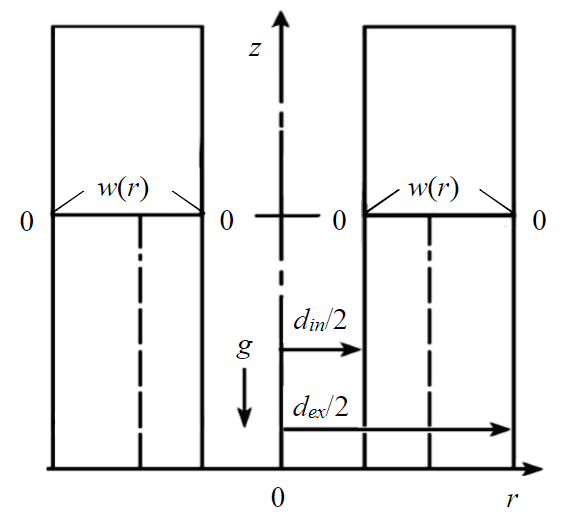
Fig.1. The well annular space scheme with boundary conditions for velocity field
In this formulation of the problem, the velocity distribution is symmetric with respect to the z-axis. Consequently, the solution will be sought for the plane form of motion in the range R1 < r < R2.
This problem is solved with the Wolfram Mathematica software, which uses the NDSolve function for the numerical solution of differential equations to find the desired velocity distribution function w(r) in the form of an interpolating function structure (Interpolating Function). Interpolating Function – is an object, which is a table of function values w(ri) at various points in the interval [R1, R2] that allows finding the function value at any point in this interval by interpolating the calculated data. The function is assumed to be even between the given points. The interpolation function can be treated as any built-in function, i.e. differentiate, integrate or build its graph. When plotting velocity distributions, a dimensionless velocity is used, which is, for each fluid, the ratio of the radial velocity distribution to the average flow velocity w$w(r)/\overline{w}$. Analysis of the velocity distributions on a scale of dimensionless variables allows a qualitative assessment of the presence of a flat profile trend.
To test the computational methods implemented in Wolfram Mathematica, the analytical solution for the problem of laminar motion of a Newtonian fluid in an annular gap is compared with the solution obtained numerically. The laminar steady flow of a viscous fluid that occurs under the effect of a longitudinal pressure gradient is also called a Poiseuille flow [13]. The analytical solution for the velocity profile is:
The input parameters for the rheological model (2) are a combination of τ0= 0, n = 1, K = 0.001 Pa·s. This set of parameters corresponds to the characteristics of water at 20 °С. The Herschel – Bulkley model takes the form of a Newtonian medium model and the consistency index corresponds to the dynamic viscosity parameter. As geometrical parameters for the calculations, a 50 mm gap between well wall and outer wall of the drill pipe was taken, with radii R2 = 107.15 and R1 = 57.15 mm respectively. Pressure gradient calculated according to [13] equals 0.09239 Pa/m. This pressure gradient corresponds to a flow rate of 0.0005 m3/s through an annular channel cross-section with the specified geometrical parameters. Reynolds number – Re = 1937 calculated for Newtonian medium flow in the annular channel at a velocity of 0.01937 m/s, confirms the existence of laminar flow mode. Comparison of the velocity profiles proves the validity of the computational method as the result of the numerical calculation coincides with the known analytical solution. Based on this comparison, it is assumed that the described calculation method can be applied to the solution of the fluid motion problem of the Herschel – Bulkley rheological model in the annular space.
To measure the formation of a flat velocity profile when comparing several fluids, a modified excess coefficient has been proposed
where μ2 and μ4 – central moments.
This modified excess coefficient, calculated using second- and fourth-order empirical central moments, is a relative value used in quantifying the uniformity of velocity distributions of fluids that differ by the rheological coefficients of the Herschel – Bulkley model and move under the same well conditions. Arguments of central moments, similar to sampling method from mathematical statistics, are values of dimensionless velocity calculated numerically along the radial component. Minimality of this parameter is the criterion of the most uniform velocity distribution along the radial flow direction in the comparative analysis. The use of such quantitative parameter may allow to determine the dependence of velocity profile type on rheological characteristics of flushing fluids.
The input data for the calculations were the parameters of 22 flushing fluids from the study [36]. The presented fluid parameters are fully suitable for numerical flow simulation and contain the rheological parameters of the Herschel – Bulkley model τ0, K, n. These parameters were determined using a Fann digital electronic rheometer model 286. As parameter τ0, a specified value of static shear stress in 10 seconds is taken for the calculation of velocity profiles. Rheological properties of the drilling fluids from the study [36] are shown in Table 1. As geometrical parameters for the calculations, a 50 mm gap between well wall and outer wall of the drill pipe with diameters of 214.3 and 114.3 mm respectively was taken. During the calculations fixed model parameters of fluid density 1200 kg/m3 and pressure gradient 500 Pa/m were used, corresponding to laminar mode of flushing fluids motion in annular space [13].
Table 1
Rheological characteristics of drilling fluids depending on the mechanism of reagent dissolution in water
|
Fluid |
Structure former |
C, % |
Static shear stress, Pa |
Consistency |
Non-linearity |
|
|
10 s |
10 min |
|||||
|
1 |
CMC HV + PAC R |
0.1 + 0.15 |
3.5 |
4.5 |
14.80 |
0.18 |
|
2 |
CMC LV + PAC L |
0.15 + 0.15 |
1.2 |
3.7 |
12.70 |
0.17 |
|
3 |
Barazan + PAC R |
0.05 + 0.15 |
3.3 |
4.1 |
12.31 |
0.18 |
|
4 |
Barazan + CMC HV |
0.05 + 0.20 |
3.4 |
3.5 |
7.51 |
0.22 |
|
5 |
Barazan + CMC LV |
0.05 + 0.35 |
3.4 |
3.5 |
13.11 |
0.22 |
|
6 |
Barazan + PAC L |
0.05 + 0.3 |
2.9 |
3.3 |
7.17 |
0.22 |
|
7 |
KSSB-2 + РАС R |
1.0 + 0.15 |
2.0 |
2.9 |
7.02 |
0.24 |
|
8 |
KSSB-2 + СМС HV |
1.0 + 0.20 |
2.0 |
2.2 |
6.21 |
0.24 |
|
9 |
Glycerine + РАС R |
3.0 + 0.15 |
2.8 |
3.5 |
10.76 |
0.24 |
|
10 |
Glycerine + СМС HV |
3.0 + 0.2 |
4.0 |
5.1 |
7.04 |
0.24 |
|
11 |
Glycerine + СМС LV |
3.0 + 0.35 |
1.5 |
2.3 |
3.97 |
0.24 |
|
12 |
Glycerine + IKPAN SL |
3.0 + 0.4 |
3.1 |
3.3 |
20.35 |
0.24 |
|
13 |
Glycerine + IKPAN R |
3.0 + 0.4 |
1.9 |
2.1 |
12.47 |
0.25 |
|
14 |
Glycerine + РАС L |
3.0 + 0.35 |
1.2 |
2.1 |
2.98 |
0.30 |
|
15 |
NTF + РАС R |
0.15 + 0.15 |
3.5 |
3.9 |
14.12 |
0.18 |
|
16 |
NTF + SMSNU |
0.15 + 0.20 |
3.5 |
3.9 |
5.70 |
0.30 |
|
17 |
РАС L + EZ MUD |
0.35 + 0.05 |
1.1 |
1.7 |
5.62 |
0.31 |
|
18 |
CMC LV + IKPAN SL |
0.2 + 0.4 |
1.7 |
2.3 |
4.01 |
0.33 |
|
19 |
РАС L + IKPAN SL |
0.2 + 0.4 |
1.8 |
2.4 |
3.81 |
0.35 |
|
20 |
CMC LV + EZ MUD |
0.35 + 0.05 |
1.1 |
1.2 |
2.39 |
0.36 |
|
21 |
NTF + IKPAN SL |
0.15 + 0.4 |
0.9 |
2.2 |
2.20 |
0.53 |
|
22 |
NTF + IKPAN R |
0.15 + 0.4 |
0.2 |
1.0 |
3.60 |
0.55 |
Discussion
As a result of numerical experiment, velocity distributions for 22 flushing fluids with pseudoplastic rheological structure described by Herschel – Bulkley model (2) were obtained for given well conditions. The solution for the equation of motion (1) in Wolfram Mathematica with consideration of (3)-(5) and boundary conditions for the well annular space (6) is an interpolating function structure with a determination area within R1≤r≤R2. The value range of the interpolating function contains dimensionless velocity distribution as a function of radial coordinate. Graphic representations of velocity distributions are shown in Fig.2. Corresponding values of modified excess coefficient are shown as a bar graph in Fig.3, a. Analysis of calculated values for the modified excess coefficient (8) shows that the smallest values were obtained for fluids 11, 14 and 20. Therefore, according to its purpose these fluids have the flattest velocity profiles, contributing to better cuttings removal than fluids 1, 2 and 3 with highest excess coefficient. Such conclusion is confirmed
by graphic analysis of velocity distributions in Fig.2, b, where the most elongated and flat profiles are presented.
In addition to velocity profile graphs, Fig.3, b shows average flow velocity values for each fluid. Significant is the observation that fluids 11, 14, 20 have the highest average velocity. High values of average flow velocity also make them most preferable. The upward flow velocity should exceed the settling velocity of the cuttings. A flat velocity profile prevents accumulation of drilled rock particles at the well walls and their further circulation in the flow [6].
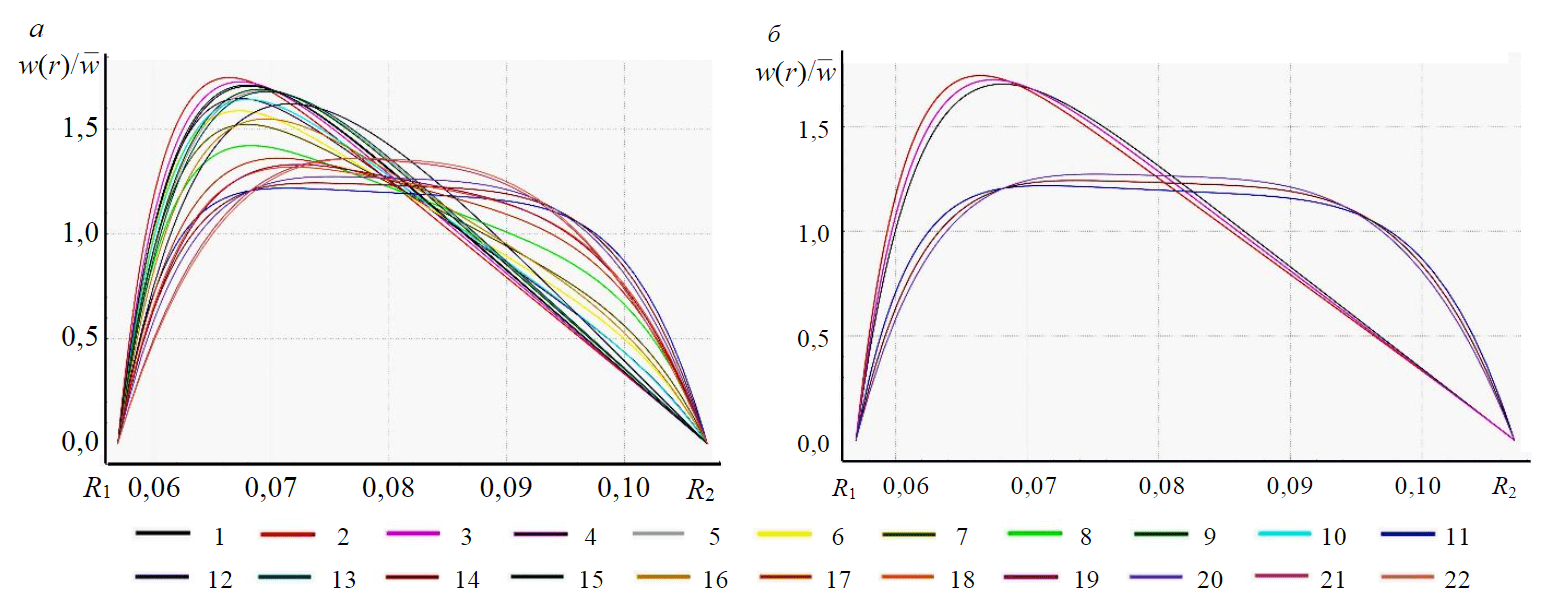
Fig.2. Velocity distributions in annular space for the 22 flushing fluids tested (a); the flattest and most peaked flushing fluid velocity profiles (b) 1-22 – fluid number (Table 1)
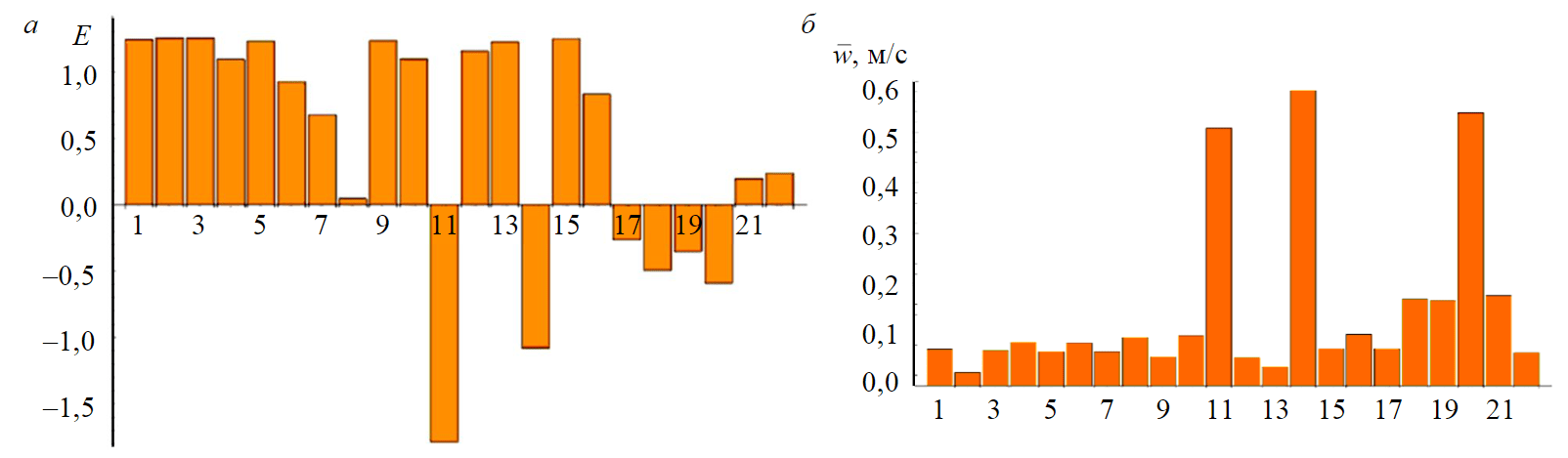
Fig.3. Characteristics of velocity distributions: modified excess coefficient (a); average velocity (b) 1-22 – fluid number (Table 1)
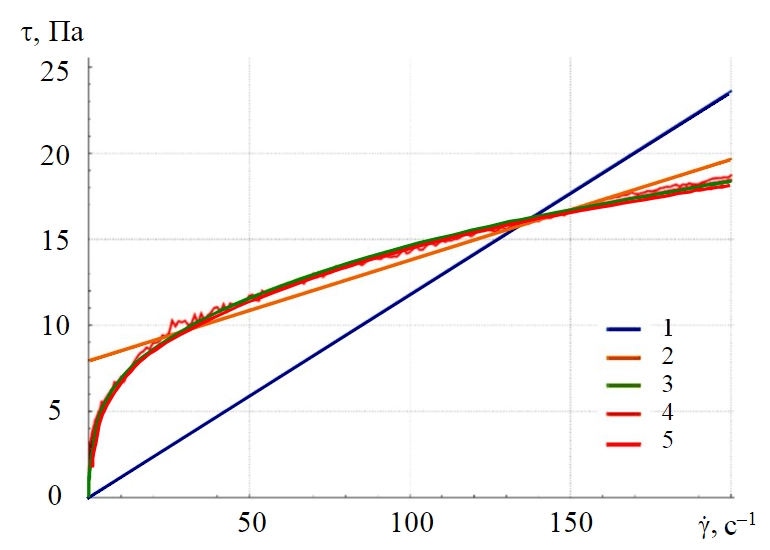
Fig.4. Approximation of the experimental dependence τ($\dot{γ}$) by rheological models 1 – Newton (0.118084$\dot{γ}$); 2 – Shvedov – Bingham (0.0585243$\dot{γ}$ + 7.96111); 3 – Ostwald – de Waale (3.17628$\dot{γ}$ 0.331203); 4 – Herschel – Bulkley (2.33712$\dot{γ}$0.375308 + 1.39014); 5 – experiment
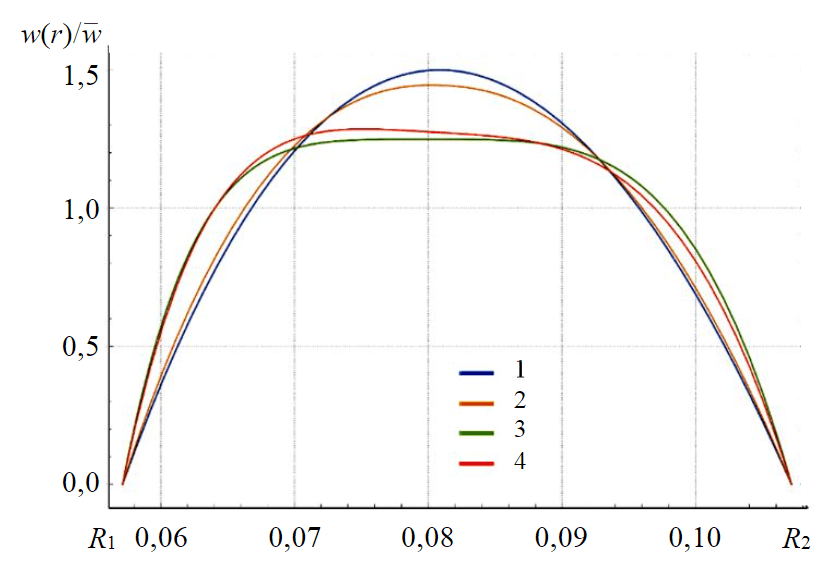
Fig.5. Velocity distributions in the annular space for different rheological models 1 – Newton; 2 – Shvedov – Bingham; 3 – Ostwald – de Waale; 4 – Herschel – Bulkley
Note, that obtained type of graphs (see Fig.2) tends to shift flow towards drill pipe axis. This tendency corresponds to the results presented in [13, 37] for Newtonian, Bingham and power-law fluid models. The significant difference of the obtained solution for Herschel – Bulkley model from the classical power-law model is dependence of velocity profile on τ0, K, n values and not only on n and K values. For the power-law model it has been found that decreasing n leads to the presence of a flat velocity profile, whereas for the Herschel – Bulkley model this statement is not true. The Bingham model takes into account the τ0 and K values, which is a significant simplification. For the Bingham model it is found that decreasing the plastic viscosity, i.e. K at , reduces the average flow velocity, and increasing t0 results in a wider flow core, namely a region in the velocity profile moving with uniform velocity. Graphs Fig.2 show that for some fluids tendency to form flow core is established (fluids 11, 14, 20), in contrast to others (fluids 1, 2, 3).
In a number of applications, drilling fluids can be described by simpler rheological equations than the Herschel – Bulkley model. Let us consider the different types of velocity profiles depending on the chosen rheological model. We will use the experimental data obtained by testing a polymer-clay flushing fluid with an Anton Paar Physica MCR52 rheometer. The experimental dependence τ(γ) was approximated by the least-squares method. The plotted rheological curves are shown in Fig.4. It is obvious that the best approximation corresponds to the Herschel – Bulkley model. Let us consider the difference between the velocity profiles for each rheological model. For this purpose, let us use sets of parameters τ0, K, n of corresponding equations. These parameters are presented in Table 2. Velocity profiles in annular space for Newton, Shvedov – Bingham, Ostwald – de Waale and Herschel – Bulkley models are presented in Fig.5. The same conditions as for the 22 previously tested fluids were used as input motion parameters. In contrast to classical hydromechanical works, in which the flow core is an assumption for the Shvedov – Bingham medium and the analytical solution is constructed in piecewise form, the numerical solution does not suppose such an assumption and the velocity profiles for Newtonian and Shvedov – Bingham media are similar for a given flushing fluid. For the Shvedov – Bingham medium, there is a slight deviation of the flow to the pipe wall and a less elongated profile. For power-law models there is a characteristic shift of the flow centre towards the pipe wall. The Ostwald – de Waale model has the flattest distribution, as indicated by the smallest value of the modified excess coefficient. The Ostwald – de Waale rheological model neglects the presence of the initial shear stress τ0, which is present in the drilling fluids. This fact is also confirmed by graphs in Fig.4 and data of Table 2.
Table 2
Parameters of rheological models for polymer-clay flushing fluid
|
Rheological model |
τ0, Pa |
Consistency index K, Pa·sn |
Non-linearity index n |
|
Newton |
0 |
0.118 |
1 |
|
Shvedov – Bingham |
7.961 |
0.059 |
1 |
|
Ostwald – de Waale |
0 |
3.176 |
0.331 |
|
Herschel – Bulkley |
1.39 |
2.337 |
0.375 |
It is reasonable to establish the relationship between the rheological parameters of the Herschel – Bulkley model and the presence of a flat velocity profile. For this purpose, correlation analysis me-thods have been used to construct correlations between the fluid parameters τ0, K, n and Е. Paired correlation fields are shown in Fig.6.
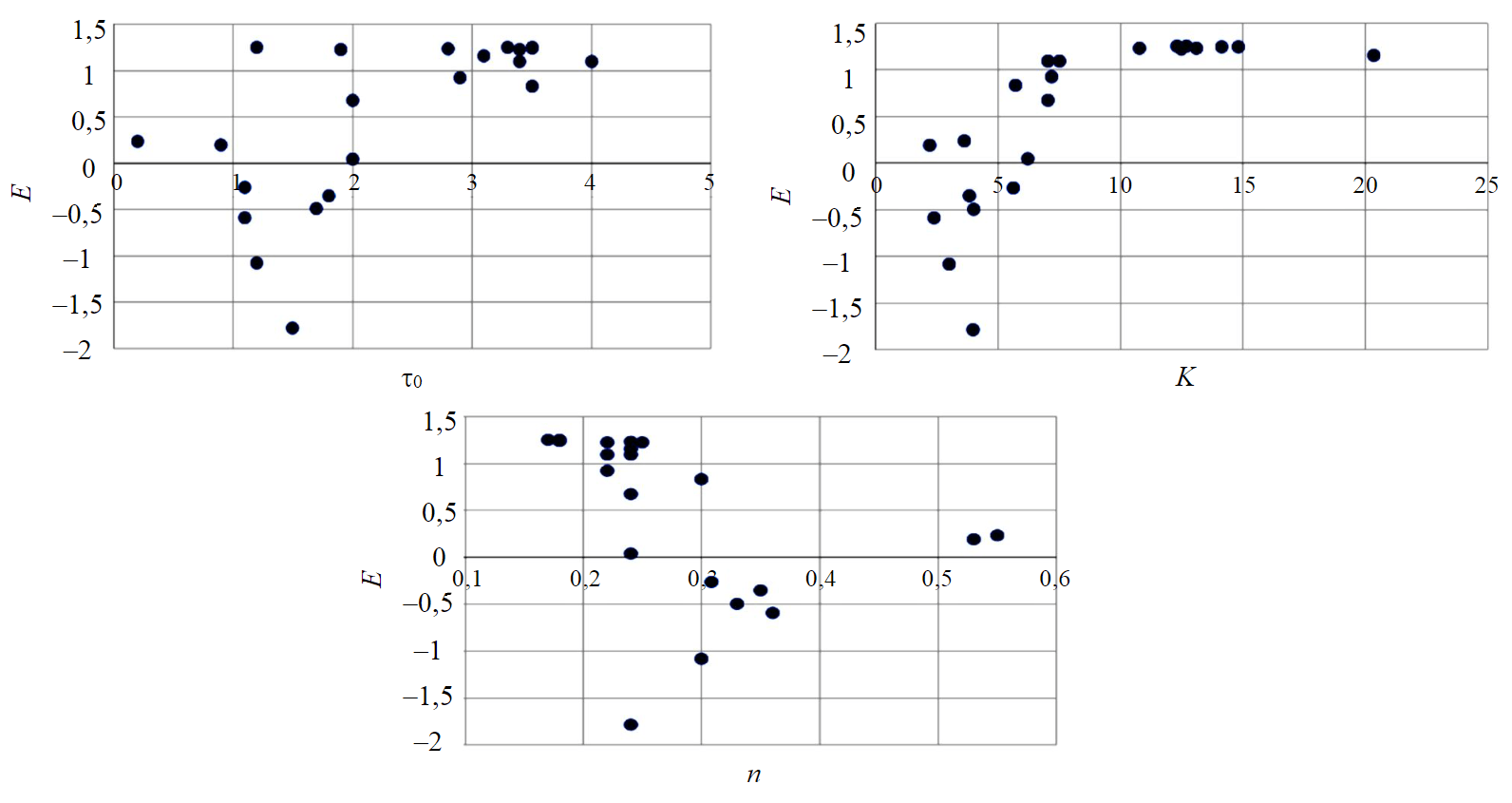
Fig.6. Correlation fields of E index dependence on coefficients of Herschel – Bulkley rheological model
Visual assessment of these relationships and correlation coefficient values does not allow to determine the best combination of τ0, K, n indicators to create the flattest velocity profile. The absolute value of the correlation coefficient calculated for each paired relationship does not exceed 0.6, which also indicates the absence of deterministic relationships or non-linear nature. It is possible that this problem can be solved using multivariate analysis methods, including neural network techniques [37, 38], as the paired correlation method does not produce successful results. This is justified by the fact that when solving the equation of motion for this type of fluids, all three parameters of the rheological model τ0, K, n are important and a flat velocity profile is achievable only with certain combinations of these parameters. Thus, it is shown that influencing the velocity profile by the non-linearity index alone is not possible, as it is assumed in the case of the power-law model [13]. From a technological point of view, it is interesting to determine the relationship between the rheological parameters of the Herschel – Bulkley model, which provide the most uniform cuttings removal in the flow. The development of new compositions, which provide the penetration of complicated intervals, able to provide high quality of cuttings removal, is a priority task, including the selection of formulations for the drilling-in the productive formations [39-41]. A promising task is to study the viscoelastic properties of some types of flushing fluids, which influence cuttings removal [42].
Conclusions
Determination of velocity profile type in annular space of the well can be performed using methods of mathematical modeling. The analysis of literary sources on the subject of mathematical modeling of hydrodynamic processes has shown the presence of considerable simplifications in the choice of rheological models for description of real properties of drilling fluids. Ma-thematical model of flushing fluid motion in a well is presented and justified. The way of finding velocity profile for rheological model of Herschel – Bulkley is shown. This rheological model is the most universal and preferable for description of modern drilling fluids. The solution for the equation of motion with boundary conditions for the well annular space of Herschel – Bulkley fluid has been realized with Wolfram Mathematica symbolic computing language. The analysis of the numerical solution demonstrated the compatibility of the velocity profiles with hydraulic principles when comparing them with the solutions for simpler rheological models. The developed approach could be used for numerical testing of drilling fluid flow parameters in order to estimate the quality of cuttings removal along the velocity profile. Based on the results of the research it is possible to select fluid with the flattest velocity profile. Modified excess coefficient as a quantitative index of the uniformity of flow velocity profile is introduced. Correlation fields of dependencies for rheological parameters of technological fluids and excess index are analyzed. It is established, that approximation of classical power-law model of Ostwald – de Waale with requirement of non-linearity parameter reduction for more uniform profile of velocity for flushing fluids is not quite correct, as the given relation is not confirmed by rheological model of Herschel – Bulkley, which approximates the experimental rheological curves most qualitatively. The task on definition of optimal ranges for rheological parameters of flushing systems, providing the most qualitative cuttings removal, including the establishment of uniform velocity distribution, requires additional numerical and experimental research. For carrying out numerical experiment, the approach described in the present work can be recommended. The results of investigation with consideration of accepted assumptions can be used for development of scientific basis for justification and optimization of drilling fluids with application of mathematical modeling methods.
References
- Ali I. Maqsood A., Ganat T. Experimental Study of Bentonite-Free Water Based Mud Reinforced with Carboxymethylated Tapioca Starch: Rheological Modeling and Optimization Using Response Surface Methodology (RSM). Polymers. 2021. Vol. 13. Iss. 19. N 3320. DOI: 10.3390/polym13193320
- Tabatabaee Moradi S.S., Nikolaev N.I., Nikolaeva T.N. Development of spacer fluids and cement slurries compositions for lining of wells at high temperatures. Journal of Mining Institute. 2020. Vol. 242, p. 174-178. DOI: 10.31897/PMI.2020.2.174
- Salehnezhad L., Heydari A., Fattahi M. Experimental investigation and rheological behaviors of water-based drilling mud contained starch-ZnO nanofluids through response surface methodology. Journal of Molecular Liquids. 2019. Vol. 276, p. 417-430. DOI: 10.1016/j.molliq.2018.11.142
- Vipulanandan C., Mohammed A.S. Hyperbolic rheological model with shear stress limit for acryla-mide polymer modified bentonite drilling muds. Journal of Petroleum Science and Engineering. 2014. Vol. 122, p. 38-47. DOI: 10.1016/j.petrol.2014.08.004
- Winiowski R., Skrzypaszek K., Maachowski T. Selection of a Suitable Rheological Model for Drilling Fluid Using Applied Numerical Methods. Energies. 2020. Vol. 13. Iss. 12. N 3192. DOI: 10.3390/en13123192
- Mitchell J. Trouble-Free Drilling. Volume 1: Stuck Pipe Prevention. Conroe: Drilbert Engineering, 2002, p. 295.
- Karimi M., Holt C., Moellendick T.E. Trouble Free Drilling with Casing Drilling; a Process Focused on Preventing the Drilling Problems. International Petroleum Technology Conference, 15-17 November 2011, Bangkok, Thailand. OnePetro, 2011. N IPTC-14866-MS. DOI: 10.2523/IPTC-14866-MS
- Ming Tang, Taiheng Zhang, Shiming He et al. Modeling of laminar flow in an eccentric elliptical annulus for YPL fluid. Journal of Natural Gas Science and Engineering. 2019. Vol. 64, p. 118-132. DOI: 10.1016/j.jngse.2019.02.001
- Bridges S., Robinson L. A Practical Handbook for Drilling Fluids Processing. Gulf Drilling Guides. 2020, p. 594. DOI: 10.1016/B978-0-12-821341-4.00001-4
- Ryltsev I.A., Ryltseva K.E., Shrager G.R Kinematics of a Power-Law Fluid Flow in a Pipe with a Varying Cross-Section. Tomsk State University Journal of Mathematics and Mechanics. 2020. Vol. 63, p. 125-138 (in Russian). DOI: 10.17223/19988621/63/11
- Epelle E.I., Obande W., Okolie J.A., Wilberforce T. CFD modelling and simulation of drill cuttings transport efficiency in annular bends: Effect of particle size polydispersity. Journal of Petroleum Science and Engineering. 2022. Vol. 208, p. 992-1004. DOI: 10.1016/j.petrol.2021.109795
- Roberts T.G., Roberts T.G., Cox S.J. An analytic velocity profile for pressure-driven flow of a Bingham fluid in a curved channel. Journal of Non-Newtonian Fluid Mechanics. 2020. Vol. 280. N 104278. DOI: 10.1016/j.jnnfm.2020.104278
- Leonov E.G., Isaev V.I. Applied Hydro-Aeromechanics in Oil and Gas Drilling. New York: John Wiley & Sons, 2010, p. 427. DOI: 10.1002/9780470542392
- Heidari M., Shahbazi K., Fattahi M. Experimental study of rheological properties of aphron based drilling Fluids and their effects on formation damage. Transactions on Chemistry and Chemical Engineering. 2017. Vol. 24. Iss. 3, p. 1241-1252. DOI: 10.24200/SCI.2017.4108
- Jimoh M.O., Salawudeen T.O., Arinkoola A.O., Daramola M.O. Rheological study of a new water-based drilling fluid using Ubakala clay in the presence of natural polymers. Chemical Engineering Communications. 2021. Vol. 208. Iss. 9, p. 1335-1343. DOI: 10.1080/00986445.2020.1774374
- Khalil M., Jan B.M. Herschel-Bulkley rheological parameters of a novel environmentally friendly lightweight biopolymer drilling fluid from xanthan gum and starch. Journal of Applied Polymer Science. 2012. Vol. 124. Iss. 1, p. 595-606. DOI: 10.1002/APP.35004
- Chandrasekhar S.V. Annular Couette-Poiseuille flow and heat transfer of a power-law fluid – analytical solutions. Journal of Non-Newtonian Fluid Mechanics. 2020. Vol. 286. N 104402. DOI: 10.1016/j.jnnfm.2020.104402
- Dobik Yu.A. The Effect of the Casing String Rotation on Drill Cuttings Transportation in a Horizontal Well. Construction of Oil and Gas Wells on Land and Sea. 2019. N 3, p. 25-29 (in Russian). DOI: 10.30713/0130-3872-2019-3-25-29
- Kharlamov S.N., Janghorbani M. Cuttings Transport in Hole Cleaning Considering Well Orientation, Pipe Eccentricity and Pipe Rotation: Problems, Results, Prospects (Survey). Bulletin of the Tomsk polytechnic university. Geo assets engineering. 2020. Vol. 331. N 7, p. 131-149 (in Russian). DOI: 10.18799/24131830/2020/7/2725
- Mohammadsalehi M., Malekzadah N. Application of New Hole Cleaning Optimization Method within All Ranges of Hole Inclinations. International Petroleum Technology Conference, 7-9 February 2012, Bangkok, Thailand. European Association of Geoscientists & Engineers, 2012. DOI: 10.2523/IPTC-14154-MS
- Ferroudji H., Rahman M.A., Hadjadj A. et al. 3D numerical and experimental modelling of multiphase flow through an annular geometry applied for cuttings transport. International Journal of Multiphase Flow. 2022. Vol. 151. N 104044. DOI: 10.1016/j.ijmultiphaseflow.2022.104044
- Tong T.A., Mengjiao Yu, Ozbayoglu E., Takach N. Numerical simulation of non-Newtonian fluid flow in partially blocked eccentric annuli. Journal of Petroleum Science and Engineering. 2020. Vol. 193. N 107368. DOI: 10.1016/j.petrol.2020.107368
- Yeo L., Feng Y., Seibi A., Temani A. Optimization of hole cleaning in horizontal and inclined wellbores: A study with computational fluid dynamics. Journal of Petroleum Science and Engineering. 2021. Vol. 205. N 108993. DOI: 10.1016/j.petrol.2021.108993
- Busch A., Johansen S.T. Cuttings transport: On the effect of drill pipe rotation and lateral motion on the cuttings bed. Journal of Petroleum Science and Engineering. 2020. Vol. 191. N 107136. DOI: 10.1016/j.petrol.2020.107136
- Tie Yan, Jingyu Qu, Xiaofeng Sun et al. Numerical investigation on horizontal wellbore hole cleaning with a four-lobed drill pipe using CFD-DEM method. Powder Technology. 2020. Vol. 375, p. 249-261. DOI: 10.1016/j.powtec.2020.07.103
- Heshamudin N.S., Katende A., Rashid H.A., Ismail I. Experimental investigation of the effect of drill pipe rotation on improving hole cleaning using water-based mud enriched with polypropylene beads in vertical and horizontal wellbores. Journal of Petroleum Science and Engineering. 2019. Vol. 179, p. 1173-1185. DOI: 10.1016/j.petrol.2019.04.086
- Liu T., Leusheva E., Morenov V. et al. Influence of Polymer Reagents in the Drilling Fluids on the Efficiency of Deviated and Horizontal Wells Drilling. Energies. 2020. Vol. 13. N 4704. DOI: 10.3390/en13184704
- Mamane Kondo Issoufou, Xianzhi Song, Zhaopeng Zhu et al. Predicting cuttings settling velocity in drilling muds and in rising-bubbles-containing muds. Journal of Petroleum Science and Engineering. 2021. Vol. 204. N 108766. DOI: 10.1016/j.petrol.2021.108766
- Turbin M.V. Investigation of initial-boundary valye problem for the herschel-bulkley mathematical fluid model. Vestnik Voronezhskogo gosudarstvennogo universiteta. Seriya: Fizika. Matematika. 2013. N 2, р. 247-258 (in Russian).
- Ming Tang, Lanfeng Yuan, Shiming He, Tao Fu. Simplified modeling of YPL fluid flow through a concentric elliptical annular pipe. Journal of Petroleum Science and Engineering. 2018. Vol. 162, p. 225-232. DOI: 10.1016/j.petrol.2017.12.030
- Nikitin V.I., Zhivaeva V.V., Nechaeva O.A., Kamaeva E.A. Influence of capillary pressure on the restoration of the bottomhole zone permeability at the filtrate-oil interfacial phase. Topical Issues of Rational Use of Natural Resources. 2019, p. 558-562. DOI: 10.1201/9781003014638-12
- Nikitin V.I., Nechaeva O.A., Mozgovoi G.S. Analysis of the results of the experiment to determine the saturation of the filtrate of drilling fluid of the core sample. AIP Conference Proceedings. 2021. Vol. 2410. Iss. 1. N 020014. DOI: 10.1063/5.0067566
- Nikitin V.I., Zhivaeva V.V., Mozgovoy G.S. Calculation of Saturation and Depth of Filtrate Penetration in the Primary Opening. Proceedings of the International Conference Engineering Innovations and Sustainable Development. Cham: Springer, 2022. Vol. 210. DOI: 10.1007/978-3-030-90843-0_30
- Nikitin V.I., Zhivaeva V.V., Kazazyan M.G. Calculation of Drilling Fluids Velocity Profile of the Herschel – Bulkley Rheological Model in the Annular Space of a Well. Construction of Oil and Gas Wells on Land and Sea. 2021. N 11, p. 22-25 (in Russian). DOI: 10.33285/0130-3872-2021-11(347)-22-25
- Vajravelu K., Sreenadh S., Devaki P., Prasad K.V. Mathematical model for a Herschel – Bulkley fluid flow in an elastic tube. Central European Journal of Physics. 2011. Vol. 9. Iss. 5, p. 1357-1365. DOI: 10.2478/s11534-011-0034-3
- Sharafutdinov Z.Z., Sharafutdinova R.Z. Water-based drilling fluids and management of their rheological parameters. Neftegazovoe delo. 2004. N 1, p. 2 (in Russian).
- Belimanea Z., Hadjadj A., Ferroudj H. et al. Modeling surge pressures during tripping operations in eccentric annuli. Journal of Natural Gas Science and Engineering. 2021. Vol. 96. N 104233. DOI: 10.1016/j.jngse.2021.104233
- Alkinani H.H., Al-Hameedi A.T.T., Norman S.D., Lian D. Application of artificial neural networks in the drilling processes: Can equivalent circulation density be estimated prior to drilling? Egyptian Journal of Petroleum. 2020. Vol. 29. Iss. 2, p. 121-126. DOI: 10.1016/j.ejpe.2019.12.003
- Dvoynikov M.V., Kuchin V.N., Mintzaev M.S. Development of viscoelastic systems and technologies for isolating water-bearing horizons with abnormal formation pressures during oil and gas wells drilling. Journal of Mining Institute. 2021. Vol. 247, p. 57-65. DOI: 10.31897/PMI.2021.1.7
- Blinov P.A., Dvoynikov M.V. Rheological and filtration parameters of the polymer salt drilling fluids based on xanthan gum. Journal of Engineering and Applied Sciences. 2018. Vol. 13. Iss. 14, p. 5661-5664. DOI: 10.3923/jeasci.2018.5661.5664
- Ulyasheva N.M., Leusheva E.L., Galishin R.N. Development of the drilling mud composition for directional wellbore drilling considering rheological parameters of the fluid. Journal of Mining Institute. 2020. Vol. 244, p. 454-461. DOI: 10.31897/PMI.2020.4.8
- Wernera B., Myrseth V., Saasenc A. Viscoelastic properties of drilling fluids and their influence on cuttings transport. Journal of Petroleum Science and Engineering. 2017. Vol. 156, p. 845-851. DOI: 10.1016/j.petrol.2017.06.063
