Метод прогноза напряженного состояния обделки подземных сооружений квазипрямоугольной и арочной форм
- 1 — д-р техн. наук доцент Санкт-Петербургский горный университет
- 2 — аспирант Санкт-Петербургский горный университет ▪ Orcid
Аннотация
Рассмотрен метод прогноза напряженно-деформированного состояния обделок подземных сооружений, форма поперечного сечения которых отлична от кругового очертания. Основной задачей исследования является разработка методики оценки влияния параметров формы поперечного сечения подземных сооружений на напряженное состояние обделки. Для решения поставленной задачи обоснован и развит метод расчета напряженного состояния обделки для тоннелей арочной с обратным сводом и квазипрямоугольной форм. Выполнена апробация методики, которая показала, что точность прогноза напряженного состояния обделки достаточна для выполнения практических расчетов. Предложен алгоритм проведения многовариантного анализа влияния формы поперечного сечения подземных сооружений арочной и квазипрямоугольной форм на напряженное состояние обделки. С использованием разработанного алгоритма выполнены параметрические расчеты и получены закономерности формирования напряженного состояния обделок подземных сооружений для различных инженерно-геологических условий, а также начального поля напряженного состояния. Выполнена количественная оценка влияния геометрических параметров тоннелей на их напряженно-деформированное состояние.
Введение
Разработки в области проектирования тоннелепроходческих комплексов позволяют использовать их для механизированного строительства тоннелей не только кругового, но и арочного, овального и квазипрямоугольного сечений. Выбор формы поперечного сечения определяется рядом факторов, среди которых наиболее значимые: назначение подземного сооружения; геотехнические условия строительства; принятая технология строительства; расчетные экономические затраты. Круговое поперечное сечение является наиболее распространенным при строительстве тоннелей в слабых грунтах, что определяется доступностью и надежностью оборудования для строительства тоннелей таких форм, а также тем, что для большинства горно-геологических условий данная форма наиболее устойчива [1, 2]. Недостатком круговой формы является низкий коэффициент использования сечения – он уменьшается с увеличением площади поперечного сечения. Тоннели некруговых очертаний имеют более высокий коэффициент использования сечения по сравнению с круговым. Однако такое изменение формы ведет к повышению напряжений и снижению устойчивости обделки тоннеля. Снизить напряжения в обделке можно за счет оптимизации формы, в частности, изменения радиуса стенок и свода. С учетом того, что рекомендации для
оптимизации геометрии некруговых сечений в общем виде отсутствуют, требуется разработка расчетного решения, которое позволит повысить эффективность использования некруговых форм поперечного сечения подземных сооружений.
Исследования в области расчета напряженного состояния обделок подземных сооружений изложены в научных работах, направленных на изучение напряженно-деформированного состояния обделки на основании аналитических решений [3-6], численного моделирования [7-9] и экспериментальных исследований [10-13]. Проведены масштабные экспериментальные исследования напряженного состояния сборных обделок для тоннелей кругового [14-16], прямоугольного [17], квазипрямоугольного [18-20], подковообразного [21] и эллиптического сечений [22]. С учетом сложности проведения масштабных экспериментальных исследований результаты таких работ не носят обобщающий характер, а нацелены на решение задач в конкретных горно-геологических условиях.
Исследователями получены детальные результаты расчета напряженного состояния обделок подземных сооружений, выполненные на основании аналитических решений и численного моделирования [23, 24], предложен подход к параметрическому анализу изменения напряженного
состояния обделки тоннелей прямоугольной и эллиптической [25], круговой и прямоугольной форм сечения [26]. В работе [27] оценивается влияние формы поперечного сечения тоннелей на величину оседания земной поверхности. В источнике [28] изучено влияние сдвоенных тоннелей различной формы поперечного сечения на формирование напряженного состояния обделки. В работе [29] выполнен ряд численных расчетов для оценки влияния формы поперечного сечения на напряженное состояние обделки. Результаты выполненных исследований показывают, что напряженное состояние обделки значительно зависит от формы поперечного сечения. Однако вопросы обоснования геометрических параметров обделок некруговых форм в научных работах не рассмотрены.
Основное внимание уделено оценке влияния различных факторов (геологических и геометрических) на формирование напряженного состояния обделок тоннелей некругового очертания. Метод расчета напряженного состояния обделки, основанный на учете породного массива через гиперстатические реакции (Hyperstatic Reaction Method, HRM), более известный как метод Метрогипротранса, доказал свою эффективность при расчете обделок тоннелей кругового очертания [13, 30]. Рассмотрено его применение для расчета обделок тоннелей некруговых форм поперечного сечения: арочной с обратным сводом и квазипрямоугольной. Основное преимущество метода HRM – скорость выполнения расчетов – использовано для решения задачи многовариантного анализа влияния формы поперечного сечения тоннеля на напряженное состояние обделки. Разработан алгоритм оценки влияния формы поперечного сечения на напряженное состояние обделки для тоннелей арочной формы с обратным сводом и квазипрямоугольного сечения.
Разработанный метод позволил выявить новые закономерности формирования напряженного состояния обделки тоннелей различной формы поперечного сечения.
Методология
Метод HRM для расчета напряженного состояния обделки подземного сооружения
Метод HRM относится к классу численных методов анализа, в которых напряженное состояние обделки, представляемой в виде одномерных стержневых элементов, может быть определено через интегральные показатели. Взаимодействие между обделкой подземного сооружения и вмещающим породным массивом формируется через набор нормальных и касательных пружин, которые соединяются со стержневыми элементами через смежные узловые точки. Механическое поведение породного массива на допредельной стадии деформирования принимается на основании линейного закона деформирования, в то время как достижение предельного состояния характеризуется идеально-пластическим течением. Узловые перемещения в методе HRM неизвестны, их определение позволяет установить величины интегральных показателей напряженного состояния стержневых элементов, т.е. определить напряженное состояние обделки. Внешнее давление в виде сосредоточенных сил прикладывается к узловым точкам. Детальное описание использования метода HRM для расчета напряженного состояния обделки кругового очертания представлено в [13, 30].
В настоящей работе метод HRM расширен для прогноза напряженного состояния некруговых обделок (арочная форма с обратным сводом, квазипрямоугольная форма).
Взаимосвязь между глобальной матрицей жесткости рассматриваемой системы K, векторами неизвестных перемещений U и узловых сил F можно представить как [31]
Раскрыв уравнение (1), получим:
где ki,a, ki,b, ki,c и ki,d – саб-матрицы матрицы ki; U1, U2, U3, … Un – компоненты вектора перемещений; F1, F2, F3, … Fn – компоненты вектора сил.
Наличие пружин по периметру тоннеля влияет на жесткость рассматриваемой системы стержневых элементов. Это учитывается за счет изменения жесткости каждого из стержневых элементов, следовательно, и глобальной матрицы жесткости.
Методика расчета нагрузок на обделку тоннелей различного очертания
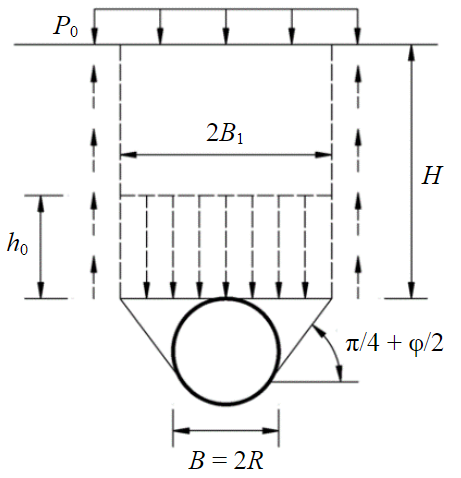
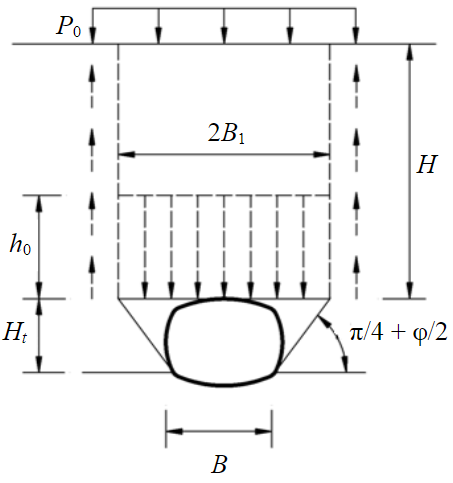
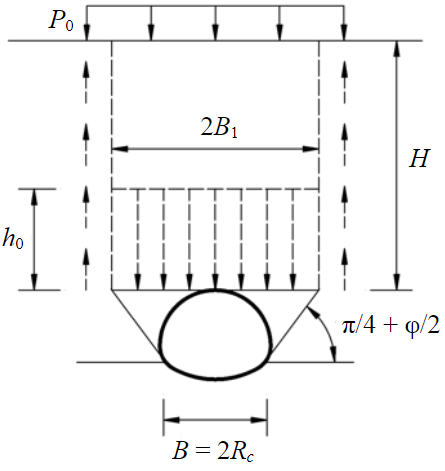
Существуют различные гипотезы формирования горного давления на обделку подземных сооружений, каждая из которых имеет свою область применения, исходя из инженерно-геологических условий и в зависимости от положения подземного сооружения относительно земной поверхности. Применимость методов расчета нагрузок на обделку исследована многими учеными и широко представлена в литературе [32-35], поэтому не является основным объектом данного исследования. Принята методика расчета нагрузки на крепь, предложенная Терцаги [36], который рассматривал формирование опускающегося столба породы шириной B1, часть нагрузки от которого передается на окружающий породный массив за счет трения, а другая составляющая удерживается обделкой подземного сооружения, что позволяет сохранить равновесие рассматриваемой системы взаимодействия «подземное сооружение – грунтовый массив».
Согласно методике, предложенной Терцаги, при глубине заложения подземного сооружения менее двух его ширин величина вертикального давления на обделку подземного сооружения определяется полным весом столба породы:
где γ – усредненный объемный вес вышележащих пород; z – расстояние от поверхности земли до расчетной отметки.
Для расчетных случаев, когда величина глубины заложения подземного сооружения составляет более двух его ширин, расчет нагрузки на обделку определяется через величину эффективной мощности пород h0, вес пород в которой определяет величину давления:
При этом принимается, что опускающийся столб породы имеет ширину B1, а в боках выработки формируются призмы сползания, угол наклона которых принимается равным (π/4 + φ/2). Величина эффективной мощности опускающегося столба породы определяется по формуле
где B1 – половина ширины опускающегося столба породы (табл.1); с – сцепление; K0 – коэффициент бокового давления; H – глубина заложения подземного сооружения; P0 – дополнительная нагрузка, приложенная на поверхности земли.
Формулы для определения ширины B1 подземных сооружений различной формы поперечного сечения сведены в табл.1.
Таблица 1
Определение ширины подземного сооружения
|
Форма поперечного |
Формула для расчета половины ширины |
Расчетная схема |
|
Круговая |
где R – радиус тоннеля; φ – угол внутреннего трения
|
|
|
Квазипрямоугольная |
где В – ширина подземного сооружения;
|
|
|
Арочная с обратным сводом |
где Rc – полуширина тоннеля
|
|
Особенности подготовки расчетной модели в рамках метода HRM
При выполнении расчетов напряженного состояния обделки тоннелей приняты схемы передачи нагрузки, обозначенные на рис.1, а-в. Взаимодействие между обделкой подземного сооружения, описанной стержневыми элементами, и породным массивом осуществляется через пружины, ориентированные в нормальном и касательном направлениях относительно контура подземного сооружения (рис.1, г). Жесткость нормальных и касательных пружин определяется как kn и ks соответственно. Значение величин kn и ks определяется через величины ηn и ηs, характеризующие способность вмещающего породного массива сопротивляться деформациям.
Нелинейная зависимость, определяющая связь между деформацией обделки δ и реакцией породного массива p на эти деформации, представлена в [13, 30]:
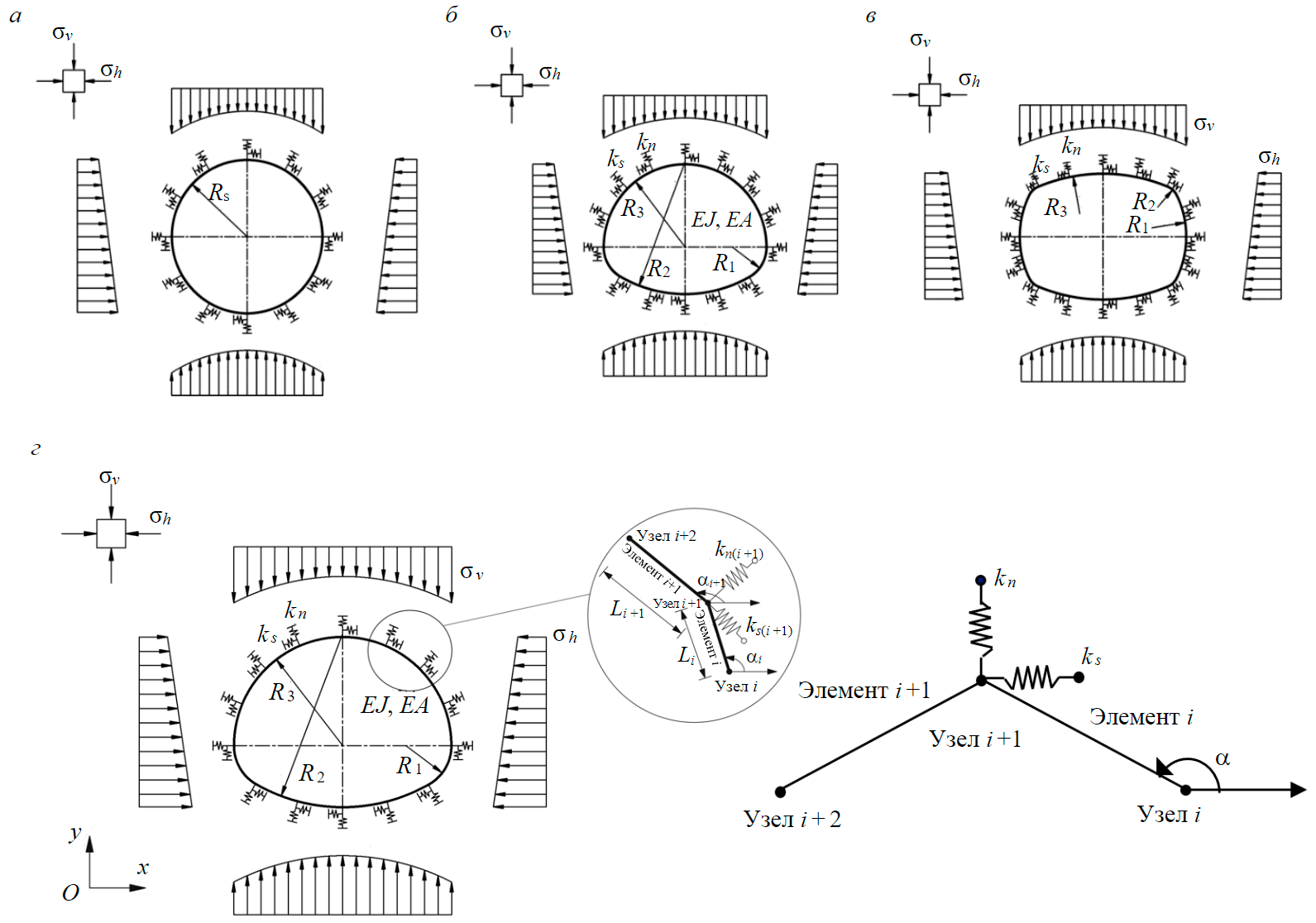
Рис.1. Расчетные схемы прогноза напряженно-деформированного состояния обделки подземных сооружений различных форм поперечного сечения: а – круговая форма; б – арочная форма с обратным сводом; в – квазипрямоугольная форма; г – схема организации взаимодействия между обделкой подземного сооружения и породным массивом σv, σh – вертикальная и горизонтальная нагрузки соответственно; EA,EJ – осевая и изгибная жесткости обделки соответственно; E – модуль деформации материала обделки; A – площадь поперечного сечения обделки; J – момент инерции обделки; R – радиус подземного сооружения (круговая форма поперечного сечения); R1 – радиус боковой стенки; R3 – радиус свода подземного сооружения; R2 – радиус обратного свода (арочная форма поперечного сечения с обратным сводом) или опорной части свода (квазипрямоугольная форма)
где plim – предельная величина реакции породного массива; η0 – начальная величина жесткости породного массива при значении δ, близком к нулю.
Показатель относительной жесткости породного массива можно выразить следующим образом:
Жесткость пружин в нормальном направлении изменяется в зависимости от радиуса подземного сооружения и определяется по формуле
в то время, как жесткость пружин в касательном направлении может быть принята равной одной трети от жесткости пружин в нормальном направлении [13]:
где Es – модуль деформации породного массива; vs – коэффициент поперечной деформации породного массива; Ri – радиус кривизны обделки в каждой рассматриваемой точке ее периметра.
Предельные величины реакции породного массива в радиальном pn,lim и в касательном ps,lim направлениях зависят от прочностных характеристик пород (сцепления и угла внутреннего трения) величины, характеризующей всестороннее обжатие пород Δσconf :
Жесткость пружин kn,1 и ks,1 может быть определена по следующим формулам:
где Li –1 – расстояние между узлами i и i – 1; Li – расстояние между узлами i и i + 1.
При выполнении расчетов было отмечено, что на формирование напряженного состояния обделки подземного сооружения значительное влияние оказывает ее вес. Так, в работе [37] было показано, что снижение давления в нижней части подземного сооружения позволяет получить лучшую сходимость с результатами прогноза, основанными на численном моделировании. При выполнении расчетов принято, что величина активного давления снижена по отношению к максимальному ее значению на 10 % [38].
Алгоритм определения формы поперечного сечения подземного сооружения по силовому фактору
Алгоритм многовариантного анализа влияния формы поперечного сечения тоннеля квази-прямоугольной формы (рис.2) на напряженное состояние обделки заключается в разбивке сечения тоннеля на отдельные сегменты, параметры (положение центра сегмента и радиус) которых контролируются через опорные точки. В первую очередь определяется площадь сечения тоннеля в соответствии с габаритом приближения строений для двухпутного тоннеля метрополитена [39, 40]. Контур сечения в свету тоннеля квазипрямоугольной формы должен перекрывать эту зону. Принимая во внимание это требование, предложен ряд математических зависимостей для определения геометрических параметров квазипрямоугольной формы сечения тоннеля с точки зрения внутренних сил, возникающих в обделке тоннеля.
Принята следующая последовательность определения геометрических параметров тоннеля квазипрямоугольного сечения (рис.3).
На начальном этапе выбирается геометрический центр O2 и вычисляется радиус R2. Центр O2 (x2, y2) дуги 2 расположен на биссектрисе отрезка прямой A1A2, которая описывается линейным уравнением y = x + (h1 – d1).
Радиус определяется по формуле
где (d2, h1) ‒ координаты точки A2.
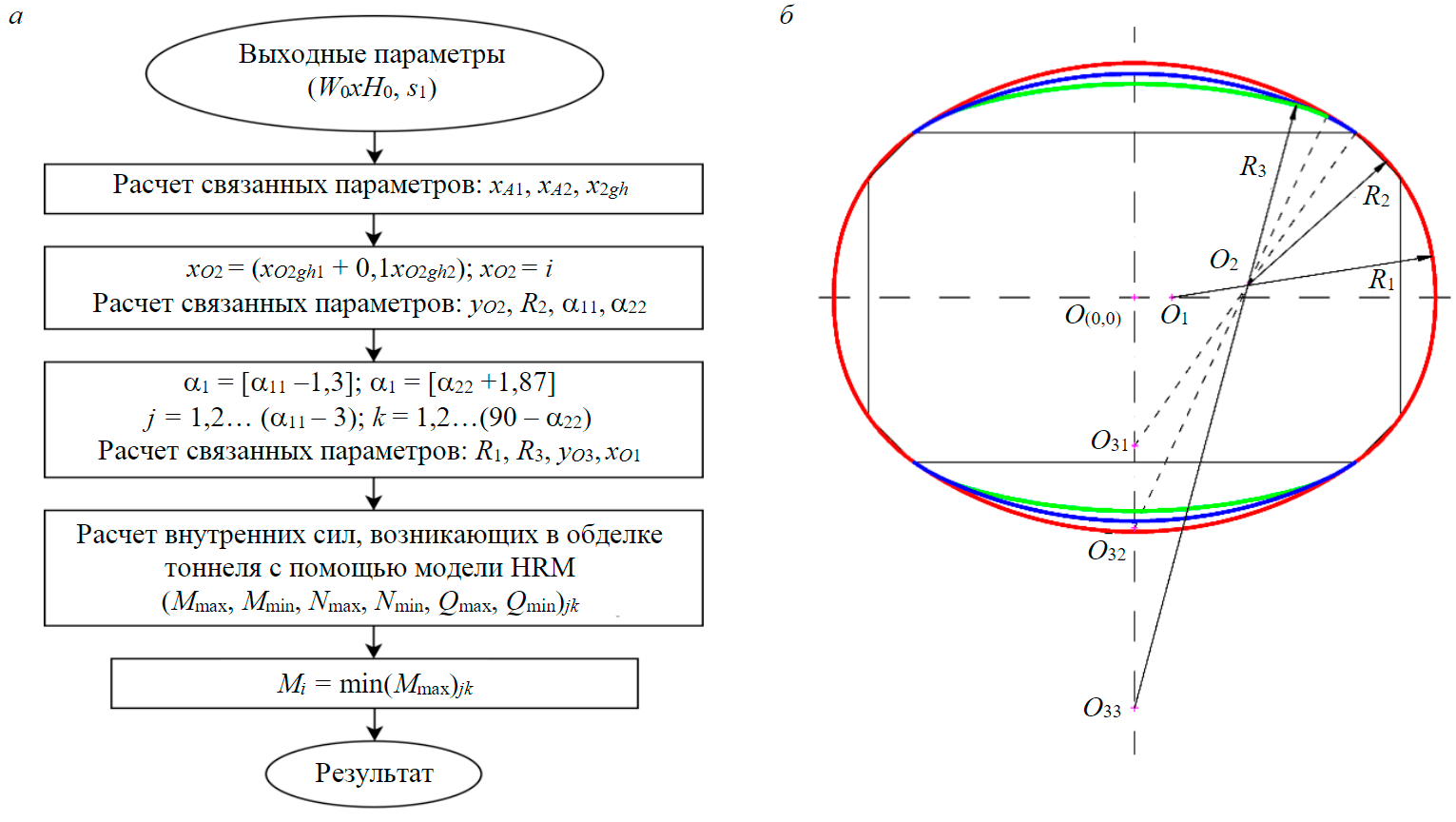
Рис.2. Общий алгоритм расчета геометрических параметров поперечного сечения (а) и различные конфигурации поперечного сечения (б) для тоннелей некруговой формы xA1, xA2 – горизонтальные координаты точек А1 и А2 соответственно; х2gh – предельная горизонтальная координата точки O2; R1, R2, R3 – радиусы боковой стенки, опорной части свода и свода; α11, α22 ‒ верхний предельный угол и нижний предельный угол углов α1 и α2 соответственно; Mi ‒ минимальное значение максимального изгибающего момента при положении точки O2 соответствующем случаю i(при изменении положения точек O1 и O3)
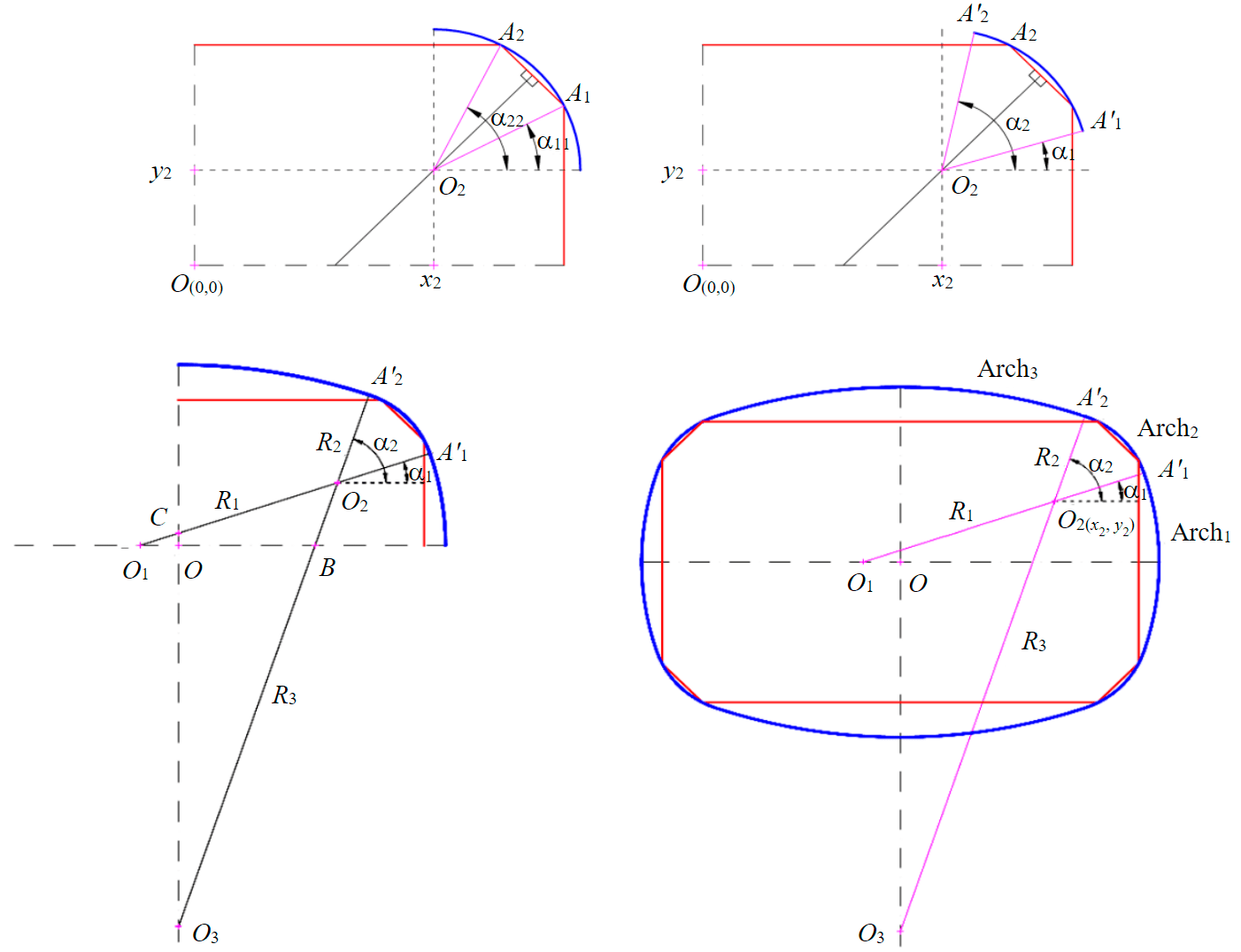
Рис.3. Принципиальная схема расчета геометрических параметров тоннеля квазипрямоугольного поперечного сечения (Arch1, Arch2, Arch3 – периметры дуги боковой стенки, опорной части свода и свода соответственно)
Определяется расположение центров O1, O3. Дуга 2 ограничена точками A1' и A2', расположенными на окружности с центром O2 и радиусом R2. Углы между прямой O2A1' , O2A2' и горизонтальной осью должны удовлетворять условию: α1 = (0, α11) и α2 = (α22, 90).
Центр O1 дуги 1 является пересечением линии, проходящей через точку O2 и имеющей наклон tg(α1), и горизонтальной оси x: O1(х1,0), x1=-y2/tg(α1)+x2. Центр О3 дуги 3 является пересечением линии, проходящей через точку O2 и имеющей наклон tg(α2), и вертикальной оси x: O3(0, y3), y3=tg(α2)(-x2)+y2. Отсюда можно выразить значения радиусов R1 и R3 (м):
где ( xA, ) и ( yA, ) ‒ координаты точки A1' и A2' соответственно.
Адаптация метода HRM для тоннеля некруговой формы поперечного сечения выполнена в ПК MatLab. Алгоритм расчета параметров поперечного сечения тоннеля также является элементом общего программного кода для выполнения расчета напряженного состояния обделки. В качестве выходных данных выступают интегральные показатели напряженного состояния обделки (перерезывающая сила, изгибающий момент, продольная сила) и положение узловых точек системы после проведения оптимизации.
Схожий алгоритм оценки влияния формы поперечного сечения тоннелей на напряженное состояние обделки разработан и для тоннелей арочной формы поперечного сечения с обратным сводом (см. рис.1, б), но в настоящей работе он не рассматривается.
Обсуждение результатов
Оценка достоверности прогноза напряженного состояния обделки в рамках метода HRM
Рассмотрено формирование напряженного состояния обделки подземных сооружений круговой, квазипрямоугольной и арочной форм поперечного сечения, параметры которых представлены на рис.1 и в табл.2. Расчет напряженного состояния обделки выполнен на основании представленной выше методики. Полученные методом HRM результаты сравнивались с результатами, полученными на основании численного моделирования взаимодействия обделки с породным массивом методом конечных элементов. Детальная постановка задачи в рамках метода конечных элементов представлена в [38]. При выполнении расчетов толщина обделки принималась равной 0,5 м. Задача решена в плоскодеформационной постановке, влияние призабойной зоны на формирование нагрузки на обделку не учитывалось. Глубина заложения (от поверхности земли до шелыги свода подземного сооружения) – 10 м, коэффициент бокового давления для всех расчетных случаев – 0,6.
Таблица 2
Геометрические параметры сечений тоннелей различной формы
|
Форма поперечного сечения |
R, м |
R1, м |
R2, м |
R3, м |
Площадь поперечного сечения, м2 |
|
Круговая |
4,89 |
– |
– |
– |
75,12 |
|
Квазипрямоугольная |
– |
5,35 |
1,00 |
9,95 |
59,78 |
|
Арочная с обратным сводом |
– |
2,45 |
8,11 |
5,24 |
69,65 |
Породный массив рассматривался как нелинейно-деформируемая среда с ограничением по величине максимальных касательных напряжений. Физико-механические характеристики породного массива, показывающие механическое поведение пород на рассматриваемом участке, и материала обделки: γ – 18/25 кН/м3; Е – 3,6/35000 МПа; v – 0,495/0,15; с – 25,6/– кПа; φ – 16,5°/– соответственно.
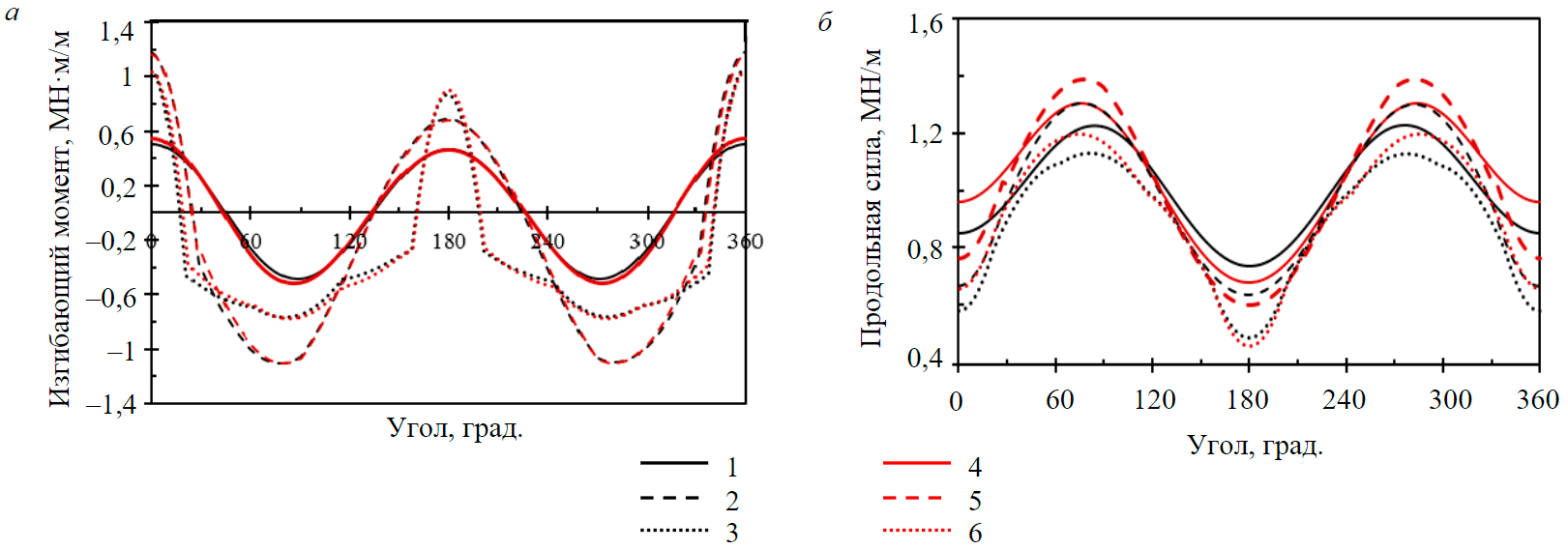
Рис.4. Напряженное состояние в обделке: а – изгибающий момент; б – продольная сила 1 – круговой (HRM); 2 – сводчатая форма (HRM); 3 – квазипрямоугольный (HRM); 4 – круговой (Plaxis); 5 – сводчатая форма (Plaxis); 6 – квазипрямоугольный (Plaxis)
Результаты расчета напряженного состояния обделки методом HRM и его сравнение с результатами, полученными на основании решения задачи методом конечных элементов, представлены в виде эпюр изгибающих моментов и продольных сил по периметру обделки тоннеля (рис.4). Результаты показывают хорошую сходимость между различными схемами взаимодействия породного массива и обделки подземного сооружения. Наибольшее отличие в результатах между двумя методами по величине изгибающего момента наблюдается при рассмотрении тоннеля кругового сечения и составляет 8,3 %, при этом для тоннелей квазипрямоугольного и арочного сечений отличие составляет 1,2 и 2,0 % соответственно. По величине продольных сил отличие между двумя методами составляет 5,8, 5,4 и 6,0 % соответственно. С качественной точки зрения наблюдается хорошая сходимость. Выполненные расчеты при других параметрах породного массива, крепи и напряженного состояния [38] также показывают хорошую сходимость двух расчетных методов.
Можно сделать вывод, что представленный метод позволяет оценить напряженное состояние обделки с достаточной для практических расчетов точностью. С учетом того, что скорость выполнения расчетов в рамках метода HRM на несколько порядков выше по сравнению с методами численного моделирования, его можно эффективно использовать для решения оптимизационных задач, где количество расчетных итераций может составлять от нескольких сотен до десятков тысяч.
Результаты оценки влияния сечения тоннеля криволинейного очертания на напряженное состояние обделки
Рассмотрим пример практической реализации предложенного алгоритма оценки влияния формы поперечного сечения тоннеля на напряженное состояние обделки. Инженерно-геологические условия строительства тоннеля квазипрямоугольного поперечного сечения приняты для г. Ханой, Вьетнам. Габарит приближения строений тоннеля для рассматриваемых условий представлен на рис.5. Глубина заложения тоннеля – 10 м, толщина обделки – 0,5 м. Расчет геометрических параметров сечения тоннеля выполняется согласно алгоритму, описанному ранее.
Для сокращения времени расчета каждый случай расчета оценивается с использованием шага 1° для углов α1 и α2 от ограниченных углов α11 и α22 соответственно; 0,1 м для изменения параметра x2. При расчете геометрических параметров сечения тоннеля выполнено 12479 расчетов напряженного состояния обделки квазипрямоугольного поперечного сечения, расчетное время для каждого случая составило около двух секунд.
Зависимость внутренних сил и радиальных смещений обделки от величины радиуса обратного свода R3 тоннеля представлена на рис.6. Влияние радиуса R3 на величину максимального изгибающего момента в сечении обделки – значительно. Увеличение радиуса R3 приводит к увеличению максимального изгибающего момента в обделке. Максимальная нормальная сила меняется незначительно при изменении радиуса R3.
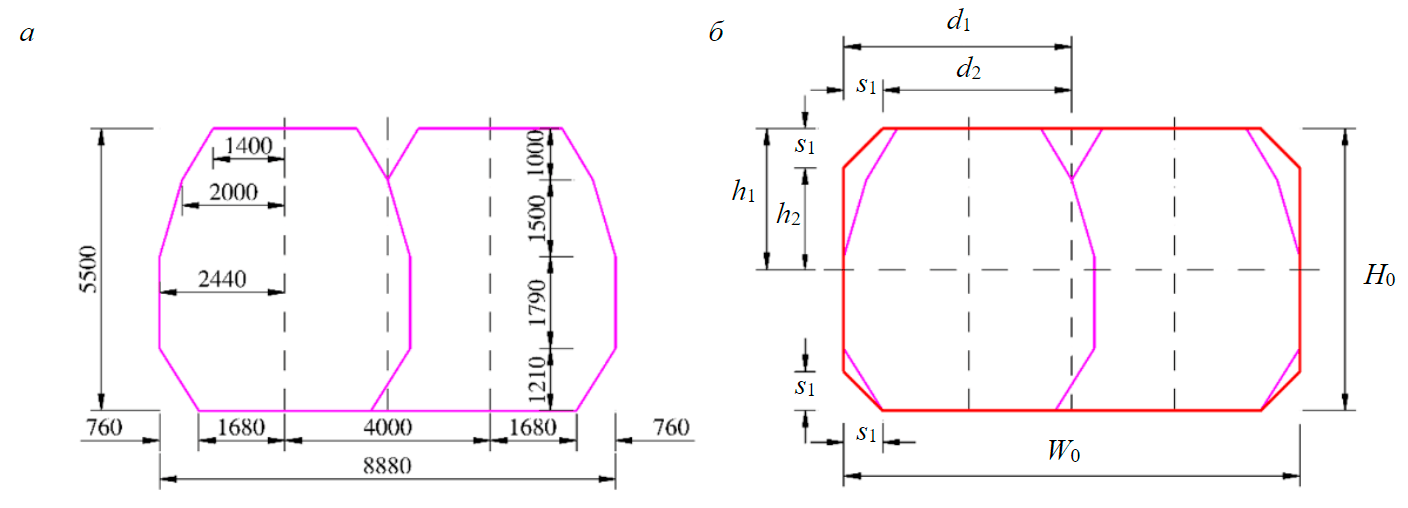
Рис.5. Построение габарита приближения строений тоннеля: а – двухпутный железнодорожный тоннель по стандартам Вьетнама; б – упрощенный габарит приближения строений тоннеля W0 = 8,88 м; H0 = 5,50 м; s1 = 0,76 м; d1 = 3,68 м; d2 = 4,44 м; h1 = 2,75 м; h2 = 1,54 м; h1 = H0/2 = h2 + s1
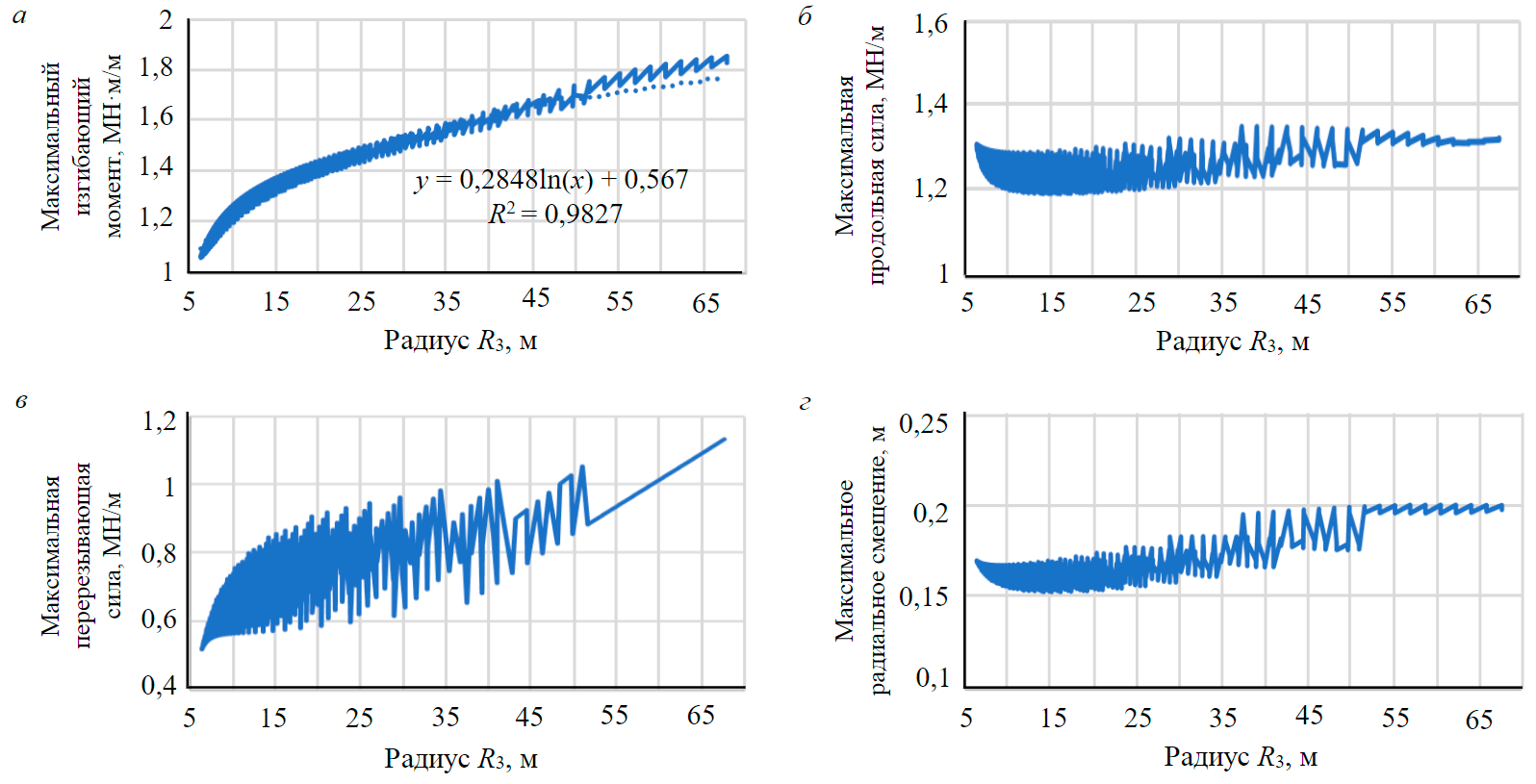
Рис.6. Внутренние силы и нормальные смещения, возникающие в обделке тоннелей: а – максимальный изгибающий момент; б – максимальная продольная сила; в – максимальная перерезывающая сила; г – максимальное радиальное смещение
Также увеличение радиуса R3 приводит к тому, что свод и обратный свод тоннеля становятся более плоскими. Тогда нормальная вертикальная нагрузка, действующая на эти сегменты обделки, увеличивается, а вертикальная поперечная нагрузка – снижается. Также снижается вертикальная нагрузка, передаваемая на боковую стенку тоннеля. Таким образом, чем более плоские свод и обратный свод тоннеля, тем выше максимальный изгибающий момент в обделке тоннеля. Максимальное нормальное смещение обделки тоннеля увеличивается с увеличением радиуса R3.
Обработка результатов расчетов позволила установить, что соотношение между радиусом R3 и максимальным изгибающим моментом в обделке тоннеля квазипрямоугольной формы поперечного сечения может быть описано уравнением
Связь между максимальным изгибающим моментом в обделке тоннеля и радиусами R2, R3, R1 с достаточной для практических расчетов точностью можно описать уравнением
Из уравнений (14) и (15) видно, что на максимальный изгибающий момент в обделке в основном влияет радиус обратного свода и незначительно – радиус боковой стенки тоннеля.
Детальный анализ результатов расчетов позволил установить, что величина максимального изгибающего момента в сечении обделки тоннеля для рассматриваемых условий изменяется от 1,05 (наилучшая форма поперечного сечения по силовому фактору) до 1,85 МН·м/м (наихудшая форма), т.е. разница в величинах изгибающего момента составляет 75 %. При этом разница в площади между наилучшей и наихудшей формами поперечного сечения составила 21 %. Можно заключить, что анализ данных, полученных на основании многовариантного расчета, позволил в значительной степени снизить напряженное состояние обделки при сохранении минимального размера площади поперечного сечения тоннеля.
Для оценки влияния различных параметров и геометрии тоннеля на напряженное состояние обделки был выполнен многовариантный расчет. В определенном диапазоне изменялись модуль деформации породного массива, глубина заложения тоннеля и коэффициент бокового давления. Модуль деформации грунта является одним из основных параметров, определяющих напряженное состояние обделки тоннеля. Его величина при выполнении расчетов изменялась от 5 до 200 МПа, при этом остальные физико-механические характеристики пород остались прежними. Всего выполнено 26031 расчетов. Результаты представлены в виде зависимостей изменения максимальной величины изгибающего момента и продольной силы в обделке тоннеля (рис.7, а). Как видно из представленных зависимостей, для всех значений модулей деформации породного массива верно следующее соотношение: чем выше значение R3, тем выше абсолютное значение изгибающего момента; при этом величина продольной силы меняется незначительно. Полученные результаты хорошо соотносятся с данными, представленными в [41].
При изменении R3 от 10 до 15 м наблюдается резкий рост величин изгибающего момента, в то время как величины максимальных нормальных сил быстро снижаются. Дальнейшее увеличение показателя R3 не оказывает серьезного влияния на напряженное состояние обделки.
Полученные результаты можно обобщить в виде зависимости, которая характеризует связь между максимальным значением изгибающего момента, геометрическими параметрами и модулем деформации породного массива:
Оценка влияния начального напряженного состояния породного массива, выраженного через величину коэффициента бокового давления K0 и глубину заложения тоннеля, представлена в виде эпюр изменения интегральных показателей напряженного состояния обделки (рис.7, б). Величина коэффициента бокового давления K0 изменялась от 0,4 до 1,0. Количество выполненных расчетов составило 22778. На основании анализа результатов расчетов можно заключить, что увеличение K0 приводит к уменьшению максимальной величины изгибающего момента, однако величина продольной силы в целом увеличивается. Такая тенденция характерна для любых значений R3. При достижении R3 величины 10 м влияние коэффициента K0 на напряженное состояние обделки повышается. С увеличением значения R3 эффект обжатия снижается, поэтому снижается и влияние показателя R3 на напряженное состояние обделки. По результатам расчетов получена зависимость для определения максимальной величины изгибающего момента через величину R3 и коэффициент бокового давления K0:
Коэффициент бокового давления K0 оказывает влияние и на формирование нормальных сил в сечении обделки, однако степень этого влияния значительно ниже влияния на изгибающий момент. Данный результат получен при различных значениях R3.
Для оценки влияния радиуса R3 на напряженное состояние обделки при различных глубинах заложения тоннеля выполнены дополнительные расчеты в объеме 19524 (рис.7, в). Величина глубины заложения H изменялась от 5 до 50 м. На основании выполненных исследований установлено, что влияние параметра R3 на величину изгибающего момента снижается по мере увеличения глубины заложения тоннеля. Это можно объяснить тем, что с ростом глубины возрастают и активные нагрузки на обделку, что приводит к возрастанию значений интегральных показателей напряженного состояния обделки. Увеличение показателя R3 приводит к тому, что обратный свод становится более плоским, а соотношение между нормальной и касательной нагрузками возрастает, что уменьшает вертикальную нагрузку в стенках тоннеля. Для расчета величины максимального изгибающего момента в обделке, в зависимости от глубины заложения тоннеля и геометрических параметров тоннеля, используется формула
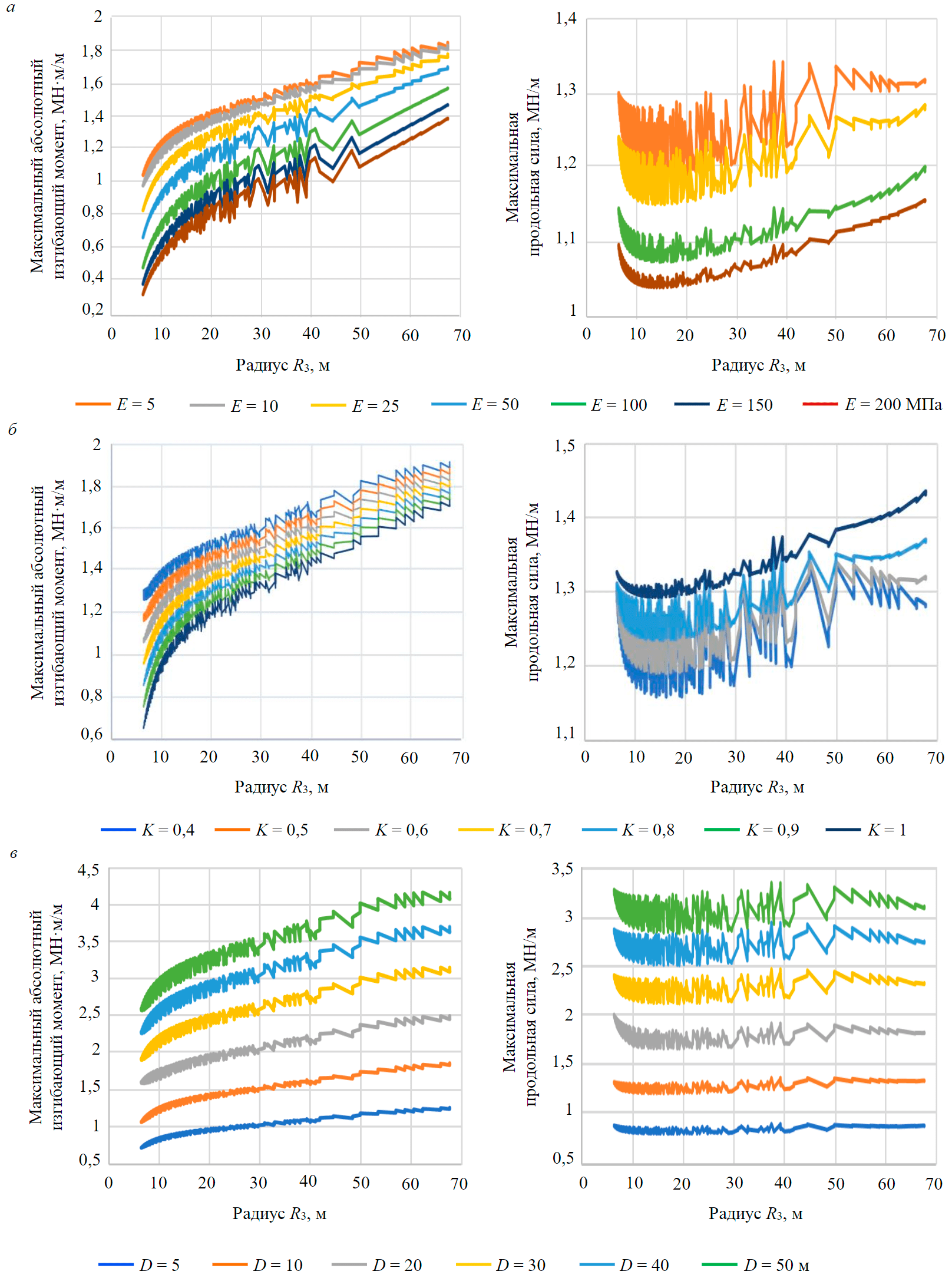
Рис.7. Влияние параметра R3 на напряженное состояние обделки тоннеля в зависимости от модуля деформации грунта (а), величины коэффициента бокового давления (б) и глубины заложения тоннеля (в)
Далее приведена формула, учитывающая влияние комбинации рассмотренных факторов: модуля деформации грунта Es, глубины тоннеля H, коэффициента давления грунта на максимальный изгибающий момент в обделке. Уравнение получено на основании анализа 956675 случаев:
Как видно из представленных результатов, предложенный алгоритм позволяет эффективно оценивать влияние контролирующих параметров сечения тоннеля на напряженное состояние обделки различной формы поперечного очертания. В то же время автоматизированного способа оптимизации формы тоннеля по заданным критериями (прочность материала, устойчивость конструкции, площадь поперечного сечения и т.д.) не предложено, но будет изучаться в дальнейших исследованиях.
Заключение
Как показывает практика строительства подземных сооружений, их формы поперечного сечения могут быть круговыми, арочными с обратным сводом, квазипрямоугольными и др. Для расчета напряженного состояния обделок некруговых форм может быть использован метод HRM, позволяющий решить поставленную задачу с достаточной для практических расчетов точностью. С учетом того, что скорость выполнения расчетов на несколько порядков выше, чем в методе конечных элементов, где породный массив рассматривается как сплошная среда, описываемая соответствующей моделью ее деформирования, метод HRM может быть использован для решения оптимизационных задач – поиска оптимальной формы поперечного сечения подземного сооружения при заданных горно-геологических условиях.
На основании выполненных исследований:
- развит метод HRM для расчета подземных сооружений некруговой формы поперечного сечения с учетом нелинейного поведения породного массива;
- разработан алгоритм проведения многовариантного расчета напряженного состояния обделки тоннелей арочной и квазипрямоугольной форм поперечного сечения;
- выполнена апробация предложенного метода для различных условий строительства тоннелей, и получена хорошая сходимость с результатами численного моделирования, полученными в программном комплексе PLAXIS 2D;
- выполнен комплекс параметрических расчетов и получены зависимости, связывающие интегральные показатели напряженного состояния обделки (изгибающий момент и продольные силы) с модулем деформации породы, напряженным состоянием породного массива и геометрическими параметрами сечения тоннелей квазипрямоугольной и арочной форм;
- получены аналитические выражения для расчета максимальных значений изгибающих моментов в сечении обделки;
- указано направление дальнейших исследований по разработке алгоритма поиска оптимальной формы поперечного сечения тоннелей по заданным критериям.
Литература
- Tatiya R. Civil excavations and tunnelling: a practical guide. London: Thomas Telford, 2005. 322 p.
- Yingyongrattanakul N., Adachi T., Tateyama K., Kurahashi M. Optimal shape of underground structure // Modern Tunneling Science and Technology. London: Taylor & Francis, 2001. 628 p.
- Господариков А.П., Выходцев Я.Н., Зацепин М.А. Математическое моделирование воздействия сейсмовзрывных волн на горный массив, включающий выработку // Записки Горного института. 2017. Т. 226. С. 405-411. DOI: 10.25515/PMI.2017.4.405
- Саммаль А.С., Фотиева Н.Н., Булычев Н.С., Хренов С.И. Расчет тоннельных обделок переменной толщины с учетом влияния земной поверхности // Записки Горного института. 2004. Т. 156. С. 24-26.
- Protosenya A.G., Lebedev M.O. Calculation of the Loads on Linings of Subway Tunnels Constructed in Physically Nonlinear Soil Masses // Journal of Mining Science. 2002. Vol. 38. Iss. 5. P. 418-424. DOI: 10.1023/A:1023975313128
- Protosenya A.G., Karasev M.A., Belyakov N.A. Elastoplastic problem for noncircular openings under Coulomb’s criterion // Journal of Mining Science. 2016. Vol. 1. P. 53-61. DOI: 10.1134/S1062739116010125
- Belyakov N.A., Smirnova O.M., Alekseev A.V., Tan H. Numerical Simulation of the Mechanical Behavior of Fiber-Reinforced Cement Composites Subjected Dynamic Loading // Applied Sciences. 2021. Vol. 11. Iss. 3. № 1112. DOI: 10.3390/app11031112
- Nguyen C.T., Gospodarikov A.P. Hyperstatic reaction method for calculations of tunnels with horseshoe-shaped cross-section under the impact of earthquakes // Earthquake Engineering and Engineering Vibration. 2020. Vol. 19. P. 179-188.
- DOI: 10.1007/s11803-020-0555-0
- Fan Wang, Biancai Gou, Yawei Qin et al. Modeling tunneling-induced ground surface settlement development using a wavelet smooth relevance vector machine // Computers and Geotechnics. 2013. Vol. 54. P. 125-132. DOI: 10.1016/j.compgeo.2013.07.004
- Безродный К.П., Лебедев М.О. О нагрузках от горного давления на обделки тоннелей закрытого способа работ // Записки Горного института. 2017. Т. 228. С. 649-653. DOI: 10.25515/PMI.2017.6.649
- Arnau O., Molins C. Experimental and analytical study of the structural response of segmental tunnel linings based on an in-situ loading test. Part 1: Test configuration and execution// Tunnelling and Underground Space Technology. 2011. Vol. 26. Iss. 6. P. 764-777. DOI: 10.1016/j.tust.2011.05.002
- Петраков Д.Г., Пеньков Г.М., Золотухин А.Б. Экспериментальное исследование влияния горного давления на проницаемость песчаника // Записки Горного института. 2022. Т. 254. С. 244-251. DOI: 10.31897/PMI.2022.24
- Do N.A., Dias D., Oreste P., Maigre I.D. The behaviour of the segmental tunnel lining studied by the hyperstatic reaction method // European Journal of Environmental and Civil Engineering. 2014. Vol. 18. Iss. 4. P. 489-510. DOI: 10.1080/19648189.2013.872583
- Blom C.B. Design philosophy of concrete linings for tunnel in soft soils. Delft, Netherlands: Delft University, 2002.
- Xiaojun Li, Zhiguo Yan, Zhen Wang et al. Experimental and analytical study on longitudinal joint opening of concrete segmental lining // Tunnelling and Underground Space Technology. 2015. Vol. 46. P. 52-63. DOI: 10.1016/j.tust.2014.11.002
- Liang Lu, Xilin Lu, Peifang Fan. Full-Ring Experimental Study of the Lining Structure of Shanghai Changjiang Tunnel // Journal of Civil Engineering and Architecture. 2011. Vol. 5. Iss. 8. P. 732-739. DOI: 10.17265/1934-7359/2011.08.007
- Nakamura H., Kubota T., Furukawa M., Nakao T. Unified construction of running track tunnel and crossover tunnel for Unified construction of running track tunnel and crossover tunnel for // Tunnelling and Underground Space Technology. 2003. Vol. 18. P. 253-262. DOI: 10.1016/S0886-7798(03)00034-8
- XinHuang, YetingZhu, ZixinZhang et al. Mechanical behaviour of segmental lining of a sub-rectangular shield tunnel under self-weight // Tunnelling and Underground Space Technology. 2018. Vol. 74. P. 131-144. DOI: 10.1016/j.tust.2018.01.016
- Xian Liu, Zhen Liu, Yuhang Ye et al.Mechanical behavior of quasi-rectangular segmental tunnel linings: Further insights from full-scale ring tests // Tunnelling and Underground Space Technology. 2018. Vol. 79. P. 304-318. DOI: 10.1016/j.tust.2018.05.016
- Xian Liu, Yuhang Ye, Zhen Liu, Dezhong Huang. Mechanical behavior of Quasi-rectangular segmental tunnel linings: First results from full-scale ring tests // Tunnelling and Underground Space Technology. 2018. Vol. 71. P. 440-453. DOI: 1016/j.tust.2017.09.019
- Trushko V.L., Protosenya A.G., Trushko O.V. Stress-strain behavior of the workings during the rich iron ores development under the confined aquifers // International Journal of Applied Engineering Research. 2016. Vol. 11. Iss. 23. P. 11153-11164.
- Feng Yang, Xinlei Sun, Jiahong Zou, Xiangcou Zheng. Analysis of an elliptical tunnel affected by surcharge loading // Proceedings of the Institution of Civil Engineers – Geotechnical Engineering. 2019. Vol. 172. Iss. 4. P. 312-319. DOI: 1680/jgeen.16.00122
- Palassi M., Mohebbi M. Design of Lining of Tunnels Excavated in Soil and Soft Rock // The Electronic Journal of Geotechnical Engineering. 2008. Vol. 3. P. 1-15.
- Protosenya A., Vilner M. Assessment of excavation intersections’ stability in jointed rock masses using the discontinuum approach // Rudarsko-geološko-naftni zbornik. 2022. Vol. 38 (2). P. 137-147. DOI: 10.17794/rgn.2022.2.12
- Wang H., Zeng G., JiangM. Analytical stress and displacement around non-circular tunnels in semi-infinite ground // Applied Mathematical Modelling. 2018. Vol. 63. P. 303-328. DOI: 10.1016/j.apm.2018.06.043
- Abdellah W.R., Ali M.A., Yang H.S. Studying the effect of some parameters on the stability of shallow tunnels // Journal of Sustainable Mining. 2018. Vol. 17. Iss. 1. P. 20-33. DOI: 10.1016/j.jsm.2018.02.001
- Rostami A., Asghari N., Ziarati M.A. et al. Investigating Effect of Tunnel Gate Investigating Effect of Tunnel Gate Inserted Forces on Its Coverage and Soil Surface Settlement // Journal of Civil Engineering. 2016. Vol. 6. Iss. 3. P. 358-369. DOI: 10.4236/ojce.2016.63030
- Vinod M., KhabbazH. Comparison of rectangular and circular bored twin tunnels in weak ground // Underground Space. 2019. Vol. 4. Iss. 4. P. 328-339. DOI: 10.1016/j.undsp.2019.03.004
- Do N.A., Dias D., Zhang Z. et al. Study on the behavior of squared and sub-rectangular tunnels using the Hyperstatic Reaction Method // Transportation Geotechnics. 2020. Vol. 22. № 100321. DOI: 10.1016/j.trgeo.2020.100321
- Oreste P. A numerical approach to the hyperstatic reaction method for the dimensioning of tunnel supports // Tunnelling and Underground Space Technology. 2007. Vol. 22. Iss. 2. P. 185-205. DOI: 10.1016/j.tust.2006.05.002
- Huebner K.H., Dewhirst D.L., Smith D.E., Byrom T.G. The finite element method for engineers. New York: John Wiley and Sons, 2001. 744 p.
- Баклашов И.В., Картозия Б.А. Механика подземных сооружений и конструкции крепей. М.: Студент, 2012. 543 c.
- Булычев Н.С. Механика подземных сооружений. М.: Недра, 1994. 382 c.
- Kolymbas D. Tunnelling and Tunnel Mechanics. A rational Approach to Tunneling. Berlin: Springer, 2005. 439 p.
- Széchy K. The Art of Tunnelling. Budapest: Akadémiai Kiadó, 1973. 1097 p.
- Takano Y.H. Guidelines for the design of shield tunnel lining // Tunneling and Underground Space Technology. 2000. Vol. 15. Iss. 3. P. 303-331. DOI: 10.1016/S0886-7798(00)00058-4
- Do N.A., Dias D. Tunnel lining design in multi-layered grounds // Tunnelling and Underground Space Technology. 2018. Vol. 81. P. 103-111. DOI: 10.1016/j.tust.2018.07.005
- Nguyen T.T., Do N.A., Karasev M.A. et al. Influence of tunnel shape on tunnel lining behaviour // Proceedings of the Institution of Civil Engineers – Geotechnical Engineering. 2021. Vol. 174. Iss. 4. P. 355-371. DOI: 10.1680/jgeen.20.00057
- Нгуен Т.Т., Карасев М.А. Расчет оптимальных геометрических параметров тоннеля квазипрямоугольного поперечного очертания по силовому фактору // Горный информационно-аналитический бюллетень. 2021. Т. 6. С. 59-71. DOI: 10.25018/0236_1493_2021_6_0_59
- Du D., Dias D., Do N. Lining performance optimization of sub-rectangular tunnels using the Hyperstatic Reaction Method // Computers and Geotechnics. 2020. Vol. 117. № 103279. DOI: 10.1016/j.compgeo.2019.103279
- Господариков А.П., Зацепин М.А. Математическое моделирование нелинейных краевых задач геомеханики // Горный журнал. 2019. № 12. С. 16-20. DOI: 10.17580/gzh.2019.12.03