Тензорная компакция пористых пород: теория и экспериментальная верификация
- 1 — канд. физ.-мат. наук заведующий лабораторией Институт механики сплошных сред УрО РАН, Пермь ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 2 — канд. физ.-мат. наук научный сотрудник Геологическая служба Израиля ▪ Orcid ▪ Scopus ▪ ResearcherID
- 3 — канд. физ.-мат. наук научный сотрудник Институт механики сплошных сред УрО РАН ▪ Orcid ▪ Elibrary ▪ Scopus
- 4 — д-р техн. наук главный научный сотрудник Институт проблем механики им. А.Ю.Ишлинского РАН ▪ Orcid ▪ Elibrary ▪ ResearcherID
- 5 — младший научный сотрудник Институт проблем механики им. А.Ю.Ишлинского РАН ▪ Orcid ▪ Elibrary ▪ ResearcherID
- 6 — канд. физ.-мат. наук научный сотрудник Геологическая служба Израиля ▪ Orcid ▪ ResearcherID
Аннотация
Уплотнение в осадочных бассейнах традиционно рассматривается как одномерный процесс, который игнорирует неупругие деформации в направлениях, ортогональных активной нагрузке. В этом исследовании представлены новые эксперименты с песчаником, демонстрирующие роль трехмерного неупругого уплотнения при циклическом истинно трехосном сжатии. Эксперименты выполнены на базе испытательной системы трехосного независимого нагружения в лаборатории геомеханики Института проблем механики им. А.Ю.Ишлинского РАН. По кривым деформирования оценены упругие модули материала и определены упругие деформации образца в каждом из трех направлений. Вычитание упругой составляющей из общей деформации позволило показать, что в направлении активного нагружения наблюдается неупругое уплотнение материала, тогда как в ортогональных направлениях имеет место разуплотнение материала. Для описания трехмерного характера уплотнения предлагается обобщение закона Ати на тензорный случай, учитывающее роль девиатора напряжений. Введен тензор уплотнения и кинетическое уравнение для описания эволюции неупругой деформации, начиная с момента приложения нагрузки. На основе экспериментов по циклическому многоосному сжатию песчаника проведены идентификация и верификация построенной модели тензорного уплотнения. Показана возможность не только качественного, но и количественного описания изменения неупругой деформации при сложном циклическом трехосном сжатии.
Введение
Ключевой фильтрационно-емкостной характеристикой пород-коллекторов является пористость. В ходе изменений полей напряжений в горном массиве, вызванных тектоническими процессами, добычей полезных ископаемых, снижением порового давления, происходит компакция – неупругое уплотнение пород. Компакция приводит к снижению пористости пород. Большинство моделей, описывающих процесс уплотнения породы в процессе осадконакопления и литогенеза, базируется на законе Ати [1] – эмпирическом законе экспоненциального падения пористости с давлением. Коэффициенты закона Ати, как правило, подбираются по данным об изменении пористости в скважинах в конкретном регионе, при этом считается, что распределение пористости по глубине зависит только от типа осадочных пород. В последние десятилетия предложены соотношения для изменения пористости с глубиной, учитывающие вариации литологического состава пород и минерального состава насыщающего их флюида [2]. Закон Ати и другие подобные соотношения (Hedberg, Weller, Теодоровича – Чернова, Burst, Beall, Overton and Zanier и др. [2]) рассматривают неупругое уплотнение как процесс, контролируемый средним напряжением, игнорируя возможное влияние компонент девиатора напряжений.
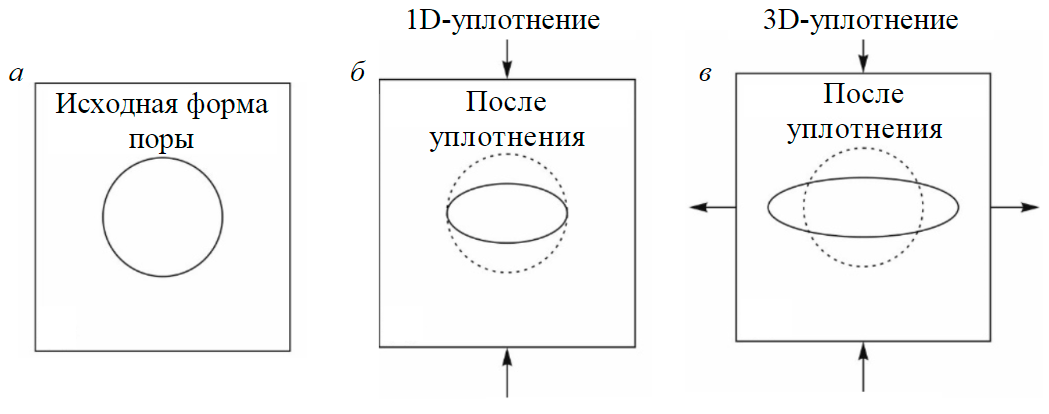
Рис.1. Схематичное представление уплотнения порового пространства
Ранние модели использовали упругую и поро-упругую реологию для описания уплотнения породы и вытеснения флюида. В этих моделях поровое давление препятствует уплотнению породы в процессе вытеснения флюида, при этом аномально высокое пластовое давление создается в случае достаточно высокой скорости уплотнения (уменьшения пористости). В последующих работах необратимое уплотнение моделировалось на основе вязкой [3-5] и вязко-пластической реологии [6-8], в том числе с учетом температурных эффектов [9] и больших деформаций [10]. Необходимо отметить, что теоретические результаты лишь частично описывают имеющиеся экспериментальные данные [11-13]. Недавние исследования показали, что уплотнение породы происходит при всех уровнях напряжений с самого начала сжатия, т.е. является беспороговым процессом, не требующим введения критериальных соотношений [14-16].
Постановка проблемы
В предыдущих исследованиях по компакции предполагалось, что деформация при уплотнении может быть аппроксимирована исключительно вертикальной компонентой (рис.1, а, б, 1D-уплотнение). Первоначально сферическое поровое пространство претерпевает вертикальное необратимое сжатие при неизменной горизонтальной деформации (рис.1, б). Такое 1D-приближение позволяет существенно упростить гидромеханическое описание процесса компакции [17]. С использованием этой гипотезы были проведены численные расчеты формирования осадочных бассейнов в двух- и трехмерных постановках [18-20]. Необходимо отметить, что недостатки такого упрощения мало изучены [17].
В настоящей работе представлены результаты испытаний песчаника в условиях истинного трехосного сжатия, демонстрирующие, что неупругое уплотнение в направлении максимального сжатия сопровождается неупругим разуплотнением в перпендикулярном направлении (рис.1, в). Для учета трехмерного характера процесса неупругого уплотнения в работе предложено обобщение закона Ати, связывающее равновесное уплотнение не только с давлением, но и с компонентами девиатора напряжений. Процесс неравномерной компакции, наблюдаемый в эксперименте, моделируется с использованием кинетических соотношений, связывающих скорость уплотнения с приложенным давлением и разностью между текущей и равновесной величинами уплотнения. Численное моделирование показало, что трехмерная (тензорная) модель неупругого уплотнения воспроизводит основные особенности деформационного поведения песчаника при циклическом нагружении в трех ортогональных направлениях.
Методология экспериментального исследования
Для изучения процесса уплотнения при сложном трехмерном нагружении используются результаты экспериментов по циклическому истинному трехосному испытанию образцов песчаника. Подробное описание условий испытаний представлено в работе [21].
Для испытаний был выбран полимиктовый песчаник, относящийся к шешминской свите уфимского яруса пермской системы. Песчаник характеризуется слоистой структурой, обусловленной чередованием прослоев, обогащенных эпидотом и обломками кремней. SEM-исследования показали, что распределение зерен минералов по объему равномерное с размером от 150 до 450 мкм. Пористость песчаника составляет 9,5 % и развита, в основном, по границам зерен, что вызвано выщелачиванием кальцита грунтовыми водами. Кубические образцы с размером ребра 40 мм изготовлены на специальном обрабатывающем комплексе в Институте проблем механики им. А.Ю.Ишлинского РАН с высокой точностью, непараллельность граней не превышала 20 мкм.

Рис.2. Образец в ИСТНН после остановки испытания на трехосное непропорциональное сжатие
Механические испытания проводились на испытательной системе трехосного независимого нагружения (ИСТНН) в лаборатории геомеханики [22-24]. Независимое нагружение в трех ортогональных направлениях осуществляется благодаря примененной в конструкции нагружающего узла оригинальной кинематической схеме, которая позволяет нажимным плитам сближаться в трех направлениях, не препятствуя друг другу [25, 26]. Перед испытаниями между гранями образца и наконечниками нажимных плит устанавливались тонкие фторопластовые прокладки со смазкой для минимизации трения при сжатии образца (рис.2). Автоматизированный комплекс управления и сбора данных ИСТНН включает LVDT-датчики перемещения и датчики усилия с разрешающей способностью 0,2 мкм и 0,03 МПа. Измерения сил и перемещений проводятся независимо по всем трем осям нагружения с частотой дискретизации 1 Гц.
Для изучения процесса уплотнения песчаника были реализованы две программы циклического трехосного нагружения (рис.3). Первая программа испытаний состояла из трех пар циклов нагружение – разгрузка и предваряющего их всестороннего сжатия до 10 МПа. В первом цикле выполнялось активное сжатие по оси X до напряжения sxx = 60 МПа с последующей разгрузкой до sxx = 10 МПа при удержании напряжений постоянными по двум другим осям syy = szz = 10 МПа. Во втором цикле нагрузка осуществлялась в том же направлении до sxx = 80 МПа с последующей разгрузкой до 10 МПа. Далее такая же пара циклов следовала при активном сжатии по оси Y с контролем постоянства напряжений в двух других направлениях, затем – в направлении оси Z (рис.3, а). Скорость активного нагружения и разгрузки в каждом из шести циклов постоянна и равна 31 кПа/с.
Вторая программа испытаний представляла собой расширенный вариант первой программы и состояла из трех троек циклов (рис.3, б). Первый цикл каждой тройки представлял собой сжатие по двум из трех направлений до 58 МПа с последующей разгрузкой до 10 МПа при удержании напряжения в третьем направлении на уровне 10 МПа. Во втором и третьем цикле осуществлялось активное сжатие (до уровня напряжений 78 МПа) и разгрузка (до 10 МПа) в каждом из двух выбранных направлений с удержанием постоянства напряжений в двух оставшихся направлениях. Первая тройка представляла собой цикл сжатие – разгрузка в направлениях X и Y, цикл сжатие – разгрузка в направлении X (удержание напряжений по осям Y, Z), цикл сжатие – разгрузка в направлении Y (удержание напряжений по осям X, Z). Вторая тройка представляла собой цикл сжатие – разгрузка в направлениях Z и Y, цикл сжатие – разгрузка в направлении Z (удержание напряжений по осям Y, X), цикл сжатие – разгрузка в направлении Y (удержание напряжений по осям X, Z). Наконец, третья тройка – циклы сжатие – разгрузка в направлениях Z и X, с последующими последовательными циклами сжатия – разгрузка в направлениях X и Z.
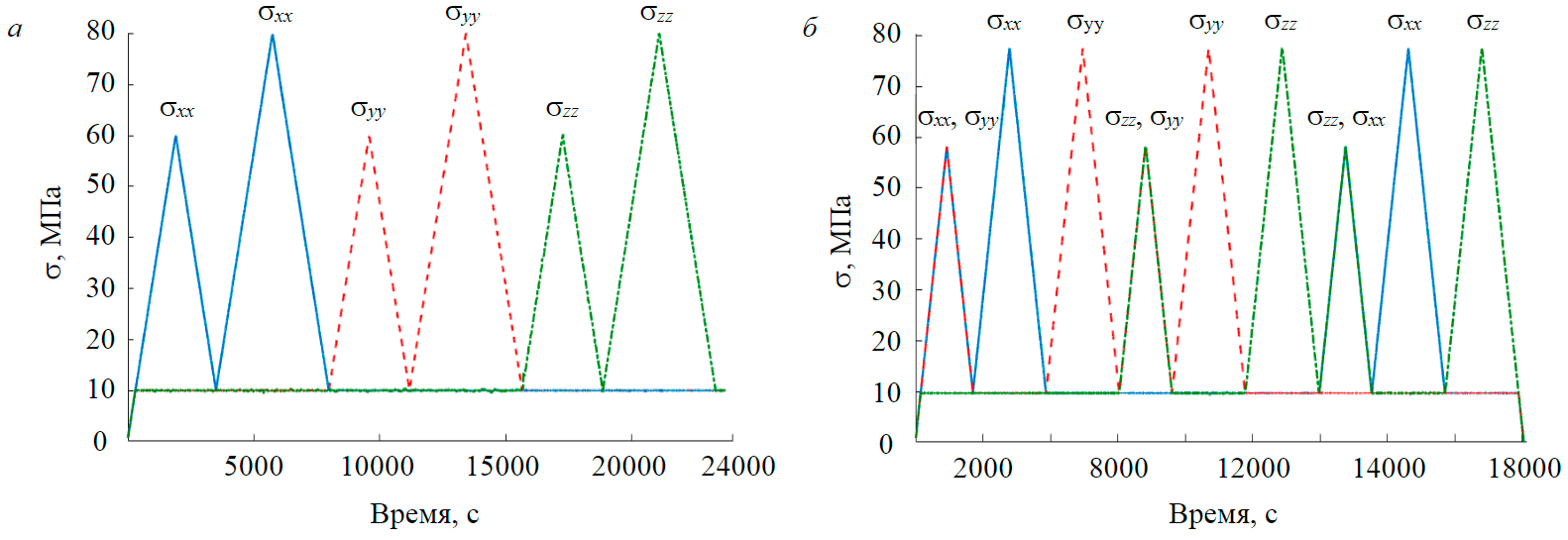
Рис.3. Первая (а) и вторая (б) программы циклических трехосных испытаний образцов песчаника (синяя сплошная линия – сжатие в направлении X, красная пунктирная – сжатие в направлении Y, зеленая штрихпунктирная – сжатие в направлении Z)
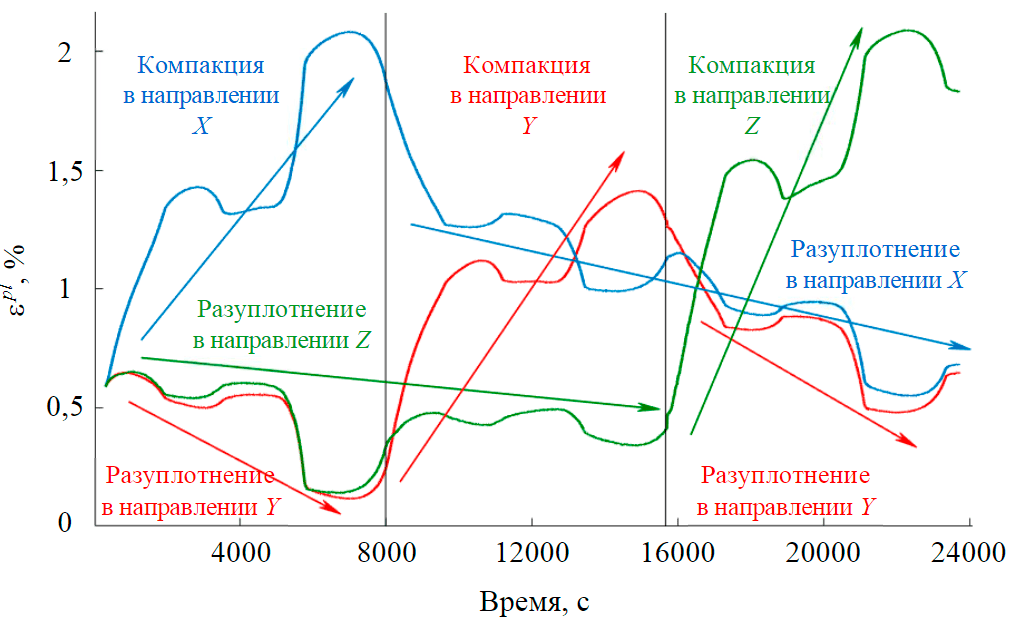
Рис.4. Кривые деформирования для сжатия в направлении оси X (a), Y (б), Z (в)
Результаты первой программы испытаний были использованы для определения материальных свойств породы, включая упругие модули и параметры, контролирующие уплотнение породы. Результаты второй программы испытаний были использованы для верификации модели тензорного уплотнения.
На рис.4 представлены кривые деформирования отдельно для каждой пары циклов при испытании песчаника по первой программе. Анализ ветвей разгрузки в каждой паре циклов позволил оценить модуль Юнга Еλ10 ГПа и коэффициент Пуассона νλ0,2. Вариации модулей от пары к паре циклов не превышают 15 %, поэтому будем считать породу изотропной, пренебрегая анизотропией упругих свойств и деградацией модулей упругости в процессе нагружения.
Используя оценку модулей упругости, вычислим упругую деформацию по каждому из трех направлений в каждом из шести циклов нагружения. Вычитание упругого отклика из общей деформации позволяет оценить вклад неупругой составляющей в деформационный отклик по каждому направлению (рис.5). Стрелки на рис.5 указывают на тенденцию изменения неупругой деформации: уплотнение (компакция) или разуплотнение. Результаты экспериментов явно показывают, что уплотнение в направлении активной нагрузки (увеличение неупругой деформации) всегда связано с растяжением в ортогональном направлении (уменьшение неупругой деформации). Во время активной нагрузки в направлении X (синяя линия) уплотнение неравномерно возрастает в течение обоих циклов, в то время как другие компоненты неупругой деформации (красная и зеленая линии) демонстрируют четкую тенденцию к разуплотнению. С началом активной нагрузки в направлении Y эта тенденция меняется, неупругая деформация в направлении активного сжатия начинает расти (красная линия) на фоне уменьшения двух других компонент. Аналогичное изменение имеет место в третьей паре циклов нагружения, соответствующей сжатию в направлении Z.

Рис.5. Изменение компонент неупругой деформации с течением времени (синяя линия – εxxpl, красная – εyypl, зеленая – εzzpl)
Представленные зависимости показывают, что все три компоненты неупругой деформации накапливаются в процессе истинного трехосного сжатия песчаника, демонстрируя как тенденцию к компакции, так и к разуплотнению. При трехосном сжатии уплотнение в одном направлении приводит к разуплотнению в перпендикулярных направлениях. Это расширение (разуплотнение) включает незначительное упругое расширение (в соответствии с коэффициентом Пуассона) и значительное неупругое расширение (рис.5), которое является в основном необратимым (см. рис.4).
Методология теоретического исследования
Общую деформацию материала при произвольной схеме приложения нагрузок можно представить суперпозицией упругой и неупругой составляющих. При этом за развитие неупругой составляющей могут отвечать различные физические механизмы. В настоящей работе под неупругой деформацией пористого материала понимается деформация уплотнения (изменения объема и структуры пористого пространства), начинающаяся с самого момента нагружения. Поскольку упругие модули практически не меняются в процессе нагружения, неупругая деформация, вызванная развитием поврежденности, пренебрежимо мала. Деформация уплотнения частично восстанавливается во время разгрузки (рис.5). Уплотнение не обязательно является изотропным, нагружение в одном направлении сопровождается деформацией растяжения (разуплотнения) в других направлениях (см. рис.1, в, рис.5). Для количественной оценки этого процесса определим тензор уплотнения Φij. Важной особенностью уплотнения по сравнению с другими механизмами неупругой деформации является то, что при постоянной нагрузке его значение приближается к определенной равновесной величине, при достижении которой порода перестает деформироваться. Если пренебречь деформацией зерен породы, изменение ее объема определяется изменением пористости. Уплотнение среды часто аппроксимируется эмпирическим законом Ати [1], который описывает изменение пористости, вызванное действующим давлением, и игнорирует вклад неизотропных механизмов, определяемых компонентами девиатора напряжений:
где φeq(P) – зависящая от давления равновесная пористость; Р – давление, P= – 1/3 (σ1+σ2+σ3), положительная величина – сжатие; A и B – материальные параметры, определяемые в результате скважинных измерений.
Применимость соотношения (1) была продемонстрирована в различных экспериментах (например, [15, 16]). Изменение пористости (объемная деформация уплотнения), связанное с увеличением давления от нуля до определенного значения P,
По аналогии с законом Ати (1), уравнение (2) описывает изменение объема материала, не принимая во внимание величину изменения деформации в различных направлениях. Мы предлагаем расширить соотношение (2) для равновесного тензора уплотнения, связав его не только с давлением, но и с девиаторной частью тензора напряжений (τij = σij +Pδij):
где Φij(0) – исходная величина тензора уплотнения, tr(Φij(0) - Aδij) – минимально возможная пористость уплотненной породы.
Вместо коэффициента B в соотношениях (1) и (2) вводятся два параметра B1 и B2, имеющие размерность напряжений. Отметим, что экспоненциальная функция тензорного аргумента – это тензор, который для произвольного аргумента X может быть представлен в виде сходящегося степенного ряда [27]:
Представленный выше ряд абсолютно сходится по норме $\| X \|=\sqrt{X\cdot \cdot X}$ для любого тензорного аргумента X и как его скалярный аналог может использоваться для вычисления тензорной экспоненциальной функции с любой заданной степенью точности. Используя (4), можно показать, что в системе координат, связанной с направлением главных напряжений, соотношение (3) можно переписать через главные напряжения и главные значения тензора уплотнения. В соответствии со свойствами экспоненциальной функции тензорного аргумента тензор уплотнения будет соосен тензору напряжений:
Для гидростатической нагрузки с нулевым девиатором напряжений (τij=0), а также для B2 → ∞ соотношение (5) эквивалентно (2) и определяет изотропное уплотнение. Если девиаторная составляющая напряжений отрицательная (сжатие), то уплотнение усиливается, в то время как растягивающее напряжение (положительные значения компонент девиатора напряжений) приводит к подавлению уплотнения и непосредственно к разуплотнению. В соотношении (3) дополнительный материальный параметр B2 отвечает за уплотнение в направлении сжимающей нагрузки и разуплотнение в направлениях, перпендикулярных ей.
Скорость уплотнения, согласно работам [3, 7], пропорциональна приложенному давлению, умноженному на разницу между равновесным и текущим значениями уплотнения. Используем эту же формулировку, отличающуюся от кинетического уравнения для пористости только тензорным характером уплотнения:
где С – положительный коэффициент, (Па∙с)–1. Следуя [15, 16], множитель C(Φij(eq) - Φij) можно рассматривать как величину, обратную вязкости, имеющую различные значения для уплотнения и разуплотнения. При постоянной нагрузке медленная релаксация деформации уплотнения до равновесного значения может рассматриваться как деформация ползучести. Поскольку равновесное уплотнение пропорционально экспоненте от девиатора напряжений (3), скорость накопления неупругой деформации (ползучести) также будет пропорциональна этой величине. Экспоненциальная зависимость скорости деформации ползучести от дифференциального напряжения подтверждается множественными лабораторными экспериментами [28-30], что указывает на непротиворечивость предложенного кинетического уравнения (6).
В случае тензорной формулировки для неупругой деформации уплотнения общая деформация материала может быть представлена в виде суммы упругой деформации и деформации уплотнения (изменения тензора уплотнения):
Соотношение (6) вместе с выражением для компонент тензора уплотнения (3) позволяют вычислить неупругую деформацию уплотнения материала при произвольной геометрии приложенных нагрузок. Прибавив вычисленную упругую деформацию для известных упругих модулей материала, получим полную деформацию (7), измеряемую в процессе нагружения образца.
Результаты
Проведем идентификацию предложенной модели тензорного уплотнения с использованием экспериментальных данных по циклическому трехосному сжатию песчаника. Для шестицикловой программы нагружения ранее были построены зависимости изменения диагональных компонент тензора неупругой деформации от времени (рис.5). Определим материальные параметры A, B1,B2 и коэффициент С, минимизируя невязку между экспериментальными и вычисленными данными с использованием разработанной модели (3D-компакции) при помощи зависимостей диагональных компонент тензора уплотнения от времени. На рис.6 представлены теоретические (в виде суммы вычисленной упругой и неупругой деформации) и экспериментальные временные кривые для компонент полной деформации. Для сравнения также были построены кривые, для которых неупругая составляющая рассчитывалась по закону Ати (1D-компакция).
Из рис.6 видно, что в течение первых двух циклов, когда активное нагружение осуществлялось в направлении оси X, 1D-модель (закон Ати) и 3D-модель (тензор уплотнения) удовлетворительно описывают экспериментальную кривую для компоненты εxxtot. Иная ситуация наблюдается для двух других компонент εyytot и εzztot, которые проявляют тенденцию к разуплотнению, и в целом для следующих пар циклов (сжатие в направлениях Y, Z). Модель тензорной компакции корректно воспроизводит тенденцию к уменьшению неупругой деформации (разуплотнению) в направлениях, перпендикулярных направлению активного сжатия, тогда как 1D-модель показывает незначительные вариации, связанные с эффектом Пуассона. Даже в направлении активного сжатия во второй и третьей парах циклов одномерная модель дает деформацию, несоответствующую экспериментальным данным. Это связано с ее неспособностью описывать частичную обратимость неупругой деформации на этапах разгружения. В целом представленные результаты показывают ожидаемый недостаток 1D-модели, использующей закон Ати, а именно неспособность описывать изменение неупругой деформации в направлениях, ортогональных направлению активного нагружения. В результате идентификации тензорной модели компакции были получены следующие значения параметров модели: A = 1,2 %, B1 = 49,2 МПа, B2 = 19,3 МПа, С = 1,6∙10–5 (Па∙с)–1. Кривые для 1D-модели получены при B= 46,8 МПа и том же значении параметра A.
Найденные параметры были использованы для верификации тензорной модели уплотнения по данным девятициклового эксперимента, моделирующего более сложный процесс компакции песчаника в трех ортогональных направлениях.
На рис.7 представлены экспериментальные (сплошные линии) и рассчитанные (пунктирные линии) зависимости компонент тензора полной деформации образца песчаника, испытанного по второй программе. Из рис.7 видно, что модель тензорной компакции корректно описывает экспериментальные данные по деформированию песчаника в трех ортогональных направлениях. Необходимо отметить, что модель качественно повторяет экспериментальные кривые как в ситуации, когда по одному направлению происходит компакция, а по двум другим разуплотнение, так и в ситуации, когда материал уплотняется в двух направлениях и расширяется в одном.
Обсуждение
Широко используемым подходом к описанию изменения пористости с глубиной является применение закона Ати и его модификаций. Согласно этому закону неупругая деформация уплотнения накапливается только в направлении активной нагрузки (см. рис.1, б). Результаты экспериментов по истинному трехосному сжатию пористого песчаника, представленные в этом исследовании, демонстрируют, что накопление неупругой деформации уплотнения в направлении активного сжатия сопровождается значительным неупругим расширением в ортогональных направлениях. Чтобы учесть трехмерный характер накопления упругой деформации, было предложено обобщение закона Ати на тензорный случай в виде (3). Введенный тензор уплотнения в обобщенной постановке зависит не только от давления, но и от компонент девиатора напряжений. Верификация и идентификация построенной тензорной модели уплотнения показала, что тензорная формулировка значительно улучшила соответствие экспериментальным данным по сравнению с одномерной моделью уплотнения. Расхождение между расчетными и экспериментальными кривыми (рис.6, 7) может быть связано как с нелинейным упругим откликом материала, так и с индуцированной поврежденностью анизотропией упругих свойств, развивающейся от цикла к циклу.
Начало неупругого деформирования, как правило, описывается тем или иным критерием текучести [31, 32]. Однако, представленные здесь результаты согласуются с недавними исследованиями [15, 16], согласно которым деформация неупругого уплотнения начинается с момента приложения нагрузки. Необходимо отметить, что введенный тензор уплотнения описывает лишь часть неупругой деформации, возникающей при нагружении пористой горной породы и связанной преимущественно с изменением объема материала (по аналогии с пластическим разрыхлением в модели Новожилова и коэффициента дилатансии в модели Друкера – Прагера – Николаевского [33]). Для учета неупругой деформации формоизменения требуется введение тензора поврежденности того или иного ранга, описывающего как деградацию упругих свойств материала, так и их индуцированную трещинообразованием анизотропию [34].
При негидростатической нагрузке скорость деформации уплотнения (соотношение (6) пропорциональна разнице между зависимым от напряжений равновесным уплотнением и его текущим значением. В случае постоянства приложенной нагрузки скорость уплотнения будет аналогична экспоненциальному закону, связывающему скорость деформации ползучести ε.cT и дифференциальное напряжение σ.d:
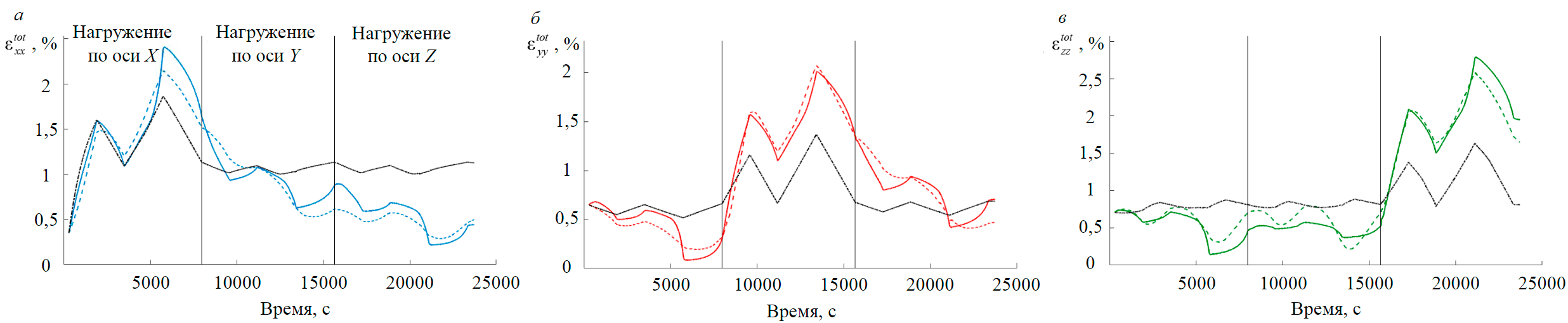
Рис.6. Совмещенные экспериментальные кривые компонент полной деформации песчаника (сплошные линии) и теоретические кривые, полученные с использованием тензорной (3D-компакция, пунктирные линии) и скалярной (1D-компакция, штрихпунктирные линии) формулировок; a – εxxtot; б – εyytot; в – εzztot
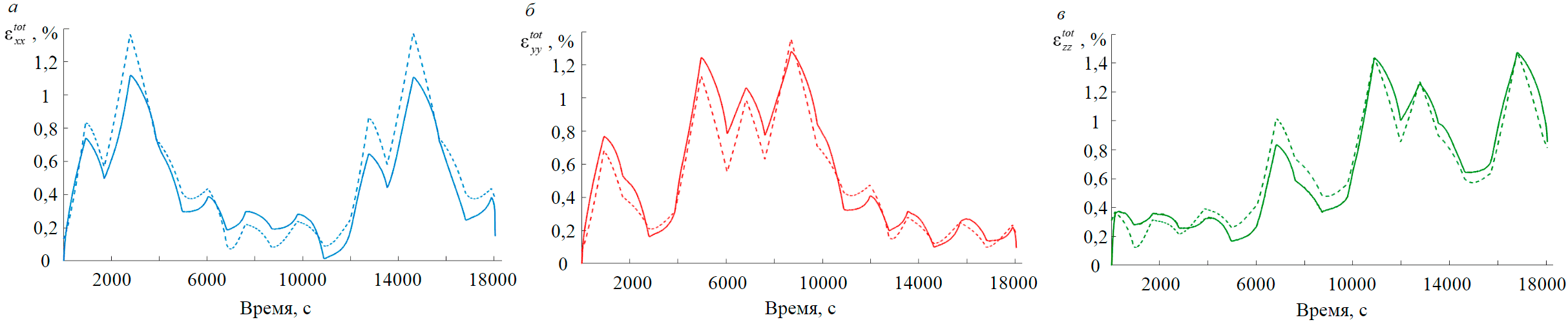
Рис.7. Совмещенные экспериментальные кривые компонент полной деформации песчаника, испытанного по второй программе (сплошные линии), и теоретические кривые, полученные с использованием тензорной модели (пунктирные линии); a – εxxtot; б – εyytot; в – εzztot
Для песчаника коэффициент Bcr варьируется в диапазоне 0,1-1,0 МПа–1 [13, 29], что очень близко к величине B2-1= 19,3–1, оцененной в результате идентификации модели для образцов песчаника.
По аналогии с отношением проницаемость – пористость, которое, как правило, представляется в виде степенной функции [35-37], можно связать уменьшение компонент тензора проницаемости Δkij с компонентами тензора уплотнения Фij в виде:
где n – показатель степени, в приближении ламинарного течения Пуазейля n = 3.
При таком предположении сильная анизотропия проницаемости в осадочных бассейнах, когда проницаемости в вертикальном и горизонтальном направлениях могут отличаться на порядки по величине, объясняется значительным вертикальным уплотнением и одновременным горизонтальным разуплотнением среды.
Заключение
В экспериментальной части работы приведены результаты циклических испытаний образцов песчаника, проведенных по двум программам трехосного нагружения. Проведена оценка упругих модулей материала, позволившая разделить общую деформацию на упругую и неупругую составляющую. Показано, что увеличение неупругой деформации в направлении активного сжатия (уплотнение) сопровождается ее уменьшением в двух ортогональных направлениях (разуплотнение).
В теоретической части работы введен тензор уплотнения, представляющий собой обобщение закона Ати на случай учета компонент девиатора напряжений. Предложено кинетическое уравнение, описывающее эволюцию компонент тензора уплотнения с течением времени. На основе экспериментальных данных по шестицикловому нагружению песчаника проведена идентификация модели, определены материальные параметры, отвечающие за процесс уплотнения и разуплотнения среды. Для верификации модели проведены численные расчеты эволюции компонент тензора уплотнения при сложном циклическом сжатии со сменой как самого направления активного сжатия, так и количества направлений активного сжатия. Сопоставление экспериментальных и расчетных кривых показало их качественное и количественное соответствие. В результате проведенных расчетов показано, что модель тензорного уплотнения позволяет успешно описывать накопление неупругих деформаций компакции и разуплотнения в различных направлениях. Применимость предложенных соотношений для описания тензорной компакции материала ограничена средне- и высокопористыми сцементированными породами.
Литература
- Athy L.F. Density, porosity, and compaction of sedimentary rocks // American Association of Petroleum Geologists Bulletin. 1930. Vol. 14. Iss. 1. P. 1-24. DOI: 10.1306/3D93289E-16B1-11D7-8645000102C1865D
- Dasgupta T., Mukherjee S. Sediment compaction and applications in petroleum geoscience. Cham: Springer, 2020. 208p. DOI: 10.1007/978-3-030-13442-6
- Токарева М., Сибин А. Численное исследование задачи фильтрации жидкости в тонком пороупругом слое // Известия Алтайского государственного университета. 2017. № 1 (93). DOI: 10.14258/izvasu(2017)1-25
- Stover S.C., Ge S., Screaton E.J. A one-dimensional analytically based approach for studying poroplastic and viscous consolidation: Application to Woodlark Basin, Papua New Guinea // Journal of Geophysical Research: Solid Earth. 2003. Vol. 108. Iss. B9. №2448. DOI: 10.1029/2001JB000466
- Suetnova E.I. Influence of the fluid-dynamic and rheological properties of sediments on the process of viscoelastic compaction at different rates of sedimentation // Izvestiya, Physics of the Solid Earth. 2010. Vol. 46. Iss. 6. P. 529-537. DOI: 10.1134/S1069351310060078
- Morency C., Huismans R., Beaumont C., Fullsack P. A numerical model for coupled fluid flow and matrix deformation with applications to disequilibrium compaction and delta stability // Journal of Geophysical Research: Solid Earth. 2007. Vol. 112. Iss. B10. № B10407. DOI: 10.1029/2006JB004701
- Holland E., Showalter R.E. Poro-Visco-Elastic Compaction in Sedimentary Basins // SIAM Journal on Mathematical Analysis. 2018. Vol. 50. Iss. 2. P. 2295-2316. DOI: 10.1137/17M1141539
- Revil A., Grauls D., Brévart O. Mechanical compaction of sand/clay mixtures // Journal of Geophysical Research: Solid Earth. 2002. Vol. 107. Iss. B11. № 2293. DOI: 10.1029/2001JB000318
- Connolly J.A.D., Podladchikov Y.Y. Temperature-dependent viscoelastic compaction and compartmentalization in sedimentary basins // Tectonophysics. 2000. Vol. 324. Iss. 3. P. 137-168. DOI: 10.1016/S0040-1951(00)00084-6
- Bruch A., Maghous S., Ribeiro F.L.B., Dormieux L. A thermo-poro-mechanical constitutive and numerical model for deformation in sedimentary basins // Journal of Petroleum Science and Engineering. 2018. Vol. 160. P. 313-326. DOI: 10.1016/j.petrol.2017.10.036
- Baud P., Reuschlé T., Ji Yu. Mechanical compaction and strain localization in Bleurswiller sandstone // Journal of Geophysical Research: Solid Earth. 2015. Vol. 120. Iss. 9. P. 6501-6522. DOI: 10.1002/2015JB012192
- Carbillet L., Heap M.J., Baud P., Wadsworth F.B., Reuschlé T. Mechanical compaction of crustal analogs made of sintered glass beads: the influence of porosity and grain size // Journal of Geophysical Research: Solid Earth. 2021. Vol. 126. Iss. 4. DOI: 10.1029/2020JB021321
- Heap M.J., Brantut N., Baud P., Meredith P.G. Time-dependent compaction band formation in sandstone // Journal of Geophysical Research: Solid Earth. 2015. Vol.120. Iss. 7. P. 4808-4830. DOI: 10.1002/2015JB012022
- Карманский А.Т. Коллекторские свойства горных пород при изменении вида напряженного состояния // Записки Горного института. 2009. Т. 183. С. 289-292.
- Pijnenburg R.P.J., Verberne B.A., Hangx S.J.T., Spiers C.J. Deformation Behavior of Sandstones From the Seismogenic Groningen Gas Field: Role of Inelastic Versus Elastic Mechanisms // Journal of Geophysical Research: Solid Earth. 2018. Vol. 123. Iss. 7. P. 5532-5558. DOI: 10.1029/2018JB015673
- Shalev E., Lyakhovsky V., Ougier-Simonin A. et al. Inelastic compaction, dilation and hysteresis of sandstones under hydrostatic conditions // Geophysical Journal International. 2014. Vol. 197. Iss. 2. P. 920-925. DOI: 10.1093/gji/ggu052
- Neuzil C.E. Hydromechanical coupling in geologic processes // Hydrogeology Journal. 2003. Vol. 11. P. 41-83. DOI: 10.1007/s10040-002-0230-8
- Brüch A., Colombo D., Frey J. et al. Coupling 3D geomechanics to classical sedimentary basin modeling: From gravitational compaction to tectonics // Geomechanics for Energy and the Environment. 2021. Vol. 28. № 100259. DOI: 10.1016/j.gete.2021.100259
- McPherson B., Bredehoeft J.D. Overpressures in the Uinta Basin, Utah: Analysis using a three-dimensional basin evolution model // Water Resources Research. 2001. Vol. 37. Iss. 4. P. 857-871. DOI: 10.1029/2000WR900260
- Torelli M., Traby R., Teles V., Ducros M. Thermal evolution of the intracratonic Paris Basin: Insights from 3D basin modelling // Marine and Petroleum Geology. 2020. Vol. 119. № 104487. DOI: 10.1016/j.marpetgeo.2020.104487
- ПантелеевИ.А., МубассароваВ.А., ЗайцевА.В. идр. Эффект Кайзера при трехосном сжатии песчаника с последовательным вращением эллипсоида заданных напряжений // Физико-технические проблемы разработки полезных ископаемых. 2020. № 3. С. 47-55. DOI: 10.1134/S1062739120036653
- Пантелеев И.А., Коваленко Ю.Ф., Сидорин Ю.В. и др. Эволюция поврежденности при сложном неравнокомпонентном сжатии песчаника по данным акустической эмиссии // Физическая мезомеханика. 2019. Т. 22. № 4. С. 56-63. DOI: 10.24411/1683-805X-2019-14006
- Shevtsov N., Zaitsev A., Panteleev I. Deformation and destruction of rocks on the true triaxial loading system with continuous acoustic emission registration // Physical and Mathematical Modeling of Earth and Environment Processes. 2018. P. 424-432. DOI: 10.1007/978-3-030-11533-3_42
- Panteleev I.A., Mubassarova V.A., Zaitsev A.V. et al. The Kaiser Effect under Multiaxial Nonproportional Compression of Sandstone // Doklady Physics. 2020. Vol. 65. P. 396-399. DOI: 10.1134/S1028335820110075
- Karev V.I., Klimov D.M., Kovalenko Yu.F., Ustinov K.B. Fracture of sedimentary rocks under a complex triaxial stress state // Mechanics of Solids. 2016. Vol. 51. Iss. 5. P. 522-526. DOI: 10.3103/S0025654416050022
- Klimov D.M., Karev V.I., Kovalenko Yu.F. Experimental study of the influence of a triaxial stress state with unequal components on rock permeability // Mechanics of Solids. 2015. Vol. 50. Iss. 6. P. 633-640. DOI: 10.3103/S0025654415060047
- Schade H., Neemann K. Tensor Analysis. Lithuania: De Gruyter, 2018. 327 p. DOI: 10.1515/9783110404265
- Rijken M.C.M. Modeling naturally fractured reservoirs: From experimental rock mechanics to flow simulation: Dissertation of Doctor of Philosophy. Austin: The University of Texas at Austin, 2005. 275 p.
- Heap M.J., Baud P., Meredith P.G. et al. Time‐dependent brittle creep in Darley Dale sandstone // Journal of Geophysical Research: Solid Earth. 2009. Vol. 114. Iss. B7. № B07203. DOI: 10.1029/2008JB006212
- Brantut N., Heap M.J., Meredith P.G., Baud P. Time-dependent cracking and brittle creep in crustal rocks: A review // Journal of Structural Geology. 2013. Vol. 52. P. 17-43. DOI: 10.1016/j.jsg.2013.03.007
- Jaeger J.C., Cook N.G.W., Zimmerman R. Fundamentals of rock mechanics. Oxford: Wiley-Blackwell, 2007. 488 p.
- Pietruszczak S. Fundamentals of plasticity in geomechanics. London: CRC Press, 2020. 206 p.
- Николаевский В.Н. Геомеханика: Собрание трудов. Т.1. Разрушение и дилатансия. Нефть и газ. Москва-Ижевск: Институт компьютерных исследований, 2010. 639 с.
- Panteleev I., Lyakhovsky V., Browning J. et al. Non-linear anisotropic damage rheology model: Theory and experimental verification // European Journal of Mechanics/A Solids. 2021. Vol. 85. № 104085. DOI: 10.1016/j.euromechsol.2020.104085
- Bernabé Y., Mok U., Evans B. Permeability-porosity Relationships in Rocks Subjected to Various Evolution Processes // Pure and Applied Geophysics. 2003. Vol. 160. P. 937-960. DOI: 10.1007/PL00012574
- Ghabezloo S., Sulem J., Saint-Marc J. Evaluation of a permeability-porosity relationship in a low-permeability creeping material using a single transient test // International Journal of Rock Mechanics and Mining Sciences. 2009. Vol. 46. Iss. 4. P. 761-768. DOI: 10.1016/j.ijrmms.2008.10.003
- Smith T.M., Sayers C.M., Sondergeld C.H. Rock properties in low-porosity/low-permeability sandstones // The Leading Edge. 2009. Vol.28. Iss. 1. P. 48-59. DOI: 10.1190/1.3064146
