Tensor compaction of porous rocks: theory and experimental verification
- 1 — Ph.D. Head of Laboratory Institute of Continuous Media Mechanics, Ural Branch of the Russian Academy of Sciences ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 2 — Ph.D. Researcher Geological Survey of Israel ▪ Orcid ▪ Scopus ▪ ResearcherID
- 3 — Ph.D. Researcher Institute of Continuous Media Mechanics, Ural Branch of the Russian Academy of Sciences ▪ Orcid ▪ Elibrary ▪ Scopus
- 4 — Ph.D., Dr.Sci. Chief Researcher Ishlinsky Institute for Problems in Mechanics, Russian Academy of Science ▪ Orcid ▪ Elibrary ▪ ResearcherID
- 5 — Junior Researcher Ishlinsky Institute for Problems in Mechanics of the Russian Academy of Sciences ▪ Orcid ▪ Elibrary ▪ ResearcherID
- 6 — Ph.D. Researcher Geological Survey of Israel ▪ Orcid ▪ ResearcherID
Abstract
Compaction in sedimentary basins has been traditionally regarded as a one-dimensional process that ignores inelastic deformation in directions orthogonal to the active load. This study presents new experiments with sandstone demonstrating the role of three-dimensional inelastic compaction in cyclic true triaxial compression. The experiments were carried out on the basis of a triaxial independent loading test system in the Laboratory of Geomechanics of the Ishlinsky Institute for Problems in Mechanics of the Russian Academy of Science. The elastic moduli of the material were estimated from the stress-strain curves and the elastic deformations of the sample in each of the three directions were determined. Subtracting the elastic component from the total deformation allowed to show that inelastic compaction of the sandstone is observed in the direction of active loading, whereas in the orthogonal directions there is a expansion of the material. To describe the three-dimensional nature of the compaction, a generalization of Athy law to the tensor case is proposed, taking into account the role of the stress deviator. The compaction tensor and the kinetic equation to describe the evolution of inelastic deformation, starting from the moment of the load application are introduced. On the basis of experiments on cyclic multiaxial compression of sandstone, the identification and verification of the constructed model of tensor compaction were carried out. The possibility of not only qualitative, but also quantitative description of changes in inelastic deformation under complex cyclic triaxial compression is shown.
Introduction
The key filtration-capacitance characteristic of reservoir rocks is porosity. During changes in stress fields in the rock mass caused by tectonic processes, mining, and a decrease in pore pressure, the compaction occurs – inelastic compaction of rocks. Compaction leads to a decrease in the porosity of rocks. Most models describing the process of rock compaction during sedimentation and lithogenesis are based on Athy law [1] – the empirical law of exponential drop in porosity with pressure. The coefficients of the Athy law, as a rule, are selected based on data on changes in porosity in boreholes in a particular region, while it is assumed that the distribution of porosity with depth depends only on the type of sedimentary rocks. In recent decades, various relations have been proposed for porosity change with depth, taking into account variations in the lithological composition of rocks and the mineral composition of the fluid saturating them [2]. Athy law and other similar relations (Hedberg, Weller, Teodorovich – Chernov, Burst, Beall, Overton and Zanier, etc. [2]) consider inelastic compaction as a process controlled by average stress, ignoring the possible influence of deviatoric stress components.
Early models used elastic and poro-elastic rheology to describe rock compaction and fluid removal. In these models, pore pressure prevents rock compaction during fluid expulsion, while an abnormally high reservoir pressure is created in the case of a sufficiently high compaction rate (porosity reduction). In subsequent studies, irreversible compaction was modeled on the basis of viscous [3-5] and visco-plastic rheology [6-8], including taking into account temperature effects [9] and large deformations [10]. It should be noted that the theoretical results only partially describe the available experimental data [11-13]. Recent studies have shown that rock compaction occurs at all stress levels from the very beginning of compression, i.e. it is a non-threshold process that does not require the introduction of a yield criteria [14-16].
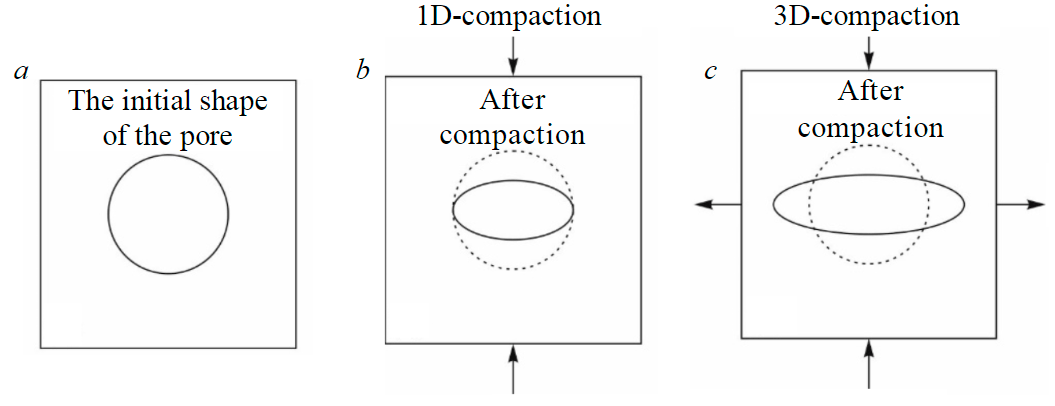
Fig.1. Schematic representation of the pore space compaction
Problem statement
In previous studies of compaction, it was assumed that the deformation during compaction can be approximated only by a vertical component (Fig.1, a, b, 1D-compaction). Initially, the spherical pore space undergoes vertical irreversible compression with constant horizontal deformation (Fig.1, b). Such a 1D-approximation makes it possible to significantly simplify the hydromechanical description of the compaction process [17]. Using this hypothesis, numerical calculations of the formation of sedimentary basins in two- and three-dimensional formulations were carried out [18-20]. It should be noted that the consequences of such simplification have been little studied [17].
This paper presents the results of sandstone tests under conditions of true triaxial compression, demonstrating that inelastic compaction in the direction of maximum compression is accompanied by inelastic decompression in the orthogonal direction (Fig.1, с). To take into account the three-dimensional nature of the inelastic compaction process, a generalization of the Athy law is proposed in the work, linking the equilibrium compaction not only with pressure, but also with the deviatoric stress components. The process of uneven compaction observed in the experiment is modeled using kinetic relations linking the compaction rate with the applied pressure and the difference between the current and equilibrium compaction values. Numerical modeling has shown that the three-dimensional (tensor) model of inelastic compaction reproduces the main features of the deformational behavior of sandstone under cyclic loading in three orthogonal directions.
Methodology of experimental research
To study the compaction process under complex three-dimensional loading, the results of experiments on cyclic true triaxial testing of sandstone samples are used. A detailed description of the experimental conditions is presented in [21].
Polymictic sandstone belonging to the Sheshmin formation of the Ufimian Strata of the Permian system was selected for testing. Sandstone is characterized by a layered structure caused by alter-nating interlayers enriched with epidote and flint fragments. SEM-studies have shown that the distribution of mineral grains by volume is uniform with a size from 150 to 450 microns. The porosity of sandstone is 9.5 % and is developed mainly along grain boundaries, which is caused by calcite leaching by groundwater. Cubic samples with an edge size of 40 mm were made on a special processing complex at the Ishlinsky Institute for Problems in Mechanics of the Russian Academy of Sciences with high accuracy, the non-parallelism of the faces did not exceed 20 microns.
Mechanical tests were carried out on the triaxial independent loading testing system (TILTS) in the laboratory of geomechanics [22-24]. Independent loading in three orthogonal directions is carried out due to the original kinematic scheme applied in the design of the loading unit, which allows the pressure plates to converge in three directions without interfering with each other [25, 26]. Before the tests, thin fluoroplastic gaskets with grease were installed between the sample faces and the tips of the pressure plates to minimize friction during compression of the sample (Fig.2). The automated TILTS control and data acquisition system includes LVDT displacement sensors and force sensors with a resolution of 0.2 microns and 0.03 MPa. Measurements of forces and displacements are carried out independently on all three loading axes with a sampling frequency of 1 Hz.
To study the process of compaction of sandstone, two programs of cyclic triaxial load were implemented (Fig.3). The first test program consisted of three pairs of loading–unloading cycles and a comprehensive compression up to 10 MPa preceding them. In the first cycle, active compression was performed along the X axis to a pressure of σxx = 60 MPa, followed by unloading to σxx = 10 MPa while keeping the stresses constant along the other two axes σyy = σzz = 10 MPa. In the second cycle, the load was carried out in the same direction up to σxx = 80 MPa, followed by unloading up to 10 MPa. Then the same pair of cycles followed with active compression along the Y axis with the control of constant stresses in the other two directions, then in the direction of the Z axis (Fig.3, a). The rate of active loading and unloading in each of the six cycles is constant and equal to 31 kPa/s.

Fig.2. Sample in TILTS after stopping the triaxial disproportionate compression test
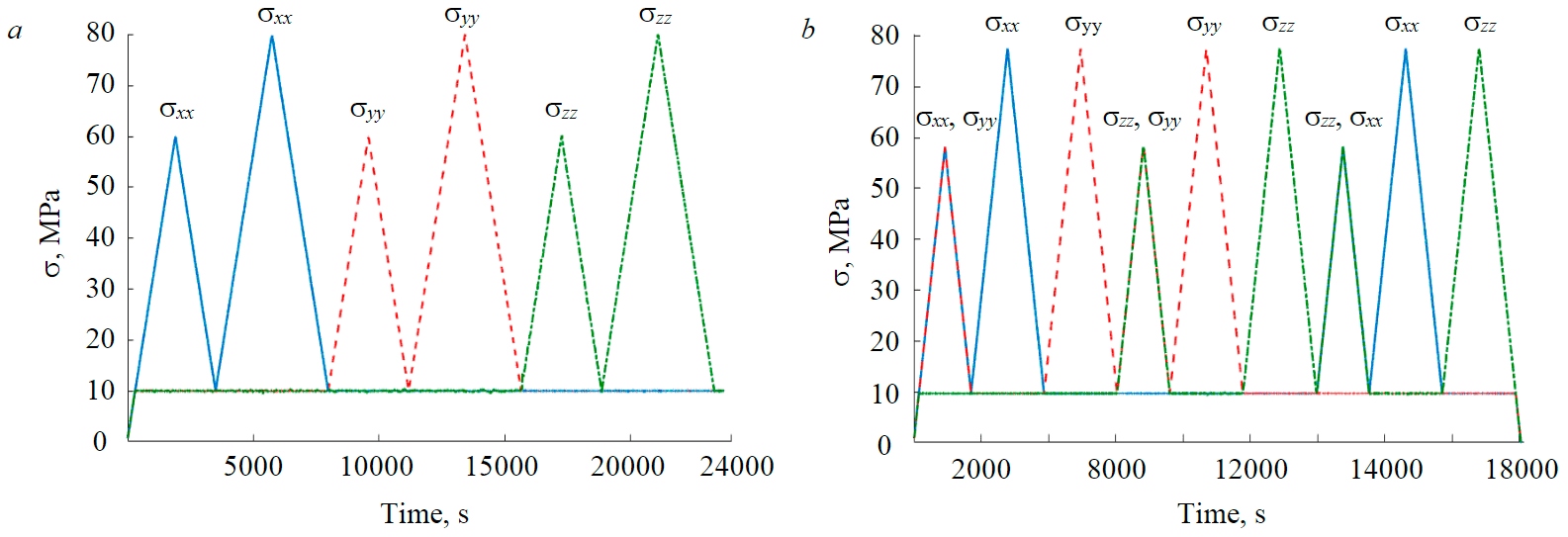
Fig.3. The first (a) and second (b) programs of cyclic triaxial testing of sandstone samples (blue solid line – compression in the X direction, red dotted line – compression in the Y direction, green dashed – compression in the Z direction)
The second test program was an extended version of the first program and consisted of three triples of cycles (Fig.3, b). The first cycle of each triple was compression in two of the three directions up to 58 MPa, followed by unloading up to 10 MPa while keeping the pressure in the third direction at 10 MPa. In the second and third cycles, active compression (up to the stress level of 78 MPa) and unloading (up to 10 MPa) were carried out in each of the two selected directions, while maintaining constant stresses in the two remaining directions. The first three represented a loading – unloading cycle in the X and Y directions, a loading – unloading cycle in the X direction (stress holding along the Y, Z axes), a loading – unloading cycle in the Y direction (stress holding along the X, Z axes). The second three was a loading – unloading cycle in the Z and Y directions, a loading – unloading cycle in the Z direction (stress holding along the Y, X axes), a loading – unloading cycle in the Y direction (stress holding along the X, Z axes). Finally, the third three are loading – unloading cycles in the Z and X directions, followed by successive loading – unloading cycles in the X and Z directions.
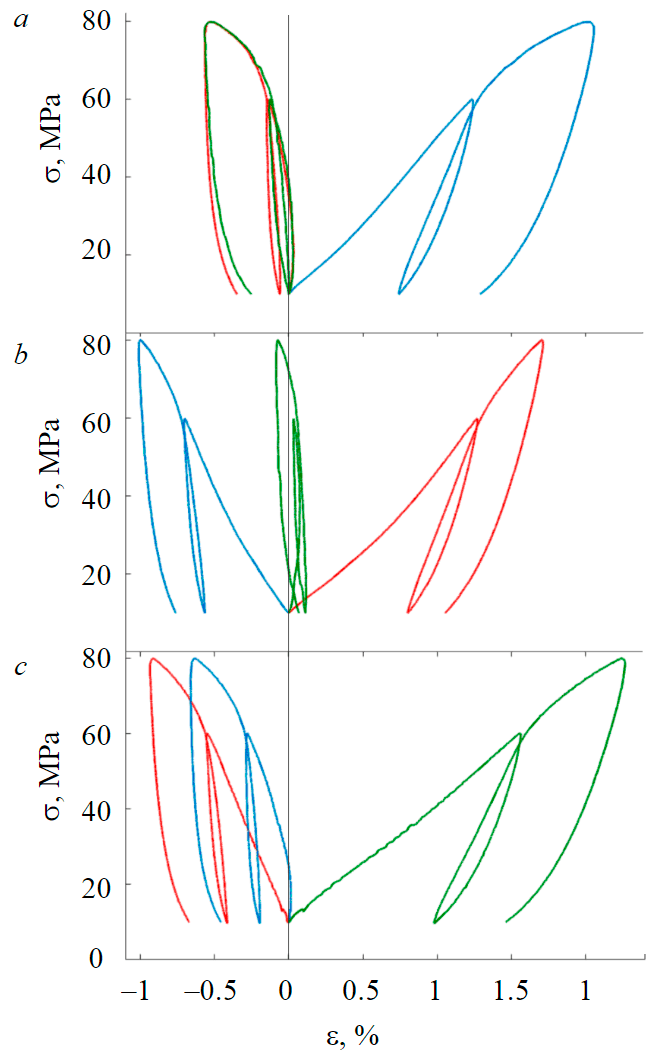
Fig.4. Deformation curves for compression in the direction of the axis X (a), Y (b), Z (c)
The results of the first test program were used to determine the material properties of the rock, including elastic moduli and parameters controlling the compaction of the rock. The results of the second test program were used to verify the tensor compaction model.
Figure 4 shows the deformation curves separately for each pair of cycles when testing sandstone according to the first program. Analysis of the unloading path in each pair of cycles allowed to estimate the Young's modulus Е~10 GPa and the Poisson coefficient ν~0.2. The modulus variations from pair to pair of cycles do not exceed 15 %, so we will consider the rock isotropic, neglecting the anisotropy of elastic properties and the degradation of elastic modulus during loading.
Using the estimated elastic moduli, we calculate the elastic strain component in each of the three directions in each of the six loading cycles. Subtracting the elastic strain from the total deformation allows to estimate the contribution of the inelastic component to the deformation response in every direction (Fig.5). The arrows in Fig.5 indicate the tendency of inelastic strain to change: compaction or expansion. The experimental results clearly show that compaction in the direction of the active load (an increase in inelastic deformation) is always associated with expansion in the orthogonal direction (a decrease in inelastic deformation). During the active load in the X direction (blue line), the compaction increases unevenly during both cycles, while other components of inelastic deformation (red and green lines) show a clear tendency to expansion. With the onset of the active load in the Y direction, this trend changes, the inelastic deformation in the direction of active compression begins to grow (red line) against the background of a decrease in the other two components. A similar change takes place in the third pair of loading cycles corresponding to compression in the Z direction.
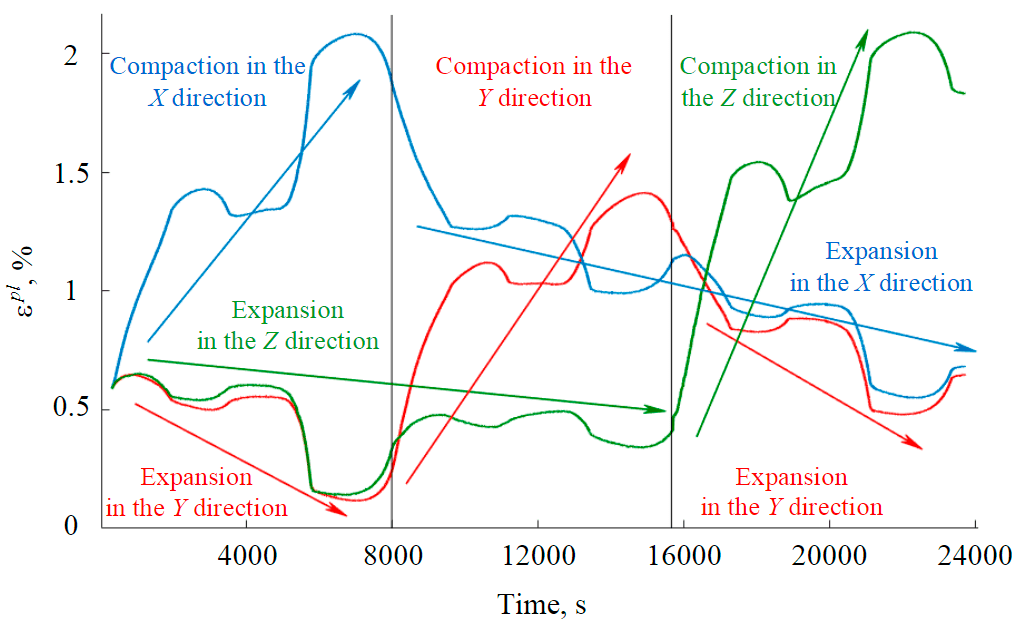
Fig.5. Change of inelastic deformation components over time(blue line – εxxpl, red – εyypl, green – εzzpl)
The presented dependences show that all three components of inelastic deformation accu-mulate in the process of true tri-axial compression of sandstone, demonstrating both a tendency to compaction and expansion. With triaxial compression, compaction in one direction leads to expansion in perpendicular directions. This extension (expansion) includes a slight elastic extension (in accordance with the Poisson's ratio) and a significant inelastic extension (Fig.5), which is basically irreversible (see Fig.4).
Methodology of theoretical research
The general deformation of the material under an arbitrary scheme of application of loads can be represented by a superposition of elastic and inelastic components. At the same time, different physical mechanisms may be responsible for the development of the inelastic component. In this paper, inelastic deformation of a porous material is understood as compaction (changes in the volume and structure of the porous space), starting from the very moment of loading. Since elastic modules practically do not change during loading, inelastic deformation caused by the development of damage is negligible. The compaction is partially restored during unloading (Fig.5). Compaction is not necessarily isotropic, loading in one direction is accompanied by expansion in other directions (see Fig.1, c, Fig.5). To quantify this process, we define the compaction tensor Fij. An important feature of compaction in comparison with other mechanisms of inelastic deformation is that, under constant load, its value approaches a certain equilibrium value, at which the rock ceases to deform. If the deformation of the rock grains is neglected, the change in its volume is determined by the change in porosity. The compaction of the medium is often approximated by the empirical Athy law [1], which describes the change in porosity caused by the acting pressure and ignores the contribution of non-isotropic mechanisms determined by the components of the stress deviator:
where φeq(P) – pressure-dependent equilibrium porosity; Р – pressure, P=-1/3(σ1+σ2+σ3) , positive value – compression; A and B – material parameters determined as a result of borehole measu-rements.
The applicability of relation (1) has been demonstrated in various experiments (for example, [15, 16]). Porosity change (volumetric deformation) associated with an increase in pressure from zero to a certain value of P,
By analogy with Athy law (1), equation (2) describes the change in the volume of the material, without taking into account the amount of deformation change in different directions. We propose to extend the relation (2) for the equilibrium tensor of compaction by associating it not only with pressure, but also with the deviatory part of the stress tensor (τij=σij+Pδij):
where Fij(0) – initial value of the compaction tensor, tr(Fij(0)-Aδij) – minimum possible porosity of compacted rock.
Instead of the coefficient B in the ratios (1) and (2), two parameters B1 and B2, having the dimension of stresses are introduced. Note that the exponential function of a tensor argument is a tensor that for an arbitrary argument X can be represented as a convergent power series [27]:
The series presented above absolutely converges according to the norm $\| X \|=\sqrt{X\cdot \cdot X}$ for any tensor argument X and as its scalar analogue can be used to calculate a tensor exponential function with any given degree of accuracy. Using (4), it can be shown that in the coordinate system associa-ted with the directions of the principal stresses, the relation (3) can be rewritten in terms of the principal values of the stress and compaction tensors. In accordance with the properties of the exponential function of the tensor argument, the compaction tenor will be aligned with the stress tensor:
For a hydrostatic load with zero stress deviator (τij=0), as well as B2→∞, the equation (5) is equivalent to (2) and it defines an isotropic compaction. If the deviatory components of the stresses is negative (compression), then the compaction increases, while the tensile stress (positive values of the stress deviator) leads to suppresses compaction and may even leads to expansion. In relation (3), the additional material parameter B2 is responsible for compaction in the direction of the compressive load and expansion in directions perpendicular to it.
The compaction rate, according to [3, 7], is proportional to the applied pressure multiplied by the difference between the equilibrium and current compaction values. We use the same formulation, which differs from the kinetic equation for porosity only by the tensor character of the compaction:
where С – positive coefficient, (Pa∙s)–1. Following [15, 16], the multiplier C(Fij(eq)-Fij) can be conside-red as the inverse of viscosity, having different values for compaction and expansion. At constant load, the slow relaxation of the deformation of the compaction to an equilibrium value can be considered as creep. Since the equilibrium compaction is proportional to the exponential of the stress deviator (3), the rate of accumulation of inelastic deformation (creep) will also be proportional to this value. The exponential dependence of the creep rate on the differential stress is confirmed by multiple laboratory experiments [28-30], which indicates the consistency with the proposed kinetic equation (6).
In the case of tensor formulation for inelastic deformation of the compaction, the total deformation of the material can be represented as the sum of elastic deformation and the compaction (changes in the tensor of the compaction):
Equation (6) together with the expression for the components of the compaction tensor (3) allow calculating the inelastic deformation of the material under arbitrary applied loads. Adding the calculated elastic deformation for the known elastic modules of the material, we obtain the total deformation (7) measured during the loading of the sample.
Results
Let us identify the proposed tensor compaction model using experimental data on cyclic triaxial compression of sandstone. For a six-cycle loading program, dependences of the change in the principal components of the inelastic deformation tensor on time were previously constructed (Fig.5). We estimate the material parameters A, B1, B2 and the coefficient С, by minimizing the discrepancy between the experimental and calculated data using the developed model (3D-compaction) using the dependencies of the principal components of the compaction tensor on time. Figure 6 presents theoretical (as a sum of the calculated elastic and inelastic strains) and experimental time curves for the components of the total deformation. For comparison, curves were also constructed for which the inelastic component was calculated according to Athy law (1D-compaction).
Figure 6 shows that during the first two cycles, when active loading was carried out in the direction of the X axis, the 1D-model (Athy law) and the 3D-model (compaction tensor) satisfactorily describe the experimental curve for the component εxxtot. A different situation is observed for the other two components εyytot and εzztot , which show a tendency to decompression, and in general for the following pairs of cycles (compression in the Y, Z directions). The tensor compaction model correctly reproduces the tendency to decrease inelastic deformation (expansion) in orthogonal directions to the active compression, whereas the 1D-model shows minor variations associated with the Poisson effect. Even in the direction of active compression in the second and third pairs of cycles, the one-dimensional model gives a deformation that does not correspond to experimental data. This is due to its inability to describe the partial reversibility of inelastic deformation during the unloading stages. In general, the presented results show the expected disadvantage of the 1D-model using Athy law, namely, the inability to describe the change in inelastic deformation in directions orthogonal to the direction of active loading. As a result of the identification of the tensor model of compaction, the following values of the model parameters were obtained: A = 1.2 %, B1 = 49.2 MPa, B2 = 19.3 MPa, С = 1.6∙10–5 (Pa∙s)–1. The curves for the 1D-model are obtained for B = 46.8 MPa and the same value of parameter A.
The constrained parameters were used to verify the tensor model of compaction according to the data of a nine-cycle experiment simulating a more complex process of compaction of sandstone in three orthogonal directions.
Figure 7 shows the experimental (solid lines) and calculated (dotted lines) dependences of the components of the tensor of the total deformation of the sandstone sample tested under the second program. Figure 7 shows that the tensor compaction model correctly describes experimental data on sandstone deformation in three orthogonal directions. It should be noted that the model qualitatively repeats experimental curves both in a situation when compaction occurs in one direction and expansion occurs in the other two, and in a situation when the material is compacted in two directions and expands in one.
Discussion
A widely used approach to describing changes in porosity with depth is the application of Athy’s law and its modifications. According to this law, inelastic deformation of the compaction accumulates only in the direction of the active load (see Fig.1, b). The results of experiments on true triaxial load of porous sandstone presented in this study demonstrate that the accumulation of inelastic compaction in the direction of active compression is accompanied by significant inelastic expansion in orthogonal directions. In order to take into account the three-dimensional nature of the accumulation of elastic deformation, a generalization of Athy law to the tensor case in the form (3) was proposed. The introduced compaction tensor in the gene-ralized formulation depends not only on the pressure, but also on the components of deviatory stress. Verification and identification of the constructed tensor model of compaction showed that the tensor formulation significantly improved compliance with experimental data compared to the one-dimensional model of compaction. The discrepancy between the calculated and experimental curves (Figs.6, 7) can be related both to the nonlinear elastic response of the material and to the damage-induced anisotropy of elastic properties that develops from cycle to cycle.
The onset of inelastic deformation is usually described by one or another yield criterion [31, 32]. However, the results presented here are consistent with recent studies [15, 16], according to which the deformation of an inelastic compaction begins at the moment of application of the load. It should be noted that the introduced compaction tensor describes only a part of the inelastic deformation that occurs when loading a porous rock and is mainly associated with a change in the volume of the material (by analogy with plastic loosening in the Novozhilov model and the dilatancy coefficient in the Drucker – Prager – Nikolaevsky model [33]). To account for the inelastic deformation of the shape change, it is necessary to introduce a damage tensor of one or another rank, describing both the deg-radation of the elastic properties of the material and their anisotropy induced by cracking [34].
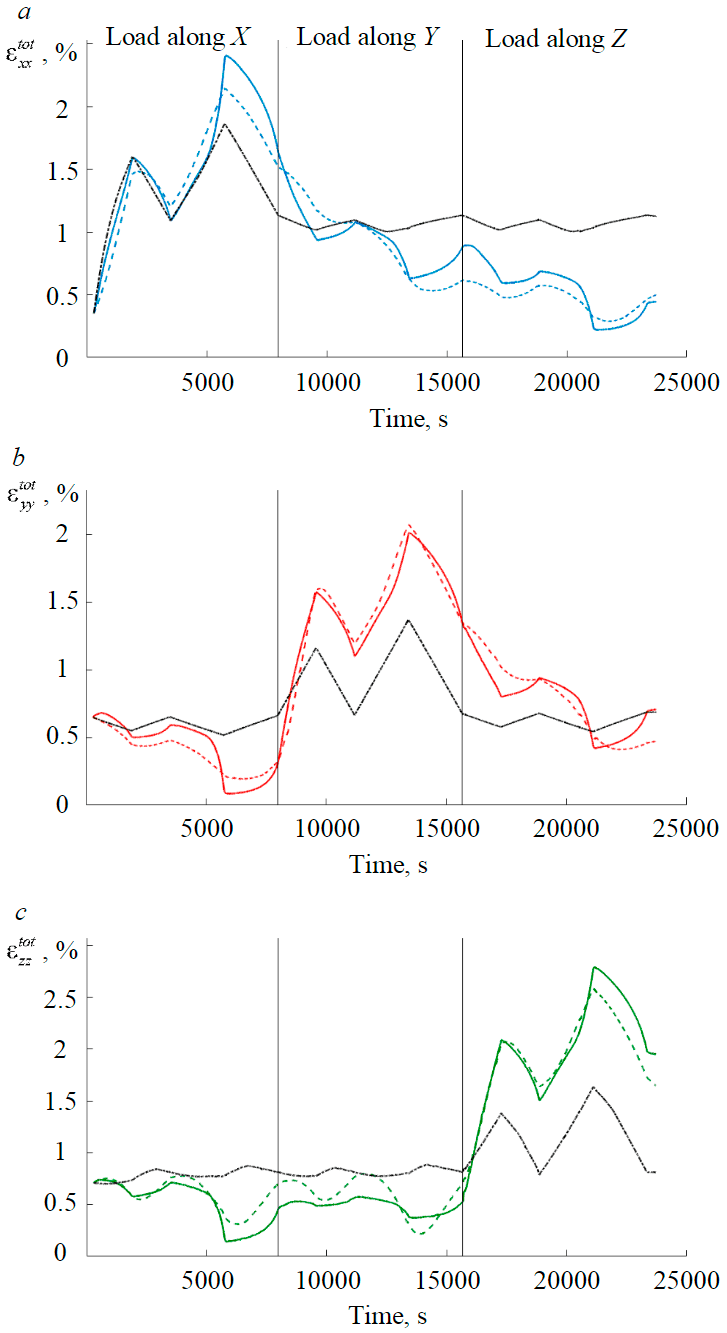
Fig.6. Combined experimental curves of the components of the total deformation of sandstone (solid lines) and theoretical curves obtained using tensor (3D-compaction, dotted lines) and scalar (1D-compaction, black lines) formulations;a – εxxtot; b – εyytot; c – εzztot
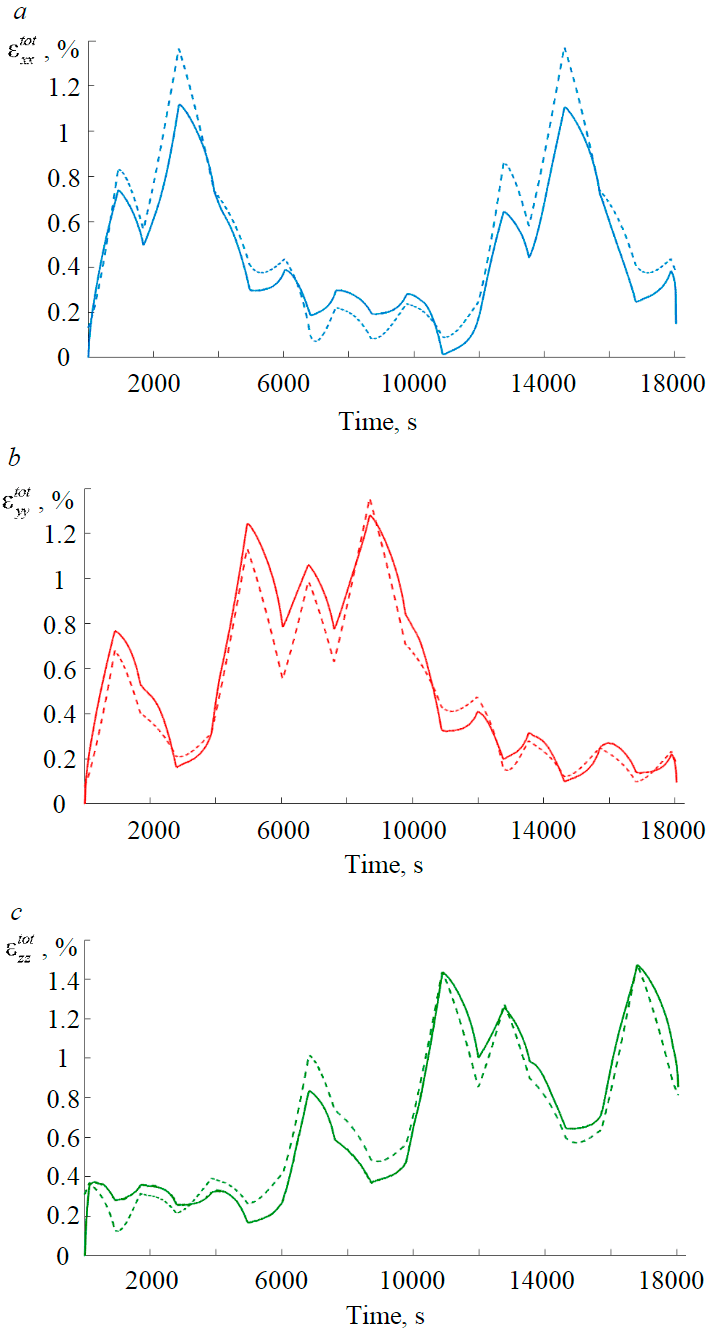
Fig.7. Combined experimental curves of the components of the total deformation of sandstone tested under the second program (solid lines) and theoretical curves obtained using the tensor model (dotted lines); a – εxxtot; b – εyytot; c – εzztot
Under non-hydrostatic load, the deformation rate of the compaction (equation (6) is proportional to the difference between the stress-dependent equilibrium compaction and its current value. If the applied load is constant, the compaction rate will be similar to the exponential law linking the creep strain rate ε.cr and the differential stress σd:
For sandstone, the coefficient Bcr varies in the range of 0.1-1.0 MPa–1 [13, 29], which is very close to the value B-12 = 19.3–1, estimated as a result of model identification for sandstone samples.
By analogy with the permeability – porosity ratio, which, as a rule, is represented as a power-law [35-37], it is possible to associate a decrease in the components of the permeability tensor Δkij with the components of the compaction tensor Fij in the form:
where n – an exponent, in the approximation of the laminar Poiseuille flow n = 3.
Under this assumption, the strong anisotropy of permeability in sedimentary basins, when the permeability in the vertical and horizontal directions may differ by the orders of magnitude, is explained by significant vertical compaction and simultaneous horizontal expansion of the medium.
Conclusion
In the experimental part of the work, the results of cyclic tests of sandstone samples conducted under two triaxial loading programs are presented. The elastic moduli of the material were evaluated, which made it possible to divide the total deformation into elastic and inelastic components. It is shown that an increase in inelastic deformation in the direction of active compression (compaction) is accompanied by its decrease in two orthogonal directions (expansion).
In the theoretical part of the work, the compaction tensor is introduced, which is a generalization of Athy’s law in the case of taking into account the components of the stress deviator. A kinetic equation describing the evolution of the components of the compaction tensor over time is proposed. Based on experimental data on the six-cycle loading of sandstone, the identification of the model was carried out, the material parameters responsible for the process of compaction and expansion of the medium was determined. To verify the model, numerical calculations of the evolution of the components of the compaction tensor under complex cyclic compression with a change in both the direction of active compression and the number of directions of active compression were carried out. Comparison of experimental and calculated curves showed their qualitative and quantitative correspondence. As a result of the calculations carried out, it is shown that the tensor compaction model makes it possible to successfully describe the accumulation of inelastic deformations of compaction and expansion in various directions. The applicability of the proposed relations to describe the tensor compaction of the material is limited to medium- and highly porous cemented rocks.
References
- Athy L.F. Density, porosity, and compaction of sedimentary rocks. American Association of Petroleum Geologists Bulletin. 1930. Vol. 14. Iss. 1, p. 1-24. DOI: 10.1306/3D93289E-16B1-11D7-8645000102C1865D
- Dasgupta T., Mukherjee S. Sediment compaction and applications in petroleum geoscience. Cham: Springer, 2020, p. 208. DOI: 10.1007/978-3-030-13442-6
- Tokareva M.A., Sibin A.N. Numerical Study of a Problem of Fluid Filtration in a Thin Poroelastic Layer. Izvestiya of Altai State University. 2017. N 1 (93) (in Russian). DOI: 10.14258/izvasu(2017)1-25
- Stover S.C., Ge S., Screaton E.J. A one-dimensional analytically based approach for studying poroplastic and viscous consolidation: Application to Woodlark Basin, Papua New Guinea. Journal of Geophysical Research: Solid Earth. 2003. Vol. 108. Iss. B9. N 2448. DOI: 10.1029/2001JB000466
- Suetnova E.I. Influence of the fluid-dynamic and rheological properties of sediments on the process of viscoelastic compaction at different rates of sedimentation. Izvestiya, Physics of the Solid Earth. 2010. Vol. 46. Iss. 6, p. 529-537.
- DOI: 10.1134/S1069351310060078
- Morency C., Huismans R., Beaumont C., Fullsack P. A numerical model for coupled fluid flow and matrix deformation with applications to disequilibrium compaction and delta stability. Journal of Geophysical Research: Solid Earth. 2007. Vol. 112. Iss. B10. N B10407. DOI: 10.1029/2006JB004701
- Holland E., Showalter R.E. Poro-Visco-Elastic Compaction in Sedimentary Basins. SIAM Journal on Mathematical Analysis. 2018. Vol. 50. Iss. 2, p. 2295-2316. DOI: 10.1137/17M1141539
- Revil A., Grauls D., Brévart O. Mechanical compaction of sand/clay mixtures. Journal of Geophysical Research: Solid Earth. 2002. Vol. 107. Iss. B11. N 2293. DOI: 10.1029/2001JB000318
- Connolly J.A.D., Podladchikov Y.Y. Temperature-dependent viscoelastic compaction and compartmentalization in sedimentary basins. Tectonophysics. 2000. Vol. 324. Iss. 3, p. 137-168. DOI: 10.1016/S0040-1951(00)00084-6
- Bruch A., Maghous S., Ribeiro F.L.B., Dormieux L. A thermo-poro-mechanical constitutive and numerical model for deformation in sedimentary basins. Journal of Petroleum Science and Engineering. 2018. Vol. 160, p. 313-326. DOI: 10.1016/j.petrol.2017.10.036
- Baud P., Reuschlé T., Ji Yu. Mechanical compaction and strain localization in Bleurswiller sandstone. Journal of Geophysical Research: Solid Earth. 2015. Vol. 120. Iss. 9, p. 6501-6522. DOI: 10.1002/2015JB012192
- Carbillet L., Heap M.J., Baud P., Wadsworth F.B., Reuschlé T. Mechanical compaction of crustal analogs made of sintered glass beads: the influence of porosity and grain size. Journal of Geophysical Research: Solid Earth. 2021. Vol. 126. Iss. 4. DOI: 10.1029/2020JB021321
- Heap M.J., Brantut N., Baud P., Meredith P.G. Time-dependent compaction band formation in sandstone. Journal of Geophysical Research: Solid Earth. 2015. Vol. 120. Iss. 7, p. 4808-4830. DOI:10.1002/2015JB012022
- Karmanskii A.T. Collecting properties of rocks in changes оf stress state type. Journal of Mining Institute. 2009. Vol. 183, p. 289-292 (in Russian).
- Pijnenburg R.P.J., Verberne B.A., Hangx S.J.T., Spiers C.J. Deformation Behavior of Sandstones From the Seismogenic Groningen Gas Field: Role of Inelastic Versus Elastic Mechanisms. Journal of Geophysical Research: Solid Earth. 2018. Vol. 123. Iss. 7, p. 5532-5558. DOI: 10.1029/2018JB015673
- Shalev E., Lyakhovsky V., Ougier-Simonin A. et al. Inelastic compaction, dilation and hysteresis of sandstones under hydrostatic conditions. Geophysical Journal International. 2014. Vol. 197. Iss. 2, p. 920-925. DOI: 10.1093/gji/ggu052
- Neuzil C.E. Hydromechanical coupling in geologic processes. Hydrogeology Journal. 2003. Vol. 11, p. 41-83. DOI: 10.1007/s10040-002-0230-8
- Brüch A., Colombo D., Frey J. et al. Coupling 3D geomechanics to classical sedimentary basin modeling: From gravitational compaction to tectonics. Geomechanics for Energy and the Environment. 2021. Vol. 28. N 100259. DOI: 10.1016/j.gete.2021.100259
- McPherson B., Bredehoeft J.D. Overpressures in the Uinta Basin, Utah: Analysis using a three-dimensional basin evolution model. Water Resources Research. 2001. Vol. 37. Iss. 4, p. 857-871. DOI: 10.1029/2000WR900260
- Torelli M., Traby R., Teles V., Ducros M. Thermal evolution of the intracratonic Paris Basin: Insights from 3D basin modelling. Marine and Petroleum Geology. 2020. Vol. 119. N 104487. DOI: 10.1016/j.marpetgeo.2020.104487
- Panteleev I.A., Mubassarova V.A., Zaitsev A.V. et al. Kaiser Effect in Sandstone in Polyaxial Compression with Multistage Rotation of an Assigned Stress Ellipsoid. Journal of Mining Science. 2020. Vol. 56, p. 370-377. DOI: 10.1134/S1062739120036653
- Panteleev I.A. Kovalenko Yu.F., Sidorin Yu.V. Damage evolution under complex nonuniform compression of sandstone according to acoustic emission data. Physical Mesomechanics. 2019. Vol. 22. N 4, p. 56-63 (in Russian). DOI: 10.24411/1683-805X-2019-14006
- Shevtsov N., Zaitsev A., Panteleev I. Deformation and destruction of rocks on the true triaxial loading system with continuous acoustic emission registration. Physical and Mathematical Modeling of Earth and Environment Processes. 2018, p. 424-432. DOI: 10.1007/978-3-030-11533-3_42
- Panteleev I.A., Mubassarova V.A., Zaitsev A.V. et al. The Kaiser Effect under Multiaxial Nonproportional Compression of Sandstone. Doklady Physics. 2020. Vol. 65, p. 396-399. DOI: 10.1134/S1028335820110075
- Karev V.I., Klimov D.M., Kovalenko Yu.F., Ustinov K.B. Fracture of sedimentary rocks under a complex triaxial stress state. Mechanics of Solids. 2016. Vol. 51. Iss. 5. P. 522-526. DOI: 10.3103/S0025654416050022
- Klimov D.M., Karev V.I., Kovalenko Yu.F. Experimental study of the influence of a triaxial stress state with unequal components on rock permeability. Mechanics of Solids. 2015. Vol. 50. Iss. 6, p. 633-640. DOI: 10.3103/S0025654415060047
- Schade H., Neemann K. Tensor Analysis. Lithuania: De Gruyter, 2018, p. 327. DOI: 10.1515/9783110404265
- Rijken M.C.M. Modeling naturally fractured reservoirs: From experimental rock mechanics to flow simulation: Dissertation of Doctor of Philosophy. Austin: The University of Texas at Austin, 2005, p. 275.
- Heap M.J., Baud P., Meredith P.G. et al. Time‐dependent brittle creep in Darley Dale sandstone. Journal of Geophysical Research: Solid Earth. 2009. Vol. 114. Iss. B7. N B07203. DOI: 10.1029/2008JB006212
- Brantut N., Heap M.J., Meredith P.G., Baud P. Time-dependent cracking and brittle creep in crustal rocks: A review. Journal of Structural Geology. 2013. Vol. 52, p. 17-43. DOI: 10.1016/j.jsg.2013.03.007
- Jaeger J.C., Cook N.G.W., Zimmerman R. Fundamentals of rock mechanics. Oxford: Wiley-Blackwell, 2007, p. 488.
- Pietruszczak S. Fundamentals of plasticity in geomechanics. London: CRC Press, 2020, p. 206.
- Nikolaevskii V.N. Geomechanics: Sobranie trudov. Vol. 1. Razrushenie i dilatansiya. Neft i gaz. Moscow-Izhevsk: Institut kompyuternykh issledovanii, 2010, p. 639 (in Russian).
- Panteleev I., Lyakhovsky V., Browning J. et al. Non-linear anisotropic damage rheology model: Theory and experimental verification. European Journal of Mechanics/A Solids. 2021. Vol. 85. N 104085. DOI: 10.1016/j.euromechsol.2020.104085
- Bernabé Y., Mok U., Evans B. Permeability-porosity Relationships in Rocks Subjected to Various Evolution Processes. Pure and Applied Geophysics. 2003. Vol. 160, p. 937-960. DOI: 10.1007/PL00012574
- Ghabezloo S., Sulem J., Saint-Marc J. Evaluation of a permeability-porosity relationship in a low-permeability creeping material using a single transient test. International Journal of Rock Mechanics and Mining Sciences. 2009. Vol. 46. Iss. 4, p. 761-768. DOI: 10.1016/j.ijrmms.2008.10.003
- Smith T.M., Sayers C.M., Sondergeld C.H. Rock properties in low-porosity/low-permeability sandstones. The Leading Edge. 2009. Vol. 28. Iss. 1, p. 48-59. DOI: 10.1190/1.3064146
