Математическая модель линейного и нелинейного повышения концентрации пропанта при проведении ГРП – решение для последовательной закачки ряда типов пропанта
- 1 — преподаватель Филиал Уфимского государственного нефтяного технического университета в г. Октябрьский ▪ Orcid
- 2 — д-р техн. наук начальник отдела Филиал Уфимского государственного нефтяного технического университета в г. Октябрьский ▪ Orcid ▪ Elibrary ▪ Scopus
- 3 — д-р техн. наук профессор Уфимский государственный нефтяной технический университет ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 4 — канд. техн. наук доцент Филиал Уфимского государственного нефтяного технического университета в г. Октябрьский ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 5 — д-р техн. наук профессор Филиал Уфимского государственного нефтяного технического университета в г. Октябрьский ▪ Orcid ▪ Elibrary ▪ Scopus
Аннотация
Известно, что значительная часть технологий, направленных на интенсификацию притока жидкости при помощи гидравлического разрыва пласта, подразумевает применение пропанта. Для транспортировки и размещения гранул в трещине обеспечивается равномерная подача пропанта заданной концентрации в жидкость разрыва. Цель работы – исключить возникновение искажений в программе закачки пропантного ГРП. Математически точный линейный набор концентрации при заданных условиях возможен только в том случае, если верно определена переходная концентрация. Предлагаемый подход позволяет корректно сформировать программу работ пропантного ГРП как для линейного, так и для нелинейного увеличения концентрации пропанта. Научная новизна работы заключается в применении новой математической модели для прямого расчета параметров программы закачки, ранее определяемых методом подбора. Разработана математическая модель линейного и нелинейного повышения концентрации пропанта при проведении ГРП. Впервые представлено аналитическое решение, позволяющее прямым вычислением определять параметры стадий основного ГРП, в том числе переходные концентрации для заданных масс пропанта различных видов. Применение математической модели при формировании плана обработки позволяет сохранить корректное распределение массы пропанта по фракциям, что облегчает внедрение информационно-аналитических систем, перенос данных напрямую из программы работ в базы данных. Предлагается провести доработку используемых в производстве форм электронных таблиц, что позволит без дополнительных трудозатрат применять математическую модель формирования программы работ на каждом процессе гидроразрыва. Получена математическая модель, которая может быть использована для совершенствования программного обеспечения, применяемого при проектировании, моделировании и инженерном сопровождении процессов ГРП.
Введение
Основной целью применения методов интенсификации добычи и увеличения степени выработки запасов углеводородного сырья является повышение эффективности разработки залежей нефти [1-3]. При этом важно правильно выбрать технологические параметры воздействий на призабойную зону и пласт [4-6]. В условиях смещения центра тяжести добычи нефти в сторону залежей с трудноизвлекаемыми запасами (ТрИЗ) решение задач обоснования управляющих решений приобретает особую актуальность в связи со значительным ростом цены ошибок [7-9]. Особая роль разработки залежей с ТрИЗ отводится гидравлическому разрыву пласта, который довольно часто обеспечивает рентабельную разработку залежей [10-12].
Значительная часть технологий интенсификации притока при помощи гидравлического разрыва пласта подразумевает использование пропанта. Для размещения гранул в трещине обеспечивается равномерная подача пропанта заданной концентрации в жидкость разрыва [13-15].
Целевая концентрация пропанта в проекте ГРП всегда выше концентрации, используемой на начальных стадиях [16, 17]. Это технологически необходимо, так как мгновенное увеличение концентрации от нуля до максимального значения приведет к осложнению при проведении ГРП [18, 19]. На начальных стадиях пропант выполняет роль абразивного материала, происходит подготовка интервала перфорации и призабойной части трещины к закачке пропанта с целевой концентрацией. Для усиления абразивного эффекта, снижения рисков технологических осложнений и выравнивания профиля фильтрации жидкости разрыва в процессе закачки на начальных стадиях используется пропант с меньшим средним диаметром частиц и при этом с бо́льшим разбросом по диаметру. На практике это достигается использованием пропанта двух фракций – незначительного количества первой и затем основной массы – более крупной фракции [20-22].
Материалы и методы
Технологический контроль при проведении ГРП включает сверку фактически закачанных объемов жидкостей и соответствующих значений концентрации пропанта [23-25]. Прозрачность технологического контроля обуславливает необходимость разделения общей массы пропанта на стадии, как правило, с равномерным шагом приращения концентрации пропанта. Шаг приращения остается постоянным на стадиях с основной фракцией пропанта, но при переходе от абразивного пропанта к основному при условии планируемого линейного повышения концентрации возникает задача с тремя взаимозависимыми переменными: масса пропанта абразивной фракции, скорость увеличения концентрации при закачке и переходная концентрация пропанта – максимальная для абразивной и минимальная для основной фракции. Из обозначенных трех переменных масса задана проектным значением напрямую, а скорость увеличения концентрации обуславливается общей массой пропанта и конечной концентрацией, что также задано в проекте.
Если для случая с закачкой двух фракций пропанта применить строгий равномерный шаг приращения концентрации от стадии к стадии, это приведет, в зависимости от начальных данных, к одной из двух ошибок. При сохранении корректной массы по стадиям будет нарушен линейный характер набора концентрации (рис.1, а). В обратном случае, при сохранении линейного характера набора концентрации, будет получено некорректное распределение массы пропанта по стадиям (рис.1, б).
Таким образом, математически точный линейный набор концентрации при условии корректного учета массы по фракциям возможен только в том случае, если переходная концентрация рассчитана для заданных условий. Это соответствующим образом нарушит кратность шага приращения концентрации по стадиям, но обеспечит корректное отображение массы каждой фракции пропанта с сохранением общего линейного набора концентрации. Приведенное на рис.1, б отклонение позволяет провести технически корректный процесс ГРП, но для моделирования и автоматизированных систем учета данный подход будет приводить к ошибкам. Предлагаемый подход позволяет корректно отобразить в программе работ момент перехода типа пропанта и, таким образом, как масса, так и набор концентрации будут соответствовать заданной технологии.
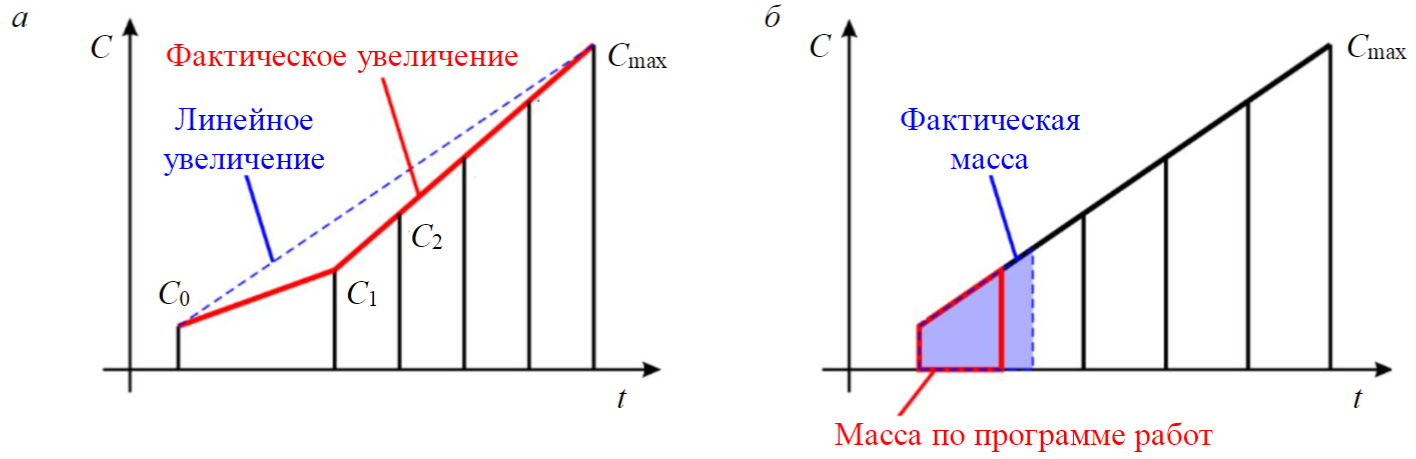
Рис.1. Искажения, возникающие при сохранении шага наращивания концентрации при переходе между фракциями: а – расхождение по линейному набору концентрации; б – расхождение по массе
Результаты и обсуждения
Для решения поставленной задачи была построена математическая модель изменения концентрации пропанта при проведении ГРП. При построении математической модели было выявлено, что для обеспечения линейного характера набора концентрации пропанта необходимо соблюдение следующего условия для стадий с повышением концентрации пропанта:
где С1, С2 – начальная и конечная концентрация рассматриваемого отрезка плана обработки; Vs – объем смеси жидкости разрыва с пропантом; K – коэффициент наклона линии набора концентрации.
Для сохранения линейного набора при переходе между фракциями пропанта в программе работ, основанной на математической модели, необходимо для заданной массы пропанта по фракциям и максимальной концентрации Cmax рассчитать концентрацию перехода Ca, на которой заканчивается стадия с фракцией № 1 и начинается фракция № 2.
На рис.2 показан линейный набор концентрации. Если представить концентрацию пропанта C как функцию от объема жидкости разрыва V, то условие линейного набора концентрации будет сохраняться при равном значении угла наклона φ для прямых C0Ca и CaCmax, как и на стандартных графиках с осью времени t при постоянном расходе закачки r. При этом масса пропанта может быть представлена как площадь трапеции, ограниченной линией концентрации, проекцией на ось V и перпендикулярами начальной и конечной концентрации к проекции,
где V – объем чистой жидкости.
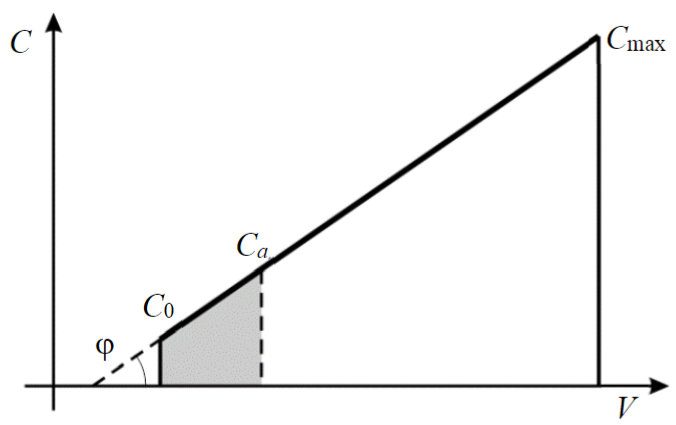
Рис.2. Линейный набор концентрации
Таким образом, зная массу пропанта по фракциям, планируемую минимальную и максимальную концентрацию, а также абсолютную плотность пропанта, можно рассчитать требуемый объем жидкости разрыва для условия линейного набора концентрации:
где M – общая масса пропанта всех фракций; C0, Cmax – начальная и максимальная концентрация.
Для расчета объема смеси жидкости разрыва с пропантом необходимо прибавить к объему жидкости разрыва (3) объем, занимаемый частицами пропанта с учетом нахождения жидкости разрыва в пространстве между частицами:
где ρ – абсолютная концентрация пропанта.
Принимая во внимание постоянство коэффициента K в формуле (1) и применение формулы (4) для пропанта фракции № 1, получена система уравнений:
где ma – масса пропанта первой (уменьшенной) фракции.
В уравнении (5) два неизвестных: Ca и Vsa. В первую очередь в практических целях нас интересует переходная концентрация Ca. Решая систему уравнений, приходим к аналитическому решению:
Таким образом, минимальное необходимое количество стадий, требуемых для описания закачки двух типов пропанта, сводится к двум, с переходной стадией Ca. В табл.1 приведен принцип формирования программы работ согласно представленной математической модели [26-28]. Дальнейшее разделение на стадии возможно по тому же принципу. При этом не возникнет необходимости расчета переходных концентраций, они могут быть заданы равными для основной фракции пропанта [29-31].
Таблица 1
Принцип формирования программы работ
|
Тип пропанта |
Масса |
Расход |
Объем жидкости |
Объем смеси |
Время |
Концентрация от |
Концентрация до |
|
№ 1 |
ma |
r |
|
|
|
C0 |
Ca |
|
№ 2 |
mb |
r |
|
|
|
Ca |
Cmax |
Примечание. mb – масса пропанта второй (основной) фракции.
При возникновении обозначенных выше искажений суммы пропанта по фракциям искажаются, и для контроля расхода материалов, хранения данных в БД инженерам требуется вручную корректировать показатели. В отличие от стандартного подхода, полученная на основе математической модели программа работ может быть напрямую загружена в информационные системы и базы данных, так как будет соответствовать фактической закачке при штатном завершении процесса [32-34].
Модель применена на практике. Пример расчета закачки 9 т пропанта, из которых 1 т фракции 30/60 и 8 т фракции 16/20, при линейном наборе концентрации представлен в табл.2.
Таблица 2
Параметры ГРП
|
Расход, м3/мин |
Объем |
Время, мин |
Тип стадии |
Концентрация от, кг/м3 |
Концентрация до, кг/м3 |
Масса по стадиям, кг |
Общая масса, кг |
Объем |
|
2,8 |
10 |
3,57 |
Буфер |
0 |
0 |
0 |
0 |
10 |
|
2,8 |
2,58 |
0,95 |
Пропант 30/60 |
120 |
200 |
415 |
415 |
2,72 |
|
2,8 |
2,51 |
0,90 |
Пропант 30/60 |
200 |
280 |
585 |
1000 |
2,72 |
|
2,8 |
3,65 |
1,31 |
Пропант 16/20 |
280 |
400 |
1242 |
2242 |
4,08 |
|
2,8 |
2,95 |
1,05 |
Пропант 16/20 |
400 |
500 |
1326 |
3568 |
3,40 |
|
2,8 |
2,86 |
1,02 |
Пропант 16/20 |
500 |
600 |
1574 |
5142 |
3,40 |
|
2,8 |
2,78 |
0,99 |
Пропант 16/20 |
600 |
700 |
1808 |
6950 |
3,40 |
|
2,8 |
2,71 |
0,97 |
Пропант 16/20 |
700 |
800 |
2050 |
9000 |
3,40 |
|
2,8 |
7,2 |
2,57 |
Продавка |
0 |
0 |
0 |
9000 |
7,2 |
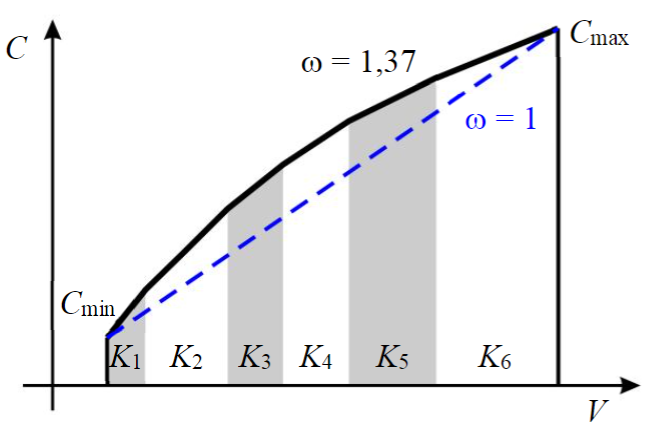
Рис.3. Нелинейное увеличение концентрации пропанта
Расчетным путем определена переходная концентрация 280 кг/м3, при которой сохраняется корректная масса пропанта и линейный набор концентрации.
Часть технологий ГРП предусматривает нелинейное увеличение концентрации пропанта в процессе закачки. При этом уменьшается требуемый объем геля с сохранением массы и концентрации пропанта. Для обеспечения условия нелинейности и плавного перехода между пропантными стадиями вносятся изменения в план обработки [9, 35].
Коэффициент K в формуле (1) для нелинейного увеличения концентрации не является постоянным для всей закачки, а изменяется от стадии к стадии. Для того, чтобы задать степень кривизны, вводится коэффициент ω, принимающий значения в пределах от 1 до 1,5. При ω = 1 будет получено линейное увеличение концентрации, а больший коэффициент соответствует большей степени нелинейности кривой увеличения концентрации пропанта. Коэффициент ωзадается при планировании ГРП как степень агрессивности закачки. В отсутствие рисков и при проведении ГРП традиционных коллекторов рекомендуется значение в пределах 1,35-1,5. При наличии рисков, связанных с потерями давления на трения в ПЗП, возможно снижение и выбор значения в пределах 1,1-1,35. При существенных рисках, либо при обработке низкопроницаемых коллекторов, рекомендуется применять линейный набор концентрации пропанта. В дальнейшем, при наработке данных для статистического анализа, граничные значения ω могут быть уточнены.
Если выразить объем стадии через коэффициент K в формуле (1), то при известном K и заданной начальной и конечной концентрации объем смеси может быть определен как
Для нелинейного случая K=Kn для каждой стадии n, начиная со стадии № 2, определяется при помощи арифметической прогрессии. Предварительно введем промежуточный множитель K', также определяемый по прогрессии,
где N – количество стадий, тогда
Соответственно, объемы стадий могут быть определены по прогрессии:
На рис.3 показано нелинейное увеличение концентрации при ω = 1,37.
Формула расчета переходной концентрации (6) может быть внедрена в используемые инженерами ГРП формы электронных таблиц, что позволит применять представленный подход на всех процессах ГРП без необходимости вручную производить вычисления. При разработке и внедрении новых специализированных информационно-аналитических систем представленная математическая модель может быть встроена в соответствующие модули для упрощения работы с системой. Внедрение нелинейности через коэффициентω не только упрощает подготовку программы работ по соответствующим технологиям, но также позволит обозначить «агрессивность» закачки в цифровом эквиваленте для учета в БД и анализа в корпоративных ИАС.
Модель применена на практике. Пример расчета закачки 7 т пропанта, из которых 1 т фракции 30/60 и 6 т фракции 12/18, при нелинейном наборе концентрации с коэффициентом агрессивности ω = 1,2 представлен в табл.3.
Таблица 3
Параметры ГРП
|
Расход, м3/мин |
Объем геля, м3 |
Время, мин |
Тип стадии |
Концентрация от, кг/м3 |
Концентрация до, кг/м3 |
Масса по стадиям, кг |
Общая масса, кг |
Объем смеси, м3 |
|
3,2 |
12 |
3,75 |
Буфер |
0 |
0 |
0 |
0 |
12 |
|
3,2 |
1,00 |
0,31 |
Пропант 30/60 |
120 |
200 |
161 |
161 |
1,05 |
|
3,2 |
1,29 |
0,40 |
Пропант 30/60 |
200 |
300 |
325 |
486 |
1,4 |
|
3,2 |
1,40 |
0,44 |
Пропант 30/60 |
300 |
400 |
514 |
1000 |
1,57 |
|
3,2 |
1,61 |
0,50 |
Пропант 16/20 |
400 |
500 |
737 |
1737 |
1,86 |
|
3,2 |
1,95 |
0,61 |
Пропант 16/20 |
500 |
600 |
1093 |
2830 |
2,32 |
|
3,2 |
2,47 |
0,77 |
Пропант 16/20 |
600 |
700 |
1647 |
4477 |
3,04 |
|
3,2 |
3,29 |
1,03 |
Пропант 16/20 |
700 |
800 |
2523 |
7000 |
4,16 |
|
3,2 |
9,4 |
2,57 |
Продавка |
0 |
0 |
0 |
7000 |
9,4 |
Применение модели позволило рассчитать объемы смеси по стадиям с учетом численно заданной характеристики агрессивности.
Выводы
- Получена математическая модель линейного и нелинейного повышения концентрации пропанта при проведении ГРП. Впервые представлено аналитическое решение, позволяющее прямым вычислением определять параметры стадий основного ГРП, в том числе переходные концентрации для заданных масс пропанта различных видов.
- Применение математической модели при формировании плана обработки позволяет сохранить корректное распределение массы пропанта по фракциям, что облегчает внедрение информационно-аналитических систем, перенос данных напрямую из программы работ в базы данных.
- Доработка используемых в производстве форм электронных таблиц позволит без дополнительных трудозатрат применять математическую модель формирования программы работ на каждом процессе ГРП.
- Полученная математическая модель может быть использована для совершенствования программного обеспечения, применяемого при проектировании, моделировании и инженерном сопровождении процессов ГРП.
Литература
- Дмитриевский А.Н. Ресурсно-инновационная стратегия развития экономики России // Нефтяное хозяйство. 2017. № 5. С. 6-7.
- Якупов Р.Ф., Мухаметшин В.Ш., Хакимзянов И.Н., Трофимов В.Е. Оптимизация выработки запасов из водонефтяных зон горизонта D3ps Шкаповского нефтяного месторождения с помощью горизонтальных скважин // Георесурсы. 2019. Т. 21. № 3. С. 55-61. DOI: 10.18599/grs.2019.3.55-61
- Сергеев В.В., Беленкова Н.Г., Зейгман Ю.В., Мухаметшин В.Ш. Физические свойства эмульсионных систем с содержанием наночастиц SiO2 // Нанотехнологии в строительстве. 2017. Т. 9. № 6. C. 37-64. DOI: 10.15828/2075-8545-2017-9-6-37-64
- Галкин В.И., Колтырин А.Н. Исследование и анализ методов определения эффективности применения технологии пропантного гидроразрыва пласта // Известия Томского политехнического университета. Инжиниринг георесурсов. 2019. Т. 330. № 11. С. 50-58. DOI: 10.18799/24131830/2019/11/2347
- ChizhovA.P., AndreevV.E., ChibisovA.V. etal. Hydraulically perfect modes of injection of grouting mixtures when isolating absorbing formations // International Conference on Extraction, Transport, Storage and Processing of Hydrocarbons & Materials (ETSaP), 24-25 August 2020, Tyumen, Russian Federation. IOP Conference Series: Materials Science and Engineering, 2020. Vol. 952. № 012040. P. 1-7. DOI: 10.1088/1757-899X/952/1/012040
- Mukhametshin V.V., Kuleshova L.S. Using the method of canonical discriminant functions for a qualitative assessment of the response degree of producing wells to water injection during the development of carbonate deposits // MEACS 2020 – International Conference on Mechanical Engineering, Automation and Control Systems, 17th September 2020, Novosibirsk, Russian Federation. IOP Conference Series: Materials Science and Engineering, 2021. Vol. 1064. № 012069. P. 1-9. DOI: 10.1088/1757-899X/1064/1/012069
- Mukhametshin V.G., Dubinskiy G.S., Andreev V.E. et al. Geological, technological and technical justification for choosing a design solution for drilling wells under different geological conditions // MEACS 2020 – International Conference on Mechanical Engineering, Automation and Control Systems, 17th September 2020, Novosibirsk, Russian Federation. IOP Conference Series:
- Materials Science and Engineering, 2021. Vol. 1064. № 012061. P. 1-9. DOI: 10.1088/1757-899X/1064/1/012061
- Tyncherov K.T., Mukhametshin V.Sh., Khuzina L.B. Method to control and correct telemtry well information in the basis of residue number system // Journal of Fundamental and Applied Sciences. 2017. Vol. 9. № 2S. P. 1370-1374. DOI: 10.4314/jfas.v9i2s.848
- Zeigman Yu.V., Mukhametshin V.V., Kuleshova L.S. Differential impact on wellbore zone based on hydrochloric-acid simulation // International Conference on Extraction, Transport, Storage and Processing of Hydrocarbons & Materials (ETSaP), 24-25 August 2020, Tyumen, Russian Federation. IOP Conference Series: Materials Science and Engineering. 2020. Vol. 952. № 012069. DOI: 10.1088/1757-899X/952/1/012069
- Мухаметшин В.Ш. Зейгман Ю.В., Андреев А.В. Экспресс-оценка потенциала добывных возможностей залежей для определения эффективности применения нанотехнологий и необходимости стимулирования ввода их в разработку // Нанотехнологии в строительстве. 2017. Т. 9. № 3. С. 20-34. DOI: 10.15828/2075-8545-2017-9-3-20-34
- Nur Wijaya, Sheng J.J. Comparative study of well soaking timing (pre vs. post flowback) for water blockage removal from matrix-fracture interface // Petroleum. 2020. Vol. 6. Iss. 3. P. 286-292. DOI: 10.1016/j.petlm.2019.11.001
- Ruimin Feng, Shengnan Chen, Steven Bryant, Jun Liu. Stress-dependent permeability measurement techniques for unconventional gas reservoirs: Review, evaluation, and application // Fuel. 2019. Vol. №115987. DOI: 10.1016/j.fuel.2019.115987
- Муслимов Р.Х. Новая стратегия освоения нефтяных месторождений в современной России – оптимизация добычи и максимизация КИН // Нефть. Газ. Новации. 2016. № 4. С. 8-17.
- Cheng Jing, Xiaowei Dong, Wenhao Cuid et al. Artificial neural network–based time-domain interwell tracer testing for ultralow-permeability fractured reservoirs // Journal of Petroleum Science and Engineering. 2020. Vol. 195. № 107558. DOI: 10.1016/j.petrol.2020.107558
- Economides J.M., Nolte K.I. Reservoir stimulation. Chichester: John Wiley and Sons, 2000. 856p.
- Галкин В.И., Колтырин А.Н. Исследование вероятностных моделей для прогнозирования эффективности технологии пропантного гидравлического разрыва пласта // Записки Горного института. 2020. Т. 246. С. 179-190. DOI: 10.31897/PMI.2020.6.7
- Prashanth Siddhamshetty, Shaowen Mao, Kan Wu, Joseph Sang-Il Kwon. Multi-Size Proppant Pumping Schedule of Hydraulic Fracturing: Application to a MP-PIC Model of Unconventional Reservoir for Enhanced Gas Production // Processes. 2020. Vol. 8. Iss. 5. № 570. DOI: 10.3390/pr8050570
- Nurgaliev R.Z., Kozikhin R.A., Fattakhov I.G. et al. Prospects for the use of new technologies in assessing the impact of geological and technological risks // IPDME 2019 – International Workshop on Innovations and Prospects of Development of Mining Machinery and Electrical Engineering, 24-27 April 2019, Saint-Petersburg Mining University, Saint-Petersburg, Russian Federation. IOP Conference Series: Earth and Environmental Science, 2019. Vol. 378. № 012117. DOI: 10.1088/1755-1315/378/1/012117
- ШляпкинА.С., ТатосовА.В. Формирование трещины гидроразрыва пласта высоковязким гелем // Геология, геофизика и разработка нефтяных и газовых месторождений. 2020. № 9 (345). С. 109-112. DOI: 10.30713/2413-5011-2020-9(345)-109-112
- Nolte K.G. Determination of proppant and fluid schedules from fracturing-pressure decline // SPE Prod. Eng. 1986. Vol. 1. Iss. 4. P. 255-265. DOI: 10.2118/13278-PA
- Seeyub Yang, Prashanth Siddhamshetty, Joseph Sang-Il Kwon. Optimal pumping schedule design to achieve a uniform proppant concentration level in hydraulic fracturing // Computers & Chemical Engineering. 2017. Vol. 101. P. 138-147. DOI: 10.1016/j.compchemeng.2017.02.035
- Yakupov R.F., Mukhametshin V.Sh., Tyncherov K.T. Filtration model of oil coning in a bottom water-drive reservoir // Periodico Tche Quimica. 2018. Vol.15. Iss. 30. P. 725-733.
- Галкин В.И., Пономарева И.Н., Черепанов С.С. и др. Новый подход к оценке результатов гидравлического разрыва пласта (на примере бобриковской залежи Шершневского месторождения // Известия Томского политехнического университета. Инжиниринг георесурсов. 2020. Т. 331. № 4. С. 107-114. DOI: 10.18799/24131830/2020/4/2598
- Fokker P.A, Borello E.S., Verga F., Viberti D. Harmonic pulse testing for well performance monitoring // Journal of Petroleum Science and Engineering. 2018. Vol. 162. P. 446-459. DOI: 10.1016/j.petrol.2017.12.053
- Humoodi A., Hamoudi M., Sarbast R. Implementation of Hydraulic Fracturing Operation for a Reservoir in KRG // UKH Journal of Science and Engineering. 2019. Vol.3. № 2. P. 10-21. DOI: 10.25079/ukhjse.v3n2y2019
- Булгакова Г.Т., Шарифуллин А.Р., Ситдиков М.Р. Математическое моделирование тепломассопереноса в вертикальной трещине гидроразрыва пласта при закачке и очистке // Вестник Тюменского государственного университета. Физико-математическое моделирование. Нефть, газ, энергетика. 2020. Т. 6. № 2 (22). С. 41-62. DOI: 10.21684/2411-7978-2020-6-2-41-62
- Нургалиев Р.З., Козихин Р.А., Фаттахов И.Г., Кулешова Л.С. Перспективы применения новых технологий при оценке влияния геолого-технологических рисков // Горный журнал. 2019. № 4 (2261). С. 36-40. DOI: 10.17580/gzh.2019.04.08
- Siddhamshetty P., Yang S., Kwon J.S. Modeling of hydraulic fracturing and designing of online pumping schedules to achieve uniform proppant concentration in conventional oil reservoirs // Computers & Chemical Engineering. 2018. Vol.114. P. 306-317. DOI: 10.1016/j.compchemeng.2017.10.032
- Масооми Р., Долгов С.В. Сравнение разных сценариев для жидкостей ГРП (гели на водной основе и пены) с помощью численного моделирования // Булатовские чтения. 2017. Т. 2. С. 150-155.
- Geertsma J., Haafkens R. Comparison of the theories for predicting width and extent of vertical hydraulically induced fractures // Journal of Energy Resource Technology. 1979. Vol. 101. Iss. 1. P. 8-19. DOI: 10.1115/1.3446866
- Keshavarz A., Yang Y., Badalyan A. et al. Laboratory-based Mathematical Modelling of Graded Proppant Injection in CBM Reservoirs // International Journal of Coal Geology. 2014. Vol. 136. P. 1-16. DOI: 10.1016/j.coal.2014.10.005
- Jiaxiang Xu, Yunhong Ding, Lifeng Yang et al. Effect of proppant deformation and embedment on fracture conductivity after fracturing fluid loss // Journal of Natural Gas Science and Engineering. 2019. Vol.71. № 102986. DOI: 10.1016/j.jngse.2019.102986
- Bahtizin R.N., Nurgaliev R.Z., Fattakhov I.G. et al. On the question of the efficiency analysis of the bottom-hole area stimulation method // International Journal of Mechanical Engineering and Technology. 2018. Vol. 9. Iss. 6. P. 1035-1044.
- Dali Guo, Yunxiang Zhao, Zixi Guo, Xianhui Cui, Bo Huang. Theoretical and Experimental Determination of Proppant Crushing Rate and Fracture Conductivity // Journal of Energy Resources Technology. 2020. Vol.142. Iss. 10. № 103005. DOI: 10.1115/1.4047079
- Нургалиев О.Т., Волченко Ю.А. Радиоизотопный метод и измерительный комплекс РИКП-01 для экспрессного определения концентрации проппанта в рабочих смесях, применяемых при гидравлическом разрыве нефтегазосодержащих пластов // Автоматизация, телемеханизация и связь в нефтяной промышленности. 2016. № 8. С. 24-28.
