Determination and verification of the calculated model parameters of salt rocks taking into account softening and plastic flow
- 1 — PhD student Belarusian State University ▪ Orcid ▪ Elibrary
- 2 — Ph.D., Dr.Sci. Professor, Head of Theoretical and Applied Mechanics Department Belarusian State University ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
Abstract
The article suggests using a combination of the modified Burgers model and the Mohr – Coulomb model with the degradation of the adhesion coefficient and the increase in the friction coefficient to determine the parameters of salt rocks. A comparative analysis of long-term laboratory tests and field observations in underground mine workings with the results obtained using a calculated model with certain parameters is carried out. The parameters of the Mohr – Coulomb model with the degradation of the adhesion coefficient and the increase in the friction coefficient were obtained from the statistically processed data of laboratory tests, and the parameters of the modified Burgers model were determined. Using numerical methods, virtual (computer) axisymmetric triaxial tests, both instantaneous and long-term, were performed on the basis of the proposed model with selected parameters. A model problem is solved for comparing the behavior of the model with the data of observation stations in underground mine workings obtained from borehole rod extensometers and contour deformation marks. The analytically obtained coefficients of the nonlinear viscous element of the modified Burgers model for all the analyzed salt rocks did not need to be corrected based on the monitoring results. At the same time, optimization was required for the viscoelastic element coefficients for all the considered rocks. The analysis of the model studies showed a satisfactory convergence with the data on the observation stations. The comparative analysis carried out on the models based on laboratory tests and observations in the workings indicates the correct determination of the parameters for salt rocks and the verification of the model in general.
Introduction. Due to the pronounced plastic flow of salt rocks, movements in the vicinity of the underground structures contour located in the salt rock mass can develop for a very long time and reach large values. Such effects in the process of operation can cause significant destruction up to the progressive rocks collapse.
Numerical methods are actively used to predict the development of rock mass deformation processes over time in the vicinity of an underground structure. Quite a lot of specialized models and methods for solving problems of rock mechanics and masses, and underground construction are implemented in the software complexes Abaqus, DIANA, FLAC, Midas, PLAXIS, ZSoil, etc.
The regulatory document SP 91.13330.2011 “Underground Mining” provides engineering methods for calculating long-term deformations and stability of underground workings, while no information is provided about the basic models underlying these methods. It is important to note that SP 91.13330.2011 in some cases does not allow calculations for the stability of deep workings in salt and potash mines, while the use of numerical methods in the design is mandatory. Other geotechnical sets of rules recommend the use of the Mohr – Coulomb and Hoek – Brown models of the elastic-ideal-plastic environment, without giving specific recommendations for taking into account rheological effects, limiting themselves only to the requirements for their consideration. In practice, the introduction of the assumption of ideal plastic behavior in a number of problems can lead to incorrect conclusions both in terms of the interaction of the host rock masses with the support [5], and in terms of estimating the size of ruptured zones of the selected criteria or taking into account plastic flow, especially when the large plastic zones formation is inevitable. In such cases, taking into account the softening makes it possible to avoid this problem and it is more correct to calculate plastic flow deformations due to the different nature of the stress distribution in the rock mass. In addition, it becomes possible to perform more accurate calculations for the study of progressive destruction cases.
Formulation of the problem. Models constructed on the basis of an integral operator with an Abelian kernel [4], and also the Mohr – Coulomb and Hoek – Brown models reflecting perfectly plastic behavior, with an empirical dependence of the Norton type [11] and similar power dependences [2, 3] are widely used in the study of rheonomic effects. At the same time, it is most correct to use the described models under certain mining-geological and mining-technical conditions (shallow depths, stowing of the worked-out space with artificial pillars, etc.), or when performing a preliminary analysis. But when designing structures at great depths, creating complex and large-scale underground geotechnical complexes, engineering underground objects of increased danger and high responsibility, often the results are not sufficient and correct. So, for example, the “scenario” of the rock mass deformation processes in the vicinity of an underground structure, according to model calculations, can only remotely correspond to real conditions [19, 26], when the process of creep of the host mass is described incorrectly and differs from the monitoring data in full-scale conditions [11, 23].
Therefore, the task of using mechanical and mathematical models, that more correctly and adequately describe the plastic flow of rock masses in the vicinity of underground structures and allow for certain specific aspects of the mechanical behavior of rock masses, remains relevant today.
Methodology. For a more correct account of the salt rocks behavior under difficult loading conditions, it is proposed to use a combined visco-elastic-plastic model consisting of a modified Burgers model and the Mohr – Coulomb model, where the main parameters (adhesion \( c(\bar {\epsilon}_{pl})\), internal friction angle \( \phi(\bar {\epsilon}_{pl})\), dilatancy angle \( \psi(\bar {\epsilon}_{pl})\) and ultimate tensile stresses \( \sigma_t(\bar {\epsilon}_{pl})\)) depend on the effective plastic relative deformations \( (\bar{\epsilon}_{pl})\) (Fig.1). In this case, the total relative deformations \( {\epsilon}\) consist of reversible (elastic \( {\epsilon}_{el}\) and viscoelastic \( {\epsilon}_{ve}\)) and irreversible (viscous \( {\epsilon}_{visc}\) and plastic \( {\epsilon}_{pl}\)) parts, and the change in the volume relative deformations occurs due to the elastic \( {\epsilon}_{v}\) происходит за счет упругой \( {\epsilon}_{v. el}\) and plastic parts \( {\epsilon}_{v. pl}\):
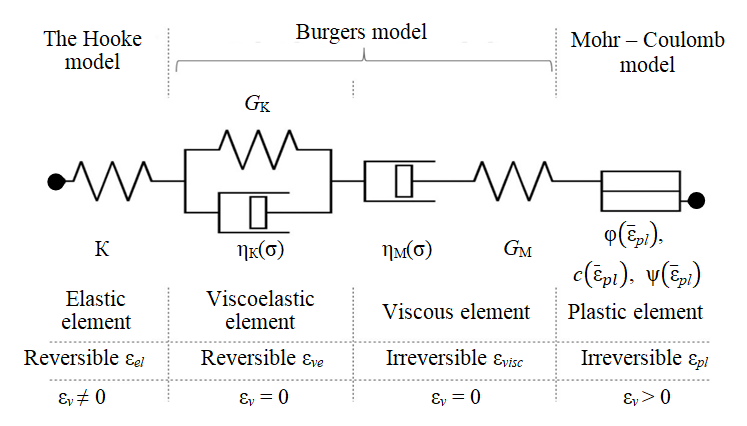
Many authors have proposed approaches to the construction of the Mohr – Coulomb model modifications, taking into account the degradation of the adhesion coefficient and the increase in the friction coefficient. The main previous approaches were to take into account the linear increase in the value of the friction coefficient, the linear decrease in the adhesion [13] and both values [12], the use of exponential dependencies [21, 25] or more complex dependencies with the determination of the stress state influence and the introduction of logarithmic functions for the dilatancy angle [18, 20]. In this case, for example, nonlinear dependences are used for the “mobilized” adhesion coefficient c' and the internal friction angle φ', proposed by Vermeer and de Borst [25], and also the dilatancy angle ψ' according to the dependence proposed by Chen and co-authors [18]:
where c, sin(φ') – are the maximum values of the adhesion and the sine of the internal friction angle; \( {\epsilon}_{c}\), \( {\epsilon}_{f}\) – are constants that affect the nature of the change in the curves c' and sin(φ') respectively; a, b, d, f – are numerical coefficients.
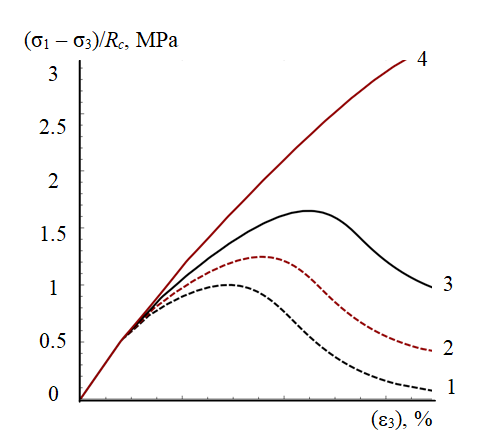
Discussion. Based on the statistical processing of the laboratory test results, the elastic modulus and decay, the ultimate strength at various compression values of the sample in the stabilometer σh, and the values of the relative longitudinal deformations \( {\epsilon}_{3}\) for the characteristic points of the diagrams were obtained. The values of the modified Mohr – Coulomb model obtained on their basis made it possible to reproduce the averaged conditional-instantaneous tests in a stabilometer (deformation curves at different compression values) (Fig.2).
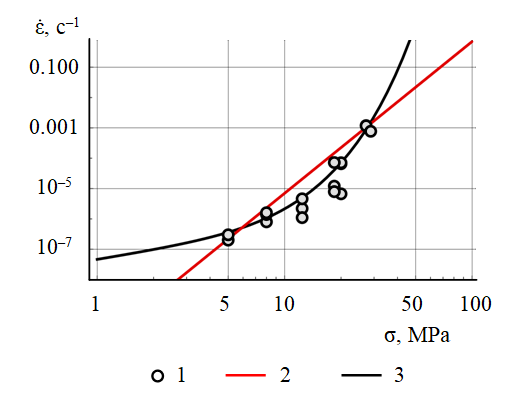
For the secondary plastic flow stage, according to laboratory tests, the parameters of the plastic flow kernels for the power-law and sine-hyperbolic dependences were analytically determined and compared. It was found that the power-law dependence does not include values higher than 18.8 MPa in the confidence interval of the stress, while the hyperbolic sine function satisfactorily “fit” into the laboratory tests for all values of the stress intensity (Fig.3, 4). A similar dependence is used in the modification of the Minkley model [7, 10]). Final view of the used function:
where \( {\dot\epsilon}_{visc}\) – is the rate of viscous relative deformations; a, b, c – are coefficients; \( \sigma_i\) – is stress intensity, \( \sigma_i=\sqrt{3j_2}\); \( \sigma_i^{'}\) – is reference pressure.
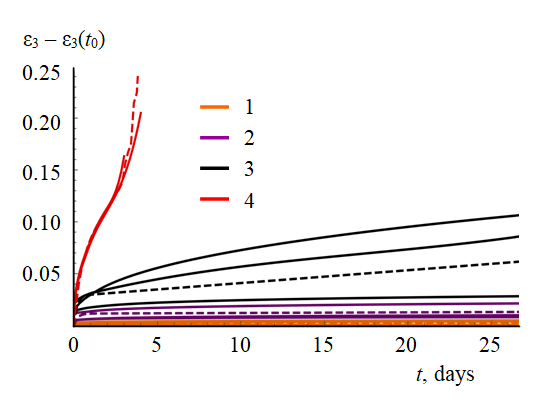
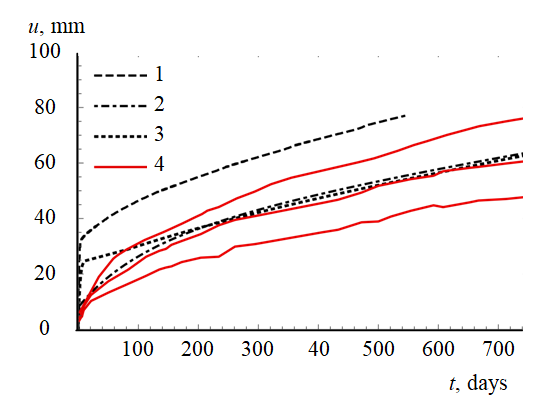
To verify the proposed model using field observation data, all observation stations were divided into groups based on similar mining-geological and mining-technical conditions, and calculations were performed for each of them (the results for one of the groups are shown in Figure 5). Initial calculations with an empirical account of the face impact (Fig.5, line “2D model”), in which a reducing factor to the components of the initial stress field was used on the production circuit according to the Bulychev dependence, showed overestimated indicators for the speed of implementation of the primary plastic flow stage. At the same time, the velocities of the steady-state plastic flow interval had a satisfactory correspondence, which is easily explained by a qualitative description of the viscous element in terms of the hyperbolic sine function, which made it possible to reliably describe a wide range of stress intensities. To exclude the significant influence of the empirical method of face accounting, the problems with the mine tunneling in time in the spacial formulation were solved (Fig.5, the line “taking into account the face impact”).The results showed that the selected parameters of the model for different groups allow to reliably calculate the value of the primary plastic flow deformations, which is very important when designing the structures of linings and supports. This indicator allows to use in projects the calculated-based values of the minimum and maximum time for the permanent anchorage construction after mining. To solve the problem of excessively rapid realization of the primary plastic flow deformations in the model calculations, the nonlinear viscoelastic element was optimized by iteratively reducing one of the coefficients. The reduction range for different groups is from 3 to 5 times (Fig.5, the line “after optimization”).
Conclusion. Verification of the considered modified Burgers model showed that it is more effective than the Mohr – Coulomb or Hoek – Brown models in combination with empirical power-law plastic flow laws of the Norton type. The advantages are as follows:
• the model is correct for a wider range of voltages, which is important for larger depths;
• it more precisely describes the stage of deformation beyond the limit of strength and allows to check for progressive destruction;
allows to correctly perform multi-stage analysis without restrictions – correct time accounting in comparison with Norton type models that take into account primary plastic flow or taking into account the effects of relaxation in comparison with visco-plastic models.
Restrictions that need to be taken into account when analyzing solutions:
• the plastic element does not depend directly on the deformation rate, in contrast to the visco-plastic models of the Dering – Kiel type [17, 27], which are widely used in the Verkhnekamskoe deposit of potassium-magnesium salts [1];
• the modified model does not take into account the humidity influence on plastic flow, in contrast to the Gampel – Schultz model, which is used for salt rocks [14] and takes into account the corresponding Gunsch – Schultz dependence;
• it does not take into account the recovery of disturbed rocks, for example, due to recrystallization [15, 22];
• the model can be extended by introducing the exponential dependence of the Arrhenius on temperature in the viscosity function, if it is necessary to take into account the combined temperature effect [24];
• in comparison with the original viscoelastic-elastic-plastic Minkley model [6] and its updated formulations [10, 16], the used function of the fracture surface is linear and has no boundary of maximum shear stresses σmax. This limitation can be critical in the case of fixing low values of σmax (a slight rise in strength with an increase in compression) when testing some salt rocks with low strength, such as carnallite.
The proposed model, in comparison with other common models of the rheological behavior of salt rocks, corresponds to the Minkley model [8, 9], while retaining its main advantages and disadvantages.It should be noted that some problems concerning the accounting of the dilatancy effect in the model can be corrected, for example, by introducing additional refined nonlinear dependences of the dilatancy angle on stresses into the used dependence on effective plastic deformations [18].
The article describes the process of determining, optimizing and verifying the parameters of the proposed calculated model of the salt rocks behavior, taking into account the softening and plastic flow. It is shown that the proposed model is correctly used for a wide range of geotechnical tasks. It combines the modified Burgers models with the dependence of the viscosity coefficients on stresses via the hyperbolic sine function and the Mohr – Coulomb model with the nonlinear dependence of the adhesion coefficient, internal friction angles and dilatancy on effective plastic deformations.
The results of the model calculations performed for virtual (computer) tests of salt rocks samples and spatial models of the rock masses behavior in the vicinity of underground structures showed a good correspondence with the results of field studies in similar mining-geological and mining-technical conditions.
