Определение и верификация параметров расчетной модели соляных пород с учетом разупрочнения и ползучести

Введение. Вследствие ярко выраженной ползучести соляных пород перемещения в окрестности контура подземных сооружений, расположенных в массиве соляных пород, могут развиваться весьма длительное время и достигать больших величин. Подобные эффекты в процессе эксплуатации могут вызывать значительные разрушения вплоть до прогрессирующего обрушения пород.

Для прогнозирования развития деформационных процессов во времени в массиве горных пород в окрестности подземного сооружения активно используются численные методы. Достаточно много специализированных моделей и методов решения задач механики горных пород и массивов, и подземного строительства реализованы в программных комплексах Abaqus, DIANA, FLAC, Midas, PLAXIS, ZSoil и др.

В нормативном документе СП 91.13330.2011 «Подземные горные выработки» приведены инженерные методики расчета долговременных деформаций и устойчивости подземных выработок, при этом никаких сведений о базовых моделях, лежащих в основе этих методик, не приводится. Важно отметить, что СП 91.13330.2011 в ряде случаев не позволяет произвести расчеты на устойчивость выработок глубокого залегания в соляных и калийных рудниках, а использование численных методов при проектировании – обязательно. Другие геотехнические своды правил рекомендуют использовать модели упруго-идеально-пластической среды Мора – Кулона и Хоека – Брауна, не приводя при этом конкретных рекомендаций по учету реологических эффектов, ограничиваясь лишь требованиями об их учете. На практике введение предположения об идеально пластическом поведении в ряде задач может привести к некорректным выводам как в части взаимодействия вмещающего массива с крепью [5], так и в части оценки размеров зон нарушения выбранных критериев или учета ползучести, особенно когда образование пластических зон больших размеров неизбежно. В таких случаях учет разупрочнения позволяет избежать указанной проблемы и корректнее проводить расчет деформаций ползучести за счет другого характера распределения напряжений в массиве. Кроме того, появляется возможность выполнения более точных расчетов на исследование случаев проявления прогрессирующего разрушения.

Постановка проблемы. Модели, построенные на основе интегрального оператора с Абелевым ядром [4], а также модели Мора – Кулона и Хоека – Брауна, отражающие идеально пластическое поведение, с эмпирической зависимостью типа Нортона [11] и подобными степенными зависимостями [2, 3] получили широкое распространение при изучении реономных эффектов. Вместе с тем наиболее корректно использовать описанные модели при определенных горно-геологических и горнотехнических условиях (малые глубины, заполнение выработанного пространства искусственными целиками и др.), либо при выполнении предварительного анализа. Но при проектировании сооружений на больших глубинах, создании сложных и крупномасштабных подземных геотехнических комплексов, инженерных подземных объектов повышенной опасности и высокой ответственности, зачастую результаты бывают недостаточно адекватными и корректными. Так, например, «сценарий» процесса разрушения массива горных пород в окрестности подземного сооружения, согласно модельным расчетам, может лишь отдаленно соответствовать реальным условиям [19, 26], когда процесс ползучести вмещающего массива описывается некорректно и отличается от данных мониторинга в натурных условиях [11, 23].

Поэтому задача использования механико-математических моделей, более корректно и адекватно описывающих ползучесть массивов горных пород в окрестности подземных сооружений и позволяющих учитывать определенные специфические аспекты механического поведения массивов горных пород, остается актуальной и сегодня.

Методология. Для более корректного учета поведения соляных пород в сложных условиях нагружения предлагается использовать комбинированную вязко-упруго-пластическую модель, состоящую из модифицированной модели Бюргерса и модели Мора – Кулона, где основные параметры (сцепление \( c(\bar {\epsilon}_{pl})\), угол внутреннего трения \( \phi(\bar {\epsilon}_{pl})\), угол дилатансии \( \psi(\bar {\epsilon}_{pl})\) и предельные растягивающие напряжения \( \sigma_t(\bar {\epsilon}_{pl})\)) зависят от эффективных пластических относительных деформаций \( (\bar{\epsilon}_{pl})\) (рис.1). При этом полные относительные деформации \(\epsilon\) состоят из обратимой (упругой \( {\epsilon}_{el}\) и вязкоупругой \( {\epsilon}_{ve}\)) и необратимой (вязкой \( {\epsilon}_{visc}\) и пластической \( {\epsilon}_{pl}\)) частей, а изменение объемных относительных деформаций \( {\epsilon}_{v}\) происходит за счет упругой \( {\epsilon}_{v. el}\) и пластической \( {\epsilon}_{v. pl}\) частей:

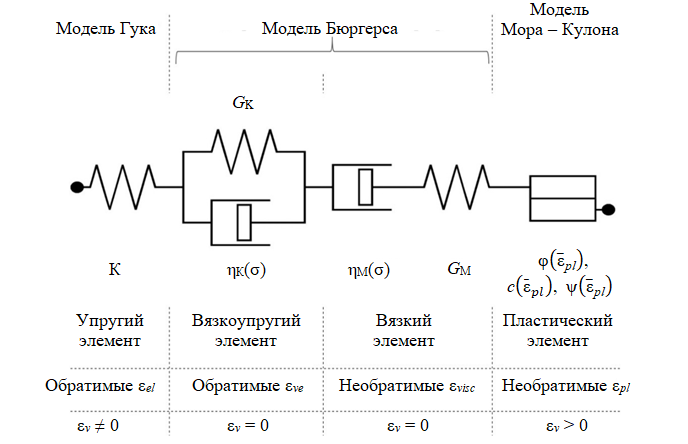
Многими авторами предлагались подходы к построению модификаций модели Мора – Кулона с учетом деградации коэффициента сцепления и возрастания коэффициента трения. Основные предшествующие подходы заключались в учете линейного роста величины коэффициента трения, линейного уменьшения сцепления [13] и обеих величин [12], использования зависимостей экспоненциального характера [21, 25] или более сложных зависимостей с определением влияния напряженного состояния и введением логарифмических функций для угла дилатансии [18, 20]. При этом, например используются нелинейные зависимости для «мобилизованных» коэффициента сцепления c' и угла внутреннего трения φ', предложенные Вермеером и де Борстом [25], а также угла дилатансии ψ' согласно зависимости, предложенной Ченом с соавторами [18]:

где c, sin(φ') – максимальные значения сцепления и синуса угла внутреннего трения; \( {\epsilon}_{c}\), \( {\epsilon}_{f}\) – константы, влияющие на характер изменения кривых c' и sin(φ') соответственно; a, b, d, f – численные коэффициенты.

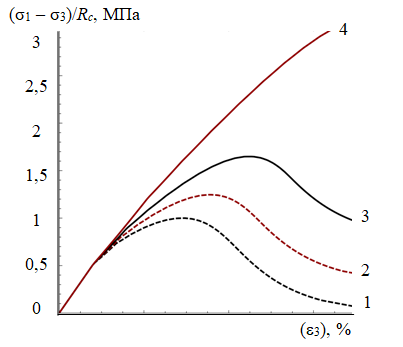
Обсуждение. На основании статистической обработки результатов лабораторных испытаний были получены модули упругости и спада, предел прочности при различных величинах обжатия образца в стабилометре σ_h, значения относительных продольных деформаций \( {\epsilon}_{3}\) для характерных точек диаграмм. Полученные на их основании значения модифицированной модели Мора – Кулона позволили воспроизвести усредненные условно-мгновенные испытания в стабилометре (кривые деформирования при разных величинах обжатия) (рис.2).

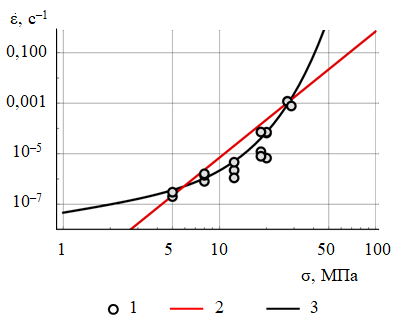
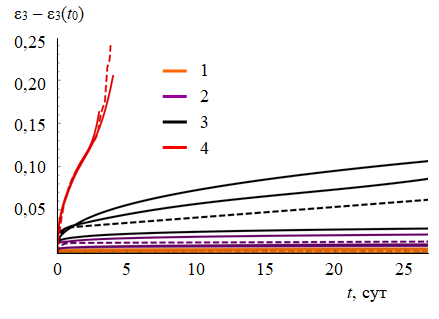
Для этапа вторичной ползучести, по данным лабораторных испытаний, выполнялось аналитическое определение параметров ядер ползучести для степенной и синус-гиперболической зависимостей и их сравнение. Установлено, что степенная зависимость не включает в доверительный диапазон напряжений значения выше 18,8 МПа, в то время как функция гиперболического синуса удовлетворительно «вписалась» в лабораторные испытания при всех значениях интенсивности напряжений (рис.3, 4). Аналогичная зависимость используется в варианте модификации модели Минкли [7, 10]). Окончательный вид используемой функции:

где \( {\dot\epsilon}_{visc}\) – скорость вязких относительных деформаций; a, b, c – коэффициенты; \( \sigma_i\) – интенсивность напряжений, \( \sigma_i=\sqrt{3j_2}\); \( \sigma_i^{'}\) – опорное давление.

Для верификации предложенной модели с использованием данных полевых наблюдений все наблюдательные станции делились на группы по схожим горно-геологическим и горнотехническим условиям и для каждой были проведены расчеты (результаты по одной из групп приведены на рис.5). Первоначальные расчеты с эмпирическим учетом влияния забоя (рис.5, линия «2D модель»), в которых на контуре выработки использовался понижающий множитель к компонентам начального поля напряжений согласно зависимости Булычева, показали завышенные показатели по скорости реализации этапа первичной ползучести. При этом скорости интервала установившейся ползучести имели удовлетворительное соответствие, которое легко объясняется качественным описанием вязкого элемента через функцию гиперболического синуса, что позволило достоверно описать широкий диапазон интенсивностей напряжений. Для исключения значительного влияния эмпирического метода учета забоя были решены задачи с проходкой выработки во времени в пространственной постановке (рис.5, линия «с учетом влияния забоя»). Результаты показали, что подобранные параметры модели для разных групп позволяют достоверно рассчитать величину первичных деформаций ползучести, что очень важно при проектировании конструкций обделок и крепи. Данный показатель позволяет использовать в проектах расчетно-обоснованные величины минимального и максимального времени возведения постоянного крепления после проходки выработки.

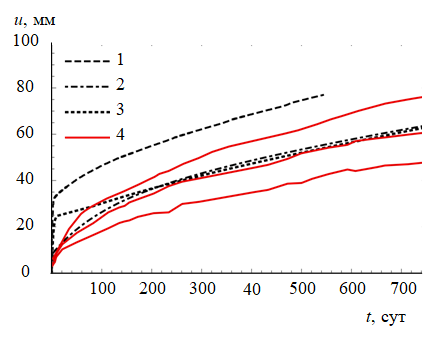
Для решения проблемы чрезмерно быстрой реализации первичных деформаций ползучести при модельных расчетах была выполнена оптимизация нелинейного вязкоупругого элемента путем итерационного уменьшения одного из коэффициентов. Диапазон уменьшения для разных групп – от 3 до 5 раз (рис.5, линия «после оптимизации»).

Заключение. Верификация рассмотренной модифицированной модели Бюргерса показала, что она является более эффективной, чем модели Мора – Кулона или Хоека – Брауна в комбинации с эмпирическими степенными законами ползучести типа Нортона. Преимущества заключаются в следующем:

• модель корректна для более широкого диапазона напряжений, что актуально для больших глубин;

• позволяет корректно выполнять многостадийный анализ без ограничений – корректный учет времени по сравнению с моделями типа Нортона, учитывающих первичную ползучесть, или учет эффектов релаксации по сравнению с вязко-пластическими моделями.

Ограничения, требующие учет при анализе решений:

• пластический элемент не зависит непосредственно от скорости деформирования, в отличие от вязко-пластических моделей типа Деринга – Киля [17, 27], получивших широкое применение на Верхнекамском месторождении калийно-магниевых солей [1];

• модифицированная модель не учитывает влияние влажности на ползучесть, в отличие от модели Гампеля – Шульца, которая используется для соляных пород [14] и учитывает соответствующую зависимость Гюнша – Шульца;

• не учитывает восстановления нарушенных горных пород, например, вследствие перекристаллизации [15, 22];

• модель может быть расширена введением экспоненциальной зависимости Аррениуса от температуры в функции вязкости при необходимости учета сопряженного температурного воздействия [24];

• по сравнению с оригинальной вязко-упруго-пластической моделью Минкли [6] и ее обновленными формулировками [10, 16], используемая функция поверхности разрушения является линейной и не имеет границы максимальных сдвиговых напряжений σmax. Данное ограничение может быть критично в случае фиксации низких величин σmax (незначительный рост прочности при увеличении обжатия) при испытаниях некоторых соляных пород с низкой прочностью, таких как карналлит.

Предложенная модель, в сравнении с другими распространенными моделями реологического поведения соляных пород, соответствует модели Минкли [8, 9], сохраняя ее основные преимущества и недостатки. Следует подчеркнуть, что некоторые проблемы, касающиеся учета эффекта дилатансии в модели, могут быть исправлены, например, путем введения дополнительных уточненных нелинейных зависимостей угла дилатансии от напряжений в используемую зависимость от эффективных пластических деформаций [18].

В статье приведен процесс определения, оптимизации и верификации параметров предложенной расчетной модели поведения соляных пород с учетом разупрочнения и ползучести. Показано, что предложенную модель корректно использовать для широкого спектра геотехнических задач. Она комбинирует модифицированные модели: Бюргерса с зависимостью коэффициентов вязкости от напряжений через функцию гиперболического синуса и Мора – Кулона с нелинейными зависимостями коэффициента сцепления, углами внутреннего трения и дилатансии от эффективных пластических деформаций.

Результаты выполненных модельных расчетов для виртуальных (компьютерных) испытаний образцов соляных пород и пространственных моделей поведения массивов горных пород в окрестности подземных сооружений продемонстрировали хорошее соответствие с результатами натурных исследований в подобных горно-геологических и горнотехнических условиях.

Литература

1. Ermashov A.O. Geomechanical substantiation of calculations of the earth surface subsidence calculations for the extraction of potash-magnesium ores (on the example of the Verkhnekamskoye potash-magnesium salt deposit): Avtoref. dis. … kand. tekhn. nauk. Perm: Gornyi institut UrO RAN, 2015, p. 22 (in Russian).
2. Karasev M.A., Buslova M.A., Vilner M.A., Nguyen T.T. Method for predicting the stress-strain state of the vertical shaft lining at the drift landing section in saliferous rocks. Journal of Mining Institute. 2019. Vol. 240, p. 628-637. DOI: 10.31897/pmi.2019.6.628 (in Russian).
3. Protosenya A.G., Ochkurov V.I., Otkupshikova I.A. Prediction of rock load on shaft lining in creep rock masses. Sbornik nauchnykh trudov III Vserossiiskoi nauchnoi konferentsii “Sovremennye obrazovatelnye tekhnologii v podgotovke spetsialistov dlya mineralno-syrevogo kompleksa”, 5-6 Marta, 2020, Sankt-Peterburg, Rossiya. St. Petersburg: Sankt-Peterburgskii gornyi universitet, 2020, p. 1091-1101. (in Russian)
4. Protosenia A.G., Nguen Ny Bai. The forecast of stress state of massif at the area of mine shaft and gallery junction. Izvestiya vysshikh uchebnykh zavedenii. Gornyi zhurnal. 2015. N 7, p. 50-55 (in Russia).
5. LiG., MaF., Liu G. et al. A Strain-Softening Constitutive Model of Heterogeneous Rock Mass Considering Statistical Damage and Its Application in Numerical Modeling of Deep Roadways. Sustainability. 2019. Vol. 11. N 8, p. 2399. DOI: 10.3390/su11082399
6. MinkleyW., MenzelW., Konietzky H., Kampte L. A visco-elasto-plastic softening model and it’s application for solving static and dynamic problems in potash mining. Proceedings of the 2nd International FlAC Symposium, 29-31 October, 2001, Lyon, France, 2001, p. 21-27.
7. Brückner D., Minkley W., Lindert A. The improved IfG gas storage cavern design concept. Mechanical Behavior of Salt VII. London: CRC Press, 2012, p. 391-398.
8. Schulze O., Heemann U., Zetsch F. et al. Comparison of advanced constitutive models for the mechanical behavior of rock salt – results from a joint research project – I. Modeling of deformation processes and benchmark calculations. The Mechanical Behavior of Salt – Understanding of THMC Processes in Salt: Proceedings of the 6th Conference (SaltMech6), 22-25 May, 2007, Hannover, Germany, 2007, p. 77-88. DOI: 10.1201/9781315106502-10
9. Hou Z., Wolters R., RokahrR. et al. Comparison of advanced constitutive models for the mechanical behavior of rock salt – results from a joint research project – II. Numerical modeling of two in situ case studies and comparison. The Mechanical Behavior of Salt – Understanding of THMC Processes in Salt: Proceedings of the 6th Conference (SaltMech6), 22-25 May, 2007, Hannover, Germany, 2007, p. 89-98. DOI: 10.1201/9781315106502-11
10. Minkley W., Bzrest P., Schleinig J.P. et al. Dynamic back-calculation of the collapse of the Saint-Maximilien mining field during mining on rock salt in Varangéville (1873). Mechanical Behavior of Salt VII. London: CRC Press, 2012, p. 241-252.
11. Firme P.A.L.P., Brandao N.B., Roehl D., Romanel C. Enhanced double-mechanism creep laws for salt rocks. Acta Geotechnica. 2018. Vol. 13, p. 1329-1340. DOI: 10.1007/s11440-018-0689-7
12. Dehkordi M.S., Lazemi H.A., Shahriar K., Dehkordi M.S. Estimation of the Rock Load in Non-squeezing Ground Condition Using the Post Failure Properties of Rock Mass. Geotechnical and Geological Engineering. 2015. Vol. 33, p. 1115-1128. DOI: 10.1007/s10706-015-9891-7
13. Hajiabdolmajid V., Kaiser P.K., Martin C.D. Modelling brittle failure of rock. International Journal of Rock Mechanics and Mining Sciences. 2002. Vol. 39. Iss. 6, p. 731-741. DOI: 10.1016/S1365-1609(02)00051-5
14. Hampel A., Schulze O. The Composite Dilatancy Model: A constitutive model for the mechanical behavior of rock salt. The Mechanical Behavior of Salt – Understanding of THMC Processes in Salt: Proceedings of the 6th Conference (SaltMech6), 22-25 May, 2007, Hannover, Germany, 2007, p. 99-108. DOI: 10.1201/9781315106502-12
15. Chen J., Peng H., Fan J. et al. Microscopic investigations on the healing and softening of damaged salt by uniaxial deformation from CT, SEM and NMR: effect of fluids (brine and oil). RSC Advances. 2020. Vol. 10, p. 2877-2886. DOI: 10.1039/C9RA05866D
16. Minkley W., Mühlbauer J. Constitutive models to describe the mechanical behavior of salt rocks and the imbedded weakness planes. The Mechanical Behavior of Salt – Understanding of THMC Processes in Salt: Proceedings of the 6th Conference (SaltMech6), 22-25 May, 2007, Hannover, Germany, 2007, p. 119-127. DOI: 10.1201/9781315106502-14
17. Missal C., Gährken A., Stahlmann J. Ein thermisch‐mechanisches Stoffmodell für Steinsalz mit Berücksichtigung von Schädigung, Bruch und Verheilung. Geotechnik. 2016. Vol. 39. N 1, p. 2-17. DOI: 10.1002/gete.201500010
18. Chen Y., Ma L., Fan P. et al. Nonlinear volumetric deformation behavior of rock salt using the concept of mobilized dilatancy angle. The Open Civil Engineering Journal. 2016. Vol. 10, p. 524-531. DOI: 10.2174/1874149501610010524
19. Poiate E.Jr. Mecânica das rochas e mecânica computacional para projeto de poços de petróleoem zonas de sal: DSc Thesis. Rio de Janeiro: Pontifícia Universidade Católica do Rio de Janeiro, 2012, p. 462. DOI: 10.17771/PUCRio.acad.34904
20. Ma L., Yang F., Xu H., Xie Z. Post-Yield Properties of Rock Salt Using the Concept of Mobilized Strength Components and the Dilation Angle. Geotechnical and Geological Engineering. 2017. Vol. 35, p. 2841-2849. DOI: 10.1007/s10706-017-0283-z
21. Rafiei Renani H., Martin C.D. Cohesion degradation and friction mobilization in brittle failure of rocks. International Journal of Rock Mechanics and Mining Sciences. 2018. Vol. 106, p. 1-13. DOI: 10.1016/j.ijrmms.2018.04.003
22. Chen J., Ren S., Yang C.et al. Self-Healing Characteristics of Damaged Rock Salt under Different Healing Conditions. Materials (Basel). 2013. Vol. 6. N 8, p. 3438-3450. DOI: 10.3390/ma6083438
23. Ślizowski J., Urbańczyk K.M. Influence of effective stress on strain rate around the gas storing cavern. The Mechanical Behavior of Salt – Understanding of THMC Processes in Salt: Proceedings of the 6th Conference (SaltMech6), 22-25 May, 2007, Hannover, Germany, 2007, p. 363-368. DOI: 10.1201/9781315106502-42
24. Günther R.-M., Lüdeling C., Popp T. et al. Vergleich aktueller Stoffgesetze und Vorgehensweisen anhand von Modellberechnungen zum thermo-mechanischen Verhalten und zur Verheilung von Steinsalz. Teilvorhaben 2. Leipzig: IfG, 2016, p. 184 (in German).
25. Vermeer P.A., de Borst R. Non-Associated Plasticity for Soils, Concrete and Rock. Heron. 1984. Vol. 29. N 3, p. 1-64. DOI: 10.1007/978-94-017-2653-5_10
26. Bérest P., Gharbi H., Brouard B. et al. Very Slow Creep Tests on Salt Samples. Rock Mechanics and Rock Engineering. 2019. Vol. 52, p. 2917-2934. DOI: 10.1007/s00603-019-01778-9
27. Wittke W. Rock Mechanics Based on an Anisotropic Jointed Rock Model (AJRM). Berlin: Wilhelm Ernst & Sohn; Verlag für Architektur und technische Wissenschaften GmbH & Co, 2014, p. 900. DOI: 10.1002/9783433604281