Transition between relieved and unrelieved modes when cutting rocks with conical picks
- 1 — Ph.D. Design Engineer LLC “Skyratovsky Experimental Plant”
- 2 — д-р техн. наук Professor Tula State University ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 3 — Ph.D., Dr.Sci. Professor Tula State University ▪ Orcid ▪ Elibrary ▪ Scopus
- 4 — Ph.D., Dr.Sci. Professor State University of Management ▪ Orcid ▪ Elibrary ▪ Scopus
- 5 — Ph.D., Dr.Sci. Professor State University of Management ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
Abstract
In the modern theory of rock cutting in production conditions, it is customary to distinguish two large classes of achievable cutting modes – relieved and unrelieved. The kinematics of rock-breaking machines in most cases determines the operation of the cutting tool in both modes in one cycle of the cutting tool. The currently available calculation methods have been developed for a stable, usually unrelieved cutting mode. In this article, the task is set to determine the conditions for the transition between cutting modes and the modernization of the calculation method for determining the forces on the cutting tool. The problem is solved by applying methods of algebraic analysis based on the search for the extremum of the force function on the cutter, depending on the ratio of the real cut spacing to the optimal spacing for the current chip thickness. As a result of solving the problem, an expression is obtained for determining the chip thickness, for which, at the specified parameters, the transition between the relieved and unrelieved cutting modes is provided. The obtained result made it possible to improve the method of calculating the forces on the cutting tool in the areas of the cutter movement with relieved cutting.
Introduction
The process of rock destruction by a cutting tool is characterized by the separation of chips in the form of rock particles from the face or rock block [11, 14, 17]. The shape of the chip is determined mainly by the kinematics of the tool movement [19]. The ratio between the width and depth of the cut, i.e. between the cut spacing t and the chip thickness h, has a great influence on the indicators of the cutting process [3, 13]. According to the mutual arrangement of the cutters, there are different types of cutting modes. The definitions by various researchers differ significantly, for example, test cuts with the use of linear cutting machines are carried out under the conditions of the so-called free cut from a smoothed surface, since in this case the necessary conditions for comparing power and energy parameters are more easily provided for the compared variants [7, 10, 22]. However, with the continuous work of the operating unit of modern rock-breaking machines, this type of cutting is practically impossible. In general, as a rule, they use the division of cutting classes into two generalized modes also known as relieved and unrelieved cutting.
An important role in the rock cutting process is played by the geometry of the cutting tool, which is understood as a set of characteristics that determine the shape of the tool and the location of its faces (surfaces) and cutting edges relative to the surfaces of the processed face [15, 18, 21]. In modern designs of rock-breaking machines of cutting action, the so-called conical picks have become the most widespread [4, 12], therefore, all further research will be carried out in relation to such cutters.
Formulation of the problem
Based on the analysis carried out in [5, 6], we will choose the initial equation for this study:
where σc – uniaxial compression strength of rock, MPa; Kg – coefficient of the cutter geometry; Kfr – rock fracturing coefficient; Kbp – coefficient of brittle-plastic properties of rock; Kob – the coefficient of non-optimality of the cutting mode; t – cut spacing (distance between adjacent cutting lines), mm; h – cutting depth (thickness of the cut chips), mm.
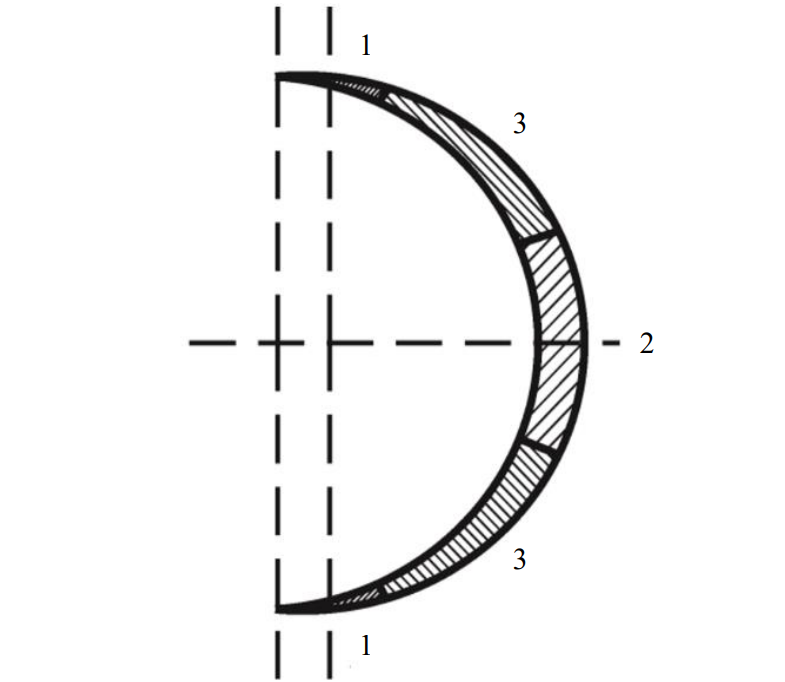
Diagram of a crescent-shaped chip [3]
Conical picks, as a rule, are used for equipping of cutting bodies of rock-breaking machines made in the form of bodies of rotation (cutters, augers, drums, etc.) [1, 3, 4, 13, 19]. Therefore, when cutting, chips are formed that have a crescent shape (see the figure).
The efficiency of rock destruction by cutters is provided with certain combinations of the cut spacing t and the chip thickness h, which allow optimizing the cutting process [13, 20]. Optimization consists in ensuring the minimum specific energy of cutting rocks with certain properties at certain values of the power characteristics of the operating unit of the mining machine.
The crescent-shaped chip diagram shows several sections: two sections 1 at the beginning and at the end of the crescent, which have t > topt; one section 2 in the middle part of the crescent with t < topt; two mid-stage sections 3, corresponding to t ≈ topt. Thus, the cutting of any rock with conical picks when they are equipped with modern cutterheads of mining machines always goes through the stages of non-optimal modes.
With a sufficiently large difference between the real and optimal cut spacings, the value of the coefficient Kob takes unnaturally large values in sections 1, tending to infinity at topt → 0, and also leads to incorrect values of the force on the tool [3]. That is, the existing mathematical model is not adequate to the real cutting process when the cutter moves along the chip sections 1, where relieved cutting is observed. In this regard, there is a need to determine the transition point between sections 1 of the relieved and 3 of the unrelieved cutting modes.
Research methodology
To solve this problem, an approach is used, which consists in finding the extremum of the force function on the cutter from the cutting depth [9]. The values of σс, Kg, Kfr and Kbp, as well as the constant 19.5, do not require disclosure, since they do not depend on the variable h [6]. This variable occurs in the Kob coefficient when calculating the optimal cut spacing topt = 3.65tgφKc , where tgφ is the criterion of brittle-plastic properties of rock, depending on the half camber angle of the cutting furrow φ, Kc – coefficient depending on the diameter of the tungsten carbide tip;
When replacing the variable x = , and also A2 = t(3.65tgφKc)–1, the initial equation (1) is transformed into an equation of the fourth degree regarding to the variable x. The fourth degree equations are generally solved by the Ferrari method. With a known root of the cubic resolvent, the roots of the fourth-degree equation according to the Ferrari method can be found from two quadratic equations, which in this case are described by the following expression:
where y is the only real root of the cubic resolvent calculated by the Cardano formula,
The solution of equation (3) will allow to determine the moment of transition between the relieved and unrelieved modes of cutting rocks with conical picks.
Results and discussion
We will find all possible solutions of equation (3) for various realistically achievable variations of the initial data, and will present the results in the form of the table.
Solutions of the fourth-degree equation for various variants of acceptable initial data
|
Initial data |
Interim calculations |
Solution of the fourth-degree equation |
|||||||
|
φ, ° |
d, mm |
t, mm |
A2 |
Q |
y |
x1 |
x2 |
x3 |
x4 |
|
45 |
15.5 |
15 |
3.56 |
239.38 |
0.61 |
– |
– |
1.69 |
–1.04 |
|
45 |
20 |
4.75 |
593.09 |
0.81 |
– |
– |
1.85 |
–1.08 |
|
|
45 |
25 |
5.93 |
1208.56 |
1.01 |
– |
– |
1.98 |
–1.11 |
|
|
45 |
30 |
7.12 |
2175.11 |
1.21 |
– |
– |
2.09 |
–1.13 |
|
|
45 |
35 |
8.30 |
3591.70 |
1.41 |
– |
– |
2.19 |
–1.14 |
|
|
60 |
15 |
2.05 |
8.06 |
0.19 |
– |
– |
1.22 |
–0.90 |
|
|
60 |
20 |
2.74 |
19.43 |
0.26 |
– |
– |
1.32 |
–0.94 |
|
|
60 |
25 |
3.42 |
38.57 |
0.33 |
– |
– |
1.42 |
–0.97 |
|
|
60 |
30 |
4.11 |
67.72 |
0.40 |
– |
– |
1.50 |
–0.99 |
|
|
60 |
35 |
4.79 |
109.23 |
0.47 |
– |
– |
1.57 |
–1.01 |
|
|
75 |
15 |
0.95 |
0.08 |
0.03 |
– |
– |
0.77 |
–0.70 |
|
|
75 |
20 |
1.27 |
0.18 |
0.04 |
– |
– |
0.84 |
–0.73 |
|
|
75 |
25 |
1.59 |
0.36 |
0.06 |
– |
– |
0.90 |
–0.76 |
|
|
75 |
30 |
1.91 |
0.63 |
0.07 |
– |
– |
0.94 |
–0.79 |
|
|
75 |
35 |
2.23 |
1.00 |
0.09 |
– |
– |
0.99 |
–0.81 |
|
|
45 |
17.5 |
15 |
3.42 |
185.86 |
0.56 |
– |
– |
1.65 |
–1.03 |
|
45 |
20 |
4.56 |
459.14 |
0.75 |
– |
– |
1.80 |
–1.07 |
|
|
45 |
25 |
5.70 |
933.07 |
0.94 |
– |
– |
1.93 |
–1.10 |
|
|
45 |
30 |
6.84 |
1675.10 |
1.12 |
– |
– |
2.04 |
–1.12 |
|
|
45 |
35 |
7.98 |
2759.67 |
1.30 |
– |
– |
2.14 |
–1.13 |
|
|
60 |
15 |
1.97 |
6.30 |
0.18 |
– |
– |
1.19 |
–0.89 |
|
|
60 |
20 |
2.63 |
15.17 |
0.24 |
– |
– |
1.29 |
–0.93 |
|
|
60 |
25 |
3.29 |
30.08 |
0.31 |
– |
– |
1.38 |
–0.96 |
|
|
60 |
30 |
3.95 |
52.75 |
0.37 |
– |
– |
1.46 |
–0.98 |
|
|
60 |
35 |
4.60 |
84.99 |
0.43 |
– |
– |
1.53 |
–1.00 |
|
|
75 |
15 |
0.92 |
0.06 |
0.02 |
– |
– |
0.75 |
–0.69 |
|
|
75 |
20 |
1.22 |
0.14 |
0.04 |
– |
– |
0.82 |
–0.72 |
|
|
75 |
25 |
1.53 |
0.28 |
0.05 |
– |
– |
0.87 |
–0.75 |
|
|
75 |
30 |
1.83 |
0.49 |
0.06 |
– |
– |
0.92 |
–0.77 |
|
|
75 |
35 |
2.14 |
0.78 |
0.08 |
– |
– |
0.97 |
–0.79 |
|
|
45 |
22 |
15 |
3.14 |
109.15 |
0.47 |
– |
– |
1.57 |
–1.01 |
|
45 |
20 |
4.18 |
268.12 |
0.63 |
– |
– |
1.71 |
–1.05 |
|
|
45 |
25 |
5.23 |
542.02 |
0.79 |
– |
– |
1.83 |
–1.08 |
|
|
45 |
30 |
6.28 |
968.31 |
0.95 |
– |
– |
1.94 |
–1.10 |
|
|
45 |
35 |
7.32 |
1587.98 |
1.10 |
– |
– |
2.03 |
–1.12 |
|
|
60 |
15 |
1.81 |
3.75 |
0.15 |
– |
– |
1.13 |
–0.86 |
|
|
60 |
20 |
2.42 |
9.00 |
0.20 |
– |
– |
1.23 |
–0.90 |
|
|
60 |
25 |
3.02 |
17.81 |
0.25 |
– |
– |
1.31 |
–0.93 |
|
|
60 |
30 |
3.62 |
31.17 |
0.31 |
– |
– |
1.39 |
–0.96 |
|
|
60 |
35 |
4.23 |
50.12 |
0.36 |
– |
– |
1.45 |
–0.98 |
|
|
75 |
15 |
0.84 |
0.04 |
0.02 |
– |
– |
0.71 |
–0.67 |
|
|
75 |
20 |
1.12 |
0.09 |
0.03 |
– |
– |
0.78 |
–0.70 |
|
|
75 |
25 |
1.40 |
0.17 |
0.04 |
– |
– |
0.83 |
–0.73 |
|
|
75 |
30 |
1.68 |
0.29 |
0.05 |
– |
– |
0.88 |
–0.75 |
|
|
75 |
35 |
1.96 |
0.47 |
0.06 |
– |
– |
0.92 |
–0.77 |
|
The table provides a wide range of possible options for real combinations of initial data. The conclusions, made on the basis of the analysis of the table, may well be accepted as final. As can be seen from the table, for any combinations of the initial data, there are no roots x1 and x2 – in fact, they are complex numbers, but we are only interested in real roots. In addition, for any combinations of the initial data, the root x4 is a negative number. This root should also be rejected, since we previously replaced $x = \sqrt h$ and the root expression cannot be a negative real number.
Thus, the only possible root in the context of this problem is found from an equation that, for any valid combinations of the initial data, allows to get a positive real number as an answer. The desired value of the cutting depth hb, at which the transition between the relieved and unrelieved cutting modes occurs for the specified conditions, is determined by squaring the value of this root:
If the current value of the cutting depth is less than the value obtained by the formula (5), then the cutting takes place in the relieved cutting mode, and if it is greater, unrelieved. Modeling of the rock mass destruction taking into account the current position of the cutters, including various schemes and cutting modes, is carried out using numerical methods such as the finite element method [8] and the discrete element method [16]. For the correct application of the obtained result in solving problems using numerical methods, it is necessary that the values of the characteristic dimensional quantities of finite or discrete elements do not exceed the values of hb.
It should be noted that the expression (5) is obtained for an idealized picture of the face destruction by the cutterhead, which does not take into account its vibrations. At the same time, as noted in [2], the oscillation ranges of the cutterhead can reach several centimeters, significantly increasing the cutting depth, including in sections 1 and 3, which introduces an error in determining the cutting mode in these sections. In this case, it is advisable to determine not the cutting depth hb, but the duration of the chip sections where relieved cutting is observed. For example, by the rotation angle of the cutter inside the chip relative to the point of initial contact. This angle φb is defined as the arcsine of the ratio hb to hmax without taking into account the vibrations of the cutterhead. Then the transition condition between the relieved and unrelieved cutting modes is transformed to the following. If the current value of the rotation angle φi of the cutter when moving through the cutting chips is less than the value of φb or greater than the value of 180° − φb, then cutting occurs in the mode of relieved cutting, otherwise – unrelieved.
Conclusion
The main theoretical conclusions can be drawn from the conducted research:
- the transition between relieved and unrelieved cutting modes does not depend on the strength properties of the rock;
- the cutting depth at which the cutting mode is changed for the specified conditions is determined by the brittle-plastic properties of the rock and also the diameter of the tungsten carbide tip and the cut spacing.
The practical use of the obtained result is as follows. The current value of the cutting depth h is compared with the value hb obtained by the formula (5). In the case of h < hb the value of hb is replaced in the formula (2) to determine the Кob coefficient, otherwise – h. The proposed approach, in comparison with the original method, allows to more accurately assess the forces on the cutter according to the formula (1) in sections 1 of the cutting chip according to the figure, i.e. in sections of irrational cutting modes.
References
- Baron L.I., Glatman L.V., Gubenkov E.K. Destruction of rocks by tunneling combines. Volume 1: Scientific and methodological foundations. Destruction by a cutting tool. Moscow: Nauka, 1968, p. 216 (in Russian).
- Kondrakhin V.P., Golovin V.L. A mathematical model of the chip formation process that takes into account the axial movements of the operating unit of a mining combine. Naukovi pratsi DonNTU. Seriya girnichno-mekhanichna. 2004. Iss. 83, p. 142-149 (in Russian).
- Zhabin A.B., Polyakov A.V., Averin E.A. et al. Consideration of non-optimal cutting conditions of rocks by conical picks. Ugol. 2019. N 7, p. 20-24. DOI: 10.18796/0041-5790-2019-7-20-24 (in Russian).
- Averin E.A., Naumov Yu.N., Smychnik A.D., Smychnik E.A. Cutterhead of shaft boring machine for hard rock destruction. Mining informational and analytical bulletin. 2019. N 2, p. 105-113 (in Russian).
- Zhabin A.B., Polyakov A.V., Averin E.A. et al. Ways of development for the theory of rock and coal destruction by picks. Ugol. 2019. N 9, p. 24-28. DOI: 10.18796/0041-5790-2019-9-24-28 (in Russian).
- Zhabin A.B., Polyakov A.V., Averin E.A., Sarychev V. I. State of scientific researches in the field of rock destruction by picks at the turn of the century. News of the Tula state university. Sciences of Earth. 2018. N 1, p. 230-247.
- Kang H., Cho J.W., Park J.Y. et al. A new linear cutting machine for assessing the rock-cutting performance of a pick cutter. International Journal of Rock Mechanics and Mining Sciences. 2016. Vol. 88, p. 129-136. DOI: 10.1016/j.ijrmms.2016.07.021
- Park J.Y., Kang H., Lee J.W. et al. A study on rock cutting efficiency and structural stability of a point attack pick cutter by lab-scale linear cutting machine testing and finite element analysis. International Journal of Rock Mechanics and Mining Sciences. 2018. Vol. 103, p. 215-229. DOI: 10.1016/j.ijrmms.2018.01.034
- Averin E.A., Zhabin A.B., Polyakov A.V. Approach to Estimate Rational Parameters of Rock Destruction from a Function of a Cutting Force. IOP Conference Series: Earth and Environmental Science. 2019. Vol. 272. Iss. 2. N 022002. DOI: 10.1088/1755-1315/272/2/022002
- Balci C., Bilgin N. Correlative study of linear small and full-scale rock cutting tests to select mechanized excavation machines. International Journal of Rock Mechanics and Mining Sciences. 2007. Vol. 3. N 44, p. 468-476. DOI: 10.1016/j.ijrmms.2006.09.001
- Liu J., Ma C., Zeng Q., Gao K. Discrete element simulation of conical pick’s coal cutting process under different cutting parameters. Shock and Vibration. 2018. Vol. 2018, p. 7975141. DOI: 10.1155/2018/7975141
- N.Bilgin, Demircin M.A., Copur H. et al. Dominant rock properties affecting the performance of conical picks and the comparison of some experimental and theoretical results. International Journal of Rock Mechanics and Mining Sciences. 2006. Vol. 43. Iss. 1, p. 139-156. DOI: 10.1016/j.ijrmms.2005.04.009
- Wang X., Su O., Wang Q.F., Liang Y.P. Effect of cutting depth and line spacing on the cuttability behavior of sandstones by conical picks. Arabian Journal of Geosciences. 2017. Vol. 10, p. 510-525. DOI: 10.1007/s12517-017-3307-3
- Wang S., Li X., Du K., Wang S. Experimental investigation of hard rock fragmentation using a conical pick on true triaxial test apparatus. Tunnelling and Underground Space Technology. 2018. Vol. 79, p. 210-223. DOI: 10.1016/j.tust.2018.05.006
- Liu J., Wan W., Xie S., Wang J. Indentation Characteristics Using Various Indenters: A Study Based on Laboratory and Numerical Tests. Geotechnical and Geological Engineering. 2019. Vol. 37, p. 4919-4931. DOI: 10.1007/s10706-019-00952-8
- Xuefeng L., Shibo W., Shirong G. Investigation on the influence mechanism of rock brittleness on rock fragmentation and cutting performance by discrete element method. Measurement. 2018. Vol. 113, p. 120-130. DOI: 10.1016/j.measurement.2017.07.043
- Li H.S., Liu S.Y., Xu P.P. Numerical simulation on interaction stress analysis of rock with conical picks. Tunnelling and Underground Space Technology. 2019. Vol. 85, p. 231-242. DOI: 10.1016/j.tust.2018.12.014
- Zakharov V.N., Linnik V.Y., Linnik Y.N., Averin E.A. Loading of coal mining machine tools after change in spatial orientation of picks. Eurasian mining. 2018. N 1, p. 40-42. DOI: 10.17580/em.2019.01.10
- Zhang Q., Han Z., Zhang M., Zhang J. New model for predicting instantaneous cutting rate of axial-type roadheaders. KSCE Journal of Civil Engineering. 2017. Vol. 21, p. 168-177. DOI: 10.1007/s12205-016-0433-5
- Zhang Q.Q., Han Z.N., Ning S.H. et al. Numerical simulation of rock cutting in different cutting mode using the discrete element method. Journal of GeoEngineering. 2015. Vol. 10. N 2. p. 35-43. DOI: 10.6310/jog.2015.10(2).1
- Prokopenko S.A., Ludzish V.S., Kurzina I.A. Improvement of cutting tools to enhance performance of heading machines in rocks. Journal of Mining Science. 2016. Vol. 52, p. 153-159. DOI: 10.1134/S1062739116010248
- Yasar S., Yilmaz A.O. Rock cutting tests with a simple-shaped chisel pick to provide some useful data. Rock Mechanics and Rock Engineering. 2017. Vol. 50, p. 3261-3269. DOI: 10.1007/s00603-017-1303-2
