Переход между блокированным и полублокированным режимами при резании горных пород тангенциальными резцами
- 1 — канд. техн. наук инженер-конструктор ООО "Скуратовский опытно-экспериментальный завод"
- 2 — д-р техн. наук профессор Тульский государственный университет ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 3 — д-р техн. наук профессор Тульский государственный университет ▪ Orcid ▪ Elibrary ▪ Scopus
- 4 — д-р техн. наук профессор Государственный университет управления ▪ Orcid ▪ Elibrary ▪ Scopus
- 5 — д-р экон. наук начальник отдела научных мероприятий и молодежной научной деятельности Государственный университет управления ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
Аннотация
В современной теории резания горных пород в производственных условиях принято выделять два больших класса достижимых режимов резания – блокированный и полублокированный. Кинематика машин для разрушения горных пород в большинстве случаев обуславливает работу резцового инструмента в обоих режимах за один цикл работы резцового инструмента. Имеющиеся в настоящее время расчетные методы разработаны для стабилизированного, как правило, полублокированного режима резания. В настоящей статье поставлена задача определения условий перехода между режимами резания и модернизации расчетного метода для определения усилий на резцовом инструменте. Задача решается за счет применения методов алгебраического анализа, основанного на поиске экстремума функции усилия на резце в зависимости от отношения реального шага резания к оптимальному шагу для текущей толщины стружки. В результате решения задачи получено выражение для определения толщины стружки, для которой при заданных параметрах обеспечивается переход между блокированным и полублокированным режимами резания. Полученный результат позволил усовершенствовать метод расчета усилий на резцовом инструменте на участках движения резца с блокированным резанием.
Введение
Процесс разрушения горной породы резцовым инструментом характеризуется отделением от забоя или породного блока стружки в виде частиц породы [11, 14, 17]. Форма стружки определяется главным образом кинематикой движения инструмента [19]. Большое влияние на показатели процесса резания оказывает соотношение между шириной и глубиной реза, т.е. между шагом резания t и толщиной стружки h [3, 13]. По взаимному расположению резов различают виды резания, их число. Определения существенно отличаются у разных исследователей, например, стендовое резание осуществляется в условиях так называемого свободного реза с выровненной поверхности, так как в этом случае легче обеспечиваются необходимые условия для сравнения силовых и энергетических параметров при сопоставляемых вариантах [7, 10, 22]. Однако при непрерывной работе исполнительного органа современных породоразрушающих машин такой вид резания практически невозможен. В целом, как правило, используют разделение классов резания на два обобщенных режима – блокированное и полублокированное резание.
Важную роль в процессе резания породы играет геометрия режущего инструмента, под которой понимается совокупность характеристик, определяющих форму инструмента и расположение его граней (поверхностей) и режущих кромок относительно поверхностей обрабатываемого забоя [15, 18, 21]. В современных конструкциях породоразрушающих машин режущего действия наибольшее распространение получили так называемые тангенциальные резцы [4, 12], поэтому все дальнейшие изыскания будут выполнены применительно к таким резцам.
Постановка задачи. На основании анализа, проведенного в работах [5, 6], выберем исходное уравнение для настоящего исследования:
где σсж – предел прочности на одноосное сжатие горной породы, МПа; Kг – коэффициент геометрии резца; Kтр – коэффициент трещиноватости горной породы; Kхп – коэффициент хрупко-пластических свойств горной породы; Kоб – коэффициент неоптимальности режима резания; t – шаг резания (расстояние между соседними линиями резания), мм; h – глубина резания (толщина срезаемой стружки), мм.
Тангенциальными резцами, как правило, оснащаются режущие органы породоразрушающих машин, выполненные в виде тел вращения (фрезы, шнеки, барабаны и т.п.) [1, 3, 4, 13, 19]. Поэтому при резании образуются стружки, имеющие серповидную форму (см. рисунок).
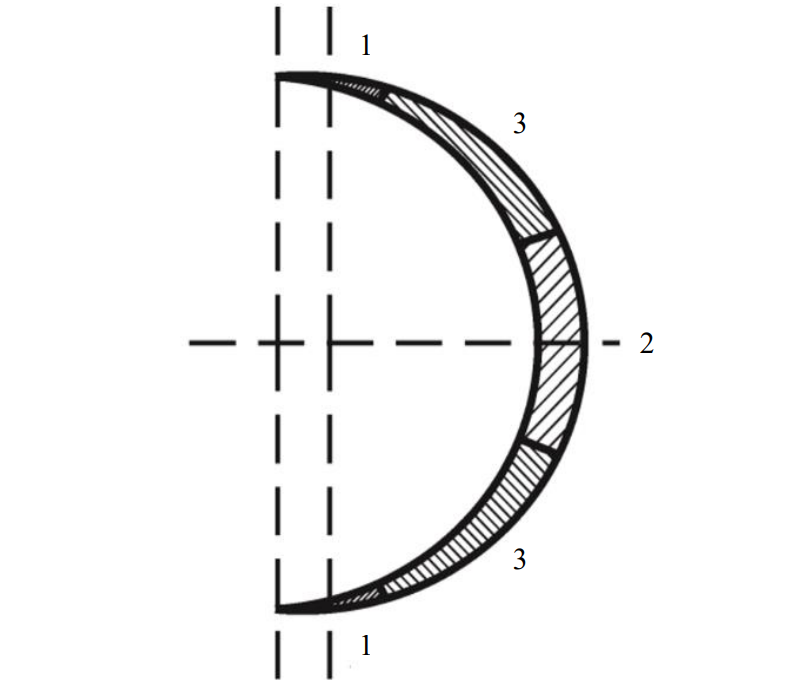
Схема серповидной стружки [3]
Эффективность разрушения горных пород резцами обеспечивается при определенных сочетаниях шага резания t и толщины стружки h, позволяющих оптимизировать процесс резания [13, 20]. Оптимизация заключается в обеспечении минимальной энергоемкости резания горных пород с определенными свойствами при определенных значениях силовых характеристик исполнительного органа горнопроходческой машины.
На схеме серповидной стружки выделено несколько участков: два участка 1 в начале и в конце серпа, у которых t > tопт; один участок 2 в средней части серпа с t < tопт; два промежуточных участка 3, соответствующих t ≈ tопт. Таким образом, резание любой горной породы тангенциальными резцами при оснащении ими современных режущих органов горнопроходческих машин всегда проходит этапы неоптимальных режимов.
При достаточно большой разнице между реальным и оптимальным шагами резания значение коэффициента Kоб принимает неестественно большие значения на участках 1, стремясь к бесконечности при tопт → 0, а также ведет к получению неправильных значений усилия на инструменте [3]. То есть имеющаяся математическая модель не адекватна реальному процессу резания при движении резца по участкам 1 стружки, на которых наблюдается блокированное резание. В связи с этим возникает необходимость в определении точки перехода между участками 1 блокированного и 3 полублокированного режимов резания.
Методика проведения исследования
Для решения поставленной задачи используем подход, заключающийся в нахождении экстремума функции усилия на резце от глубины резания [9]. Величины σсж, Kг, Kтр и Kхп, как и константа 19,5, не требуют раскрытия, поскольку не зависят от переменной h [6]. Эта переменная встречается в коэффициенте Kоб при вычислении оптимального шага резания tопт = 3,65tgφKв, где tgφ – критерий хрупко-пластических свойств горной породы, зависящий от значения половины угла развала борозды резания φ, Kв – коэффициент, зависящий от диаметра твердосплавной вставки;
Произведем замену переменной $ x=\sqrt h $, а также $A_2 = t(3,65tgφK_В)^{-1}$. Тогда исходное выражение (1) преобразуется в уравнение четвертой степени относительно переменной x. Уравнения четвертой степени в общем виде решаются методом Феррари. При известном корне кубической резольвенты корни уравнения четвертой степени по методу Феррари могут быть найдены из двух квадратных уравнений, которые в данном случае описываются следующим выражением:
где y – единственный вещественный корень кубической резольвенты, вычисляемый по формуле Кардано,
Решение уравнения (3) позволит определить момент перехода между блокированным и полублокированным режимами резания горных пород тангенциальными резцами.
Результаты и обсуждение
Найдем все возможные решения уравнения (3) при различных реально достижимых вариациях исходных данных, а результаты представим в виде таблицы.
Решения уравнения четвертой степени при различных вариантах допустимых исходных данных
|
Исходные данные |
Промежуточные расчеты |
Решение уравнения 4-й степени |
|||||||
|
φ, ° |
d, мм |
t, мм |
A2 |
Q |
y |
x1 |
x2 |
x3 |
x4 |
|
45 |
15,5 |
15 |
3,56 |
239,38 |
0,61 |
– |
– |
1,69 |
–1,04 |
|
45 |
20 |
4,75 |
593,09 |
0,81 |
– |
– |
1,85 |
–1,08 |
|
|
45 |
25 |
5,93 |
1208,56 |
1,01 |
– |
– |
1,98 |
–1,11 |
|
|
45 |
30 |
7,12 |
2175,11 |
1,21 |
– |
– |
2,09 |
–1,13 |
|
|
45 |
35 |
8,30 |
3591,70 |
1,41 |
– |
– |
2,19 |
–1,14 |
|
|
60 |
15 |
2,05 |
8,06 |
0,19 |
– |
– |
1,22 |
–0,90 |
|
|
60 |
20 |
2,74 |
19,43 |
0,26 |
– |
– |
1,32 |
–0,94 |
|
|
60 |
25 |
3,42 |
38,57 |
0,33 |
– |
– |
1,42 |
–0,97 |
|
|
60 |
30 |
4,11 |
67,72 |
0,40 |
– |
– |
1,50 |
–0,99 |
|
|
60 |
35 |
4,79 |
109,23 |
0,47 |
– |
– |
1,57 |
–1,01 |
|
|
75 |
15 |
0,95 |
0,08 |
0,03 |
– |
– |
0,77 |
–0,70 |
|
|
75 |
20 |
1,27 |
0,18 |
0,04 |
– |
– |
0,84 |
–0,73 |
|
|
75 |
25 |
1,59 |
0,36 |
0,06 |
– |
– |
0,90 |
–0,76 |
|
|
75 |
30 |
1,91 |
0,63 |
0,07 |
– |
– |
0,94 |
–0,79 |
|
|
75 |
35 |
2,23 |
1,00 |
0,09 |
– |
– |
0,99 |
–0,81 |
|
|
45 |
17,5 |
15 |
3,42 |
185,86 |
0,56 |
– |
– |
1,65 |
–1,03 |
|
45 |
20 |
4,56 |
459,14 |
0,75 |
– |
– |
1,80 |
–1,07 |
|
|
45 |
25 |
5,70 |
933,07 |
0,94 |
– |
– |
1,93 |
–1,10 |
|
|
45 |
30 |
6,84 |
1675,10 |
1,12 |
– |
– |
2,04 |
–1,12 |
|
|
45 |
35 |
7,98 |
2759,67 |
1,30 |
– |
– |
2,14 |
–1,13 |
|
|
60 |
15 |
1,97 |
6,30 |
0,18 |
– |
– |
1,19 |
–0,89 |
|
|
60 |
20 |
2,63 |
15,17 |
0,24 |
– |
– |
1,29 |
–0,93 |
|
|
60 |
25 |
3,29 |
30,08 |
0,31 |
– |
– |
1,38 |
–0,96 |
|
|
60 |
30 |
3,95 |
52,75 |
0,37 |
– |
– |
1,46 |
–0,98 |
|
|
60 |
35 |
4,60 |
84,99 |
0,43 |
– |
– |
1,53 |
–1,00 |
|
|
75 |
15 |
0,92 |
0,06 |
0,02 |
– |
– |
0,75 |
–0,69 |
|
|
75 |
20 |
1,22 |
0,14 |
0,04 |
– |
– |
0,82 |
–0,72 |
|
|
75 |
25 |
1,53 |
0,28 |
0,05 |
– |
– |
0,87 |
–0,75 |
|
|
75 |
30 |
1,83 |
0,49 |
0,06 |
– |
– |
0,92 |
–0,77 |
|
|
75 |
35 |
2,14 |
0,78 |
0,08 |
– |
– |
0,97 |
–0,79 |
|
|
45 |
22 |
15 |
3,14 |
109,15 |
0,47 |
– |
– |
1,57 |
–1,01 |
|
45 |
20 |
4,18 |
268,12 |
0,63 |
– |
– |
1,71 |
–1,05 |
|
|
45 |
25 |
5,23 |
542,02 |
0,79 |
– |
– |
1,83 |
–1,08 |
|
|
45 |
30 |
6,28 |
968,31 |
0,95 |
– |
– |
1,94 |
–1,10 |
|
|
45 |
35 |
7,32 |
1587,98 |
1,10 |
– |
– |
2,03 |
–1,12 |
|
|
60 |
15 |
1,81 |
3,75 |
0,15 |
– |
– |
1,13 |
–0,86 |
|
|
60 |
20 |
2,42 |
9,00 |
0,20 |
– |
– |
1,23 |
–0,90 |
|
|
60 |
25 |
3,02 |
17,81 |
0,25 |
– |
– |
1,31 |
–0,93 |
|
|
60 |
30 |
3,62 |
31,17 |
0,31 |
– |
– |
1,39 |
–0,96 |
|
|
60 |
35 |
4,23 |
50,12 |
0,36 |
– |
– |
1,45 |
–0,98 |
|
|
75 |
15 |
0,84 |
0,04 |
0,02 |
– |
– |
0,71 |
–0,67 |
|
|
75 |
20 |
1,12 |
0,09 |
0,03 |
– |
– |
0,78 |
–0,70 |
|
|
75 |
25 |
1,40 |
0,17 |
0,04 |
– |
– |
0,83 |
–0,73 |
|
|
75 |
30 |
1,68 |
0,29 |
0,05 |
– |
– |
0,88 |
–0,75 |
|
|
75 |
35 |
1,96 |
0,47 |
0,06 |
– |
– |
0,92 |
–0,77 |
|
В таблице широко представлены возможные варианты реальных комбинаций исходных данных. Выводы, сделанные на основе анализа таблицы, вполне можно принять окончательными. Как видно из таблицы, при любых комбинациях исходных данных корни x1 и x2 отсутствуют – на самом деле они являются комплексными числами, но нас интересуют только вещественные корни. Кроме того, при любых комбинациях исходных данных корень x4 является отрицательным числом. От этого корня также следует отказаться, поскольку ранее мы производили замену $x = \sqrt h$, а подкоренное выражение не может быть отрицательным вещественным числом.
Таким образом, единственный возможный в контексте настоящей задачи корень находится из выражения, которое при любых допустимых комбинациях исходных данных позволяет получить положительное вещественное число в качестве ответа. Искомое значение глубины резания hб, при которой для заданных условий происходит переход между блокированным и полублокированным режимами резания, определяется возведением в квадрат значения этого корня:
Если текущее значение глубины резания меньше величины, полученной по формуле (5), то резание происходит в режиме блокированного резания, а если больше – полублокированного.
Моделирование разрушения горного массива с учетом текущего положения резцов, в том числе с учетом различных схем и режимов резания, осуществляется с использованием численных методов, таких как метод конечных элементов [8] и метод дискретных элементов [16]. Для корректного применения полученного результата в решении задач с использованием численных методов необходимо, чтобы значения характерных размерных величин конечных или дискретных элементов не превышали величины hб.
Следует отметить, что выражение (5) получено для идеализированной картины разрушения забоя режущим органом, не учитывающей его колебаний. Вместе с тем, как отмечалось в работе [2], размахи колебаний режущего органа могут достигать нескольких сантиметров, существенно увеличивая глубину резания, в том числе на участках 1 и 3, что вносит ошибку в определение режима резания на данных участках. В таком случае целесообразно определять не глубину резания hб, а продолжительность участков стружки, на которых наблюдается блокированное резание. Например, по углу поворота резца внутри стружки относительно точки первоначального контакта. Этот угол φб определяется как арксинус отношения hб к hmax без учета колебаний режущего органа. Тогда условие перехода между блокированным и полублокированным режимами резания трансформируется к следующему. Если текущее значение угла поворота φi резца при движении по стружке резания меньше величины φб или больше величины 180° − φб, то резание происходит в режиме блокированного резания, иначе – полублокированного.
Заключение
Из проведенного исследования можно сделать основные теоретические выводы:
- переход между блокированным и полублокированным режимами резания не зависит от прочностных свойств горной породы;
- глубина резания, при которой для заданных условий осуществляется изменение режима резания, определяется хрупко-пластическими свойствами горной породы, а также диаметром твердосплавной вставки и шагом резания.
Практическое использование полученного результата заключается в следующем. Текущее значение глубины резания h сравнивается со значением hб, полученным по формуле (5). В случае h < hб в формулу (2) для определения коэффициента Коб подставляется значение hб, иначе – h. Предложенный подход позволяет более точно в сравнении с исходным методом оценивать усилия на резце по формуле (1) на участках 1 стружки резания согласно рисунку, т.е. на участках нерациональных режимов резания.
Литература
- Барон Л.И. Разрушение горных пород проходческими комбайнами. Том 1: Научно-методические основы. Разрушение резцовым инструментом / Л.И.Барон, Л.В.Глатман, Е.К.Губенков. M.: Наука, 1968. 216 с.
- Кондрахин В.П. Математическая модель процесса стружкообразования, учитывающая осевые перемещения исполнительного органа горного комбайна / В.П.Кондрахин, В.Л.Головин // Науковi працi ДонНТУ. Серiя гiрнично-механична. 2004. Вып. 83. С. 142-149.
- Об учете неоптимальных режимов резания горных пород тангенциальными резцами / А.Б.Жабин, А.В.Поляков, Е.А.Аверин и др. // Уголь. 2019. № 7. С. 20-24. DOI: 10.18796/0041-5790-2019-7-20-24
- Проектирование фрезы стволопроходческого комбайна / Е.А.Аверин, Ю.Н.Наумов, А.Д.Смычник, Е.А.Смычник // Горный информационно-аналитический бюллетень. 2019. № 2. С. 105-113. DOI: 10.25018/0236-1493-2019-02-0-105-113
- Пути развития теории разрушения углей и горных пород резцовым инструментом / А.Б.Жабин, А.В.Поляков, Е.А.Аверин и др. // Уголь. 2019. № 9 (1122). С. 24-28. DOI: 10.18796/0041-5790-2019-9-24-28
- Состояние научных исследований в области разрушения горных пород резцовым инструментом на рубеже веков / А.Б.Жабин, А.В.Поляков, Е.А.Аверин, В.И.Сарычев // Известия Тульского государственного университета. Науки о Земле. 2018. № 1. С. 230-247.
- A new linear cutting machine for assessing the rock-cutting performance of a pick cutter / H.Kang, J.W.Cho, J.Y.Park et al. // International Journal of Rock Mechanics and Mining Sciences. 2016. Vol. 88. P. 129-136. DOI: 10.1016/j.ijrmms.2016.07.021
- A study on rock cutting efficiency and structural stability of a point attack pick cutter by lab-scale linear cutting machine testing and finite element analysis / J.Y.Park, H.Kang, J.W.Lee et al. // International Journal of Rock Mechanics and Mining Sciences. 2018. Vol. 103. P. 215-229. DOI: 10.1016/j.ijrmms.2018.01.034
- Averin E.A. Approach to Estimate Rational Parameters of Rock Destruction from a Function of a Cutting Force / E.A.Averin, A.B.Zhabin, A.V.Polyakov // IOP Conference Series: Earth and Environmental Science. 2019. Vol. 272. Iss. 2. № 022002. DOI: 10.1088/1755-1315/272/2/022002
- Balci C. Correlative study of linear small and full-scale rock cutting tests to select mechanized excavation machines / C.Balci, N.Bilgin // International Journal of Rock Mechanics and Mining Sciences. 2007. Vol. 3. № 44. P. 468-476. DOI: 10.1016/j.ijrmms.2006.09.001
- Discrete element simulation of conical pick’s coal cutting process under different cutting parameters / J.Liu, C.Ma, Q.Zeng, K.Gao // Shock and Vibration. 2018. Vol. 2018. P. 7975141. DOI: 10.1155/2018/7975141
- Dominant rock properties affecting the performance of conical picks and the comparison of some experimental and theoretical results / N.Bilgin, M.A.Demircin, H.Copur et al. // International Journal of Rock Mechanics and Mining Sciences. 2006. Vol. 43. Iss. 1. P. 139-156. DOI: 10.1016/j.ijrmms.2005.04.009
- Effect of cutting depth and line spacing on the cuttability behavior of sandstones by conical picks / X.Wang, O.Su, Q.F.Wang, Y.P.Liang //Arabian Journal of Geosciences. 2017. Vol. 10. P. 510-525. DOI: 10.1007/s12517-017-3307-3
- Experimental investigation of hard rock fragmentation using a conical pick on true triaxial test apparatus / S.Wang, X.Li, K.Du, S.Wang // Tunnelling and Underground Space Technology. 2018. Vol. 79. P. 210-223. DOI: 10.1016/j.tust.2018.05.006
- Indentation Characteristics Using Various Indenters: A Study Based on Laboratory and Numerical Tests / J.Liu, W.Wan, S.Xie, J.Wang // Geotechnical and Geological Engineering. 2019. Vol. 37. P. 4919-4931. DOI: 10.1007/s10706-019-00952-8
- Investigation on the influence mechanism of rock brittleness on rock fragmentation and cutting performance by discrete element method / L.Xuefeng, W.Shibo, G.Shirong, // Measurement. 2018. Vol. 113. P. 120-130. DOI: 10.1016/j.measurement.2017.07.043
- Li H.S. Numerical simulation on interaction stress analysis of rock with conical picks / H.S.Li, S.Y.Liu, P.P.Xu // Tunnelling and Underground Space Technology. 2019. Vol. 85. P. 231-242. DOI: 10.1016/j.tust.2018.12.014
- Loading of coal mining machine tools after change in spatial orientation of picks / V.N.Zakharov, V.Y.Linnik, Y.N.Linnik, E.A.Averin // Eurasian mining. 2018. № 1. P. 40-42. DOI: 10.17580/em.2019.01.10
- New model for predicting instantaneous cutting rate of axial-type roadheaders / Q.Zhang, Z.Han, M.Zhang, J.Zhang // KSCE Journal of Civil Engineering. 2017. Vol. 21. P. 168-177. DOI: 10.1007/s12205-016-0433-5
- Numerical simulation of rock cutting in different cutting mode using the discrete element method / Q.Q.Zhang, Z.N.Han, S.H.Ning et al. // Journal of GeoEngineering. 2015. Vol. 10. № 2. P. 35-43. DOI: 10.6310/jog.2015.10(2).1
- Prokopenko S.A. Improvement of cutting tools to enhance performance of heading machines in rocks / S.A.Prokopenko, V.S.Ludzish, I.A.Kurzina // Journal of Mining Science. 2016. Vol. 52. P. 153-159. DOI: 10.1134/S1062739116010248
- Yasar S. Rock cutting tests with a simple-shaped chisel pick to provide some useful data / S.Yasar, A.O.Yilmaz // Rock Mechanics and Rock Engineering. 2017. Vol. 50. P. 3261-3269. DOI: 10.1007/s00603-017-1303-2
