Совершенствование структуры имитационной модели тягового асинхронного электропривода рудничного электровоза

Введение. Процесс транспортировки руды с помощью электровозной тяги показывает, что условия работы оборудования определяются расположением, длиной и профилем железнодорожного пути, состоянием контактирующих поверхностей колесо-рельс, напряженностью грузопотоков и т.д. В подземных условиях чаще всего перемещают до 700 т грузов в сутки на расстояния до двух километров (93,6 %); потоки грузов более 1000 т в сутки составляют около 3 %, а на расстояния более трех километров не более 1,5 % [5]. Рабочий цикл движения подземного транспорта состоит из нескольких этапов: работа на перегонах – 28, вспомогательные и маневровые работы – 19,2, простой подвижного состава – 50 %. На режим маневрирования подземных грузовых составов и, соответственно, тяговых электроприводов тратится основное рабочее время, при этом за один час работы электровоза осуществляется более 700 переключений контроллера скорости. Следовательно, на электромеханическую систему подземного рельсового транспорта значительное влияние оказывают именно динамические режимы работы.

Постановка проблемы. По регламенту железнодорожного транспорта для горных выработок скорость груженого состава должна быть не более 9 км/ч, в том числе на участках маневрирования – 3,6-5,4 км/ч. Также существуют нормативы на предельно допустимые значения уклона или подъема рельсового пути – 3-7 ‰ (3-7 м на 1 км). Однако в случае начала движения груженого состава на подъеме из неподвижного состояния при низком значении коэффициента сцепления колес с рельсами возникает эффект буксования, т.е. появляется значительная разница между линейной скоростью ведущего колеса в точке контакта с рельсом и линейной скоростью оси ведущего колеса электровоза относительно неподвижной системы координат. Таким образом, происходит неконтролируемое увеличении скорости скольжения, приводящее к трению контактирующих поверхностей с большими потерями мощности и значительным их износом. В динамических режимах разгона и торможения с буксованием и юзом ведущих колес следует учитывать степень загрязненности поверхности рельсов, бандажей колес и их взаимный износ [4]. Показатели состояния поверхности [2]: чистые – 0,7; сухие – 2,5; покрытые водой – 1,3; погруженные в грязь – 9; засохшая грязь – 23,4; жидкая грязь – 24,7 %.

Анализ переходных процессов разгона и торможения при возникновении буксования и юза ведущих колес позволяет сделать вывод о том, что для увеличения тягового усилия рудничных электровозов следует разработать алгоритмы управления тяговыми электродвигателями [8, 10, 13].

Для решения этой задачи необходимо создать математическую модель распределенной механической системы, состоящей из электровоза и нескольких вагонеток, с учетом их загрузки, рельефа рельсового пути, а также коэффициентов сцепления колес с рельсами и трения качения.

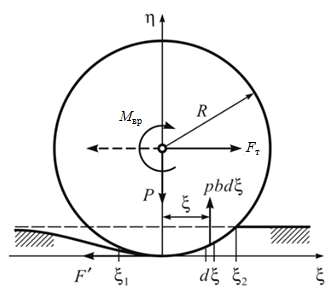
Методика исследований. Академик А.Ю.Ишлинский [3] изучил качение абсолютно жесткого колеса по частично деформируемому основанию. Для рассматриваемого случая рельсы уложены по шпалам на основании из утрамбованного щебня (рис.1).

Система уравнений равновесия сил и моментов сил относительно нижней точки колеса в плоской системе координат (ξ, η) описывает поведение системы с малой погрешностью из-за малой величины деформации поверхности рельса (плечо силы трения качения), вызванной давлением на него нагруженного колеса:

где ξ₁, ξ₂ – расстояния начала и конца соприкосновения рельса с колесом; М_вр – момент вращения; F_т – горизонтальная сила давления колеса; р(ξ) – реакции рельса на колесо; Р – вертикальная сила давления колеса на рельс; F' – сила сцепления колеса с рельсом; R – радиус колеса, b – ширина колеса.

Сила трения качения Fт ведущего колеса, к которому приложен движущий момент М_вр > 0 тягового электропривода, направлена в противоположную сторону от движения колеса и является сопротивлением электровоза, приводимого в движение ведущими колесами. При этом уравнение моментов приводит к такому соотношению:

Произведение F_тR есть момент полезного сопротивления равномерному движению. Тогда момент трения качения \(M_{вр}=\int_{\xi_1}^{\xi_2} bp(\xi)\xi d\xi=0\). Чтобы колесо пришло в движение, необходимо выполнить главное условие:

где ψ – коэффициент трения скольжения поверхности колеса; Р – вес электровоза.

Если не соблюсти условие, колесо начнет проскальзывать относительно рельса, т.е. движение электровоза за счет тяги ведущих колес всегда сопровождается наличием скорости скольжения – разницы линейных скоростей ведущих колес в точке их контакта с рельсами и скорости оси ведущей колесной пары. Продолжение такого режима приведет к значительному превышению силы трения относительно силы тяги ведущего колеса, а значит возникнет неуправляемое буксование. Таким образом, для эффективного разгона и торможения электровоза необходимо удерживать эту величину на допустимом уровне.

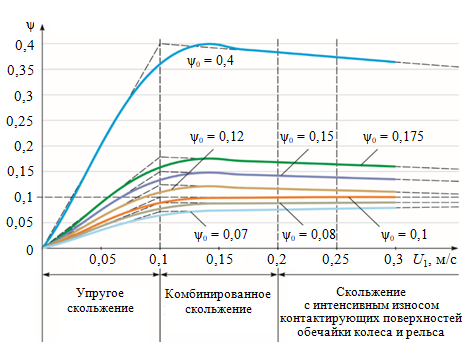
Практические исследования зависимости коэффициента трения скольжения проведены профессором А.А.Ренгевичем [7]. При проведении натурных экспериментов в подземных условиях было установлено, что при используемых материалах бандажей колес и рельсов, состоянии их контактных поверхностей, а также постоянной нагрузке на оси колесной пары и линейной скорости электровоза коэффициент сцепления ψ зависит только от скорости скольжения колеса. Данные экспериментов приведены на рис.2 в виде зависимостей в абсолютных величинах.

Полученные А.А.Ренгевичем зависимости подчиняются эмпирическим выражениям:

где \(tg\alpha=0,016-0,03 \sqrt{10\psi_0-0,7};\) ψ – коэффициент сцепления; ψ₀ – потенциальный коэффициент сцепления; U – скорость скольжения; U₀ = 0,1 м/с – рекомендуемая величина скольжения.

На участке упругого скольжения коэффициент сцепления имеет линейный возрастающий характер от нуля до максимального значения ψ = 0-ψ₀, на участке комбинированного скольжения и далее при коэффициенте трения ψ₀ > 0,1 (чистые и сухие рельсы) медленно уменьшается, а при ψ₀ < 0 медленно возрастает, приближаясь к значению ψ₀ = 0,1.

Обеспечить значительный рост тягового усилия на сцепке электровоза за счет увеличения его собственного веса не представляется возможным при малых значениях коэффициента трения скольжения (загрязненные рельсы). Увеличение мощности тяговых двигателей не дает эффекта из-за того, что излишний тяговый момент, приложенный к ведущим колесам, вызывает их неконтролируемое буксование относительно рельсов при достаточно малом коэффициенте сцепления. В настоящее время основным способом увеличения коэффициента сцепления является подсыпка песка под ведущие колеса. Очень быстро песок под действием проходящих груженых составов измельчается, и трение скольжение уменьшается в 2-2,5 раза. Необходимость регулярно убирать загрязненный песок с путей только осложняет ситуацию.

В течение нескольких лет различными коллективами ученых, специалистов в области подвижного состава под руководством профессоров В.В.Процива, А.А.Сердюка и других были проведены эксперименты по установлению зависимости коэффициента сцепления ведущих колес рудничных электровозов от скорости скольжения [3, 9, 11]. Экспериментальные данные подтверждают результаты аналитических исследований [12, 19]. Установлено, что коэффициент трения скольжения и, соответственно, сцепление ведущих колес с рельсами могут изменяться в широких пределах, сопровождаясь появлением неэффективных режимов буксования и юза [14-17].

В математической модели подземного электровоза учитывались: момент изгиба относительно центра массы при возникновении тяговых усилий; упругое крепление корпусного элемента локомотива; размеры зазоров в сцепках подвижного состава между собой, а также с тяговым электровозом. Данная механическая система рассматривалась как система с распределенными параметрами. Электромеханическая часть локомотива представлена двумя колесными парами (КП) с тяговым электроприводом. Механическая часть представляет собой систему локомотива совместно со сцепкой из 12 вагонеток. Для измерения скорости движения был применен метод прямого измерения скорости движения состава с помощью датчика скорости на ведомой оси.

Электрическая часть системы состоит из двух тяговых асинхронных двигателей (ТАД) с управлением от индивидуальных преобразователей частоты с векторным управлением. Рассматривается такая система дифференциальных уравнений, которая учитывает ориентацию вектора потокосцепления ротора \(\Psi_{r_x}=\vert \bar{\Psi_{r_{ном}}}\vert,\Psi_{r_y}=0,\) на ось x координат подвижной системы x, y [1, 19].

Механическая часть включает массу электровоза, массы 12 вагонеток, обладающими двухсоставными упругими связями с демпфированием. Динамика механической части описывается системой уравнений [6, 18]:

где U_i – избыточная скорость скольжения i-й КП; \(F_{сц_i}\) – сила сцепления i-й колесной пары; \(v_{эв}\) – величина линейной скорости электровоза; \(v_{k_i}\) – величина линейной скорости на ободе колеса; ψ(U) – коэффициент сцепления; P – вес локомотива; R – радиус колеса; \(M_{i}\) – момент КП; \(F_{n}\) – сила n-го вагона; \(m_{эв}\) – масса локомотива; \(\alpha\) – угол наклона пути; \(\omega_i\) – угловая частота вращения КП; \(\frac{h}{l}\) – отношение высоты сцепки от головки рельса к расстоянию между осями КП; i = 1-m, n = 1-l; l – количество вагонов; m – количество КП.

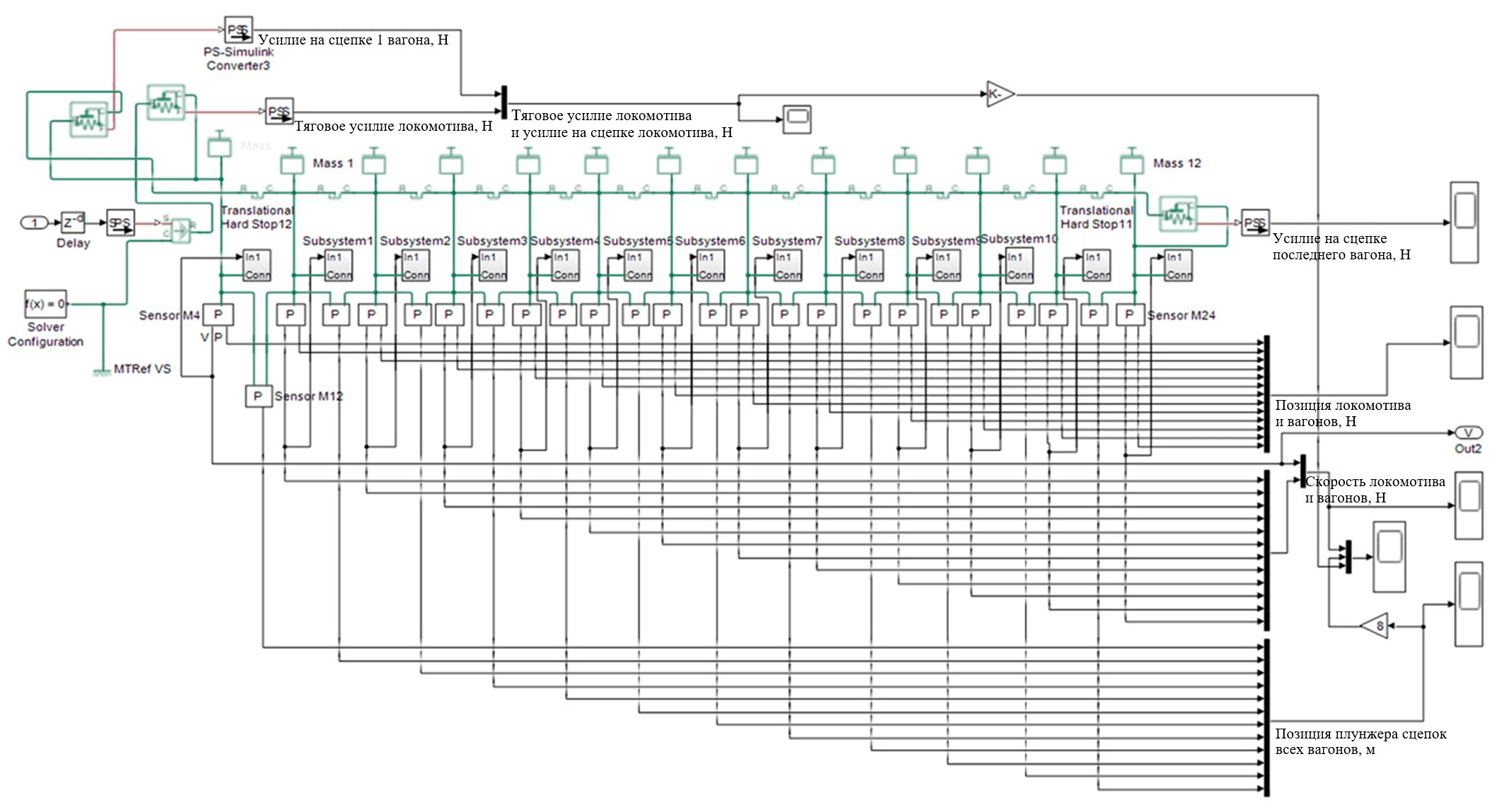
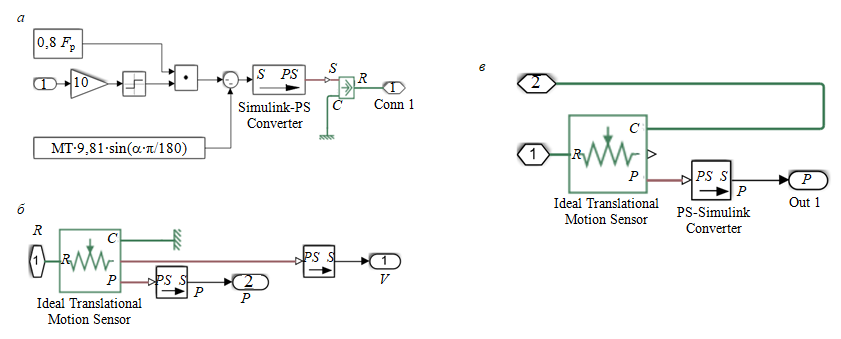
На базе математической модели впервые предложена структура имитационной модели распределенной механической системы подвижного состава. Основу имитационной модели составляют массы локомотива Mass (14 т) и 12 вагонов по 10 т Mass 1-12, которые соединяются плунжерной сцепкой. Это позволяет изменять тяговое усилие на величину усилия сопротивления движению вагона для каждого последующего вагона. Параметры заданы в пределах \(±\)0,025 м для диапазона позиции плунжера сцепки. Датчики скорости, перемещения массы и перемещения плунжера сцепки представлены на рис.3.

Контактная жесткость и коэффициент демпфирования приняты как 108 Н/м и 106 Н/(м/с) соответственно в верхнем и нижнем упоре. В подсистемах 0-12 формируются как активная сила F_a (от уклона пути), так и реактивные силы сопротивления движению F_p (рис.4).

Для обеспечения высокой эффективности работы необходимо обозначить принципы построения алгоритма управления:

1. Поскольку скорость скольжения имеет случайный характер и зависит от разных факторов, управление должно быть индивидуальным для каждой колесной пары.

2. Основная управляемая величина – линейная скорость движения, поэтому должна существовать закономерная связь при управлении скоростью скольжения и линейной скоростью. Главным критерием эффективности является точность стабилизации диапазона скорости

3. Коэффициент сцепления растет в зоне упругого скольжения от нуля до почти максимального значения, поэтому скорость скольжения поддерживается меньше 0,1 м/с для режимов малой тяги.

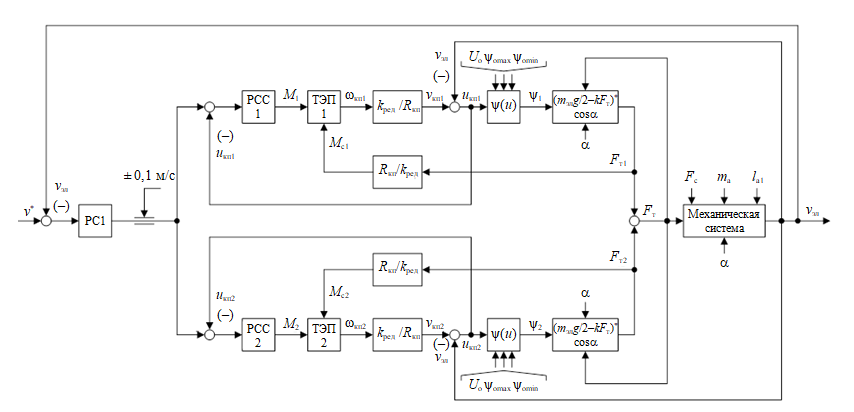
4. При значениях комбинированного скольжения менее 0,1 м/с возникает максимум коэффициента сцепления. Превышение этих границ приводит к потерям электроэнергии, износу рельсового пути и бандажей колес. Участок перехода между режимами размыт в силу вероятностного характера процессов трения. В различных источниках часто упоминается приближение вероятности к 100 %, скольжение имеет комбинированный характер при скорости 0,12 м/с, т.е. для моделирования принимается предельная скорость вращения за 0,1 м/с. Разработанная функциональная схема системы управления двухдвигательным тяговым электроприводом (ТЭП) представлена на рис.5.

Функциональная схема системы регулирования состоит из внешнего основного контура регулирования линейной скорости \(v_{эв}\), двух внутренних подчиненных контуров регулирования скорости скольжения двух КП \(v_{1}\), \(v_{2}\). Основные элементы – блок ограничения сигнала регулятора линейной скорости (РС) локомотива в пределах \(\pm\)0,1 м/с и два регулятора скорости скольжения РСС1, РСС2. Таким образом обеспечивается работа ТЭП1, ТЭП2 при максимальной тяге в режимах упругого и комбинированного скольжения.

При выполнении алгоритма в первую очередь производится вычисление разности желаемой скорости \(v^{*}\) и линейной фактической скорости \(v_{эв}\), которая передается на ПИ-регулятор линейной скорости локомотива. Далее сигнал преобразуется в сигнал задания скорости скольжения для двух КП в виде \(u_{1}^{*}\),\(u_{2}^{*}\) с ограничением диапазона 0,1 м/с.

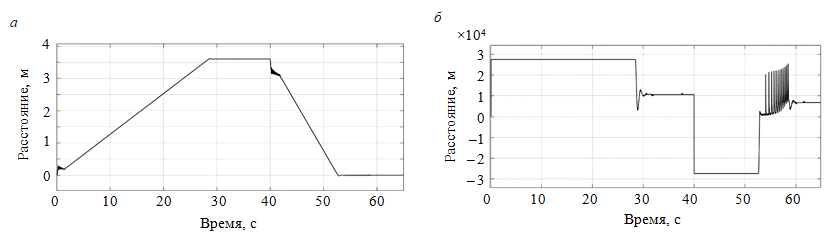
Результаты. Практические результаты моделирования системы регулирования представлены диаграммами в нескольких режимах, включающих разгон, равномерное движение и торможение (рис.6). В диаграммах скорости и тягового усилия отражаются три характерных участка, в отличие от известных имитационных моделей.

С первых секунд начала движения происходит сцепка электровоза со всеми вагонами. Далее состав (134 т) разгоняется до скорости 3,6 м/с в течении 29 с, что не противоречит исследованиям [6]. После равномерного движения с заданной скоростью (3,6 м/с) происходит торможение с 40-й секунды в течении 12,5 с до полного останова, при этом возникают небольшие колебания скорости (40-42 с) из-за смещения плунжеров сцепок.

Далее при нулевой скорости в интервале 53-58 с наблюдаются 12 рывков скорости электровоза, связанные с переключением сцепных устройств под воздействием скатывающей силы, направленной против движения, так как локомотив движется на подъем. Аналогичные импульсы повышения тяговых усилий возникают в процессе удержания состава на нулевой скорости до установившихся значений силы тяги в покое.

Выводы.

1. Определен критерий управления тяговым асинхронным электроприводом с контролем допустимой величины скорости скольжения ведущих колес относительно рельсового пути.

2. Предложен закон управления и структура системы управления тяговым электроприводом рудничного электровоза на основе контроля скорости скольжения для исключения нежелательных режимов буксования при разгоне и юзе колесных пар электровоза в процессе торможения.

3. Разработана имитационная модель электромеханической системы подвижного состава с распределенными параметрами, отличающаяся от известных наличием сцепки, а также введением дополнительных устройств механической системы для учета их влияния на процессы движения вагонов на участках пути с переменным профилем.

4. Практическое применение предлагаемого способа управления асинхронными тяговыми электроприводами подземного электровоза заключается в возможности трогания тяжело груженного состава с места на участке подъема в условиях недостаточного сцепления при загрязненных путях. Это позволит реже подсыпать песок под ведущие колесные пары электровоза и снизить затраты на уборку песка с рельсового пути и его утилизацию.

Литература