Traction asynchronous electric drive of mine electric locomotivesimulation model structure improvement
Abstract
The article discusses the solution to the problem of underground railway transport slipping in dynamic modes, which occurs when there is a significant difference in the speeds of the driving and driven pairs of wheels. The state of the rail surfaces largely determines the coefficient of adhesion, therefore, using a mathematical model, the condition for the dependence of the magnitude of slipping and tractive effort is selected. For effective acceleration and deceleration of an electric locomotive, it is necessary to control the coefficient of adhesion at a certain level. A simulation model of rolling stock has been created, which for the first time takes into account a mechanical system with distributed parameters. In the structural diagram of the automatic control system of traction electric drives with frequency regulation, such factors as the volume of goods being moved, rolling friction, slope (rise) levels and the state of the rail track are taken into account. The simulation results show the features of the movement and stops of the freight train not only by the diagrams of speed and forces in the modes of acceleration-deceleration and uniform movement, but also the positions of the plungers and tractive forces on the couplings of the electric locomotive and all trolleys involved in the movement of goods. The practical application of the proposed method lies in the possibility of starting a heavily laden train from its place on the ascent section in conditions of insufficient adhesion coefficient with contaminated roads.
Introduction. The process of transporting ore using electric locomotive traction shows that the operating conditions of the equipment are determined by the location, length and profile of the railway track, the state of the wheel-rail contacting surfaces, the intensity of freight flows, etc. Inunderground conditions, up to 700 tons of cargo per day are most often moved over distances of up to two kilometers (93.6 %); cargo flows of more than 1000 tons per day are about 3 %, and at distances of more than three kilometers no more than 1.5 % [5]. The working cycle of the underground transport movement consists of several stages: work on the tracks – 28, auxiliary and shunting works – 19.2, idle rolling stock – 50 %. The main working time is spent on the mode of maneuvering underground freight trains and, accordingly, traction electric drives, while more than 700 switches of speed controller are performed per one hour of electric locomotive operation. Consequently, it is the operation dynamic modes that have a significant impact on the electromechanical system of underground rail transport.
Formulation of problem. According to the regulations of railway transport for mine workings, the speed of a loaded train should be no more than 9 km/h, including 3.6-5.4 km/h in maneuvering sections. There are also standards for the maximum permissible slope or rise values of the rail track – 3-7 ‰ (3-7 m per 1 km). However, in the case movement start of the loaded train on the rise from a stationary state with a low value of the adhesion coefficient of the wheels to the rails, the effect of slipping occurs, i.e., there is a significant difference between the linear speed of the driving wheel at the point of contact with the rail and the linear speed of the driving wheel of the electric locomotive axis relative to the stationary coordinate system. Thus, an uncontrolled increase in slipping speed occurs, leading to friction of the contacting surfaces with large losses of power and significant wear. In dynamic modes of acceleration and braking with slipping and skidding of the driving wheels, one should take into account the degree of surface of the rails contamination, wheel rims and their mutual wear. [4]. Surface condition indicators [2]: clean – 0.7; dry – 2.5; covered with water – 1.3; immersed in mud – 9; dried mud – 23.4; liquid mud – 24.7 %.
The analysis of the transient processes of acceleration and deceleration in the event of slipping and skidding of the driving wheels allows us to conclude that in order to increase the tractive effort of mine electric locomotives, it is necessary to develop control algorithms for traction electric motors [8, 10, 13].
To solve this problem, it is necessary to create a mathematical model of a distributed mechanical system, consisting of an electric locomotive and several trolleys, taking into account their load, the topography of the track, as well as the coefficients of adhesion of wheels to rails and rolling friction.
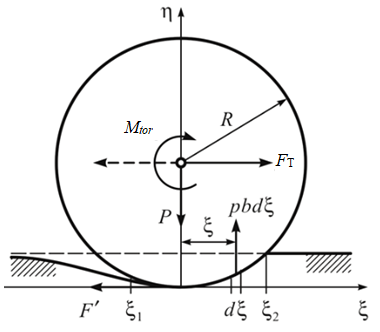
Methodology. Academician A.Yu.Ishlinsky [3] studied the rolling of an absolutely rigid wheel on a partially deformable base. For the considered case, the rails are laid along the sleepers on the basis of compacted rubble (Fig.1).
The system of equations for the equilibrium of forces and moments of forces relative to the lower point of the wheel in a plane coordinate system (ξ, η) describes the behavior of the system with a small error due to the small amount of deformation of the rail surface (arm of the rolling friction force) caused by the pressure of the loaded wheel on it:
where ξ1, ξ2 – distances of the beginning and end of the rail with the wheel contact; Мtor – torque; Fт – horizontal wheel pressure force; р(ξ) – rail-to-wheel reactions; Р – vertical force of wheel pressure on the rail; F' – wheel-to-rail adhesion; R – wheel radius, b – wheel width.
The rolling friction force Fт of the driving wheel, to which the driving moment Мtor > 0 of the traction electric drive is applied, is directed in the opposite direction from the wheel movement and is the resistance of the electric locomotive driven by the driving wheels. In this case, the equation of moments leads to the following relation:
The product FтR is the moment of useful resistance to uniform motion. Then the rolling friction moment \(M_{tor}=\int_{\xi_1}^{\xi_2} bp(\xi)\xi d\xi=0\). For the wheel to start moving, the main condition must be met:
whereе ψ – slipping friction coefficient of the wheel surface; Р – electric locomotive weight.
If the condition is not met, the wheel will begin to slip relative to the rail, i.e. the movement of an electric locomotive due to the traction of the driving wheels is always accompanied by the presence of a slipping speed – the difference between the linear speeds of the driving wheels at the point of their contact with the rails and the speed of the axle of the driving wheel pair. Continuation of this mode will lead to a significant excess of the friction force relative to the traction force of the drive wheel, which means uncontrolled slipping will occur. Thus, for effective acceleration and deceleration of an electric locomotive, it is necessary to keep this value at an acceptable level.
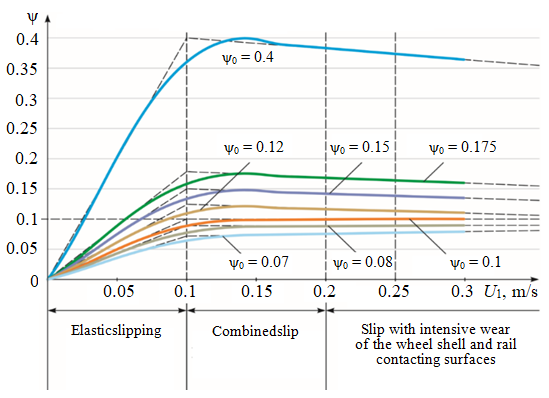
Practical studies of the dependence of the slipping friction coefficient were carried out by Professor A.A.Rengevich [7]. When carrying out full-scale experiments in underground conditions, it was found that with the materials used for the tires of wheels and rails, the state of their contact surfaces, as well as the constant load on the axle of the wheelset and the linear speed of the electric locomotive, the coefficient of adhesion ψ depends only on the slipping speed of the wheel. The experimental data are shown in Fig.2 in the form of dependences in absolute values.
The dependences obtained by A.A.Rengevich obey the empirical expressions:
where \(tg\alpha=0,016-0,03 \sqrt{10\psi_0-0,7};\) ψ – adhesion coefficient; ψ0 – potentialadhesion coefficient; U – slipping speed; U0 = 0,1 м/с – recommended slip value.
In the section of elastic slipping, the coefficient of adhesion has a linear increasing character from zero to the maximum value ψ = 0-ψ0, in the area of combined slipping and further with the friction coefficient ψ0 > 0,1 (clean and dry rails)decreases slowly, and at ψ0 < 0 slowly increases, approaching the value ψ0 = 0,1.
It is not possible to provide a significant increase in the tractive effort on the coupling of an electric locomotive by increasing its own weight at low values of the slipping friction coefficient (dirty rails). An increase in the power of traction motors does not give an effect due to the fact that an excessive traction moment applied to the driving wheels causes them to slip uncontrollably relative to the rails with a sufficiently low coefficient of adhesion. Currently, the main way to increase the coefficient of adhesion is to add sand under the drive wheels. Very quickly the sand under the action of passing coarse compositions is crushed, and the slipping friction reduce by 2-2.5 times. The need to regularly remove contaminated sand from the tracks only complicates the situation.
For several years, various teams of scientists, specialists in the field of rolling stock under the guidance of professors V.V.Protsiv, A.A.Serdyuk and others have carried out experiments to establish the dependence of the adhesion coefficient of the driving wheels of mine electric locomotives on the slipping speed [3, 9, 11]. Experimental data confirms analytical results [12, 19]. It has been established that the slipping friction coefficient and, accordingly, the adhesion of the driving wheels to the rails can vary over a wide range, accompanied by the appearance of ineffective slipping and skidding modes [14-17].
In the mathematical model of an underground electric locomotive, the following were taken into account: the moment of bending relative to the center of mass when traction forces occur; elastic fastening of the locomotive body element; the dimensions of the gaps in the couplings of the rolling stock with each other, as well as with the traction electric locomotive. This mechanical system was considered as a system with distributed parameters. The electromechanical part of the locomotive is represented by wheelsets pairs (WP) with a traction electric drive. The mechanical part is a locomotive system together with a coupling of 12 trolleys. To measure the speed of movement, the method of direct measurement of the speed of the train was applied using a speed sensor on the driven axle.
The electrical part of the system consists of two traction asynchronous motors (TAM) controlled by individual frequency converters with vector control. A system of differential equations is considered that takes into account the orientation of the rotor flux linkage vector \(\Psi_{r_x}=\vert \bar{\Psi_{r_{ном}}}\vert,\Psi_{r_y}=0,\) on the x-axis of the coordinates of the moving system x, y [1, 19].
The mechanical part includes the mass of the electric locomotive, the mass of 12 trolleys, which have two-piece elastic connections with damping. The dynamics of the mechanical part is described by the system of equations [6, 18]:
where Ui – excess slipping speed of ith WP; \(F_{ad_i}\) – adhesion force of the ith wheelset; \(v_{EL}\) – the electric locomotive linear speed value; \(v_{wh_i}\) – the linear speed value at the wheel rim; ψ(U) – adhesion coefficient; P – electric locomotive weight; R – wheel radius; \(M_{i}\) – WP torque; \(F_{n}\) – nth railway carriage force; \(m_{EL}\) – electrical locomotive weight; \(\alpha\) – track angle; \(\omega_i\) – WP velocity; \(\frac{h}{l}\) – the ratio of the hitch height from the rail head to the distance between the gearbox axles of WP; i = 1-m, n = 1-l; l – railway carriage number; m – WP number.
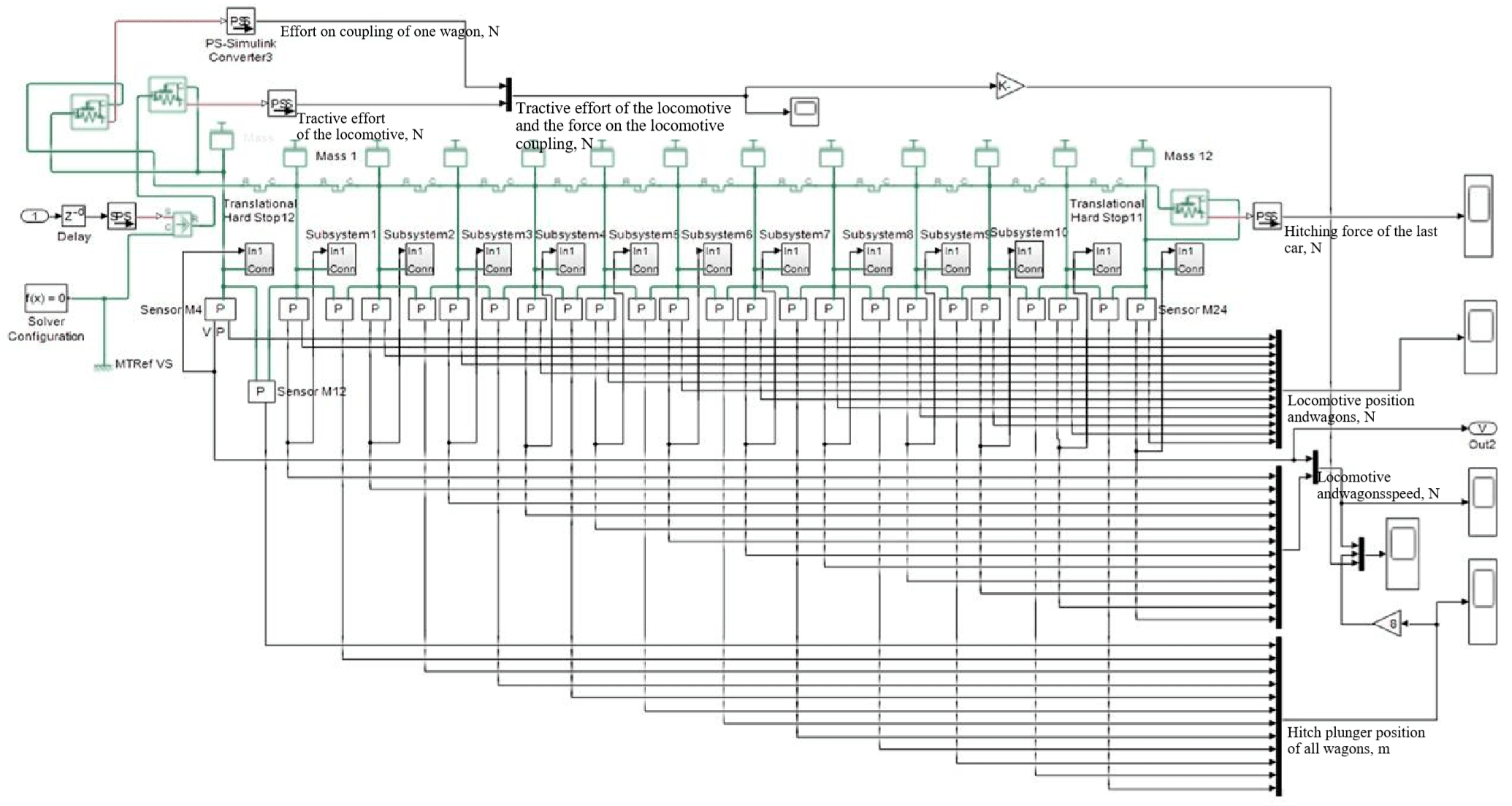
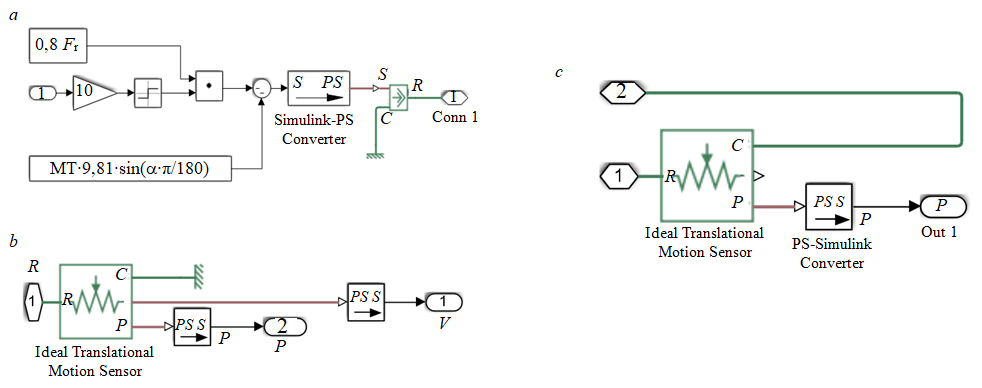
On the basis of a mathematical model, for the first time the structure of a simulation model of a distributed mechanical system of a rolling stock is proposed. The basis of the simulation model is the masses of the Mass locomotive (14 t) and 12 wagons of 10 t Mass 1-12, which are connected by a plunger coupling. This allows to change the tractive effort by the amount of resistance to the movement of the car for each subsequent car. The parameters are set within \(±\)0,025 m for the hitch plunger position range. The sensors for speed, mass displacement and displacement of the hitch plunger are shown in Fig.3.
Contact stiffness and damping coefficient are taken as 108 N/m and 106 N/(m/s), respectively, in the upper and lower stops. In subsystems 0-12, both the active force Fa (from the slope of the path) and the reactive forces of resistance to motion Fp are formed (Fig.4).
To ensure high efficiency, it is necessary to outline the principles of construction of the control algorithm:
1. Since the slipping speed is random and depends on various factors, the control must be individual for each wheelset.
2. The main controlled variable is the linear speed of movement, therefore, there must be a natural connection when controlling the slipping speed and linear speed. The main criterion of efficiency is the accuracy of stabilization of the slipping speed range.
3. The adhesion coefficient increases in the elastic slipping zone from zero to almost maximum value, so the slipping speed is kept below 0.1 m/s for low thrust modes.
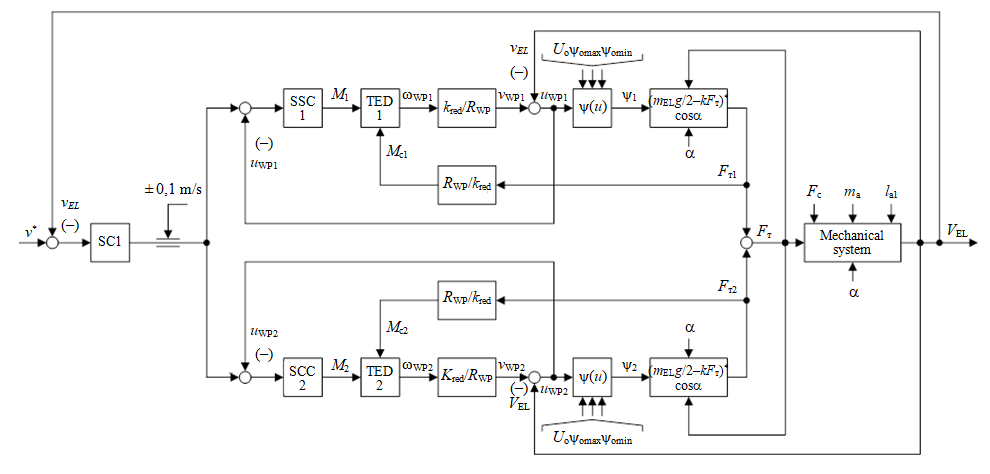
4. When combined slip values are less than 0.1 m/s, a maximum adhesion coefficient occurs. Exceeding these limits leads to losses of electricity, wear of the track and wheel rims. The section of the transition between the modes is blurred due to the probabilistic nature of the friction processes. In various sources, the probability approaching 100 % is often mentioned; slip has a combined character at a speed of 0.12 m/s, i.e. for simulation the limiting rotation speed is taken as 0.1 m/s. The developed functional diagram of the control system for a two-engine traction electric drive (TED) is shown in Fig.5.
The functional diagram of the control system consists of an external main loop for linear speed control \(v_{EL}\), two internal slave control loops of slipping speed of two WP \(v_{1}\), \(v_{2}\). The main elements are a block for limiting the signal of the linear speed controller (SC) of the locomotive within \(\pm\)0,1 м/s and two slip speed controllers SSC1, SSC2. This ensures the operation of TED1, TED2 at maximum thrust in the modes of elastic and combined slipping.
When executing the algorithm, first of all, the difference of the desired speed \(v^{*}\) and the actual linear speed \(v_{EL}\), which is transmitted to the PI-controller of the locomotivelinear speed are calculated. Further, the signal is converted into a signal for setting the slipping speed for two WPs in the form of \(u_{1}^{*}\),\(u_{2}^{*}\) with limited range of 0.1 m/s.
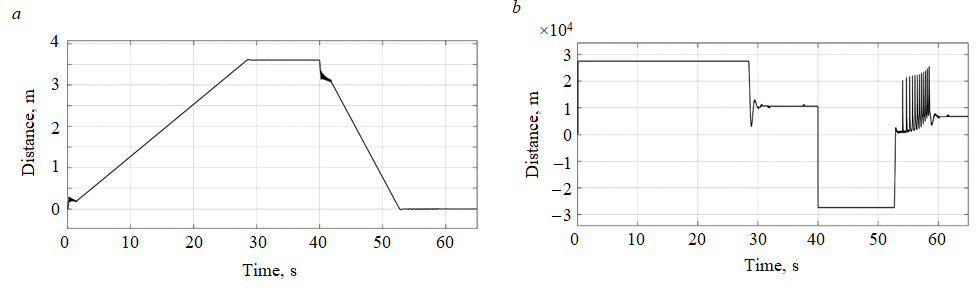
Results. The practical results of modeling the control system are presented by diagrams in several modes, including acceleration, uniform movement and braking (Fig.6). In the diagrams of speed and tractive effort, three characteristic areas are reflected, in contrast to the known simulation models.
From the first seconds of the start of movement, the electric locomotive is coupled with all the cars. Further, the train (134 t) accelerates to a speed of 3.6 m/s for 29 s, which does not contradict the research [6]. After a uniform movement at a given speed (3.6 m/s), braking occurs from the 40th second for 12.5 s to a complete stop, while small fluctuations in speed (40-42 s) occur due to the displacement of the plunger couplings.
Further, at zero speed in the interval of 53-58 s, 12 jerks of the speed of the electric carriage are observed, associated with the switching of the coupling devices under the influence of the rolling force directed against the movement, since the locomotive is moving uphill. Similar impulses of increasing tractive effort arise in the process of keeping the train at zero speed until the steady values of the traction force at rest.
Conclusion.1. The criterion for the control of the traction asynchronous electric drive with the control of the permissible value of the slipping speed of the driving wheels relative to the rail track has been determined.
2. A control law and the structure of a control system for a traction electric drive of a mine electric locomotive based on slipping speed control to eliminate unwanted slipping modes during acceleration and skidding of an electric locomotive wheelsets during braking are proposed.
3. A simulation model of the electromechanical system of rolling stock with distributed parameters has been developed, which differs from the known ones by the presence of a coupling, as well as the introduction of additional devices of the mechanical system to take into account their influence on the processes of movement of cars on track sections with a variable profile.
4. The practical application of the proposed method for controlling asynchronous traction electric drives of an underground electric locomotive lies in the possibility of starting a heavily laden train from its place on the ascent section in conditions of insufficient adhesion with contaminated tracks. This will make it possible to sprinkle sand under the driving wheelsets of an electric locomotive less often and reduce the cost of cleaning sand from the rail track and its disposal.