Интерпретируемое машинное обучение для определения негерметичности скважин
- 1 — инженер 1 категории Институт «ТатНИПИнефть» ПАО «Татнефть» имени В.Д.Шашина ▪ Orcid ▪ Elibrary
- 2 — д-р техн. наук директор по повышению нефтеотдачи пластов, волновым и биотехнологиям Институт «ТатНИПИнефть» ПАО «Татнефть» имени В.Д.Шашина ▪ Orcid
Аннотация
Вопрос своевременной и точной оценки технического состояния скважин становится все более актуальным в условиях разработки месторождений на поздней стадии, высокой обводненности продукции и увеличения доли стареющего фонда скважин. Для диагностики эксплуатационной колонны традиционно применяются геофизические методы, позволяющие выявить наличие повреждений и определить их интервал, но значительная загрузка специалистов на месторождениях препятствует оперативной отправке геофизических партий для проверки состояния скважин. Это приводит к потере добычи нефти, росту обводненности, негативному воздействию на окружающую среду, увеличению объемов непродуктивной закачки и снижению ключевых экономических показателей. Для решения этих проблем предложен новый подход к оценке технического состояния колонн, основанный на применении моделей машинного обучения. Представлены методика применения интерпретируемого машинного обучения для диагностики негерметичности эксплуатационных колонн скважины и сравнение данного подхода с методом статистического анализа ROC-AUC. Разработанный подход объединяет алгоритм машинного обучения LightGBM и методы SHAP-анализа, что позволяет оценивать вклад ключевых факторов в прогнозирование состояния скважины и определять их граничные значения. Для обучения модели использованы данные 14318 скважинных исследований, проведенных с 2000 по 2022 гг. Результаты показывают, что наиболее значимыми признаками являются содержание сульфатов, коэффициент перенасыщения раствора и обводненность продукции. Исследование подтверждает эффективность методов интерпретируемого машинного обучения в задачах диагностики сложных технических объектов. Полученные результаты демонстрируют потенциал внедрения таких моделей в практику мониторинга состояния скважин и планирования ремонтных работ. Предложенный подход также может быть адаптирован для других задач нефтегазовой отрасли, включая прогнозирование осложнений и оптимизацию работы скважин.
Введение
Проблема негерметичности эксплуатационных колонн скважин (НЭК) остается одной из наиболее актуальных при разработке нефтяных месторождений. Нарушение целостности колонны приводит к снижению дебита нефти, увеличению обводненности и существенным экологическим рискам [1]. Для диагностики НЭК традиционно используются геофизические методы, химический анализ воды и математическое моделирование [2-4]. Однако эти методы обладают рядом недостатков – высокая стоимость, сложность интерпретации данных и длительное время выполнения исследований [5, 6]. Магнитно-импульсная дефектоскопия имеет ограничения при высоких температурах и давлении, что снижает ее эффективность в сложных условиях эксплуатации [5], а тепловая конвекция требует точной калибровки и специализированного оборудования, что увеличивает затраты на диагностику [6]. В связи с этим возникает необходимость внедрения современных технологий для диагностики негерметичности, в частности методов машинного обучения, которые позволяют повысить точность прогнозов и оперативность выявления нарушений.
Геофизические исследования, такие как шумометрия, термометрия и акустический каротаж, являются наиболее распространенными методами диагностики НЭК, например трассерные исследования позволяют эффективно локализовать заколонные перетоки [7].
Анализ химического состава попутно добываемой воды является альтернативным и более доступным методом диагностики. Изменения в концентрации химических компонентов, таких как сульфаты и хлориды, могут указывать на заколонные перетоки и проникновение флюидов из других горизонтов [8]. Водонефтяное отношение и анализ обводненности продукции являются важными индикаторами нарушения герметичности колонн [9, 10], тем не менее в условиях сложных геохимических разрезов данный метод уступает геофизическим подходам по точности.
Применение математического моделирования позволяет прогнозировать развитие заколонных перетоков и оптимизировать ремонтно-изоляционные работы. В статье [11] представлены модели, учитывающие динамику процессов в период ожидания затвердевания цемента. В работе [12] предложен инновационный метод проведения изоляционных работ, который позволяет минимизировать экономические риски и повысить эффективность изоляции. Таким образом, сочетание геофизических методов, химического анализа и математического моделирования создает основу для комплексной диагностики НЭК. Однако недостатки традиционных методов требуют внедрения более инновационных подходов, таких как машинное обучение. Методы машинного обучения позволяют анализировать большие массивы данных, учитывать нелинейные зависимости и повышать точность прогнозирования параметров разработки [11-14], активно применяются для прогнозирования дебита нефти, пластового давления и других параметров. В статье [11] представлена методика прогнозирования пластовых свойств нефти с использованием нейросетей. Авторы статьи [14] усовершенствовали традиционные методы анализа кривых падения добычи, применив алгоритмы случайного леса и градиентного бустинга, что позволило повысить точность прогнозов. В работе [15] предложен метод восстановления давления на приеме насоса в скважинах с установкой электроцентробежного насоса на основе анализа обводненности и других параметров.
В статье [16] рассматривается многоцелевая регрессия на основе алгоритма случайного леса для прогнозирования добычи сланцевого газа. Использование ансамблевых подходов, таких как ElasticNet и XGBoost, показало высокую точность в краткосрочном прогнозировании дебита скважин [17-19]. Для обработки временных рядов применяются нейронные сети с долгой краткосрочной памятью (LSTM), позволяющие учитывать долгосрочные зависимости в данных [20-22].
Оптимизация технологических режимов работы скважин является еще одним перспективным направлением применения машинного обучения. В статье [23] описан гибридный метод, объединяющий нейросети и алгоритм оптимизации роя частиц, что позволило повысить точность оценки производительности скважин. Модели машинного обучения также применяются для интегрированного моделирования скважин, где забойное давление моделируется в зависимости от динамических параметров [24].
В исследованиях [25, 26] предложена система прогнозирования оптимальных режимов нагнетательных скважин, которая позволяет максимизировать добычу нефти. Глубокое обучение используется для совместного предсказания добычи нефти, газа и воды, а также других динамических показателей разработки месторождений, что особенно актуально для нетрадиционных месторождений [27, 28].
Методы машинного обучения активно применяются для прогнозирования осложнений и аварийных ситуаций. В статье [29] представлен пилотный проект по прогнозированию инцидентов на нагнетательных скважинах, включая заколонные перетоки, нештатные изменения давления и выход оборудования из строя, с использованием алгоритмов машинного обучения. Применение нейросетей для выявления аномального поведения технологических параметров при бурении описано в работах [30-32]. Кроме того, методы машинного обучения используются для автоматизации процессов [33, 34] и оптимизации размещения скважин. В статье [35] предложена модель обучения с подкреплением для оптимального проектирования сетки скважин. Применение методов машинного обучения для обработки данных геофизических исследований с целью определения литологических типов описывается в статье [36]. В статье [37] рассматриваются PVT-свойства (давление, объем, температура) флюидов, которые определяются с применением моделей на основе искусственного интеллекта, нейронные сети и машинное обучение используются для моделирования зависимостей.
Ряд зарубежных статей посвящен изучению негерметичности скважины с использованием методов машинного обучения. Например, в статье [38] модели машинного обучения были использованы для анализа нарушений целостности скважин в системах механизированной добычи, в исследованиях [39, 40] машинное обучение используется для прогнозирования качества воды, позволяя не только выявлять изменения в химическом составе, но и снижать неопределенность моделей благодаря современным методам обработки данных и анализа временных изменений.
Современные методы машинного обучения позволяют значительно повысить точность прогнозирования динамических параметров разработки, оптимизировать режимы работы скважин и автоматизировать процессы. Их применение в сочетании с традиционными геофизическими и химическими методами обеспечивает комплексный подход к решению проблемы негерметичности эксплуатационных колонн скважин.
Целью данного исследования является определение абсолютных значений признаков, влияющих на возникновение негерметичности эксплуатационных колонн, с использованием методов интерпретируемого машинного обучения, а также анализ фактических результатов работы модели.
Методологическая основа исследования частично опирается на подходы, представленные в работах [41, 42], где рассмотрен процесс создания и тестирования модели машинного обучения, а также ключевые признаки, влияющие на состояние эксплуатационной колонны, включая химический состав воды, возраст скважины и динамику работы.
Настоящее исследование развивает предложенную методику путем более глубокого анализа интерпретируемости моделей машинного обучения. В качестве инструментов для оценки влияния признаков на предсказания используются методы SHAP-анализа [43], что позволяет не только определить значимые факторы, но и выявить их граничные значения, превышение которых коррелируется с ростом вероятности возникновения негерметичности.
Также в задачи исследования входит сравнение значений признаков, полученных на основе статистического анализа промысловых данных и результатов интерпретации модели машинного обучения.
Методология
В промысловых условиях одним из первичных способов выявления отклонений в продукции является отбор проб на химический (шестикомпонентный) анализ воды, который заключается в определении концентрации шести основных ионов: натрий, кальций, магний, хлор, гидрокарбонаты и сульфаты. По изменению шестикомпонентного состава попутно добываемой воды производится предварительная оценка герметичности эксплуатационных колонн добывающих скважин. На рис.1 приведены примеры химического анализа проб попутно добываемой воды по скважинам месторождения N.
Графики анализа проб добываемой воды (рис.1) показывают, что содержание компонентов и общая минерализация по скважинам с негерметичной колонной в разы превышает значение по скважинам с герметичной колонной. Таким образом, химический анализ попутно добываемой воды стал одним из факторов, способствующих определению негерметичности эксплуатационной колонны скважины по сильному отклонению параметров от нормы.
Одним из показателей, которые применяются для определения наличия негерметичности скважин, является отношение Cl/Ca. Анализ значений данного показателя, характерных для скважин с герметичной и негерметичной колонной, приведен в статье [42]. Это пример определения негерметичности по скважине. Таких подходов может быть большое количество, и для изучения отношения концентраций веществ компонентного состава требуется много времени и средств.
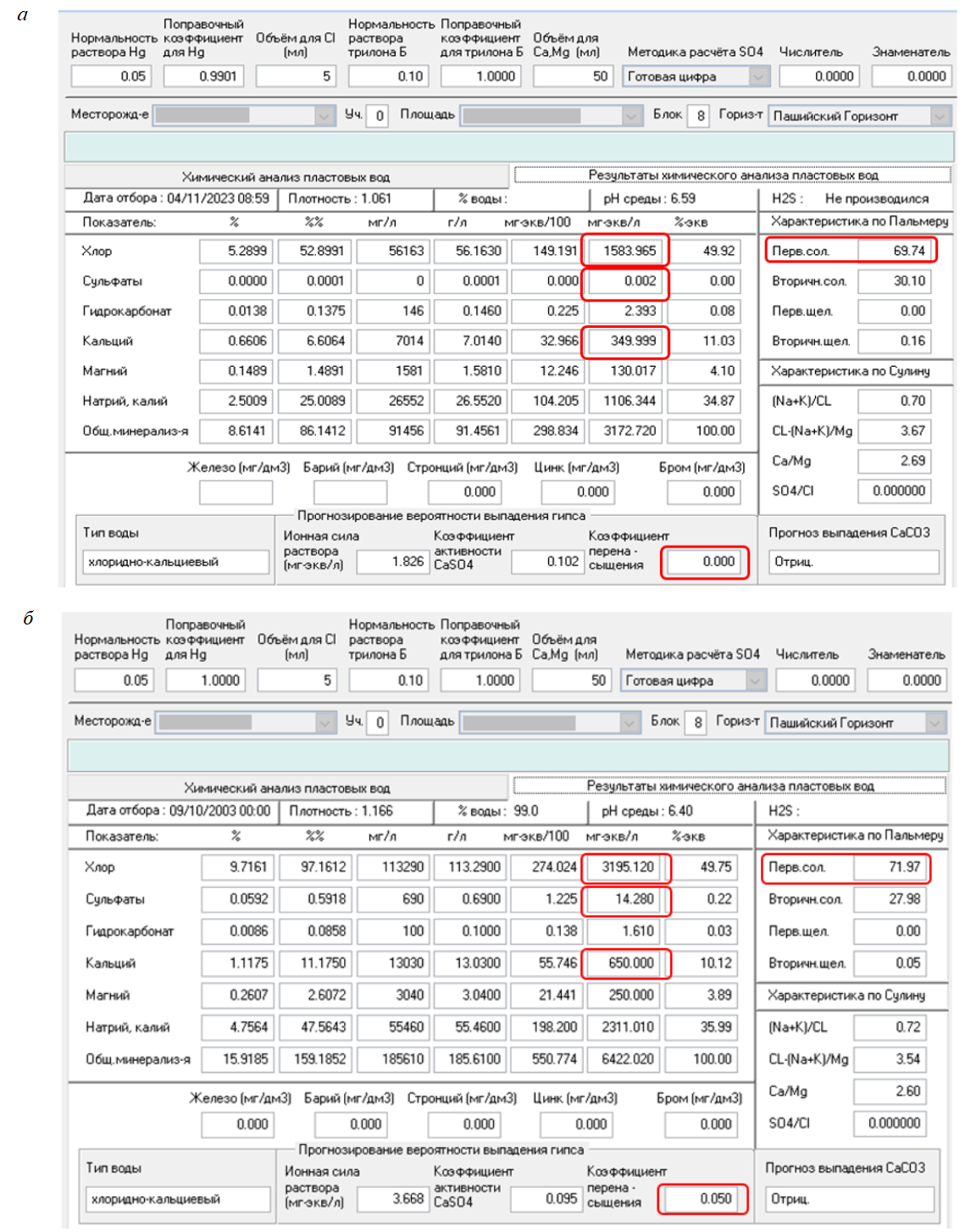
Рис.1. Результат химического анализа воды: для скважин с герметичной (а) и негерметичной (б) эксплуатационными колоннами
Все приведенные вычисления и анализ данных в исследовании были выполнены с использованием языка программирования Python 3.10.5 в среде программирования Jupyter Notebook, запущенного в интегрированной среде разработки Visual Studio Code v.1.99.3. Для предобработки данных, построения моделей машинного обучения, а также оценки их производительности использовалась библиотека scikit-learn v.1.2.2, для реализации градиентного бустинга на деревьях решений применялась библиотека LightGBM v.4.1.0, для интерпретации предсказаний модели и анализа важности признаков использовалась библиотека shap v.0.44.1, для обработки и анализа табличных данных применялась библиотека pandas v.2.3.1, для математических операций и работы над массивами использовалась библиотека numpy v.1.26.4, для визуализации результатов использовались библиотеки matplotlib v.3.8.4 и seaborn v.0.13.2.
Для оценки распределения исследуемых параметров по площадям месторождения N было проанализировано 14318 исследований, полученных из корпоративных баз данных, за 2000-2022 гг. В качестве рассматриваемых признаков были отобраны параметры, характеризующие химический состав воды, динамику работы скважины, а также возраст скважины.
В первую очередь была проведена оценка распределений каждого параметра для анализа аномалий и выбросов. Под выбросом понимаются значения данных, которые существенно отличаются от большинства остальных значений в выборке [44, 45]. Для определения выбросов был выбран подход с использованием межквартильного размаха (IQR) [46].
На рис.2 представлено схематичное изображение диаграммы размаха, которую также называют «ящик с усами». Данный вид диаграммы позволяет отобразить все квартили по исходным данным. Квартиль Q1 – число, отделяющее первую четверть выборки, т.е. 25 % данных меньше данного значения в выборке, а 75 % – больше. Далее идет медиана (второй квартиль Q2), которая делит выборку пополам, т.е. 50 % данных в выборке меньше этого значения, а 50 % – больше. Третий квартиль Q3 – число, отделяющее три четверти всей выборки, т.е. 75 % данных в выборке меньше данного значения, а 25 % данных больше этого значения. При этом межквартильным размахом называется расстояние между третьим и первым квартилем. Также на данной диаграмме имеются «усы», которые простираются влево от первого квартиля и вправо от третьего квартиля. Размер «усов» равен полуторному межквартильному размаху. Все точки в данных, находящиеся за пределами «усов», можно считать выбросами.
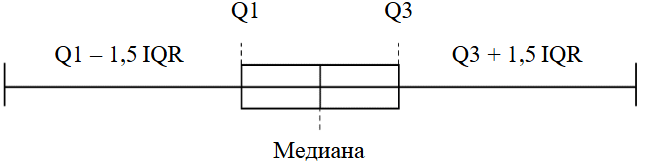
Рис.2. Диаграмма размаха
На основе описанного подхода были проанализированы выбросы по параметрам в разрезе площадей месторождения N. Для начала рассмотрим выбросы по исследуемым параметрам для скважин с герметичной колонной. К параметрам с наибольшим средним значением доли выбросов относится химический анализ воды, а именно показатель Ca/Mg – 0,19, содержание сульфатов – 0,15, Cl–(Na+K)/Mg – 0,14.
По параметрам, характеризующим динамику работы скважины, выбросов практически не наблюдается, что говорит о достаточно хорошей представительности данных. А по параметрам, характеризующим состав воды, картина не такая однозначная. Параметры, доля выбросов которых не превышает 10 % – плотность воды, ионная сила раствора, водородный показатель, содержание хлора, гидрокарбонатов, кальция, магния, натрия, общая минерализация, показатель (Na+K)/Cl, а также содержание первичных и вторичных солей. Параметры, доля выбросов которых выше 10 % – коэффициент активности CaSO4, коэффициент перенасыщения, содержание сульфатов, показатели Cl–(Na+K)/Mg, Ca/Mg и содержание вторичных щелочей.
В группе параметров для скважин с негерметичной колонной количество выбросов меньше, чем в скважинах с герметичной колонной. Среди параметров с наибольшей долей выбросов можно выделить содержание вторичных щелочей, дебит жидкости и содержание кальция. В целом по выборке для скважин с негерметичной колонной процент выбросов по параметрам не превышает 10 %, что говорит о достаточной однородности выборки.
Наиболее интересные заключения можно сделать для выборки с герметичной колонной, по которой наблюдается больший процент выбросов. Возможно, измерения были некорректно проведены, и по ряду параметров скважина проходила как негерметичная, но в целом на основе исследований и других анализов она была признана герметичной. По этой причине возможно возникновение выбросов в общей выборке. Предлагаемый в данной работе способ позволяет проанализировать множество параметров и корректно оценить техническое состояние скважины.
Следующим этапом стало заполнение пропущенных значений, когда пустые значения сначала заполнялись предыдущим значением для каждой конкретной скважины, а затем для оставшихся пропущенных значений по скважине происходило заполнение снизу вверх, т.е. последующим значением.
После предобработки данных была проведена проверка признаков на мультиколлинеарность с помощью матрицы корреляции Пирсона, позволяющей понять, насколько сильно и в каком направлении связаны различные признаки в наборе данных [47].
Матрица корреляции Пирсона строится на основе коэффициентов линейной корреляции между всеми парами числовых переменных в датафрейме:
где xi– значение признака x в i-м наблюдении; yi – значение признака y в i-м наблюдении; x‾ – среднее значение признака x; y‾ — среднее значение признака y; n – количество наблюдений.
На рис.3 в виде тепловой карты представлена матрица корреляции Пирсона по признакам, которые были выделены для анализа их влияния на возникновение негерметичности эксплуатационной колонны: F1 – код площади; F2 – возраст скважины на момент исследования; Y – состояние колонны; F3 – плотность воды; F4 – ионная сила раствора; F5 – коэффициент активности CaSO4; F6 – коэффициент перенасыщения; F7 – водородный показатель; F8 – хлор; F9 – сульфаты; F10 – гидрокарбонат; F11 – кальций; F12 – магний; F13 – натрий; F14 – общая минерализация; F15 – (Na+K)/Cl; F16 – Cl–(Na+K)/Mg; F17 – Ca/Mg; F18 – первичные соли; F19 – вторичные соли; F20 – вторичные щелочи; F21 – дебит жидкости; F22 – дебит нефти; F23 – обводненность; F24 – пластовое давление; F25 – забойное давление; F26 – количество ремонтов. На пересечении горизонтальной и вертикальной осей нанесены коэффициенты линейной корреляции.
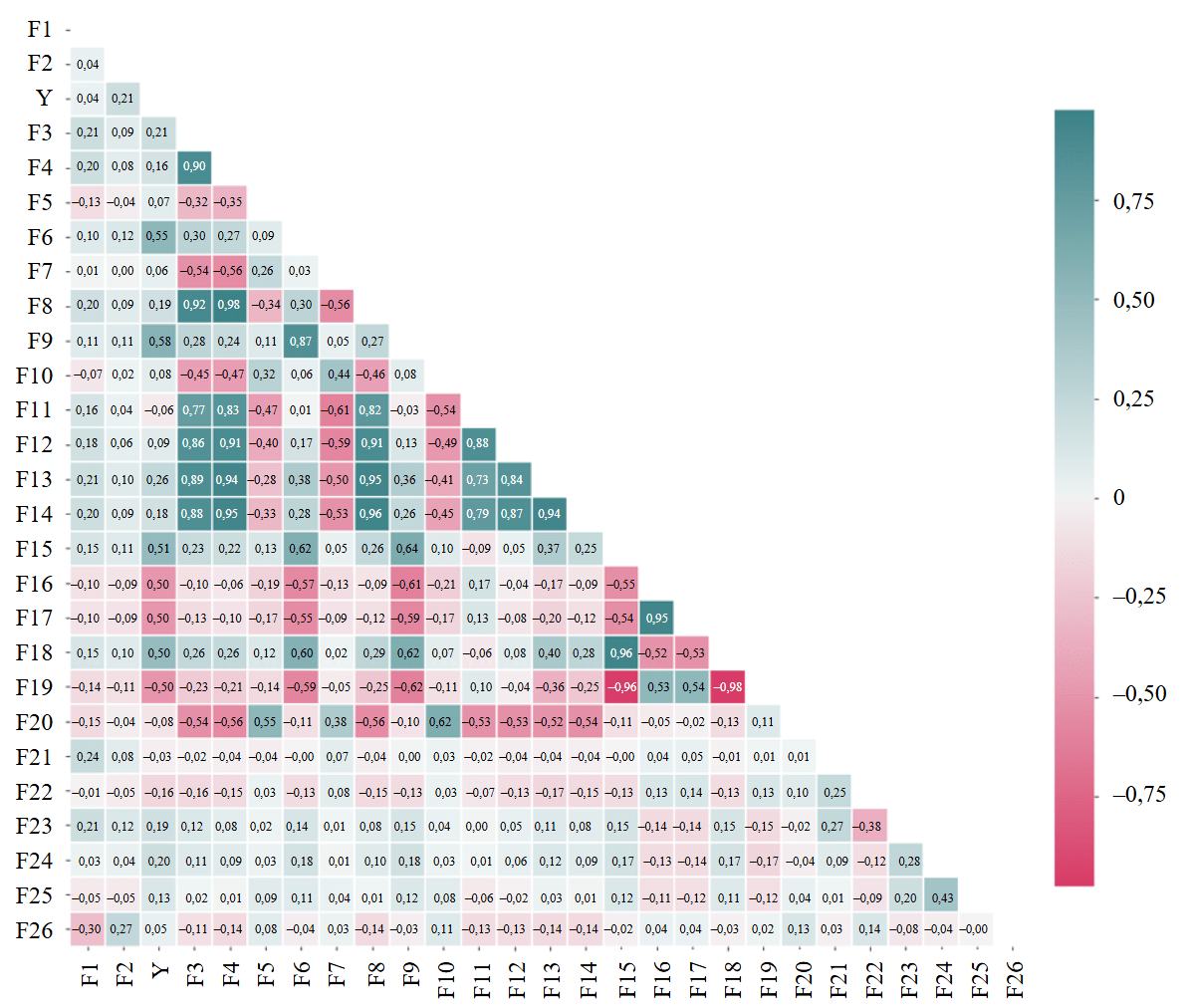
Рис.3. Матрица корреляции признаков в общем наборе данных с учетом обработки выбросов
Наибольшая прямая зависимость наблюдается между признаками, которые характеризуют химический состав воды (рис.3). Из-за влияния сильной корреляции признаков на обучение модели и дальнейшее ее применение было принято решение об удалении одного из пары зависимых параметров. Из обучающего датасета были удалены следующие параметры: ионная сила раствора, содержания хлора, кальция, магния, натрия, коэффициент Ca/Mg.
На этапе подготовки данных было проведено масштабирование признаков с помощью метода стандартизации с использованием модуля StandardScaler, входящего в состав библиотеки scikit-learn для языка программирования Python [48]. Применение стандартизации необходимо из-за неоднородности величины признаков, участвующих в обучении. Если не провести стандартизацию, то модель решит, что признаки с большей величиной важнее признаков с меньшей величиной. Значения признаков преобразованы по формуле
где zi – стандартизированное значение параметра; хi – исходное значение параметра; μi – среднее значение параметра (среднее арифметическое всех значений параметра); σi – стандартное отклонение параметра (мера разброса значений параметра относительно среднего).
Среднее значение признака вычитается в начале, это позволяет собрать распределение вокруг нуля. Вторым действием происходит деление на значение стандартного отклонения, данный шаг позволяет привести данные к масштабу, где одно стандартное отклонение соответствует единичной длине. После стандартизации мы получаем значение, которое представляет собой отклонение исходного значения от среднего в стандартных единицах.
В ряде параметров наблюдается значительный разброс значений между разными площадями месторождения, что связано с геолого-физическими особенностями каждого эксплуатационного объекта. С учетом этой специфики была доработана методика обучения модели путем включения признака площади и применения метода переноса знаний [49]. Данный подход заключается в проведении кластеризации эксплуатационных объектов на основе химического анализа воды и динамических параметров работы скважин с использованием метода силуэта и алгоритма K-средних, что позволило выявить группы схожих объектов и объединить данные по объектам с малым количеством наблюдений с данными объектов-аналогов. Обучение модели проводилось с учетом кластерной принадлежности скважин и регистрацией специфики каждого объекта. Применение данного метода позволило повысить точность прогнозирования на 13 % и улучшить другие метрики качества модели. В настоящем исследовании этот подход обеспечил учет принадлежности скважин к определенному объекту при прогнозировании негерметичности эксплуатационных колонн.
Для оценки значимости отдельных признаков и их способности разделять случаи для герметичных и негерметичных скважин использован метод статистического анализа ROC-AUC (площадь под кривой рабочих характеристик) [50]. Он позволяет оценить важность признаков на основе их способности разделять различные классы. Процесс определения показателя AUC (площади под кривой ROC) заключается в построении ROC-кривой, которая отражает зависимость между долями верно предсказанных положительных случаев (TPR) и ложных срабатываний (FPR) по признаку. Чем выше значение показателя AUC, тем лучше исследуемый признак разделяет классы.
Для каждого объекта выборки с известным значением признака xi и меткой класса yi (θ) {0, 1} определяется бинарный классификатор по порогу θ:
где yi (θ) – предсказанный класс для i-го объекта при заданном пороге классификации θ, если хi ≥ θ, то объект считается положительным, иначе – отрицательным.
Для каждой точки θ рассчитываются чувствительность (TPR) и специфичность (FPR):
где TP(θ) – число верно классифицированных скважин как негерметичные; FN(θ) – число ошибочно классифицированных скважин как герметичные; FP(θ) – число ошибочно классифицированных скважин как негерметичные; TN(θ) – число верно классифицированных скважин как герметичные.
С изменением порога классификации θ по всему диапазону значений признакастроится ROC-кривая – график сопоставления TPR(θ) и FPR(θ).Интеграл под этой кривой определяет метрику AUC:
где f – доля ложных положительных классификаций (FPR); TPR(f) – чувствительность при заданной FPR.
Помимо определения важности признаков, необходимо определить пороговые значения признаков. Одним из статистических параметров, использующихся для определения порогового значения признаков при классификации, является индекс Юдена [51]:
Индекс Юдена позволяет найти пороговое значение, при котором достигается максимальное различие между TPR и FPR в задаче бинарной классификации:
где θ*– оптимальное значение порога классификации.
Кроме статистических также применяются методы, основанные на данных моделей машинного обучения. Одним из таких методов является SHAP-анализ [52]. Методы SHAP-анализа позволяют оценить вклад каждого признака в предсказание модели, что помогает выявить наиболее значимые факторы, влияющие на результат. Это делает его незаменимым инструментом для анализа сложных систем, таких как диагностика состояния скважин, где множество факторов влияет на возникновение негерметичности. Каждая точка, отображенная на SHAP-графике, представляет собой SHAP-значение для каждого конкретного случая. Совокупность этих точек для каждого признака формирует его распределение на горизонтальной оси. Плотность этого распределения несет важную информацию: широкие, плотные участки графика указывают на диапазон SHAP-значений, характерный для большинства наблюдений, и отражают типичный вклад признака. Напротив, узкие и вытянутые участки («хвосты» графика) соответствуют редкому, но потенциально сильному влиянию, которое может быть связано с выбросами или специфическими взаимодействиями признаков. Низкие значения признака отображаются синим цветом, высокие – красным. Положение точек относительно нулевой линии показывает направление и силу влияния признака. Если величины находятся с правой стороны, это увеличивает предсказание положительного класса, т.е. наличие нарушения по скважине, если же точки находятся с левой стороны, то увеличивается предсказание отрицательного класса, т.е. герметичность скважины. Влияние каждого признака оценивается как разница между предсказанием модели с учетом этого признака и без него, это обеспечивает справедливое распределение вклада каждого признака.
Предсказание модели с учетом вклада признаков по SHAP-анализу рассчитывается следующим образом:
где ϕ0 – базовая линия; ϕi(x) – SHAP-значение для i-го признака; n – количество признаков.
SHAP-значения являются относительными оценками влияния признаков, выраженными в условных единицах отклонения от базовой линии ϕ0. Однако для практического применения модели важно понимать, какие абсолютные значения признаков соответствуют ключевым переходным точкам между герметичными и негерметичными скважинами.
В частности, для каждого признака существует пороговое значение, при котором SHAP-вклад близок нулю, т.е. предсказание модели не склоняется ни в сторону положительного, ни в сторону отрицательного класса. Такие значения признаков можно трактовать как граничные значения, разделяющие области «низкого риска» и «повышенного риска» негерметичности.
Для получения граничных значений было выполнено обратное преобразование стандартизированных признаков в их исходные физические шкалы. Исходя из параметров масштабирования каждого признака, значение, соответствующее нейтральному SHAP-вкладу, рассчитывается по формуле:
где zi(0) – стандартизированное значение, при котором SHAP-вклад равен нулю; zi(0) = 0; γi – абсолютное пороговое значение признака.
Научная новизна данного исследования заключается в разработке интерпретируемой модели машинного обучения на базе алгоритма LightGBM [53] с применением SHAP-анализа, впервые адаптированной для задач диагностики негерметичности эксплуатационных колонн. В отличие от традиционных реализаций, LightGBM применяет стратегию роста деревьев, что обеспечивает более высокую точность и эффективность обучения, а также использует метод гистограммной дискретизации признаков для ускорения вычислений и снижения потребления памяти.
LightGBM относится к методам градиентного бустинга на решающих деревьях. Предсказание модели выражается как сумма предсказаний отдельных деревьев:
где T – количество деревьев в ансамбле; ft – функция-дерево решений, построенное на t-й итерации; F – пространство всех возможных деревьев решений; ki– вектор признаков объекта i.
SHAP-анализ был применен как метод постобработки результатов модели LightGBM для количественной оценки вклада отдельных признаков в прогноз. Это позволило интерпретировать работу модели и выделить ключевые параметры, определяющие вероятность негерметичности.
SHAP-метод рассчитывает маржинальный вклад каждого признака в предсказание модели, учитывая все возможные комбинации признаков. В данной работе важность признаков оценивалась по среднему абсолютному значению SHAP-значений по всей выборке:
где ϕij – SHAP-значение признака j для наблюдения i; N – количество объектов в выборке.
Чем выше значение Ij, тем в среднем признак оказывает более сильное влияние на предсказание модели.
Обсуждение результатов
На рис.4 показан пример ROC-анализа для признака «содержание сульфатов». Данный параметр хорошо разделяет случаи для герметичных и негерметичных скважин, так как значение площади под кривой ROC составляет 0,8 д.ед. Красной точкой обозначен показатель оптимального порога для данного признака по индексу Юдена (2,08 мг-экв/л) – значение, выше которого чаще наблюдаются скважины с негерметичной колонной, а ниже – скважины с герметичной колонной. Подобным образом были проанализированы остальные признаки, результаты анализа представлены в табл.1.
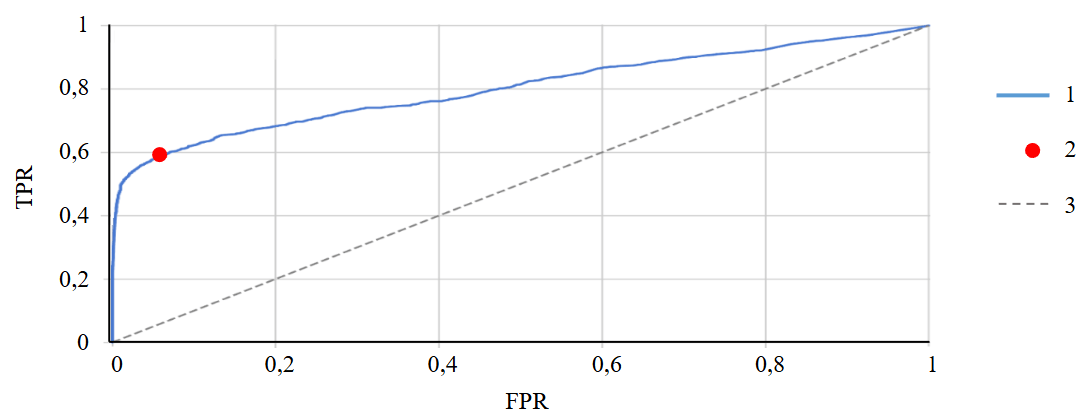
Рис.4. Пример ROC-анализа cодержания сульфатов
1 – ROC-кривая (AUC = 0,8); 2 – оптимальный порог, AUC = 2,08; 3 – случайное угадывание фактического значения модели
Таблица 1
Значения AUC и граничные значения рассматриваемых признаков для разделения герметичных и негерметичных скважин по статистическому методу ROC-AUC
|
Признак |
AUC, д.ед. |
Граничное значение признака |
|
Сульфаты, мг-экв/л |
0,802 |
2,082 |
|
Коэффициент перенасыщения, д.ед. |
0,776 |
0,114 |
|
(Na+K)/Cl, д.ед. |
0,747 |
0,74 |
|
Первичные соли, мг-экв/л |
0,741 |
73,68 |
|
Обводненность, % |
0,647 |
93,83 |
|
Пластовое давление, атм |
0,647 |
158 |
|
Плотность воды, г/см3 |
0,646 |
1,118 |
|
Возраст скважины, лет |
0,645 |
36 |
|
Общая минерализация, мг-экв/л |
0,627 |
5810,998 |
|
Коэффициент активности CaSO4, д.ед. |
0,619 |
0,101 |
|
Забойное давление, атм |
0,58 |
114 |
|
Гидрокарбонат, мг-экв/л |
0,571 |
2,098 |
|
Количество ремонтов |
0,558 |
10 |
|
Водородный показатель, д.ед. |
0,531 |
5,82 |
|
Дебит жидкости, м3/сут |
0,503 |
13,145 |
|
Вторичные щелочи, мг-экв/л |
0,467 |
0,04 |
|
Дебит нефти, м3/сут |
0,368 |
0,004 |
|
Вторичные соли, мг-экв/л |
0,257 |
38,62 |
|
Cl–(Na+K)/Mg, д.ед. |
0,25 |
5,1 |
Для интерпретации силы предсказательной способности признака была использована качественная шкала [54], согласно которой AUC = 0,5 д.ед. – классификатор на уровне случайного угадывания; AUC = 0,7-0,8 – приемлемый; AUC = 0,8-0,9 – отличный; AUC > 0,9 – выдающийся.
Согласно данной шкале, такие признаки, как содержание сульфатов, коэффициент перенасыщения раствора, а также коэффициент (Na+K)/Cl и содержание первичных солей, обладают наибольшей значимостью при статистическом анализе, так как значение AUC для данных признаков больше 0,7. Такие признаки, как обводненность, пластовое давление и возраст скважины, демонстрируют умеренное влияние на классификацию, особенно в комбинации с другими факторами. Признаки с AUC менее 0,6 д.ед. имеют слабую разделяющую способность и, вероятно, играют вспомогательную роль в предсказании негерметичности скважин. Однако данный метод статистического анализа не учитывает нелинейную зависимость в данных и взаимодействие между признаками, которые могут быть критически важны для точного предсказания. ROC-AUC оценивает только индивидуальную способность каждого признака разделять классы, что ограничивает его применимость в таких задачах как определение негерметичности скважин.
Модели машинного обучения совместно с дальнейшим SHAP-анализом позволяют обойти ограничения, которые характерны только для статистических методов.
На рис.5 представлен SHAP-анализ важности признаков, рассчитанный с использованием формул (1) и (3). Представленные на графике признаки упорядочены по уменьшению степени влияния на предсказание модели.
Наибольшее влияние по среднему абсолютному SHAP-значению на возникновение негерметичности по модели LightGBM оказывают следующие признаки: SHAP-значение содержания сульфатов 0,872; SHAP-значение коэффициента перенасыщения раствора 0,644; SHAP-значение обводненности продукции 0,436; SHAP-значение возраста скважины на момент исследования 0,420; SHAP-значение гидрохимический коэффициент Cl–(Na+K)/Mg 0,374.
В процессе исследования были определены абсолютные пограничные значения признаков по SHAP-анализу с использованием формулы (2), изменение которых приводит к повышенной вероятности возникновения негерметичности: сульфаты – 2,36 мг-экв/л; коэффициент перенасыщения – 0,10 д.ед.; обводненность – 77,27 %; возраст скважины – 33 года; Cl–(Na+K)/Mg – 3,86 д.ед.; первичные соли – 69,50 мг-экв/л; пластовое давление – 151,14 атм; (Na+K)/Cl – 0,70 д.ед.; вторичные соли – 30,29 мг-экв/л; количество ремонтов – 15 шт.; плотность воды – 1,10 г/см3; дебит жидкости – 27,04 м3/сут; коэффициент активности CaSO4 – 0,10 д.ед.; общая минерализация – 4776,53 мг-экв/л; водородный показатель – 6,31 д.ед.; дебит нефти – 3,13 м3/сут; вторичные щелочи – 0,11 мг-экв/л; гидрокарбонат – 2,19 мг-экв/л; забойное давление – 95,86 атм.
Наибольшее влияние на предсказание негерметичности оказывают сульфаты и коэффициент перенасыщения, причем разница в величинах признаков невелика (табл.1). Также в обоих случаях отмечается высокая важность первичных солей, возраста скважины, обводненности и пластового давления. А гидрохимический коэффициент Cl–(Na+K)/Mg по статистическому анализу ROC-AUC имеет самое низкое влияние на возникновение негерметичности, при этом по SHAP-анализу данный признак на пятом месте по важности. Это связано с тем, что SHAP-анализ дает более точные и интерпретируемые граничные значения, поскольку учитывает нелинейности и сочетания признаков, которые не видны в простом статистическом анализе ROC-AUC.
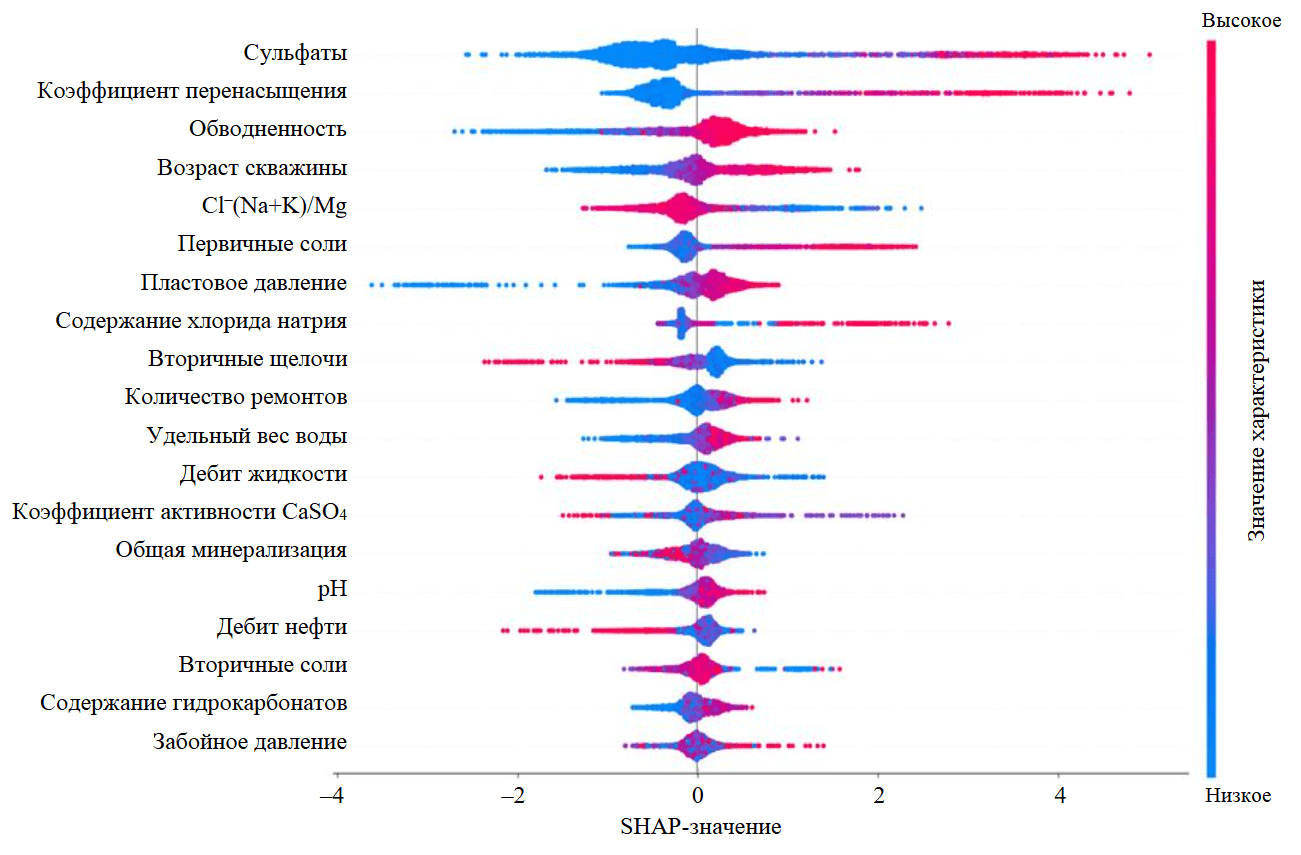
Рис.5. Оценка влияния признаков на возникновение негерметичности
На рис.6 представлены графики интерпретации для пяти признаков, в большей степени влияющих на предсказание негерметичности скважины.
Значение сульфатов, при котором SHAP-значение является нейтральным, равно 2,36 мг-экв/л (рис.6, а), т.е. значения ниже этого уровня уменьшают вероятность негерметичности, а выше – увеличивают.
Для коэффициента перенасыщения граничное значение равно 0,1 (рис.6, б). Более высокие значения характерны для скважин с негерметичной колонной. В рамках исследования рассчитано значение коэффициента перенасыщения в водах терригенного девона. В среднем оно равняется 0,017, при этом значение коэффициента перенасыщения для нижнего и среднего карбона изменяется в пределах 0-2,48, в среднем 0,69. Следовательно, можно сделать вывод о том, что при повышении коэффициента перенасыщения в пробе, полученной в скважине, высока вероятность притока флюида из вышележащих горизонтов, в частности из карбона.
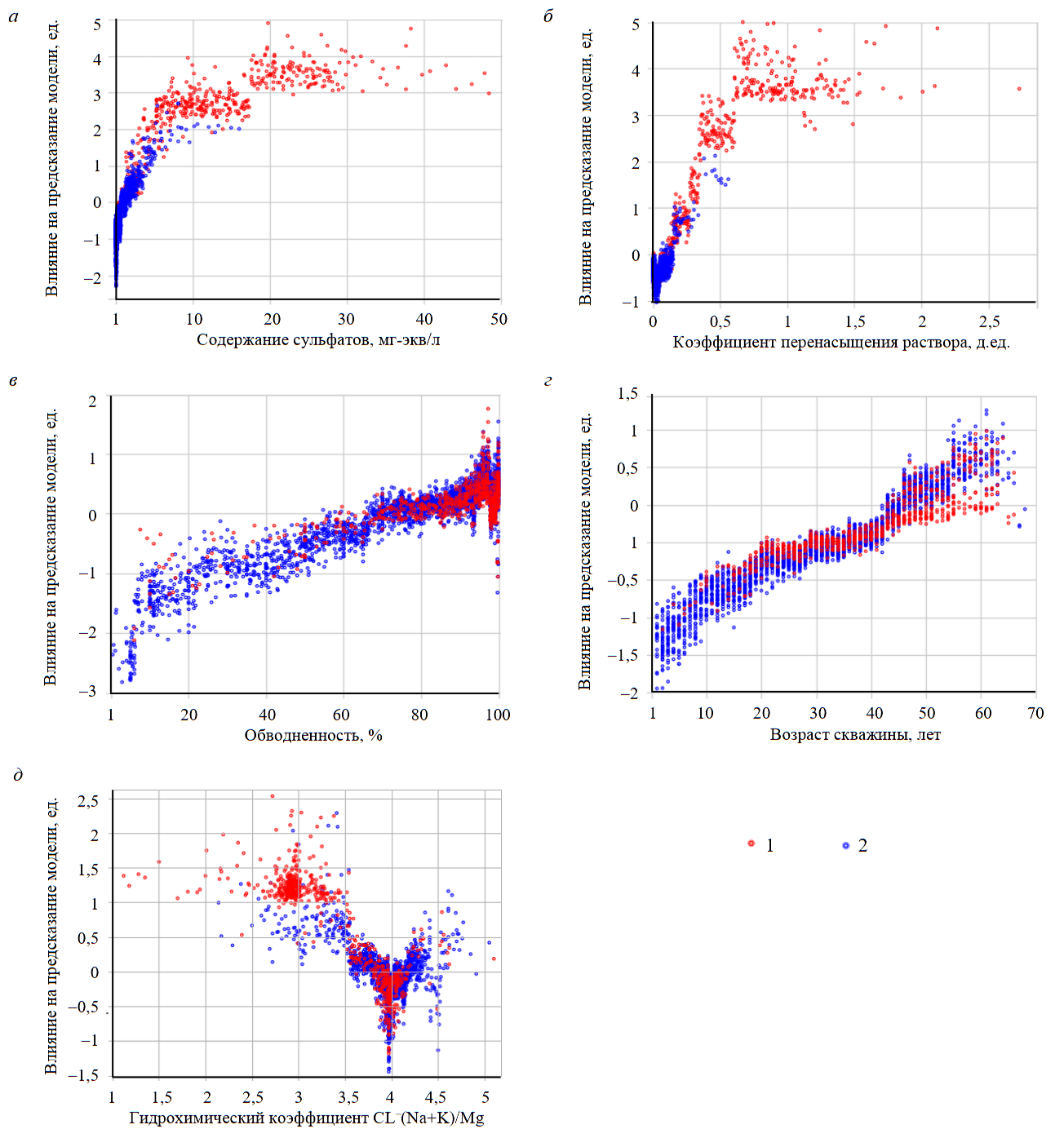
Рис.6. Графики влияния признаков на вероятность возникновения негерметичности эксплуатационной колонны: а – содержание сульфатов; б – коэффициент перенасыщения; в – обводненность; г – возраст скважины; д – гидрохимический коэффициент Cl–(Na+K)/Mg
1 – негерметичная скважина; 2 – герметичная
С увеличением значения обводненности возрастает вероятность предсказания негерметичности скважины (рис.6, в). Значение обводненности, при котором SHAP-значение является граничным, равно 77,27 %.
С увеличением возраста скважины на момент исследования возрастает вероятность предсказания негерметичности скважины (рис.6, г). Пороговое значение по SHAP-анализу по признаку возраста скважины равняется 33 годам.
С понижением значения гидрохимического коэффициента Cl–(Na+K)/Mg увеличивается вероятность негерметичности колонны (рис.6, д). При значениях гидрохимического коэффициента Cl–(Na+K)/Mg около 3,86 наблюдается пограничная область между случаями с герметичной и негерметичной колонной. В рамках исследования рассчитано значение гидрохимического коэффициента Cl–(Na+K)/Mg в водах терригенного девона, в среднем оно равняется 4,08, при этом значение Cl–(Na+K)/Mg вод нижнего и среднего карбона изменяется в пределах 0,89-3,17, в среднем 2,40. При понижении величины гидрохимического коэффициента Cl–(Na+K)/Mg в пробе, полученной в скважине, высока вероятность притока флюида из вышележащих горизонтов, в частности из карбона.
Сравнение полученных результатов определения граничных значений с помощью статистических методов и модели машинного обучения с последующим SHAP-анализом представлено в табл.2.
Таблица 2
Сравнение граничных значений исследуемых признаков по методу ROC-AUC и SHAP-анализу
|
Признак |
Граничное значение |
Разница между показателями, % |
|
|
ROC-AUC |
SHAP |
||
|
Сульфаты, мг-экв/л |
2,082 |
2,36 |
–13 |
|
Коэффициент перенасыщения, д.ед. |
0,114 |
0,1 |
12 |
|
(Na+K)/Cl, д.ед. |
0,74 |
0,7 |
5 |
|
Первичные соли, мг-экв/л |
73,68 |
69,5 |
6 |
|
Обводненность, % |
93,83 |
77,27 |
18 |
|
Пластовое давление, атм |
158 |
151,14 |
4 |
|
Плотность воды, г/см3 |
1,118 |
1,1 |
2 |
|
Возраст скважины, лет |
36 |
33 |
8 |
|
Общая минерализация, мг-экв/л |
5810,998 |
4776,53 |
18 |
|
Коэффициент активности CaSO4, д.ед. |
0,101 |
0,1 |
1 |
|
Забойное давление, атм |
114 |
95,86 |
16 |
|
Гидрокарбонат, мг-экв/л |
2,098 |
2,19 |
–4 |
|
Количество ремонтов |
10 |
15 |
–50 |
|
Водородный показатель, д.ед. |
5,82 |
6,31 |
–8 |
|
Дебит жидкости, м3/сут |
13,145 |
27,04 |
–106 |
|
Вторичные щелочи, мг-экв/л |
0,04 |
0,11 |
–175 |
|
Дебит нефти, м3/сут |
0,004 |
3,13 |
–78150 |
|
Вторичные соли, мг-экв/л |
38,62 |
30,29 |
22 |
|
Cl–(Na+K)/Mg, д.ед. |
5,1 |
3,86 |
24 |
В 12 признаках по статистическому анализу ROC-AUC наблюдаются более высокие граничные значения по сравнению с SHAP-анализом (табл.2), например по коэффициенту перенасыщения 0,114 и 0,1 соответственно. В семи признаках, наоборот, ROC-AUC ставит более низкие значения, например, по сульфатам – 2,082 и 2,36 соответственно. В первом случае можно говорить о том, что SHAP-анализ делает акцент на распознавании даже небольших изменений в признаках. Во втором случае ROC-AUC пытается охватить весь диапазон значений, который может быть важен для классификации. Для дебита нефти наблюдаются сильные различия по граничным значениям в зависимости от метода анализа. Вероятно, это связано с тем, что данный признак влияет на предсказание негерметичности нелинейно, и метод ROC-AUC не смог обнаружить зависимость значений этого признака от наличия негерметичности по скважине.
В отличие от ранее применявшихся моделей машинного обучения и статистических методов, предложенный подход обеспечивает не только высокую точность предсказаний, но и интерпретацию граничных значений ключевых признаков, таких как содержание сульфатов, коэффициент перенасыщения, обводненность продукции и возраст скважины. Также впервые продемонстрирована высокая значимость ранее недооцениваемых признаков, выявленных за счет использования SHAP, что было невозможно при стандартном ROC-AUC-анализе.
Заключение
В ходе проведенного исследования проанализированы возможности применения методов машинного обучения для диагностики негерметичности эксплуатационных колонн скважин.
SHAP-анализ позволил установить абсолютные граничные значения ключевых признаков. Например, граничное значение для содержания сульфатов, превышение которого с большей вероятностью приводит к возникновению негерметичности, равно 2,36 мг-экв/л, граничное значение коэффициента перенасыщения – 0,1, а обводненности – 77,27 %.
Анализ ROC-AUC показал, что отдельные признаки, такие как сульфаты и коэффициент перенасыщения, обладают высокой разделяющей способностью. Однако SHAP-анализ обеспечивает более глубокую интерпретацию модели за счет учета нелинейностей и синергетических эффектов между параметрами. Это делает его незаменимым инструментом для анализа сложных систем, таких как эксплуатация скважин, где множество факторов влияет на возникновение негерметичности. Таким образом, сочетание методов машинного обучения и SHAP-анализа позволяет повысить точность предсказаний и достоверность выводов, предоставляя более надежную основу для принятия решений.
Практическая значимость исследования заключается в возможности применения интерпретируемых моделей машинного обучения для различных задач нефтяной отрасли, в том числе для мониторинга состояния эксплуатационных колонн скважин. Это позволит оперативно выявлять зоны риска, снижать экологические, а также экономические потери при геофизических исследованиях и эксплуатации скважин.
Литература
- Черненко А.В., Лышко Г.Н. Предотвращение заколонных перетоков пластовых флюидов на основе математического моделирования процессов в скважине // Нефть. Газ. Новации. 2018. № 3 (208). С. 30-33.
- Набиуллин А.Ш., Синицына Т.И., Воронцов С.Ю. Изучение причин возникновения нарушений герметичности эксплуатационных колонн добывающих скважин. Разработка превентивных методов по защите обсадной колонны // Экспозиция Нефть Газ. 2023. № 8 (101). С. 88-93. DOI: 10.24412/2076-6785-2023-8-88-93
- Аникеев Д.П., Закиров С.Н., Аникеева Э.С., Лысенко А.Д. Негерметичность скважин − глобальная проблема, а не локальная // Актуальные проблемы нефти и газа. 2019. Вып. 4 (27). 14 с. DOI: 10.29222/ipng.2078-5712.2019-27.art15
- Трунов Э.И., Оздоева А.Х., Блоцкая А.И. и др. Новые подходы к применению акустического метода для непрерывного мониторинга герметичности крепления скважины // Нефтяное хозяйство. 2024. № 2. С. 38-42. DOI: 10.24887/0028-2448-2024-2-38-42
- Шарипов А.Ф., Волков А.Н. Система контроля и оценки качества газоконденсатных исследований скважин // Вести газовой науки. 2016. № 4 (28). С. 173-180.
- Валиуллин Р.А., Шарафутдинов Р.Ф., Федотов В.Я. и др. Изучение тепловой конвекции на модели скважины с индукционным нагревателем при заколонном перетоке «сверху» // Вестник Башкирского университета. 2017. Т. 22. № 2. С. 325-329.
- Patidar A.K., Joshi D., Dristant U., Choudhury Y. et al. A review of tracer testing techniques in porous media specially attributed to the oil and gas industry // Journal of Petroleum Exploration and Production Technology. 2022. Vol. 12. Iss. 12. P. 3339-3356. DOI: 10.1007/s13202-022-01526-w
- Batista G. dos S., Takimi A.S., da Costa E.M. Chemical Changes in the Composition of Oil Well Cement with Core/Shell Nanoparticle Addition under CO2 Geological Storage Conditions // Energy & Fuels. 2024. Vol. 38. Iss. 23. P. 22947-22958. DOI: 10.1021/acs.energyfuels.4c03686
- Азаматов М.А., Шорохов А.Н. Метод определения негерметичности эксплуатационной колонны // Недропользование XXI век. 2015. № 6 (56). С. 43-47.
- Щербакова К.О. Анализ проблемы высокой обводненности добываемой продукции горизонтальных скважин // Известия высших учебных заведений. Геология и разведка. 2022. Т. 64. № 6. С. 29-38. DOI: 10.32454/0016-7762-2022-64-6-29-38
- Джабаров К.А. Математическое моделирование процессов формирования заколонных перетоков в скважине в период ожидания затвердевания цемента // Нефтяное хозяйство. 2019. № 5. С. 67-71. DOI: 10.24887/0028-2448-2019-5-67-71
- Буркова А.А. Применение новой технологии проведения ремонтно-изоляционных работ // Строительство нефтяных и газовых скважин на суше и на море. 2022. № 8 (356). С. 39-44. DOI: 10.33285/0130-3872-2022-8(356)-39-44
- Фрейман О.А., Еремин Н.А. Разработка методики прогнозирования пластовых свойств нефти при помощи машинного обучения // Экспозиция Нефть Газ. 2023. № 7. С. 118-120. DOI: 10.24412/2076-6785-2023-7-118-120
- Tadjer A., Hong A., Bratvold R.B. Machine learning based decline curve analysis for short-term oil production forecast // Energy Exploration & Exploitation. 2021. Vol. 39. Iss. 5. P. 1747-1769. DOI: 10.1177/01445987211011784
- Пашали А.А., Азбуханов А.Ф., Сухарев К.В., Топольников А.С. Восстановление значений давления на приеме насоса нефтедобывающих скважин с использованием методов искусственного интеллекта // Нефтегазовое дело. 2022. Т. 20. № 6. С. 165-172. DOI: 10.17122/ngdelo-2022-6-165-172
- Liang Xue, Yuetian Liu, Yifei Xiong et al. A data-driven shale gas production forecasting method based on the multi-objective random forest regression // Journal of Petroleum Science and Engineering. 2021. Vol. 196. № 107801. DOI: 10.1016/j.petrol.2020.107801
- Евсеенков А.С., Гузь В.С., Шпетный Д.Н., Юдин Е.В. Краткосрочное прогнозирование дебита скважин на основе ансамблевого подхода // Нефтяное хозяйство. 2023. № 2. С. 78-82. DOI: 10.24887/0028-2448-2023-2-78-82
- Arief I.H., Tao Yang. A Machine-Learning Approach to Predict Gas-Oil Ratio Based on Advanced Mud Gas Data // Petrophysics. 2024. Vol. 65. Iss. 4. P. 433-454.
- Negash B.M., Yaw A.D. Artificial neural network based production forecasting for a hydrocarbon reservoir under water injection // Petroleum Exploration and Development. 2020. Vol. 47. Iss. 2. P. 383-392. DOI: 10.1016/S1876-3804(20)60055-6
- Габитова С.И., Давлетбакова Л.А., Климов В.Ю. и др. Методика прогнозирования темпов падения нефти проектных скважин на основе алгоритма машинного обучения // PROНЕФТЬ. Профессионально о нефти. 2020. № 4 (18). С. 69-74. DOI: 10.7868/S2587739920040102
- Werneck R. de O., Prates R., Moura R. et al. Data-driven deep-learning forecasting for oil production and pressure // Journal of Petroleum Science and Engineering. 2022. Vol. 210. № 109937. DOI: 10.1016/j.petrol.2021.109937
- Xuanyi Song, Yuetian Liu, Liang Xue et al. Time-series well performance prediction based on Long Short-Term Memory (LSTM) neural network model // Journal of Petroleum Science and Engineering. 2020. Vol. 186. № 106682. DOI: 10.1016/j.petrol.2019.106682
- Ahmadi M.A., Soleimani R., Lee M. et al. Determination of oil well production performance using artificial neural network (ANN) linked to the particle swarm optimization (PSO) tool // Petroleum. 2015. Vol. 1. Iss. 2. P. 118-132. DOI: 10.1016/j.petlm.2015.06.004
- Печко К.А., Сенькин И.С., Белоногов Е.В. Моделирование скважин методами машинного обучения для задач интегрированного моделирования // PROНЕФТЬ. Профессионально о нефти. 2022. Т. 7. № 2 (23). С. 114-120. DOI: 10.51890/2587-7399-2022-7-2-114-120
- Vikara D., Khanna V. Application of a Deep Learning Network for Joint Prediction of Associated Fluid Production in Unconventional Hydrocarbon Development // Processes. 2022. Vol 10. Iss. 4. № 740. DOI: 10.3390/pr10040740
- Ng C.S.W., Ghahfarokhi A.J., Amar M.N. Application of nature-inspired algorithms and artificial neural network in waterflooding well control optimization // Journal of Petroleum Exploration and Production Technology. 2021. Vol. 11. Iss. 7. P. 3103-3127. DOI: 10.1007/s13202-021-01199-x
- Мартюшев Д.А., Пономарева И.Н., Захаров Л.А., Шадров Т.А. Применение машинного обучения для прогнозирования пластового давления при разработке нефтяных месторождений // Известия Томского политехнического университета. Инжиниринг георесурсов. 2021. Т. 332. № 10. С. 140-149. DOI: 10.18799/24131830/2021/10/3401
- Пономарев Р.Ю., Мигманов Р.Р., Зиазев Р.Р. Оценка возможностей применения гибридного моделирования для оптимизации добычного потенциала нефтегазового месторождения // Экспозиция Нефть Газ. 2023. № 5. С. 64-68. DOI: 10.24412/2076-6785-2023-5-64-68
- Мехоношин Р.О., Вильданов Т.Ф., Кордик К.Е. и др. Прогнозирование возникновения инцидентов на нагнетательных скважинах с использованием алгоритмов машинного обучения // Нефтепромысловое дело. 2023. № 9 (657). С. 16-21. DOI: 10.33285/0207-2351-2023-9(657)-16-21
- Черников А.Д., Еремин Н.А., Столяров В.Е. и др. Применение методов искусственного интеллекта для выявления и прогнозирования осложнений при строительстве нефтяных и газовых скважин: проблемы и основные направления решения // Георесурсы. 2020. Т. 22 № 3. С. 87-96. DOI: 10.18599/grs.2020.3.87-96
- Шибаев А.А., Шраго И.Л., Васинкин И.А., Чернышов А.С. Применение методов машинного обучения в задаче анализа аномального поведения технологических параметров, при классификации технологических операций, цикла строительства скважины // Бурение и нефть. 2023. № 7-8. С. 28-31.
- Dexin Ma, Hongbo Yang, Zhi Yang et al. An Intelligent Method for Real-Time Surface Monitoring of Rock Drillability at the Well Bottom Based on Logging and Drilling Data Fusion // Processes. 2025. Vol. 13. Iss. 3. № 668. DOI: 10.3390/pr13030668
- Шаляпин Д.В., Бакиров Д.Л., Фаттахов М.М. и др. Применение методов машинного обучения для повышения качества крепления скважин // Известия высших учебных заведений. Нефть и газ. 2020. № 5 (143). С. 81-93. DOI: 10.31660/0445-0108-2020-5-81-93
- Шлыков С.В. Применение методов машинного обучения для автоматизации процессов в нефтегазовой отрасли // Транспорт и хранение нефтепродуктов и углеводородного сырья. 2023. № 2. С. 46-53. DOI: 10.24412/0131-4270-2023-2-46-53
- Майоров К.Н. Применение алгоритмов машинного обучения для решения задач нефтегазовой сферы // Интеллектуальные системы в производстве. 2021. Т. 19. № 3. С. 55-64. DOI: 10.22213/2410-9304-2021-3-55-64
- Сахнюк В.И., Новиков Е.В., Шарифуллин А.М и др. Применение методов машинного обучения в обработке данных геофизических исследований скважин отложений викуловской свиты // Георесурсы. 2022. Т. 24. № 2. С. 230-238. DOI: 10.18599/grs.2022.2.21
- Rammay M.H., Abdulraheem A. PVT correlations for Pakistani crude oils using artificial neural network // Journal of Petroleum Exploration and Production Technology. 2017. Vol. 7. Iss. 1. P. 217-233. DOI: 10.1007/s13202-016-0232-z
- Salem A.М., Yakoot M.S., Mahmoud O. A novel machine learning model for autonomous analysis and diagnosis of well integrity failures in artificial-lift production systems // Advances in Geo-Energy Research. 2022. Vol. 6. № 2. P. 123-142. DOI: 10.46690/ager.2022.02.05
- Sadiki N., Jang D.-W. Estimation of Hydraulic and Water Quality Parameters Using Long Short-Term Memory in Water Distribution Systems // Water. 2024. Vol. 16. Iss. 21. № 3028. DOI: 10.3390/w16213028
- Xiaohui Yan, Tianqi Zhang, Wenying Du et al. A Comprehensive Review of Machine Learning for Water Quality Prediction over the Past Five Years // Journal of Marine Science and Engineering. 2024. Vol. 12. Iss. 1. № 159. DOI: 10.3390/jmse12010159
- Ишкулов И.М., Вафин Р.Р., Тахауов Д.Д. и др. О методах определения негерметичности эксплуатационной колонны скважины // Нефтяное хозяйство. 2024. № 7. С. 56-60. DOI: 10.24887/0028-2448-2024-7-56-60
- Ишкулов И.М., Тахауов Д.Д., Вафин Р.Р. и др. Определение негерметичности колонны скважин с использованием моделей машинного обучения // Нефтегазовое дело. 2024. Т. 22. № 4. С. 260-267. DOI: 10.17122/ngdelo-2024-4-260-267
- Xianlin Ma, Mengyao Hou, Jie Zhan, Zhenzhi Liu. Interpretable Predictive Modeling of Tight Gas Well Productivity with SHAP and LIME Techniques // Energies. 2023. Vol. 16. Iss. 9. № 3653. DOI: 10.3390/en16093653
- Smiti A. A critical overview of outlier detection methods // Computer Science Review. 2020. Vol. 38. № 100306. DOI: 10.1016/j.cosrev.2020.100306
- Kiani R., Wei Jin, Sheng V.S. Survey on extreme learning machines for outlier detection // Machine Learning. 2024. Vol. 113. Iss. 8. P. 5495-5531. DOI: 10.1007/s10994-023-06375-0
- Dash C.S.K., Behera A.K., Dehuri S., Ghosh A. An outliers detection and elimination framework in classification task of data mining // Decision Analytics Journal. 2023. Vol. 6. № 100164. DOI: 10.1016/j.dajour.2023.100164
- Morais É.T., Barberes G.A., Souza I.V.A.F. et al. Pearson Correlation Coefficient Applied to Petroleum System Characterization: The Case Study of Potiguar and Reconcavo Basins, Brazil // Geosciences. 2023. Vol. 13. Iss. 9. № 282. DOI: 10.3390/geosciences13090282
- Thippa Reddy G., Swarna Priya R.M., Parimala M. et al. A deep neural networks based model for uninterrupted marine environment monitoring // Computer Communications. 2020. Vol. 157. P. 64-75. DOI: 10.1016/j.comcom.2020.04.004
- Ишкулов И.М., Сафаров А.Х., Фаттахов И.Г., Дьяконов А.А. Применение метода переноса знаний для предсказания негерметичности скважин // Нефтепромысловое дело. 2025. № 5 (677). С. 24-28.
- Chicco D., Jurman G. The Matthews correlation coefficient (MCC) should replace the ROC AUC as the standard metric for assessing binary classification // BioData Mining. 2023. Vol. 16. № 4. DOI: 10.1186/s13040-023-00322-4
- Старовойтов В.В., Голуб Ю.И. Сравнительный анализ оценок качества бинарной классификации // Информатика. 2020. Т. 17. № 1. С. 87-101. DOI: 10.37661/1816-0301-2020-17-1-87-101
- Ishkulov I., Vafin R., Takhauov D. еt al. Innovative approach to diagnostics of well integrity using machine learning // Norwegian Journal of Development of the International Science. 2024. № 144. P. 29-34. DOI: 10.5281/zenodo.14169109
- Guolin Ke, Qi Meng, Finley T. et al. LightGBM: A Highly Efficient Gradient Boosting Decision Tree // Advances in Neural Information Processing Systems 30: 31st Annual Conference on Neural Information Processing Systems (NIPS 2017), 4-9 December 2017, Long Beach, CA, USA. Curran Associates Inc., 2018. P. 3147-3155. DOI: 10.5555/3294996.3295074
- Hosmer D.W., Lemeshow S. Applied Logistic Regression. Wiley, 2000. 392 p. DOI: 10.1002/0471722146
