Поиск равновесия по Нэшу для системы из двух взаимосвязанных рынков сырья и продукции
- 1 — аспирант Сколковский институт науки и технологий ▪ Orcid
- 2 — канд. техн. наук старший преподаватель Сколковский институт науки и технологий ▪ Orcid
Аннотация
Исследуется новая модель комплексной экономической системы, которая состоит из двух рынков – сырья и продукции, связанных между собой посредством продажи и переработки сырья в продукцию. Данная модель при достижении рынками равновесного состояния позволяет оценивать товарные потоки и экономическую эффективность каждого производителя сырья или продукции с учетом рыночной конъюнктуры. При такой структуре взаимосвязанных товарных рынков производители продукции на рынке сырья являются покупателями сырья, а на рынке продукции – продавцами. Эта особенность рыночной системы приводит к тому, что функция спроса на сырье задается неявно, и стандартные методы поиска равновесия представляются неэффективными в приложении к данной задаче. С целью поиска равновесного состояния для представленной структуры из взаимосвязанных товарных рынков был разработан алгоритм поиска равновесия по Нэшу, который учитывает стремление каждого рыночного игрока максимизировать свою прибыль с учетом рыночных условий и поведения конкурентов. Благодаря применению методов теории игр и экономического моделирования настоящее исследование дает представление о конкурентной динамике и стратегических взаимодействиях как между игроками в рамках одного товарного рынка с точки зрения конкуренции, так и между самими рынками с точки зрения формирования взаимосвязанного ценообразования. Результаты имеют прикладное значение для разработки рыночных и инвестиционных стратегий предприятий из реальных секторов экономики, программ модернизации производств и оптимизации программ выделения государственных субсидий.
Введение
Поиск новых подходов к оптимизации рыночных стратегий в условиях нестабильной геополитической ситуации и усиливающихся системных изменений в мире является актуальным вопросом. Одним из способов исследовать эффекты от применения той или иной рыночной стратегии является определение состояния рынка, при котором достигается равновесие по Нэшу. Равновесие по Нэшу представляет собой такое состояние экономической системы, при котором ни один из участников экономического процесса не может увеличить прибыль, изменив свою стратегию в одностороннем порядке.
Рассматривается поиск равновесия по Нэшу в системе из двух рынков сырья и продукции, взаимосвязанных посредством переработки сырья в продукцию с добавленной стоимостью. Исследование равновесия по Нэшу на таких рынках имеет важное практическое применение. Например, понимание состояний равновесия может помочь в оптимизации программ модернизации производства, повышении эффективности рыночной стратегии и обосновании политики государственного регулирования. Это исследование также особенно актуально, учитывая нестабильный характер рынков минерально-сырьевого и топливно-энергетического комплексов, где стратегическое взаимодействие производителей, потребителей и регулирующих органов может значительно влиять на общее состояния рынка. Таким образом, стимулом к этому исследованию послужила необходимость разработки надежных алгоритмов, способных находить равновесие по Нэшу в сложных рыночных системах.
Тема поиска равновесия по Нэшу активно исследуется достаточно давно в различных профессиональных областях. Так, поиск равновесия Нэша на несовершенном рынке важен для работы электросети с дерегулированным рынком [1]. С ростом числа возобновляемых источников энергии становится труднее найти равновесие по Нэшу, которое могло бы решить проблему неопределенности возобновляемых источников энергии [2]. Были предложены различные решения этого вопроса с целью максимизации прибыли игроков в некооперативных играх [3]. В статье [4] исследуется динамическая модель международных транзакций «бизнес – бизнес», в которых продавцы и покупатели ищут равновесное состояние в системе спрос – предложение, причем вероятность совпадения зависит как от индивидуальных, так и от совокупных усилий по поиску, в работе [5] исследуется динамика скоординированной монополии с устоявшимися, нейтральными к риску фирмами, и условия, при которых на рынок могут выйти новые конкуренты, а исследование [6] посвящено разработке игровой модели для поиска решений по ценообразованию в конкурентной цепочке поставок, состоящей из доминирующего производителя, который производит один скоропортящийся продукт, и двух ритейлеров, которые вынуждены действовать в условиях нелинейной функции спроса. В статье [7] предлагается метод поиска равновесного состояния рынка на основе аукциона, который применяет методы теории игр с неполной информацией о некооперативной среде. В работе [8] предлагается совершенная конкурентная модель рынка, где цены определяются условиями порога рентабельности. В статье [9] учитываются факторы оптимальных стратегий торгов на рынках со значительной долей возобновляемых источников энергии. В исследовании [10] представлена иерархическая структура распределенного обучения с подкреплением (HNDRL) для поиска равновесий по Нэшу в стратегиях торгов на несовершенных рынках электроэнергии. Помимо равновесия по Нэшу исследователи иногда рассматривают конкурентное равновесие в контексте оптимизации рынков. Например, в статье [11] исследуются различия между равновесием по Нэшу и конкурентным равновесием в контексте рынков электроэнергии. В некоторых работах предлагаются более сложные модели рыночного равновесия, например, в публикации [12] приводится исследование чистых равновесий Нэша в квантовой игре, которая выходит за рамки классической биматричной игры. А в материале [13] исследуется игровой подход Нэша – Штакельберга для анализа стратегических взаимодействий в устойчивых энергетических системах. В статье [14] рассматриваются аналитические и функциональные проблемы понимания влияния добровольных рынков возобновляемой энергии. Авторы подчеркивают отсутствие строгих эмпирических данных и соответствующих статистических методов для выявления этих воздействий.
В современных исследованиях также часто применяют методы теории игр, использующейся для изучения взаимосвязей стратегического поведения рациональных участников рынка, который обычно анализируется с использованием моделей равновесного программирования. Модели равновесия на рынках могут быть классифицированы как модели Курно (для моделирования количеств) [15], Штакельберга (комбинирующие количества и цены) [16], модели, основанные на агентах [17], и др.
В некоторых статьях также рассматриваются расширенные рыночные системы. Так, в работе [5] проводится исследование динамики координированной монополии с устоявшимися, нейтральными к риску фирмами, а в статье [18] показано, что в дилемме заключенных первый наилучший результат достижим, но не может быть интерпретирован как равновесие Нэша. В игре «подсказки» может быть достижим только второй наилучший результат, но существует равновесие Нэша, которое строго предпочтительнее, чем в дилемме заключенных. В статье [19] с помощью теории игр рассматриваются стратегические последствия быстрого энергетического перехода, а в источнике [20] исследуется применение теории игр для долгосрочного энергетического планирования. В статье [21] рассматривается применение теории игр для моделирования поведения участников фондового рынка. Применение методов теории игр и алгоритмов поиска равновесия по Нэшу изучаются в контексте не только моделирования экономических систем, что наглядно показано в источнике [22]. При этом в экономических моделях часто рассматриваются региональные рынки. В статье [23] представлена обобщенная игровая модель Нэша для описания конкурентных отношений между централизованными и локальными энергетическими рынками, а в работе [24] продемонстрирован сравнительный анализ равновесия по Нэшу и последовательного равновесия в контексте региональных энергетических рынков. При этом в источнике [25] исследуется игра, влияющая на рынок, в которой участвуют инвесторы, не склонные к риску.
В некоторых работах, например в [26], рассматриваются исследования методов теории игр, в которых игроки не имеют полной информации об истинном распределении вероятностей, но им необходимо принять решение до реализации рассматриваемых событий. Другие исследования рассматривают сложные рыночные системы из множества продуктовых цепочек, состоящих из поставщиков сырья, поставщиков услуг, производственных интеграторов и потребителей. Тогда модель равновесия для лиц, принимающих решения на всех уровнях, устанавливается вариационным неравенством, что показано в статье [27]. Также в некоторых работах рассматривается влияние поведения участников рынка на ценообразование [28], изучается сеть цепочек поставок сельскохозяйственной продукции [29], для которой устанавливается обобщенная модель равновесия по Нэшу со стохастическими параметрами среди фирм, производящих свежие продукты. Затем происходит преобразование этой модели в смешанную систему с использованием условий Каруша – Куна – Таккера. Иногда исследователи еще больше усложняют задачу, рассматривая не только равновесие, но и так называемые задачи о сделках по Нэшу. Так, в работе [30] предлагается некооперативная модель торгов, которая расширяет модель Рубинштейна.
Точные и аппроксимационные алгоритмы для разных видов игр предлагались с разных точек зрения. Совсем недавно появился ряд работ, продвигающих эти фундаментальные концепции аппроксимации для поиска равновесия по Нэшу. С другой стороны, эмпирические исследования аппроксимации равновесия по Нэшу довольно редки даже для двух игроков [31]. В литературе также рассматривают непрерывные игры, в которых у каждого игрока есть пространство непрерывного действия. В данном случае концепция решения, называемая локальным равновесием по Нэшу, характеризует стратегию, в котором ни один игрок не может получить больший положительный эффект при отклонении от локальной окрестности своей стратегии. Некоторые авторы рассматривают сложные рыночные системы с олигополистическими механизмами ценообразования в цепочках поставок. Однако существующий механизм последовательного ценообразования не в полной мере учитывает ограничения, такие как объем закупок фирм и информацию об изменении каждого параметра, что приводит к отрыву механизма ценообразования от реального рынка [32]. Однако существует и другая проблема, связанная со сходимостью сложных систем, особенно когда методы теории игр применяют для исследования не только экономики, а, например, для моделирования взаимодействующих биологических и социальных систем. Если система не настроена для достижения равновесия, то ее поведение может быть непредсказуемым [33]. Также иногда исследователи рассматривают равновесие Байеса [34], которое является обобщением равновесия по Нэшу в смешанных стратегиях.
На основании приведенного анализа можно сделать вывод, что в большинстве существующих научных работ, так или иначе затрагивающих тему равновесия по Нэшу на различных рынках, рассматриваются в основном энергетические рынки, в меньшей степени исследуются товарные рынки. При этом вопросы поиска равновесия на взаимосвязанных рынках сырья и продукции встречаются намного реже, что подчеркивает актуальность настоящей работы.
Научная новизна и цель работы заключается в создании алгоритма поиска равновесий по Нэшу на двух взаимосвязанных рынках сырья и продукции (вместе – товары). Данная рыночная система характеризуется следующими особенностями:
- на рынке продукции и рынке сырья участвуют по несколько игроков;
- производители продукции на рынке сырья являются покупателями сырья, а на рынке продукции – продавцами;
- покупатели продукции в явном виде задают функцию спроса на продукцию, которая определяется моделью Курно;
- функция спроса на рынке сырья задается неявно c учетом рыночной конъюнктуры на рынке продукции;
- для каждого рынка рассматривается бескоалиционная игра;
- передача сырья и продукции от продавца к покупателю происходит в рамках единых межрыночных бирж, которые хранят весь объем произведенного товара, т.е. продавцы не могут выбирать, кому из покупателей они продают товар и в каком количестве;
- удельные операционные издержки на единицу товара каждого рыночного игрока постоянны и включают в себя все возможные затраты, которые игроки несут в рамках своей операционной деятельности, в том числе затраты на производство, логистику, налоги и иные издержки.
Методы
Постановка проблемы. Рассматривается бескоалиционная игра, в которой часть игроков участвует на обоих рынках: потребители сырья на одном рынке являются производителями продукции на другом. Как следствие, функция спроса на рынке сырья задается неявно, и стандартные методы поиска равновесия сведением к одному рынку не эффективны в приложении к представленной задаче. Рассмотрим общую математическую постановку задачи для поиска равновесия по Нэшу на каждом рынке. Игроки на каждом рынке стремятся максимизировать свою прибыль:
где Pij – прибыль каждого игрока, у.е.; i = 1, 2 – индексы рынков (1 – рынок продукции, 2 – рынок сырья); j = 1, 2, 3 …Si – индексы игроков на каждом рынке (Si – общее количество игроков на каждом i-м рынке);xij – суммарное количество товара, проданного j-м игроком на i-м рынке; R+– множество неотрицательных действительных чисел.
Прибыль каждого игрока рассчитывается из разницы между полученной от продажи товара выручкой и понесенными операционными издержками:
где Rij – выручка каждого игрока, полученная от продажи товара, у.е.; Cij – итоговые операционные издержки каждого игрока, у.е.
Выручка каждого игрока рассчитывается из произведения суммарного количества проданного товара каждого типа и стоимости этого товара на рынке, которая зависит от функции спроса на соответствующем рынке:
где pricei(Qi) – функция спроса на товар на i-м рынке; Qi – суммарное количество товара, произведенного на i-м рынке.
Функция спроса на рынке продукции задается в явном виде:
где а – коэффициент функции спроса на рынке продукции, у.е.; Q1 – суммарное количество произведенной игроками продукции, , ед.
Функция спроса на рынке сырья price2(Q2) задается в неявном виде.
Итоговые операционные издержки производителей продукции зависят от удельных операционных издержек, а также стоимости сырья на рынке сырья. С учетом того, что количество произведенной продукции пропорционально количеству потребленного сырья для каждого игрока, итоговые операционные издержки производителей продукции определяются по формуле:
где с1j – удельные операционные издержки на производство единицы продукции, у.е./ед.; u – коэффициент преобразования сырья в продукцию, описывающий количество единиц сырья, необходимое для производства одной единицы продукции; price2(Q2) – функция спроса на сырье; Q2 – суммарное количество сырья, приобретаемого производителями продукции на рынке сырья, ед.;x1j – объем продукции, произведенный каждым игроком на рынке продукции, ед.
Итоговые понесенные издержки производителей сырья определяются по формуле:
где c2j – удельные операционные издержки на производство единицы сырья, у.е./ед.; x2j – объем сырья, произведенного каждым игроком на рынке сырья, ед.
Предлагаемое решение. Алгоритм поиска равновесного состояния между взаимосвязанными рынками сырья и продукции выглядит следующим образом:
- В явном виде задать функцию спроса на рынке продукции.
- Для каждого игрока на всех рынках задать значения удельных издержек на производство единицы товара.
- Выполнить аппроксимацию функции спроса на рынке сырья:
а) осуществить поиск равновесия по Нэшу для рынка продукции при каждом заданном значении стоимости сырья; стоимость сырья задать в определенном диапазоне с N количеством точек;
б) на основе полученного множества значений объема спроса на сырье и стоимости сырья выполнить аппроксимацию функции спроса на рынке сырья методом наименьших квадратов. - Реализовать поиск равновесия по Нэшу для рынка сырья с учетом полученной функции спроса на рынке сырья. Рассчитать значения параметров рынка сырья (общий объем произведенного сырья и его удельная стоимость), при которых достигается равновесие по Нэшу.
- Выполнить поиск равновесия по Нэшу на рынке продукции с учетом полученной удельной стоимости сырья. Рассчитать значение объема произведенной продукции.
Равновесное состояние между взаимосвязанными рынками сырья и продукции считается достигнутым, когда полученные в результате выполнения предлагаемого алгоритма объемы производства сырья и продукции сходятся.
Для поиска равновесия по Нэшу для каждого рынка предлагается использовать метод нащупывания, который подразумевает, что каждый игрок в рамках соответствующего рынка и согласно условиям бескоалиционной игры стремится максимизировать свою прибыль с учетом известных исторических данных о рыночных стратегиях конкурентов. Для решения задачи максимизации прибыли каждого игрока применялась библиотека алгоритмов для научных и инженерных расчетов SciPy. В качестве метода оптимизации применялся симплекс-метод Нелдера – Мида. Блок-схема описанного алгоритма отображена на рис.1.
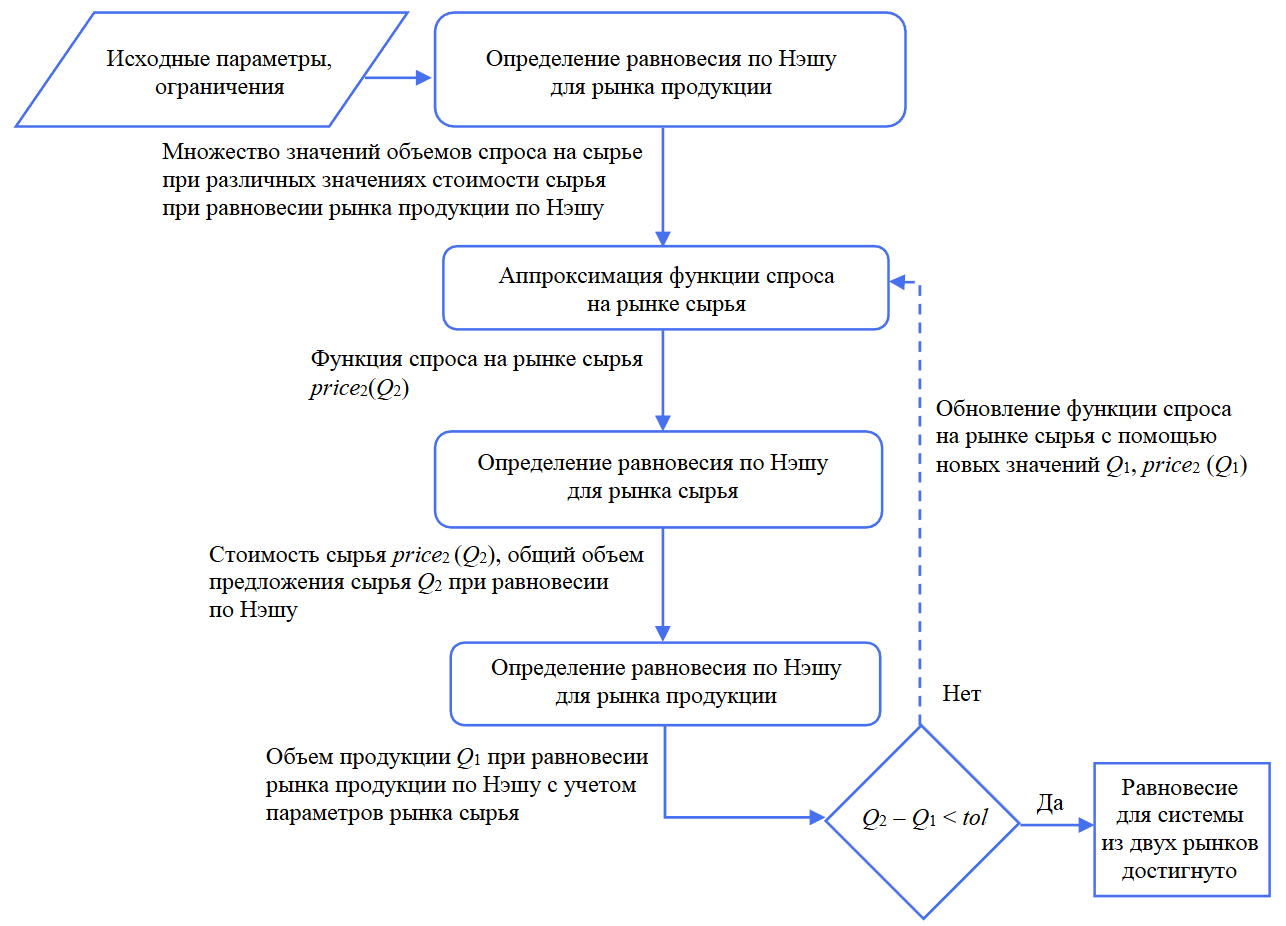
Рис.1. Алгоритм поиска равновесного состояния между взаимосвязанными рынками сырья и продукции
Численный эксперимент. Применим предложенный алгоритм для поиска равновесного состояния между взаимосвязанными рынками сырья и продукции. Для наглядности предположим, что в качестве сырья выступает сырая нефть, а в качестве продукции – нефтепродукты. Таким образом, примем u = 1. Зададим исходные значения параметров (табл.1). Удельные операционные издержки на производство единицы товара для производителей нефти и нефтепродуктов выберем случайно из диапазонов c1j ∈ |60,160|, c2j ∈ |20,160|. Обозначим данный набор значений исходных параметров под рыночным сценарием № 1.
Таблица 1
Исходные значения параметров для рыночного сценария № 1
|
Параметр |
Значение |
|
Коэффициент функции спроса на рынке продукции (нефтепродукты) а, у.е. |
200 000 |
|
Удельные операционные издержки на производство единицы товара, у.е./ед. |
|
|
Производитель продукции (нефтепродуктов) 1 с11 |
25 |
|
Производитель продукции (нефтепродуктов) 2 с12 |
40 |
|
Производитель продукции (нефтепродуктов) 3 с13 |
80 |
|
Производитель продукции (нефтепродуктов) 4 с14 |
120 |
|
Производитель продукции (нефтепродуктов) 5 с15 |
160 |
|
Производитель сырья (нефти) 1 с21 |
110 |
|
Производитель сырья (нефти) 2 с22 |
135 |
|
Производитель сырья (нефти) 3 с23 |
80 |
|
Производитель сырья (нефти) 4 с24 |
105 |
|
Производитель сырья (нефти) 5 с25 |
120 |
Рассмотрим результаты каждого шага алгоритма:
1. В явном виде зададим функцию спроса на рынке нефтепродуктов в соответствии с формулой (1):
2. Для каждого игрока зададим значения удельных операционных издержек на производство (табл.1).
3. Выполним аппроксимацию функции спроса на рынке нефти методом наименьших квадратов:
а) зададим диапазон значений стоимости нефти с количеством точек N = 50:
Результаты поиска равновесия по Нэшу на рынке нефтепродуктов методом нащупывания с учетом выбранных точек в заданном диапазоне значений стоимости нефти представлены в табл.2;
б) выполним аппроксимацию функции спроса на рынке нефти методом наименьших квадратов с учетом значений в табл.2. Примем, что функция спроса имеет вид полинома четвертой степени, так как полином четвертой степени достигает лучшего значения коэффициента детерминации в рамках данного численного эксперимента (R2 = 0,99904 для полинома четвертой степени; R2 = 0,97498 для полинома третьей степени; R2 = 0,85784 для гиперболы):
где Q2 – суммарный объем произведенной игроками нефти, ед., .
В результате были получены следующие значения коэффициентов функции спроса на рынке нефти для рыночного сценария № 1: А = 1,72·10–11; В = –1,50·10–7; С = 4,95·10–4; D = –7,55·10–1; E = 4,79·102.
Таблица 2
Результаты расчета объемов спроса на нефть при различной удельной стоимости нефти для рыночного сценария № 1
|
Параметр |
Значения |
||||
|
Удельная стоимость нефти, у.е./ед. |
0,00 |
3,06 |
6,12 |
9,18 |
12,24 |
|
Объем спроса на нефть, ед. |
3076,61 |
2811,84 |
2589,01 |
2398,94 |
2234,90 |
|
Удельная стоимость нефти, у.е./ед. |
15,31 |
18,37 |
21,43 |
24,49 |
27,55 |
|
Объем спроса на нефть, ед. |
2095,14 |
1998,98 |
1911,26 |
1830,92 |
1757,06 |
|
Удельная стоимость нефти, у.е./ед. |
30,61 |
33,67 |
36,73 |
39,80 |
42,86 |
|
Объем спроса на нефть, ед. |
1688,92 |
1625,88 |
1567,37 |
1512,93 |
1462,14 |
|
Удельная стоимость нефти, у.е./ед. |
45,92 |
48,98 |
52,04 |
55,10 |
58,16 |
|
Объем спроса на нефть, ед. |
1414,65 |
1370,15 |
1328,36 |
1289,05 |
1252,00 |
|
Удельная стоимость нефти, у.е./ед. |
61,22 |
64,29 |
67,35 |
70,41 |
73,47 |
|
Объем спроса на нефть, ед. |
1217,01 |
1183,93 |
1152,60 |
1122,89 |
1094,67 |
|
Удельная стоимость нефти, у.е./ед. |
76,53 |
79,59 |
82,65 |
85,71 |
88,78 |
|
Объем спроса на нефть, ед. |
1067,83 |
1042,27 |
1017,92 |
994,67 |
972,46 |
|
Удельная стоимость нефти, у.е./ед. |
91,84 |
94,90 |
97,96 |
101,02 |
104,08 |
|
Объем спроса на нефть, ед. |
951,23 |
930,90 |
913,47 |
896,75 |
880,64 |
|
Удельная стоимость нефти, у.е./ед. |
107,14 |
110,20 |
113,27 |
116,33 |
119,39 |
|
Объем спроса на нефть, ед. |
865,09 |
850,08 |
835,58 |
821,57 |
808,03 |
|
Удельная стоимость нефти, у.е./ед. |
122,45 |
125,51 |
128,57 |
131,63 |
134,69 |
|
Объем спроса на нефть, ед. |
794,92 |
782,23 |
769,94 |
758,03 |
746,48 |
|
Удельная стоимость нефти, у.е./ед. |
137,76 |
140,82 |
143,88 |
146,94 |
150,00 |
|
Объем спроса на нефть, ед. |
735,28 |
724,41 |
713,85 |
703,60 |
693,64 |
Малые значения коэффициентов А и В полинома четвертой степени объясняются тем, что значения аргумента функции (суммарного объема нефти) достигают нескольких тысяч единиц. Отобразим рассчитанные значения удельной стоимости нефти и соответствующего объема спроса на нефть из табл.2, а также аппроксимированную функцию спроса на нефть (рис.2).
4. В результате расчета равновесия по Нэшу для рынка нефти с учетом аппроксимированной функции спроса получим значение удельной стоимости нефти при равновесии рынка нефти по Нэшу price2(Q2)=146,39 у.е./ед.
5. Выполним поиск равновесия по Нэшу для рынка нефтепродуктов с учетом значения удельной стоимости нефти, рассчитанного на шаге 4. На рис.3 представлены графики изменения прибыли каждого производителя нефти и нефтепродуктов при каждом шаге поиска равновесия по Нэшу для соответствующего рынка. Значения рыночных параметров игроков при достижении равновесия по Нэшу на каждом рынке продемонстрированы в табл.3.
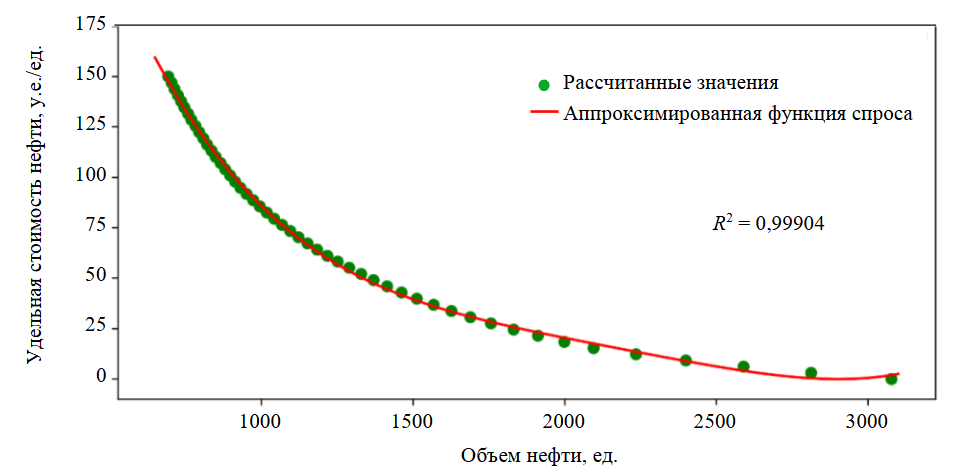
Рис.2. Результат аппроксимации функции спроса на рынке нефти для рыночного сценария № 1
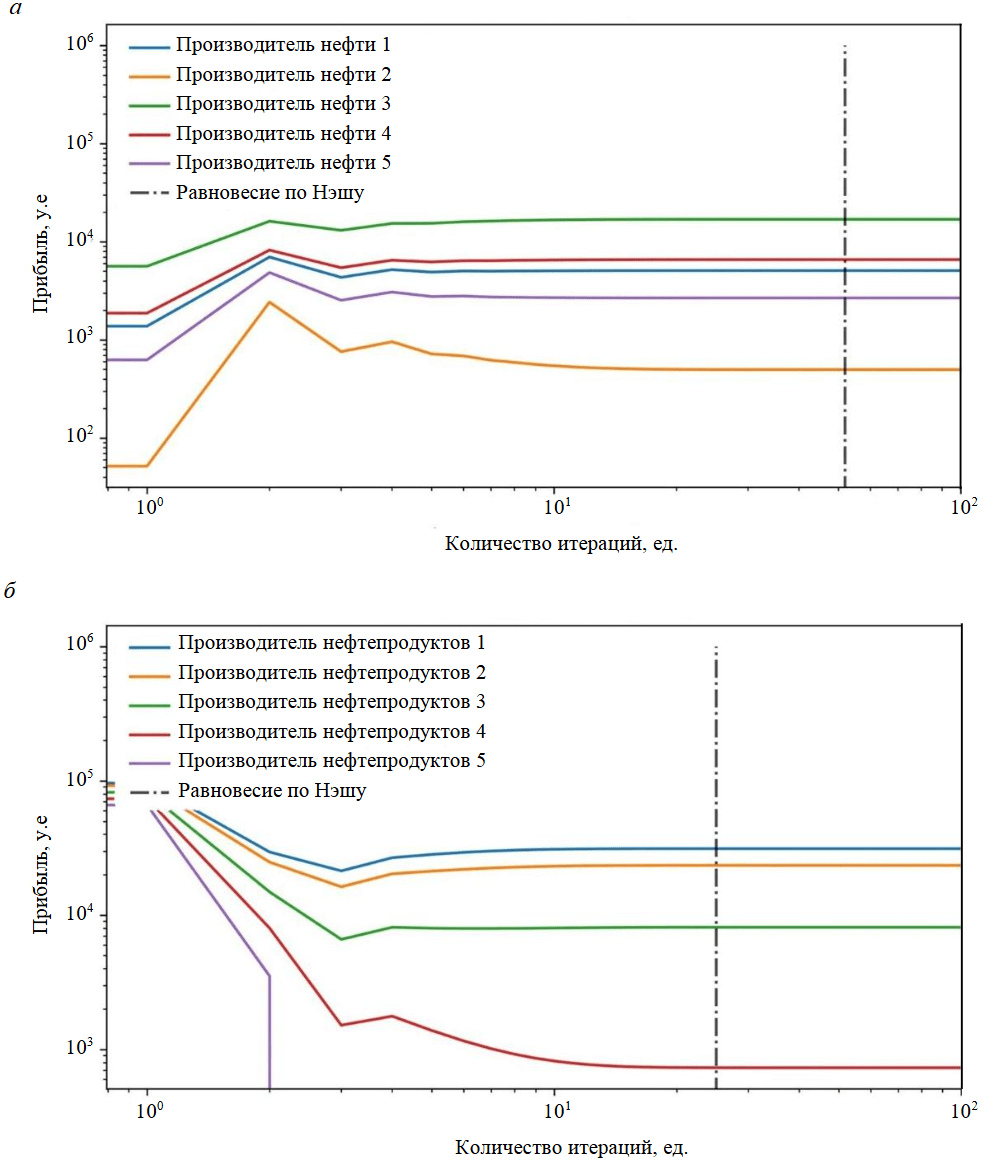
Рис.3. Результаты поиска равновесия по Нэшу для рынка нефти – сырья (а) и рынка нефтепродуктов – продукции (б) для рыночного сценария № 1
Исходя из приведенных результатов (рис.3, табл.3) можно сделать следующие выводы:
- Разница между итоговыми значениями объемов производимой нефти и нефтепродуктов пренебрежительно мала, что позволяет утверждать о достижении равновесного состояния между взаимосвязанными рынками сырья и продукции за одну итерацию алгоритма.
- При данной рыночной конъюнктуре производитель нефтепродуктов 5 оказался неконкурентоспособным по причине повышенных операционных издержек по сравнению с другими производителями, что привело к снижению его объема производства и, соответственно, прибыли до нуля. При этом производитель нефтепродуктов 1, обладающий наиболее эффективным производством с наименьшими операционными издержками, занял лидирующую позицию на рынке как по объемам производства, так и прибыли. Данное наблюдение подтверждает способность алгоритма отражать рыночную динамику, которая соответствует заданной конъюнктуре рынка.
- Метод нащупывания показывает быструю сходимость: равновесие по Нэшу для рынка нефти было достигнуто за 53 итерации, а равновесие по Нэшу для рынка нефтепродуктов – за 26 итераций.
Таблица 3
Рыночные параметры игроков на рынке нефти и рынке нефтепродуктов при достижении равновесия по Нэшу для рыночного сценария № 1
|
Параметр |
Значение |
||||
|
Индекс игрока |
|||||
|
1 |
2 |
3 |
4 |
5 |
|
|
Рынок сырья |
|||||
|
Прибыль, у.е. |
5076,98 | 497,58 | 16897,09 | 6567,85 | 2670,24 |
|
Объем производимой нефти, ед. |
139,50 |
43,67 | 254,50 | 158,67 | 101,17 |
|
Объем производимой нефти (всего), ед. |
697,52 |
||||
|
Удельная стоимость нефти, у.е./ед. |
146,39 | ||||
| Рынок продукции | |||||
|
Прибыль, у.е. |
31282,49 | 23472,85 | 8120,71 | 730,16 |
0,00 |
|
Объем производимых нефтепродуктов, ед. |
278,97 | 241,65 | 142,13 | 42,65 |
0,00 |
|
Объем производимых нефтепродуктов (всего), ед. |
705,41 |
||||
|
Удельная стоимость нефтепродуктов, у.е./ед. |
283,52 | ||||
При аппроксимации функции спроса на сырье гиперболой в результате применения алгоритма объем нефти составил Q2 = 640,73 ед., объем нефтепродуктов Q1 = 736,19 ед., а коэффициент детерминации R2 = 0,85784. Такая разница между итоговыми значениями объемов не позволяет говорить о достижении равновесного состояния между взаимосвязанными рынками сырья и продукции. Точность аппроксимации функции спроса на сырье непосредственно влияет на поиск конечного состояния равновесия рыночной системы.
Для демонстрации практической значимости предложенного подхода рассмотрим ситуацию, когда производитель нефтепродуктов (продукции) 5 выполнил оптимизацию своего производства, что привело к снижению его удельных операционных издержек на 20 %: с15 = 128 у.е./ед. Обозначим данный набор значений исходных параметров рыночным сценарием № 2.
Для рыночного сценария № 2 выполним все шаги алгоритма поиска равновесного состояния между двумя взаимосвязанными рынками нефти и нефтепродуктов. Результаты расчета объемов спроса на нефть при различной удельной стоимости нефти представлены в табл.4. На рис.4 укажем результат аппроксимации функции спроса на рынке нефти. Значения коэффициентов функции спроса на рынке нефти для рыночного сценария № 2: А = 1,83·10–11; В = –1,59·10–7; С = 5,18·10–4; D = –7,82·10–1; Е = 4,91·102. Результаты поиска равновесия по Нэшу на рынках нефти и нефтепродуктов показаны на рис.5, итоговые рыночные параметры игроков на рынке нефти и нефтепродуктов при достижении равновесия по Нэшу продемонстрированы в табл.5.
Таблица 4
Результаты расчета объемов спроса на нефть при различной удельной стоимости нефти для рыночного сценария № 2
|
Параметр |
Значения |
||||
|
Удельная стоимость нефти, у.е./ед. |
0,00 |
3,06 |
6,12 |
9,18 |
12,24 |
|
Объем спроса на нефть, ед. |
3076,65 |
2811,83 |
2589,01 |
2398,89 |
2234,88 |
|
Удельная стоимость нефти, у.е./ед. |
15,31 |
18,37 |
21,43 |
24,49 |
27,55 |
|
Объем спроса на нефть, ед. |
2095,15 |
1998,98 |
1911,26 |
1830,92 |
1757,06 |
|
Удельная стоимость нефти, у.е./ед. |
30,61 |
33,67 |
36,73 |
39,80 |
42,86 |
|
Объем спроса на нефть, ед. |
1688,93 |
1625,88 |
1567,37 |
1512,93 |
1462,14 |
|
Удельная стоимость нефти, у.е./ед. |
45,92 |
48,98 |
52,04 |
55,10 |
58,16 |
|
Объем спроса на нефть, ед. |
1414,65 |
1370,15 |
1328,36 |
1289,05 |
1252,00 |
|
Удельная стоимость нефти, у.е./ед. |
61,22 |
64,29 |
67,35 |
70,41 |
73,47 |
|
Объем спроса на нефть, ед. |
1217,01 |
1183,93 |
1152,60 |
1122,89 |
1094,66 |
|
Удельная стоимость нефти, у.е./ед. |
76,53 |
79,59 |
82,65 |
85,71 |
88,78 |
|
Объем спроса на нефть, ед. |
1067,83 |
1042,28 |
1017,92 |
994,67 |
972,46 |
|
Удельная стоимость нефти, у.е./ед. |
91,84 |
94,90 |
97,96 |
101,02 |
104,08 |
|
Объем спроса на нефть, ед. |
951,23 |
930,90 |
913,47 |
896,75 |
880,63 |
|
Удельная стоимость нефти, у.е./ед. |
107,14 |
110,20 |
113,27 |
116,33 |
119,39 |
|
Объем спроса на нефть, ед. |
865,09 |
850,08 |
835,58 |
821,57 |
808,13 |
|
Удельная стоимость нефти, у.е./ед. |
122,45 |
125,51 |
128,57 |
131,63 |
134,69 |
|
Объем спроса на нефть, ед. |
795,83 |
783,89 |
772,31 |
761,06 |
750,14 |
|
Удельная стоимость нефти, у.е./ед. |
137,76 |
140,82 |
143,88 |
146,94 |
150,00 |
|
Объем спроса на нефть, ед. |
739,52 |
729,21 |
719,17 |
709,41 |
699,91 |
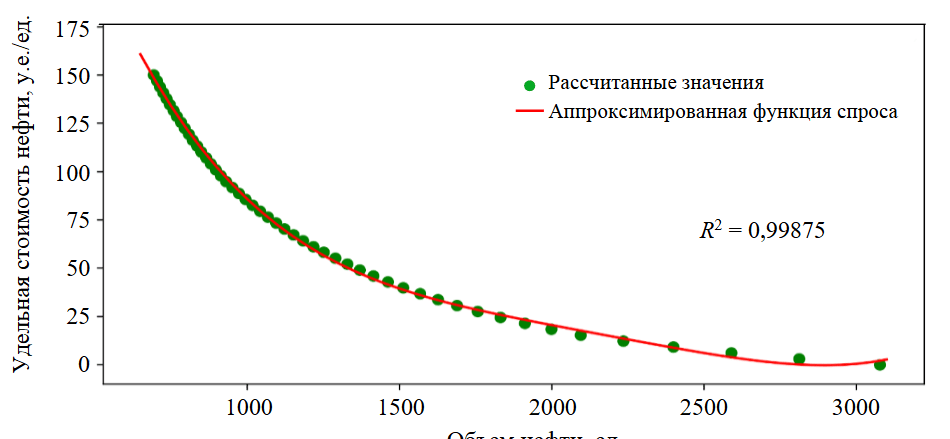
Рис.4. Результат аппроксимации функции спроса на рынке нефти для рыночного сценария № 2
Исходя из приведенных результатов (рис.5, табл.5), можно сделать следующие выводы:
- Разница между итоговыми значениями объемов производимой нефти и нефтепродуктов пренебрежительно мала, что позволяет утверждать о достижении равновесного состояния между взаимосвязанными рынками сырья и продукции за одну итерацию алгоритма.
- Снижение удельных операционных издержек производителя нефтепродуктов 5 привело к повышению его конкурентоспособности, что позволило ему восстановить экономически целесообразное производство, занять долю на рынке и возобновить получение экономической прибыли. Данный результат еще раз демонстрирует способность алгоритма отражать рыночную динамику при заданной рыночной структуре и особенностях каждого из игроков.
- Метод нащупывания показывает быструю сходимость: равновесие по Нэшу для рынка нефти было достигнуто за 79 итераций, а равновесие по Нэшу для рынка нефтепродуктов – за 52 итерации.
Дополнительно рассмотрим ситуацию, когда на рынках представлено неравное количество производителей сырья и продукции: три производителя нефтепродуктов и семь производителей нефти (сценарий № 3). Выполним все шаги алгоритма поиска равновесного состояния между двумя взаимосвязанными рынками нефти и нефтепродуктов. В качестве исходных значений для рыночного сценария примем значения табл.1. При этом на рынках будут присутствовать производители нефтепродуктов под индексами j = 1, 2, 3 (см. табл.1), а к производителям нефти с индексами j = 1, 2, 3, 4, 5 присоединятся новые производители нефти j = 6, 7 и удельными операционными издержками с26 = 90 у.е./ед., с27 = 75 у.е./ед. соответственно.
В результате применения алгоритма объем производимой нефти составил Q2 = 792,18 ед., а объем производимых нефтепродуктов – Q1 = 787,47 ед. Разница между итоговыми значениями объемов производимой нефти и нефтепродуктов пренебрежительно мала, что позволяет говорить о достижении равновесного состояния между взаимосвязанными рынками сырья и продукции за одну итерацию алгоритма, а также демонстрирует возможность его применения для рыночных систем с неравным количеством игроков на рынках сырья и продукции.
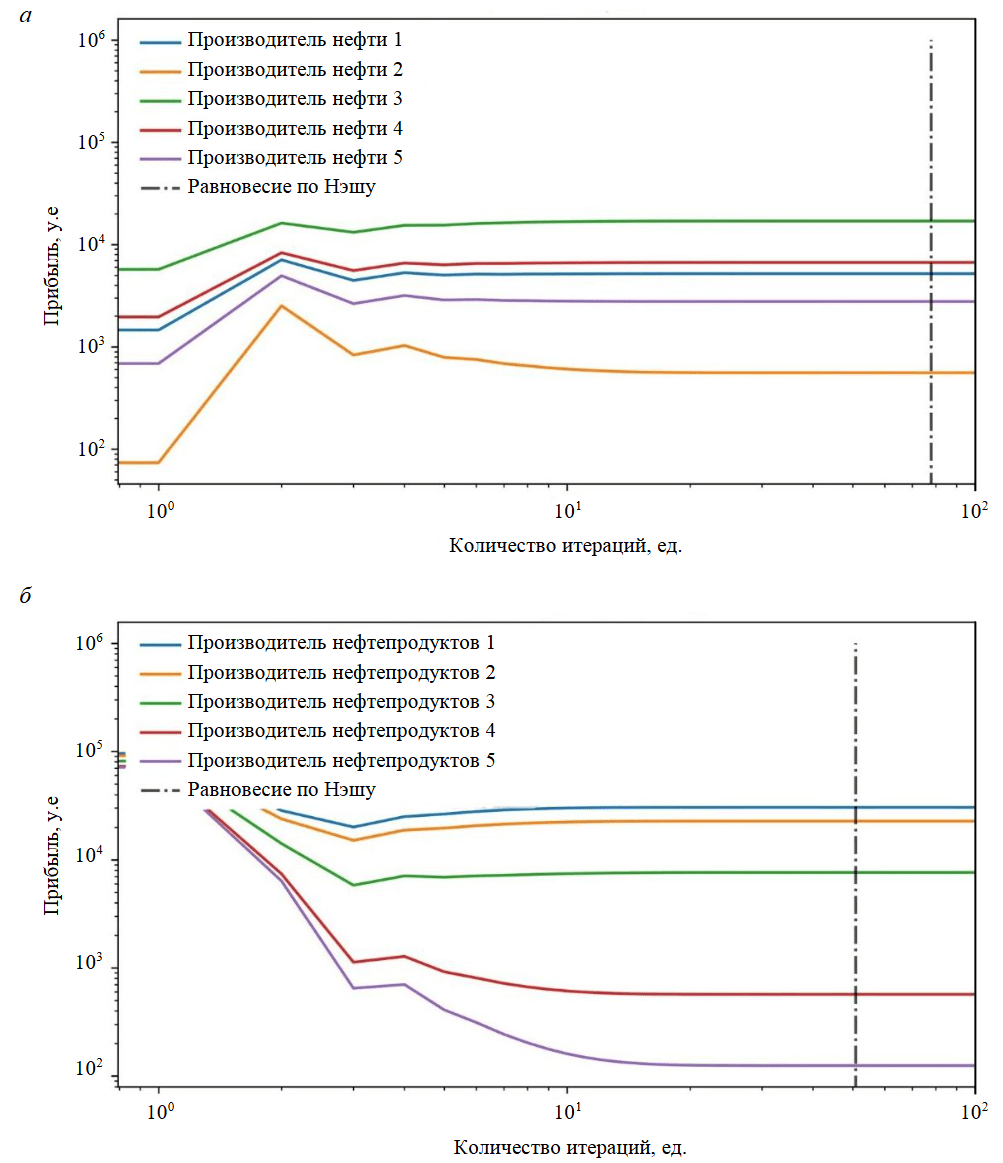
Рис.5. Результаты поиска равновесия по Нэшу для рынка нефти – сырья (а) и рынка нефтепродуктов – продукции (б) для рыночного сценария № 2
Таблица 5
Рыночные параметры игроков на рынке нефти и рынке нефтепродуктов при достижении равновесия по Нэшу для рыночного сценария № 2
|
Наименование параметра |
Значение |
||||
|
Индекс игрока |
|||||
|
1 |
2 |
3 |
4 |
5 |
|
|
Рынок сырья |
|||||
|
Прибыль, у.е. |
5194,07 | 557,69 | 16956,02 | 6684,83 | 2776,04 |
|
Объем производимой нефти, ед. |
139,68 |
45,77 | 252,38 | 158,47 | 102,12 |
|
Объем производимой нефти (всего), ед. |
698,42 |
||||
|
Удельная стоимость нефти, у.е./ед. |
147,18 | ||||
| Рынок продукции | |||||
|
Прибыль, у.е. |
30406,85 | 22682,49 | 7608,08 | 568,42 |
124,66 |
|
Объем производимых нефтепродуктов, ед. |
276,31 | 238,65 | 138,21 | 37,78 |
17,69 |
|
Объем производимых нефтепродуктов (всего), ед. |
708,64 |
||||
|
Удельная стоимость нефтепродуктов, у.е./ед. |
282,23 | ||||
Результаты
Несмотря на неявный вид функции спроса на рынке сырья, а также комплексность рыночной системы, которая заключается в участии производителей продукции сразу на обоих рынках, предложенный алгоритм, включающий в себя применение метода нащупывания для поиска равновесия по Нэшу для каждого рынка и подхода к аппроксимации функции спроса, успешно продемонстрировал свою способность выполнять поиск равновесного состояния в системе из двух взаимосвязанных рынков сырья и продукции. При этом численные эксперименты, представленные в работе, продемонстрировали следующее:
- Рыночная динамика и итоговое положение игроков на рынках соответствует заданной рыночной конъюнктуре.
- Предложенный алгоритм не приводит к неустойчивости системы, несмотря на комплексное взаимодействие рынков и игроков.
- Численные эксперименты демонстрируют быструю сходимость предложенного алгоритма.
- Подход к аппроксимации функции спроса на рынке сырья является достаточно точным для решения поставленной задачи.
Заключение
Поиск равновесного состояния между взаимосвязанными рынками сырья и продукции является важной прикладной задачей, особенно в случаях, когда рассматриваются рынки стратегических товаров, относящихся к минерально-сырьевому и топливно-энергетическому комплексам, которые кроме прочего могут зависеть не только от комплексной рыночной конъюнктуры, но и испытывать влияние со стороны внешних регуляторных органов, геополитических изменений.
Результаты численных экспериментов при различных рыночных сценариях продемонстрировали практическую значимость применения алгоритма для оптимизации рыночных стратегий игроков, планирования различных мероприятий по повышению рыночной конкурентоспособности и эффективности производства, а также снижения операционных издержек. Предложенный алгоритм также позволяет анализировать изменения в системе из двух взаимосвязанных рынков в целом – оценивать влияние рынков друг на друга при изменениях в конъюнктуре на одном и них.
В качестве дальнейшего шага предполагается внедрение в алгоритм возможности учета дополнительных факторов, которые могут влиять на итоговое равновесное состояние рыночной системы, таких как углеродное регулирование, логистика, различные инфраструктурные риски. Данное улучшение позволит точнее учитывать особенности комплексной рыночной конъюнктуры стратегических товаров, которые относятся к минерально-сырьевому и топливно-энергетическому комплексам. Таким образом управленческие решения, определяющие рыночные стратегии игроков, будут более эффективны.
Литература
- Nan Shang, Yi Ding, Wenqi Cui. Review of Market Power Assessment and Mitigation in Reshaping of Power Systems // Journal of Modern Power Systems and Clean Energy. 2022. Vol. 10. P. 1067-1084.
- Jian-jian Shen, Chun-tian Cheng, Ze-bin Jia et al. Impacts, challenges and suggestions of the electricity market for hydro-dominated power systems in China // Renewable Energy. 2022. Vol. 187. P. 743-759. DOI: 10.1016/j.renene.2022.01.089
- Sharifi R., Anvari-Moghaddam A., Fathi S.H., Vahidinasab V. A bi-level model for strategic bidding of a price-maker retailer with flexible demands in day-ahead electricity market // International Journal of Electrical Power & Energy Systems. 2020. Vol. 121. № 106065. DOI: 10.1016/j.ijepes.2020.106065
- Eaton J., Jinkins D., Tybout J.R., Daniel Xu. Two-Sided Search in International Markets. National Bureau of Economic Research Working Paper Series, 2022. № 29684.
- Forrest J.Y.-L., Buttermore J., Wajda T.A. At Nash equilibrium when new market competitions appear? // Kybernetes. 2017. Vol. 46. Iss. 2. P. 256-271. DOI: 10.1108/K-11-2016-0311
- Rajabi N., Mozafari M., Naimi-Sadigh A. Bi-level pricing and inventory strategies for perishable products in a competitive supply chain // RAIRO – Operations Research. 2021. Vol. 55. № 4. P. 2395-2412. DOI: 10.1051/ro/2021106
- Nezarat A., Dastghaibifard G.H. Efficient Nash Equilibrium Resource Allocation Based on Game Theory Mechanism in Cloud Computing by Using Auction // PLOS ONE. 2015. Vol. 10 (10). № e0138424. DOI: 10.1371/journal.pone.0138424
- Azevedo E.M., Gottlieb D. Perfect Competition in Markets with Adverse Selection // Econometrica. 2017. Vol. 85. Iss. 1. P. 67-105. DOI: 10.3982/ECTA13434
- Xiu Ji, Cong Li, Dexin Li, Chenglong Qi. Bidding Strategy of Two-Layer Optimization Model for Electricity Market Considering Renewable Energy Based on Deep Reinforcement Learning // Electronics. 2022. Vol. 11. Iss. 19. № 3107. DOI: 10.3390/electronics11193107
- Liying Yu, Peng Wang, Zhe Chen et al. Finding Nash equilibrium based on reinforcement learning for bidding strategy and distri-buted algorithm for ISO in imperfect electricity market // Applied Energy. 2023. Vol. 350. № 121704. DOI: 10.1016/j.apenergy.2023.121704
- Haibing Wang, Jian Deng, Chengmin Wang et al. Comparing Competition Equilibrium with Nash Equilibrium in Electric Power Market // CSEE Journal of Power and Energy Systems. 2018. Vol. 4. № 3. P. 299-304. DOI: 10.17775/CSEEJPES.2015.01140
- Frąckiewicz P., Szopa M., Makowski M., Piotrowski E. Nash Equilibria of Quantum Games in the Special Two-Parameter Strategy Space // Applied Sciences. 2022. Vol. 12. Iss. 22. № 11530. DOI: 10.3390/app122211530
- Zhenxing Lei, Mingbo Liu, Zhijun Shen et al. A Nash–Stackelberg game approach to analyze strategic bidding for multiple DER aggregators in electricity markets // Sustainable Energy, Grids and Networks. 2023. Vol. 35. № 101111. DOI: 10.1016/j.segan.2023.101111
- O’Shaughnessy E., Sumner J. The need for better insights into voluntary renewable energy markets // Frontiers in Sustainable Energy Policy. 2023. Vol. 2. № 1174427. DOI: 10.3389/fsuep.2023.1174427
- Acemoglu D., Kakhbod A., Ozdaglar A. Competition in Electricity Markets with Renewable Energy Sources // The Energy Journal. 2017. Vol. 38. Suppl. 1. P. 137-155. DOI: 10.5547/01956574.38.SI1.dace
- Yujing Huang, Yudong Wang, Nian Liu. A two-stage energy management for heat-electricity integrated energy system considering dynamic pricing of Stackelberg game and operation strategy optimization // Energy. 2022. Vol. 244. Part A. № 122576. DOI: 10.1016/j.energy.2021.122576
- Yanchang Liang, Chunlin Guo, Zhaohao Ding, Huichun Hua. Agent-Based Modeling in Electricity Market Using Deep Deterministic Policy Gradient Algorithm // IEEE Transactions on Power Systems. 2020. Vol. 35. Iss. 6. P. 4180-4192. DOI: 10.1109/TPWRS.2020.2999536
- Barrett S., Dannenberg A. Tipping Versus Cooperating to Supply a Public Good // Journal of the European Economic Association. 2017. Vol. 15. Iss. 4. P. 910-941. DOI: 10.1093/jeea/jvw022
- Yujiao Liu, Yan Li, Yiping Rong et al. Benefit allocation of electricity–gas–heat–hydrogen integrated energy system based on Shapley value // Clean Energy. 2023. Vol. 7. Iss. 6. P. 1381-1390. DOI: 10.1093/ce/zkad062
- Pfeifer A., Feijoo F., Duić N. Fast energy transition as a best strategy for all? The nash equilibrium of long-term energy planning strategies in coupled power markets // Energy. 2023. Vol. 284. № 129109. DOI: 10.1016/j.energy.2023.129109
- Hannafey K. Modeling the Stock Market Through Game Theory: Thesis submitted in partial fulfillment of the requirements for Honors in Mathematical Science. Georgia Southern University, 2021. № 590. 35 p.
- Samuelson L. Game Theory in Economics and Beyond // Journal of Economic Perspectives. 2016. Vol. 30. № 4. P. 107-130.
- Dong Xie, Mingbo Liu, Lixin Xu, Wentian Lu. Generalized Nash equilibrium analysis of transmission and distribution coordination in coexistence of centralized and local markets // International Journal of Electrical Power & Energy Systems. 2022. Vol. 137. № 107762. DOI: 10.1016/j.ijepes.2021.107762
- Michelacakis N.J. Nash versus consistent equilibrium: A comparative perspective on a mixed duopoly location model of spatial price discrimination with delegation // Regional Science and Urban Economics. 2023. Vol. 99. № 103860. DOI: 10.1016/j.regsciurbeco.2022.103860
- Xiangge Luo, Schied A. Nash Equilibrium for Risk-Averse Investors in a Market Impact Game with Transient Price Impact // Market Microstructure and Liquidity. 2019. Vol. 5. № 01n04. № 2050001. DOI: 10.1142/S238262662050001X
- Yongchao Liu, Huifu Xu, Shu-Jung Sunny Yang, Jin Zhang. Distributionally robust equilibrium for continuous games: Nash and Stackelberg models // European Journal of Operational Research. 2018. Vol. 265. Iss. 2. P. 631-643. DOI: 10.1016/j.ejor.2017.07.050
- Yongtao Peng, Dan Xu, Yaya Li, Kun Wang. A Product Service Supply Chain Network Equilibrium Model considering Capacity Constraints // Mathematical Problems in Engineering. 2020. Vol. 2020. Iss. 1. № 295072. DOI: 10.1155/2020/1295072
- Xiao Chen, Choi J.H., Larsen K., Seppi D.J. Price impact in Nash equilibria // Finance and Stochastics. 2023. Vol. 27. Iss. 2. P. 305-340. DOI: 10.1007/s00780-023-00499-w
- Pin-bo Chen, Gui-hua Lin, Weina Xu, Xide Zhu. Supply chain network equilibrium with outsourcing for fresh agricultural products under stochastic demands // IMA Journal of Management Mathematics. 2024. № dpae024. DOI: 10.1093/imaman/dpae024
- Collard-Wexler A., Gowrisankaran G., Lee R.S. «Nash-in-Nash» Bargaining: A Microfoundation for Applied Work // Journal of Political Economy. 2019. Vol. 127. № 1. P. 163-195. DOI: 10.1086/700729
- Zhaohua Chen, Xiaotie Deng, Wenhan Huang et al. On tightness of Tsaknakis-Spirakis descent methods for approximate Nash equilibria // Information and Computation. 2023. Vol. 293. № 105046. DOI: 10.1016/j.ic.2023.105046
- Huilin Yao, Rizhao Gong, Zhihui Yuan. Multi-Oligopoly Sequential Pricing Mechanisms and Their Game Analysis in Raw Material Supply Chains // Sustainability. 2022. Vol. 14. Iss. 23. № 16231. DOI: 10.3390/su142316231
- Pangallo M., Heinrich T., Farmer J.D. Best reply structure and equilibrium convergence in generic games // Science Advances. 2019. Vol. 5. Iss. 2. № eaat1328. DOI: 10.1126/sciadv.aat1328
- Bosshard V., Bünz B., Lubin B., Seuken S. Computing Bayes-Nash Equilibria in Combinatorial Auctions with Verification // Journal of Artificial Intelligence Research. 2020. Vol. 69. P. 531-570. DOI: 10.1613/jair.1.11525
