Nuclear magnetic resonance as a method for revisiting the theory and practice of filtration consolidation in water-saturated clay soils
- 1 — Ph.D., Dr.Sci. Professor Empress Catherine ΙΙ Saint Petersburg Mining University ▪ Orcid
- 2 — Postgraduate Student Empress Catherine ΙΙ Saint Petersburg Mining University ▪ Orcid
- 3 — Engineer Saint Petersburg State University ▪ Orcid
- 4 — Researcher Saint Petersburg State University ▪ Orcid
Abstract
This article outlines the key principles and assumptions that form the basis of the filtration consolidation model for water-saturated clay soils described by K.Terzaghi in 1925 for calculating the settlement of structures. One of the main assumptions that requires revision is the notion that the pore water in clay soils has properties identical to those of bulk water. In the modern context, pore water should be considered in terms of its structuredness under the influence of the active centers of solid particles, ions, and other factors. The results of experimental studies on the effect of active centers of the solid surface, primarily clay particles, on the change in water structure via nuclear magnetic resonance relaxometers of various generations are presented. The patterns of changes in the structure of pore water in water-saturated clay soils of different granulometric and mineral compositions in the range of changes in their conditional physical state by moisture are shown. The structuredness of pore water in soils contributes to its inertness to the perception of external pressure and to the need to revise the concepts of filtration consolidation in favour of the rheological model for predicting the development of settlements as the main criterion for their stability.
Funding
The experimental part of this work was supported by an internal grant of Saint Petersburg State University initiative project (ID 100349765).
Introduction
The theory and practice of foundation design and stability calculations for structures on water-saturated clay soils are based on K.Terzaghi’s filtration consolidation model, which was proposed in 1925 [1]. Its main purpose involves analysing the compression of water-saturated clay soils through pore water outflow (filtration) under the influence of external pressure. This model is applied for not only solving problems related to the construction and operation of structures on clay soils but also for addressing specific practical hydrogeological tasks. It is believed that the observed increase in the yields of operating wells during continuous pumping occurs due to the outflow (filtration) of pore water from clay aquitards as the groundwater level decreases by a value S, resulting in increased normal stresses on the aquitards (σz = γwS, where γw is the water specific weight) [2].
The mathematical formulation of K.Terzaghi’s filtration consolidation model was based on the following assumptions:
- analysis of a one-dimensional consolidation problem of water-saturated clay soils without the possibility of lateral expansion (where the clay soil layer thickness h, divided by the loaded area width b, is less than or equal to 0.25);
- the clay soil is fully water-saturated and the pore fluid possesses properties identical to those of bulk water;
- structural bonds between soil particles are absent;
- the filtration of water through soils obeys the linear Darcy’s law:
where v is the filtration velocity; ∂H\∂l is the hydraulic gradient; and k is the coefficient of permeabi-lity of the soil;
- at any time t≠ 0, the total external pressure p = p2 – p1 is distributed between the pore water pw (pore water pressure) and the soil skeleton pер (effective pressure) (Fig.1).
The main equation of the filtration consolidation model relates the change in pore water pressure in clay soil over time t to the change of pressures H with layer depth z:
where Cu is the coefficient of consolidation, equal to:
where e1 is the initial void ratio of clay soils and a is the coefficient of compressibility of the soils in the pressure range p2 – p1.
In soil mechanics practice, when the coefficient of consolidation is Cu ≤ 107 cm2/year, the filtration consolidation process develops so slowly that it may be neglected.
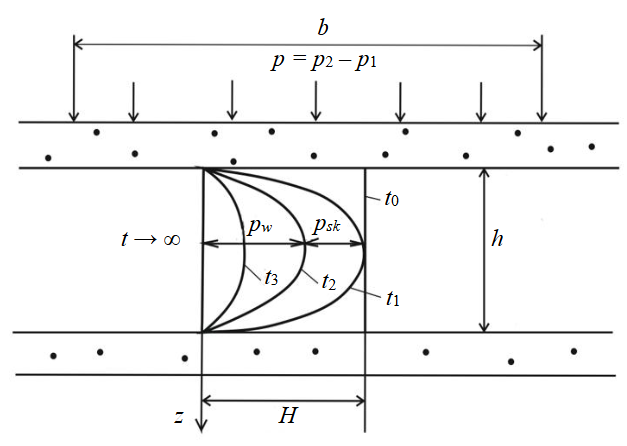
Fig.1. The isochrones of pore pressure distribution along the height of the clay soil layer z at different time t of pressure loading (according to K.Terzaghi’s hypothesis)
The development of the filtration consolidation theory of water-saturated clay soils, which accounts for pore water anomalies, has been conducted by several researchers [3, 4]. Special attention should be given to the works of A.I.Ksenofontov, who employed rheological models to describe the deformation behaviour of water-saturated clay soils as single-phase media when their permeability coefficient decreases to k ≤ 10–3 m/day.
The study of water structure in clay soils is of fundamental scientific and practical importance when analyzing the long-term stability of structures for various purposes, at the base of which lie water-saturated clay deposits of diverse genesis and age [5]. These such soils have different mineral and granulometric compositions, physical states, structural bonds, and variabilities in strength and bearing capa-city [6, 7]. The application of the filtration consolidation model in the design of structures results in a significant overestimation of the allowable pressure R due to soil compaction during experimental studies to obtain shear strength parameters: the angle of internal friction φ and cohesion c. These parameters are regarded as fundamental and are employed in stability calculations (allowable pressure determinations) for above-ground structures for various purposes [8-10]. Exceeding allowable pressures through the use of incorrect (overestimated) values of φ and c above design pressures ps can compromise the stability and safety of construction and operating structures, leading to structurally unsafe buildings [11].
Methods for studying water structure transformation under the influence of the active centres of solid surfaces
Research into changes in water structures on various substrates (quartz and mica sheets) was conducted in the 1960-1980s by specialists in physics and physical chemistry. Particular mention should be given to studies examining water state alterations under the influence of SiO2 active centres, along with research by M.S.Metsik’s scientific school (experiments on mica sheets). When the water structure in quartz capillaries measuring 0.03-0.04 μm was examined, a 35-40 % increase in the visco-sity of the adsorbed water compared with that of the bulk water was recorded [12]. Quartz substrates, owing to their relatively simple crystallochemical structure, possess fewer active centres than aluminosilicates do, such as feldspars, mica, and clay minerals, with clay particles being characterized by the most complex structure.
An important feature of the research conducted by M.S.Metsik’s scientific school is the performance of experimental work on mica sheets under conditions of changing surface states and, consequently, the activity and number of energy centres [13, 14]. The results of these studies demonstrated that the dielectric constant of water εw decreases from 80 to 4.5 as the thickness of the adsorbed water film decreases from 2 to 0.07 μm. The thermal conductivity λ at this same film thickness on a fresh mica surface becomes comparable to the λ of metals, reaching 60 W/m·deg. Washing the freshly cleaved mica surface in boiling water significantly reduces the λ value to 0.6 W/m·deg (equivalent to bulk water).
The following questions should be addressed: what role do the active centres of various minerals play, and how does their radius of influence increase – this being determined by the crystallochemical features of the mineral lattice structure and their degree of dispersion. Research on such energetically non-uniform active centres associated with point defects on solid surfaces of various media (both metallic and non-metallic) was conducted by G.I.Distler. It was established that the active centres are divided into two groups: epitaxial centres, which increase the water density; and polarising centres, which are long-range centres that stop the translational movement of water molecules at distances up to 10 μm. The model of translational movement – involving jump-like displacements of water molecules from equilibrium positions (remaining in equilibrium for 10–13 s) combined with vibrational and rotational movements – was first proposed by Ya.I.Frenkel, when substantiating the liquid state of matter. Such motion is absent in solid-state bodies.
The most precise method for determining the crystallochemical structure of both liquid and solid substances is nuclear magnetic resonance (NMR), which registers transitions between magnetic energy levels of atomic nuclei induced by radiofrequency (RF) radiation [15]. In foreign countries, NMR is actively used to study the pore space of soils of various compositions [16-18].
Pore water in soils contains ions and complex compounds of both organic and inorganic compositions at varying concentrations [19]. Moreover, soil pores contain microorganisms and their metabolites, along with gases of various origins (biochemical, deep, and catalytic) [20-22].
Research into the influence of the cation content in perchlorate salt solutions on water structuring (HClO4– being an anion that does not affect the structure of bulk water) was conducted by V.I.Chizhik [23]. All the studied perchlorate solutions were prepared via fully degassed water, whose spin-lattice relaxation time T1 is approximately 3.5 s, whereas the T1 value of the distillate is slightly lower and is 2.5 s. It has been experimentally established that the T1 parameter decreases approximately threefold in the presence of positive-hydration ions compared with fully degassed water, with the smallest decrease observed in sodium perchlorate solutions and the most significant – in magnesium solutions.
The hypothesis regarding the absence of bulk water in clay soils of various compositions and states was first proposed and confirmed through the work of R.E.Dashko, which was conducted via an ECHO-4 NMR relaxometer (1H frequency of 20 MHz) while investigating changes in the structural characteristics of pore water in fine-dispersed soils [24]. The experiments were carried out on water-saturated clay soils of varying granulometric and mineral compositions, as well as varying physical states. It should be emphasised that clay soils possess the greatest quantity of active centres, which is related not only to the crystallochemical structure peculiarities of various aluminosilicates and silicates but also to the content of living components and their metabolites (gases, proteins, lipids, acids, etc.) [25-27]. Not only living but also dead cells most frequently carry a positive charge [28]. The main polyhedra comprising the structure of clay layered aluminosilicates are silicon-oxygen tetrahedra, along with octahedra containing various cations (Al3+, Mg2+, Ca2+, Na+, K+).
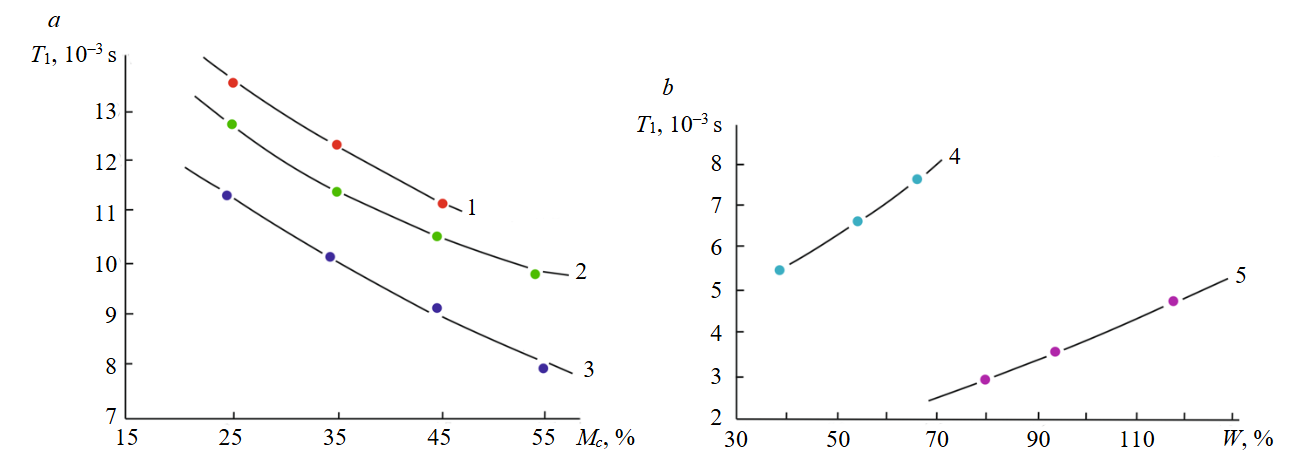
Fig.2. Variation of spin-lattice relaxation time T1 of pore water with clay fraction content Мс and moisture content at liquid limit WL (a) and clay mineral composition (b) [24]
1 – W = 1.1 WL; 2 – W = WL; 3 – Wp < W < WL; 4 – hydromica clay; 5 – bentonite clay
When conducting research via the ECHO-4 relaxometer the structural characteristics of the pore water in the dispersed soils were examined with respect to the following factors:
- content of the clay fraction Мс while maintaining a constant mineral composition (hydromica group) (Fig.2, а);
- the variation in the soil moisture content W as an indicator of their physical state, where WL is the moisture content at the liquid limit (Fig.2, а) [29];
- influence of the activity of the clay fraction’s mineral composition on the Т1 – montmorillonite group (bentonite) and hydromica (Fig.2, b);
- variation in the mineralization of pore water with different chemical compositions (Fig.3).
The conducted research has demonstrated that bulk water is entirely absent under such variations in clay soil composition and state, as the average T1 parameter measures n·10–3 s compared to bulk water (Т1= 2.5 s). Moreover, the greatest decrease in T1 occurs at the lowest moisture content (with constant mineral composition) and in the presence of more active clay minerals from the montmorillonite group (bentonite), even at very high moisture contents (W > 70 %).
Investigation into how the mineralisation and ionic composition of pore solutions affect water structure revealed that the active centres of clay particles exert a predominant influence. This is evidenced by the T1 values measured in the presence of negative-hydration ions (K+) and positive-hydration ions (Na+, Mg2+, Ca2+, and Al3+), with all T1 measurements remaining within n·10–3 s.
Researches of the structure of pore water in water-saturated clay soils was continued via modern NMR equipment (ECHO-12 relaxometer with a 1H frequency of 20 MHz, designed at the Department of Radio Physics of Saint Petersburg State University). The spin-lattice relaxation times were measured via a standard inversion-recovery pulse sequence. The 90° RF pulse duration was 3.8 μs, the “dwell” time was 32 μs, and the signal-to-noise ratio was ~900. A Spin Core pulse generator with a 100 MHz clock frequency served as the sequence synthesizer. The “EchoScan” hardware-software interface for the entire system was programmed in the object-oriented language LabVIEW. The pulse intervals ranged from 0.2 to 400 μs and were divided into 60 discrete values. All investigations were conducted under standard conditions. Experimental investigations were carried out using the equipment of the Department of Nuclear Physics Research Methods and of the Centre for Magnetic Resonance Research of the Science Park of Saint Petersburg State University.
The experimental results enabled the evaluation of pore water structural changes in water-saturated clay soils, which were analyzed layer-by-layer with increasing distance from the active centres of the solid particles.
A series of investigations were conducted to examine the influence of varying clay fraction contents in soils maintaining a constant physical state corresponding to the quasi-liquid limit according to regulatory provisions in soil mechanics and engineering geology. This clay soil condition corresponds to the soil moisture content at the boundary of the beginning of decay of the root system of plants WL under conditions of excessive moisture. All the tested soils had the same mineral composition (hydromica group).
Soil mechanics and engineering geology practices demonstrate that soils in a quasi-liquid state (W ≈ WL) contain bulk water in their pore space that can respond to minimal pressures and be removed from the soil according to Darcy’s law.
The variations in the clay fraction content and physical state parameters of the investigated soils are presented in Table 1.
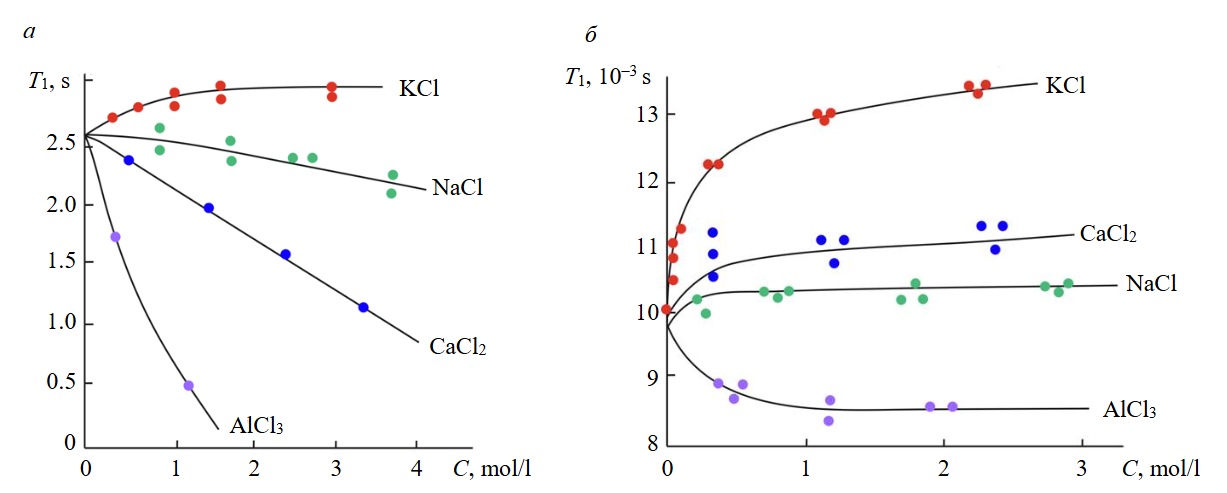
Fig.3. Variations in spin-lattice relaxation time T1 of water protons: a – in solutions on their concentrations C; b – in pore solutions of clay hydromica soils at concentration C; Мс = 54 %, W = WL [24]
Table 1
Granulometric composition and some physical properties of the studied clay soils
|
Sample |
Soil type |
Diameter of fractions and their content in the samples, % |
Water content W, % |
Limits, % |
Plasticityindex,IР, % |
||
|
Clay (<0.002 mm) |
Silt (0.002-0.05 mm) |
Liquid limit WL |
Plasticlimit WP |
||||
|
1 |
Siltloam |
16 |
84 |
26.7 |
26.7 |
15.8 |
10.9 |
|
2 |
Siltloam |
28 |
72 |
34.2 |
34.2 |
19.5 |
14.7 |
|
3 |
Siltyclay |
40 |
60 |
45.0 |
45.0 |
24.0 |
21.0 |
The soil types followed the V.V.Okhotin classification system widely used in engineering geology, which is based on the sand, silt, and clay fraction contents. The clay fraction content determines the characteristics of the WL and WP listed in Table 1.
Results and discussion
During experimental investigations of clay samples (Table 1) via an ECHO-12 relaxometer (20 MHz frequency), Т1 parameter values were obtained that characterize the degree of pore water structuring as water protons move away from active centres on solid particle surfaces. The results were processed via the “EchoScan” hardware-software interface using the Levenberg – Marquardt approximation method (Table 2).
Table 2
Spin-lattice relaxation times T1 for clay soils of the liquid state with varying clay fraction contents
|
Sample label |
Soil type |
Clay fraction (<0.002 mm)content, % |
W = WL, % |
Spin-lattice relaxation time, ms |
|
|
T1S |
T1C |
||||
|
1 |
Silt loam |
16 |
26.7 |
0.4 |
17.6 |
|
2 |
Silt loam |
28 |
34.2 |
0.7 |
11.9 |
|
3 |
Silty clay |
40 |
45.0 |
0.9 |
10.8 |
Note. T1S – characterizes the structure of the pore water at the solid surface of the particles, and T1C – in the central part of the pore.
The general trend of T1 variation with increasing clay fraction content, which determines the greatest number of active centres in soil samples, manifests in reduced maximum T1 values. This results from decreased pore sizes and, consequently, the enhanced influence of fine-dispersed particles on the pore water structure. The main conclusion, according to the results of these studies, is the absence of bulk water in the pores of water-saturated clay soils at their most unstable liquid state. Notably, even the maximum obtained T1С value of 17.62 ms remains more than two orders of magnitude below the bulk water’s T1 (2.5 s).
A comparison of modern pore water structure research results from the ECHO-12 relaxometer with previously established patterns (ECHO-4) confirms their numerical equivalence. The weighted mean T1 values (based on percentage distributions of the most probable T1 values) match those obtained for clay soils of varying granulometric compositions at the liquid state (W = WL) (Table 3).
Table 3
Comparison of T1 values obtained with the ECHO-4 and ECHO-12 relaxometers
|
Clay fraction (<0.002 mm) content, % |
Spin-lattice relaxation time T1, ms |
Note |
|
|
ECHO-4 |
ECHO-12 |
||
|
16 |
– |
13.22 |
Experimental studies were carried out on soils of the same mineral and granulometric composition, as well as physical state |
|
28 |
12.10 |
9.36 |
|
|
40 |
11.10 |
8.60 |
|
For samples with varying clay fraction contents, free induction decay (FID) signal spectra were recorded following fast Fourier transformation via the ECHO-12 relaxometer (Fig.4, а-c). As the relaxometer receiver employs a synchronous phase detector without quadrature detection capability, all the spectra were acquired with a 47.5 kHz resonance frequency offset at 500 Hz spectral resolution. Figure 4, d displays the superimposed spectra with amplitude-axis normalization.
Interpretation of the pore water proton spectra for three clay soil samples at W = WL explains their structural organization at varying distances from the active centres of the solid particles (denoted as the 1st and 2nd components in Table 4). The pore water structural transformation spectrum is compared with the bulk water spectrum.
Component 1 reveals increasing pore water structuring in various clay soils with increasing clay fraction content at maximum distances from solid surfaces – in the central part of the pore (representing polarizing centres according to G.I.Distler). Component 2 demonstrates equivalent patterns in the vicinity of the solid surface (epitaxial centres). Notably, the HWHM of the 1st component in the outermost water layers exceeds the bulk water value (0.2 kHz) by 4-6 times.
The consistent value of the 3rd component most likely represents crystallization water within the clay mineral structure. This structural water typically requires clay firing temperatures of 300-600 °C for removal.
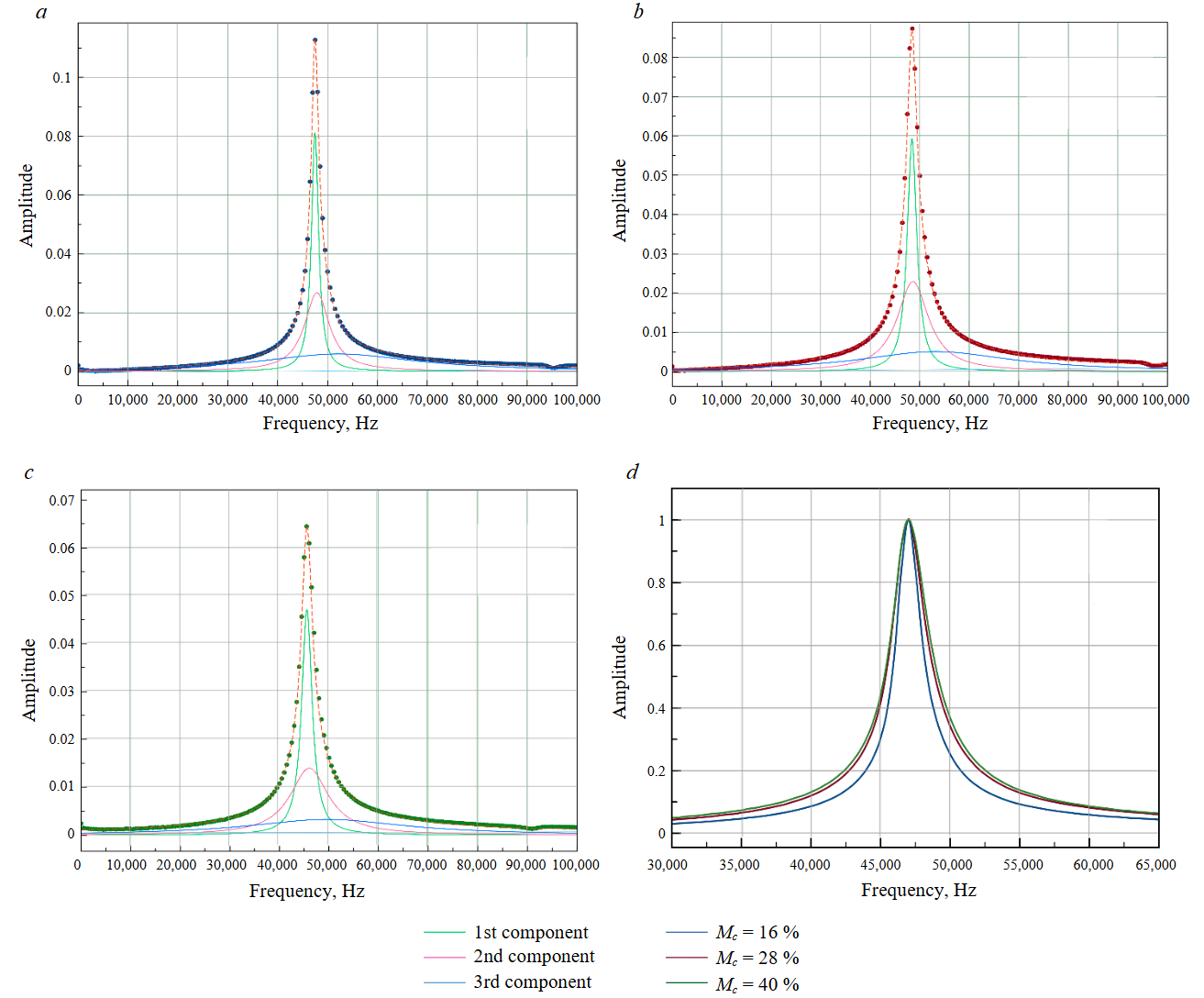
Fig.4. Spectra of FID signals recorded for water-saturated clay soils of varying granulometric composition at constant physical state (W = WL): a – Mс = 16 %; b – Mс = 28 %; c – Mс = 40 %; d – superimposed spectrum of three tested samples
Table 4
HWHM values derived from signal spectrum processing
|
Components |
HWHM, kHz |
|||
|
Мс = 16 % |
Мс = 28 % |
Мс = 40 % |
Bulk water |
|
|
1 |
0.86 |
1.17 |
1.29 |
0.2 |
|
2 |
3.0 |
3.9 |
4.7 |
– |
|
3 |
19.0 |
19.0 |
19.0 |
– |
Note. The HWHM parameter is used in the spectra analysis and indicates the half width at the half maximum amplitude.
In additional to investigating pore water structure in water-saturated clay soil at quasi-liquid conditions, experiments were also conducted on soil samples at W = WP. Under current soil classification systems in soil mechanics and engineering geology, this state is classified as quasi-solid, with WP defined as the moisture content at the plastic limit. The WP parameter in soil science corresponds to the moisture content at the beginning of wilting of the plant root system, the vacuum pumps of which are not able to “pump out” the soil moisture. This parameter fixes the maximum physically-bound water content in clay soil, defined as the maximum molecular water holding capacity Wm max – a value closely approximating the plastic limit moisture content WP. The Wm max value is determined by removing water from 2 mm-thick clay soil samples under a pressure of 6.55 MPa.
The water structure in the water-saturated clay sample (Mс = 40 %) was determined at a moisture content approaching the plastic limit (W = WP = 26 %). The T1 values measured via the ECHO-12 relaxometer ranged from 4.76 to 9.62 ms. The narrower T1 variation range may be attributed to both minimal pore diameters and the stronger in-fluence of epitaxial centres on pore water structuring relative to polarising centres. The signal spectrum analysis revealed only two components: crystallization water within the clay mineral structure (19 kHz) and a unified component that represent the structural integrity of the pore water in the soil (Fig.5).
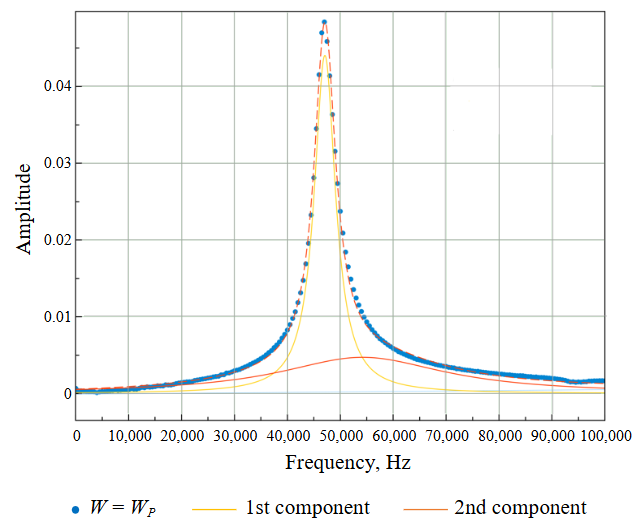
Fig.5. FID spectrum of water-saturated clay soil at W = WP with 40 % clay fraction content
The Fig.5 analysis reveals that the HWHM value for this water-saturated clay soil in the quasi-solid state exceeds that of the bulk water by a factor of 12.5, indicating that it has the most hardened pore water structure among all the tested samples.
When external pressure is transferred to water-saturated soils, it redistributes between solid particles and pore water. Researchers have adopted various approaches to filtration consolidation in water-saturated clay soils, whose development intensity depends on the dynamics of pore pressure changes.
The earliest theoretical models of one-dimensional compression by K.Terzaghi and V.A.Florin describe pore pressure gradually decreasing from initial values of 100 % (K.Terzaghi) and 80 % (V.A.Florin) to zero values over time. N.A.Tsytovich’s model presents pore pressure development as a process featuring an initial gradual increase, followed by dissipation to residual values dependent on the clay soil state and structural bond strength.
Experimental investigations of the relative pore pressure ratios pw/p during one-dimensional compaction with varying clay fraction contents Mс at similar physical states demonstrated identical reductions in pw/p as pore water structuring increased, consequently resulting in greater pressure p inertia (Fig. 6).
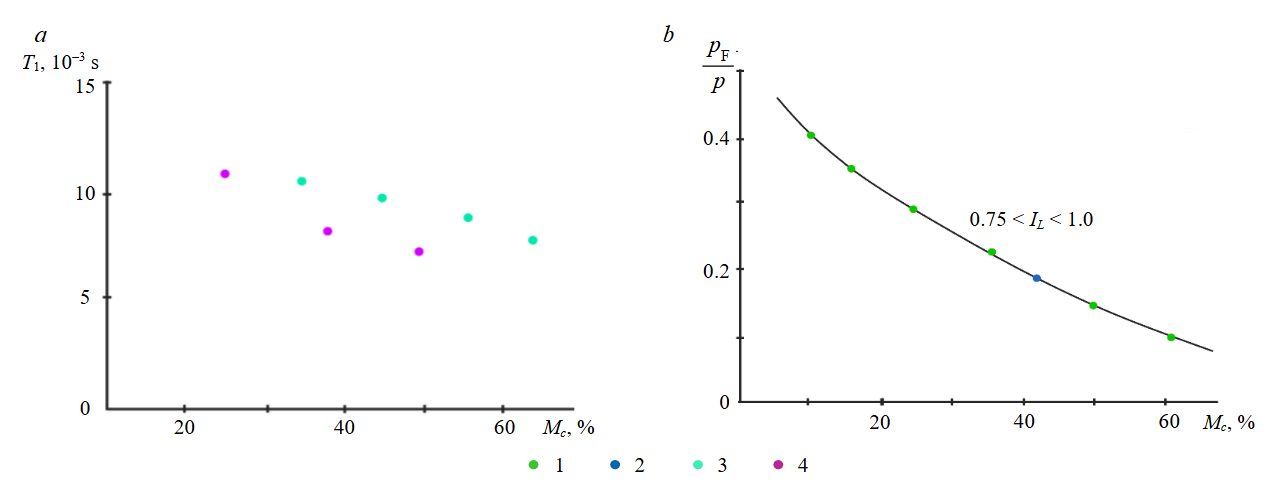
Fig.6. Variation in water structuring degree by Т1 value (a) and relativepore pressure ratio pw/p (b) versus clay fraction content Mс and liquidity index IL
1 – laboratory tests; 2 – tests in situ; 3 – ECHO-4; 4 – ECHO-12
As established, the one-dimensional consolidation problem (without the possibility of lateral expansion) represents a theoretical case. Under conditions of simultaneous vertical and lateral deformations development, the pore pressures decrease to zero.
Deformations develop due to soil skeleton creep, meaning that structured pore water acts as an inert component. Consequently, the principal physical model for water- and water-gas-saturated clay soils should be interpreted through rheological laws that reflect the actual behaviour of foundation soils.
Conclusion
Current practices necessitate the revision of K.Terzaghi’s filtration consolidation model, which remains widely used for designing structures for various purposes, including unique ones, on water- and water-gas-saturated clay soils of diverse geneses and ages [30-32]. These soils account for 60-80 % of the sedimentary section of the Earth’s crust globally, not just in Russia.
The revision of the K.Terzaghi model can be based on assessing pore water structuring in fine-dispersed soils, which affects the interaction of special characteristics in the structure – clay soils system.
The most reliable data on water structure transformation under the influence of various energy centres can be obtained only based on nuclear magnetic resonance. A review of previous studies on the structure of water using alternative methods demonstrates limited influence of the active centres of silicate and aluminosilicate surfaces on the water transformation within the soils pores.
Soil mechanics and engineering-geology practice demonstrates that clay soils in quasi-liquid and similar states contain significant amounts of bulk water, which absorb a portion of the external pressure, is filtered out from clay deposits. This process reduces the moisture content while increasing the density and strength. Employing incorrect shear strength parameters creates conditions for the transition to structural unsafe buildings through unjustified overestimation of the foundation soil bearing capacity.
Expert assessments of such situations typically limit themselves to formally conducting analyses and identifying errors in engineering surveys or construction code violations. Crucially, these assessments completely lack critical evaluation of the reliability of the shear strength parameters used in bearing capacity calculations for water-saturated clay soils in structures designed according to the second limit state.
This paper analyses pore water structuring in various clay soils as a function of their physical state, granulometric and mineral composition, and pore water chemistry via different-generation nuclear magnetic resonance relaxometers (ECHO-4 and ECHO-12). Comparative results demonstrate that even liquid-consistency clays contain no bulk water. The pore water exhibits progressively decreasing structural organization with increasing distance from the active centres of the solid particles, as evidenced by spin-lattice relaxation time T1 measurements and spectral line widths (HWHM).
The structural organization of pore water in fine-dispersed soils determines its pressure response inertness under new stress states within structure-clay soil interaction zones [33, 34]. This necessitates the application of rheological principles that characterize clay soil behaviour as a quasi-homogeneous medium.
References
- Powrie W. Soil mechanics. Concepts and applications. CRC Press, 2014, p. 682.
- Mironenko V.A., Serdyukov L.I., Kotov I.G. On the influence of “aquitard” rock compressibility on filtration processes in aquifers. Journal of Mining Institute. 1971. Vol. 62. N 2, p. 39.
- Florin V.A. Fundamentals of soil mechanics. In 2 vol. Leningrad; Moscow: Gosstroiizdat, 1959-1961.
- Zaretskii Yu.K. Theory of soil consolidation. Мoscow: Nauka, 1967, p. 270.
- Bernal J.D., Fowler R.H. A Theory of Water and Ionic Solution, with Particular Reference to Hydrogen and Hydroxyl Ions. The Journal of Chemical Physics. 1933. Vol. 1. N 8, p. 515-548. DOI: 10.1063/1.1749327
- Mustafin M.G., Nguyen Huu Viet. The Estimation of the Building’s Vertical Shifts and Construction Groundworks on the Basis of Deformation Network Element Analysis. Geodesy and Cartography. 2019. N 3, p. 11-19 (in Russian). DOI: 10.22389/0016-7126-2019-945-3-11-19
- Shulyatev O.A., Isaev O.N., Nayatov D.V., Sharafutdinov R.F. Forecast of base strains development for a multifunctional residential complex. Geotechnics. 2017. N 2, p. 4-15 (in Russian).
- Travush V.I., Shulyatev O.A., Shulyatev S.O. et al. Analysis of the Results of Geotechnical Monitoring of “Lakhta Center” Tower. Soil Mechanics and Foundation Engineering. 2019. Vol. 56. N 2, p. 15-21. DOI: 10.1007/s11204-019-09576-9
- Vasenin V.A., Shashkin A.G. Secular sediments of Saint Petersburg buildings. St. Petersburg: Izd-vo Instituta “Georekonstruktsiya”, 2022, p. 440.
- Shashkin A.G., Zentsov V.N., Ulitsky V.M. Development of underground space of megapolis. Housing Construction. 2018. N 9, p. 30-36 (in Russian).
- Kornilov Yu.N., Tsareva O.S. Perfecting the methods of monitoring the buildings and structures deformation. Geodesy and Cartography. 2020. N 4, p. 9-18 (in Russian). DOI: 10.22389/0016-7126-2020-958-4-9-18
- Deryagin B.V., Churaev N.V. New properties of liquids. Мoscow: Nauka, 1971, p. 176.
- Metsik M.S. Splitting of Mica Crystals and Surface Energy. The Journal of Adhesion. 1972. Vol. 3. Iss. 4, p. 307-314. DOI: 10.1080/00218467208072201
- Gudkov O.I., Metsik M.S. Dielectric properties of mica at shf. Soviet Physics Journal. 1973. Vol. 16. N 5, p. 664-667. DOI: 10.1007/BF00898805
- Jacobsen N.E. NMR Data Interpretation Explained: Understanding 1D and 2D NMR Spectra of Organic Compounds and Natural Products. Wiley, 2017, p. 656.
- Meyer M., Buchmann C., Schaumann G.E. Determination of quantitative pore-size distribution of soils with 1H NMR relaxometry. European Journal of Soil Science. 2018. Vol. 69. Iss. 3, p. 393-406. DOI: 10.1111/ejss.12548
- Jäger A., Bertmer M., Schaumann G.E. The relation of structural mobility and water sorption of soil organic matter studied by 1H and 13C solid-state NMR. Geoderma. 2016. Vol. 284, p. 144-151. DOI: 10.1016/j.geoderma.2016.08.024
- Brax M., Köhne M., Kroener E., Schaumann G.E. Potential of NMR relaxometry to unravel the properties of mucilage in several pore sizes. Geoderma. 2019. Vol. 340, p. 269-278. DOI: 10.1016/j.geoderma.2019.01.013
- Moritsugu N., Nara T., Koda S. et al. Molecular Mechanism of Acceleration and Retardation of Collective Orientation Relaxation of Water Molecules in Aqueous Solutions. The Journal of Physical Chemistry B. 2020. Vol. 124. Iss. 51, p. 11730-11737. DOI: 10.1021/acs.jpcb.0c10036
- Baryakh A.A., Andreiko S.S., Fedoseev A.K. Gas-dynamic roof fall during the potash deposits development. Journal of Mining Institute. 2020. Vol. 246, p. 601-609. DOI: 10.31897/PMI.2020.6.1
- Shuangbiao Han, Zhiyuan Tang, Chengshan Wang et al. Hydrogen-rich gas discovery in continental scientific drilling project of Songliao Basin, Northeast China: new insights into deep Earth exploration. Science Bulletin. 2022. Vol. 67. Iss. 10, p. 1003-1006. DOI: 10.1016/j.scib.2022.02.008
- Mukhopadhyay S., Parai R. Noble Gases: A Record of Earth’s Evolution and Mantle Dynamics. Annual Review of Earth and Planetary Sciences. 2019. Vol. 47, p. 389-419. DOI: 10.1146/annurev-earth-053018-060238
- Chizhik V.I. NMR relaxation and microstructure of aqueous electrolyte solutions. Molecular Physics. 1997. Vol. 90. Iss. 4, p. 653-660.
- Dashko R.E. Engineering-geological analysis and assessment of water-saturated clayey soils as a base for structures. St. Petersburg: Izd-vo Instituta “Georekonstruktsiya”, 2015, p. 384.
- Pereiro I., Fomitcheva-Khartchenko A., Petrini L., Kaigala G.V. Nip the bubble in the bud: a guide to avoid gas nucleation in microfluidics. Lab on a Chip. 2019. Vol. 19. N 14, p. 2296-2314. DOI: 10.1039/C9LC00211A
- Cheremisina O., Litvinova T., Sergeev V. et al. Application of the Organic Waste-Based Sorbent for the Purification of Aqueous Solutions. Water. 2021. Vol. 13. Iss. 21. N 3101. DOI: 10.3390/w13213101
- Kulikova N.V., Danilev S.M., Efimova N.N., Kulikov A.I. Simulation of seismotomography and electrotomography data for a sand-clay section with the presence of subsurface gas accumulations. Monitoring. Science and Technologies. 2020. N 2 (44), p. 26-30 (in Russian). DOI: 10.25714/MNT.2020.44.004
- Bacterial paleontology / Ed. by. A.Yu.Rozanova. Мoscow: Rossiiskaya akademiya nauk, 2021, p. 124.
- O’Kelly B.C. Review of Recent Developments and Understanding of Atterberg Limits Determinations. Geotechnics. 2021. Iss. 1, p. 59-75. DOI: 10.3390/geotechnics1010004
- Protosenya A.G., Kumov V.V. Effect of soil body structure of mixed-type tunnel face on shape and size of subsidence trough on ground surface. Mining Informational and Analytical Bulletin. 2024. N 4, p. 5-21 (in Russian). DOI: 10.25018/0236_1493_2024_4_0_5
- Karasev M., Astapenka T. Assessment of the Influence of Formation Conditions of Embankments and Spoil Heaps on Their Stability When Dumped on Clay-Salt Slurries. Eng. 2025. Vol. 6. Iss. 1. N 2. DOI: 10.3390/eng6010002
- Yakovleva A.A., Movchan I.B., Medinskaia D.K., Sadykova Z.I. Quantitative interpretations of potential fields: from parametric to geostructural recalculations. Bulletin of the Tomsk Polytechnic University. Geo Assets Engineering. 2023. Vol. 334. N 11, p. 198-215 (in Russian). DOI: 10.18799/24131830/2023/11/4152
- Morozov K.V., Demekhin D.N., Bakhtin E.V. Multicomponent strain gauges for assessing the stress-strain state of a rock mass. Mining Informational and Analytical Bulletin. 2022. N 6-2, p. 80-97 (in Russian). DOI: 10.25018/0236_1493_2022_62_0_80
- Demenkov P.A., Romanova Е.L., Kotikov D.A. Stress–strain analysis of vertical shaft lining and adjacent rock mass under conditions of irregular contour. Mining Informational and Analytical Bulletin. 2023. N 11, p. 33-48 (in Russian). DOI: 10.25018/0236_1493_2023_11_0_33
