Исследования точности построения цифровых моделей рельефа техногенных массивов по данным спутниковых определений координат
- 1 — д-р техн. наук профессор Петербургский государственный университет путей сообщения Императора Александра I ▪ Orcid
- 2 — д-р техн. наук заведующий кафедрой Санкт-Петербургский горный университет императрицы Екатерины II ▪ Orcid
- 3 — канд. техн. наук главный специалист отдела АО «Газпром диагностика» ▪ Orcid
- 4 — канд. техн. наук ведущий инженер Санкт-Петербургский горный университет императрицы Екатерины II ▪ Orcid
Аннотация
На всех этапах жизненного цикла зданий и сооружений выполняется геодезическое сопровождение электронными средствами измерений – системой лазерного сканирования, беспилотными воздушными суднами и спутниковым оборудованием. При этом получают набор геопространственных данных, которые можно представить в виде цифровой модели. Актуальность настоящей работы – практические рекомендации для построения локальной модели квазигеоида и цифровой модели рельефа (ЦМР) определенной точности. В качестве объектов исследования выбраны локальная модель квазигеоида и ЦМР. Отмечено, что ЦМР часто создается на обширные территории, и тогда на такие модели необходимо создавать локальную модель квазигеоида. Рассматривается задача оценки точности построения таких моделей, решение которой позволит получить лучшее приближение к реальным данным на заданных наборах полевых материалов. Представлен общий алгоритм создания как ЦМР, так и локальных моделей квазигеоида в программном продукте Golden Software Surfer. Построения выполнялись методами пространственной интерполяции. При построении локальной модели квазигеоида для площадного объекта отмечены методы триангуляции с линейной интерполяцией (наименьшее значение средней квадратической погрешности (СКП) интерполяции составило 0,003 м) и кригинга (0,003 м). Наименьшее значение СКП определения высот по контрольным точкам для площадного объекта получено методами естественного соседа (0,004 м) и кригинга (0,004 м). При построении локальной модели квазигеоида на линейный объект выделены методы кригинга (0,006 м) и триангуляции с линейной интерполяцией (0,006 м). Построение цифровой модели рельефа привело к наименьшему совокупному значению оцениваемых параметров: на равнинном участке земной поверхности – метод естественного соседа, для горного участка местности с антропогенным рельефом – метод квадратичного кригинга, для горного участка местности – квадратичный кригинг.
Введение
Важным аспектом обеспечения проектирования, строительства и эксплуатации зданий и сооружений, в том числе и объектов минерально-сырьевого комплекса, является геодезическое сопровождение, которое включает инженерно-геодезические изыскания, разбивочные работы и исполнительные съемки. Во время эксплуатации может выполняться мониторинг деформаций объектов [1]. На всех этапах жизненного цикла объектов минерально-сырьевого комплекса возможно применение передовых технологий: информационного [2, 3], численного [4-6] и имитационного моделирования [7], а также нейронных сетей [8, 9]. В таком случае возможно осуществлять контроль основных характеристик изучаемого объекта безопасно и с высокой детальностью, что приводит к повышению качества передаваемых полевых материалов и расширению набора информации относительно объекта исследования. Применительно к геодезическому обеспечению ведения работ использование передовых технологий позволяет объединить геопространственные данные в единый набор достоверной информации, используемый при принятии технических решений и создании комплексных моделей для безопасной эксплуатации инженерных сооружений [10-12]. Активно применяются бесконтактные методы съемки местности, такие как лазерное сканирование [13] и фотограмметрические методы [14], в том числе беспилотные летательные аппараты [15-17]. Отметим, что в последнее время для определения высотного положения элементов сооружений используются и методы наблюдений со спутниковой системой навигации (ГНСС) [18], для эффективного применения которых необходимо иметь на объект строительства модель высот квазигеоида или модель аномалий высот. Подчеркнем, что в процессе проектирования и строительства объектов, а также при различных градостроительных работах, в том числе по освоению территорий, создание цифровой модели рельефа (ЦМР) по полученным данным является важным этапом получения пространственной информации об участке работ. Оценка точности и автоматизации создания ЦМР – актуальная задача, так как качество и скорость построения позволяют увеличить производительность всех связанных процессов. Таким образом, возникает задача исследования точности создания локальной модели квазигеоида и ЦМР при отсутствии общих рекомендаций их построения [19, 20] и оценки точности [21, 22]. Например, в работах [23-25] приведены рекомендации по использованию методов пространственной интерполяции [26, 27] для построения математических моделей рельефа.
Отметим, что построение ЦМР возможно как с применением локальной модели квазигеоида, так и без ее использования. Однако это может привести к искажению информации о рельефе [19, 25]. Для предоставления результатов геодезического обеспечения применяется нормальная система высот [18, 28, 29]. В случае получения геодезических высот встает вопрос о переходе к ней. Тогда необходима локальная модель квазигеоида [30-32], для создания которой важно иметь совмещенные пункты [33, 34] (с известными геодезическими высотами из ГНСС-определений и нормальными или ортометрическими высотами из геометрического нивелирования). Моделирование поверхности аномалий высот [34] было вызвано прежде всего развитием территорий Польши [28], Словении [31], прибрежных городов Красного моря [20], Эфиопии [34].
Авторами работ [21, 35] отмечено, что создание таких моделей в труднодоступных горных районах является важным этапом точного определения высот при использовании ГНСС-оборудования. В статье [28] указано, что при создании локальной модели на территории Кракова достигнута точность на уровне 5 мм. Создание таких моделей важно для развития регионов [33]. Зачастую решается задача моделирования поверхности аномалий высот для площадного объекта. При этом отсутствуют исследования, направленные на создание локальной модели квазигеоида для линейного объекта большой протяженности. Не разработаны рекомендации о необходимом числе пунктов или о способе назначения достаточного их числа для создания модели, точность определения высот по которой отвечала бы точности, указанной в техническом задании на каждом этапе строительства.
При определении поправок в геодезические высоты для дальнейшего построния ЦМР необходимо выбрать метод пространственной интерполяции, который будет использован для построения математической модели аномалий высот [36]. Построение ЦМР по данным, полученным различными методами съемки [37], активно изучается [35]. При этом результаты могут быть использованы как пространственная сетка с регулярным шагом (GRID) или облако точек [38]. Выбор метода пространственной интерполяции оказывает непосредственное влияние на итоговую точность построения математической модели рельефа [39]. Самым распространенным методом считается триангуляционная нерегулярная сеть (TIN) [25]. Однако в работах [40-42] отмечается целесообразность применения и других методов пространственной интерполяции:
- Метод кригинга используется для задачи построения рельефа как земной, так и подводной поверхности [43, 44] при правильном определении вариограммы [45, 46], формирующей пространственную зависимость.
- Радиальная базисная функция. Данные о рельефе местности, полученные в результате воздушного лазерного сканирования (ВЛС), подвержены выбросам, которые оказывают негативное влияние на точность цифровых моделей рельефа. Однако экспериментальные результаты в исследовании [47] показали, что использование сплайн-функций предоставляет более точную модель по натурным данным, а не созданным синтетически.
На полученную точность построений влияют плотность исходных геопространственных данных [48, 49] и источник информации [50]. Цель работы – оценить точность создания математических моделей рельефа и квазигеоида на основе методов пространственной интерполяции, а также разработать начальные положения общей методики создания локальной модели квазигеоида и цифровой модели рельефа.
Методы
Исходные данные
Построение локальной модели квазигеоидаВ качестве исходных данных для площадного объекта выступали 300 совмещенных геодезических пунктов, на которых были определены геодезические и нормальные высоты. Из общего числа пунктов, расположенных на приблизительно одинаковом расстоянии друг от друга в разных частях объекта, 10 % (30 пунктов) использовались как контрольные и не участвовали в создании модели. Средние квадратические погрешности (СКП) определения нормальных высот пунктов не превышали 3 мм. Площадь объекта исследования составила 776,39 км2.
При создании локальной модели квазигеоида с целью строительства автомобильной дороги в равнинной местности из общего числа совмещенных геодезических пунктов отобрано 28 пунктов, расположенных по разные стороны и на равном расстоянии от оси проектируемого объекта в разных его частях. Ограничение в количестве пунктов обусловлено существующей планово-высотной основой. Аналогично для контроля качества построения из процесса создания моделей исключена часть пунктов (10 %), которая противоречила принципу равномерного распределения данных, а также могла привести к коллизиям в интерпретации результатов оценки точности из-за локальной нестабильности.
Построение ЦМР
Исходными данными послужили результаты воздушного лазерного сканирования трех обширных участков земной поверхности с различными типами рельефа (табл.1). При помощи ПО TerraScan компании Terrasolid с применением макроса из облаков точек автоматически классифицированы два облака точек, содержащие:
- ключевые точки, которые использованы для построения ЦМР;
- точки земной поверхности, которые не являются обязательными (ключевыми) для построения. При этом они содержат пространственную информацию о земной поверхности, которая может быть использована для оценки точности.
В дальнейшем участки визуально оценены на предмет наличия точек с нехарактерными отклонениями, которые свидетельствуют об ошибочной классификации отдельных точек земной поверхности.
Таблица 1
Краткая характеристика участков
|
Участок |
Средний угол наклона, град |
Минимальная высота, м |
Максимальная высота, м |
Площадь, м2 |
|
A |
0,5 |
8,30 |
35,40 |
53423 |
|
B |
29,3 |
194,95 |
918,07 |
10872 |
|
C |
25,6 |
460,63 |
1726,00 |
32541 |
Участок A – равнинная местность (рис.1, а) с незначительным изменением кривизны поверхности на локальных областях. В качестве участка B (рис.1, б) выбран горный регион со значительными перепадами высот и областями со значительным изменением кривизны поверхности. Участок C – горная местность (рис.1, в) с выраженным антропогенным рельефом. Видны поверхностные проявления нарушений и характерные для открытого способа отработки бровки и откосы.
Общее описание методики построения моделей
Использованы шесть методов пространственной интерполяции. Построения выполнялись в программе Golden Software Surfer. Предлагается создание локальной модели квазигеоида:
- импорт набора геопространственных данных в программный продукт;
- переход от облака точек к GRID (пространственная сетка с регулярным шагом);
- построение математических моделей при помощи выбранных методов пространственной интерполяции с использованием различных параметров;
- расчет метрик для оценки точности построений с применением контрольных точек;
- сравнительный анализ метрик, характеризующих точность построения математических моделей, полученных выбранными методами пространственной интерполяции;
- определение метода пространственной интерполяции по значениям выбранных метрик для построения математической модели схожих участков.
Создание ЦМР:
- преобразование при большой протяженности объекта работ или согласно поставленной задаче геодезических высот к нормальным с помощью созданной локальной модели квазигеоида;
- разделение большого по площади объекта на фрагменты размером 1000×1000 м;
- выбор характерного участка на основе общих морфометрических характеристик из множества полученных фрагментов;
- построение ЦМР на характерном участке и выработка практических рекомендаций по выбору метода пространственной интерполяции на основе оценки точности для всего объекта работ;
- создание ЦМР на весь объект работ выбранным методом пространственной интерполяции.
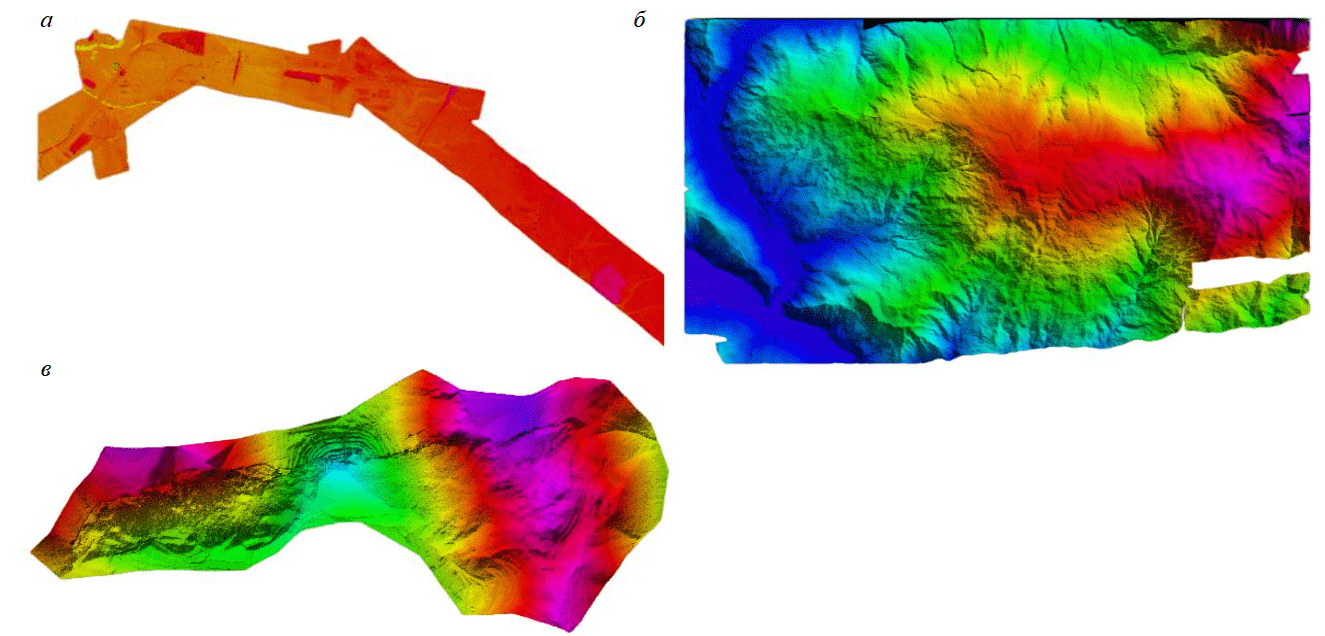
Рис.1. Участки работ, построенные по классифицированным данным
Анализ методов построения моделей
Триангуляция с линейной интерполяцией
В программе Surfer строится триангуляционная поверхность на исходном наборе данных. При попадании точки с неизвестной координатой Z в построенную плоскость, ограниченную тремя точками, определяемую уравнением
коэффициенты определяются выражениями:
Неизвестная координата Z для новой точки, вставляемой в поверхность, вычисляется формулой
С использованием метода наименьших квадратов вычисляется такая математическая поверхность, которая включает все исходные данные:
Разность между результирующими значениями построения и точками с известными координатами определяется формулой
На следующем этапе вычисляются значения высот в узлах регулярной сети. Возникает задача решения модифицированного дифференциального уравнения
где Ti – коэффициент натяжения.
Требуется учитывать граничные условия:
где ∇2 – оператор Лапласа; n – нормаль к границе; Tb – параметр натяжения на границе.
Тогда итоговая оценка Z определяется выражением
С помощью метода минимальной кривизны построены поверхности с изменением двух параметров The Internal Tension (степень прогиба) и The Boundary Tension (значение прогиба на краях). Чем выше значения указанных параметров, тем менее выраженный изгиб.
Метод ближайшего соседа
Для определения значения новой точки, добавляемой в поверхность, используется значение ближайшей выборочной точки
где Zi – значение ближайшей выборочной точки.
В процессе создания моделей использовались различные варианты области поиска значений с целью выявления изменения области на точность цифровой модели.
Естественный сосед
Определение весов для вычисления значений координат в узлах регулярной сетки осуществляется на основе пропорциональных площадей [40]:
где wi0 – весi-й точки (вычисляется при помощи диаграмм Вороного).
При использовании такого метода высоты интерполируемых точек не выйдут за пределы диапазона высот исходных данных [41].
Радиальная базисная функция
Для вычисления координаты Zдля вставляемой точки используется выражение
где di0 – расстояние между определяемой точкой и известной i-й точкой; λi – коэффициент i-й точки с известными координатами; B – радиальная базисная функция, аргументом которой является расстояние di0.
В качестве вычислительного ядра для метода в исследовании использованы функции, доступные в программе Surfer:
- Multiquadric
- Inverse Multiquadric
- Miltilog
- Thin Plate Spline
- Natural Cubic Spline
где d – расстояние от точки с неизвестным значением Z до точки с известными пространственным координатами; R2 – параметр сглаживания.
Кригинг
Преимущество такого метода – применение статистических моделей, которые в том числе позволяют выполнять прогноз с оценкой его точности. Важным фактором, влияющим на коэффициент корреляции, является расстояние между исходными точками.
Определение координаты Z для добавляемой к математической поверхности точки выполняется по формуле
где n весов λi является решением системы кригинга
Выбор методов пространственной интерполяции обусловлен отечественным и зарубежным опытом применения их для построения цифровых моделей рельефа и квазигеоида. Кроме того, такие методы разработчики программного обеспечения Surfer указывают для построения цифровых моделей рельефа.
Обсуждение результатов
Построение локальной модели квазигеоида площадного объекта
После выполнения этапа построения модели проведено сравнение методов на основе анализа значений СКП пространственной интерполяции и СКП определения аномалий высот по контрольным точкам (табл.2). Отметим, что для расчета СКП определения аномалии высоты по контрольным точкам применялась формула Гаусса. При аналитическом рассмотрении результатов оценки точности построений выделяются особенности:
- наименьшее значение СКП интерполяции достигнуто при использовании методов триангуляции с линейной интерполяцией (0,003м) и кригинга (0,003 м);
- наименьшее значение СКП определения высот по контрольным точкам было получено методами естественного соседа (0,004 м) и кригинга (0,004м).
Таблица 2
Оценка точности построения локальной модели квазигеоида площадного объекта
|
Метод |
Количество точек |
Количество |
СКП |
СКП определения |
|
Триангуляция с линейной интерполяцией |
268 |
30 |
0,003 |
0,008 |
|
Минимальная кривизна |
269 |
30 |
0,010 |
0,006 |
|
Ближайший сосед |
265 |
30 |
0,014 |
0,006 |
|
Естественный сосед |
265 |
30 |
0,007 |
0,004 |
|
Радиальная базисная функция (cubic spline) |
263 |
30 |
0,007 |
0,006 |
|
Кригинг |
270 |
30 |
0,003 |
0,004 |
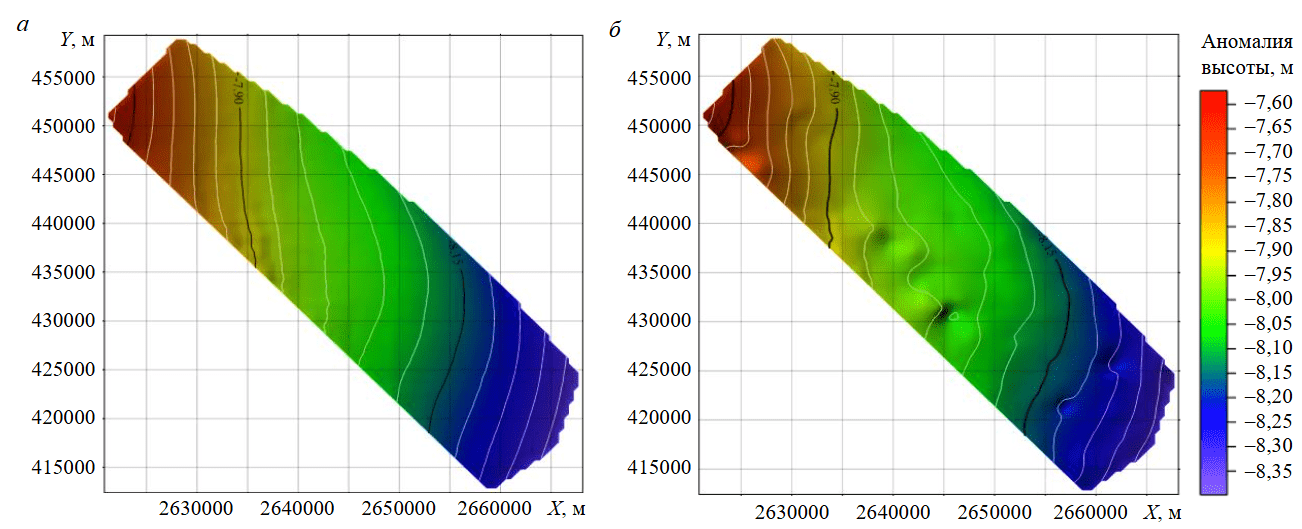
Рис.2. Локальная модель квазигеоида, построенная методами триангуляции с линейной интерполяцией (а); кригинга (б)
Построение локальной модели квазигеоида линейного объекта
Для построения модели использованы данные геодезических и нормальных высот пунктов, которые располагались вдоль проектируемой трассы. Выполнены аналогичные построения (табл.3). Наименьшая СКП определения высот по модели была получена методами кригинга (0,006 м) и триангуляции с линейной интерполяцией (0,006 м). При оценке точности построения модели по контрольным точкам наименьшее значение СКП определения высот получено методом кригинга (0,007 м). Метод кригинга по оцениваемым параметрам предпочтителен для обоих объектов. При определении оптимального количества исходных пунктов, необходимых для построения локальной модели квазигеоида, точки были равноудалены друг от друга. Расстояние между соседними точками составляло 5-6 км, при этом они располагались на одной линии. Для оценки необходимого числа пунктов решено последовательно исключать исходные точки и оценивать точность построения модели по контрольным точкам. Для построения модели из 27 пунктов решено оставить 10 при условии их равномерного расположения. Модель была построена методом кригинга, СКП определения высот которой по формуле Гаусса составила 4 мм. СКП построения модели данным методом 7 мм. При дальнейшем исключении точек и построении модели (с расстоянием между точками 10 км) СКП составила 26 см, что не удовлетворяет требуемой точности построения. Таким образом, при выполнении проектирования необходимого количества пунктов в данном районе рекомендуемое расстояние между совмещенными пунктами – 5 км.
Таблица 3
Оценка точности построения локальной модели квазигеоида линейного объекта
|
Метод |
Количество точек |
Количество |
СКП |
СКП определения |
|
Триангуляция с линейной интерполяцией |
27 |
10 |
0,006 |
0,009 |
|
Минимальная кривизна |
28 |
9 |
0,01 |
0,009 |
|
Ближайший сосед |
27 |
9 |
0,021 |
0,016 |
|
Естественный сосед |
26 |
9 |
0,011 |
0,008 |
|
Радиальная базисная функция (cubic spline) |
26 |
10 |
0,015 |
0,009 |
|
Кригинг |
28 |
10 |
0,006 |
0,007 |
Построение ЦМР по результатам воздушного лазерного сканирования
Разделение участков на фрагменты
Классифицированные данные воздушного лазерного сканирования были разделены на фрагменты размером 1000×1000 м. После этого по углу наклона и методом визуальной оценки выбраны фрагменты, которые в наибольшей степени характеризуют каждый участок.
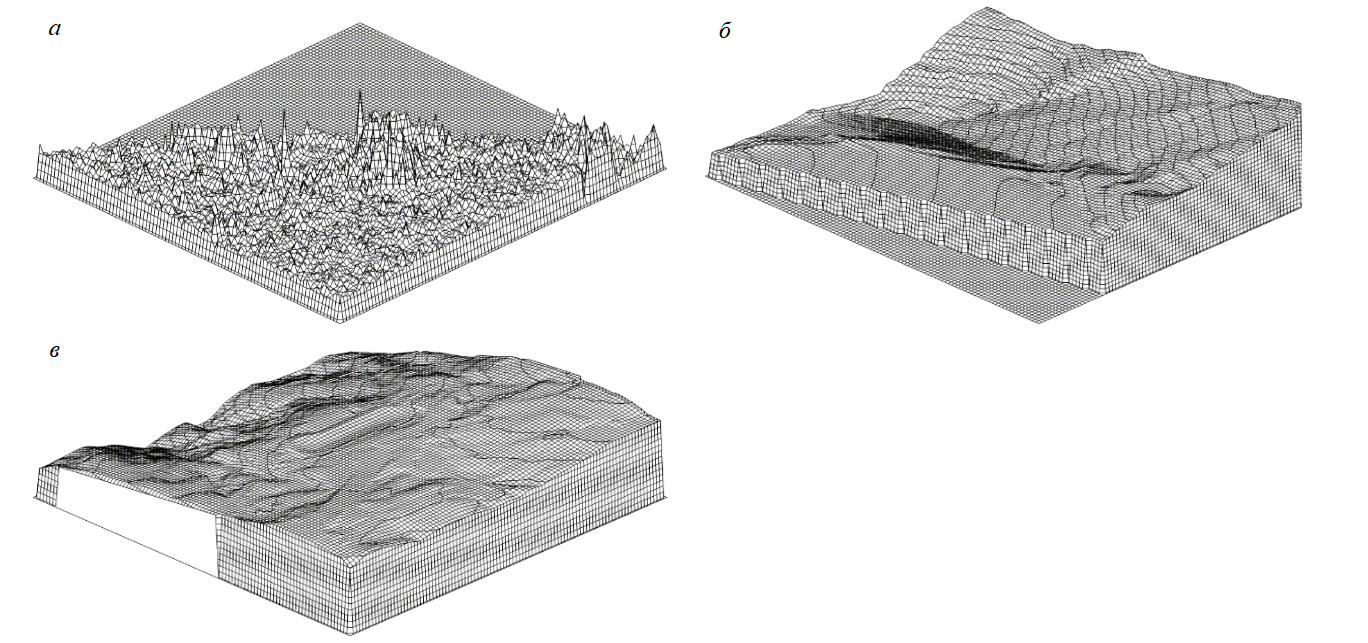
Рис.3. Характерные фрагменты: a – равнинного участка А; б – горного участка с выраженным антропогенным рельефом В; в – горного участка С
Оценка точности построенных моделей по характерным фрагментам различными методами пространственной интерполяции
Для оценки точности построены ЦМР с использованием шести методов пространственной интерполяции в программном продукте Surfer. В сумме использовали 180 ЦМР, по 60 моделей для трех участков (рис.3). Такой подход увеличивает скорость построения ЦМР на весь объект, так как при анализе методов пространственной интерполяции на одном характерном фрагменте из количества фрагментов Nснижается время оценки точности построения моделей использованными методами в N раз, при условии, что гипотеза верна.
Для анализа методов пространственной интерполяции по точности использовалось вычисление отклонения точки земной поверхности (два набора данных), которые можно рассматривать как избыточные измерения, так как они не участвовали в построении цифровых моделей рельефа. Выбор параметров «Процент точек, отклонившихся более чем на 0,33 м», «Процент точек, отклонившихся более чем на 1 м» обусловлен принятой высотой сечения рельефа для участков с равнинным рельефом. Первый параметр – процент точек с отклонением от построенной поверхности более 1/3 от высоты сечения рельефа, второй параметр – с отклонением от построенной топографической поверхности не менее высоты сечения рельефа. Высота рельефа для равнинного фрагмента а и участка А принята равной 1 м (табл.4). Таким образом, наименьшее значение параметров «СКП определения высоты» и «Процент точек, отклонившихся более чем на 0,33 м» получено при использовании методов естественного соседа (0,06 м, 1,13 %), триангуляции с линейной интерполяцией (0,07 м, 1,50 %), ординарного кригинга с вариограммой Power (0,07 м, 1,82 %).
Таблица 4
Оценка точности построеных моделей на равнинном фрагменте a
|
Метод |
Параметры |
СКП |
Процент точек, |
Процент точек, |
|
Естественный сосед |
Стандартный |
0,06 |
1,13 |
0,00 |
|
Триангуляция с линейной интерполяцией |
Стандартный |
0,07 |
1,50 |
0,00 |
|
Кригинг |
Ординарный тип |
0,07 |
1,82 |
0,04 |
|
Минимальная кривизна |
Internal Tension: 0,75 |
0,07 |
1,95 |
0,02 |
|
Радиальная базисная функция |
Мультилогарифмическая |
0,07 |
2,18 |
0,05 |
|
Ближайший сосед |
Стандартный |
0,09 |
2,58 |
0,08 |
Выполнено построение ЦМР на горном фрагменте с выраженным антропогенным фактором. Выбор параметров «Процент точек, отклонившихся более чем на 1,66 м», «Процент точек, отклонившихся более чем на 5 м» обусловлен принятой высотой сечения рельефа для горного участка с антропогенным рельефом. Первый параметр – процент точек с отклонением от построенной поверхности более 1/3 от высоты сечения рельефа, второй параметр – с отклонением от построенной ЦМР не менее высоты сечения рельефа. В исследовании высота сечения рельефа для горного участка с антропогенным рельефом принята равной 5 м (табл.5).
Таблица 5
Оценка точности построенных ЦМР на горном фрагменте с антропогенным рельефом b
|
Метод |
Параметры |
СКП |
Процент точек, |
Процент точек, |
|
Естественный сосед |
Стандартный |
0,88 |
14,24 |
1,59 |
|
Кригинг |
Квадратичный тип |
0,89 |
15,21 |
1,64 |
|
Триангуляция с линейной интерполяцией |
Стандартный |
0,94 |
15,31 |
2,12 |
|
Радиальная базисная функция |
Мультиквадратичная функция |
0,92 |
16,06 |
1,92 |
|
Ближайший сосед |
Стандартный |
0,95 |
16,13 |
1,81 |
|
Минимальная кривизна |
Internal Tension: 0,75 Boundary Tension: 0,75 |
1,21 |
22,60 |
3,20 |
Наименьшее значение СКП и параметра «Процент точек, отклонившихся более чем на 1,66 м» получены методами естественного соседа (0,88 м, 14,24 %), квадратичного кригинга с компонентом вариограммы по гауссовому (нормальному) распределению (0,89 м, 15,21 %) и триангуляцией с линейной интерполяцией (0,94 м, 15,31 %).
Выполнено построение ЦМР на горном участке. Выбор параметров «Процент точек, отклонившихся более чем на 1,66 м», «Процент точек, отклонившихся более чем на 5 м» обусловлен принятой высотой сечения рельефа для горного участка и аналогичен фрагменту b. Результаты оценки точности для горного фрагмента с приведены в табл.6.
Таблица 6
Оценка точности построенных цифровых моделей на горном фрагменте c
|
Метод |
Параметры |
СКП |
Процент точек, |
Процент точек, |
|
Кригинг |
Квадратичный тип |
0,30 |
1,04 |
0,00 |
|
Естественный сосед |
Стандартный |
0,31 |
1,28 |
0,00 |
|
Радиальная базисная функция |
Мультиквадратичная функция |
0,32 |
1,29 |
0,00 |
|
Минимальная кривизна |
Internal Tension: 0,75 |
0,39 |
1,34 |
0,00 |
|
Ближайший сосед |
Стандартный |
0,35 |
1,47 |
0,00 |
|
Триангуляция с линейной интерполяцией |
Стандартный |
0,33 |
1,74 |
0,18 |
Исходя из комплексной оценки параметров СКП определения высоты и параметра «Процент точек, отклонившихся более чем на 1,66м» можно выделить метод квадратичного кригинга со сферическим компонентом вариограммы (0,30 м, 1,04 %).
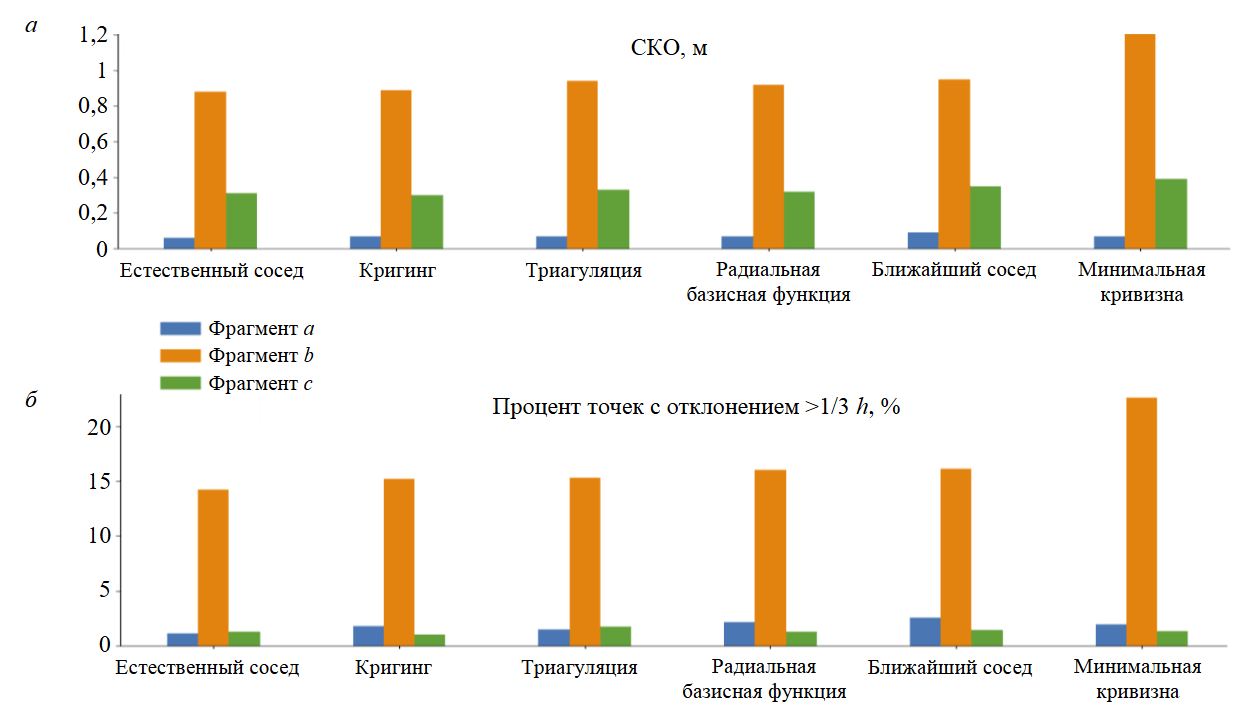
Рис.4. Оценка точности методов построения ЦМР на заданных фрагментах
Проверка точностной оценки построенных ЦМР методами пространственной интерполяции на весь объект
Выполнено построение и оценка точности цифровых моделей рельефа, созданных на всю площадь участков A, B и C. Таким образом, результаты, полученные на предыдущем этапе, нацелены на получение предварительного представления о точности построенных ЦМР для каждого участка земной поверхности, так как различия в типах рельефа явно указывают на необходимость использования дифференцированного подхода. Гистограмма с оцениваемыми параметрами для фрагментов a,b и cотражена на рис.4. Комплексная оценка точности построенных моделей для участков A, B и Cприведена в табл.7.
Таблица 7
Оценка точности цифровых моделей рельефа
|
Метод |
СКП определения высоты, м |
Количество точек |
Процент точек, |
Процент точек, |
|
Равнинный участок A |
||||
|
Естественный сосед |
0,11 |
53288238 |
5,84 |
0,84 |
|
Кригинг |
0,12 |
53288238 |
6,78 |
1,06 |
|
Триангуляция с линейной интерполяцией |
0,12 |
53288238 |
6,93 |
1,09 |
|
Горный участок с антропогенным рельефом B |
||||
|
Кригинг |
0,55 |
4556172 |
6,63 |
0,77 |
|
Естественный сосед |
0,57 |
4556172 |
7,17 |
0,80 |
|
Радиальная базисная функция |
0,57 |
4556172 |
7,08 |
0,95 |
|
Горный участок C |
||||
|
Кригинг |
0,29 |
17476315 |
0,83 |
0,01 |
|
Естественный сосед |
0,29 |
17476315 |
0,91 |
0,01 |
|
Радиальная базисная функция |
0,29 |
17476315 |
0,94 |
0,01 |
Отметим методы пространственной интерполяции согласно рассматриваемым участкам:
- Естественный сосед для участка A. Согласуется с оценкой точности характерного фрагмента.
- Квадратичный кригинг с компонентом вариограммы по гауссовому (нормальному) распределению и естественного соседа для участка B. Частично согласуется с оценкой точности характерного фрагмента. Различия в комплексной оценке оказались незначительными, так как метод естественного соседа показал большую устойчивость к образованию выбросов в топографической поверхности. Метод кригинга незначительно превзошел метод естественного соседа в остальных оцениваемых параметрах.
- Квадратичный кригинг со сферическим компонентом вариограммы для участка C. Согласуется с комплексной оценкой точности характерного фрагмента.
Заключение
В труднодоступных регионах проблематично развивать или оценивать сохранность имеющейся высотной основы. Создание цифровых моделей позволит значительно снизить производственные издержки на повторные измерения исследуемых участков и выполнить поиск наиболее производительных решений по выбору алгоритма построения математического аналога с заданной точностью. Снижение затрат на построение цифровых моделей приведет к увеличению доступности единого набора достоверной геопространственной информации, который применяется при проектировании, строительстве и дальнейшем мониторинге зданий и инженерных сооружений, при оценке опасности развития оползневых процессов, наблюдении за паводками и является основой для исследований в науках о Земле, основывающихся на информации как вспомогательной.
Исследование точности локальной модели квазигеоида показало:
- Наименьшее значение СКП интерполяции для площадного объекта достигнуто при использовании методов триангуляции с линейной интерполяцией (0,003 м) и кригинга (0,003 м). Наименьшее значение СКП определения высот по контрольным точкам для площадного объекта получено методами естественного соседа (0,004 м) и кригинга (0,004 м).
- Наименьшее СКП определения высот по модели показали методы кригинга (0,006м) и триангуляции с линейной интерполяцией (0,006 м). При оценке точности построения модели по контрольным точкам наименьшее значение СКП определения высот получено при использовании метода кригинга (0,007 м).
- При построении моделей квазигеоида необходимо определить количество исходных пунктов в районе работ, которое зависит от аномальности региона. При выполнении проектирования необходимого количества пунктов в данном районе рекомендуемое расстояние между совмещенными пунктами – 5 км.
Исследование точности построения ЦМР показало:
- Построение цифровой модели рельефа методом естественного соседа на равнинном участке земной поверхности А привело к наименьшему совокупному значению оцениваемых параметров: СКП, «Процент точек, отклонившихся более чем на 0,33 м», «Процент точек, отклонившихся более чем на 5 м».
- Для построения ЦМР на горном участке земной поверхности с выраженным антропогенным рельефом B авторы отметили метод квадратичного кригинга с компонентом вариограммы по гауссовому (нормальному) распределению.
- Для участка горной местности C по наименьшим значениям оцениваемых параметров авторы выделили метод квадратичного кригинга со сферическим компонентом вариограммы.
- Подход к оценке точности построения по характерным равнинному и горному фрагменту оказался действенным, так как был подтвержден при построении ЦМР на весь равнинный и горный объект работы. Это обусловлено близкими морфометрическими характеристиками. На горном фрагменте с антропогенным рельефом такой подход требует дополнительного контроля двумя методами пространственной интерполяции, близкими по оцениваемым параметрам к оптимальному, что объясняется областями с резким изменением кривизны поверхности;
Все методы пространственной интерполяции привели к отклонениям выше допустимых к топографическим поверхностям на равнинном, горном с антропогенным рельефом и горном участках земной поверхности при наименьших процентных отклонениях 5,84; 6,63 и 0,83 % соответственно.
Литература
- Пономаренко М.Р., Кутепов Ю.И., Шабаров А.Н. Информационно-аналитическое обеспечение мониторинга состояния объектов открытых горных работ на базе технологий веб-картографии // Горный информационно-аналитический бюллетень. 2022. № 8. С. 56-70. DOI: 10.25018/0236_1493_2022_8_0_56
- Рагузин И.И., Быкова Е.Н., Лепихина О.Ю. Метод полигональной метрической сетки для оценки кадастровой стоимости земельных участков // Вестник Московского университета. Серия 5. География. 2023. Т. 78. № 3. С. 92-103. DOI: 10.55959/MSU0579-9414.5.78.3.8
- Bykowa E., Skachkova M., Raguzin I. et al. Automation of Negative Infrastructural Externalities Assessment Methods to Determine the Cost of Land Resources Based on the Development of a «Thin Client» Model // Sustainability. 2022. Vol. 14. Iss. 15. № 9383. DOI: 10.3390/su14159383
- Бажин В.Ю., Масько О.Н., Мартынов С.А. Автоматизированный контроль и управление балансом шихты при производстве металлургического кремния // Цветные металлы. 2023. № 4. С. 53-60. DOI: 10.17580/tsm.2023.04.07
- Bazhin V.Yu., Masko O.N., Huy H. Nguyen. Increasing the speed of information transfer and operational decision-making in metallurgical industry through an industrial bot // Non-ferrous Metals. 2023. № 1. P. 62-67. DOI: 10.17580/nfm.2023.01.10
- Гендлер С.Г., Крюкова М.С. Управление тепловым режимом линий метрополитена, включающих в себя двухпутные и однопутные тоннели // Горный информационно-аналитический бюллетень. 2023. № 9-1. С. 248-269. DOI: 10.25018/0236_1493_2023_91_0_248
- Карасев М.А., Поспехов Г.Б., Астапенко Т.С., Шишкина В.С. Анализ моделей прогноза напряженно-деформированного состояния техногенных грунтов низкой прочности // Горный информационно-аналитический бюллетень. 2023. № 11. С. 49-69. DOI: 10.25018/0236_1493_2023_11_0_49
- Кульчицкий А.А., Мансурова О.К., Николаев М.Ю. Распознавание дефектов грузоподъемных канатов металлургического оборудования оптическим методом с помощью нейронных сетей // Черные металлы. 2023. № 3. С. 81-88. DOI: 10.17580/chm.2023.03.13
- Петров П.А., Шестаков А.К., Николаев М.Ю. Сбор и обработка данных алюминиевого электролизера с использованием многофункционального пробойного устройства и системы технического зрения // Цветные металлы. 2023. № 4. С. 45-53. DOI: 10.17580/tsm.2023.04.06
- Петрова Т.А., Астапенко Т.С., Кологривко А.А., Есман Н.М. Снижение геоэкологических последствий при складировании галитовых отходов // Горный информационно-аналитический бюллетень. 2022. № 10-1. С. 155-162 (in English). DOI: 10.25018/0236_1493_2022_101_0_155
- Беликов А.А., Беляков Н.А. Методика прогноза напряженно-деформированного состояния междукамерных целиков, закрепленных податливой тросовой крепью // Горный информационно-аналитический бюллетень. 2023. № 4. С. 20-34. DOI: 10.25018/0236_1493_2023_4_0_20
- Беляков Н.А., Беликов А.А. Прогноз целостности водозащитной толщи на Верхнекамском месторождении калийных руд // Горный информационно-аналитический бюллетень. 2022. № 6-2. С. 33-46. DOI: 10.25018/0236_1493_2022_62_0_33
- Huxiong Li, Weiya Ye, Jun Liu et al. High-Resolution Terrain Modeling Using Airborne LiDAR Data with Transfer Learning // Remote Sensing. 2021. Vol. 13. Iss. 17. № 3448. DOI: 10.3390/rs13173448
- Hashemi-Beni L., Jones J., Thompson G. et al. Challenges and Opportunities for UAV-Based Digital Elevation Model Generation for Flood-Risk Management: A Case of Princeville, North Carolina // Sensors. 2018. Vol. 18. Iss. 11. № 3843. DOI: 10.3390/s18113843
- Гусев В.Н., Блищенко А.А., Санникова А.П. Исследование комплекса факторов, оказывающих влияние на погрешность реализации маркшейдерской съемки горных объектов с применением геодезического квадрокоптера // Записки Горного института. 2022. № 254. С. 173-179. DOI: 10.31897/PMI.2022.35
- Кремчеев Э.А., Данилов А.С., Смирнов Ю.Д. Состояние метрологического обеспечения систем мо-ниторинга на базе беспилотных воздушных судов // Записки Горного института. 2019. Т. 235. C. 96-105. DOI: 10.31897/PMI.2019.1.96
- Меньшиков С.Н., Джалябов А.А., Васильев Г.Г. и др. Пространственные модели, разрабатываемые с применением лазерного сканирования на газоконденсатных месторождениях северной строительно-климатической зоны // Записки Горного института. 2019. Т. 238. С. 430-437. DOI: 10.31897/PMI.2019.4.430
- Luethje F., Tiede D., Eisank C. Terrain Extraction in Built-Up Areas from Satellite Stereo-Imagery-Derived Surface Models: A Stratified Object-Based Approach // ISPRS International Journal of Geo-Information. 2017. Vol. 6. Iss. 1. № 9.DOI: 10.3390/ijgi6010009
- Das R.K., Samanta S., Jana S.K., Rosa R. Polynomial interpolation methods in development of local geoid model // The Egyptian Journal of Remote Sensing and Space Science. 2018. Vol. 21. Iss. 3. P. 265-271. DOI: 10.1016/j.ejrs.2017.03.002
- Ahmed H.M., Mohamed E.A., Bahaa S.A. Evaluating two numerical methods for developing a local geoid model and a local digital elevation model for the Red Sea Coast, Egypt // Journal of King Saud University – Engineering Sciences. 2023. Vol. 35. Iss. 6. P. 384-392. DOI: 10.1016/j.jksues.2021.04.004
- Banasik P., Bujakowski K. The Use of Quasigeoid in Leveling Through Terrain Obstacles // Reports on Geodesy and Geoinformatics. 2017. Vol. 104. Iss. 1. P. 57-64. DOI: 10.1515/rgg-2017-0015
- Borowski Ł., Banaś M. The Best Robust Estimation Method to Determine Local Surface // Baltic Journal of Modern Computing. 2019. Vol. 7. № 4. P. 525-540. DOI: 10.22364/bjmc.2019.7.4.06
- Habib M., Alzubi Y., Malkawi A., Awwad M. Impact of interpolation techniques on the accuracy of large-scale digital elevation model // Open Geosciences. 2020. Vol. 12. Iss. 1. P. 190-202. DOI: 10.1515/geo-2020-0012
- Amodio A.M., Aucelli P.P.C., Garfì V., Rosskopf C.M. Digital photogrammetric analysis approaches for the realization of detailed terrain models // Rendiconti Online della Società Geologica Italiana. 2020. Vol. 52. P. 69-75. DOI: 10.3301/ROL.2020.21
- Bui L.K., Glennie C.L., Hartzell P.J. Rigorous Propagation of LiDAR Point Cloud Uncertainties to Spatially Regular Grids by a TIN Linear Interpolation // IEEE Geoscience and Remote Sensing Letters. 2022. Vol. 19. № 7003105. DOI: 10.1109/LGRS.2021.3134587
- Boreggio M., Bernard M., Gregoretti C. Evaluating the Differences of Gridding Techniques for Digital Elevation Models Generation and Their Influence on the Modeling of Stony Debris Flows Routing: A Case Study From Rovina di Cancia Basin (North-Eastern Italian Alps) // Frontiers in Earth Science. 2018. Vol. 6. № 89. DOI: 10.3389/feart.2018.00089
- Fazilova D., Magdiev H. Comparative Study of Interpolation Methods in Development of Local Geoid // International Journal of Geoinformatics. 2018. Vol. 14. № 1. P. 29-33.
- Banasik P., Bujakowski K., Kudrys J. et al. Development of a precise local quasigeoid model for the city of Krakow – QuasigeoidKR2019 // Reports on Geodesy and Geoinformatics. 2020. Vol. 109. Iss. 1. P. 25-31. DOI: 10.2478/rgg-2020-0004
- Mysen E. On the uncertainty of height anomaly differences predicted by least-squares collocation // Journal of Geodetic Science. 2020. Vol. 10. Iss. 1. P. 53-61. DOI: 10.1515/jogs-2020-0111
- Hosseini-Asl M., Amiri-Simkooei A.R., Safari A. Establishment of a corrective geoid surface by spline approximation of Iranian GNSS/levelling network // Measurement. 2022. Vol. 197. № 111341. DOI: 10.1016/j.measurement.2022.111341
- Medved K., Kuhar M., Koler B. Regional gravimetric survey of central Slovenia // Measurement. 2019. Vol. 136. P. 395-404. DOI: 10.1016/j.measurement.2018.12.065
- Chymyrov A. Comparison of different DEMs for hydrological studies in the mountainous areas // The Egyptian Journal of Remote Sensing and Space Science. 2021. Vol. 24. Iss. 3. Part 2. P. 587-594. DOI: 10.1016/j.ejrs.2021.08.001
- Mahbuby H., Safari A., Foroughi I. Local gravity field modeling using spherical radial basis functions and a genetic algorithm // Comptes Rendus Geoscience. 2017. Vol. 349. № 3. P. 106-113. DOI: 10.1016/j.crte.2017.03.001
- Belay E.Y., Godah W., Szelachowska M., Tenzer R. ETH-GQS: An estimation of geoid-to-quasigeoid separation over Ethiopia // Geodesy and Geodynamics. 2022. Vol. 13. Iss. 1. P. 31-37. DOI: 10.1016/j.geog.2021.09.006
- Qingwang Liu, Liyong Fu, Qiao Chen et al. Analysis of the Spatial Differences in Canopy Height Models from UAV LiDAR and Photogrammetry // Remote Sensing. 2020. Vol. 12. Iss. 18. № 2884. DOI: 10.3390/rs12182884
- Мустафин М.Г., Баландин В.Н., Брынь М.Я. и др. Топографо-геодезическое и картографическое обеспечение Арктической зоны Российской Федерации // Записки Горного института. 2018. Т. 232. С. 375-382. DOI: 10.31897/PMI.2018.4.375
- Mustafin M.G., Valkov V.A., Kazantsev A.I. Monitoring of Deformation Processes in Buildings and Structures in Metropolises // Procedia Engineering. 2017. Vol. 189. P. 729-736. DOI: 10.1016/j.proeng.2017.05.115
- Rusli N., Majid M.R., Nur Fakihin Auni A. Razali, Nur Fatma Fadilah Yaacob. Accuracy Assessment of DEM from UAV and TanDEM-X Imagery // 2019 IEEE 15th International Colloquium on Signal Processing & Its Applications, 8-9 March 2019, Penang, Malaysia. IEEE Xplore, 2019. P. 127-131. DOI: 10.1109/CSPA.2019.8696088
- Habib M. Evaluation of DEM interpolation techniques for characterizing terrain roughness // Catena. 2021. Vol. 198. № 105072. DOI: 10.1016/j.catena.2020.105072
- Li L., Nearing M.A., Nichols M.H. et al. The effects of DEM interpolation on quantifying soil surface roughness using terrestrial LiDAR // Soil and Tillage Research. 2020. Vol. 198. № 104520. DOI: 10.1016/j.still.2019.104520
- Chuanfa Chen, Yixuan Bei, Yanyan Li, Weiwei Zhou. Effect of interpolation methods on quantifying terrain surface roughness under different data densities // Geomorphology. 2022. Vol. 417. № 108448. DOI: 10.1016/j.geomorph.2022.108448
- Cățeanu M., Ciubotaru A. Accuracy of Ground Surface Interpolation from Airborne Laser Scanning (ALS) Data in Dense Forest Cover // ISPRS International Journal of Geo-Information. 2020. Vol. 9. Iss. 4. № 224. DOI: 10.3390/ijgi9040224
- Tao Zhang, Xiaosu Xu, Shengbao Xu. Method of establishing an underwater digital elevation terrain based on kriging interpolation // Measurement. 2015. Vol. 63. P. 287-298. DOI: 10.1016/j.measurement.2014.12.025
- Ikechukwu M.N., Ebinne E., Idorenyin U., Raphael N.I. Accuracy Assessment and Comparative Analysis of IDW, Spline and Kriging in Spatial Interpolation of Landform (Topography): An Experimental Study // Journal of Geographic Information System. 2017. Vol. 9. № 3. P. 354-371. DOI: 10.4236/jgis.2017.93022
- Павлова А.И. Анализ методов интерполирования высот точек для создания цифровых моделей рельефа // Автометрия. 2017. Т. 53. № 2. С. 86-94. DOI: 10.15372/AUT20170210
- Helwig Z.D., Guggenberger J., Elmore A.C., Uetrecht R. Development of a variogram procedure to identify spatial outliers using a supplemental digital elevation model // Journal of Hydrology X. 2019. Vol. 3. № 100029. DOI: 10.1016/j.hydroa.2019.100029
- Arun P.V. A comparative analysis of different DEM interpolation methods // The Egyptian Journal of Remote Sensing and Space Science. 2013. Vol. 16. Iss. 2. P. 133-139. DOI: 10.1016/j.ejrs.2013.09.001
- Bui L.K., Glennie C.L. Estimation of lidar-based gridded DEM uncertainty with varying terrain roughness and point density // ISPRS Open Journal of Photogrammetry and Remote Sensing. 2023. Vol. 7. № 100028. DOI: 10.1016/j.ophoto.2022.100028
- Agüera-Vega F., Agüera-Puntas M., Martínez-Carricondo P. et al. Effects of point cloud density, interpolation method and grid size on derived Digital Terrain Model accuracy at micro topography level // International Journal of Remote Sensing. 2020. Vol. 41. Iss. 21. P. 8281-8299. DOI: 10.1080/01431161.2020.1771788
- McRoberts R.E., Domke G.M., Qi Chen et al. Using genetic algorithms to optimize k-Nearest Neighbors configurations for use with airborne laser scanning data // Remote Sensing of Environment. 2016. Vol. 184. P. 387-395. DOI: 10.1016/j.rse.2016.07.007
