Учет геомеханического состояния трещинно-порового коллектора при гидродинамическом моделировании
- 1 — д-р техн. наук профессор Пермский национальный исследовательский политехнический университет ▪ Orcid ▪ ResearcherID
- 2 — канд. техн. наук Ведущий научный сотрудник Пермский национальный исследовательский политехнический университет ▪ Orcid
- 3 — канд. техн. наук Ведущий научный сотрудник Пермский национальный исследовательский политехнический университет ▪ Orcid
Аннотация
Представлено гидродинамическое моделирование залежи углеводородов с трещинно-поровым коллектором с учетом геомеханических эффектов смыкаемости трещинного пространства в процессе изменения пластового давления. Параметр трещинной проницаемости получен на основе представлений о влиянии напряженного состояния массива на стенки трещин, параметр трещиноватости определен на основе обработки данных сейсморазведки по методологии 3D. Модель со снижением проницаемости реализована в гидродинамическом симуляторе tNavigator. Применение нового подхода позволило улучшить сходимость динамики пластовых давлений в скважинах в созданной гидродинамической модели при неизменном качестве адаптации дебитов и обводненности, а также повысить надежность прогнозирования пластовых давлений и в результате оптимизировать систему поддержания пластового давления.
Введение
При интенсивном снижении пластового давления во время разработки залежи с трещинным типом коллектора происходят процессы, которые затруднительно воспроизвести в рамках модели одной среды. Эти процессы, описанные в научно-технической литературе, связаны с эффектами смыкания трещин и изменения трещинной проницаемости, т.е. с геомеханическим состоянием продуктивного объекта [1-3].
В настоящее время при создании гидродинамических моделей нефтяных и газовых залежей даже при наличии трещинно-порового коллектора используется модель единой пористости. Ее создание является хорошо отработанной и даже рутинной операцией. Адаптация подобной модели к начальным условиям разработки также не вызывает затруднений. Дебиты по скважинам и забойные давления определяются фильтрационно-емкостными свойствами прискважинной области пласта. Обводненность продукции скважин является функцией фазовых проницаемостей и активности законтурной области. Одним из наиболее важных и при этом сложно настраиваемых параметров является динамика пластовых давлений по отдельным скважинам. От пластового давления зависят режим работы скважины, выбор скважинного оборудования, планирование мероприятий по интенсификации притока. С точки зрения физики пласта от пластового давления зависят содержание в порах свободного газа и, как следствие, фазовые проницаемости, а также раскрытие трещин в коллекторе и абсолютная проницаемость.
Наиболее корректным способом моделирования трещинного коллектора является создание модели дискретной сети трещин (DFN) с последующим использованием при создании гидродинамической модели с двойной пористостью/проницаемостью. Основной недостаток такой модели – сложность реализации из-за расширенного параметрического обеспечения [4].
В статье предложен подход к геолого-гидродинамическому моделированию залежей углеводородов с трещинно-поровым коллектором, основанный на учете геомеханических эффектов смыкаемости трещинного пространства в процессе изменения пластового давления. При этом распределение по разрезу проницаемости носит динамический характер. В начальных пластовых условиях коллектор представлен как поровой средой, так и системами открытых трещин. При снижении пластового давления происходит интенсивное уменьшение трещинной проницаемости, вследствие чего целые области пласта, ранее считавшиеся коллектором, перестают фильтровать углеводороды. Начальная величина проницаемости, как и ее изменение, являются функцией напряжений.
Исследования проводились для турнейско-фаменского пласта (ТФм) одного из месторождений Пермского края – пластовой массивной карбонатной залежи с высокой расчлененностью (до 19) при общей толщине пласта 50-75 м. Работа скважин характеризуется высокими дебитами в первое время работы (до 100 м3/сут и выше). Для большинства скважин в течение первых 5-10 лет работы наблюдается падение дебитов в несколько раз.
Методы
Для учета динамического характера поведения фильтрационно-емкостных свойств трещинного коллектора при гидродинамическом моделировании процесс создания модели в соответствии с новым подходом можно разбить на несколько этапов:
- анализ промысловых данных и гидродинамических исследований скважин, выявление областей с эффектом снижения проницаемости;
- выбор геолого-геофизических критериев, определяющих интенсивность процесса снижения трещинной проницаемости или отсутствие данного процесса;
- создание трехмерной геомеханической модели пласта и вмещающих пород;
- подготовка к гидродинамическому моделированию, расчет кубов проницаемости и параметров сжимаемости трещин;
- корректировка и адаптация новой гидродинамической модели с учетом эффекта смыкания трещин и новых проницаемостей.
С целью выявления эффекта изменения фильтрационных свойств коллектора на первом этапе был проведен анализ результатов гидродинамических исследований скважин, а также промысловых данных работы скважин. Факт изменения фильтрационных свойств может быть предварительно установлен по снижению проницаемости скважины, определенное по кривым восстановления давления, по вогнутым к оси дебитов индикаторных диаграмм скважин, а также по отрицательной динамике коэффициента продуктивности [5, 6]. При этом наиболее надежным является первый способ выделения данного эффекта, поскольку динамика проницаемости анализируется на контуре скважины, где отсутствует процесс кольматации. Согласно распространенной практике, зависимость проницаемости от давления аппроксимируется экспоненциальной функцией вида
где k0 и k – начальная и текущая проницаемость; p0 и p – начальное и текущее пластовые давления; β – степень снижения проницаемости.
Неизвестными величинами являются начальная проницаемость при пластовых условиях k0 и параметр снижения проницаемости β. Подобный анализ возможен при наличии достаточно широкого диапазона пластовых давлений исследований скважины на нестационарных режимах, при низких значениях обводненности и пластовых давлениях, превышающих давление насыщения. На рассматриваемом объекте этим условиям соответствует 10 скважин, для которых в дальнейшем был определен β.
При выборе геолого-геофизических критериев для трехмерного распределения параметра снижения проницаемости возможно использование нескольких подходов. Например, в работе [7] проводилось ранжирование по скорости пробега продольной волны. Сжимаемость стенок трещины определялось прочностными свойствами породы, которые, в свою очередь, зависели от скорости продольной волны. Преимуществом данного способа является распространенность материалов акустического каротажа для большинства объектов, главный недостаток – отсутствие привязки к трещиноватости. В случае порово-трещинного коллектора, где трещиноватость распространена не повсеместно, на основе интервального времени пробега продольной волны можно ложно выделить высокую сжимаемость породы даже в областях с поровым типом коллектора.
В связи с этим в данной работе изучалось распределение трещиноватости пласта по скважинным данным и исследованиям керна. Поскольку скважин, охваченных исследованиями трещиноватости, недостаточно для простой интерполяции, осуществлялся поиск взаимосвязи трещиноватости с материалами 3D-сейсмики. Была собрана воедино и проанализирована совокупность данных исследований, связанных с выделением трещин [8]. Изучалась трещиноватость восьми скважин объекта ТФм анализируемого месторождения. Исследования включали геофизическое изучение скважин методом ЭМС с помощью приборов КарСар МС-110 и MicroScope, а также определение трещиноватости в ориентированном керне.
Из всей совокупности данных выделяется распределение субвертикальной трещиноватости с преимущественными азимутами простирания 90-130° и углами падения 70-85°. При этом зависимость результатов от используемого прибора не прослеживалась. Полученные распределения в дальнейшем использовались для построения объемной вероятностной модели трещиноватости исследуемого объекта, осуществлялась классификация с использованием методов машинного обучения на языке Python. В качестве исходных параметров для обучения модели использовались кубы угловых сумм амплитуд сейсморазведки 3D напрямую (без преобразования в атрибуты). Идея заключалась в использовании отрезка сейсмической трассы, проходящей через исследуемую точку в интервале ±50 м относительно этой точки с применением методов сжатия (методы главных векторов, сингулярного разложения матриц и т.д.), в качестве входных параметров методов машинного обучения. В качестве моделей машинного обучения применялись различные бустинги.
Качество классификации оценивалось методом кросс-валидации с использованием метрики ROC AUC и достигло значений 0,88-0,91 для разных моделей. При этом на основе фактических данных были выделены два класса (вида) пустотного пространства – без трещин (0) и с трещинами (1). На рис.1 приведены распределения плотностей вероятностей встречаемости данных классов в зависимости от вероятности прогнозов моделей машинного обучения. Классы хорошо разделены таким образом, что при увеличении предсказанной вероятности увеличивается отношение класса 1 к классу 0.
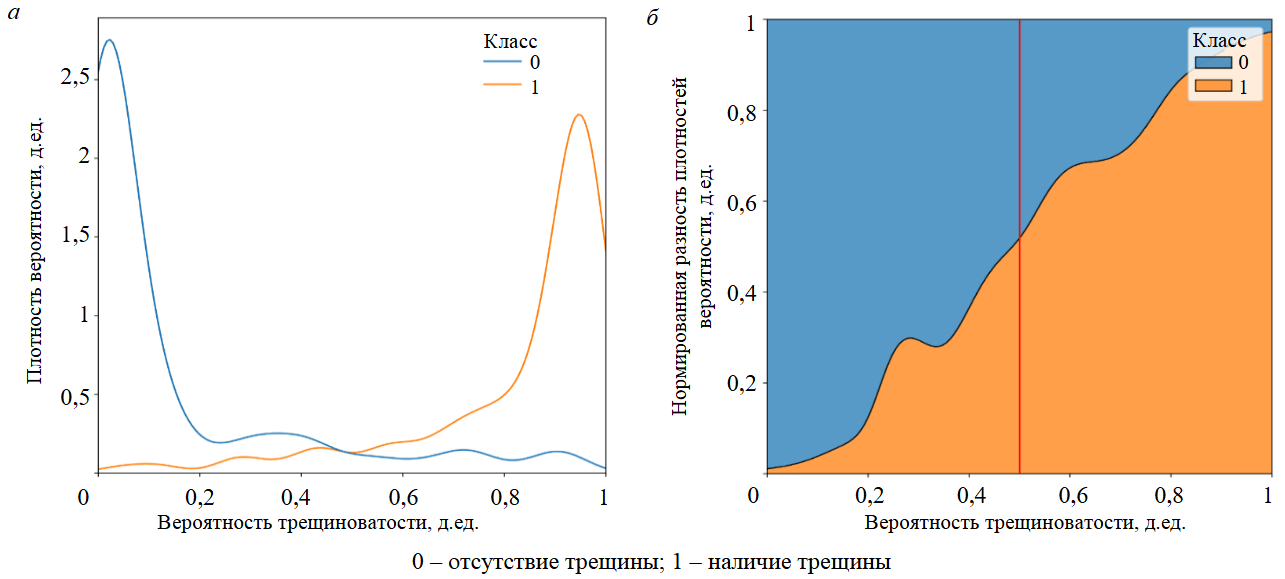
Рис.1. Распределение плотностей вероятностей трещиноватости для выделенных классов (а) и нормированная разность плотностей вероятности (б)
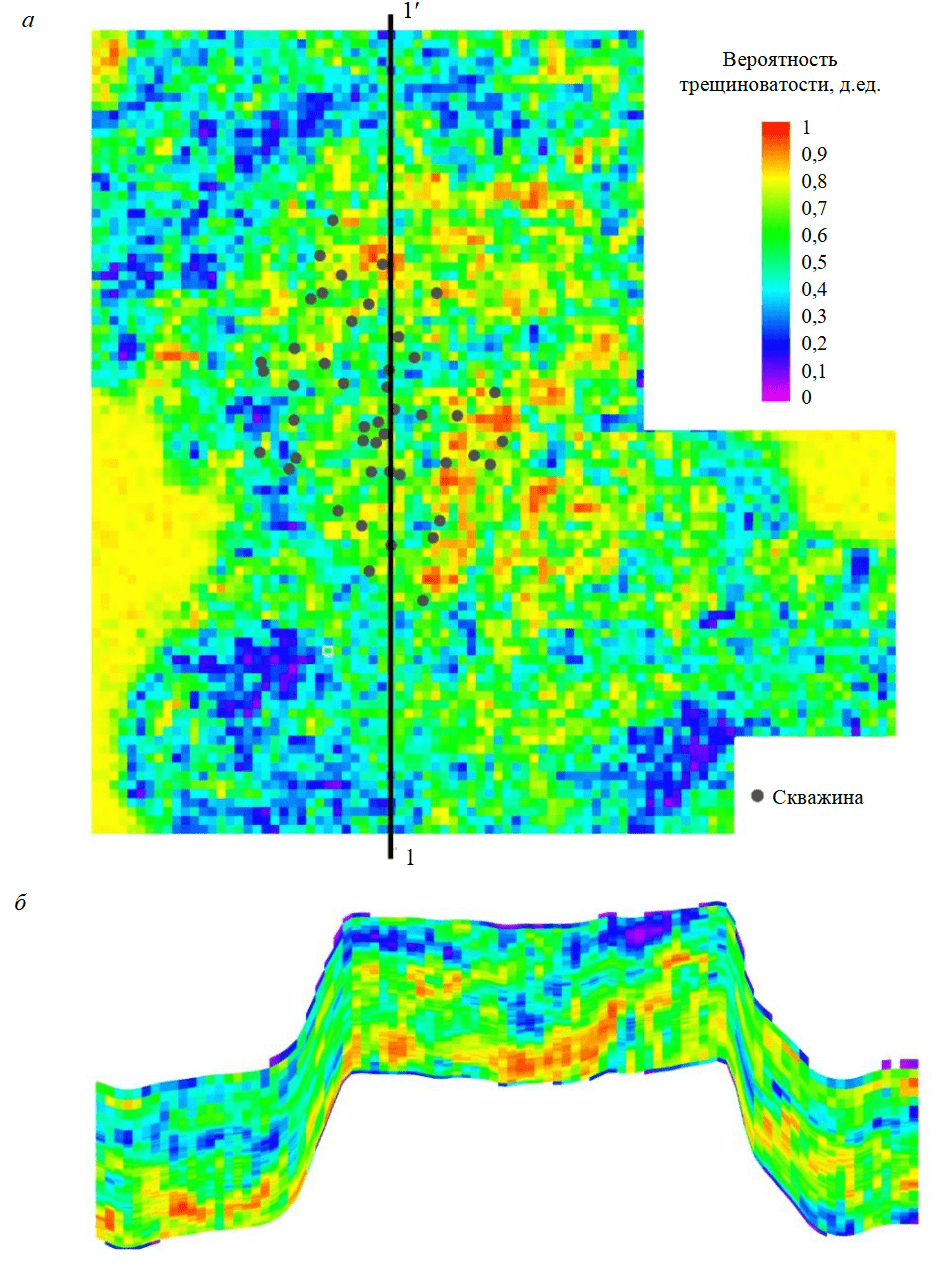
Рис.2. Вероятность распределения трещиноватости по кровле пласта ТФм (а) и по разрезу 1-1 (б)
На основании полученного куба трехмерного распределения вероятности трещиноватости (рис.2) было определено среднее значение этого параметра в интервале перфорации для всех скважин. Дальнейший анализ параметра для группы скважин с достаточным количеством КВД, продемонстрировал его линейную взаимосвязь со снижением проницаемости
где CD – вероятностный параметр наличия трещиноватости (диапазон изменения от 0 до 1).
Эта зависимость использовалась в дальнейшем для выделения регионов снижения проницаемости в процессе гидродинамического моделирования, а также для расчета таблиц зависимости фильтрационно-емкостных свойств от пластового давления в каждом выделенном регионе.
В настоящее время для получения трехмерного распределения проницаемости в гидродинамической модели трещинных и трещинно-поровых объектов в большинстве случаев по-прежнему используются корреляции от пористости с последующей калибровкой на результаты гидродинамических исследований (ГДИ) скважин. Для определения распределения проницаемости применялся геомеханический подход.
В научно-технической литературе имеется множество сведений о влиянии напряженного состояния пород на проницаемость коллекторов трещинно-порового и трещинного типов [9-11]. В то же время проницаемость коллекторов порового типа не столь существенно зависит от напряженного состояния, как проницаемость трещиноватой горной породы [12-14]. С учетом этого выполнялся поиск взаимосвязи напряженного состояния массива [15, 16] с трещинной проницаемостью, определенной на основе ГДИ.
Очевидно, что проницаемость тех или иных систем трещин и нарушений существенно зависит от их ориентировки относительно главных нормальных напряжений. Гипотеза критически напряженного нарушения [16, 17] утверждает, что «нарушения, которые являются механически активными, также являются гидравлически активными, а нарушения, которые не являются механически активными, не являются гидравлически активными», и подтверждается многочисленными исследованиями [16, 18, 19]. Под механически активными понимаются нарушения, находящиеся в таком напряженном состоянии, при котором действующие на нем нормальные и касательные напряжения способствуют раскрытию трещин нарушения, что в свою очередь позволяет осуществляться движению флюида по данному нарушению. При этом очевидно, что проницаемость определенной системы трещин будет зависеть от нормальных напряжений, которые сжимают ее, и от касательных напряжений, которые стремятся сдвинуть горную породу по данной системе трещин [20]. Уравнения для расчета касательных и нормальных напряжений, действующих по трещине, широко известны [1, 15].
Тенденция к сдвигу по трещине будет определяться не только уровнем действующих напряжений, но и прочностными параметрами. Критерий напряженного состояния для поверхности ослабления (трещины или нарушения) в общем случае:
где μ – параметр трения; τ, σn – касательное и нормальное к поверхности стенок трещины напряжения соответственно.
Таким образом, вычислив действующие на анализируемой системе трещин нормальные и касательные напряжения и сопоставив их с данными проницаемости продуктивного объекта, зафиксированными в определенном интервале, можно судить о степени активности системы трещин.
Проницаемость трещинного массива при использовании простейшей модели, представленная системой плоскопараллельных трещин (при условии непроницаемой матрицы), определяется следующей зависимостью:
где е – раскрытие трещин; d – расстояние между трещинами.
В качестве параметра, характеризующего густоту трещин (величина, обратная расстоянию между трещинами), можно использовать куб вероятности трещиноватости.
Таким образом, принимая вероятность трещиноватости как характеристику густоты трещин (p = 1/d) и величину е (е = τ/σn) как параметр, характеризующий раскрытие, можно составить выражение, определяющее проницаемость трещинного коллектора:
где Prob – значение вероятности трещиноватости; τ/σn – отношение нормальных (σn) и касательных (τ) напряжений по системе трещин; a – эмпирический коэффициент [20].
В расчете трещинной проницаемости учитывалось два вида трещиноватости: упорядоченная, соответствующая максимальной концентрации трещин (азимут 115°, угол падения 80°), и условно упорядоченная, связанная с кривизной стратиграфических слоев, азимут простирания которой составляет нормаль к направлению максимальной кривизны. Азимут максимальной кривизны рассчитывался как физическое направление (т.е. не из сопоставления векторов по взаимно перпендикулярным направлениям, как это реализовано в большинстве пакетов геологического моделирования); угол падения второй системы трещин определялся из решения задачи оптимизации. В конечном выражении к трещинной проницаемости также была добавлена поровая проницаемость, взятая из геологической модели. В таком случае итоговое расчетное выражение полной проницаемости коллектора выглядит следующим образом:
где Kпор – поровая составляющая проницаемости.
Для последующих гидродинамических расчетов трещинную составляющую проницаемости, полученную в локальной системе координат трещины, необходимо преобразовать в глобальную систему координат модели (2). Для каждой системы трещин вычисляется тензор проницаемости в глобальной системе координат гидродинамической модели [15]:
где α – угол падения данной системы трещин; θ – азимут простирания системы трещин; m – количество систем трещин.
Создание геомеханической модели
Величины касательных и нормальных напряжений, а также направления их приложения в каждой ячейке для расчета проницаемости были получены из геомеханической модели. Построение геолого-геомеханической модели [1, 18, 19] продуктивных объектов или месторождения в целом предполагает оценку его исходного напряженного состояния, т.е. определение следующих параметров: вертикальной компоненты горного давления; минимальной и максимальной горизонтальных компонент горного давления; азимута действия горизонтальной компоненты; порового давления; распределенных значений физико-механических свойств пород продуктивного объекта и вмещающих пород [21-23].
Построение объемной геомеханической конечно-элементной сетки модели выполнялось посредством ее экспорта из программы геологического моделирования (в виде координат восьми узлов для каждого элемента) и преобразования данных в формат, поддерживаемый геомеханическим симулятором.
Латеральные размеры ячейки сетки составили 100×100 м. В области исследуемого продуктивного объекта было проведено значительное сгущение конечно-элементной расчетной сетки (до 0,4 м). Особенностью построения данной модели является отсутствие воспроизведения вышележащей толщи целиком. Вместо этого создан выравнивающий слой, к которому на этапе геомеханического расчета прикладывается нагрузка, соответствующая весу вышележащих пород.
Величина вертикального горного давления определяется весом вышележащих пород. Распределение плотности в разрезе вычислялось путем интерполяции каротажных данных плотностного каротажа с последующим интегрированием плотности пород с учетом толщин ячеек геомеханической модели для определения вертикального горного давления. Значения физико-механических свойств пород продуктивного объекта были приняты по полученным в результате керновых испытаний зависимостям между статическими и динамическими геомеханическими характеристиками [24-27].
Расчет компонент бокового горного давления выполнялся по модели изотропной упругой пористой среды [16, 28, 29]:
где Sh, SH – минимальная и максимальная компоненты горизонтальных напряжений соответственно; р – пластовое (поровое) давление; σv – вертикальное напряжение, Biot– коэффициент Био; v – коэффициент Пуассона, E – модуль упругости, ɛh, ɛH – компоненты дополнительных тектонических деформаций.
Распределение пластового давления по разрезу было принято в соответствии с действующей гидродинамической моделью и впоследствии корректировалось при наличии текущих данных по пластовому давлению (ГДИ скважин, замеры при производстве операций гидравлического разрыва пласта (ГРП) и т.д.) [30].
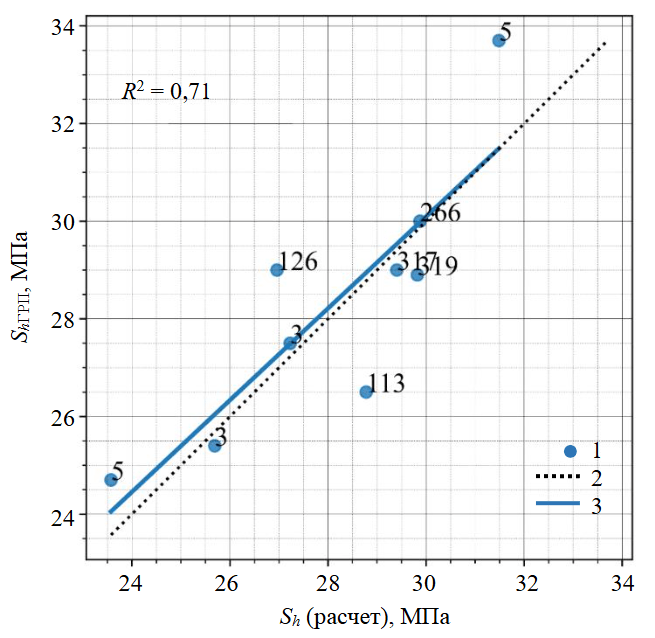
Рис.3. Сопоставление расчетных напряжений с замеренными величинами давлений смыкания трещин ГРП
1 – значения в скважинах; 2 – линия ровных значений; 3 – регрессивная прямая
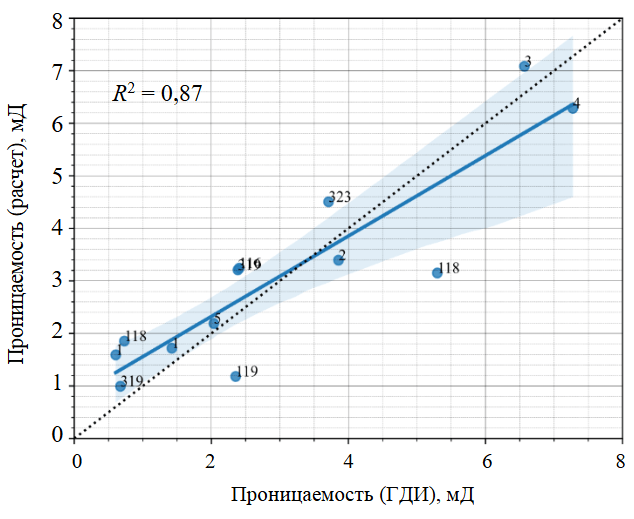
Рис.4. Кроссплот кубического корня расчетной и определенной из ГДИ проницаемостей
Условные обозначения см. на рис.3
Калибровка расчетного профиля минимального горизонтального напряжения выполнялась путем сопоставления расчетных напряжений с замеренными величинами давлений смыкания трещин при производстве операций ГРП (рис.3).
Далее методом конечных элементов был выполнен расчет напряженно-деформированного состояния массива в программе Ansys. Калькуляция выполнялась в сопряженной постановке с учетом течения флюида в деформируемой поровой среде. В модели были заданы кинематические граничные условия на нижней и боковых гранях для учета тектонических деформаций.
После завершения геомеханических вычислений с использованием соотношений (2)-(4) был построен куб проницаемости, который в дальнейшем использовался для гидродинамического моделирования. Расчитанная по данной методике проницаемость показала хорошую взаимосвязь с результатами ГДИ (рис.4).
В заключительной части работы проводилось гидродинамическое моделирование с использованием новых кубов проницаемости и представлений о смыкании трещин.
В исходной гидродинамической модели залежь имеет значительную расчлененность, при которой у отдельных пропластков отсутствует гидродинамическая взаимосвязь. При этом не учитывается развитая система трещиноватости, выявленная исследованиями керна и отчетов испытаний микроимиджерами. Данные участки залежи могут формально считаться неколлектором, поскольку общая пустотность, включающая в себя пористость и трещинную пористость, является весьма незначительной, но при этом через трещины может происходить фильтрация пластовых флюидов.
Для учета трещиноватости в процессе гидродинамического моделирования предложен промежуточный вариант между исходной моделью и моделью двойной среды, имеющий следующие особенности:
- неактивные ячейки из исходной гидродинамической модели были заданы активными;
- в ячейках исходного неколлектора была задана незначительная пористость (0,2 %, при этом начальные запасы нефти по всей модели увеличились на 3 %);
- проницаемость была определена по формулам (2)-(4) во всех ячейках модели;
- анизотропия проницаемости рассчитывалась с использованием выявленных и принятых в расчетах угловых параметров систем трещин [21];
- снижение проницаемости было задано необратимым, что подтвердилось значительным объемом компрессионных испытаний образцов керна с единичной трещиной.
Снижение проницаемости учитывалось с помощью 10 таблиц изменения проницаемости rocktab [31]. Регионы применения данных таблиц определялись величиной вероятности трещиноватости. Первому региону соответствуют области залежи с минимальным количеством трещин, десятому – области с наибольшей густотой трещин и максимальным снижением проницаемости. Параметр β определен по линейной зависимости (1). Методика учета эффекта снижения проницаемости гидродинамических расчетов реализована в программном пакете tNavigator.
Обсуждение результатов
Гидродинамические расчеты показали, что при снижении пластового давления выделяются области, где проницаемость падает особенно интенсивно. В случае невысокой начальной проницаемости и быстрого снижения проницаемости возможно возникновение зон, где прекращается фильтрация флюидов. Это свидетельствует о непостоянном (динамическом) по времени характере литологического разреза (рис.5).
Применение нового подхода позволило улучшить адаптацию расчетных пластовых давлений к фактическим значениям при гидродинамическом моделировании разработки объекта (рис.6). Снижение пластового давления по скважине 3 сопровождалось снижением дебита жидкости от 80 до 20 м3/сут. При этом, согласно исходной модели, меньший отбор жидкости в скважине при одновременной работе соседних нагнетательных скважин позволяет восстановить пластовое давление, чего не наблюдается в фактических данных. Объяснить данный факт можно, исходя из концепции динамического характера литологического строения коллектора в области дренирования данной скважины. В гидродинамической модели на основе геомеханического подхода снижение пластового давления повлекло за собой существенное необратимое снижение проницаемости в обширных областях залежи, в результате чего была нарушена гидродинамическая связь добывающей скважины с нагнетательными скважинами и законтурной областью. Данный результат подчеркивает важность своевременного введения системы поддержания пластового давления в залежах углеводородов с трещинным типом коллектора. Также можно сделать вывод о критической важности корректного определения и учета в гидродинамических расчетах параметра сжимаемости горных пород [32, 33].
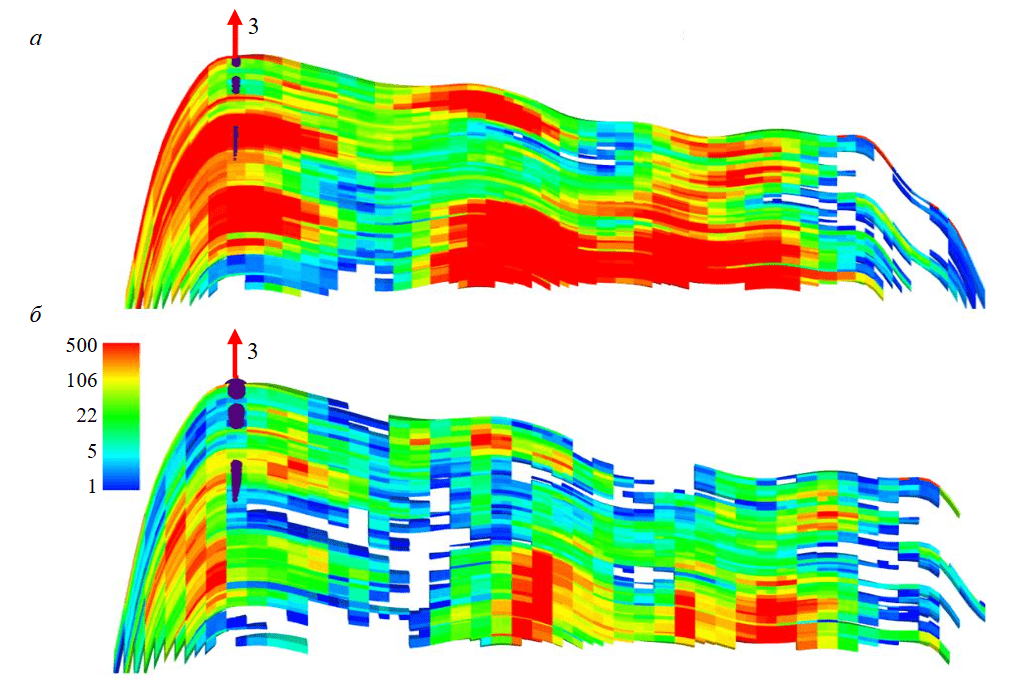
Рис.5. Распределение по разрезу проницаемости породы скважины 3 на начало разработки (а) и через 10 лет (б)
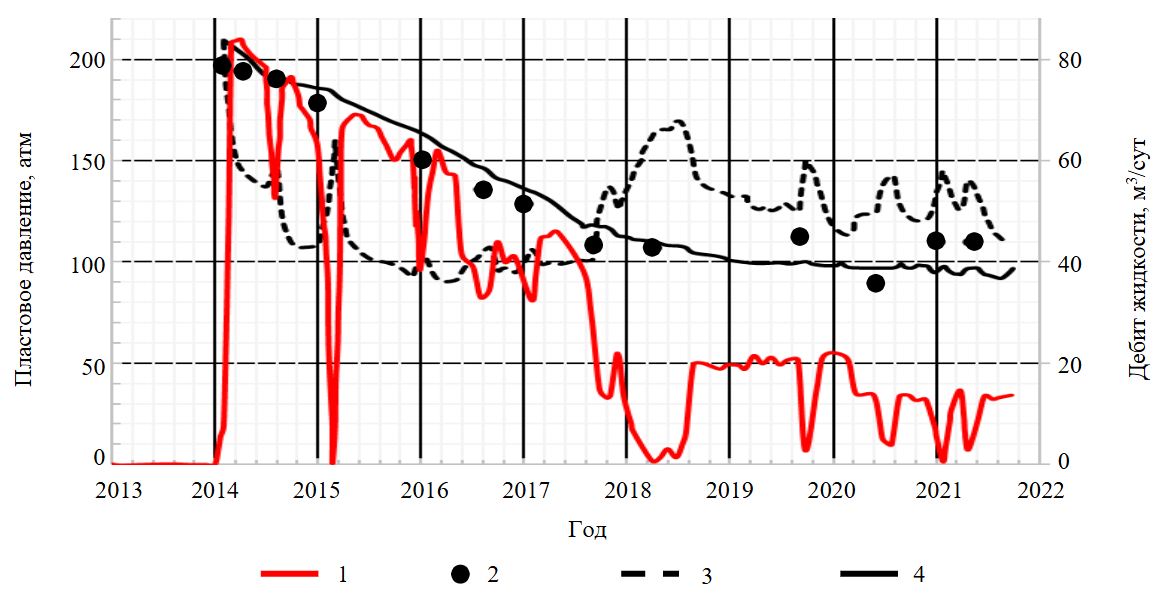
Рис.6. Динамика дебита жидкости и пластового давления скважины 3
1 – дебит жидкости, м3/сут; 2 – фактические данные; 3 – исходная гидродинамическая модель; 4 – гидродинамическая модель на основе геомеханического подхода
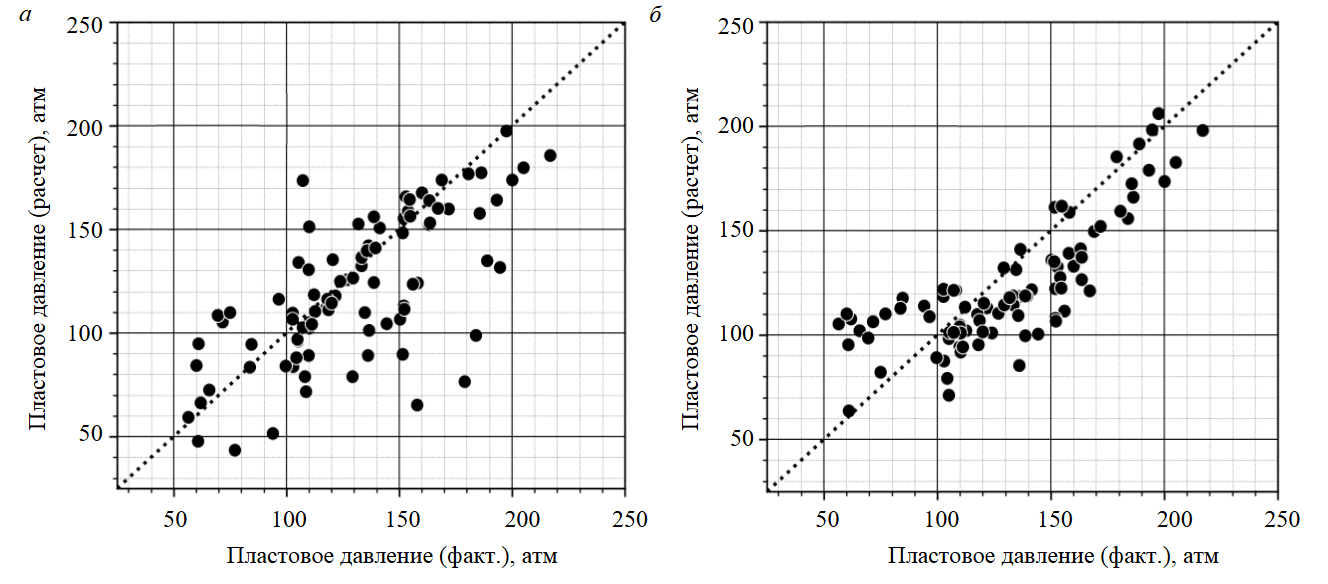
Рис.7. Кроссплот соответствия фактических и расчетных пластовых давлений по скважинам для исходной (а) и модифицированной с использованием геомеханического моделирования (б) моделей
На рис.7 приведены кроссплоты фактических и расчетных пластовых давлений по всем скважинам. В модели, модифицированной на основе использования геомеханического моделирования, соответствие фактических и расчетных пластовых давлений более выражено, чем в исходной модели. При этом качество адаптации по дебитам скважин и обводненности по сравнению с исходной моделью не ухудшилось.
В результате расчетов можно сделать вывод о применимости представленной концепции для повышения качества адаптации гидродинамических моделей залежей углеводородов с трещинным типом коллектора.
Заключение
Поиск новых подходов гидродинамического моделирования трещинных коллекторов остается актуальной задачей при проектировании и сопровождении разработки месторождений углеводородов.
Лучшим способом учета трещиноватости при создании модели остается разработка модели дискретной сети трещин (DFN) с ее последующим использованием при создании гидродинамической модели с двойной пористостью/проницаемостью, однако данная модель требует расширенного параметрического обеспечения.
В настоящее время все большее распространение получают трехмерные геомеханические модели, в которых по исходным физико-механическим свойствам с использованием метода конечных элементов рассчитывается трехмерное распределение направлений и величин главных нормальных напряжений. Как правило, большинство геомеханических моделей строится для планирования и сопровождения операций бурения скважин и операций ГРП, но результаты моделирования могут быть использованы для оценки степени раскрытия трещин в трещинных коллекторах и, как развитие этого направления, для построения трехмерного распределения кубов проницаемости.
Обобщение результатов исследований трещиноватости позволило определить генеральные угловые параметры систем трещин для рассмотренного объекта. Путем классификации методами машинного обучения с использованием кубов угловых сумм трехмерной сейсмической съемки был получен куб вероятности трещиноватости. Выявлена хорошая взаимосвязь между проницаемостью коллектора и состоянием горной породы, определенным при геомеханическом моделировании. Благодаря выявленной взаимосвязи удалось получить полный тензор проницаемости для объекта ТФм.
В программном пакете tNavigator реализована методика учета эффекта снижения проницаемости в гидродинамических расчетах. При этом общее снижение проницаемости залежи моделируется с помощью встроенных ключевых слов симулятора.
Гидродинамическое моделирование с использованием описанных подходов позволило значительно улучшить сходимость динамики пластовых давлений при приемлемом качестве сходимости динамики добычи и обводненности. Повышение надежности прогнозирования пластовых давлений позволяет планировать мероприятия по интенсификации притока с более предсказуемым результатом, создавать более реальные характеристики трещин при разработке дизайнов ГРП, а также оптимизировать систему поддержания пластового давления.
Литература
- Кашников Ю.А., Ашихмин С.Г. Механика горных пород при разработке месторождений углеводородного сырья. М.: Горная книга, 2019. 496 c.
- Щипанов А.А. Влияние динамической информации трещинно-порового коллектора на эффект от увеличения депрессии // Геология, геофизика и разработка нефтяных и газовых месторождений. 2003. № 2. С. 33-37.
- Черемисин Н.А., Сонич В.П., Ефимов П.А. Роль неупругой деформации коллекторов в нефтеотдаче пластов // Нефтяное хозяйство. 2001. № 9. С. 76-79.
- Закревский К.Е., Кундин А.С. Особенности геологического 3D моделирования карбонатных и трещинных резервуаров. М.: ООО «Белый Ветер», 2016. 404 с.
- Викторин В.Д. Влияние особенностей карбонатных коллекторов на эффективность разработки нефтяных залежей. М.: Недра, 1988. 149 с.
- Lun Zhao, Zifei Fan, Mingxian Wang et al. Productivity Evaluation of Vertical Wells Incorporating Fracture Closure and Reservoir Pressure Drop in Fractured Reservoirs // Mathematical Problems in Engineering. 2020. Vol. 2020. Iss. 1. № 9356178. DOI: 10.1155/2020/9356178
- Якимов С.Ю. Геолого-геомеханические основы оценки изменения трещинной проницаемости в процессе изменения пластового давления в карбонатных коллекторах: Автореф. дис. … канд. техн. наук. Пермь: Пермский национальный исследовательский политехнический университет, 2018. 26 с.
- Черепанов С.С., Пономарева И.Н., Ерофеев А.А., Галкин С.В. Определение параметров трещиноватости пород на основе комплексного анализа данных изучения керна, гидродинамических и геофизических исследований скважин // Нефтяное хозяйство. 2014. № 2. С. 94-96.
- Brace W.F. Permeability of crystalline and argillaceous rocks // International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1980. Vol. 17. Iss. 5. P. 241-251. DOI: 10.1016/0148-9062(80)90807-4
- Kranzz R.L., Frankel A.D., Engelder T., Scholz C.H. The permeability of whole and jointed Barre Granite // International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1979. Vol. 16. Iss. 4. P. 225-234. DOI: 10.1016/0148-9062(79)91197-5
- Barton N., Bandis S., Bakhtar К. Strength, deformation and conductivity coupling of rock joints // International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. 1985. Vol. 22. Iss. 3. P. 121-140. DOI: 10.1016/0148-9062(85)93227-9
- Barton N., Bandis S. Effects Of Block Size On The Shear Behavior Of Jointed Rock // The 23rd U.S Symposium on Rock Mechanics (USRMS), 25-27 August 1982, Berkeley, CA, USA. OnePetro, 1982. № ARMA-82-739.
- Fischer K. Geomechanical reservoir modeling – workflow and case study from the North German Basin: vom Fachbereich Material- und Geowissenschaften der Technischen Universität Darmstadt zur Erlangung des akademischen Grades Doktor der Naturwissenschaften (Dr. rer. nat.) genehmigte Dissertation. Darmstadt: Technische Universität, 2013. 265 p.
- Zhang Zhang, Shunli He, Daihong Gu et al. Effects of stress-dependent permeability on well performance of ultra-low permeability oil reservoir in China // Journal of Petroleum Exploration and Production Technology. 2018. Vol. 8. Iss. 2. P. 565-575. DOI: 10.1007/s13202-017-0342-2
- Wittke W. Rock Mechanics Based on an Anisotropic Jointed Rock Model (AJRM). Ernst & Sohn, 2014. 876 p. DOI: 10.1002/9783433604281
- Zoback M.D. Reservoir Geomechanics. Cambridge: Cambridge University Press, 2007. 449 p. DOI: 10.1017/CBO9780511586477
- Zoback M.D., Kohli A.H. Unconventional Reservoir Geomechanics. Shale Gas, Tight Oil, and Induced Seismicity. Cambridge University Press, 2019. 495 p. DOI: 10.1017/9781316091869
- Shustov D.V., Kashnikov Yu.A., Ashikhmin S.G., Kukhtinskiy A.E. 3D Geological Geomechanical Reservoir Modeling for the Purposes of Oil and Gas Field Development Optimization // Geomechanics and Geodynamics of Rock Masses. CRC Press, 2018. Vol. 2. P. 1425-1430.
- Tavaf Saeed, Abdideh M. Using petrophysical and geomechanical modeling of reservoir rock in well completion // Modeling Earth Systems and Environment. 2022. Vol. 8. Iss. 4. P. 5639-5652. DOI: 10.1007/s40808-022-01440-4
- Шустов Д.В., Кашников Ю.А. Разработка геолого-геомеханической модели участка Юрубчено-Тохомского месторождения // Геология, геофизика и разработка нефтяных и газовых месторождений. 2015. № 4. С. 26-31.
- Charlez Рh.A. Rock Mechanics. In 2 volumes. Vol. 2: Petroleum Applications. Technip Editions, 1997. 661 p.
- Hampton J., Boitnott G. Integration of Fine-Scale, Plug, and Well-Log Geomechanical Properties // 53rd U.S. Rock Mechanics/Geomechanics Symposium, 23-26 June 2019, New York City, NY, USA. OnePetro, 2019. № ARMA-2019-2077.
- Boitnott G., Louis L., Hampton J. et al. High Resolution Geomechanical Profiling in Heterogeneous Source Rock From the Vaca Muerta Formation, Neuquén Basin, Argentina // 52nd U.S. Rock Mechanics/Geomechanics Symposium, 17-20 June 2018, Seattle, WA, USA. OnePetro, 2018. № ARMA-2018-129.
- Gowida A., Elkatatny S., Moussa T. Comparative Analysis Between Different Artificial Based Models for Predicting Static Poisson’s Ratio of Sandstone Formations // International Petroleum Technology Conference, 13-15 January 2020, Dhahran, Kingdom of Saudi Arabia. OnePetro, 2020. № IPTC-20208-MS. DOI: 10.2523/IPTC-20208-MS
- Qi Li, Aguilera R., Cinco-Ley H. A Correlation for Estimating the Biot Coefficient // SPE Drilling & Completion. 2020. Vol. 35. Iss. 2. P. 151-163. DOI: 10.2118/195359-PA
- Rekoske J., Walton G. Estimating Mechanical Properties of Sandstone from Petrographic and Physico-Mechanical Indices // 53rd U.S. Rock Mechanics/Geomechanics Symposium, 23-26 June 2019, New York City, NY, USA. OnePetro, 2019. № ARMA-2019-0101.
- Tariq Z., Mahmoud M.A., Abdulraheem A., Al-Shehri D.A. On Utilizing Functional Network to Develop Mathematical Model for Poisson’s Ratio Determination // 52nd U.S. Rock Mechanics/Geomechanics Symposium, 17-20 June 2018, Seattle, WA, USA. OnePetro, 2018. № ARMA-2018-744.
- Sone H. Mechanical Properties of Shale Gas Reservoir Rocks and its Relation to the in-Situ Stress Variation Observed in Shale Gas Reservoirs: Dissertation for the Degree of Doctor of Philosophy. Stanford University, 2012. 247 p.
- Sone H., Zoback M.D. Mechanical properties of shale-gas reservoir rocks – Part 2: Ductile creep, brittle strength, and their relation to the elastic modulus // Geophysics. 2013. Vol. 78. № 5. P. D393-D402. DOI: 10.1190/geo2013-0051.1
- Захаров Л.А., Мартюшев Д.А., Пономарева И.Н. Прогнозирование динамического пластового давления методами искусственного интеллекта // Записки Горного института. 2022. Т. 253. С. 23-32. DOI: 10.31897/PMI.2022.11
- Индрупский И.М., Ибрагимов И.И., Цаган-Манджиев Т.Н. и др. Лабораторная, численная и промысловая оценка эффективности циклического геомеханического воздействия на карбонатном коллекторе турнейского яруса // Записки Горного института. 2023. Т. 262. С. 581-593. DOI: 10.31897/PMI.2023.5
- Жуков В.С., Кузьмин Ю.О. Экспериментальная оценка коэффициентов сжимаемости трещин и межзерновых пор коллектора нефти и газа // Записки Горного института. 2021. Т. 251. С. 658-666. DOI: 10.31897/PMI.2021.5.5
- Жуков В.С., Кузьмин Ю.О. Сопоставление подходов к оценке сжимаемости порового пространства // Записки Горного института. 2022. Т. 258. С. 1008-1017. DOI: 10.31897/PMI.2022.97
