Use of the UNIFAC model in the calculation of physicochemical properties of ecotoxicants for technological and ecoanalytical purposes
- 1 — Ph.D., Dr.Sci. Scientific Supervisor of the Project of the Administrative Staff of the Scientific Centre “Assessment of Technogenic Transformation of Ecosystems” Saint Petersburg Mining University ▪ Orcid
- 2 — Postgraduate Student Saint Petersburg Mining University ▪ Orcid
Abstract
Modern development vector of environmental monitoring leads to elaboration of analytical methods for qualitative and quantitative analysis of different ecotoxicants. Many studies face the lack of information on isomers and homologues of already studied compounds. This problem cannot always be solved experimentally due to the difficulty of separating or synthesizing certain compounds; the use of group theories of solutions will help partly; using them, solubility in water or partition coefficient between two immiscible solvents is calculated for ecotoxicants. These parameters are important for solving the analytical and ecological problems. The partition coefficient in the octanol – water system is associated with a possibility of accumulation of different compounds in living organisms; the partition coefficient in the hexane – acetonitrile system can be used in gas chromatographic analysis. Solubility in water is closely associated with accumulation of ecotoxicants in water bodies, as well as with their ability to be transferred. This paper presents the capabilities of the UNIFAC model for solving physicochemical problems using the example of calculating the properties of real ecotoxicants on the basis of the available thermodynamic data. All the obtained calculated values were compared with those determined experimentally. In the case of pyrene derivatives, solubility data were obtained for the first time using a correlation group model to calculate the heat of fusion and melting temperature.
Introduction
Determination of physicochemical properties of ecotoxicants is an important task from the viewpoint of ecology and physical chemistry. Among such properties is the partition coefficient of a substance between two immiscible solvents, solubility in water, and octanol – water partition coefficient. Information about the partition coefficients in two-phase solvent systems can be used in sample preparation for extraction and subsequent analysis of toxic compounds [1, 2]. The partition coefficient octanol – water is of particular importance since it is associated with the ability of substances to penetrate through organic membranes [3]. Solubility in water is closely related to the ability of a substance to accumulate in water bodies, as well as to penetrate into groundwater [4]. All these physicochemical properties were studied only for a number of ecotoxicants, since some substances are either extremely difficult to separate in pure form, or they have not yet been synthesized. There are a large number of isomers and homologues for ecotoxicants, which are also toxic [5, 6]. An urgent problem is the development of methods for predicting the physicochemical properties of individual compounds based on their presumed structure.
The most common methods for predicting the properties of chemical compounds are the group approach methods. In these methods, the molecules are separated into fragments, most often functional groups. The most actively applied model realising this approach is the UNIFAC model [7]. It allows calculating the activity coefficients of individual components in a complex mixture by dividing them into separate fragments. For organic molecules, this approach is efficient since they are built from a limited set of functional groups. A set of groups CH3, CH2, CH, C and OH allows designing any alkane, cycloalkane or aliphatic alcohol, including a polyhydric one. For example, n-hexane (СН3-(СН2)4-СН3) consists of two СН3 groups and four СН2 groups. Ethanol contains one CH3, one CH2 and one OH group. Adding a group for ethers (C-O-C) and for esters (R1OOR2) it is possible to build molecules not only of ethers and esters, but also of hydroxyethers and hydroxyesters. For the consideration of amines, the NH2 group is introduced, and for aromatic compounds, two groups of aromatic carbon are introduced – ACH – aromatic carbon with a hydrogen atom and AC – aromatic carbon without a hydrogen atom.
Some substances (CH3OH, H2O, CH3CN) are distinguished as separate groups. Usually, these are the parent compounds of homologous series or substances that differ markedly in their properties from the typical organic substances. The ability to calculate the activity coefficients of components in the mixture allows estimating a large number of physicochemical properties using the equations of chemical thermodynamics. Using Raoult's law, it is possible to describe the liquid – vapour equilibrium, which is applied in modelling of rectification, distillation and evaporation [8, 9]. The Schroeder equation allows describing solubility in mixed solvents [10]. In the UNIFAC model, the activity factor is broken down into two components:
where γ is the activity coefficient; γcomb – combinatorial component of the activity coefficient; lnγres – residual component of the the activity coefficient.
The combinatorial component takes into account the difference in the shape of molecules. The residual component is associated with energy interactions between molecules in solution. An obvious presence of the combinatorial component makes it possible to describe the properties of solutions of polymers and macromolecules [11]. In practice, all the parameters, which are necessary for the model, are determined by regression of experimental data based on liquid – vapour, liquid – liquid and solubility equilibria. Such an approach to describing the properties of multicomponent systems can be efficiently used in environmental monitoring and chemical analysis; further, it will be shown by the example of calculating the solubility and partition coefficients.
Methods
Chromatographic analysis
Chromatographic measurements were conducted on a Shimadzu GC-QP2010SE chromato-mass spectrometer equipped with an RTX-5MS column (30 m×0.25 mm×0.25 μm) of Restek Company. The chromatograph operated in a constant flow rate mode (1.03 ml/min). Helium was the carrier gas. Evaporator temperature was 250 °C. Injection volume was 1 µl, reset 20:1. The oven program consisted of an initial isotherm of 50 °C (for 10 min), then the temperature raised to 290 °C at a rate of 10 °C/min and was maintained for 10 min. Temperature of the ion source of mass detector equalled 200 °C, interface temperature was 290 °C. Mass scanning range was chosen as 45-500 m/z with imaging duration of 0.3 s.
Calculation of solubility according to the UNIFAC model
With a gradual change of the mole fraction of a component in solution from zero to one it is possible to find the equality point of both parts (if it exists at all). A smooth change in the composition of the solvent will correspond to a smooth change in the mole fraction of asphaltene. Thus, it is possible to construct a solubility isotherm using the Schroeder equation:
where ΔHf is the substance heat of fusion; T – temperature of the system; Tf – substance melting point; R – universal gas constant; ха – mole fraction.
Calculation of the asphaltene solubility in one solvent was carried out by the dichotomy method (halving the segment). At each calculated point, the asphaltene activity coefficient was calculated according to the UNIFAC model, after which the error was determined from formula (2). The calculation continued until the error became less than 10–20. When calculating the solubility in two solvents, the solubility in one of the two-phase systems (in the absence of the third component) was taken as the first point. Then, there was a movement along the solubility line using the confidence interval method. The accuracy of the calculations was controlled by the calculation error.
Discussion of results
Group approach in the calculation of partition coefficients for ecoanalyti-cal purposes
In gas chromatography-mass spectrometry (GCMS) analysis, some analytes might not be in the databases, which either completely excludes their identification or leads to erroneous identification. This problem is especially acute in analytical studies [12, 13] and in the development of modern technologies [14-16]. In this case, for many known ecotoxicants, several homologues or isomers can be proposed, which will have no less toxic properties, but will not be available in databases. For example, in the NIST MS 2018 mass spectra database, there are no mass spectra of any C20H18 tetramethyl pyrenes, although there are 16 substances with such a molecular formula in the database. These 16 spectra may well become a source of false identification, if tetramethyl pyrene is present in the analysed sample. At the same time, there are studies on the toxicity of pyrene [17], but the toxicity of its homologues was not investigated. If we take the extremely toxic 2,3,7,8-tetrachlorodibenzodioxine [18] as an example, there are no mass spectra of even a monomethyl derivative for it, and there are only two other substances with the same molecular formula. Due to the lack of information, any studies of the toxicity of such homologues and isomers will face the difficulty of their identification in complex matrices [19]. For this reason, it is important to identify the noninvestigated compounds and to increase the reliability of identification of the already studied compounds.
In practice other identification features can be used in addition to the mass spectrum. In case of identification on capillary columns the retention indices are applied [20], which make it possible to exclude the identification options that are unreliable for a given release time from the list of substances with similar mass spectra. It is possible to vary the ionization energy (in electron impact mass spectrometry, the energy of electrons in an ion source is varied). Sometimes, this makes it possible to reliably determine the molecular formula and even make reasonable assumptions about the structure of the analyte [21]. However, this significantly complicates the analysis and does not work well with substances with a weak intensity of molecular ion in the spectrum.
Back in the mid-1960s, it was proposed to use the partition coefficient Kd of a substance between two immiscible phases as an additional structure-dependent parameter for specifying the structure of molecules in gas chromatographic (GC) analysis [22]. Such a coefficient (concentration partition coefficient) is the ratio of the equilibrium concentrations of a substance distributed between two liquid phases. Examples of such phases are water – octanol, hexane – ethylene glycol solvent systems. During partition, polar substances will predominantly concentrate in a more polar solvent, and non-polar substances in a less polar one. If you take a mixture of methanol and heptane and distribute them between ethylene glycol and hexane, methanol will be collected in ethylene glycol, and heptane in hexane. If GC analysis of each phase is performed separately, then with equal volumes injected into the injector of the chromatograph, methanol partition coefficient can be calculated as the ratio of peak areas of methanol in the hexane and ethylene glycol phases:
where Shexane is the peak area of the component in hexane phase; Seg – peak area of the component in ethylene glycol phase.
On the one hand, this complicates the analysis, since now it is necessary to obtain two chromatograms instead of one. However, this allows solving several problems. First, each of the two chromatograms is simpler since not all sample components are present in the investigated phase. Secondly, by comparing the calculated partition coefficient of an unknown analyte with the known values, it can be used as an additional identification feature. Since the partition coefficient does not depend linearly on the retention index (which is also calculated from the chromatogram), the result is two independent identification features. When using mass spectrometric detector, it is possible to determine three independent identification features for each analyte. This methodology was successfully applied until the beginning of 1990 [23]. During this time, a number of important improvements were proposed. The list of the used solvent systems was expanded. First of all, this is due to hexane – acetonitrile system, an active use of which started in the analysis of essential oils and petroleum products [24]. In [25] a method for Kd measurement on the basis of an internal standard was proposed. A substance with a known partition coefficient was taken as a standard. Then, formula (3) for hexane – ethylene glycol pair of solvents is converted to the form
where Kst is the partition coefficient of the standard; – peak area of the standard in the hexane phase; – peak area of the standard in the ethylene glycol phase.
This modification makes it possible to avoid errors associated with inaccurate dosing of the sample into the chromatograph evaporator. Empirical formulas for calculating Kd of substances based on their known physicochemical properties, such as molecular weight, boiling point, number of carbon atoms in a molecule also appeared [26]. The LSER model [27, 28] that makes it possible to calculate the partition coefficients in previously studied solvent systems with a sufficiently high accuracy is most actively used in analytical practice. This made it possible to apply this method not only to confirm the results of identification, but also to check the assumptions about the structure of analyte molecules. However, the approach appeared to be much more efficient when the chromato-partition method was combined with group theories of solutions [29], which is due to a possibility of working with systems of solvents of variable composition. Group theories of solutions make it possible to estimate the partition coefficients for the non-investigated compounds.
Calculation of the activity coefficients of groups, and then of individual molecules, is rather complicated, but its result can be easily applied to the calculation of the Kd value. As an example, let us consider a system of a and b phases. For a two-phase equilibrium, the activities of any component i distributed between phases are equal to each other. Thermodynamic activity of ai is equal to the product of the activity coefficient γi and the mole fraction of the component xi, provided that it is normalized to a pure substance. Normalization is interpreted as a choice of composition at which the activity coefficient is assumed to be equal to one. Now, it is possible to write down the condition of thermodynamic equilibrium of phases:
where a and b indicate the belonging of characteristics to phases a and b.
After transformations we get:
Kx value is the ratio of mole fractions of the component in coexisting phases and differs from Kd value only by a simple factor equal to the ratio of molar volumes of the same phases,
where Vα and Vβ are molar volumes of a and b phases.
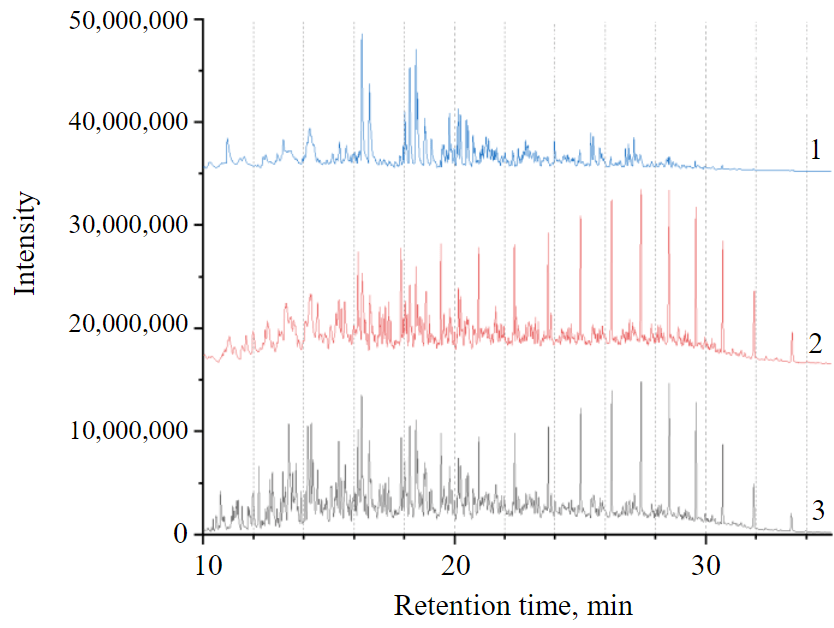
Fig.1. General view of chromatograms of equilibrium solutions of diesel fuel in acetonitrile (1); hexane (2) and initial diesel fuel (3). Chromatograms are shifted from each other by a constant without distortion of peak heights
Using equations (5)-(7) for any organic molecule that can be built from the known groups with the known parameters, it is possible to calculate the partition coefficient. The calculated value can then be compared with the measured value, and the assumptions about the structure of the analyte can be verified. It appears that the partition coefficient is a rather structure-sensitive parameter. Thus, for 3-carene and a-terpinene (general formula C10H16, both are components of the essential oil of coniferous plants), the Kovats retention indices are 1011 and 1018 [30]. Mass spectrum of these substances consists of ion series with the main masses 41-43; 77-79; 93; 121 and 136. In the conditions of routine GC-MS analysis on a 30-meter column, a difference in retention indices of 100 units corresponds to 1-2 min of time, i.e., the difference in the release time of these substances is from 3 to 6 s. This is not enough to reliably distinguish between substances. However, the situation changes when the partition coefficients are taken into account. For the hexane – acetonitrile system, Kd values are 6.7 and 4.3 for 3-carene and a-terpinene, respectively [23]. UNIFAC calculations give values of 7.5 and 4.4, which are extremely close to the experimental values. It is important to note that for any data set, the partition coefficient for 3-carene is 1.55-1.7 times higher than that for a-terpinene. This is a quite measurable difference and, therefore, the substances can be distinguished.
One example of using this approach is the identification of polyaromatic compounds in middle-distillate petroleum pro-ducts. Figure 1 illustrates the possibilities of the chromato-partition method. A sample of commercial diesel fuel was taken as an object. Six largest peaks in the centre of the chromatogram (1) are mono-, di- and trimethyl naphthalenes. Large peaks in the right part of the chromatogram (2) of the hexane phase are С14-С22 n-alkanes. If there was no interphase partition, chromatogram (3) would be observed, obtained by summing lines 1 and 2 (original fuel). It can be seen that in this case, many peaks would simply overlap each other.
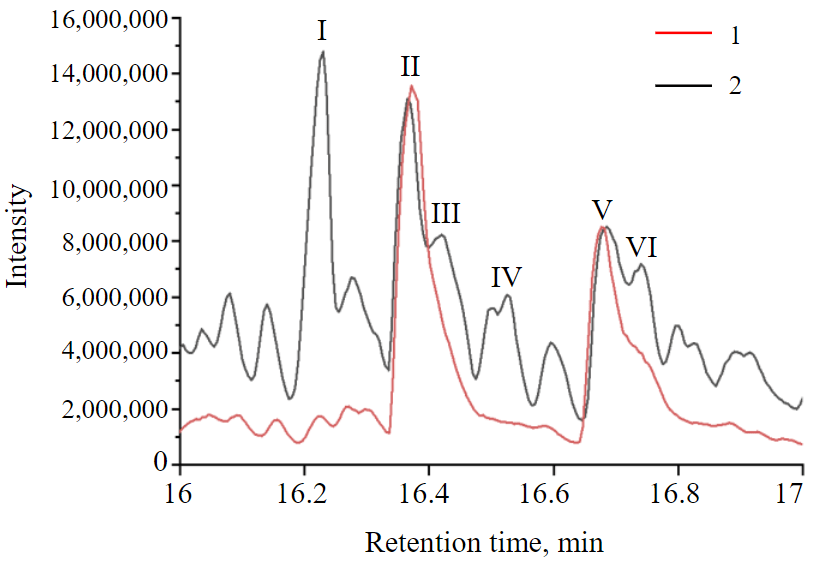
Fig.2. Section of chromatograms shown in Fig.1, in the interval of release time 16-17 min 1 – hexane extract; 2 – acetonitrile extract
Figure 2 shows a section of the chromatogram of hexane and acetonitrile phases. Two large peaks can be found on the chromatogram of acetonitrile extract, while there are more of them in the hexane phase. Peak I is an n-alkane, peaks III and IV are isomeric alkanes, peaks II and V are isomers of methyl naphthalene, peak VI is an alkyl derivative of benzene with a long radical. There is a clear tendency of non-aromatic compounds to concentrate in the hexane phase, which makes it possible to analyse them separately and calculate the partition coefficient as an additional identification feature. In addition to identification of aromatic compounds, this approach can also be useful in the study of other fuel components [31].
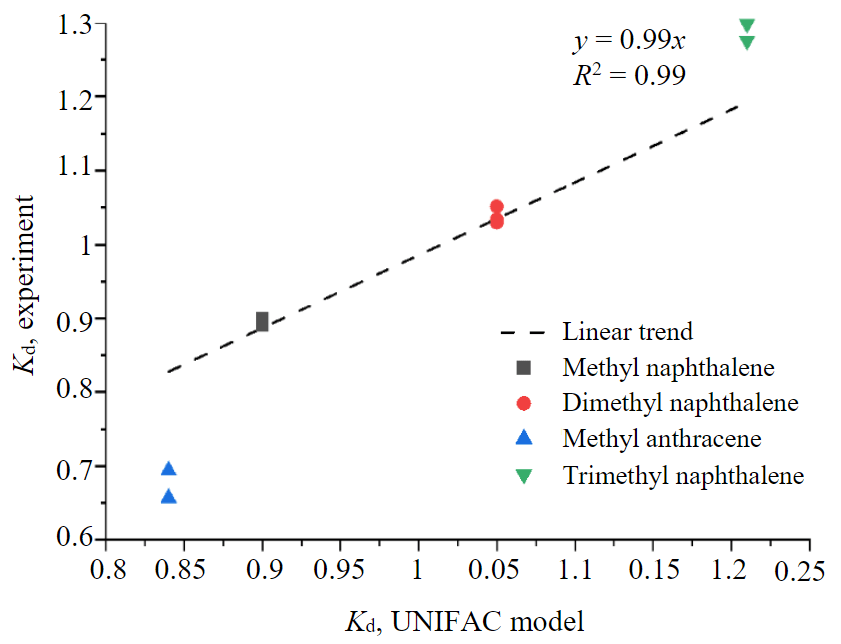
Fig.3. Calculated and experimental values of partition coefficients of some components of diesel fuel
Figure 3 shows the degree of correlation between the calculated and experimental values of the partition coefficients of methyl naphthalenes and anthracene. It can be seen that model calculations correlate well with experimental data. This makes it possible to use the partition coefficients calculated according to the UNIFAC model as an additional identification feature. In a similar way, it is possible to identify different polyaromatic and heterocyclic compounds: methyl derivatives of naphthalene, anthracene, fluorene, biphenyl, tetrahydro naphthalene, dibenzothiophene, dibenzofuran, carbazole [29].
Group approach in calculating the solubility of ecotoxicants in water and hydrocarbons
In mass spectrometry the use of partition coefficients is of an auxiliary nature, whereas in modelling of natural and technological processes these values are included in the list of the main ones. One of the most important indicators of any ecotoxicant is its solubility in water. However, if the substance is not in the database and is not isolated as a pure compound, the only way to estimate the solubility is to calculate it. Even if the solubility data are available, there is a possibility of experimental error due to the fact that the solubility of many ecotoxicants in water is very low (10-100 µg/l). The UNIFAC model makes it possible to calculate the solubility of such substances, for this it is necessary to take into account the effects of fusion of the substance under study. In practice such accounting is made using the Schroeder-van Laar equation. Since melting points of many important ecotoxicants are much higher than 0 °C, only the heat and fusion of the ecotoxicant should be taken into account when calculating the solubility in water. According to the Schroeder – van Laar equation, in this case, the activity of an ecotoxicant calculated according to the UNIFAC model in a solution, which is in equilibrium with a solid ecotoxicant, is related to the heat of fusion and melting temperature of the substance by the following formula:
It can be seen that the right side of formula (8) does not depend on the composition of solution. This means that it can be considered as a constant factor when calculating the total activity coefficient of the ecotoxicant:
With such a calculation of solubility, the main difficulty may be the lack of information on the heat of fusion of an ecotoxicant. However, it is possible to calculate these values using group contribution methods [32]. In such methods, a certain physical property of a substance is estimated as a linear combination of the contributions of individual molecular groups. For example, for the heat of fusion, the equation will look as:
where Ni, Mj, Oi are the numbers of groups of the first, second and third order in the molecule; Hfus,1, Hfus,2, Hfus,3 – the contribution of each group to the heat of fusion; Hfus,0 – constant value.
First order groups are the simplest functional groups. For example, methyl (CH3), hydroxo (OH) or aromatic with hydrogen (ACH). Groups of the second and third orders are combinations of simple groups; it is necessary to take them into account for correcting the obtained values with regard for the mutual influence of closely spaced groups or the shape of a molecule. Pyrene molecule in this calculation will consist of 16 groups of the first order (6 AC and 10 ACH) and 4 groups of the third order (two conjugations of aromatic rings according to the type of phenalene and two conjugations of aromatic rings of the phenanthrene type). The value calculated in this way is 421 K, which is extremely close to the experimentally determined value of 424 K [33].
Table 1 presents the results of solubility calculations for several important ecotoxicants and their homologues. It can be seen that the discrepancies between the calculated and experimental values are one order of magnitude. In the case of methyl and ethyl pyrene, the values were obtained using the calculated heat of fusion. Although a discrepancy of one order is significant for analytical practice, in the case of solubility estimation such accuracy will be sufficient. When working with the non-investigated substances, such an estimated calculation is, in fact, the only method for determining the solubility of ecotoxicants in mixed solvent systems.
Table 1
Examples of calculating the solubility of ecotoxicants according to the UNIFAC model (equation (8)
|
Substance |
Formula |
Equilibrium mole fraction |
Heat of fusion, J/mol |
Solubility, mg/l |
Experimental solubility, mg/l |
|
DDT, 1,1,1-trichloro-2,2-bis(4-chlorophenyl)ethane |
C14H9Cl5 |
9.60·10–9 |
26,280 [34] |
1.9·10–1 |
2.5·10–2 [35] |
|
DDE, 1,1-dichloro-2,2-bis(n-chlorophenyl) ethylene |
C14H8Cl4 |
1.00·10–7 |
23,550 [36] |
1.8 |
1.2·10–1 [35] |
|
Hexachloroethane |
C2Cl6 |
3.10·10–6 |
9,750 [33] |
4.1·101. |
1.1·102 [37] |
|
Hexachlorane |
C6H6Cl6 |
3.1·10–8 |
25,930 [38] |
5.0·10–1 |
7.3 [39] |
|
Benzpyrene |
C20H12 |
4.70·10–11 |
14,700 [34] |
6.6·10–4 |
3.8·10–3 [37] |
|
Pyrene |
C16H10 |
2.50·10–9 |
16,700 [33] |
2.8·10–2 |
1.3·10–1 [37] |
|
Methyl pyrene |
C17H12 |
1.60·10–9 |
18,283* |
1.9·101 |
No data |
|
Ethyl pyrene |
C18H14 |
1.30·10–9 |
17,922* |
1.7·10,0001 |
No data |
*Values obtained from formula (10).
Group models of solutions are used to solve the environmental and technological problems in the calculation of solubility diagrams for hydrocarbon mixtures. Such a calculation itself would be a standard physicochemical problem if the researchers had exhaustive data on physicochemical pro-perties of components. However, in practice the researchers face the lack of information about the system under consideration [40]. When preparing fuel for marine engines, fuel oil or other residual products of deep oil refining (oil tar, visbreaker tar) are often added to it. Since the solubility of high-molecular non-volatile products in fuels based on n-alkanes is low, for increasing it, it is necessary to add a diesel fraction with a high content of aromatic compounds to the fuel. The resulting fuel should be stable and, at the same time, meet a number of environmental and economic requirements [41]. Among the environmental constraints, one of the most important is low sulphur content in fuel (less than 0.5 wt.% according to the requirements of the International Maritime Organization). This value is easy to calculate if sulphur content in the residual product is known (sulphur content in the initial volatile diesel fractions is much lower and can usually be neglected) and the concentration of the residual product. Solubility in a mixture of alkanes and substituted arenes depends on their ratio and should be determined experimentally. The situation is complicated by the fact that such solutions are usually dark and can precipitate with time. For this reason, the calculation of the solubility of such compounds is an important ecological problem, which can also be solved using group models.
Molecular and group composition of the alkane-arene mixture can be determined from the data of GC-MS analysis. If the group and molecular composition of the residual product is known, it is possible to calculate its solubility using the Schroeder formula. The problem is that the residual products are also multicomponent, and it is customary to distinguish four main classes of compounds in their composition: paraffins, aromatic compounds, resins, and asphaltenes. This classification is based on SARA analysis. This is the procedure for successive isolation of the four above fractions using a set of solvents. Asphaltenes are the first to precipitate from the residual fuel; therefore, the remaining components only contribute to the change in the composition of the solvent. In order to correctly take into account these changes, it was proposed to use the average molecular weights of each of the above groups and the results of infrared (IR) spectroscopy and nuclear magnetic resonance (NMR). In this case, the molecular weight can be determined by cryoscopy or from the solvent vapour pressure.
At the stage of choosing a solvent for cryoscopy, UNIFAC model calculations are very useful. The UNIFAC model makes it possible to choose such a solvent, the solution of the substance in which will be close to ideal, for asphaltenes it appeared to be benzene. In addition to the average molecular weight, the elemental composition (or the equivalent average gross formula of the simulated compound) is needed for calculations, as well as IR or NMR spectra, which allow to determine the composition of the functional groups present in the compound. Based on these data, the group composition of an average molecule of asphaltene or hydrocarbon mixture can be obtained. As an example, Table 2 shows the group composition of asphaltenes of various compositions in the range of molecular weights 617-1,574 g/mol. The group composition was calculated based on the fact that only the AC, ACH, CH2, and CH3 groups are present in the asphaltene molecule. Thus, if the asphaltene empirical formula had the form CNHM, then the number of groups was calculated using the system of equations
where N(AC), N(ACH), and N(CH2) are the numbers of UNIFAC groups comprised in one asphaltene molecule (the number of CH3 groups is assumed to be one); k is the ratio of the number of ASN groups to the number of AC groups.
Table 2
Data on composition and molecular weight of different asphaltenes [42]
|
Parameter |
Sample 1 |
Sample 2 |
Sample 3 |
|
Mw, g/mol |
617 |
1,135 |
1,574 |
|
C, wt.% |
89.18 |
86.14 |
87.65 |
|
H, wt.% |
5.68 |
6.39 |
6.5 |
|
S, wt.% |
2.45 |
5.5 |
3.22 |
|
AC |
20.9 |
33.1 |
46.5 |
|
ACH |
15.9 |
25.3 |
35.6 |
|
CH2 |
8.1 |
22.1 |
31.9 |
|
CH3 |
1 |
1 |
1 |
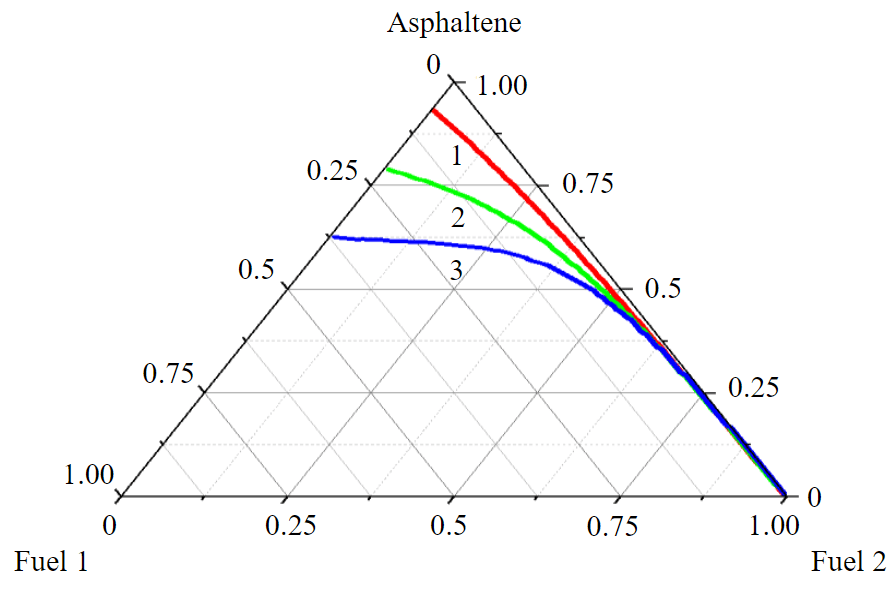
Fig.4. Calculated asphaltene solubility isotherms (1-3) from Table 2 at a temperature of 373 K
Parameter k can be estimated from the NMR spectroscopy data, or one of the known polyaromatic compounds can be taken as a sample. Thus, for benzopyrene k = 11/8 = 1.375. Such calculations can be performed even with N and M not rounded to integers and not rounding the obtained values of N(AC), etc. As an illustration of this method, Fig. 4 shows the solubility isotherms of asphaltenes with characteristics from Table 2 in mixtures of two diesel fractions. Fraction 1 consists mainly of alkanes and isoalkanes (98 wt.%), and fraction 2 of aromatic compounds (75 wt.%). As can be seen from the calculation results, asphaltenes dissolve better in highly aromatized fractions; also with an increase in molecular weight the solubility in alkane fractions decreases significantly.
Conclusion
The given examples do not exhaust the application field of group theories of solutions for solving technological and ecoanalytical problems. The efficiency of such application depends on the availability and reliability of the physicochemical characteristics of the substances under study. These characteristics can be determined both experimentally and using different correlation dependences. In this work, it was demonstrated that the UNIFAC model can give satisfactory results when calculating the solubility of ecotoxicants in water and can also be used in the estimation of partition coefficients in two-phase systems.
References
- Ponomareva M.A., Cheremisina O.V., Mashukova Y.A., Lukyantseva E.S. Increasing the efficiency of rare earth metal
- recovery from technological solutions during processing of apatite raw materials. Journal of Mining Institute. 2021. Vol. 252,
- p. 917-926. DOI: 10.31897/PMI.2021.6.13
- Sudarikov S.M., Yungmeister D.A., Korolev R.I., Petrov V.A. On the possibility of reducing man-made burden on benthic biotic communities when mining solid minerals using technical means of various designs. Journal of Mining Institute. 2022. Vol. 253, p. 82-96. DOI: 10.31897/PMI.2022.14
- Cumming H., Rücker C. Octanol-Water Partition Coefficient Measurement by a Simple 1H NMR Method. ACS Omega. 2017. Vol. 2. N 9, p. 6244-6249. DOI: 10.1021/acsomega.7b01102
- Roy D.N., Goswami R., Pal A. The insect repellents: A silent environmental chemical toxicant to the health. Environmental Toxicology and Pharmacology. 2017. Vol. 50, p. 91-102. DOI: 10.1016/j.etap.2017.01.019
- Gonçalves N.P.F., Vargaet Z., Nicol E. et al. Comparison of Advanced Oxidation Processes for the Degradation of Maprotiline in Water-Kinetics, Degradation Products and Potential Ecotoxicity. Catalysts. 2021. Vol. 11. Iss. 2. N 240.
- DOI: 10.3390/CATAL11020240
- Pashkevich M.A., Kharko P.A. The use of a composite mix to remove metals from acidic drainage waters at tailings facilities. Obogashchenie rud. 2022. N 4, p. 40-47 (in Russian). DOI: 10.17580/or.2022.04.07
- Fredenslund A., Jones R.L., Prausnitz J.M. Group‐contribution estimation of activity coefficients in nonideal liquid mixtures. AIChE Journal. 1975. Vol. 21. N 6, p. 1086-1099. DOI: 10.1002/aic.690210607
- Rodriguez-Donis I., Gerbaud V., Joulia X. Thermodynamic Insights on the Feasibility of Homogeneous Batch Extractive Distillation. 4. Azeotropic Mixtures with Intermediate Boiling Entrainer. Industrial & Engineering Chemistry Research. 2012. Vol. 51. N 18, p. 6489-6501. DOI: 10.1021/ie2019432
- Seyf J.Y., Shojaeian A. Vapor-liquid (azeotropic systems) and liquid-liquid equilibrium calculations using UNIFAC and NRTL-SAC activity coefficient models. Fluid Phase Equilibria. 2019. Vol. 494, p. 33-44. DOI: 10.1016/J.FLUID.2019.04.029
- Coto B., Suárez I., Tenorio M.J., Huerga I. Extraction of aromatic and polyaromatic compounds with NMP: experimental and model description. Fluid Phase Equilibria. 2022. Vol. 554. N 113293. DOI: 10.1016/J.FLUID.2021.113293
- Pazuki G., Seyfi Kakhki S. A hybrid GMDH neural network to investigate partition coefficients of Penicillin G Acylase in polymer-salt aqueous two-phase systems. Journal of Molecular Liquids. 2013. Vol. 188, p. 131-135. DOI: 10.1016/j.molliq.2013.10.001
- Raupov I., Burkhanov R., Lutfullin A. et al. Experience in the Application of Hydrocarbon Optical Studies in Oil Field Development. Energies. 2022. Vol. 15. Iss. 10. N 3626. DOI: 10.3390/EN15103626
- Khalifa A.A., Bazhin V.Y., Ustinova Y.V., Shalabi M.E.K. Study of the kinetics of the process of producing pellets from red mud in a hydrogen flow. Journal of Mining Institute. 2022. Vol. 254, p. 261-270. DOI: 10.31897/PMI.2022.18
- Kudinova A.A., Poltoratckaya M.E., Gabdulkhakov R.R. et al. Parameters influence establishment of the petroleum coke genesis on the structure and properties of a highly porous carbon material obtained by activation of KOH. Journal of Porous Materials. 2022. Vol. 29. Iss. 5, p. 1599-1616. DOI: 10.1007/S10934-022-01287-1
- Leusheva E., Alikhanov N., Morenov V. Barite-Free Muds for Drilling-in the Formations with Abnormally High Pressure. Fluids. 2022. Vol. 7. Iss. 8. N 268. DOI: 10.3390/FLUIDS7080268
- Sergeev V.V., Cheremisina O.V., Fedorov A.T. et al. Interaction Features of Sodium Oleate and Oxyethylated Phosphoric Acid Esters with the Apatite Surface. ACS Omega. 2022. Vol. 7. Iss. 3, p. 3016-3023. DOI: 10.1021/acsomega.1c06047
- Bielská L., Kah M., Sigmund G. et al. Bioavailability and toxicity of pyrene in soils upon biochar and compost addition. Science of the Total Environment. 2017. Vol. 595, p. 132-140. DOI: 10.1016/J.SCITOTENV.2017.03.230
- Mehrle P.M., Buckler D.R., Little E.E. et al. Toxicity and bioconcentration of 2,3,7,8-tetrachlorodibenzodioxin and
- ,3,7,8-tetrachlorodibenzofuran in rainbow trout. Environmental Toxicology and Chemistry. 1988. Vol. 7. Iss. 1, p. 47-62.
- DOI: 10.1002/ETC.5620070108
- Pashkevich M.A., Bykova M.V. Methodology for thermal desorption treatment of local soil pollution by oil products at the facilities of the mineral resource industry. Journal of Mining Institute. 2022. Vol. 253, p. 49-60. DOI: 10.31897/PMI.2022.6
- Xiaoli Wei, Imhoi Koo, Seongho Kim, Xiang Zhang. Compound identification in GC-MS by simultaneously evaluating the mass spectrum and retention index. The Analyst. 2014. Vol. 139. Iss. 10, p. 2507-2514. DOI: 10.1039/C3AN02171H
- Alam M.S., Stark C., Harrison R.M. Using Variable Ionization Energy Time-of-Flight Mass Spectrometry with Comprehensive GC×GC to Identify Isomeric Species. Analytical Chemistry. 2016. Vol. 88. Iss. 8, p. 4211-4220. DOI: 10.1021/acs.analchem.5b03122
- Bowman M.C., Beroza M. Identification of Compounds by Extraction p-Values Using Gas Chromatography. Analytical Chemistry. 1966. Vol. 38. Iss. 11, p. 1544-1549. DOI: 10.1021/ac60243a022
- Isidorov V.A., Zenkevich I.G., Dubis E.N. et al. Group identification of essential oils components using partition coefficients in a hexane-acetonitrile system. Journal of Chromatography A. 1998. Vol. 814. Iss. 1-2, p. 253-260.
- DOI: 10.1016/S0021-9673(98)00398-7
- Tkachenko K.G., Zenkevich I.G. The Essential Oil of the Flowers of Heracleum antasiaticum Manden. Grown in Russia. Journal of Essential Oil Research. 1993. Vol. 5. Iss. 2, p. 227-228. DOI: 10.1080/10412905.1993.9698208
- Berezkin V.G., Pankov A.G., Loshchilova V.D. Combined partition-chromatographic methods. Chromatographia. 1976. Vol. 9. Iss. 10, p. 490-496. DOI: 10.1007/BF02282661
- Isidorov V.A., Kotowska U., Vinogorova V.T. GC Identification of Organic Compounds Based on Partition Coefficients of Their TMS Derivatives in a Hexane-Acetonitrile System and Retention Indices. Analytical Sciences. 2005. Vol. 21. Iss. 12, p. 1483-1489.
- DOI: 10.2116/analsci.21.1483
- Poole C.F. Partition constant database for totally organic biphasic systems. Journal of Chromatography A. 2017. Vol. 1527, p. 18-32. DOI: 10.1016/j.chroma.2017.10.061
- Poole C.F., Karunasekara T., Ariyasena T.C. Totally organic biphasic solvent systems for extraction and descriptor determinations. Journal of Separation Science. 2013. Vol. 36. Iss. 1, p. 96-109. DOI: 10.1002/jssc.201200709
- Efimov I., Povarov V.G., Rudko V.A. Comparison of UNIFAC and LSER Models for Calculating Partition Coefficients in the Hexane-Acetonitrile System Using Middle Distillate Petroleum Products as an Example. Industrial & Engineering Chemistry
- Research. 2022. Vol. 61. Iss. 27, p. 9575-9585. DOI: 10.1021/acs.iecr.2c01093
- Adams R.P., González-Elizondo M.S., González-Elizondo M., Slinkman E. DNA fingerprinting and terpenoid analysis of Juniperus blancoi var. huehuentensis (Cupressaceae), a new subalpine variety from Durango, Mexico. Biochemical Systematics and Ecology. 2006. Vol. 34. Iss. 3, p. 205-211. DOI: 10.1016/J.BSE.2005.11.004
- Rekhletskaya E.S., Ershov M.A., Savelenko V.D. et al. Unraveling the Superior Role of Characterizing Methyl Ester of Isohexene as an Innovative High-Octane Gasoline Mixing Component. Energy & Fuels. 2022. Vol. 36. Iss. 19, p. 11829-11838.
- DOI: 10.1021/acs.energyfuels.2c01973
- Marrero J., Gani R. Group-contribution based estimation of pure component properties. Fluid Phase Equilibria. 2001. Vol. 183-184, p. 183-208. DOI: 10.1016/S0378-3812(01)00431-9
- Domalski E.S., Hearing E.D. Heat Capacities and Entropies of Organic Compounds in the Condensed Phase. Volume III. Journal of Physical and Chemical Reference Data. 1996. Vol. 25. Iss. 1, p. 1-525. DOI: 10.1063/1.555985
- Acree W.E. Thermodynamic properties of organic compounds: enthalpy of fusion and melting point temperature compilation. Thermochimica Acta. 1991. Vol. 189. Iss. 1, p. 37-56. DOI: 10.1016/0040-6031(91)87098-H
- Toxicological Profiles. ATSDR. URL: https://www.atsdr.cdc.gov/toxprofiledocs/index.html (accessed 02.11.2022).
- Donnelly J.R., Drewes L.A., Johnson R.L. et al. Purity and heat of fusion data for environmental standards as determined by differential scanning calorimetry. Thermochimica Acta. 1990. Vol. 167. Iss. 2, p. 155-187. DOI: 10.1016/0040-6031(90)80476-F
- IUPAC-NIST Solubility Database, Version 1.1. URL: https://srdata.nist.gov/solubility/ (accessed 30.05.2022).
- DOI: 10.18434/T4QC79
- Sabbah R., Xu Wu An. Enthalpies de fusion et de sublimation de l’isomère γ d’hexachlorocyclohexane. Thermochimica Acta. 1991. Vol. 178, p. 339-341. DOI: 10.1016/0040-6031(91)80326-E
- Richardson L.T., Miller D.M. Fungitoxicity of Chlorinated Hydrocarbon Insecticides in Relation to Water Solubility and Vapor Pressure. Canadian Journal of Botany. 1960. Vol. 38. N 2, p. 163-175. DOI: 10.1139/b60-015
- Rogachev M.K., Aleksandrov A.N. Justification of a comprehensive technology for preventing the formation of asphalt-resin-paraffin deposits during the production of highlyparaffinic oil by electric submersible pumps from multiformation deposits. Journal of Mining Institute. 2021. Vol. 250, p. 596-605. DOI: 10.31897/PMI.2021.4.13
- Gabdulkhakov R.R., Rudko V.A., Pyagay I.N. Methods for modifying needle coke raw materials by introducing additives of various origin (review). Fuel. 2022. Vol. 310. Part A. N 122265. DOI: 10.1016/J.FUEL.2021.122265
- Gauthier T., Danial-Fortain P., Merdrignac I. et al. Studies on the evolution of asphaltene structure during hydroconversion of petroleum residues. Catalysis Today. 2008. Vol. 130. Iss. 2-4, p. 429-438. DOI: 10.1016/j.cattod.2007.10.005
