Математическое моделирование развития процесса сдвижения при отработке калийных руд длинными очистными забоями
Аннотация
В благоприятных горно-геологических условиях, в частности на Старобинском месторождении калийных солей (Беларусь), применяются системы отработки длинными очистными забоями, которые обуславливают высокую техногенную нагрузку на недра, включая интенсивную деформацию земной поверхности. Представленные исследования направлены на изучение динамики сдвижения земной поверхности в процессе подвигания забоя лавы. Математическое моделирование осуществлялось в упруго-пластической постановке с численной реализацией методом конечных элементов. Условием обрушения пород кровли являлось раскрытие контакта между слоями при достижении его границ трещинами сдвига или формирование области растягивающих напряжений на обнажении. При движении фронта очистных работ наблюдается рост оседаний с последующей их стабилизацией до величины, определяемой технологическими параметрами ведения горных работ и физико-механическими свойствами обрушенных пород. При этом каждая точка земной поверхности испытывает знакопеременные горизонтальные деформации: при приближении фронта – растяжения, при удалении – сжатия. Полученные результаты математического моделирования хорошо согласуются с данными инструментальных измерений сдвижений земной поверхности, что свидетельствует об адекватности описания процесса деформирования породного массива при слоевой выемке сильвинитовых пластов длинными очистными забоями.
Введение
Освоение калийных и соляных месторождений полезных ископаемых осуществляется камерно-столбовой системой разработки. Это обусловлено необходимостью обеспечения сохранности водозащитной толщи и предотвращения прорыва пресных вод в горные выработки [1-4]. Лишь в благоприятных горно-геологических условиях, в частности на Старобинском месторождении калийных солей (Республика Беларусь), применяются различные варианты столбовых систем разработки [5-7], характерные для угольных бассейнов. В связи с этим целевые исследования процесса сдвижения при очистной выемке длинными столбами связаны с угольными месторождениями [8-10], а разработанные для них инженерные методы прогноза оседаний земной поверхности базируются на многолетних инструментальных наблюдениях. Результаты этих исследований составили основу нормативной базы охраны объектов земной поверхности от вредного влияния подземных разработок угля. Вместе с тем, современный опыт освоения угольных месторождений и переход на более глубокие горизонты показывает, что нормативные инженерные методы прогноза оседаний существенно отличаются от результатов фактических наблюдений [11-13]. Для нивелирования этих расхождений используют эмпирические корректирующие коэффициенты [11, 14, 15], переходят к статистическим оценкам [16, 17], применяют методы математического моделирования [11, 18, 19], позволяющие учесть в расчетах деформаций земной поверхности особенности строения подработанного массива и физико-механические свойства слагающих его пород [20-22].
Прогнозирование сдвижений земной поверхности при отработке сильвинитовых пластов длинными очистными забоями базируется на эмпирических подходах и соотношениях, характерных для угольных месторождений. По аналогии максимальное оседание земной поверхности определяется по следующей формуле [23]:
где Nx, Ny – коэффициенты, зависящие от соотношения размеров выработанного пространства и глубины горных работ; m – вынимаемая мощность пласта; ω – коэффициент извлечения руды.
Натурные исследования процесса сдвижения на Старобинском месторождении, связанные с изучением расслоения подработанного массива и формирования зоны водопроводящих трещин, освещены в работах [24, 25]. Предпринимались также попытки математического моделирования процесса сдвижения [26], основанные на применение аналитических подходов, что не позволило достаточно адекватно описать динамику деформаций земной поверхности.
Целью представленных исследований являлось изучение динамики сдвижения земной поверхности в процессе подвигания забоя лавы. Численное моделирование осуществлялось в упругопластической постановке методом конечных элементов.
Методология
Оценка изменения напряженно-деформированного состояния (НДС) породного массива выполнялась применительно к валовой отработке трех слоев Третьего калийного горизонта. Соответствующая схема расчета, построенная по направлению движения лавы, представлена на рис.1. Принималось, что расчетная область испытывает действие массовых сил, интенсивностью (где – удельный вес пород ‑го элемента геологического разреза), на боковых границах ограничиваются горизонтальные перемещения, на нижней – вертикальные. Верхняя граница (земная поверхность) является свободной. Геомеханическая модель отражала основные особенности строения подработанного массива. Механические свойства пород, слагающих геологический разрез, принимались в соответствии с результатами лабораторных испытаний [27, 28].
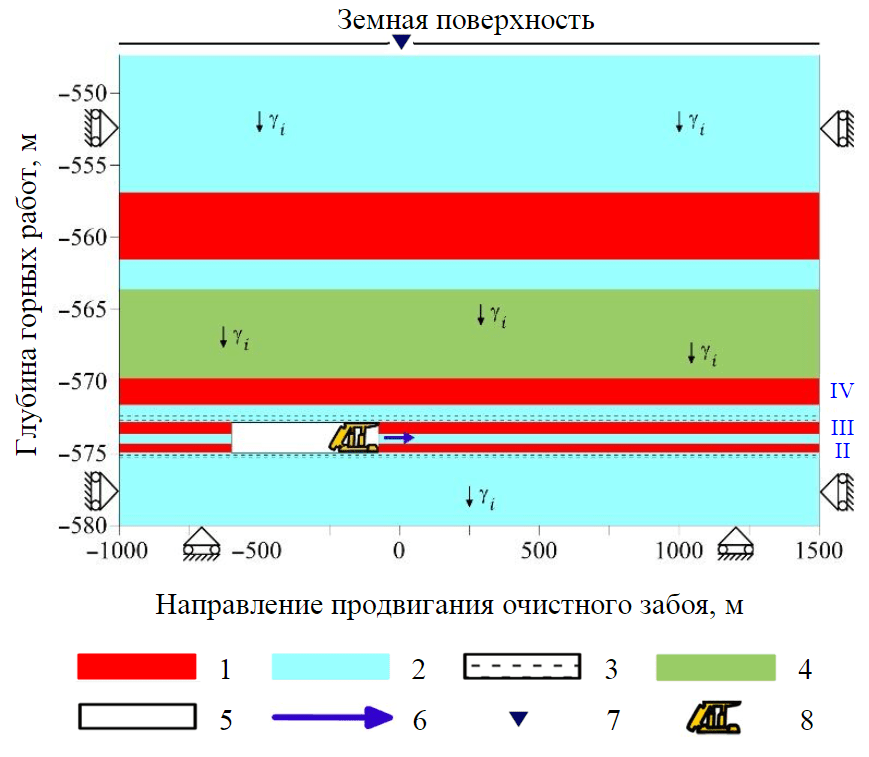
Рис.1. Принципиальная схема расчета НДС подработанного массива 1 – сильвинит; 2 – каменная соль; 3 – глинистые прослои; 4 – глинисто-карналлитовая пачка; 5 – выработанное пространство лавы; 6 – направление движения лавы; 7 – точка наблюдений; 8 – забойная крепь
Определение напряженно-деформированного состояния пород основывалось на модели идеальной упругопластической среды, которая в области действия напряжений сжатия реализовывалась в варианте параболического критерия Кулона – Мора [29]:
а в области напряжений растяжения упругое деформирование ограничивалось пределом прочности на растяжение
где τmax = (σ1 – σ3)/2 – максимальное касательное напряжение; σ = (σ1 – σ3)/2 – нормальное напряжение; σ1, σ3 – главные напряжения, вычисляемые по результатам математического моделирования; r = σс/σt – отношение предела прочности на одноосное сжатие σс к пределу прочности на одноосное растяжение σt;
В физическом выражении формирование зон пластических деформаций в областях сжатия и растяжения связывается с процессами трещинообразования, из-за развития трещин сдвига и отрыва.
Численное решение задачи осуществлялось по стандартной процедуре метода конечных элементов [30], в рамках которой учет пластического характера деформирования пород проводился методом секущей матрицы [31]. Взаимодействие слоев, залегающих в кровле и почве выработанного пространства, моделировалось контактными элементами Гудмана [32-34] в модификации полной диаграммы деформирования [35]. Механические свойства контактов принимались по результатам лабораторных испытаний контактов в режиме «сдвиг со сжатием» [36].
Критерием обрушения пород кровли являлось раскрытие контакта между слоями при достижении его границ трещинами сдвига или формирование зоны растягивающих напряжений на обнажении [37]. В численных расчетах он реализовывался в рамках итерационной процедуры путем локализации и последующего исключения из расчетов элементов, в которых выполняется критерий обрушения. В расчетную схему математического моделирования в виде геоматериала включались заполняющие выработанное пространство разрушенные породы, деформационные свойства которых принимались на порядок ниже соответствующих показателей породного массива [38].
Обсуждение результатов
Разрушение пород в процессе движения лавы
Результаты математического моделирования показывают, что в процессе подвигания забоя лавы в почве выработки локализуется область пластических деформаций, связанная с формированием трещин отрыва. Обрушение пород кровли начинает происходить при продвижении лавы на расстояние около 5 м (рис.2, а).
По мере дальнейшего подвигания фронта очистных работ (рис.2, б-г) наблюдаются расширение области трещиноватости в почве и увеличение объема обрушенных пород кровли. При протяженности выработанного пространства более 25 м (рис.2, в, г) происходит стабилизация области трещиноватости в почве и в дальнейшем фиксируется лишь ее увеличение по латерали. Принятый коэффициент разуплотнения обуславливает полное заполнение выработанного пространства разрушенными породами, что предотвращает дальнейшее развитие зон трещиноватости в кровле. Таким образом, обрушению оказываются подвержены породы до глиносто-карналлитовой пачки включительно. При существенно большей протяженности выработанного пространства процесс трещинообразования и возможного обрушения кровли может затрагивать и вышележащие пласты. Одновременно с этим в выработанном пространстве формируется неоднородная техногенная геосреда.
В характере разрушения породного массива в окрестностях выработанного пространства наблюдается периодичность. Сначала фиксируется увеличение зон трещиноватости в почве и увеличение объема обрушенных пород в кровле. Затем происходит заполнение выработанного пространства геоматериалом, предотвращающее дальнейшее увеличение зон трещиноватости в вертикальном направлении. После этого процесс повторяется.
Как показывают выполненные расчеты, определяющее влияние на деформирование подработанного массива оказывают свойства разрушенных пород. В зависимости от принятых в расчете их деформационных свойств существенно изменяется величина оседаний земной поверхности (рис.3). Повышение этих показателей резко снижает максимальные оседания земной поверхности на этапе движения лавы, что влияет на изменение градиента вертикальных сдвижений в точке измерения (реперная точка, рис.3).
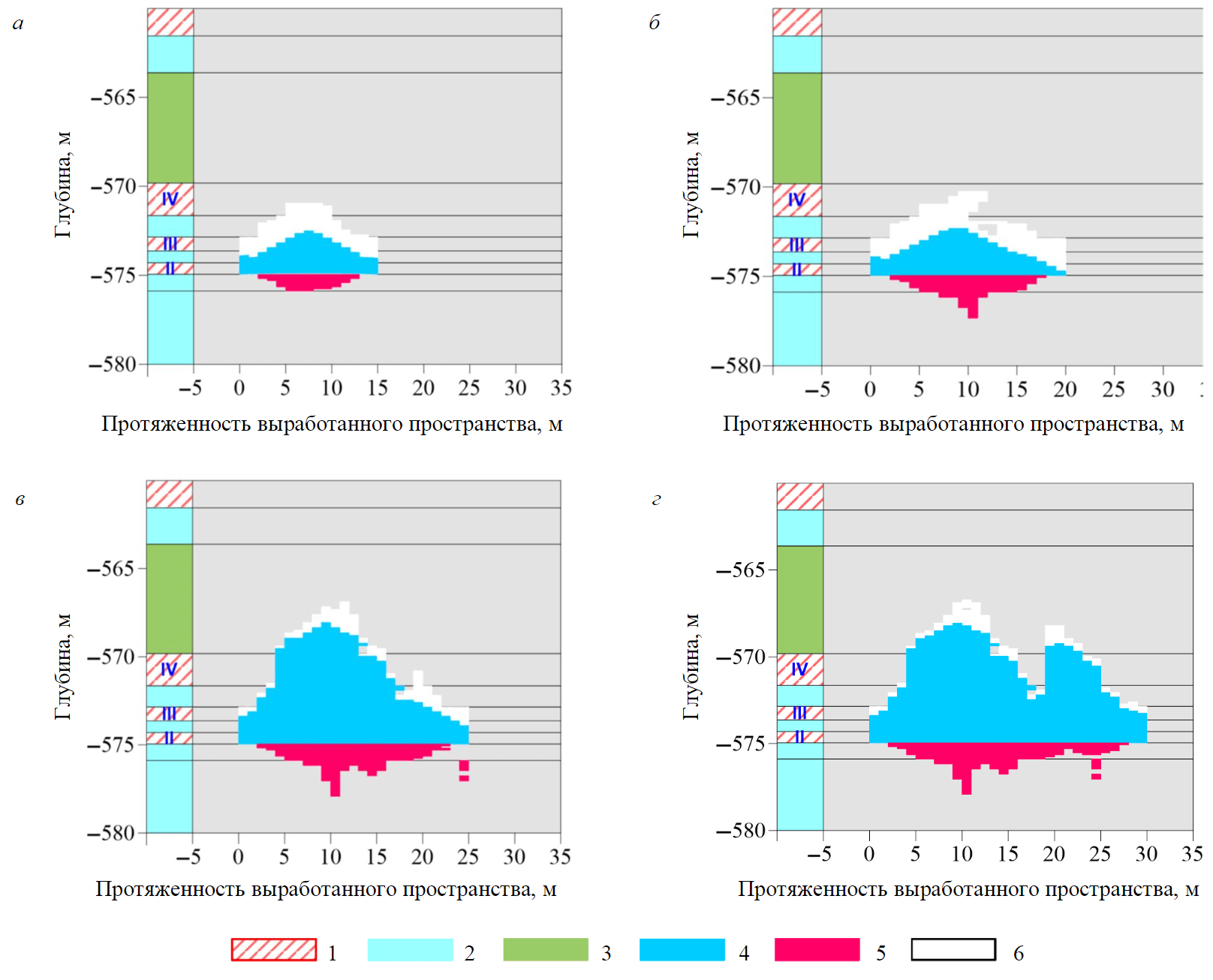
Рис.2. Характер разрушения породного массива в процессе подвигания фронта очистных работ на расстоянии 15 (а), 20 (б), 25 (в), 30 (г) м 1 – сильвинит; 2 – каменная соль; 3 – глинисто-карналлитовая пачка; 4 – обрушившаяся порода; 5 – область трещинообразования; 6 – выработанное пространство лавы
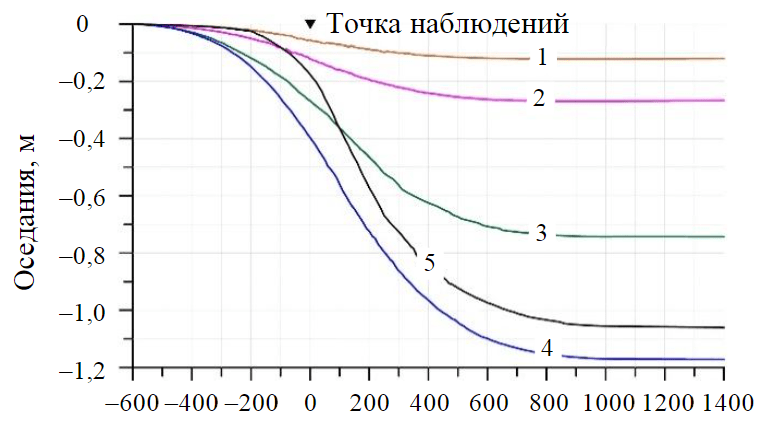
Рис.3. Кривые зависимости оседаний земной поверхности в точке наблюдения от уровня снижения модуля деформаций обрушенных пород относительно исходных показателей 1 – в 5 раз; 2 – в 15 раз; 3 – в 25 раз; 4 – в 35 раз; 5 – постепенное снижение от 5 до 30 раз
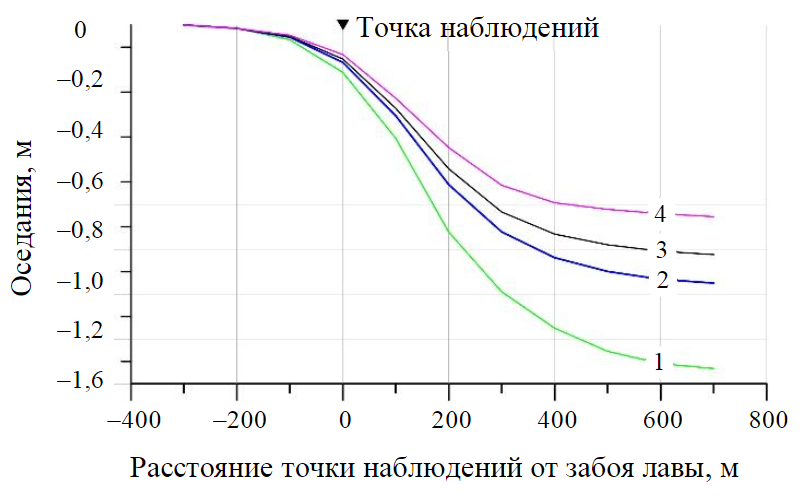
Рис.4. Кривые зависимости оседаний земной поверхности в точке наблюдений от скорости подвигания очистного забоя
1 – 1; 2 – 2; 3– 3; 4 – 10 м/сут
На рис.3-6 ось абсцисс определяет расстояние между точкой маркшейдерских наблюдений за сдвижением земной поверхности (реперной точкой) и проекцией на нее очистного забоя лавы. Отрицательные значения расстояния соответствуют приближению лавы к точке маркшейдерских наблюдений 0, положительные – удалению от нее. Вариация деформационных свойств обрушенных пород позволяет откалибровать геомеханическую модель по данным маркшейдерских измерений, но добиться приемлемого согласования на участке формирования значительных градиентов не удается. Можно предположить, что снижение деформационных свойств разрушенных пород происходит постепенно, по мере движения фронта очистных работ. С учетом этого обеспечиваются относительно высокие градиенты оседаний земной поверхности в активной стадии процесса сдвижения (рис.3, кривая 5).
Динамика развития процесса сдвижения
Существенное влияние на оседания земной поверхности в пределах динамической части мульды сдвижения оказывает скорость подвигания очистного забоя: чем выше скорость, тем больше оседания. Факт пропорциональной зависимости скорости оседания точки наблюдения от скорости подвигания очистных работ для угольных месторождений отмечался Г.Кратчем [8]. Для условий Старобинского калийного месторождения по результатам обработки маркшейдерских наблюдений данная зависимость конкретизирована в виде линейного соотношения
где Vзаб – скорость подвигания очистного забоя, м/сут;X,V – коэффициенты, зависящие от горно-геологических и горно-технических условий отработки.
Основная сложность использования выражения (2) заключается в определении коэффициентов X, B при отсутствии данных маркшейдерских наблюдений. Тем не менее, общий анализ соотношения показывает, что на значительном удалении очистного забоя от точки наблюдения оседания земной поверхности будут уменьшаться с увеличением скорости подвигания лавы. Это подтверждается и результатами математического моделирования (рис.4). При удалении забоя на 700 м от точки наблюдения и увеличении скорости движения лавы с 1 до 10 м/сут оседания уменьшатся с 1,51 до 0,85 м, или на 45 %. Таким образом, чем выше скорость движения забоя, тем меньшая часть конечных оседаний земной поверхности реализуется в динамической части мульды сдвижения. Резкое уменьшение оседаний происходит в диапазоне 1-4 м/сут, и дальнейшее увеличение скорости подвигания очистного забоя не приводит к столь значительному снижению оседаний.
Математическое моделирование процесса деформирования массива проводилось на примере отработки лавы № 102 рудника 1 РУ ОАО «Беларуськалий». Скорость движения очистного забоя принималась постоянной – 2 м/сут. При геомеханическом моделировании постепенно равномерно увеличивалось выработанное пространство, имитируя движение очистного забоя, а деформационные свойства обрушенных пород кровли уменьшались по линейной зависимости. При этом максимальное «ослабление» деформационных свойств обрушенных пород должно было обеспечивать переход процесса сдвижения в затухающую стадию и достижение оседаний земной поверхности, соответствующие выбранной скорости движения забоя.
На рис.5 показана динамика развития оседаний земной поверхности в процессе движения очистного фронта, построенная по результатам математического моделирования. По мере увеличения выработанного пространства с постоянной скоростью вначале наблюдается рост оседаний с последующей их стабилизацией до величины, определяемой технологическими параметрами ведения горных работ (скоростью отработки, вынимаемой мощностью и т.д.) и физико-механическими свойствами обрушенных пород. Затем происходит лишь расширение мульды сдвижения по латерали вслед за движением фронта очистных работ. После отработки лавы нарастание оседаний земной поверхности до конечных значений, определяемых выражением (1), будет реализовываться в затухающем режиме.
На рис.6 приведены кривые нарастания вертикальных сдвижений земной поверхности в точке наблюдений в процессе ведения очистной выемки (кривая 1), также для сравнения показаны оседания, построенные по эмпирической формуле (2) при скорости подвигания очистного забоя 2 м/сут (кривая 2), и фактические оседания (кривая 3). Можно заметить, что наблюдается хорошее соответствие оседаний земной поверхности как по величине, так и по скорости их нарастания. Некоторое отличие фактических оседаний (кривая 3) от расчетных после завершения активной стадии сдвижения связано, по-видимому, с тем, что реальная скорость движения лавы являлась переменной и варьировалась в диапазоне 0,9-5,2 м/сут.
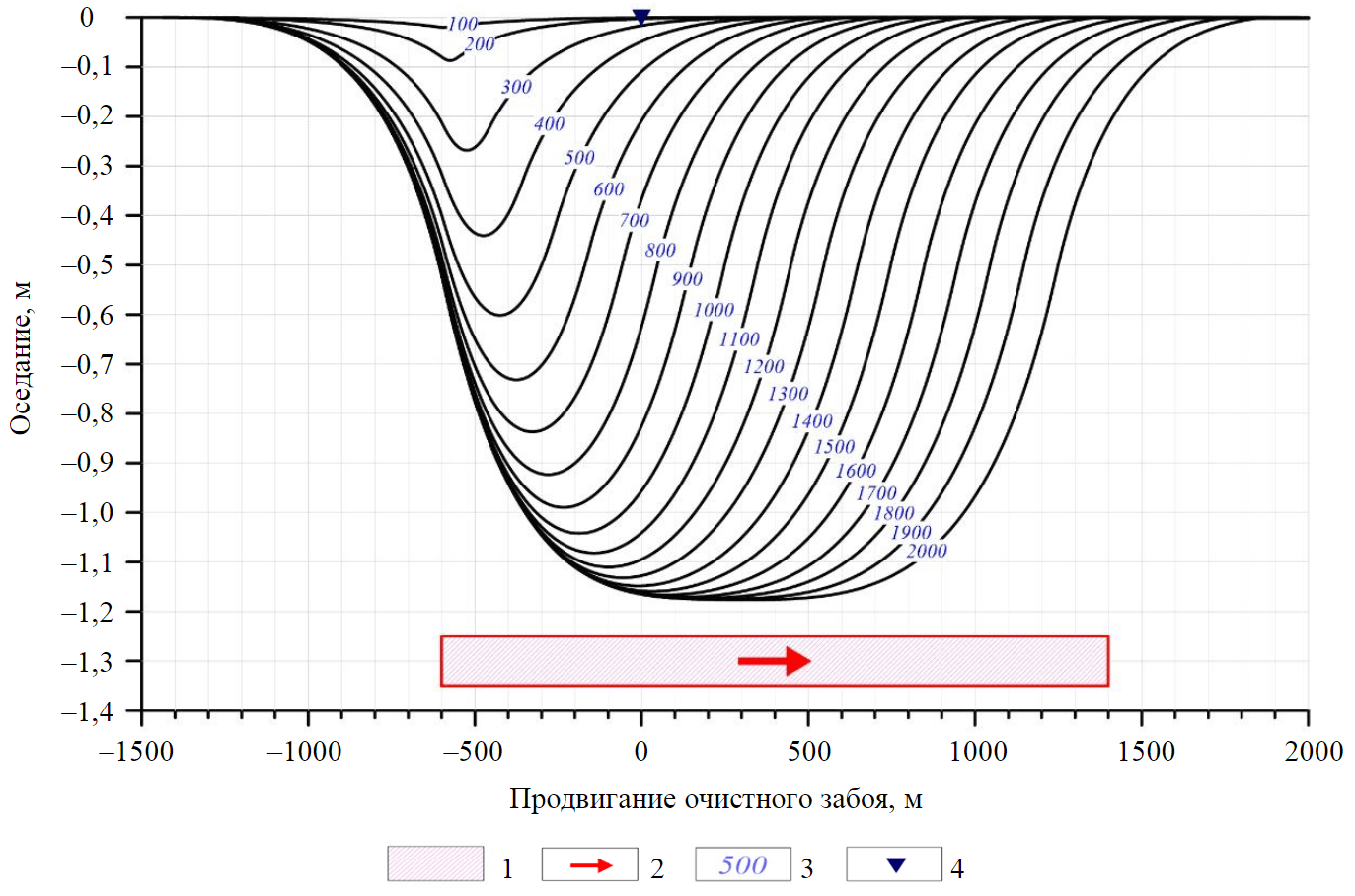
Рис.5. Динамика формирования мульды сдвижения при движении фронта очистных работ 1 – выработанное пространство лавы; 2 – направление движения забоя; 3 – размер выработанного пространства; 4 – точка наблюдений
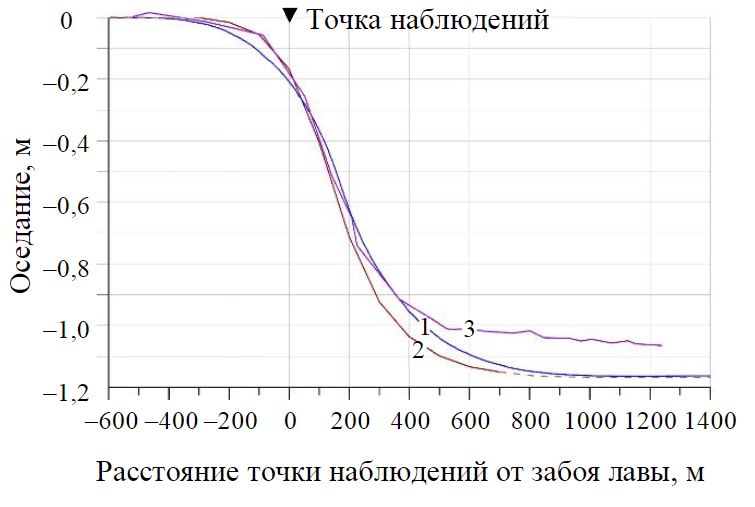
Рис.6. Кривые оседаний земной поверхности в точке наблюдений при движении фронта очистных работ 1 – результаты математического моделирования; 2 – расчетные по эмпирической формуле (2) при скорости подвигания забоя 2 м/сут; 3 – фактические (репер 1, лава № 102 рудника 1 РУ)
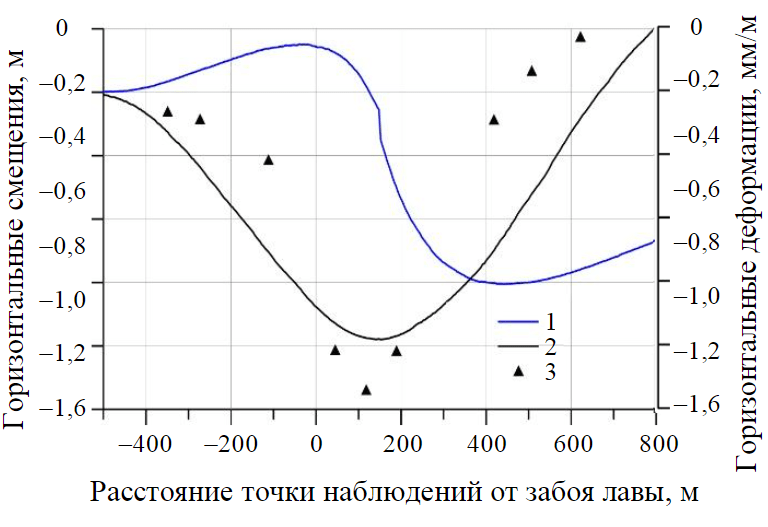
Рис.7. Горизонтальные смещения и деформации земной поверхности в точке наблюдения 1 – деформации; 2 – расчетные смещения; 3 – фактические смещения
Обычно [39, 40] в процессе подвигания забоя лавы на земной поверхности, наряду с ее оседанием, фиксируются горизонтальные смещения. Причем вначале происходит прямое перемещение навстречу движущемуся забою, а затем точка наблюдений возвращается обратно (рис.7). В случае, если точка наблюдений расположена на продольной оси выемочного столба, и отсутствуют другие влияющие факторы (неоднородное строение подработанного массива, наличие соседних отработанных участков, подработки, надработки и т.д.), то прямая и обратная траектории точки наблюдений будут совпадать по направлению, но обратная, как правило, оказывается более длинной. Другими словами, точка наблюдений не возвращается в исходное положение. Эта тенденция отражается в результатах математического моделирования. Некоторое отклонение фактических измерений от расчетных (рис.7) можно объяснить влиянием группы горно-геологических и горно-технических факторов, которые не учтены в расчетах.
Представляет интерес изменение горизонтальных деформаций земной поверхности в точке наблюдения, которые определяют уровень негативного воздействия горных работ на промышленные и гражданские объекты (рис.7, положительные значения – деформации растяжения, отрицательные – деформации сжатия). Как видно, в процессе движения фронта очистных работ точка наблюдений испытывает знакопеременные деформации: при приближении имеет место растяжение, при удалении – сжатие. Нулевые горизонтальные деформации фиксируются примерно в 100 м за забоем лавы.
Заключение
Построенная геомеханическая модель породного массива в полной мере отражает основные особенности строения массива, подвигание забоя лавы и технологические параметры ведения горных работ. Модель включает в себя обрушение пород кровли отрабатываемого пласта. Ее реализация позволяет исследовать изменение напряженно-деформированного состояния подработанного породного массива и выявить основные закономерности происходящих геомеханических процессов, в том числе характер развития деформаций земной поверхности.
Показана принципиальная возможность достижения соответствия между расчетными оседаниями и натурными наблюдениями за сдвижением земной поверхности с помощью вариации свойств обрушенных пород, образующихся в процессе движения забоя лавы. В этом случае появляется возможность прогнозирования процесса сдвижения земной поверхности при слоевой выемке сильвинитовых пластов длинными очистными забоями.
Литература
- Rauche H. Die Kaliindustrie im 21. Jahrhundert. Springer-Verlag Berlin Heidelberg, 2015. 580 p.
- Барях А.А., Смирнов Э.В., Квиткин С.Ю., Тенисон Л.О. Калийная промышленность России: проблемы рационального и безопасного недропользования // Горная промышленность. 2022. № 1. С. 41-50. DOI: 10.30686/1609-9192-2022-1-41-50
- Зубов В.П., Ковальский Е.Р., Антонов С.В., Пачгин В.В. Повышение безопасности рудников при отработке Верхнекамского месторождения калийно-магниевых солей // Горный информационно-аналитический бюллетень. 2019. № 5. С. 22-33. DOI: 10.25018/0236-1493-2019-05-0-22-33
- Беляков Н.А., Беликов А.А. Прогноз целостности водозащитной толщи на Верхнекамском месторождении калийных руд // Горный информационно-аналитический бюллетень. 2022. № 6-2. С. 33-46. DOI: 10.25018/0236_1493_2022_62_0_33
- Подлесный И.А., Гетманов В.Н., Петровский Б.И., Носуля И.Е. Технология слоевой выемки при разработке пласта Третьего калийного горизонта Старобинского месторождения // Горный журнал. 2018. № 8. С. 59-64. DOI: 10.17580/gzh.2018.08.08
- Ковалев О.В., Мозер С.П., Мозер И.Ю., Лейсле А.В. Обоснование рациональных технологий отработки IV горизонта в условиях Старобинского месторождения калийных солей // Записки Горного института. 2011. Т. 190. С. 9-15.
- Ковалев О.В., Ковальский Е.Р., Сиренко Ю.Г., Тхориков И.Ю. Разработка технологических схем селективной выемки калийных пластов сложного строения в условиях Старобинского месторождения // Записки Горного института. 2011. Т. 190. С. 16-21.
- Kratzsch H. Mining Subsidence Engineering. Berlin, Heidelberg, New York: Springer-Verlag, 1983. 558 p.
- Викторов С.Д., Гончаров С.А., Иофис М.А., Закалинский В.М. Механика сдвижения и разрушения горных пород. М.: Институт проблем комплексного освоения недр им. академика Н.В.Мельникова РАН, 2019. 360 с.
- Galvin J.M. Ground Engineering – Principles and Practices for Underground Coal Mining. Switzerland: Springer International Publishing, 2016. 684 р.
- Kulibaba S., Miletenko N. Influence of the mining depth factor on accuracy of the forecast of the earth’s surface subsidence in Kuzbass // E3S Web of Conferences. VIII International Scientific Conference «Problems of Complex Development of Georesources». 2020. Vol. 192. № 04009. DOI: 10.1051/e3sconf/202019204009
- Аверин Г.А., Доценко О.Г., Корецкая Е.Г. Учет влияния песчаников и известняков на максимальное оседание земной поверхности, вызванное горными работами // Сборник научных трудов Донбасского государственного технического института. 2021. № 22 (65). С. 21-27.
- Ghabraie B., Ghabraie K., Ren G., Smith J.V. Numerical modelling of multistage caving processes: insights from multi-seam longwall mining-induced subsidence // International Journal for Numerical and Analytical Methods in Geomechanics. 2017. Vol. 41. Iss. 7. P. 959-975. DOI: 10.1002/nag.2659
- Ларченко В.Г., Коваленко Е.В., Маталкина Ю.А. Прогноз вероятных оседаний земной поверхности при ее подработке на больших глубинах // Сборник научных трудов Донбасского государственного технического института. 2021. № 24 (67). С. 40-44.
- Tao Xu, Tian-hong Yang, Chong-feng Chen et al. Mining induced strata movement and roof behavior in underground coal mine // Geomechanics and Geophysics for Geo-Energy and Geo-Resources. 2015. Vol. 1. P. 79-89. DOI: 10.1007/s40948-015-0010-2
- Гордиенко М.Э., Колесник Н.А., Козловский Г.И., Назимко В.В. Совершенствование методики расчета деформаций подрабатываемых зданий и сооружений // Проблеми гірського тиску. 2013. № 1-2 (22-23). С. 137-166.
- Zhixian Hou, Keming Yang, Yanru Li et al. Dynamic prediction model of mining subsidence combined with D-InSAR technical parameter inversion // Environmental Earth Sciences. 2022. Vol. 81 (11). № 307. DOI: 10.1007/s12665-022-10423-8
- Корецкая Е.Г. Моделирование оседаний земной поверхности в условиях подработки лавой № 35вост, пл. h8 шахты им. М.В.Фрунзе // Сборник научных трудов Донбасского государственного технического института. 2018. № 12 (55). С. 23-28.
- Макеева Т.Г., Трофимов В.А. Расчет оседания земной поверхности горнопромышленных объектов (на примере угольных месторождений Донбасса) // Геоэкология. Инженерная геология, гидрогеология, геокриология. 2022. № 1. С. 69-76. DOI: 10.31857/S086978092201009X
- Jiránková E., Waclawik P., Nemcik J. Assessment of models to predict surface subsidence in the Czech part of the Upper Silesian Coal Basin – Case study // Acta Geodynamica et Geomaterialia. 2020. Vol. 17. № 4 (200). P. 469-484. DOI: 10.13168/AGG.2020.0034
- Tajduś K. Numerical simulation of underground mining exploitation influence upon terrain surface // Archives of Mining Sciences. 2013. Vol. 58. № 3. P. 605-616. DOI: 10.2478/amsc-2013-0042
- Hongwei Wang, Yaodong Jiang, Yixin Zhao et al. Numerical investigation of the dynamic mechanical state of a coal pillar during longwall mining panel extraction // Rock Mechanics and Rock Engineering. 2013. № 46 (5). P. 1211-1221. DOI: 10.1007/s00603-012-0337-8
- Новокшонов В.Н., Данилова А.Ф., Усова Н.М. Горизонтальное смещение земной поверхности в зависимости от максимального оседания в мульде сдвижения // Горная механика и машиностроение. 2015. № 1. С. 5-8.
- Новокшонов В.Н., Данилова А.Ф., Дешковский В.Н., Зейтц В.Э. Исследование процесса развития техногенных трещин в подрабатываемом массиве горных пород на Старобинском месторождении // Горный журнал. 2014. № 2. С. 19-22.
- Новокшонов В.Н., Данилова А.Ф., Дешковский В.Н., Богдан С.И. Развитие деформаций внутри подработанного массива пород при столбовой системе разработки калийных пластов // Рудник будущего. 2011. № 2 (6). С. 17-20.
- Журавков М.А., Круподеров А.В. К задаче моделирования перемещений земной поверхности в регионе ведения крупномасштабных горных работ // Вестник Белорусского государственного университета. Серия 1. Физика. Математика. Информатика. 2008. № 3. С. 52-55.
- Проскуряков Н.М., Антонов А.А., Ливенский В.С. Исследование физико-механических свойств соляных пород Старобинского месторождения // Записки Горного института. 1972. Т. 61 (1). С. 101-104.
- Петровский А.Б., Прушак В.Я., Лутович Е.А. Физико-механические свойства пород, слагающих и перекрывающих третий калийный пласт Старобинского месторождения // Доклады Национальной академии наук Беларуси. 2021. Т. 65. № 4. С. 484-494. DOI: 10.29235/1561-8323-2021-65-4-484-494
- Ding-Jian Wang, Huiming Tang, Peiwu Shen, Yi Cai. A Parabolic Failure Criterion for Transversely Isotropic Rock: Modification and Verification // Mathematical Problems in Engineering. Vol. 2019. № 8052560. P. 1-12. DOI: 10.1155/2019/8052560
- Zienkiewicz O.C., Taylor R.L., Zhu J.Z. The Finite Element Method: Its Basis and Fundamentals. Oxford: Butterworth-Heinemann, 2013. 756 p. DOI: 10.1016/C2009-0-24909-9
- Huang C., Lu R., Hsu W. Power Flow Analysis Based on the Secant Method in the Environment of the Offshore Wind Farm // Journal of Physics: Conference Series. 2020. Vol. 1583. № 012007. DOI: 10.1088/1742-6596/1583/1/012007
- Goodman R.E. The Mechanical Properties of Joints // Advanced Rock Mechanics. 1974. Vol. 1. Part. A. P. 127-140.
- Hatzor Y., Ma G., Shi G.-H. Discontinuous Deformation Analysis in Rock Mechanics Practice. London, UK: Taylor & Francis Group, 2017. Vol. 5. 410 p. DOI: 10.4324/9781315687032
- Delong Huang, Aiping Tang, Zhongyue Wang. Analysis of pipe-soil interactions using Goodman contact element under seismic action // Soil Dynamics and Earthquake Engineering. 2020. Vol. 139. № 106290. DOI: 10.1016/j.soildyn.2020.106290
- Барях А.А., Паньков И.Л. Взаимодействие слоев в соляном массиве. Сообщение 2: Математическое моделирование геомеханических процессов с учетом деформации контактов // Физико-технические проблемы разработки полезных ископаемых. 1992. № 3. С. 21-27.
- Барях А.А., Дудырев И.Н., Асанов В.А., Паньков И.Л. Взаимодействие слоев в соляном массиве. Сообщение 1. Механические свойства контактов // Физико-технические проблемы разработки полезных ископаемых. 1992. № 2. С. 7-11.
- Барях А.А., Андрейко С.С., Федосеев А.К. Газодинамическое обрушение кровли при разработке месторождений калийных солей // Записки Горного института. 2020. Т. 246. С. 601-609. DOI: 10.31897/PMI.2020.6.1
- Барях А.А., Андрейко С.С., Федосеев А.К. О механизме локализации очагов газодинамических явлений в почве сильвинитовых пластов // Вестник Пермского национального исследовательского политехнического университета. Геология. Нефтегазовое и горное дело. 2017. Т. 16. № 3. С. 247-254. DOI: 10.15593/2224-9923/2017.3.5
- Tajduś K., Misa R., Sroka A. Analysis of the surface horizontal displacement changes due to longwall panel advance // International Journal of Rock Mechanics and Mining Sciences. 2018. Vol. 104. P. 119-125. DOI: 10.1016/j.ijrmms.2018.02.005
- Barbato J., Hebblewhite B., Mitra R., Mills K. Prediction of horizontal movement and strain at the surface due to longwall coal mining // International Journal of Rock Mechanics and Mining Sciences. 2016. Vol. 84. P. 105-118. DOI: 10.1016/j.ijrmms.2016.02.006
