Мониторинг состояния измельчения в барабанных мельницах по результирующему моменту на валу
Аннотация
Измельчение является самым энергоемким процессом среди всех этапов подготовки сырья и определяет протекание последующих стадий обогащения руды. В соответствии с нагрузочными характеристиками, формируемыми в результате разрушения руды в мельнице, определяется уровень потребления электроэнергии. Скорость барабана мельницы – один из технологических параметров, за счет которого можно осуществлять управление механизмами разрушения руды при выборе скоростного режима работы регулируемого электропривода мельницы. Представленное исследование повышения энергоэффективности за счет использования электропривода мельницы основано на комплексном моделировании технологической части – процесса измельчения и электромеханической части – электропривода процесса измельчения. За счет оценки нагрузочного момента с помощью его разложения в спектр осуществляется идентификация состояния мельницы по смене знаков частотных составляющих спектра момента, а при исследовании электромагнитного момента электропривода осуществляется мониторинг процесса измельчения. Оценка и выбор эффективного режима работы электропривода проводится на основе полученного спектра электромагнитного момента. Результаты исследований показали, что при увеличении скорости барабана мельницы – повышении энергии удара, значения нагрузочных моментов сопоставимы для заданных параметров моделирования. По полученным спектрам можно идентифицировать состояние мельничной загрузки – скорость и уровень заполнения. Представленный подход позволяет оценить влияние изменения технологических показателей процесса измельчения на показатели электромеханической системы. Изменение скоростного режима работы позволит повысить производительность измельчения за счет сокращения времени измельчения руды и не приведет к повышению энергозатрат. Интеграция цифровых моделей технологического процесса и системы автоматизированного электропривода позволяет сформировать основу для построения комплексных способов мониторинга и оценки энергетической эффективности всей технологической цепочки обогащения руды.
Введение
Процесс измельчения является самым энергоемким процессом при подготовке сырья на горно-обогатительных предприятиях. В соответствии с тенденциями устойчивого развития [1, 2], которые оказывают существенное влияние на промышленные объекты за счет сформировавшейся политики ресурсосбережения, необходимо рассматривать способы повышения эффективности процесса измельчения [3, 4].
Существуют следующие способы повышения эффективности процесса измельчения [5]: усовершенствование конструкторских решений; применение усовершенствованных систем управления (Advanced Process Control – APC); диагностика процесса измельчения и оценка остаточного ресурса; технологические решения повышения энергоэффективности; электромеханические решения.
Конструкторские решения
Барабанные мельницы – самые распространенные измельчительные агрегаты, характеризуются высокой энергоемкостью в сравнении с другими типами оборудования для дезинтеграции сырья. Актуально развитие схем рудоподготовки за счет использования гравитационных вертикальных мельниц (Vertical Mill) и валковых прессов (Roller Press) [6]. Удельное энергопотребление данного оборудования на 1 т продукции в среднем на 25 % меньше барабанных мельниц. Исследователи подчеркивают важность оптимизации геометрических параметров лифтеров барабанных мельниц с целью снижения энергопотребления [7]. В последнее время использование DEM-моделирования получило широкое распространение для решения многих технологических задач процесса измельчения.
Метод дискретных элементов (Discrete Element Method, DEM) предназначен для расчета поведения сыпучих сред и основан на вычислении контактных взаимодействий между условно неделимыми гранулированными частицами [8, 9]. Метод DEM пришел на смену классическим теориям расчета энергетических затрат. В классической теории расчет энергопотребления осуществляется по основным эмпирическим формулам: Олевского, Chen Bingchen, Davis, Levinson, Bond [10]. Однако почти все классические методы не учитывают влияние лифтеров и позволяют отразить только влияние скорости вращения, степени заполнения шихты, размер и форму мелющих тел. Метод DEM позволяет оценить потребляемую мощность на основании взаимодействия материалов, участвующих в процессе измельчении.
В работе [11] была проведена валидация DEM-модели с экспериментальными данными, было установлено, что модель является корректной при разработке конструкции лифтеров мельниц. В работе [12] отмечено, что при выборе подходящей комбинации конструкторских параметров лифтеров с технологическими (скорость и заполнение мельницы) параметрами повышается энергетическая эффективность процесса измельчения. Подбор такой комбинации для полномасштабных мельниц на практике является затруднительным, что подчеркивает актуальность DEM-моделирования.
Усовершенствованные системы управления
Синтез системы управления осуществляется согласно математическому описанию объекта управления. Химико-технологические процессы протекают в движущихся потоках, перемещение которых оказывает влияние на эффективность данных процессов. Использование гидродинамических уравнений для описания механического перемещения потоков измельчаемой продукции является распространенным способом при проектировании измельчительных агрегатов и их систем управления [13].
Классические контуры управления процессом измельчения строятся по принципу стабилизации основных технологических параметров. Расход исходного сырья в барабане мельницы является основным параметром, в соответствии с которым происходит управление. Для поддержания заданного класса –0,074 мм на контрольном сите дополнительно происходит управление расходом воды в мельнице и в гидроциклоне [14]. Повышенные требования к современным горно-обогатительным комбинатам приводят к необходимости внедрения контуров оптимизации в существующие системы управления. Построение подобных систем управления предполагает сложное математическое моделирование процессов, протекающих в технологических аппаратах на полном цикле получения готового продукта [15, 16]. Таким образом, задача усовершенствованных систем управления заключается не только в поддержании номинальной производительности процесса измельчения, но и в оптимизации с целью снижения приходящихся затрат.
Диагностика процесса измельчения и оценка остаточного ресурса
Данные способы повышения эффективности направлены на снижение дополнительных потерь потребляемой энергии, которые возникают при эксплуатации неисправного оборудования. Своевременное предотвращение поломок на стадии их развития позволяет снизить вероятность возникновения простоев технологического оборудования, исключить выход из строя конструкторских и электромеханических узлов системы мельница-электропривод и снизить количество планово-предупредительных работ по замене отдельных элементов оборудования. При диагностике конструкторских узлов мельницы идентифицируется динамическое состояние мельницы, как правило, посредством акустических сигналов [17] и вибрации [18, 19]. В соответствии с полученными данными можно охарактеризовать состояние износа футеровки мельницы и ее лифтеров. Контроль за состоянием основных электромеханических узлов привода мельницы удобнее всего осуществлять посредством мониторинга токов статора [20, 21]. Влияние технологических переменных на электромеханическую систему можно увидеть в сигналах электропривода.
Электромеханические решения
Внедрение регулируемого электропривода механизма вращения мельницы является одним из способов повышения энергоэффективности процесса измельчения [22]. Это позволяет осуществлять управление динамикой внутримельничной загрузки мельниц, исключить зоны руды, которые не измельчаются, и повысить эффективность процесса измельчения [23, 24].
Как правило, эффект от приведенных способов наблюдается при их комплексном использовании, что стало возможным в эпоху четвертой промышленной революции [25, 26]. Внедрение киберфизических систем в горной промышленности на основе таких ключевых тенденций Индустрии 4.0, как промышленный интернет вещей (IIoT), аналитика больших данных, искусственный интеллект и цифровое моделирование позволяют обеспечить взаимодействие оборудования на всей цепочке создания конечного продукта и адаптацию технологических процессов к внешним и внутренним изменениям [27, 28]. Подобный предиктивный анализ открывает возможности перед предприятиями по прогнозированию технического состояния оборудования и выдаче соответствующих рекомендаций для повышения эффективности работы на основе данных об эксплуатации за счет изучения процессов в виртуальной среде [29, 30].
Технологические решения
Основные регулируемые технологические параметры, за счет которых можно повысить производительность, – уровень загрузки, количество измельчающих тел и скорость вращения барабанной мельницы [31]. Особенности конструкции лифтеров также влияют на поведение загрузки внутри мельницы. Если управление динамикой внутримельничной загрузкой не осуществляется, то большая часть энергии расходуется не на измельчение руды, а на разрушение измельчающих тел и повреждение футеровки и других механических частей мельницы [23].
Ряд исследователей из профильных институтов, изучающих процесс измельчения считают, что скорость мельницы необходимо изменять в процессе измельчения. Основным фактором, требующим изменения скоростного режима мельницы, является непостоянство физико-механических свойств руды в процессе разработки месторождения [32].
Как правило, управляемые электроприводы мельниц полусамоизмельчения используются для их пуска. Однако, не на всех фабриках преобразователи частоты осуществляют только плавный пуск. Например, на фабриках компании Copper Mountain мельницы, оснащенные управляемым электроприводом, не вращались с постоянной скоростью в течение двух месяцев эксплуатации, а изменялись в диапазоне от 7 до 10 об/мин. Изменение скорости в таком диапазоне покрывает все режимы работы мельниц.
Загрузка мельницы или уровень заполнения является главным параметром, так как он определяет технологическую устойчивость процесса измельчения. Неправильная идентификация данного параметра может привести не только к снижению производительности (при его пониженном значении), но и к нарушению работы технологической системы, повреждению узлов мельницы (при его повышенном значении).
Главной трудностью при изучении поведения загрузки является невозможность установить измерительные устройства внутри корпуса мельницы. В таком случае реализуются только методы косвенного мониторинга [22, 24].
Существуют разные способы получения информации о процессах, протекающих в мельнице. Мониторинги акустических эмиссий и вибраций получили широкое распространение при определении заполнения мельниц [33, 34]. Однако, данные способы при определении текущего заполнения мельницы обладают существенными неточностями, обусловленными помехами механизмов [35, 36]. Главным недостатком способов при мониторинге уровня загрузки мельницы на определенных частотах является влияние собственных частотных компонентов механических частей мельниц [37, 38].
В отличие от вибро- и акустических сигналов момент на валу зависит непосредственно от изменений технологических параметров и не зависит от собственной частоты механических частей [39]. Сигнал момента может быть получен доступным способом при помощи наблюдателя координат за счет токовых сигналов, так как данные измерители устанавливаются вместе с управляемым электроприводом мельницы.
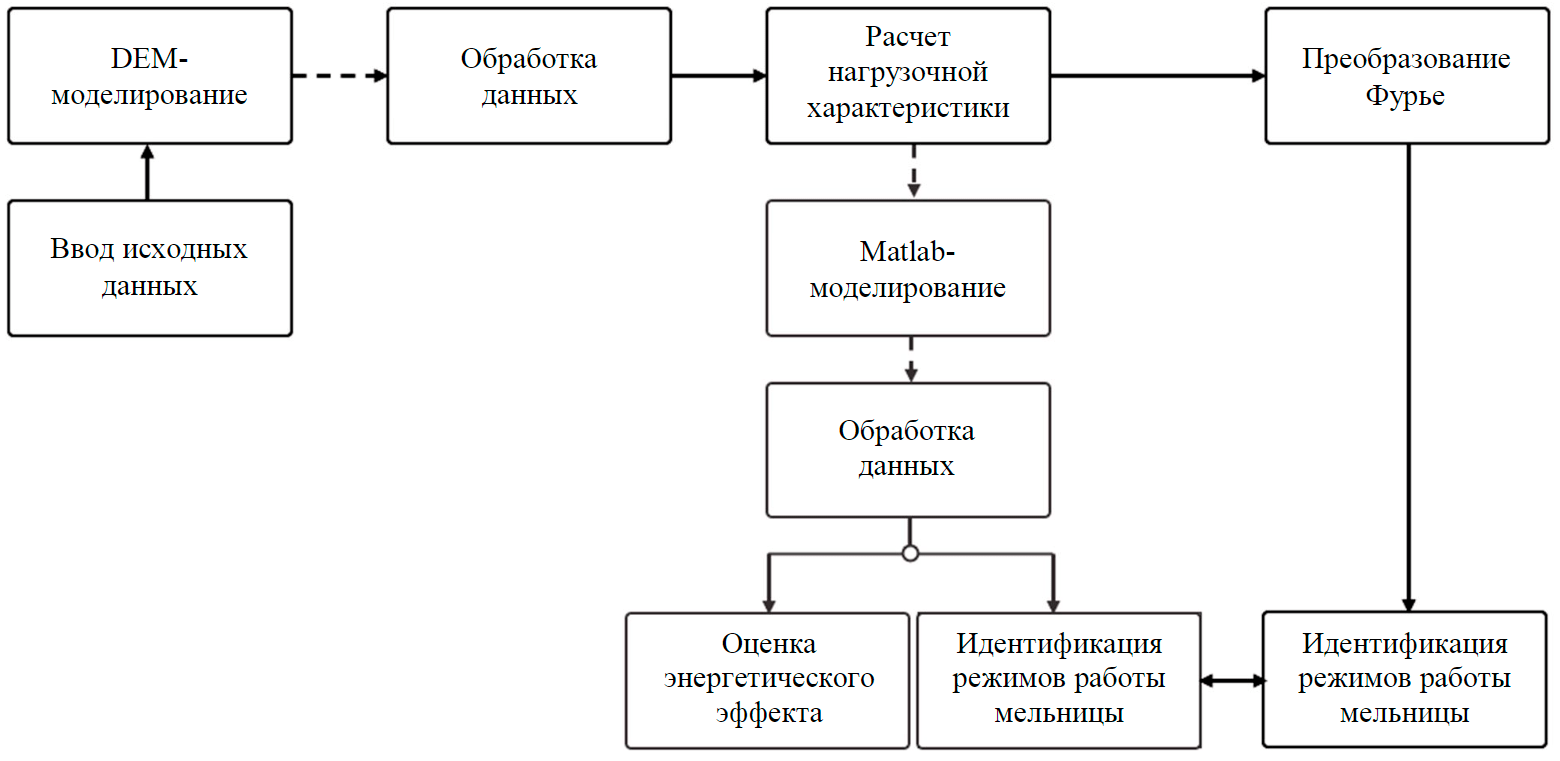
Рис.1. Методика исследований
Целью статьи является исследование влияния на спектральные составляющие электромагнитного момента двигателя в системе автоматизированного электропривода технологических параметров процесса измельчения для определения оптимального режима работы. При оптимальном режиме работы электропривода измельчение руды будет осуществляться при минимальных энергозатратах, обеспечивая номинальные технологические характеристики. Так как идентификация состояния мельницы (определение уровня заполнения) имеет трудности, предложено рассматривать спектральный состав электромагнитного момента двигателя для исключения ложных рекомендаций для выбора режима работы мельницы.
Существует ряд исследований поведения загрузки мельницы с помощью оценки момента [39, 40]. Возникающие соударения между частицами и движение пульпы внутри мельницы создают интенсивную вибрацию в механических частях, которая приводит к колебаниям крутящего момента на валу мельницы. Колебания отражаются в потребляемом токе, формируемом моменте и угловой скорости электропривода. Таким образом, сигнал момента является информативным как с точки зрения электромеханической части, так и технологической.
Методология
Исследования базировались на комплексном моделировании технологической и электромеханической частей системы мельница-электропривод. Методика состоит из двух ветвей и девяти основных этапов (рис.1). В первой ветви проводились исследования поведения внутримельничной загрузки с помощью DEM-моделирования в ПО Rocky DEM. При создании модели барабанной мельницы необходимо выбрать физические модели (алгоритм моделирования) по расчету внутренних усилий между частицами и объектом моделирования – мельницей; задать геометрию объекта; задать вращательное движение объекта; создать внутреннее объемное заполнение мельницы.
Во второй ветви исследований осуществляется оценка энергетического моделирования на основании моделирования электропривода мельницы и оценки электромагнитного момента в ПО Matlab.
Алгоритмы моделирования
Алгоритмы DEM-моделирования строятся на вычислении [41] нормальной и тангенциальной составляющих сил взаимодействия пар: частица-частица и частица-граница объекта симуляции.
В соответствии с линейной упругой моделью гистерезиса [42], нормальная составляющая силы взаимодействия к плоскости контакта вычисляется следующим образом:
где Knl и Knu – значения нагрузочной и разгрузочной контактных жесткости; Ftn и Ft-Δtn – нормальные упругопластические контактные силы в текущий момент времени t и в предыдущий момент времени t-Δt; Δt – шаг моделирования; ΔSn – изменение нормального перекрытия контактов частиц в течение текущего времени (положительное, когда частицы приближаются друг к другу, и отрицательное, когда отдаляются); stn и st-Δtn – значения нормального перекрытия в текущий и предыдущий момент времени; λ – константа, λ = 0,001.
Упругофрикционная тангенциальная составляющая вычисляется по предельной упругой модели Кулона (Linear spring Coulomb limit model) [43]:
где Ft-Δtn – значение тангенциальной силы в предыдущий момент времени; ΔSτ – тангенциальное относительное смещение частиц в течение временного интервала; Kτ – тангенциальная жесткость; μ – коэффициент трения.
Так как моделируемые частицы, находящиеся внутри мельницы, имеют сферическую форму, используется модель сопротивления частиц качению. В соответствии с моделью [44] «Тип С: предел качения линейной пружины»
где Mtr – вектор момента сопротивления качению; Mr,lim – предельное значение момента сопротивления качению; Mt-Δtr – вектор момента сопротивления качению в предыдущий момент времени; Kr – жесткость качения; ωrel – вектор относительной угловой скорости.
Геометрия барабанной мельницы
Для сокращения времени моделирования процесса расчет или вычисление проводились для участка барабанной мельницы длиной 0,9 м. В данной статье осуществлялось моделирование мельницы полусамоизмельчения. В модели принято допущение, что все частицы, взаимодействующие внутри мельницы, являются сферическими. Такое решение позволяет упростить проведение расчетов и сократить время моделирования, однако не позволяет учесть геометрию реальных измельчаемых частиц. Изменение геометрии частиц не рассматривается как фактор, оказывающий влияние на поведение нагрузочной характеристики для последующего моделирования электропривода. Однако нельзя отрицать факт влияния геометрии измельчаемых частиц на изменение поведения внутримельничной загрузки, скорости и момента [45].
Геометрические и технологические параметры мельницы, заданные при моделировании: внешний диаметр мельницы 11,5 м; длина участка 0,9 м; номинальная масса руды mр1 = 30 т; номинальная масса измельчающих тел mт = 8 т; плотность руды 2800 кг/м3; плотность измельчающих тел 7800 кг/м3.
Длительность моделирования составляла 35 с с шагом моделирования 0,0005 с. Скорости вращения барабана выбраны в соответствии с рекомендованными режимными значениями при проектировании обогатительных фабрик. Как правило, диапазон регулирования находится в пределах 0,5-0,85 от критической скорости nкр.
Процесс измельчения протекает под воздействием трех основных механизмов разрушения: удар, истирание и абразивный износ. Влияние данных механизмов будет различным в зависимости от режима работы мельницы. Режим работы определяется скоростью мельницы. Согласно [46] можно выделить семь скоростных режимов работы. Принято выражать режим работы относительно критической частоты вращения. При превышении значения критической скорости частицы начинают центрифугировать и прилипать к барабану под действием центробежных сил [47],
Данный режим работы недопустим, воздействия разрушающих сил не происходит – измельчение руды не осуществляется. Можно выделить три основных режима работы мельницы:
- каскадный (частота вращения барабана 50-60 % от критической скорости);
- водопадный (частота вращения барабана 70-85 % от критической скорости);
- смешанный (промежуточный между каскадным и водопадным с частотой вращения барабана 60-70 % от критической скорости).
При пониженных значениях скорости частицы перекатываются из одной части барабана в другую, разрушение происходит под действием истирания и абразивного износа. С увеличением скорости вращения мельницы верхние слои частиц отрываются от других, поднимаются и в верхней точке траектории падают под действием сил тяжести. Разрушение данных слоев происходит под действием удара. На практике удар используется для разрушения крупных крепких частиц, а истирание – для сокращения размера материала менее крепких пород для получения заданного класса крупности при последующих стадиях обогащения.
Выбраны характерные значения скорости, соответствующие трем рассматриваемым режимам работы мельниц: n1 – каскадный – 65 % от nкр = 0,84 рад/с (8 об/мин); n2 – водопадный – 80 % от nкр = 1,05 рад/с (10 об/мин); n3 – критический – 100 % от nкр = 1,31 рад/с (12,5 об/мин).
На рис.2 представлены режимы работы мельницы при моделировании процесса измельчения в Rocky DEM.
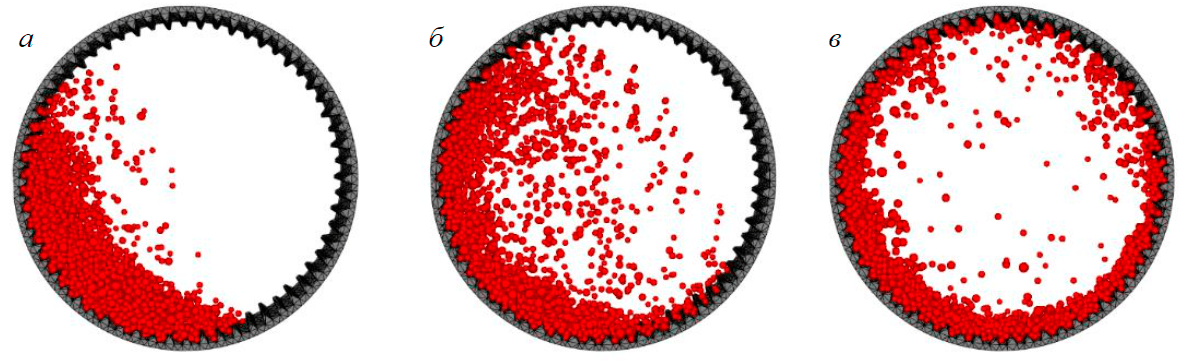
Рис.2. Режимы работы мельницы: а – каскадный; б – водопадный; в – критический
При проведении исследований учитывался фактор изменения загрузки мельницы. В модели мельницы задавалось три насыпи исходного сырья: mр1 = 25 т, mр2 = 35 т и mр3 = 40 т. Для каждой насыпи осуществлялось измельчение при трех скоростях n1, n2 и n3.
Извлечение полезного компонента осуществляется из пульпы (при обогащении методами флотации или «уголь в пульпе»), поэтому кроме руды в мельницу загружается и вода. Добавление воды оказывает существенное влияние на получение необходимого готового продукта –0,074 мм, поэтому ее наличие в барабане мельницы необходимо учитывать [48, 49]. Учет добавления воды не производился, так как ее наличие подразумевает проведение дополнительного CFD-моделирования, а исследование ориентировано на реализацию электромеханической системы процесса измельчения.
После каждого эксперимента данные экспортировались в Microsoft Excel. Далее осуществлялся расчет модуля эквивалентного момента по трем проекциям x, y и z в соответствии с данными Rocky DEM:
Полученный момент использовался в качестве нагрузочной характеристики для модели электропривода в Matlab Simulink на втором этапе проведения исследований.
После проведения операции быстрого преобразования Фурье получены спектры модулей эквивалентных моментов, по которым произведена идентификация режимов работы мельницы. Таким образом, получена матрица состояний барабанной мельницы по спектральным составляющим нагрузочного момента. Далее необходимо перейти к второй ветви исследований в Matlab Simulink, чтобы состояние мельницы можно было определить в процессе ее эксплуатации по спектральным составляющим электромагнитного момента.
Тренд на сокращение технологических цепочек и увеличение пропускных мощностей измельчительных агрегатов является актуальным до сих пор, что повышает требования к мельницам при проектировании и эксплуатации [50]. Электропривод процесса измельчения является главным потребителем на горнопромышленном предприятии, управление которым необходимо осуществлять в соответствии с технологическими параметрами для повышения эффективности барабанных мельниц [51]. Для электропривода процесса измельчения могут использоваться кинематические структуры: однодвигательная, двухдвигательная, безредукторная. Переход к двухдвигательной структуре обоснован максимальным механическим моментом, который можно передать через зубчатое зацепление. При мощностях выше 9 МВт передача момента через одну шестерню невозможна. Безредукторный электропривод характеризуется самой высокой энергоэффективностью, так как в его составе отсутствуют передаточные устройства. Данный электропривод целесообразно применять в диапазоне мощностей от 12 до 36 МВт.
Наиболее перспективными двигателями, используемыми в электроприводе, являются асинхронные двигатели с короткозамкнутыми роторами (АДКР), вентильно-индукторные двигатели (ВИД) и синхронные двигатели с постоянными магнитами (СДПМ). Ввиду высокой стоимости изготовления СДМП целесообразно рассматривать и разрабатывать способы повышения эффективности асинхронных и вентильно-индукторных электроприводов, используемых для управления процессом измельчения [52, 53].
Электроприводы мельничных агрегатов характеризуются тяжелым режимом работы. Существующие технологические особенности процесса измельчения усложняют процесс эксплуатации электроприводов. Электропривод, выбранный на основе расчетных методик под номинальный режим работы мельницы может не сформировать пусковой момент при затвердевании руды. В таком случае мощность машины будет завышена, а при выходе на номинальный режим работы энергетические показатели КПД и коэффициент мощности будут иметь пониженные значения.
Мельницы работают в продолжительном режиме, их работа приостанавливается только на время планово-предупредительного ремонта по замене футеровки и других узлов один раз в месяц. В статье исследуется работа асинхронного электропривода процесса измельчения, работающего под нагрузкой при наступлении установившегося режима работы мельничного агрегата.
На рис.3 представлена имитационная модель электропривода мельницы. Барабанные мельницы питаются от напряжения 6/10 кВ. На горно-обогатительных комбинатах с малым и средним объемом выпуска готовой продукции мощность шаровых мельниц составляет 1 МВт. Для моделирования электропривода был взят асинхронный двигатель со следующими параметрами: мощность 1 МВт, напряжение питания 6 кВ, номинальная скорость 595 об/мин, cosφ = 0,85, КПД = 0,972, перегрузочная способность 4,5. Обмоточные параметры двигателя рассчитаны согласно методике И.П.Копылова.
В результате имитационного моделирования функция электромагнитного момента была разложена на спектральные составляющие с помощью преобразования Фурье. На основании этих составляющих проведена идентификация режимов работы мельницы и сравнение со спектром нагрузочного момента, полученного в первой части исследования.
В процессе обработки данных необходимо снять энергетические и нагрузочные характеристики, по которым производится оценка энергетического эффекта и идентификация режимов работы мельницы. В данном исследовании оценка энергетических характеристик и критериев энергоэффективности не проводилась.
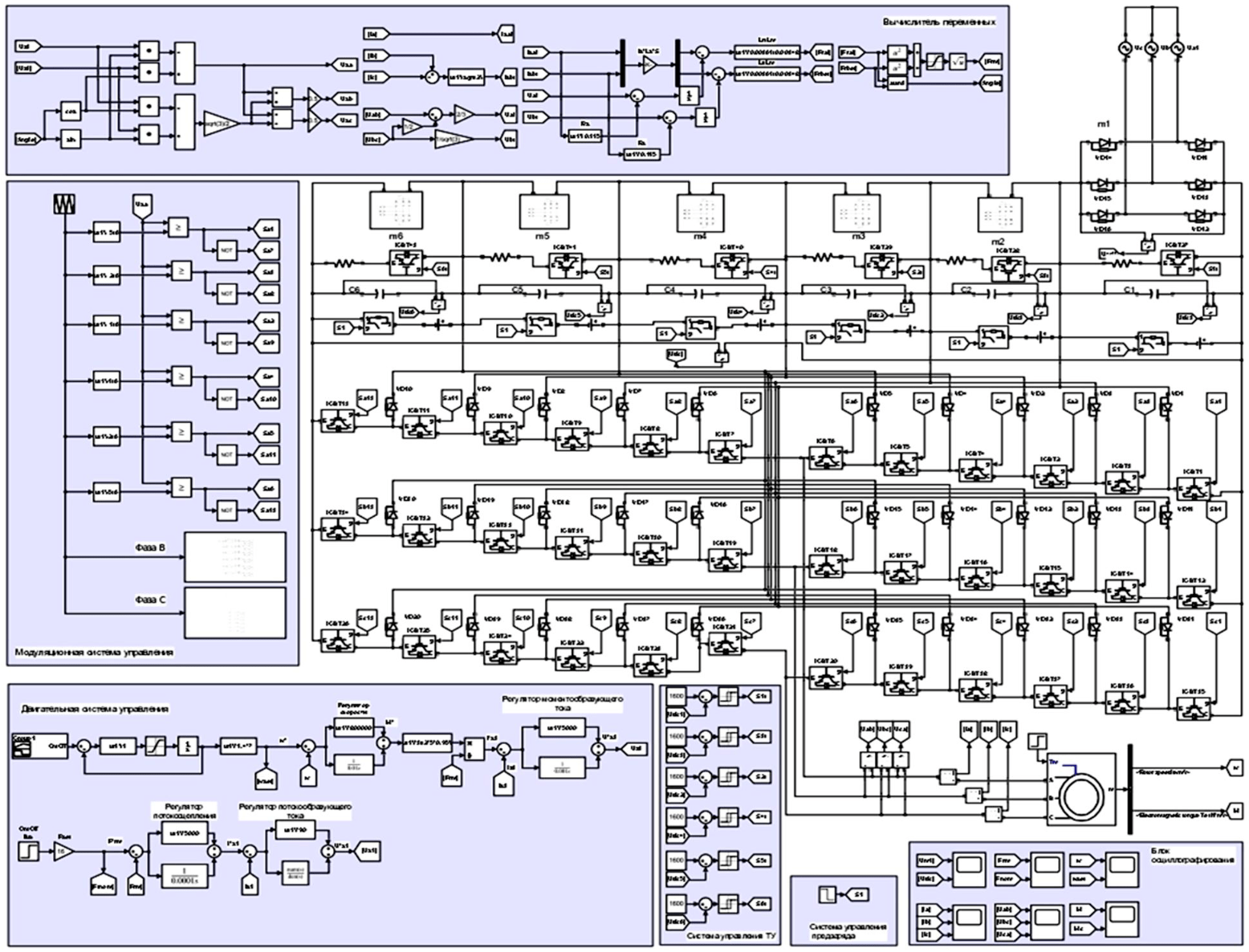
Рис.3. Имитационная модель электропривода процесса измельчения
Для сокращения времени моделирования был взят промежуток времени, соответствующий выходу мельницы в установившийся режим работы мельницы. Такой режим считается достигнутым, если средние координаты всех частиц по вертикальной и горизонтальной осям приходят к условно неизменным значениям [53]. Установившийся режим работы достигается в момент времени 16 с. Таким образом, выбран интервал нагрузки, соответствующий 2 с времени нагрузочной характеристики при загрузке 35 т и скорости 1,05 рад/с от 16 до 18 с.
Моделирование асинхронного электропривода проводилось с шагом моделирования 0,000002 с. Такой шаг выбран в соответствии с частотой несущего сигнала модуляционной системы управления автономного инвертора.
Обсуждение результатов
Результаты экспериментов приведены на рис.4, 5. Чем больше скорость мельницы, тем больше момент приобретает форму периодического сигнала (рис.4). При скорости 1,31 рад/с загрузка начинает центрифугировать и момент нагрузки уменьшается. В соответствии с каскадным режимом работы мельницы 0,84 рад/с руда будет измельчаться до более тонкой фракции. При разрушении руды ударом 1,05 рад/с требуется большая мощность, однако исследования показали, что каскадный и водопадный режимы могут быть сопоставимы по мощности. Изменение скорости в процессе эксплуатации мельницы практически не скажется на потребляемой электроэнергии, но позволит повысить производительность измельчения за счет сокращения времени измельчения руды.
Для каждого состояния мельницы можно получить характерный набор частотных составляющих спектра момента (ЧССМ) определенной амплитуды (рис.5, табл.1). Предположим, что отследить уровень загрузки мельницы на определенной скорости можно по смене знаков частотных составляющих спектра (табл.2). Однако для этого необходимы непрерывный мониторинг сигнала момента и сравнение спектральных составляющих друг с другом.

Рис.4. Модуль эквивалентного момента мельницы при загрузке 25 т (а), 35 т (б) и 40 т (в) на скоростях 0,84 рад/с (1), 1,05 рад/с (2) и 1,31 рад/с (3)
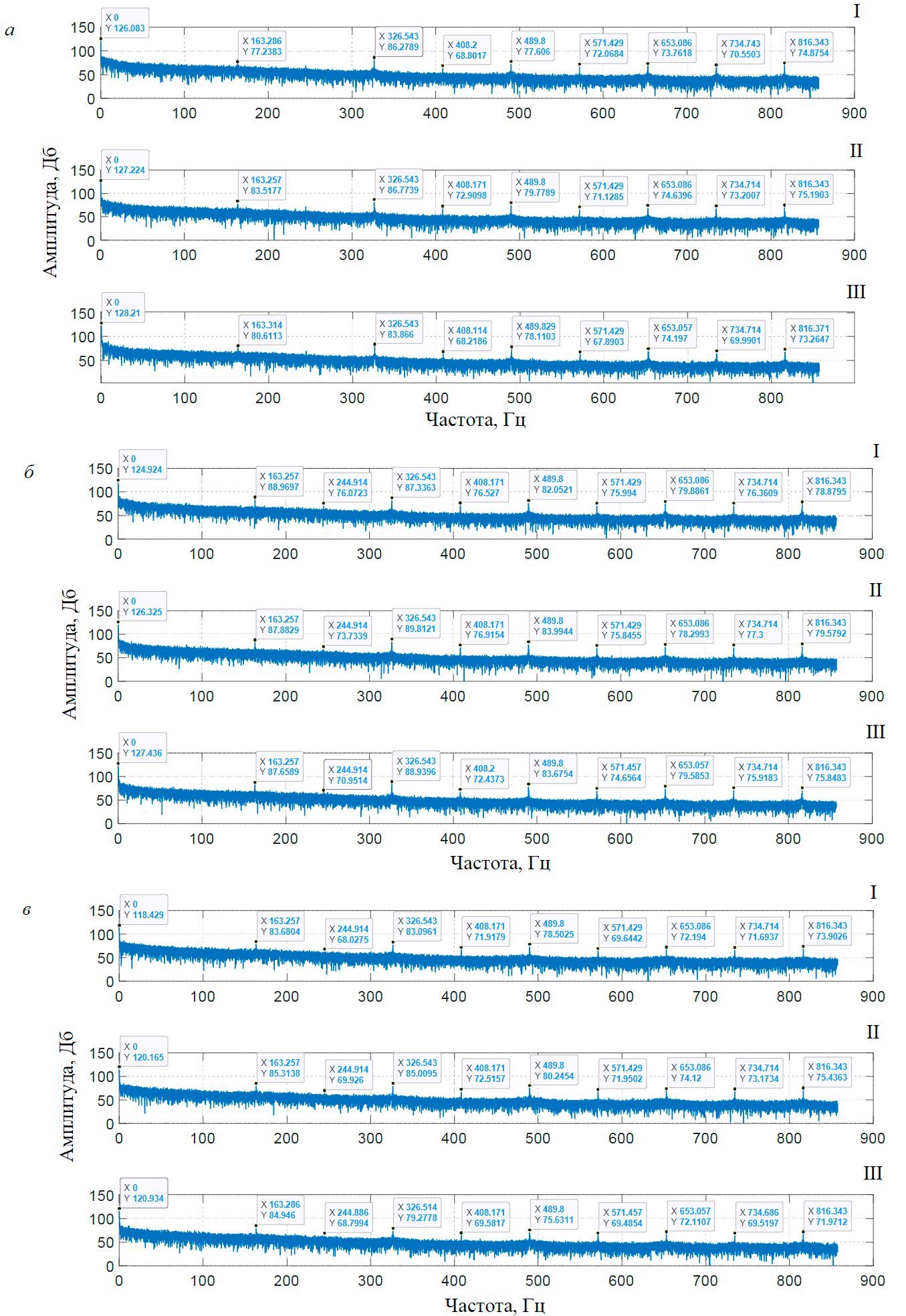
Рис. 5. Спектры нагрузочных моментов при загрузке 25 т (I), 35 т (II), 40 т (III) и скорости 0,84 рад/с (а), 1,05 рад/с (б) и 1,31 рад/с (в)
Таблица 1
Матрица состояний мельниц
|
Скорость, рад/c (об,мин) |
3arpyзка, т |
1 ЧCCM |
2 ЧCCM |
3 ЧCCM |
4 ЧCCM |
5 ЧCCM |
6 ЧCCM |
7 ЧCCM |
8 ЧCCM |
9 ЧCCM |
10 ЧCCM |
||||||||||
|
ƒ1, Гц |
М1, Дб |
ƒ2, Гц |
М2, Дб |
ƒ3, Гц |
М3, Дб |
ƒ4, Гц |
М4, Дб |
ƒ5, Гц |
М5, Дб |
ƒ6, Гц |
М6, Дб |
ƒ7, Гц |
М7, Дб |
ƒ8, Гц |
М8, Дб |
ƒ9, Гц |
М9, Дб |
ƒ10, Гц |
М10, Дб |
||
|
0,84 (8) |
25 35 40 |
0 0 0 |
126,1 127,2 128,2 |
163,3 163,3 163,3 |
77,2 83,5 80,6 |
244,9 244,9 244,9 |
68,7 70,5 68,6 |
326,5 326,5 326,5 |
86,3 86,8 83,9 |
408,2 408,2 408,2 |
68,8 72,9 68,2 |
489,8 489,8 489,8 |
77,6 79,8 78,1 |
571,4 571,4 57I,4 |
72,1 71,1 67,9 |
653,1 653,1 653,1 |
73,8 74,6 74,2 |
734,7 734,7 734,7 |
70,7 73,2 70,0 |
816,3 816,3 816,4 |
74,9 75,2 73,3 |
|
1,05(10) |
25 35 40 |
0 0 0 |
124,9 126,3 127,4 |
163,3 163,3 163,3 |
89,0 87,9 87,7 |
244,9 244,9 244,9 |
76,1 73,7 71,0 |
326,5 326,5 326,5 |
87,3 89,8 88,9 |
408,2 408,2 408,2 |
76,5 76,9 72,4 |
489,8 489,8 489,8 |
82,5 84,0 83,7 |
571,4 571,4 571,4 |
76,0 75,9 74,7 |
653,1 653,1 653,1 |
80,0 78,3 79,6 |
734,7 734,7 734,7 |
76,3 77,3 75,9 |
816,3 816,3 816,3 |
78,9 79,6 75,9 |
|
1,31(12,5) |
25 35 40 |
0 0 0 |
118,4 120,2 120,9 |
163,3 163,3 153,3 |
83,7 85,3 85,0 |
244,9 244,9 244,9 |
68,0 69,9 68,8 |
326,5 326,5 326,5 |
83,1 85,0 79,3 |
408,2 408,2 408,2 |
71,9 72,5 69,6 |
489 489,9 489,9 |
78,5 80,2 75,6 |
571,4 571,4 571,4 |
69,6 72,0 69,5 |
653,1 653,1 653,1 |
72,2 74,1 72,1 |
734,7 734,7 734,7 |
71,7 73,2 69,5 |
816,3 816,3 816,3 |
73,9 75,4 72,0 |
Таблица 2
Индентификация внтримельничной загрузки
|
Скорость, рад/c (об,мин) |
3arpyзка, т,
|
1 ЧCCM |
2 ЧCCM |
3 ЧCCM |
4 ЧCCM |
5 ЧCCM |
6 ЧCCM |
7 ЧCCM |
8 ЧCCM |
9 ЧCCM |
10 ЧCCM |
||||||||||
|
ƒ1, Гц |
М1, Дб |
ƒ2, Гц |
М2, Дб |
ƒ3, Гц |
М3, Дб |
ƒ4, Гц |
М4, Дб |
ƒ5, Гц |
М5, Дб |
ƒ6, Гц |
М6, Дб |
ƒ7, Гц |
М7, Дб |
ƒ8, Гц |
М8, Дб |
ƒ9, Гц |
М9, Дб |
ƒ10, Гц |
М10, Дб |
||
|
0,84 (8) |
25 35 |
0 0 |
↑ |
163,3 163,3 |
↑ |
244,9 244,9 |
↑ |
326,5 326,5 |
↑ |
408,2 408,2 |
↑ |
489,8 489,8 |
↑ |
571,4 571,4 |
↓ |
653,1 653,1 |
↑ |
734,7 734,7 |
↑ |
816,3 816,3 |
↑ |
|
35 40 |
0 0 |
↑ |
163,3 163,3 |
↓ |
244,9 244,9 |
↓ |
326,5 326,5 |
↓ |
408,2 408,2 |
↓ |
489,8 489,8 |
↓ |
571,4 571,4 |
↓ |
653,1 653,1 |
↓ |
734,7 734,7 |
↓ |
816,3 816,4 |
↓ |
|
|
1.05(10) |
25 35 |
0 0 |
↑ |
163,3 163,3 |
↓ |
244,9 244,9 |
↓ |
326,5 326,? |
↑ |
408,2 408,2 |
↑ |
489,8 489,8 |
↑ |
571,4 571,4 |
↓ |
653,1 653,1 |
↑ |
734,7 734,7 |
↑ |
816,3 816,3 |
↑ |
|
35 40 |
0 0 |
↑ |
163,3 163,3 |
↓ |
244,9 244,9 |
↓ |
326,5 326,5 |
↓ |
408,2 408,2 |
↓ |
489,8 489,8 |
↓ |
571,4 571,4 |
↓ |
653,1 653,1 |
↓ |
734,7 734,7 |
↓ |
816,3 816,3 |
↓ |
|
|
1,31 (1 2,5) |
25 35 |
0 0 |
↑ |
163.3 163,3 |
↑ |
244,9 244,9 |
↑ |
326,5 326,5 |
↑ |
408,2 408,2 |
↑ |
489,8 489,9 |
↑ |
571,4 571,4 |
↑ |
653,1 653,1 |
↑ |
734,7 734,7 |
↑ |
816,3 816,3 |
↑ |
|
35 40 |
0 0 |
↑ |
163,3 163,3 |
↓ |
244,9 244,9 |
↓ |
326,5 326,5 |
↓ |
408,2 408,2 |
↓ |
489,8 489,9 |
↓ |
571,4 571,4 |
↑ |
653,1 653,1 |
↓ |
734,7 734,7 |
↓ |
816,3 816,3 |
↓ |
|
Примечание. Увеличение ↑ и снижение ↓ амплитуды сооствляющей спектра относительно предудыщего значения.
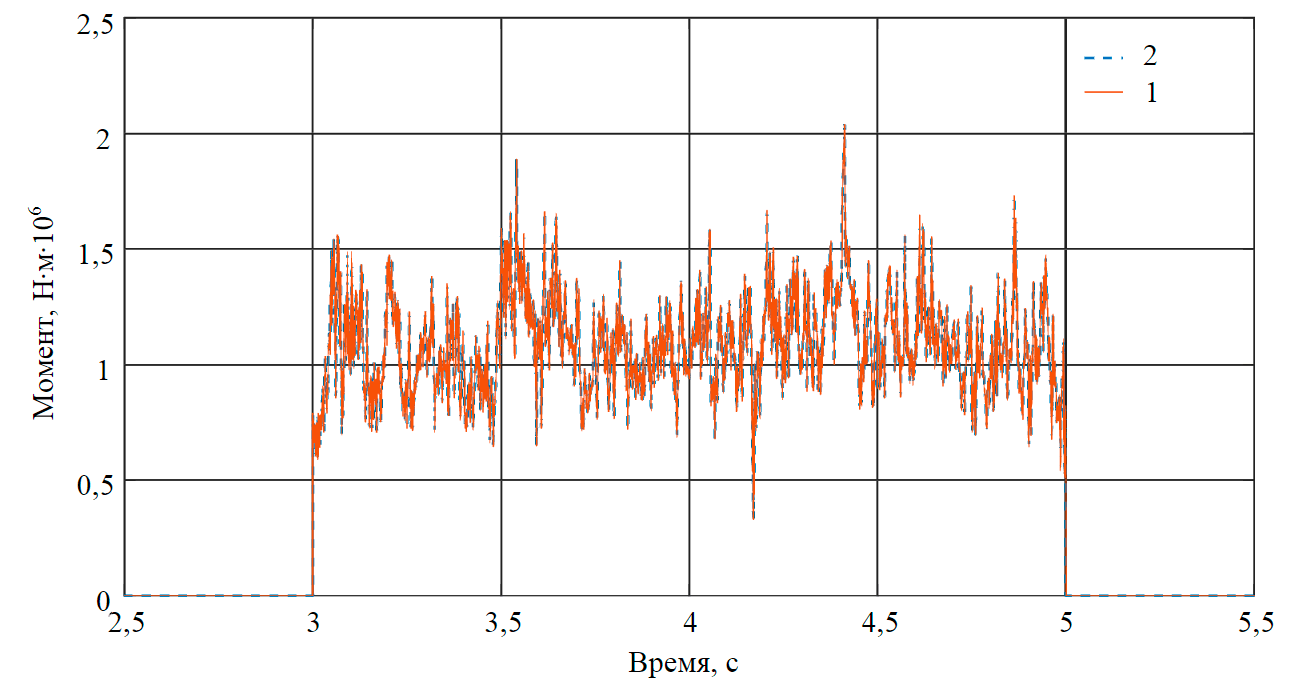
Рис.6. Электромагнитный момент двигателя (1) и момент сопротивления (2) при нагрузке 35 т и скорости 1,05 рад/с
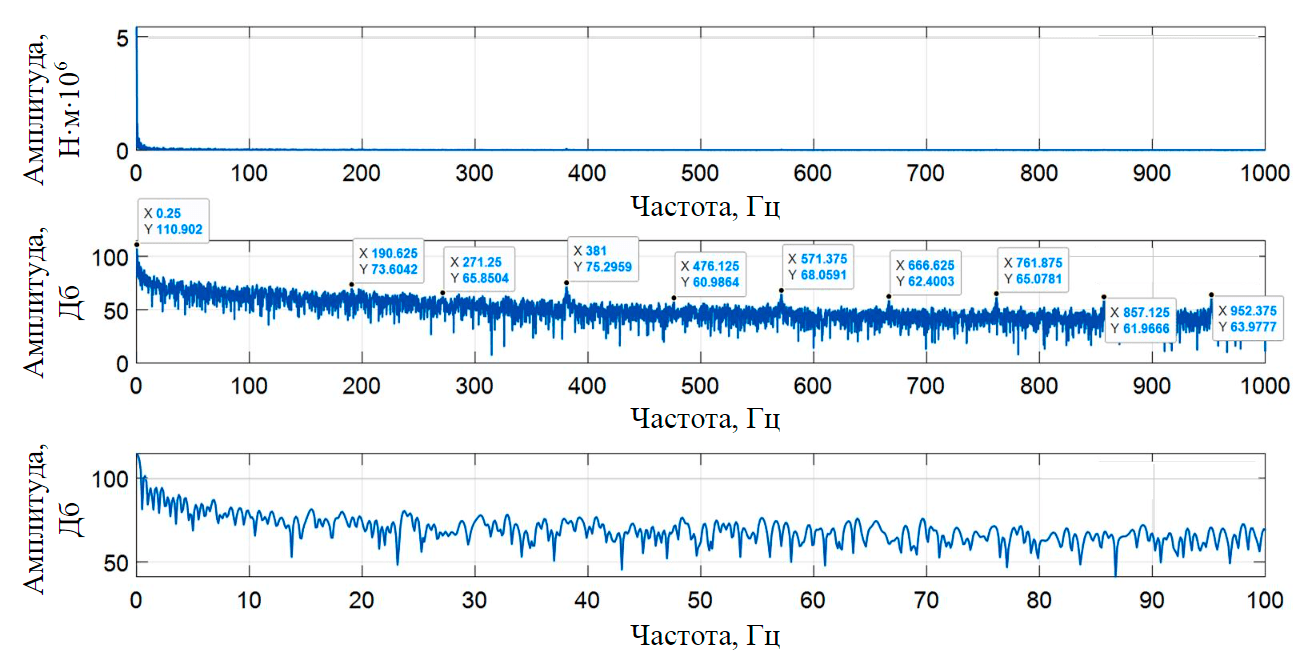
Рис.7. Спектр электромагнитного момента при нагрузке 35 т и скорости 1,05 рад/с
На рис.6, 7 представлены результаты исследований электропривода процесса измельчения. Так как на данном этапе исследований рассмотрен только установившейся режим работы, на рис.6 отсутствуют промежутки разгона и торможения двигателя. Промежуток времени 3-5 с соответствует работе двигателя под нагрузкой. Соответственно, в момент времени 3 с осуществляется наброс нагрузки, 5 с – сброс. Амплитуда колебаний составляет около 1,5 МН∙м. Повышенные колебания электромагнитного момента приводят к колебаниям двигателя и, как следствие, к возникновению вибраций и к биению ротора.
Согласно полученным результатам исследований повышение скоростного режима работы мельницы позволит снизить среднее значение момента. Если для текущих характерик измельчаемого продукта такое изменение не скажется на качестве измельчения, то это позволит снизить потребляемую мощность электроприводом из сети и амплитуду колебаний.
По полученному спектру на рис.7 можно сделать вывод, что в сигнале электромагнитного момента прослеживается периодическая составляющая. В спектре электромагнитного момента прослеживаются те же составляющие, что и в спектре нагрузочной характеристики, однако наблюдается смещение зафиксированных пиков по частотной оси.
Заключение
Несмотря на то, что мельницы, как правило, проектируются с нерегулируемым электроприводом, эффект, который можно получить от регулируемой скорости, представляет практический интерес. Управление силами разрушения руды можно осуществлять за счет изменения скорости вращения мельницы.
Проведенные исследования показали, что за счет комплексного моделирования технологической и электромеханической частей можно оптимизировать энергетические затраты. При увеличении скорости вращения с 0,84 до 1,05 рад/с увеличивается энергия удара, позволяющая обеспечить разрушение руды. При этом значения нагрузочного момента сопоставимы, а значит возможно повысить ударную энергию на измельчение без повышения затрат электроэнергии.
По полученным спектрам можно идентифицировать состояние мельничной загрузки – скорость и уровень заполнения.
Разработанная методика может использоваться для определения более эффективного режима работы при изменении объемного заполнения мельницы за счет вариативности свойств руды. Результаты исследований имеют практическую значимость как при эксплуатации мельничного агрегата, так и при проектировании электромеханических комплексов. Исследования позволяют учесть особенности объекта автоматизации и при разработке электроприводов мельниц. Показана возможность получения энергетического эффекта в процессе эксплуатации мельницы в результате проведения комплексного цифрового моделирования технологической и электромеханической частей. Это позволяет оценить влияние изменения одних показателей технологической системы на другие показатели электромеханической системы на основе относительно быстрого полученного отклика модели в ходе виртуальных испытаний. Исследования, проведенные авторами, могут лечь в основу создания комплексного инструмента по оценке эффективности – энергетической цепочки звеньев процесса измельчения. Данную идею возможно реализовать за счет одной из ключевых тенденций Индустрии 4.0 – цифрового моделирования.
Направление будущих исследований будет заключаться в оценке энергетической эффективности при изменении режимов работы барабанных мельниц.
Литература
- Litvinenko V.S. Digital Economy as a Factor in the Technological Development of the Mineral Sector // Natural Resources Research. 2020. Vol. 29. P. 1521-1541. DOI: 10.1007/s11053-019-09568-4
- Filatova I., Nikolaichuk L., Zakaev D., Ilin I. Public-private partnership as a tool of sustainable development in the oil-refining sector: Russian case // Sustainability. 2021. Vol. 13. Iss. 9. № 5153. DOI: 10.3390/su13095153
- Zhukovskiy Y.L., Batueva D.E., Buldysko A.D. et al. Fossil Energy in the Framework of Sustainable Development: Analysis of Prospects and Development of Forecast Scenarios // Energies. 2021. Vol. 14. Iss. 17. № 5268. DOI: 10.3390/en14175268
- Федосеев С.В., Цветков П.С. Ключевые факторы общественного восприятия проектов захвата и захоронения углекислого газа // Записки Горного института. 2019. Т. 237. С. 361-368. DOI: 10.31897/PMI.2019.3.361
- Cleary P.W., Owen P. Effect of operating condition changes on the collisional environment in a SAG mill // Minerals Engineering. 2019. Vol. 132. P. 297-315. DOI: 10.1016/j.mineng.2018.06.027
- Ruonan Meng, Qinglin Zhao, Miaomiao Wu et al. A Survey and Analysis on Electricity Consumption of Raw Material Mill System in China Cement Industry between 2014 and 2019 // Sustainability. 2021. Vol. 13. Iss. 3. № 1126. DOI: 10.3390/su13031126
- Zixin Yin, Tongqing Li, Yuxing Peng, Guiyi Wu. Effect of Lifter Shapes on the Mill Power in a Ball Mill // IOP Conference Series: Materials Science and Engineering. 2018. Vol. 452. Iss. 4. № 042201. DOI: 10.1088/1757-899X/452/4/042201
- Djordjevic N., Shi F.N., Morrison R. Determination of lifter design, speed and filling effects in AG mills by 3D DEM // Minerals Engineering. 2004. Vol. 17. Iss. 11-12. P. 1135-1142. DOI: 10.1016/j.mineng.2004.06.033
- Mishra B.K., Rajamani R.K. The discrete element method for the simulation of ball mills // Applied Mathematical Modelling. 1992. Vol. 16. Iss. 11. P. 598-604. DOI: 10.1016/0307-904X(92)90035-2
- Xiaolei Bian, Guoqiang Wang, Hongdi Wang et al. Effect of lifters and mill speed on particle behaviour, torque, and power consumption of a tumbling ball mill: Experimental study and DEM simulation // Minerals Engineering. 2017. Vol. 105. P. 22-35. DOI: 10.1016/j.mineng.2016.12.014
- Hlungwani O., Rikhotso J., Dong H., Moys M.H. Further validation of DEM modeling of milling: effects of liner profile and mill speed // Minerals Engineering. 2003. Vol. 16. № 10. P. 993-998. DOI: 10.1016/j.mineng.2003.07.003
- Djordjevic N., Shi F.N., Morrison R. Determination of lifter design, speed and filling effects in AG mills by 3D DEM // Minerals Engineering. 2004. Vol. 17. Iss. 11-12. P. 1135-1142. DOI: 10.1016/j.mineng.2004.06.033
- Александров А.В., Литвинова Н.М. Экспериментально-теоретические исследования процесса измельчения руд // Горный информационно-аналитический бюллетень. 2009. Т. 4. №. 12. С. 242-249.
- Bouchard J., Desbiens A., Poulin É. Reducing the energy footprint of grinding circuits: the process control paradigm // IFAC-PapersOnLine. 2017. Vol. 50. Iss. 1. P. 1163-1168. DOI: 10.1016/j.ifacol.2017.08.402
- Александрова Т.Н., Потемкин В.А. Разработка методики оценки процесса гидроциклонирования c учетом реологических параметров минеральной суспензии // Записки Горного института. 2021. Т. 252. С. 908-916. DOI: 10.31897/PMI.2021.6.12
- Александрова Т.Н., Ромашев А.О., Кузнецов В.В. Развитие методического подхода к определению флотационной способности тонковкрапленных сульфидов // Обогащение руд. 2020. № 2. С. 9-14. DOI: 10.17580/or.2020.02.02
- Dongling Wu, Wei Chen, Hongjie Yanet al. Identifying grinding mill dynamics using acoustic beamforming and numerical modelling // Powder Technology. 2020. Vol. 371. P. 231-243. DOI: 10.1016/j.powtec.2020.05.092
- Campbell J.J., Holmes R.J., Spencer S.J. et al. The collection and analysis of single sensor surface vibration data to estimate operating conditions in pilot-scale and production-scale AG/SAG mills // Proceedings of the XXII International Mineral Processing Congress, 9 September – 3 October 2003, Cape Town, South Africa. South African Institute of Mining & Metallurgy, 2003.
- P. 280-288.
- Kuzba B., Pawlosa W., Konieczny A., Krzeminska M. Optimisation Platform for copper ore processing at the Division of Concentrator of KGHM Polska Miedz SA // Mineral Engineering Conference MEC 2016, 25-28 September 2016, Swieradow-Zdroj, Poland. E3S Web of Conferences, 2016. Vol. 8. № 01037. DOI: 10.1051/e3sconf/20160801037
- Korolev N.A., Solovev S.V. AC motor diagnostics system based on complex parametric analysis // International Conference on Mechanical Engineering, Automation and Control Systems 2016, 27-29 October 2016, Tomsk, Russian Federation. IOP Conference Series: Materials Science and Engineering, 2017. Vol. 177. № 012007. DOI: 10.1088/1757-899X/177/1/012007
- Kozjaruk A.E., Vasilev B.U., Shtop S.A., Serdukov N.A. Currents in bearings of induction motors of electric drives with semiconductor converter // 17th International Ural Conference on AC Electric Drives (ACED), 26-30 March 2018, Ekaterinburg, Russia. IEEE, 2018. № 17719959. DOI: 10.1109/ACED.2018.8341707
- Góralczyk M., Krot P., Zimroz R., Ogonowsk S. Increasing Energy Efficiency and Productivity of the Comminution Process in Tumbling Mills by Indirect Measurements of Internal Dynamics – An Overview // Energies. 2020. Vol. 13. Iss. 24. № 6735. DOI: 10.3390/en13246735
- Cleary P.W., Owen P. Effect of operating condition changes on the collisional environment in a SAG mill // Minerals Engineering. 2019. Vol. 132. P. 297-315. DOI: 10.1016/j.mineng.2018.06.027
- Weerasekara N.S., Liu L.X., Powell M.S. Estimating energy in grinding using DEM modelling // Minerals Engineering. 2016. Vol. 85. P. 23-33. DOI: 10.1016/j.mineng.2015.10.013
- Koteleva N., Khokhlov S., Frenkel I. Digitalization in Open-Pit Mining: A New Approach in Monitoring and Control of Rock Fragmentation // Applied Sciences. 2021. Vol. 11. Iss. 22. № 10848. DOI: 10.3390/app112210848
- Beloglazov I.I., Petrov P.A., Bazhin V.Y. The concept of digital twins for tech operator training simulator design for mining and processing industry // Eurasian Mining. 2020. № 2. P. 50-54. DOI: 10.17580/em.2020.02.12
- Boikov A., Payor V., Savelev R., Kolesnikov A. Synthetic data generation for steel defect detection and classification using deep learning // Symmetry. 2021. Vol. 13. Iss. 7. №1176. DOI: 10.3390/sym13071176
- Vasilyeva N., Fedorova E., Kolesnikov A. Big data as a tool for building a predictive model of mill roll wear // Symmetry. 2021. Vol. 13. Iss. 5. № 859. DOI: 10.3390/sym13050859
- Николаев А.В., Фет Ш., Кычкин А.В. Использование кибернетического подхода к ценозависимому управлению спросом на потребляемую подземным горно-добывающим предприятием электроэнергию // Записки Горного института. 2022. C.1-12 (Online first). DOI: 10.31897/PMI.2022.33
- Boikov A.V., Savelev R.V., Payor V.A., Potapov A.V. Evaluation of bulk material behavior control method in technological units using dem. Part 2 // CIS Iron and Steel Review. 2020. Vol. 20. P. 3-6. DOI: 10.17580/cisisr.2020.02.01
- Behera B., Mishra B.K., Murty C.V.R. Experimental analysis of charge dynamics in tumbling mills by vibration signature technique // Minerals Engineering. 2007. Vol. 20. Iss. 1. P. 84-91. DOI: 10.1016/j.mineng.2006.05.007
- Peng Gao, Wentao Zhou, Yuexin Hanet al. Enhancing the capacity of large-scale ball mill through process and equipment optimization: An industrial test verification // Advanced Powder Technology. 2020. Vol. 31. Iss. 5. P. 2079-2091. DOI: 10.1016/j.apt.2020.03.001
- Jian Tang, Tianyou Chai, Lijie Zhaoet et al. Soft sensor for parameters of mill load based on multi-spectral segments PLS sub-models and on-line adaptive weighted fusion algorithm // Neurocomputing. 2012. Vol. 78. Iss. 1. P. 38-47. DOI: 10.1016/j.neucom.2011.05.028
- Jian Tang, Lijie Zhao, Heng Yue et al. Vibration analysis based on empirical mode decomposition and partial least square // Procedia Engineering. 2011. Vol. 16. P. 646-652. DOI: 10.1016/j.proeng.2011.08.1136
- Gugel K., Palacios G., Ramirez J., Parra M. Improving ball mill control with modern tools based on digital signal processing (DSP) technology // Cement Industry Technical Conference, 2003. Conference Record. IEEE-IAS/PCA 2003, 4-9 May 2003, Dallas, USA. IEEE, 2003. P. 311-318. DOI: 10.1109/CITCON.2003.1204732
- Gugel K.S., Moon R.M. Automated mill control using vibration signal processing // 2007 IEEE Cement Industry Technical Conference Record, 29 April 2007 – 2 May 2007, Charleston, USA. IEEE, 2007. P. 17-25. DOI: 10.1109/CITCON.2003.1204732
- Esteves P.M., Stopa M.M., Cardoso Filho B.J., Galery R. Charge behavior analysis in ball mill by using estimated torque // IEEE Transactions on Industry Applications. 2014. Vol. 51. Iss. 3. P. 2600-2606. DOI: 10.1109/TIA.2014.2377372
- Behera B., Mishra B.K., Murty C.V.R. Experimental analysis of charge dynamics in tumbling mills by vibration signature technique // Minerals Engineering. 2007. Vol. 20. Iss. 1. P. 84-91. DOI: 10.1016/j.mineng.2006.05.007
- Pedrayesa F., Norniellaa J.G., Meleroet M.G. et al. Frequency domain characterization of torque in tumbling ball mills using DEM modelling: Application to filling level monitoring // Powder Technology. 2018. Vol. 323. P. 433-444. DOI: 10.1016/j.powtec.2017.10.026
- Walton O.R., Braun R.L. Viscosity, granular‐temperature, and stress calculations for shearing assemblies of inelastic, frictional disks // Journal of Rheology. 1986. Vol. 30. Iss. 5. P. 949-980. DOI: 10.1122/1.549893
- Thornton C., Cummins S.J., Cleary P.W. An investigation of the comparative behaviour of alternative contact force models during elastic collisions // Powder Technology. 2011. Vol. 210. Iss. 3. P. 189-197. DOI: 10.1016/j.powtec.2011.01.013
- Wensrich C.M., Katterfeld A. Rolling friction as a technique for modelling particle shape in DEM // Powder Technology. 2012. Vol. 217. P. 409-417. DOI: 10.1016/j.powtec.2011.10.057
- Lei Xu, Kun Luo, Yongzhi Zhao et al. Influence of particle shape on liner wear in tumbling mills: A DEM study // Powder technology. 2019. Vol. 350. P. 26-35. DOI: 10.1016/j.powtec.2019.03.033
- Bibak Z., Banisi S. A combined physical and DEM modelling approach to investigate particle shape effects on load movement in tumbling mills // Advanced Powder Technology. 2021. Vol. 32. Iss. 3. P. 916-930. DOI: 10.1016/j.apt.2021.01.034
- Bbosa L.S., Govender I., Mainza A. Development of a novel methodology to determine mill power draw // International Journal of Mineral Processing. 2016. Vol. 149. P. 94-103. DOI: 10.1016/j.minpro.2016.02.009
- МелехинаК.А., АнаньевП.П., ПлотниковаА.В. идр. Моделирование и оптимизация процесса рудоподготовки комплексных руд при их дезинтеграции в мельнице самоизмельчения // Горный информационно-аналитический бюллетень. 2020. № 10. С. 95-105. DOI: 10.25018/0236-1493-2020-10-0-95-105
- Seong-Hyeon Hong, Byoung-Kee Kim. Effects of lifter bars on the ball motion and aluminum foil milling in tumbler ball mill // Materials Letters. 2002. Vol. 57. Iss. 2. P. 275-279. DOI: 10.1016/S0167-577X(02)00778-4
- Осипова Н.В. Выбор параметров алгоритма управления загрузкой мельницы мокрого самоизмельчения железной руды // Горный информационно-аналитический бюллетень. 2021. № 10. С. 146-156. DOI: 10.25018/0236_1493_2021_10_0_146
- Ruonan Meng, Qinglin Zhao, Miaomiao Wu et al. A Survey and Analysis on Electricity Consumption of Raw Material Mill System in China Cement Industry between 2014 and 2019 // Sustainability. 2021. Vol. 13. Iss. 3. № 1126. DOI: 10.3390/su13031126
- Бельский А.А., Добуш В.С., Хайкал Ш.Ф. Эксплуатация однофазного автономного инвертора в составе ветроэнергетического комплекса малой мощности // Записки Горного института. 2019. Т. 239. С. 564-569. DOI: 10.31897/PMI.2019.5.564
- Сычев Ю.А., Зимин Р.Ю. Повышение качества электроэнергии в системах электроснабжения минерально-сырьевого комплекса гибридными фильтрокомпенсирующими устройствами // Записки Горного института. 2021. Т. 247. С. 132-140. DOI: 10.31897/PMI.2021.1.14
- Васильев Б.Ю., Шпенст В.А., Калашников О.В., Ульянов Г.Н. Обеспечение энергетической развязки электроприводов и сетей электроснабжения промышленных электротехнических комплексов // Записки Горного института. 2018. Т. 229. С. 41-49. DOI: 10.25515/PMI.2018.1.41
- Lvov V., Chitalov L. Semi-Autogenous Wet Grinding Modeling with CFD-DEM // Minerals. 2021. Vol. 11. Iss. 5. №485. DOI: 10.3390/min11050485
