Estimation of the influence of fracture parameters uncertainty on the dynamics of technological development indicators of the Tournaisian-Famennian oil reservoir in Sukharev oil field
Abstract
Issues related to the influence of reservoir properties uncertainty on oil field development modelling are considered. To increase the reliability of geological-hydrodynamic mathematical model in the course of multivariate matching, the influence of reservoir properties uncertainty on the design technological parameters of development was estimated, and their mutual influence was determined. The optimal conditions for the development of the deposit were determined, and multivariate forecasts were made. The described approach of history matching and calculation of the forecast of technological development indicators allows to obtain a more reliable and a less subjective history match as well as to increase the reliability of long-term and short-term forecasts.
Introduction
The need to streamline the development of oil and gas fields has increased. To improve the efficiency of design solutions and minimize the risks emerging in the development process, it is necessary to apply mathematical tools. One of the relevant tools for monitoring the state of the fields and designing the development is the geological-hydrodynamic mathematical reservoir model (HDM) [1, 2]. The HDM integrates all source data on the reservoir under study. The ability of the model to reproduce physicochemical, filtration and geomechanical processes depends on the amount and quality of the considered information [3]. Often, the reservoirs developed at the initial stage are not adequately explored, which leads to major uncertainties that can affect the technological and economic efficiency of the entire asset. Uncertainty is a state of complete or partial absence of information about the reservoir modelled which is necessary to understand a certain event, its consequences, and their probability.
E.A.Gladkov analysed the process of history matching to actual indicators [4]. It is noted that a high degree of the source data uncertainty when constructing a reservoir model makes history matching according to observation data a necessary step in modelling. At this stage, by solving the inverse problem, the reservoir porosity and permeability incorporated into the model are identified. This process is called history matching. Usually, the parameters that have the greatest uncertainty and a stronger influence on the decision are corrected; most often these are absolute and phase permeabilities, volume of edge water zone, pore compressibility factors, productivity and injectivity of wells. E.A.Gladkov also noted the importance of the stage of multivariate modelling with estimation of uncertainties of the geological model and the risks of well location. This stage is virtually standard abroad but is rarely used in Russia.
In [5], a quantitative assessment of uncertainties of oil reservoirs parameters is considered in detail. Primary task of the analysis of uncertainties and risks in estimation of reserves is quantification of the variation of parameters that affect the calculation of reserves. The main way to quantify the uncertainties is based on calculation of random errors, the calculation methods of which differ depending on the parameter investigated. Random errors, in contrast to systematic ones, inevitably occur when determining the volumetrics from geophysical data (seismic surveying, well logging) and the results of laboratory studies. In this paper, the assessment of random errors in reservoir parameters is considered as an uncertainty assessment for statistical Monte Carlo modelling or construction of a multivariate geological model.
In [6], an algorithm for estimating the uncertainty is considered, which includes the following steps: choosing the uncertainty of parameters that are critical for the problem solved; compiling a representative sample of experiments, on the basis of which the response surfaces will be constructed; constructing a response surface using neural networks; prediction of results taking into account the probabilistic distribution of uncertain parameters; analysis of results.
C.C.B.Cavalcante presented a data-based continuous learning algorithm for solving the tasks of the HDM history matching [7]. The algorithm consists of a two-stage optimization strategy in which different types of reservoir uncertainty are processed at each stage. The proposed approach constantly estimates the data of all model implementations and makes a strategic choice of input data that can be used for HDM.
Direction of a multivariate HDM is relevant. The main advantage of multivariate history matching is a possibility to implement many versions of the reservoir model and assess the risks probabilistically [8].
The purpose of the work is to increase the reliability of forecasting technological development indicators for reservoirs developed at an early stage. The following tasks have been set:
- Definition of the study object; assessment of exploration degree of reservoir properties.
- Construction of a single-medium HDM with indirect consideration of fractures. Determination of uncertainty parameters and the most sensitive HDM parameters for the target function by means of multivariate history matching.
- Assessment of exploration degree of fracturing parameters of reservoir.
- Construction of a dual-medium HDM. Determination of fracturing uncertainty parameters and sensitivity of fracturing uncertainty parameters to the target function by means of multivariate history matching.
- Determining the relationship between the fracturing uncertainty parameters and the calculated technological parameters of reservoir development.
Scientific novelty consists in development of a scientifically grounded systemic approach to forecasting the technological indicators of development under the conditions of source data uncertainty, which ensures an increase in reliability of long-term and short-term forecasts.
Methods
The study object was selected according to the following criteria: a significant level of recoverable and residual oil reserves; development of reservoir at the initial stage; a high degree of source date uncertainty. Based on these criteria, the Tournaisian-Famennian (T-Fm) reservoir of Sukharev oil field was considered.
The T-Fm reservoir is at the initial stage of development. According to a brief geological and physical characteristic (Table 1), it is clear that the T-Fm sheet is reservoir, massive, characterized by low reservoir properties. Oil is characterized as light, low-viscosity, sulphurous, paraffinic, resinous. The average productivity factor for the reservoir is high; at the same time, the reservoir is low-permeable. It can be assumed that the system of fractures through which fluid is filtered to production wells is well developed.
Table 2 presents the exploration degree of reservoir properties and physicochemical properties of reservoir fluids according to well logging data, well flow test (WFT), core studies, deep and wellhead oil samples. According to core studies, rocks of both effective and dense parts of reservoir are unevenly fractured. Layering fractures are differently oriented, intersecting, closed, healed with calcite, to 0.45 mm wide, openness < 0.01-0.12 mm.
Table 1
Geological-physical characteristics of the T-Fm reservoir
|
Parameters |
T-Fm |
|
Deposit type |
Sheet massive |
|
Reservoir type |
Carbonate |
|
Average effective net pay, m |
11.0 |
|
Porosity coefficient, unit fraction |
0.08 |
|
Reservoir saturation coefficient, unit fraction |
0.91 |
|
Permeability, µm2 |
0.002 |
|
Initial reservoir pressure, MPa |
21.46 |
|
Viscosity of oil in reservoir conditions, mPa∙s |
2.46 |
|
Density of oil in surface conditions, g/cm3 |
0.837 |
|
Sulphur content in oil, % |
1.47 |
|
Paraffin content in oil, % |
5.37 |
|
Productivity coefficient, m3/day∙MPa |
24.9 |
Table 2
Exploration degree of reservoir properties and physicochemical properties of formation fluids
|
Parameter |
Method |
Number |
Number |
|
Porosity |
Core |
148 |
4 |
|
Logging |
53 |
5 |
|
|
Permeability |
Core |
141 |
4 |
|
Logging |
53 |
5 |
|
|
Well flow test |
16 |
6 |
|
|
Oil saturation |
Core |
49 |
3 |
|
Logging |
43 |
5 |
|
|
Physicochemical properties of oil |
Deep samples |
5 |
4 |
|
Wellhead samples |
6 |
4 |
A small number of wells were studied. All wells are in the same area; thus, it is impossible to characterize the reservoir as a whole. It can be concluded that the T-Fm reservoir shows a high degree of source data uncertainty.
A single-medium HDM of three-phase filtration was constructed (Fig.1); current geological model of the reservoir under study was taken as a basis. Dependences of PVT properties of reservoir fluids are taken according to the research based on the latest project documentation. For distribution of filtration properties within the model volume, petrophysical dependence permeability – porosity constructed on the basis of core studies was applied. For this reservoir, the functions of relative phase permeabilities (RPP) in oil-water system were determined by the analytical method from capillary pressure curves using (the Bourdain method) due to the lack of direct research.
Based on the analysis of geological field description of the reservoir, it is assumed that rocks are fractured, while the average permeability of the reservoir taken from the results of core studies is characterized by a low value and does not reflect the production capabilities of wells [9, 10]. Therefore, to indirectly take into account the natural fracturing, it was decided to increase the values of absolute permeability of the reservoir in the area of production wells by applying a multiplier [11].
To find the optimal permeability value, the multiplier is set as an uncertainty. The choice of maximum and minimum permeability values was carried out taking into account actual measurements from core studies, well logging, well flow test as well as using these comparable reservoirs [12, 13] (Table 3).
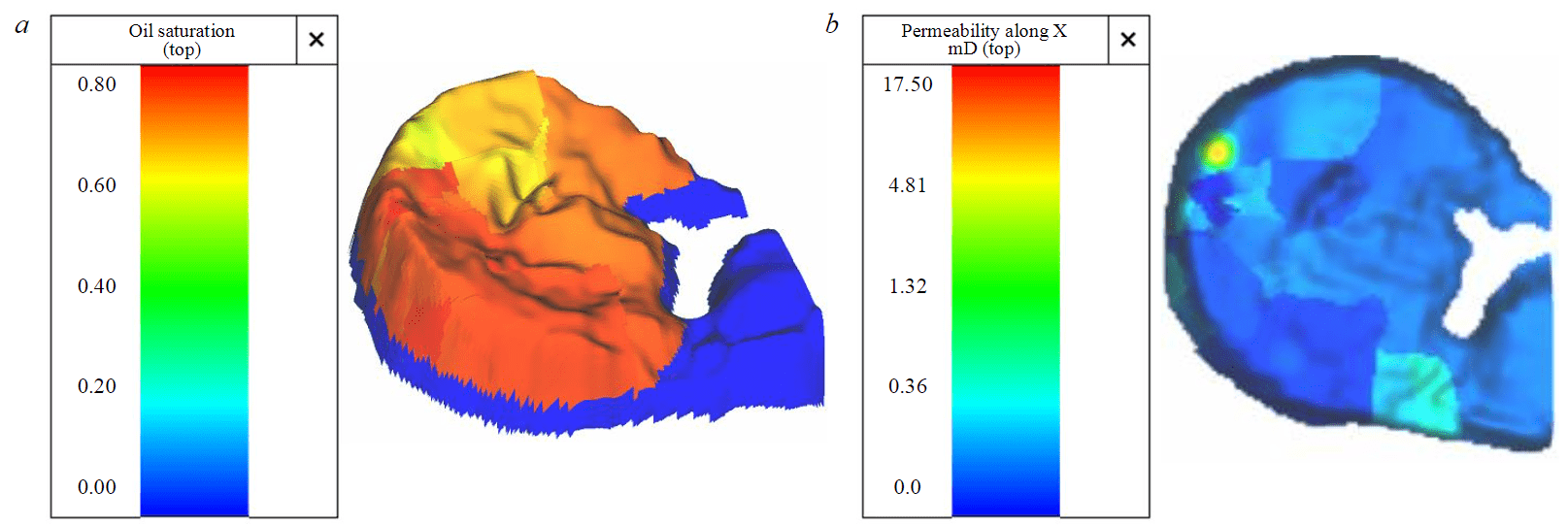
Fig.1. General view of single-medium reservoir model: cube of initial oil saturation (а) and permeability (b)
Table 3
Range of uncertainty parameters
|
Uncertainty parameters |
Value of parameter |
||
|
Minimum |
Average |
Maximum |
|
|
Aquifer permeability k |
2 |
111 |
221 |
|
Aquifer porosity m |
0.06 |
0.08 |
0.11 |
|
Average effective aquifer thickness h |
3.2 |
11 |
19.8 |
|
Absolute permeability multiplier (presence of fracture systems) |
1.5 |
8.2 |
15 |
|
Uncertainty of RPP |
– |
– |
– |
|
Skin factor |
–5 |
0 |
5 |
|
Well-reservoir connectivity |
0.5 |
5 |
10 |
Further, as an uncertainty parameter, RPP functions of oil-water system are set to select the optimal dependence that closely characterizes the displacement process in fractured reservoirs.
Influence of the edge water zone has a high degree of uncertainty, which is adjusted in the HDM proceeding from actual dynamics of reservoir pressure [14, 15]. It is possible to adapt the influence of water edge zone by average permeability, porosity, and effective thickness beyond the oil pool outline; therefore, these parameters were chosen as uncertainty. Variation range of these parameters was selected based on dynamics of actual reservoir pressure measurements and with involvement of comparable reservoirs. Such parameters as skin factor and well-reservoir connectivity characterizing well productivity were also chosen as uncertainty [16]. These parameters are dynamic in the development process, so they have a high degree of uncertainty.
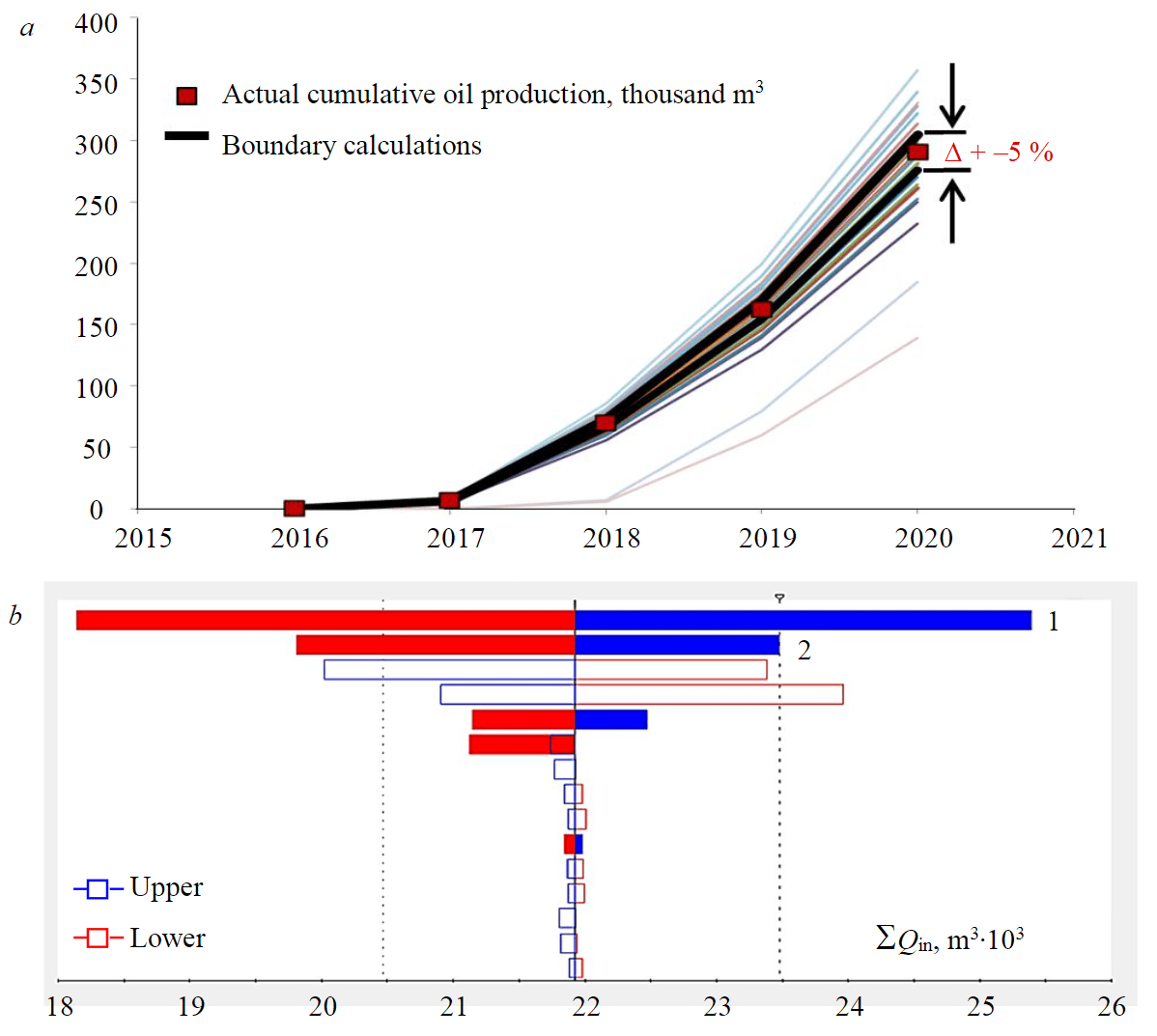
Fig.2. Estimation of the influence of uncertainty parameters on oil production: а – schedule on cumulative design oil production of multivariate history matching; b – tornado diagram 1 – multiplier of absolute permeability 2 – RPP multiplier
The process of HDM adjustment to data on the production and injection wells operation is defined as history matching [17]. Quality of history matching is checked in accordance with current temporary regulations for assessing the quality and injectivity of three-dimensional digital geological-hydrodynamic models. The regulations imply that the deviation of the estimated cumulative production of liquid and oil should not exceed 5 %, and the deviation of the estimated annual production of liquid and oil – 10 %.
At this stage of work, a multivariate history matching was carried out taking into account the selected range of uncertainty parameters in the Enable (Roxar) software. Next, the quality of all calculations was assessed in accordance with current regulatory document, and the sensitivity was analysed which showed the degree of influence of each uncertainty parameter on levels of cumulative oil production [18]. A total of 95 calculations were made, of which 32 are within the scope of the regulation, i.e., history matching has 32 equiprobable solutions. Black lines show the boundary calculations, and the calculations distributed above or below the boundary ones are not included in the current regulation (Fig.2, a). It can be seen from the tornado diagram that the most influencing uncertainty parameters is an absolute permeability multiplier, which indirectly considers the presence of fracturing, and the RPP dependence (Fig.2, b). In view of the fact that core studies revealed fracturing and the accepted average permeability for the reservoir identified by well logging is characterized by low values and amounts to 2 mD, and the WFT recorded an average value for the reservoir equal to 123 mD, it can be concluded that filtration mostly occurs via a well-developed system of fractures [19, 20]. To approximate the HDM to the characteristics of a real reservoir, it is necessary to construct a dual-medium HDM, which considers filtration via the matrix and fractured components of reservoir [21].
For a comprehensive study of fracturing of the T-Fm reservoir, well logging, well flow test, studies of directed core and 3D seismic were considered [22]. Since fracture parameters are dynamic depending on reservoir pressure, it was decided to take well logging data, core studies and 3D seismic data as initial fracturing conditions and use well flow test to consider the effect of reservoir pressure. Special logging (VAK-D and EMS) carried out in three wells 4, 113, 215, and studies of directed core in wells 2, 3 made it possible to determine the intervals and direction of fracturing [23].
Hydrodynamic studies were performed in all operating wells using pressure recovery curve (PRC) method. PRC during processing (in accordance with the Warren – Root model) confirmed the occurrence of fracturing [24]. Processing of PRC according to the Warren – Root method makes it possible to determine several fracture parameters and record their change in accordance with reservoir pressure dynamics [25]. Fracture indices were calculated in accordance with the Warren – Root model using the example of wells 3, 118, 121 of the T-Fm reservoir (Table 4).
Table 4
Results of PRC treatment in accordance with Warren – Root model
|
Well number |
Year |
qin.fl.rate, m3/day |
Рin.r.pr, MPa |
Win.fr.op, µm |
qс.f rate, m3/day |
Рc.r.pr, MPa |
Wc.fr.op, µm |
|
|
3 |
2017 |
83.7 |
21.46 |
40.2 |
53.5 |
13.39 |
68.6 |
|
|
118 |
2018 |
62.5 |
8.5 |
8.66 |
30.3 |
|||
|
121 |
2018 |
67.7 |
67.3 |
15.49 |
196.7 |
|||
Notes: qin.fl.rate – initial fluid rate; Рin.r.pr – initial reservoir pressure; Win.fr.op – initial fracture openness; qс. fl.rate – current fluid rate; Рc.r.pr – current reservoir pressure; Wc.fr.op – current fracture openness.
One of notable features of the development of fractured reservoirs are the pronounced deformation processes occurring at a decreasing reservoir pressure. As a result, filtration characteristics can change significantly during exploitation of the field [26]. An example of the T-Fm reservoir of Sukharev field is the area of well 118. This area is characterized by geological isolation; therefore, there is a strong decrease in reservoir pressure below the saturation pressure. Figure 3 shows the dynamics of changes in total permeability and reservoir pressure.
To consider the deformation processes, a dependence of changes in fracture permeability on reservoir pressure was obtained based on methodological provisions [27]. The main theoretical dependencies are:
where Ktot is total permeability; Km – matrix permeability; βfr – fracture compressibility factor; Kfr – fracture permeability.
These dependencies imply that for keeping vertical fractures open, reservoir pressure should exceed lateral rock pressure, which is determined from the formula:
where Klat is the coefficient of lateral expansion; ν – Poisson's ratio; mabs – total porosity of the rock, %.
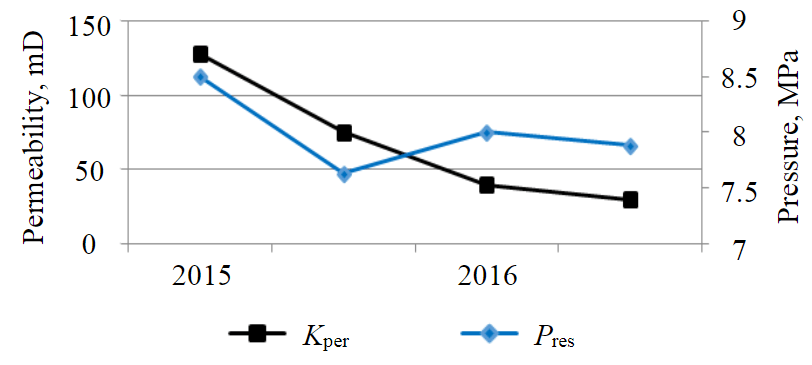
Fig.3. Reservoir pressure change dynamics and total reservoir permeability in area of well 118
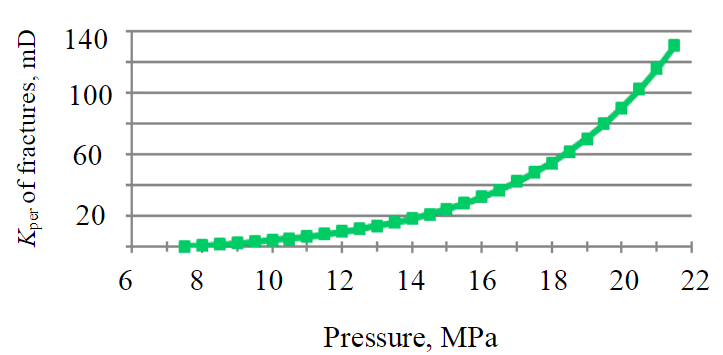
Fig.4. Dependence of changes in fracture permeability on reservoir pressure
According to the statistical data on comparable fields, for the T-Fm reservoirs vertical rock pressure at average rock density of 2,450 kg/m3 is 48.2 MPa. At average mabs = 11 %, ν = 0.134, and Klat = = 0.155 values lateral rock pressure is 7.45 MPa, which is consistent with the results presented in [28].
Based on the above dependencies, an averaged theoretical curve of changes in fracture permeability values depending on reservoir pressure was obtained (Fig.4).
To create a dual-medium model, FracaFlow software (Beicip-Franlab) was used, which allows analysing a set of source data on fracturing, creating a discrete fracture model (DFN-model), and distributing fracturing within the reservoir volume [29]. At the first stage, as a result of analysing special logging data and core, four groups of fractures were identified according to the Schmidt diagram. Fracture density of the four families is determined, and on the basis of seismofacies analysis, a relationship is established between fracture zones and facies. Next, a DFN-model is constructed applying the stochastic method in a reduced part of the reservoir (near-wellbore zone), which is used to calibrate the statistical parameters of the fracture system (average orientation, length, etc.) and the parameters used in calculating the equivalent properties (porosity, permeability tensors, etc.).
For the distribution of fracturing within the reservoir volume a discrete parameter was used which characterizes the probability distribution of fractures in each block of the grid. The parameter was obtained at the stage of geological modelling by superimposing the results of seismofacies analysis on a three-dimensional grid and the studies on distinguishing low-porosity carbonate reservoirs with secondary porosity based on well logging results. The obtained parameter was loaded into FracaFlow as a three-dimensional cube and used as a corrective property for the probability of fractures.
At the first stage of constructing the dual-medium HDM, it is necessary to determine the type of model. For this, the Nelson classification of carbonate fractured reservoirs was used [30]. It was ascertained that the filtration of reservoir fluid mainly occurs via fractures. The main reserves calculated by the volumetric method are concentrated in the pore component of the reservoir. Based on a comparison of the classification and filtration processes occurring in the T-Fm reservoir, it was decided to perform calculations on the dual-porosity HDM.
In the process of constructing the dual-porosity HDM the grid is duplicated in order to assign properties for the matrix and fracture components. At the next stage, deformation processes are modelled. To consider deformation, a certain dependence of fracture permeability on current reservoir pressure was taken as a basis and converted into a dependence of the ratio of current fracture permeability to the initial one on the value of current reservoir pressure. In the hydrodynamic model, this dependence was assigned as a KVSP table [31]. Since reservoir pressure has different dynamics in each zone of production wells, it was decided to set the dependence of fracture deformation for each region of production and injection wells [32]. The most important characteristic of multiphase filtration is RPP for fluids saturating the void space [33]. The functions obtained as a result of laboratory core studies were taken as basic dependences of RPP for the pore component of carbonate reservoir. Lack of data on the RPP in the fracture component complicates construction of the dual-porosity model. Shape of the RPP curves for fractures is taken as a cross [34].
When creating a dual-porosity model, it becomes necessary to set the Sigma parameter, which characterizes a hydrodynamic association between the matrix and the fracture. This parameter was selected empirically using the data obtained during the PRC processing in accordance with Warren – Root model focusing on reproduction of actual well performance on dual-porosity hydrodynamic model.
For fractures, as a rule, the saturation value is judgement-based [35]. Considering multiple opinions on determining the value of the initial saturation coefficient Kin, the value of Kin in fractures is taken as 0.9. Such high oil saturation value does not have a decisive influence on overall reserves of the reservoir, since average fracture porosity is 0.01 unit fraction. Thus, a HDM with dual-porosity system was constructed (Table 5). General view of the dual-medium HDM cubes is shown in Fig.5.
Table 5
Comparison of HDM characteristics
|
Parameters |
HDM within design technical documentation |
Dual-porosity HDM |
|
|
Matrix porosity, unit fractions |
0.08 |
0.08 |
|
|
Fracture porosity, unit fractions |
0.01 |
|
|
|
Oil saturation of matrix, unit fractions |
0.91 |
0.745 |
|
|
Oil saturation of fractures, unit fractions |
0.9 |
|
|
|
Geological oil reserves in pore part of reservoir, % |
100 |
86.2 |
|
|
Geological oil reserves in fractured part of reservoir, % |
13.8 |
|
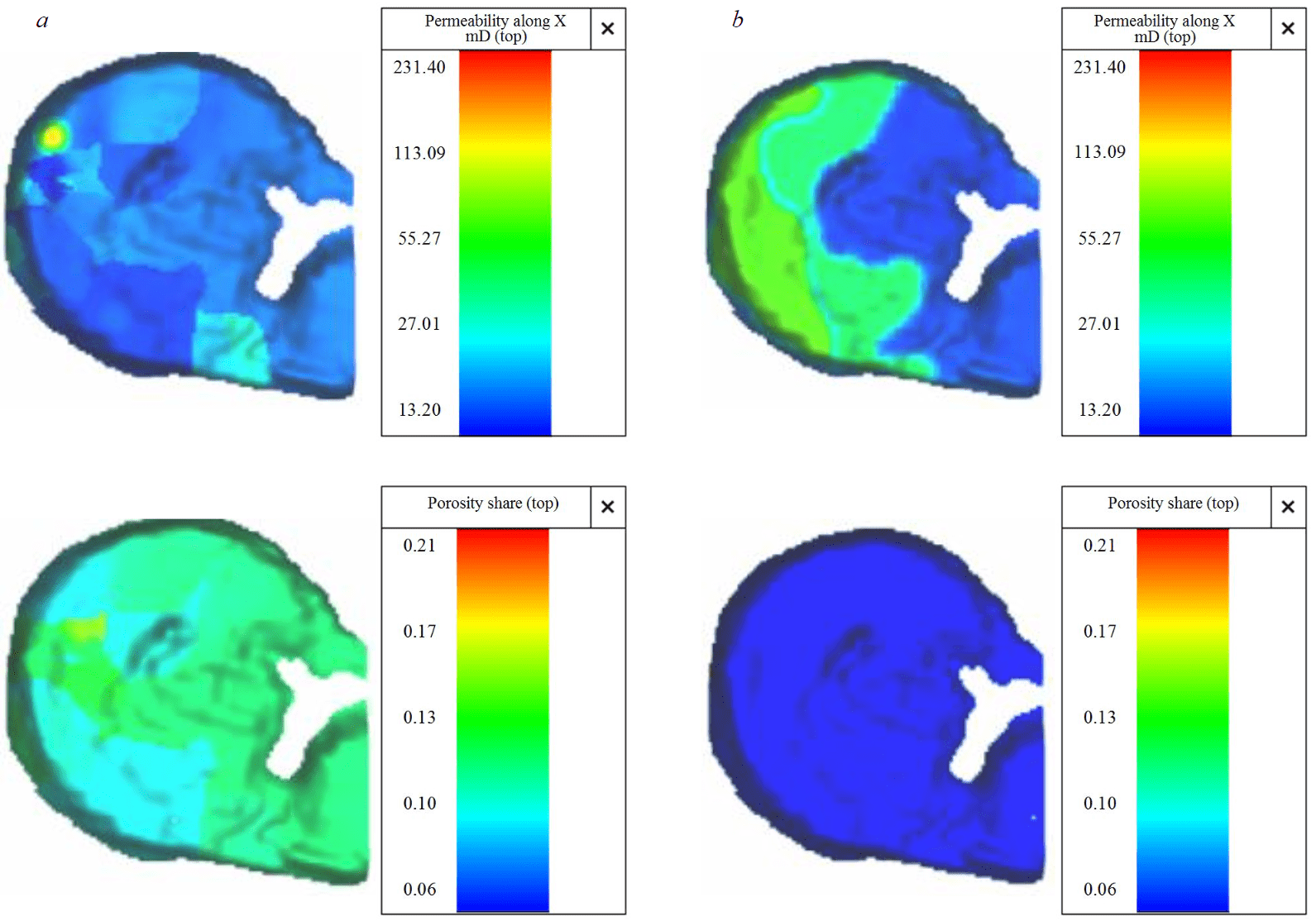
Fig.5. General view of dual-medium reservoir model: а – permeability cube of pore and fracture component; b – porosity cube of pore and fracture component
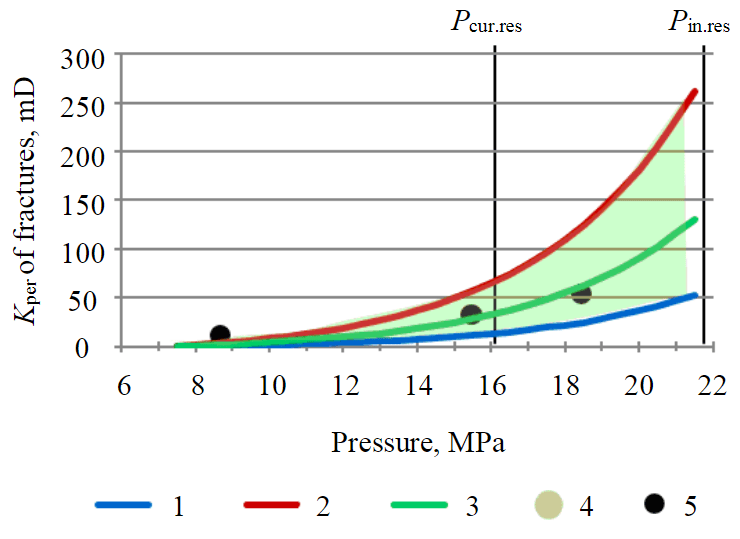
Fig.6. A set of dependences of changes in fracture permeability on reservoir pressure 1-3 – Kper of fractures, mD: 1 – min, 2 – max, 3 – average; 4 – distribution area; 5 – Kper after Warren – Root model, mD
For a more detailed study of the influence of fractures on oil production levels, fracture parameters are considered as uncertainty. Based on the analysis of source data necessary to construct a dual-medium model it was found that the parameter characterizing the deformation process has a high degree of uncertainty, since it was obtained from theoretical dependencies and averaged estimate parameters. It is necessary to consider the range of values of estimate parameters and the fact that in the area of each production well different permeability values of the matrix component of carbonate reservoir are recorded. Thus, there is a possibility of multiple dependences of a change in fracture permeability from reservoir pressure. Figure 6 shows the dependences characterized by the maximum, minimum and average values of fracture permeability and highlights the area within which the dependences can be distributed.
Sigma coefficient which characterizes the relationship between the matrix and fractures was selected empirically using the data obtained during PRC processing (in accordance with Warren – Root model; it can be concluded that this fracture parameter is highly uncertain [36]. As an uncertainty, the fracture compressibility coefficient was set, since this parameter was obtained from PRC interpretations in accordance with Warren – Root model. The range of changes of these parameters was chosen based on PRC processing with involvement of comparable reservoirs.
Range of uncertainty parameters values (minimum/average/maximum): matrix-to-fracture connectivity (Sigma) – 1/5/10; fracture compressibility coefficient βfr – 0.078/0.114/0.15 MPa–1.
To analyse the sensitivity and identify the parameter that has the greatest impact, a multivariate history matching was accomplished under conditions of fracturing parameters uncertainty. 95 calculations were performed, 42 of them comply with the regulations. According to results of sensitivity analysis of uncertainty parameters to oil production levels, it was found that deformation of the fractured component had the greatest effect on oil production levels.
Other parameters had a minor impact on cumulative oil production levels; therefore, to identify the dependence of deformation processes on cumulative oil production, the parameters were excluded from uncertainties for prediction calculations [37].
Dependence of deformation impact on oil production levels was determined by multivariate forecasts under conditions of deformation uncertainty. To avoid a possible error in assessing the effect of fracture deformation on oil production levels, a multivariate forecast was made for the current development system, i.e., only for the studied part of the reservoir. During multivariate modelling, it was ascertained that with a dependence characterizing the maximum values of fracture permeability, no maximum oil production is recorded, which indicates premature flooding. By comparing oil production and fracture permeability at fixed current reservoir pressure, an estimated empirical dependence of cumulative oil production on current fracture permeability was obtained. The dependence shows the range of fracture permeability (27.3-48.2 mD), at which the maximum oil production is recorded. Areas of the most intense fracture closure and premature flooding were identified [38]. Coming back to the dependence of fracture deformation, it is possible to determine the range of reservoir pressure (14.8-17.1 MPa), at which the maximum oil production is predicted (Fig.7).
A multivariate forecast under conditions of uncertainty of the dependence of a change in permeability of the fracture component of reservoir on reservoir pressure values made it possible to determine the rational reservoir pressure, at which an intense closure of fractures and premature flooding are not recorded.
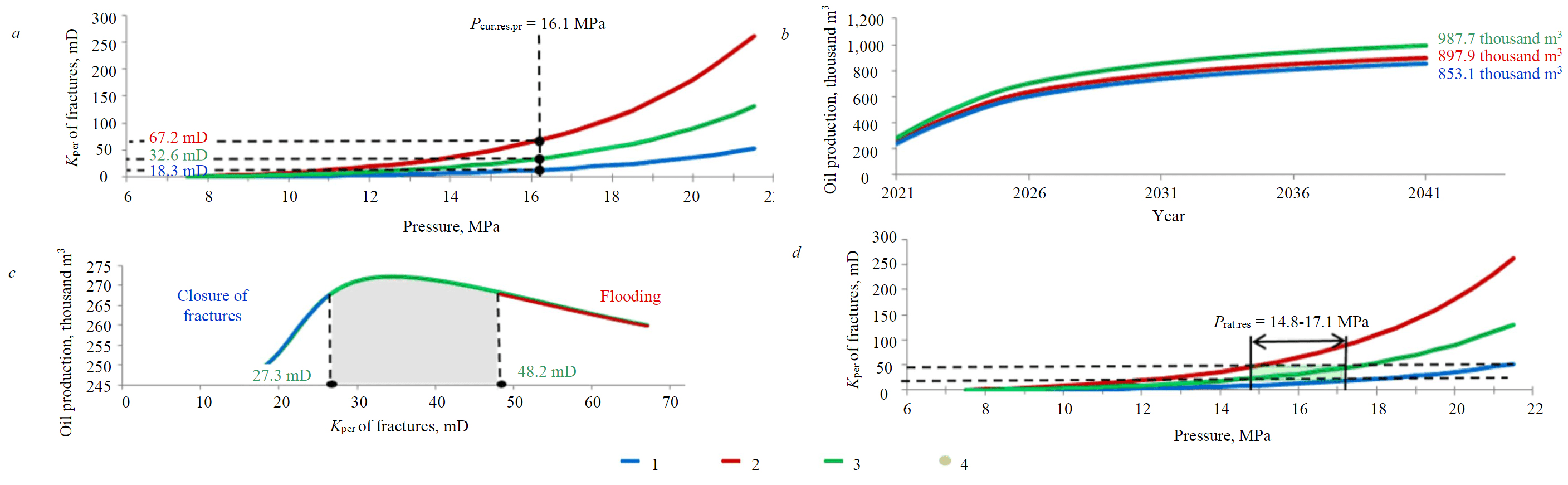
Fig.7. Results of multivariate forecast for HDM: a – dependences of change in fracture permeability from reservoir pressure values; b – cumulative oil production for different values of fracture permeability; c – dependence of cumulative oil production on fracture permeability; d – dependence of changes in fracture permeability on reservoir pressure values with a mark of the zone characteristic of maximum cumulative oil production 1-3 – Kper of fractures, mD: 1 – min, 2 – max, 3 – average; 4 – Prat.res zone
Discussion of results
The study object was chosen according to criteria that provide a lot of uncertainties which can significantly affect the technological and economic efficiency of the asset. Primary parameters of uncertainty and their ranges are established according to actual studies with involvement of comparable reservoirs. A multivariate history matching was accomplished; using its results 32 solutions were found. To determine the most significant uncertainty parameters, the sensitivity analysis to oil production levels was performed. It was ascertained that the values of absolute reservoir permeability affect oil production levels and oil recovery factor. Accordingly, this parameter requires a more detailed study using reservoir fracturing data. With the help of a comprehensive analysis of the results of hydrodynamic, core, geophysical and seismic studies, a significant effect of fracturing on reservoir permeability values was established. Thus, it was decided to construct the dual-medium model that describes the filtration processes in the matrix and fractured components of the reservoir.
As a result of collection and analysis of source data, uncertainty parameters of fractures were determined. In the course of multivariate history matching and sensitivity analysis, it was revealed that the dependence of a change in permeability on reservoir pressure values has a decisive influence on oil production levels. It was decided only to evaluate the effect of fracture permeability dependence on reservoir pressure values on oil production levels. According to the results of a multivariate forecast for 20 years, the optimal reservoir pressure has been determined, at which the maximum oil production levels will be recorded. Maintaining reservoir pressure in the identified range will ensure a rational development of this reservoir and the maximum oil recovery factor.
Conclusion
Consideration of uncertainty parameters in the HDM allows setting model parameters that have a significant impact on oil production levels, which serves as the basis for its further detailed and comprehensive study. The use of multivariate modelling technology under conditions of model parameters uncertainty makes it possible to obtain a set of equally probable implementations of hydrodynamic reservoir models and evaluate the technological efficiency of the reservoir considering the risks of further non-confirmation of reservoir properties. Multivariate modelling made it possible not only to reduce the degree of uncertainty by means of history matching, but also to identify the range of rational reservoir pressure, which will ensure the maximum oil production level for the reservoir under consideration.
References
- Dikalov D.V. Comprehensive Approach to the Construction of a Permanently Working Geological-Technological Model on the Example of the Western-Tugrovsky Deposit. Geology, Geophysics and Development of Oil and Gas Fields. 2018. N 9, p. 34-40 (in Russian). DOI: 10.30713/2413-5011-2018-9-34-40
- Bozhenyuk N.N., Strekalov A.V. Some history matching techniques for the hydrodynamic model. Neftegazovoe delo. 2016. Vol. 14. N 2, p. 42-49 (in Russian).
- Kozyrev N.D., Kochnev A.A., Mengaliev A.G. et al. Refinement of the Geological and Hydrodynamic Model of a Complex Oil Reservoir by Means of Acomprehensive Data Analysis. Bulletin of the Tomsk Polytechnic University. Geo Аssets Engineering. 2020. Vol. 331. N 10, p. 164-177 (in Russian).
- Gladkov E.A., Gladkova E.E. Ambiguity of geological-technological information in the history matching process. Burenie i neft. 2008. N 10, p. 40-41(in Russian).
- Kuznetsova Yu.V. Specific features of variable geological modelling. Molodoi uchenyi. 2019. N 24 (262), p. 56-58 (in Russian).
- Maiorov K.N. Use of machine learning algorithms for solving problems in oil and gas industry. Intellektualnye sistemy v proizvodstve. 2021. Vol. 19. N 3, p. 55-64 (in Russian). DOI: 10.22213/2410-9304-2021-3-55-64
- Cavalcante C.C.B., de Souza C.C., Maschio C. et al. A learning-from-data approach with soft clustering and path relinking to the history-matching problem. Journal of Petroleum Exploration and Production. Vol. 11. Iss. 7, p. 3045-3077. DOI: 10.1007/s13202-021-01176-4
- Olenchikov D.M. Interactive stepwise calculation as a basis for automating history matching of hydrodynamic models with a large number of wells. Nauchno-tekhnicheskii vestnik OAO “NK “Rosneft”. 2007. N 2, p. 38-40 (in Russian).
- Galkin S.V., Krivoshchekov S.N., Kozyrev N.D., Kochnev A.A., Mengaliev A.G. Accounting of geomechanical layer properties in multilayer oil field development. Journal of Mining Institute. 2020. Vol. 244, p. 408-417. DOI: 10.31897/PMI.2020.4.3
- Gimazov A.A., Fokeeva E.E., Khairullin R.U., Minikhanov D.M. Integrated Approach to Adapting and Forecasting the Parameters of Secondary Porosity for the R. Trebs Oilfield. Oil Industry. 2018. N 10, p. 20-23 (in Russian). DOI: 10.24887/0028-2448-2018-10-20-23
- Ermekov R.I., Korovin M.O., Merkulov V.P., Chernova O.S. Construction of Anisotropy Simulation Model and Studying the Effect of Permeability Anisotropy on the Example of Field Unit Modeling. Bulletin of the Tomsk Polytechnic University. Geo Аssets Engineering. 2019. Vol. 330. N 11, p. 86-93 (in Russian). DOI: 10.18799/24131830/2019/11/2351
- Akmal Aulia, Daein Jeong, Ismail Mohd Saaid et al. A Random Forests-based sensitivity analysis framework for assisted history matching. Journal of Petroleum Science and Engineering. 2019. Vol. 181. N 106237. DOI: 10.1016/j.petrol.2019.106237
- Katterbauer K., Arango S., Sun S., Hoteit I. Multi-data reservoir history matching for enhanced reservoir forecasting and uncertainty quantification. Journal of Petroleum Science and Engineering. 2015. Vol. 128, p. 160-176. DOI: 10.1016/j.petrol.2015.02.016
- Krasovskiy A., Sventskiy S., Shandrygolov Z., Zimin E. Geology and Field Data Processing using Neural Networks for Production History Matching. Burenie i neft. 2014. N 10, p. 44-46 (in Russian).
- Repina V., Galkin V., Galkin S. Complex Petrophysical Correction in the Adaptation of Geological Hydrodynamic Models (on the Example of Visean Pool of Gondyrev Oil Field). Journal of Mining Institute. 2018. Vol. 231, p. 268-274. DOI: 10.25515/PMI.2018.3.268
- Martyushev D.A., Martyushev D.A. Assessment of Informative Value in Determination of Reservoir Filtration Parameters Based on Interpretation of Pressure Stabilization Curves. Bulletin of the Tomsk Polytechnic University. Geo Аssets Engineering. 2019. Vol. 330. N 10, p. 26-32 (in Russian). DOI: 10.18799/24131830/2019/10/2295
- Chernykh I.A., Galkin V.I., Ponomareva I.N. Comparative analysis of the methods for defining bottom hole pressure at well operation of Shershnevsky field. Bulletin of the Tomsk Polytechnic University. Geo Assets Engineering. 2017. Vol. 328. Iss. 8, p. 41-47.
- Gutman I.S, Balaban I.J. Methods of Risks and Uncertainties Evaluation According to Spe-Prms Classification of Reserves and Resources. Oil Industry. 2014. N 1, p. 88-93 (in Russian).
- Akhmerova A.V., Gallyamova D.Ch., Melnikov A.V., Kharitontseva P.A. Evolution of the conceptual model of a low-permeability fractured reservoir. Bulletin of the Tomsk Polytechnic University. Geo Assets Engineering. 2020. Vol. 331. N 9, p. 39-48 (in Russian). DOI: 10.18799/24131830/2020/9/2802
- Repina V.A., Galkin V.I., Galkin S.V. Complex petrophysical correction in the adaptation of geological hydrodynamic models (on the example of Visean pool of Gondyrev oil field). Journal of Mining Institute. 2018. Vol. 231, p. 268-274. DOI: 10.25515/PMI.2018.3.268
- Huafeng Sun, Hadi Belhaj, GuoTao et al. Rock properties evaluation for carbonate reservoir characterization with multi-scale digital rock images. Journal of Petroleum Science and Engineering. 2019. Vol. 175, p. 654-664. DOI: 10.1016/j.petrol.2018.12.075
- Benjamin Brigaud, Benoît Vincent, Christophe Durlet et al. Characterization and origin of permeability–porosity heterogeneity in shallow-marine carbonates: From core scale to 3D reservoir dimension (Middle Jurassic, Paris Basin, France). Marine and Petroleum Geology. 2014. Vol. 57, p. 631-651. DOI: 10.1016/j.marpetgeo.2014.07.004
- Denney D. Digital core laboratory: reservoir-core properties derived from 3D images. Journal of Petroleum Technology. 2004. Vol. 56. Iss. 5, p. 66-88. DOI: 10.2118/0504-0066-JPT
- Martiushev D.A., Lekomtsev A.V., Kotousov A.G. Determining Openness and Compressibility of Natural Fractures of Carbonate Reserves in the Logovskoye Deposit. Perm Journal of Petroleum and Mining Engineering. 2015. Vol. 14. N 16, p. 61-69 (in Russian). DOI: 10.15593/2224-9923/2015.16.7
- Karev V.I., Kovalenko Yu.F., Zhuravlev A.B., Ustinov K.B. Model of Filtration to the Well Accounting for Dependence of Filtration on Stresses. Processes in GeoMedia. 2015. N 4, p. 34-44 (in Russian).
- Kashnikov Ju.A., Ashihmin S.G., Shustov D.V. et al. Improving the efficiency of hydrocarbon field development based on comprehensive geomechanical studies. Oil Industry. 2019. N 3, p. 66-69 (in Russian). DOI: 10.24887/0028-2448-2019-3-66-69
- Takougang E.M.T., Bouzidi Y., Ali M.Y. Characterization of small faults and fractures in a carbonate reservoir using waveform inversion, reverse time migration, and seismic attributes. Journal of Applied Geophysics. 2019. Vol. 161, p. 116-123. DOI: 10.1016/j.jappgeo.2018.12.012
- Meng Chen, Zhifang Zhou, Lei Zhao et al. Study of the Scale Effect on Permeability in the Interlayer Shear Weakness Zone Using Sequential Indicator Simulation and Sequential Gaussian Simulation. Water. 2018. Vol. 10. Iss. 6. N 779. DOI: 10.3390/w10060779
- Zhen Yin, Tao Feng, Colin MacBeth. Fast assimilation of frequently acquired 4D seismic data for reservoir history matching. Computers & Geosciences. 2019. Vol. 2019. Iss. 128, p. 30-40. DOI: 10.1016/j.cageo.2019.04.001
- Mohamed Soufiane Jouini, Ali AlSumaiti, Moussa Tembely et al. Permeability upscaling in complex carbonate samples using textures of micro-computed tomography images. International Journal of Modelling and Simulation. 2020. Vol. 40. Iss. 4, p. 245-259. DOI: 10.1080/02286203.2019.1596728
- Sablok R., Aziz K. Upscaling and Discretization Errors in Reservoir Simulation. Petroleum Science and Technology. 2008. Vol. 26. Iss. 10-11, p. 1161-1186. DOI: 10.1080/10916460701833863
- Osho Ilamah. A multiobjective dominance and decomposition algorithm for reservoir model history matching. Petroleum. 2019. Vol. 5. Iss. 4, p. 352-366. DOI: 10.1016/j.petlm.2019.07.004
- Khasanov D.I., Lonshakov M.A. Investigation of scale effect and the concept of an elementary representative volume of rocks in relation to porosity. Georesursy. 2020. Vol. 22. N 4, p. 55-69 (in Russian). DOI: 10.18599/grs.2020.4.55-69
- Ching-Hsien Liu, Krishna Nunna, Imroj Syed, King M.J. Evaluation of Upscaling Approaches for the Amellago Carbonate Outcrop Model. SPE Europec featured at 81st EAGE Conference and Exhibition, 3-6 June 2019, London, UK. OnePetro, 2019. N SPE-195560-MS. DOI: 10.2118/195560-MS
- Ipatov A.I., Kremenetskiy M.I., Gulyaev D.N. et al. Eservoir Surveillance When Hard-To-Recover Reserves Developing. Oil Industry. 2015. N 9, p. 68-72 (in Russian).
- Putilov I.S., Popov N.A., Yuriev A.V., Chizhov D.B. Scale effect on the reservoir permeability and porosity over a wide range of void structure (example of the Tedinskoye oil field). Arctic Evironmental Research. 2019. Vol. 19. Iss. 3, p. 93-98. DOI: 10.3897/issn2541-8416.2019.19.3.93
- Kozyrev N.D., Vishnyakov A.Yu., Putilov I.S. Evaluation of the influence of uncertainty parameters on forecasting of development indicators. Nedropolzovanie. 2020. Vol. 20. N 4, p. 356-368 (in Russian). DOI: 10.15593/2712-8008/2020.4.5
- Nasybyllin A.V., Shutov A.A., Antonov O.G. Raising Efficiency of Oil Production While Optimizing Water-Flooding System on the Basis of Neironet and Hydrodynamic Modeling. Equipment and Technologies for Oil and Gas Complex. 2014. N 5, p. 47-51 (in Russian).
