Совершенствование метода оценки изгибных напряжений в стенке подземного трубопровода
- 1 — д-р техн. наук ректор Ухтинский государственный технический университет ▪ Orcid
- 2 — аспирант Санкт-Петербургский горный университет ▪ Orcid
Аннотация
Приведены краткие сведения о современных методах определения изгибных напряжений протяженных участков подземных магистральных трубопроводов без доступа к образующей трубопровода. Обоснована необходимость модернизации методов, основанных на определении конфигурации оси трубопровода с поверхности грунта с последующим расчетом по полученным данным изгибных напряжений. Предложена математическая модель, позволяющая при планировании исследования рассчитать оптимальные параметры съемки оси трубопровода с поверхности грунта для трубопровода произвольной конфигурации и глубины залегания. Проведены стендовые испытания трассоискателя БИТА-1 для определения погрешности в измерении глубины залегания оси трубопровода. Доказано, что отклонения показаний трассоискателя относительно истинных значений в узких интервалах глубин залегания подчиняются нормальному распределению и не меняют свой знак. Представлены доверительные интервалы погрешности в определении глубины залегания оси трубопровода для прибора БИТА-1.
Введение
Углеводороды играют важную роль в современном топливно-энергетическом балансе, являясь неотъемлемой частью современной промышленности [1-3]. С помощью магистральных трубопроводов возможна постоянная и бесперебойная поставка углеводородов от мест добычи до потребителя [4, 5]. Поэтому важное место занимают методы и технологии, позволяющие осуществлять надежную и исправную работу магистральных трубопроводов.
Аварии на действующих газонефтепроводах связаны с колоссальным уроном окружающей среде и огромным материальным ущербом [6-8], вызванными потерями перекачиваемого продукта и сбоями в сроках поставок, а также остановкой всей системы для проведения внеплановых ремонтов [9, 10].
К наиболее трудно прогнозируемым типам аварий относятся аварии, связанные с воздействием на трубопровод внешних силовых факторов, которые приводят к образованию ненормативного изгиба трубопровода [11-13]. Как правило, при проектировании прочность трубопровода закладывается в расчет толщины стенки труб [14-16], который учитывает воздействие постоянных нагрузок [17]. Однако данный расчет не берет во внимание возможность влияния на трубопровод иных нагрузок и воздействий, возникающих в период эксплуатации, поскольку их учет в произвольный момент времени не поддается математическому описанию [18-20]. Реальные условия эксплуатации магистральных газонефтепроводов различны, что подтверждается большим числом поправочных коэффициентов, вводимых в прочностные расчеты.
Несмотря на существование обширного числа методов оценки напряженно-деформированного состояния стальных конструкций [21, 22], большинство из них малоприменимы к магистральным трубопроводам из-за сложности определения механических напряжений на протяженных участках подземных трубопроводов, а периодичность внутритрубной диагностики не позволяет отнести ее к системам постоянного мониторинга технического состояния трубопровода. Поэтому необходима оценка фактического состояния подземного газонефтепровода в течение всего периода его эксплуатации в произвольный момент времени в соответствии с изменяющимися инженерно-геологическими условиями. В данных условиях методы, позволяющие оценить техническое состояние в произвольный момент времени, приобретают особую актуальность.
Современные методы и проблемы определения технического состояния протяженных участков подземных трубопроводов
Под техническим состоянием трубопровода обычно понимается совокупность факторов, влияющих на надежную и безотказную эксплуатацию трубопровода. Одним из наиболее важных параметров, определяющих техническое состояние трубопровода, считается напряженно-деформирование состояние (НДС) металла стенок трубопровода, которое, в свою очередь, также зависит от большого количества нагрузок и воздействий, оказывающих влияние на трубопровод. Среди основных источников напряженного состояния можно выделить изгибные напряжения [11, 14, 18]. Рассмотрим основные методы определения НДС на участках подземных трубопроводов, не требующие постоянного доступа к образующей трубы.
Хорошо зарекомендовали себя методы, основанные на измерении физических полей трубопровода: магнитометрические [16, 23], с использованием интеллектуальных вставок [24, 25], ультразвуковые [25]. При наличии информации о начальном напряженном состоянии данное семейство методов является самым точным, а некоторые методы [23, 26] показывают высокую точность определения НДС без информации о начальном напряженном состоянии. Самым существенным недостатком этих методов является необходимость доступа к образующей трубопровода для возможности установки специализированного оборудования. Кроме того, их применение подразумевает наличие априорных знаний об участках трубопровода, в которых возможно появление дополнительных изгибающих напряжений, однако распределение данных участков по длине трубопровода не носит постоянный характер при его эксплуатации.
Расчет НДС трубопровода возможен по нормативным стандартам при наличии информации о значениях изгибных напряжений, действующих на подконтрольных участках [16, 27]. В последнее время большое внимание уделяется методам, основанным на использовании волоконно-оптических датчиков, позволяющих дистанционно оценивать изгиб трубопровода в произвольный момент времени при его эксплуатации [19, 28, 29]. Данная система, например, применяется для мониторинга особо опасных участков магистрального газопровода «Сахалин – Хабаровск – Владивосток» диаметром 1220 мм. Использование данного метода позволяет оперативно установить развитие непроектных изгибов на участках подземных магистральных трубопроводов, в том числе залегающих на границах активных тектонических разломов [19, 29]. При эксплуатации данных систем возникали проблемы – повреждение волоконно-оптических сенсоров деформации геологической средой, что влекло за собой выход из строя и ложноположительные срабатывания системы. Для эффективного использования данных методов необходима разработка методов вспомогательных, которые позволят подтвердить (или опровергнуть) наличие непроектных изгибов на подконтрольных участках.
Таким может быть метод определения изгибных напряжений в стенке подземного магистрального трубопровода на основании данных о конфигурации оси трубопровода, главными преимуществами которого являются дешевизна, простота и возможность использования для мониторинга протяженных участков магистральных трубопроводов. Широкое применение данного метода ограничено слабо развитой научно-технической базой.
Ряд работ исследователей предлагает различные варианты оценки изгибных напряжений на основе данных съемки оси трубопровода. Так, в работах [30, 31] рекомендуется использование полиномов высокой степени для аппроксимации оси трубопровода, в источниках [25, 32] авторы предлагают использовать метод хорд. Кроме того, существуют стандарты ВРД 39-1.10-026-2001 и рекомендации ВНИИСТ Р-352-79, предлагающие использовать фиксированный шаг при проведении съемки оси трубопровода. Данные подходы опираются на допущения, которые не всегда выполняются на практике [12, 14, 28]. Например, при использовании метода хорд требуется фиксированное расстояние между точками измерений, а в расчетах, согласно данному методу, за фактическую глубину залегания оси трубопровода во всех точках измерений принимается максимальная на участке измерений глубина. Также предполагается, что погрешность используемых для определения глубины залегания оси трубопровода приборов не меняется при проведении съемки.
Основные проблемы и возможности модернизации данной методики описаны в работе [33]. Главное ограничение всех существующих методов – использование максимальной глубины на участке контроля при проведении расчетов, а также фиксированная погрешность трассоискателя на всем участке контроля. Опираясь на литературные источники [34, 35], можно сказать, что при переходе через естественные и искусственные препятствия участки подземного трубопровода могут быть заглублены более чем на 10 м, в то время как в 100 м от данного перехода глубина может не достигать и 2-3 м. Погрешность прибора в различных точках измерений также может существенно колебаться в зависимости от условий съемки (влажности, температуры и др.). Все граничные случаи указывают на необходимость доработки методик [25, 31, 32] для оценки изгибных напряжений при различных конструктивных параметрах как самого трубопровода и условий прокладки, так и используемого оборудования и места проведения съемки.
Методология исследования
Доработка математической модели, подобной описанной в источнике [33], сопряжена с необходимостью поиска большого количества данных для подбора регрессионных коэффициентов. Эти данные могут быть получены путем моделирования упругого изгиба участка трубопровода при зафиксированных параметрах. В работе используются данные, аналогичные применяемым в работе [33], с добавлением нескольких новых входных переменных. Подробная схема модели описана в материалах [25, 32, 33].
Разрабатываемая математическая модель задается следующими параметрами:
где D – диаметр исследуемого трубопровода, м; hl, hr, hm – глубина залегания оси трубопровода в левой, правой и центральной точках измерений, м; Δl, Δr, Δm – погрешность измерений глубины залегания оси трубопровода в левой, правой и центральной точках измерений, %; L – шаг между точками измерений глубины залегания оси трубопровода, м; σ – максимальная погрешность в определении изгибных напряжений при использовании данных параметров, МПа.
Для разрабатываемой математической модели (1) необходимо подобрать регрессионные коэффициенты, минимизирующие некоторую метрику, по которой можно судить о качестве разработанной модели. Традиционной метрикой качества задач регрессии является среднеквадратичная ошибка измерений, однако для данной задачи она будет сложно интерпретируемой ввиду большого разброса значений прогнозируемой величины (погрешности в определении изгибных напряжений). Поэтому за целевую метрику принято использовать среднюю абсолютную процентную ошибку, которая показывает в процентах, на сколько в среднем не точен прогноз модели. Средняя абсолютная процентная ошибка выражается через соотношение
где y1, yˆi – истинное значение величины и спрогнозированное моделью соответственно; ε – произвольная положительная малая величина, применяемая во избежание деления на ноль.
Применение данной метрики позволяет учитывать одинаковые веса при ошибках на значения отклика любого порядка, т.е. масштаб прогнозируемой величины.
Значения hl, hr, hm; Δl, Δr, Δm; L являются непрерывными величинами, поэтому их можно добавлять в регрессионную модель в первоначальном виде. Значение диаметра трубопровода – величина дискретная, применительно к задачам оптимизации данные величины обычно называют порядковыми, подразумевая отсутствие возможности сравнить их между собой, как это можно сделать с непрерывными. С этой целью применяются различные подходы для кодирования порядковых переменных [36], в данной работе использовался метод One Hot Encoding – кодирование с одной «горячей» переменной [36]. Диаметр трубопровода кодируется n-мерным вектором, где n – количество уникальных категорий данного признака. В нашей задаче рассматривается только магистральные трубопроводы, поэтому ряд исследуемых диаметров включает 1420, 1220, 1020, 820, 720, 520, 320, 220 мм.
Тогда математическая модель будет принимать на вход 14 признаков, а на выходе выдавать один, равный погрешности в расчете изгибных напряжений при использовании данных признаков:
где n – количество примеров.
Задача оптимизации будет выглядеть следующим образом:
где X – матрица входных данных, представленных в табличном виде путем конкатенации столбцов; l – количество элементов в выборке данных.
Обсуждения и результаты
Решение задачи оптимизации (2) подразумевает выбор не только оптимальных значений весов матриц W, но и минимального их размера, поскольку размер матриц W будет существенно влиять на алгоритмическую сложность вычислений на приборах, где данная математическая модель будет реализована. Для поиска коэффициентов использовалось API [36], в качестве метода минимизации был выбран Adam [36, 37] с параметрами по умолчанию. Для ускорения процесса обучения все целочисленные переменные, подаваемые на вход модели, были нормированы для приведения их распределений к нормальным с нулевым математическим ожиданием и единичной дисперсией. Итоговый вид нелинейной математической модели зависимости диаметра трубопровода, погрешности используемого оборудования, шага между точками измерений и глубины залегания оси трубопровода от максимальной погрешности в определении изгибных напряжений:
где W1-4 – матрицы подобранных в процессе оптимизации коэффициентов (весов); b1-4 – значения смещений, подобранных в процессе оптимизации; sigm – функция сигмоиды, применяемая поэлементно, равная sigm(x)=1/(1+exp(-x)).
Размеры итоговых матриц с коэффициентами, полученными в процессе оптимизации, представлены в табл.1.
Таблица 1
Параметры разработанной математической модели (3)
|
Параметр |
Размер матрицы |
Параметр |
Размер матрицы |
|
W1 |
(14, 15) |
b1 |
(15, 1) |
|
W2 |
(15, 20) |
b2 |
(20, 1) |
|
W3 |
(20, 15) |
b3 |
(15, 1) |
|
W4 |
(20, 1) |
b4 |
(1, 1) |
После оптимизации MAPE = 0,67 %, таким образом средняя ошибка между истинным значением погрешности в определении изгибных напряжений и значением, определенным на основе модели (3), достаточно мала, и данную модель целесообразно использовать для дальнейших исследований. Для контроля переобучения модели под данные результат представлен для тестовой выборки, которая получена случайным семплированием 15 % исходной выборки, подготовленной для обучения. Для контроля переобучения использовались L1, L2-регуляризации.
Как разработанная математическая модель (3), так и модели других исследователей [25, 31, 32] предполагают, что значение погрешности прибора, с помощью которого измеряется глубина залегания оси трубопровода, не превышает некоторую константную величину, которая для современных трассоискателей составляет около ±5 %. Однако для получения адекватных результатов также необходимо, чтобы значения отклонений показаний трассоискателя от фактических значений при измерениях на одной глубине были одного знака, в противном случае рассчитанные на основе этих данных изгибные напряжения могут либо не соответствовать действительности, либо быть не консервативными по отношению к истинным изгибным напряжениям.
В современных литературных источниках не отражена информация по дисперсии погрешности трассоискателей при измерениях в узких интервалах глубин, таким образом мы имеем методологию, которую необходимо апробировать с помощью экспериментальных исследований. Для этих целей были определены погрешности трассоискателя типа БИТА-1 при различных значениях глубин залегания оси трубопровода. Поскольку грунты не оказывают существенного влияния на точность трассоискателей [38], измерялась не глубина трубопровода, а расстояние между осью трубопровода и приемником, что в данных условиях является допущением (рис.1). Максимальная паспортная погрешность прибора составляет ±5 %.
Погрешность определения глубины залегания оси трубопровода трассоискателем (±5 %) указана с учетом действия на прибор максимально консервативной совокупности факторов, в то время как на реальном трубопроводе данные факторы могут отсутствовать, что способно повысить точность прибора.
Важным фактором при съемке глубины залегания оси подземного трубопровода также является дисперсия полученных данных. При проведении съемки с помощью трассоискателя подразумевается, что при фиксированной глубине залегания оси трубопровода отклонения в определении расстояний от оси трубопровода до приемника трассоискателя (глубина залегания) будут одного знака. Например, на глубине 1-2 м прибор ошибается в диапазоне от 1 до 3 %.
Цели экспериментального исследования заключаются в определении доверительных интервалов погрешности прибора в узких интервалах глубин (по 1 м) и подтверждении гипотезы об гомоскедастичности дисперсии ошибки в узких интервалах глубин (по 1 м).
Для достижения поставленных целей необходимо выполнить следующее:
- зафиксировать показания прибора для выбранного диапазона расстояний от приемника прибора до оси исследуемого трубопровода;
- сверить полученные прибором данные и истинные значения, измеренные с помощью рулетки;
- оценить точечные статистики погрешности прибора;
- вывести интервальные оценки погрешности прибора при разном расстоянии от приемника до оси трубопровода;
- сделать выводы по полученным данным.
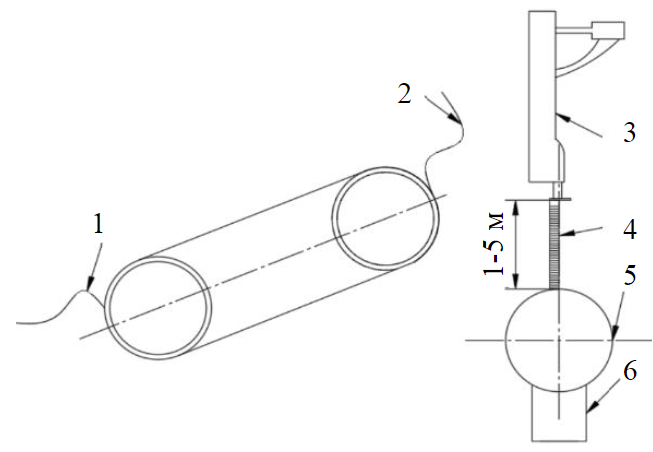
Рис.1. Схема измерительного стенда 1 – подключение к источнику тока; 2 – заземление; 3 – трассоискатель БИТА-1; 4 – рулетка; 5 – трубопровод; 6 – опора трубопровода
Для каждого расстояния от оси трубопровода до приемника производится восемь измерений, каждое измерение состоит из трех, которые далее усредняются. Таким образом, для каждого значения расстояния между осью трубопровода и приемником имеется восемь показаний прибора. В качестве истинного расстояния используются показания, полученные с помощью измерений рулеткой с погрешностью не более ±0,45 мм/м. Точная установка прибора над осью трубопровода гарантируется встроенными в прибор БИТА-1 средствами определения оси трубопровода. При измерениях использовался участок трубопровода диаметром 220 мм и длиной 35 м с изоляционным битумным покрытием (рис.1). Для работы трассоискателей необходимо, чтобы по телу трубопровода протекал электрический ток. На реально действующих трубопроводах возможность поиска оси трубопровода трассоискателями обеспечивается его подключением к станциям катодной защиты. На измерительном стенде источником тока служит входящий в комплект прибора БИТА-1 генератор, который подключается с помощью зажимов к торцам трубопровода, другой конец трубопровода заземляется. Частота тока при измерениях, согласно рекомендациям источника [38], 640 Гц. Интервал исследуемых глубин в один метр принят экспертно с целью фиксации статистически значимых отличий на основании результатов работ [25, 33].
Пример результатов измерений, проведенных согласно описанным положениям, представлен в табл.2. Измерения вблизи подключений к заземлению и источнику тока от генератора сопряжены с возникновением существенных помех от наводимых источников тока, что вызывает дополнительную погрешность при измерениях. Для нивелирования погрешности измерения на экспериментальном стенде производились по центру трубопровода.
Таблица 2
Результаты измерений при частоте 640 Гц
|
Lдейств, м |
Lизм1, м |
Lизм2, м |
Lизм, м |
Погрешность, % |
|
1,1 |
1,090 |
1,090 |
1,100 |
–0,61 |
|
1,1 |
1,100 |
1,100 |
1,100 |
0,00 |
|
1,1 |
1,090 |
1,100 |
1,100 |
–0,30 |
|
1,1 |
1,100 |
1,100 |
1,080 |
–0,61 |
|
1,1 |
1,090 |
1,090 |
1,100 |
–0,61 |
|
1,1 |
1,080 |
1,100 |
1,100 |
–0,61 |
|
1,1 |
1,089 |
1,096 |
1,090 |
–0,77 |
|
1,1 |
1,090 |
1,086 |
1,099 |
–0,78 |
|
… |
… |
… |
… |
… |
|
5,1 |
5,140 |
5,120 |
5,130 |
0,59 |
|
5,1 |
5,190 |
5,150 |
5,160 |
1,31 |
|
5,1 |
5,150 |
5,140 |
5,170 |
1,05 |
|
5,1 |
5,180 |
5,180 |
5,180 |
1,57 |
|
5,1 |
5,180 |
5,200 |
5,180 |
1,70 |
|
5,1 |
5,240 |
5,200 |
5,200 |
2,22 |
|
5,1 |
5,190 |
5,150 |
5,170 |
1,37 |
|
5,1 |
5,150 |
5,140 |
5,170 |
1,05 |
Среднее значение установленной прибором глубины залегания вычисляется по формуле:
где Lизм – расстояние от приемника до оси цилиндрического проводника (трубопровода), м.
Среднее значение погрешности прибора в определении глубины рассчитывается по формуле:
где Lhiист – истинное значение глубины залегания оси трубопровода, м.
Выборочные статистики по группам глубин залегания приведены в табл.3. При обработке результатов экспериментальных исследований в качестве выборки использовалась погрешность в определении глубины залегания оси трубопровода, вычисленная как среднее трех измерений (4).
Таблица 3
Выборочные статистики по группам глубин залегания при частоте тока 640 Гц
|
Параметр |
Глубина залегания оси h, м |
||||
|
1,1 |
2,1 |
3,1 |
4,1 |
5,1 |
|
|
Минимальная погрешность Δmin, % |
–1,32 |
–1,27 |
1,51 |
0,41 |
0,59 |
|
Максимальная погрешность Δmax, % |
0 |
0,48 |
2,37 |
1,22 |
2,22 |
|
Средняя погрешность Δhiavg% |
–0,552 |
–0,734 |
1,986 |
0,746 |
1,356 |
|
Стандартное отклонение выборки, % |
0,353 |
0,544 |
0,274 |
0,309 |
0,461 |
При малых значения глубины залегания оси (до 2 м) прибор показывает более низкие значения глубин относительно истинных (табл.3). При увеличении глубины залегания прибор показывает более высокие значения глубин залегания относительно истинных. При исследовании глубин залегания на реально действующих трубопроводах и последующем использовании полученных данных для оценки уровня изгибных напряжений необходимо определить максимальные значения погрешности в определении глубины залегания оси трубопровода, а также дисперсию отклонений в узких интервалах. Исследуем характер распределения с помощью непараметрического способа оценки плотности случайной величины – ядерной оценки плотности (рис.2) [34].
Распределения погрешностей схожи с нормальными (рис.2), но для каждой глубины залегания свои параметры среднего и среднеквадратичного отклонения. Нормальное распределение обладает рядом хороших свойств, которые можно использовать на практике. Так, зная статистику нормального распределения можно построить доверительные интервалы для погрешности при измерении на определенной глубине и пользоваться полученными данными для расчета изгибных напряжений.
Оценим более строго, имеет ли погрешность измерений глубины залегания оси трубопровода прибором БИТА-1 нормальное распределение. Наиболее мощным критерием соответствия распределения нормальному является критерий Шапиро – Уилка [35]. Статистика критерия Шапиро – Уилка:
где s2 – дисперсия выборки; а – табличный коэффициент.
Критические значения статистики W являются табличными. Оценим, будет ли распределение выборочных данных соответствовать нормальному с помощью критерия Шапиро – Уилка на уровне значимости α = 0,95.
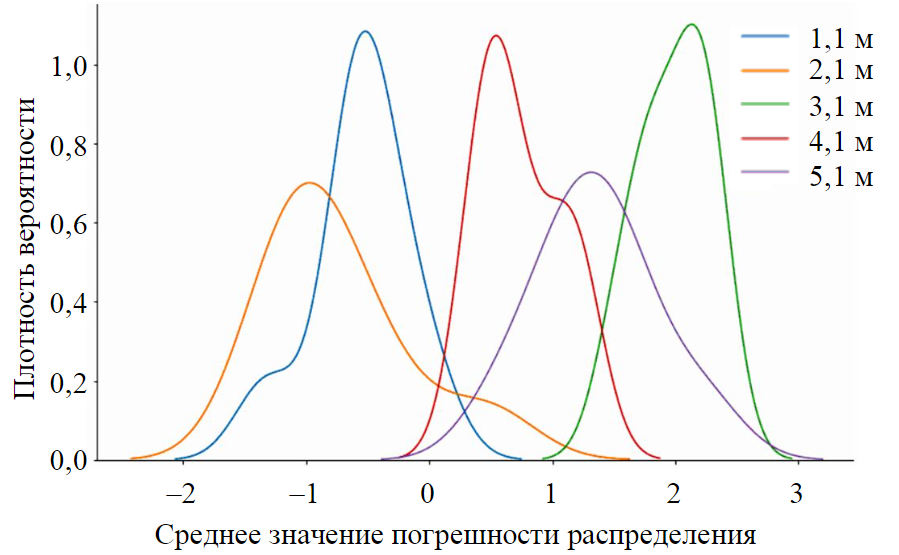
Рис.2. Ядерная оценка плотности распределения при исследовании глубин залегания h
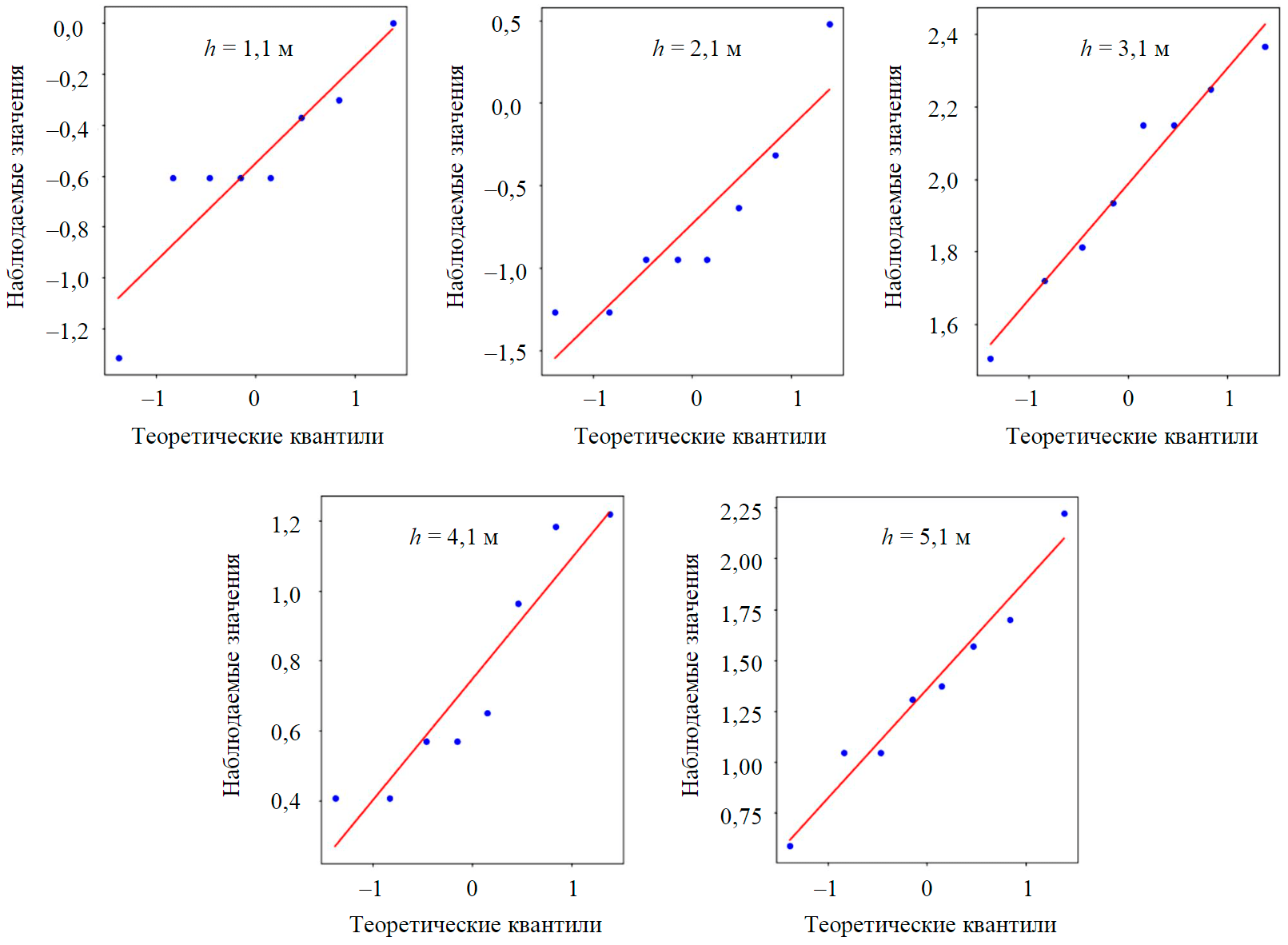
Рис.3. Оценка распределения с помощью Q-Q-графика
Для автоматизации процесса воспользуемся реализацией расчета критерия Шапиро – Уилка, представленной в пакете stats языка программирования Python.
Значение p-value (на уровне значимости 0,95) для глубины залегания оси трубопровода 1,1 м составляет 0,036, что не соответствует нормальному распределению. Значения, соответствующие нормальному распределению: 0,084 (глубина залегания 2,1 м); 0,975 (3,1 м); 0,637 (4,1 м); 0,968 (5,1 м).
При глубине залегания 1,1 м распределение погрешности измерений глубины оси трубопровода отлично от нормального. Далее при построении доверительных интервалов погрешностей измерений планируется использование Т-статистики, одной из особенностей которой является то, что она не требует полного соответствия распределения нормальному: достаточно, чтобы распределение лишь визуально соответствовало нормальному [39]. Одним из способов визуальной оценки нормальности распределения является Q-Q-график (quantile-quantile график).
Анализ данных по Q-Q-графику основан на сравнении теоретических квантилей нормального распределения распределению значений полученной по результатам экспериментов выборки. Воспользуемся реализацией Q-Q plot из пакета stats. Оценим визуально, могли ли данные выборки быть сформулированы нормальным распределением (рис.3).
При глубине залегания 1,1 м (рис.3) существует некоторая дискретность вокруг среднего, что, возможно, свидетельствует о настройке фильтров используемого оборудования. Т-статистика позволяет строить доверительные интервалы на основе распределений, отличных от нормального в случае, если они не сильно скошены [39], распределение погрешностей при глубине залегания 1,1 м удовлетворяют требуемым условиям.
Поскольку дисперсия генеральной совокупности не известна, 99 % доверительных интервалов средней погрешности измерений при каждой глубине залегания будем оценивать с помощью Т-статистики распределения Стьюдента со степенями свободы n – 1:
где X– – среднее по выборке; µ – среднее генеральной совокупности; n – количество элементов выборки; S – несмещенное выборочное стандартное отклонение.
Тогда доверительный интервал неизвестной средней погрешности в определении глубины залегания оси трубопровода µ при условии наблюдаемой средней X– будет равняться
где t – искомый квантиль распределения Стьюдента.
Доверительные интервалы для средней погрешности в определении глубины залегания оси трубопровода на основе Т-распределения Стьюдента: при h = 1,1 м доверительный интервал –0,9 ≤ µ ≤ –0,2; при h = 2,1 м интервал –1,5 ≤ µ ≤ 0; при h = 3,1 м интервал 1,6 ≤ µ ≤ 2,3; при h = 4,1 м интервал 0,2 ≤ µ ≤ 1; при h = 5,1 м интервал 0,7 ≤ µ ≤ 2.
По результатам расчета погрешности трассоискателя БИТА-1 в определении глубины залегания трубопровода установлено, что в узких интервалах глубин отклонение измерений относительно истинных значений не меняет свой знак, а абсолютное значение погрешности не превышает паспортных величин.
Таким образом, для расчета изгибных напряжений участка подземного трубопровода на основании данных о конфигурации оси трубопровода необходимо рассчитать требуемый шаг между точками измерений с помощью математической модели (3) и методики, описанной в статье [33], провести съемку конфигурации оси подземного трубопровода и по полученным значениям с помощью геометрических положений [25, 32, 33] произвести пересчет полученных радиусов изгиба на участке в изгибные напряжения.
Заключение
Доработана математическая модель определения оптимального шага измерений при съемке глубины залегания оси подземного трубопровода с поверхности грунта для последующего расчета по полученным данным изгибных напряжений в стенке трубопровода. Математическая модель позволяет учесть переменную погрешность и глубину залегания оси в каждой точке измерений, а также конструктивные особенности исследуемого трубопровода и условий прокладки. Максимальная погрешность разработанной модели на отложенной выборке по метрике МАРЕ = 0,67 %, по метрике МАЕ = 3,5 МПа.
На основе экспериментальных исследований по определению погрешности трассоискателя БИТА-1 в узком интервале глубин (по 1 м) установлено, что дисперсия ошибки в определении глубины залегания оси трубопровода всегда одного знака относительно истинной глубины залегания, что позволит с достаточной точностью производить расчеты после съемки по полученным данным. Доказано, что погрешность прибора в узком интервале глубин подчиняется нормальному распределению, либо не сильно от него отличается. Вычислены 99 % доверительных интервалов погрешности в определении глубины залегания оси трубопровода в процентах для трассоискателя БИТА-1. Показано, что данные значения погрешности всегда не превышают паспортных значений прибора.
Литература
- Litvinenko V. The Role of Hydrocarbons in the Global Energy Agenda: The Focus on Liquefied Natural Gas // Resources. 2020. Vol. 9. Iss. 5. № 59. DOI: 10.3390/resources9050059
- Литвиненко В.С., Цветков П.С., Двойников М.В., Буслаев Г.В. Барьеры реализации водородных инициатив вконтексте устойчивого развития глобальной энергетики // Записки Горного института. 2020. Т. 244. C. 428-438. DOI: 10.31897/PMI.2020.4.5
- Двойников М.В., Будовская М.Е. Разработка углеводородной системы заканчивания скважин с низкими забойными температурами для условий нефтегазовых месторождений Восточной Сибири // Записки Горного института. 2022. Т. 253. С. 12-22. DOI: 10.31897/PMI.2022.4
- Fetisov V.G., Tcvetkov P.S., Müller J.M. Tariff Approach to Regulation of the European Gas Transportation System: Case of Nord Stream // Energy Reports. 2021. Vol. 7. № 6. P. 413-425. DOI: 10.1016/j.egyr.2021.08.023
- Zhengbing Li, Yongtu Liang, Weilong Ni et al. Pipesharing: economic-environmental benefits from transporting biofuels through multiproduct pipelines // Applied Energy. 2022. Vol. 311. № 18684. DOI: 10.1016/j.apenergy.2022.118684
- Biezma M.V., Andrés M.A., Agudo D., Briz E. Most fatal oil & gas pipeline accidents through history: A lessons learned approach // Engineering Failure Analysis. 2020. Vol. 110. № 104446. DOI: 10.1016/j.engfailanal.2020.104446
- Guoyun Shi, Weichao Yu, Kun Wang et al. Time-dependent economic risk analysis of the natural gas transmission pipeline system // Process Safety and Environmental Protection. 2021. Vol. 146. P.432-440. DOI: 10.1016/j.psep.2020.09.006
- Исламов Р.Р., Фриндлянд Я.М., Агиней Р.В. Ретроспективный анализ причин отказов на магистральных нефтегазопроводах, работающих в осложненных инженерно-геологических условиях // Оборудование и технологии для нефтегазового комплекса. 2017. № 6. С. 80-87.
- Chio Lam, Wenxing Zhou. Statistical analyses of incidents on onshore gas transmission pipelines based on PHMSA database // International Journal of Pressure Vessels and Piping. 2016. Vol. 145. P. 29-40. DOI: 10.1016/j.ijpvp.2016.06.003
- Гольянов А.И., Гольянов А.А., Кутуков С.Е. Обзор методов оценки энергоэффективности магистральных нефтепроводов // Проблемы сбора, подготовки и транспорта нефти и нефтепродуктов. 2017. №4 (110). С. 156-170. DOI: 10.17122/ntj-oil-2017-4-156-170
- Овчинников Н.Т. Методические вопросы применения радиусов изгиба при мониторинге состояния трубопроводов // Наука и технологии трубопроводного транспорта нефти и нефтепродуктов. 2018. Т.8. № 3. С. 278-289. DOI: 10.28999/2541-9595-2018-8-3-278-289
- Аскаров Р.М., Валеев А.Р., Исламов И.М., Тагиров М.Б. Оценка влияния геодинамических зон, пересекающих магистральные газопроводы, на их напряженно-деформированное состояние // Известия Томского политехнического университета. Инжиниринг георесурсов. 2019. Т. 330. № 11. С. 145-154. DOI: 10.18799/24131830/2019/11/2358
- Bakesheva A.T., Fetisov V.G., Pshenin V.V. A refined algorithm for leak location in gas pipelines with determination of quantitative parameters // International Journal of Engineering Research and Technology. 2019. Vol. 12. № 12. P. 2867-2869.
- Гумеров А.К., Сильвестров С.А. Совершенствование методов оценки допустимых значений радиуса упругого изгиба трубопровода // Нефтегазовое дело. 2018. Т. 16. № 4. С. 96-107. DOI: 10.17122/ngdelo-2018-4-96-107
- Sultanbekov R., Islamov Sh., Mardashov D. et al. Research of the influence of marine residual fuel composition on sedimentation due to incompatibility // Journal of Marine Science and Engineering. 2021. Vol. 9. № 1067. DOI: 10.3390/jmse9101067
- Krivokrysenko E.A., Popov G.G., Bolobov V.I., Nikulin V.E. Use of Magnetic Anisotropy Method for Assessing Residual Stresses in Metal Structures // Key Engineering Materials. 2020. Vol. 854. P. 10-15. DOI: 10.4028/www.scientific.net/KEM.854.10
- Xia Mengying, Hong Zhang. Stress and Deformation Analysis of Buried Gas Pipelines Subjected to Buoyancy in Liquefaction Zones // Energies. 2018. Vol. 11. № 9. № 2334. DOI: 10.3390/en11092334
- МастобаевБ.Н., АскаровР.М., КитаевС.В. идр. Выявление потенциально опасных участков магистральных газопроводов на пересечениях с геодинамическими зонами // Трубопроводный транспорт: теория и практика. 2017. № 3 (61). С. 38-43.
- Adegboye M.A., Wai-Keung Fung, Karnik A. Recent Advances in Pipeline Monitoring and Oil Leakage Detection Technologies: Principles and Approaches // Sensors. 2019. Vol. 19(11). № 2548. DOI: 10.3390/s19112548
- Варшицкий В.М., Студенов Е.П., Козырев О.А., Фигаров Э.Н. Упругопластический изгиб трубопровода при комбинированном нагружении // Наука и технологии трубопроводного транспорта нефти и нефтепродуктов. 2021. Т. 11. № 4. С. 372-377. DOI: 10.28999/2541-9595-2021-11-4-372-377
- Болобов В.И., Попов Г.Г. Методика испытаний трубопроводных сталей на стойкость к «ручейковой» коррозии // Записки Горного института. 2021. Т. 252. С. 854-860. DOI: 10.31897/PMI.2021.6.7
- Коршак А.А., Гайсин М.Т., Пшенин В.В. Использование метода структурной минимизации среднего риска для идентификации массоотдачи испаряющейся нефти при наливе в танкеры // Нефтяное хозяйство. 2019. № 10. С. 108-111. DOI: 10.24887/0028-2448-2019-10-108-111
- Агиней Р.В., Исламов Р.Р., Мамедова Э.А. Определение напряженно-деформированного состояния участка трубопровода под давлением по результатам измерения коэрцитивной силы // Наука и технологии трубопроводного транспорта нефти и нефтепродуктов. 2019. Т. 9. № 3. С. 284-294. DOI: 10.28999/2541-9595-2019-9-3-284-294
- Yi Shuai, Xin-Hua Wang, Can Feng et al. A novel strain-based assessment method of compressive buckling of X80 corroded pipelines subjected to bending moment load // Thin-Walled Structures. 2021. Vol. 167. № 108172. DOI: 10.1016/j.tws.2021.108172
- Мамедова Э.А. Совершенствование методов оценки и мониторинга изгибных напряжений в стенках труб подземных магистральных нефтегазопроводов: Автореф. дис. … канд. техн. наук. Ухта: Ухтинский государственный технический университет, 2021. 23 с.
- Chmelko V., Garan M., Šulko M. Strain measurement on pipelines for long-term monitoring of structural integrity // Measurement. 2020. Vol. 163. № 107863. DOI: 10.1016/j.measurement.2020.107863
- Щипачев А.М., Горбачев С.В. Влияние послесварочной обработки на скорость сплошной коррозии и микроструктуру сварных соединений сталей 20 и 30ХГСА // Записки Горного института. 2018. Т. 231. C. 307-311. DOI: 10.25515/PMI.2018.3.307
- Andres M. Biondi, Jingcheng Zhou, Xu Guo et al. Pipeline structural health monitoring using distributed fiber optic sensing textile // Optical Fiber Technology. 2022. Vol. 70. № 102876. DOI: 10.1016/j.yofte.2022.102876
- Zhaoming Zhou, Jia Zhang, Xuesong Huang, Xishui Guo. Experimental study on distributed optical-fiber cable for high-pressure buried natural gas pipeline leakage monitoring // Optical Fiber Technology. 2019. Vol. 53. № 02028. DOI: 10.1016/j.yofte.2019.102028
- Кузьбожев А.С., Бирилло И.Н., Бердник М.М. Исследование влияния шага измерений профиля газопровода на точность расчета радиусов изгиба его оси // Научные труды НИПИ Нефтегаз ГНКАР. 2018. № 4. С. 43-49. DOI: 10.5510/OGP20180400370
- Варшицкий В.М., Фигаров Э.Н., Лебеденко И.Б. Исследование напряженного состояния трубопроводов с ненормативной кривизной оси // Наука и технологии трубопроводного транспорта нефти и нефтепродуктов. 2018. Т. 8. № 3. С. 273-277. DOI: 10.28999/2541-9595-2018-8-3-273-277
- Середенок В.А. Разработка методики реконструкции магистральных газопроводов методов «труба в трубе» на осложненных участках трассы: Автореф. дис. … канд. техн. наук. Ухта: Ухтинский государственный технический университет, 2020. 22 с.
- Aginey R.V., Firstov A.A., Kapachinskikh Zh.Yu. To the question of determining bending stress of a buried pipeline from the ground surface // International Conference on Innovations, Physical Studies and Digitalization in Mining Engineering (IPDME) 2020, 23-24 April 2020, St. Petersburg, Russian Federation. Journal of Physics: Conference Series. Vol. 1753. № 012068. DOI: 10.1088/1742-6596/1753/1/012068
- Rosenblatt M. Remarks on Some Nonparametric Estimates of a Density Function // The Annals of Mathematical Statistics. 1956. Vol. 27. Iss. 3. P. 832-837 DOI: 10.1214/aoms/1177728190
- Shapiro S.S., Wilk M.B. An analysis of variance test for normality (complete samples) // Biometrika. 1965. Vol. 52. Iss. 3-4, P. 591-611. DOI: 10.1093/biomet/52.3-4.591
- Pedregosa F., Varoquaux G., Gramfort A. et al. Scikit-learn: Machine Learning in Python // Journal of Machine Learning Research. 2011. Vol. 12. P. 2825-2830.
- Kingma D.P., Ba J. Adam: A method for stochastic optimization // 3rd International Conference for Learning Representations, San Diego, 2015. http://arxiv.org/abs/1412.6980 (дата обращения 15.01.2021).
- Спиридович Е.А. Повышение надежности магистральных газопроводов в условиях коррозионного растрескивания под напряжением: Автореф. дис. … д-ра техн. наук. М.: ООО «Гизпрогазцентр», 2014. 50 с.
- Lumley T., Diehr P., Emerson S., Lu Chen. The Importance of the Normality Assumption in Large Public Health Data Sets // Annual Review of Public Health. 2002. Vol. 23. P. 151-169. DOI: 10.1146/annurev.publhealth.23.100901.140546
