Применение метода опорных векторов для обработки результатов обогащения оловянных руд методом центробежной концентрации
- 1 — канд. техн. наук доцент Иркутский национальный исследовательский технический университет ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
- 2 — канд. техн. наук доцент Иркутский национальный исследовательский технический университет ▪ Orcid ▪ Scopus
- 3 — генеральный директор ООО «Сибикон» ▪ Orcid ▪ Scopus
- 4 — канд. техн. наук профессор Иркутский национальный исследовательский технический университет ▪ Orcid ▪ Scopus
Аннотация
Актуальность исследований обусловлена получением новых знаний об особенностях применимости метода опорных векторов, относящегося к инструментам машинного обучения, для решения задач математического моделирования горно-обогатительного оборудования. Цель исследований – статистический анализ результатов полупромышленных испытаний технологии Knelson CVD на оловянном сырье с помощью метода опорных векторов и разработка математических моделей, пригодных для дальнейшей оптимизации технологических параметров оборудования. Объектами исследований являлись продукты, полученные в результате работы гидроциклонов, а также технологические параметры работы центробежных концентраторов. В работе применяются классические методы математической статистики, метод наименьших квадратов для построения модели линейной регрессии, метод опорных векторов, реализованный на базе библиотеки Scikit-learn, а также метод верификации получаемых моделей на базе библиотеки ShuffleSplit. Представлено общее описание процесса проведения испытаний концентратора Knelson с непрерывной регулируемой разгрузкой применительно к обогащению оловянных руд. Полученные результаты обработаны с помощью метода опорных векторов. Получены регрессионные модели в виде полиномов второй степени и в виде радиально-базисных функций. Показана существенная нелинейность в зависимости между содержанием ценного компонента в хвостах и значениями технологических параметров аппарата.
Введение
Добыча и переработка минерального сырья всегда являлись ключевыми вопросами национальной безопасности нашей страны [1]. На территории Российской Федерации выявлены практически все виды полезных ископаемых, а по некоторым из них наша страна входит в число мировых лидеров: железные руды, никель, медь, цинк, вольфрам и др. [2, 3]. Ключевым металлом, который используется в различных областях промышленности, является олово. Благодаря своим свойствам [4] олово находит широкое применение в легировании, лужении, пайке, и – самое важное – в электронной и микроэлектронной промышленностях.
В конце 90-х – начале 2000-х гг. добыча олова в РФ была почти полностью прекращена. В 2010 г. было получено всего 100 т концентрата, хотя на территории России сосредоточены крупнейшие запасы олова в мире – более 2 млн т, из них более трех четвертей подсчитаны по категориям А + В + С1. Лидирующие позиции в оловодобывающей отрасли традиционно занимают Китай, который с середины 1990-х гг. обеспечивает не менее 30 % мировой добычи металла (около 900 месторождений), и Индонезия (20 %). В РФ в настоящее время на государственном учете находятся более 250 месторождений олова (рис.1).
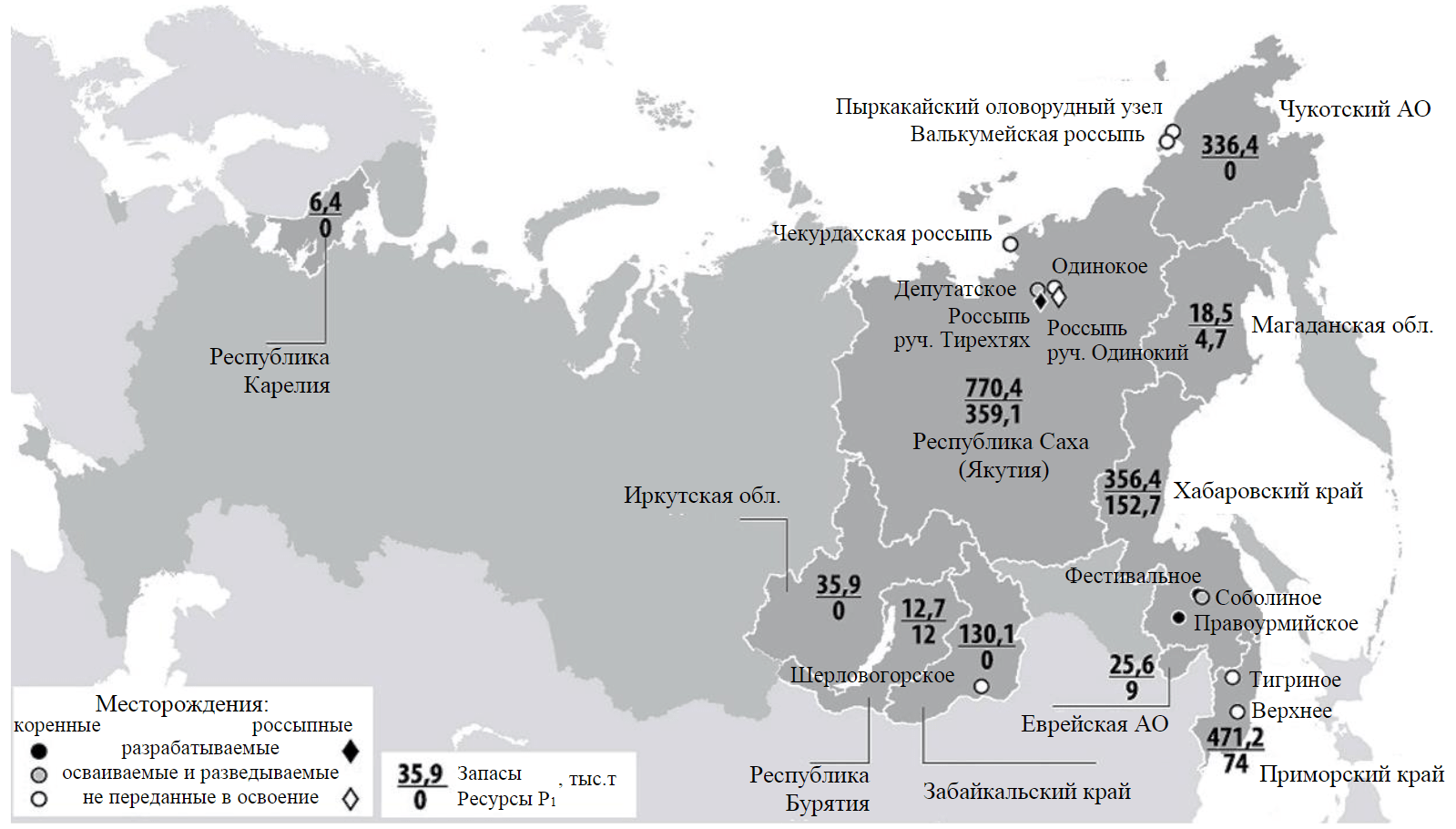
Рис.1. Состояние сырьевой базы олова Российской Федерации
Объекты и методы
Металл в основном получают в результате переработки касситерита, который, как правило, обогащают с применением гравитационных методов и флотационного обогащения. Для достижения наибольших показателей эффективности извлечения на стадии флотационного обогащения используются новые реагентные режимы [5-7], проектируется новое оборудование – например, применение скоростной флотации в контуре измельчения, разработанная компанией Metso Outotec. Предлагаемая технология позволяет минимизировать переизмельчение ценного компонента, повысить производительность извлечения и снизить обводнение схемы обогащения [8].
Для извлечения крупных частиц металла применяют гравитационное обогащение, в частности центробежную концентрацию [9-11]. Однако в связи с особенностями минералогического состава [12] и несовершенством применяемых технологий, с хвостами обогащения уходит значительное количество ценного компонента, который при правильном подходе может быть извлечен и переработан.
Существуют различные технологии переработки таких материалов, которые постоянно обновляются [13, 14]. Тем не менее наиболее распространенными методами остаются именно обогащение с помощью гравитационных методов и флотационное обогащение.
Применение центробежных концентраторов [15, 16] в гравитационных методах переработки оловянных руд и продуктов их обогащения является показателем современности и эффективности схемы разработки сырья [17].
Ручная настройка (технологических параметров центобежных конденсаторов, скорости вращения чаши, влияния характеристик исходного сырья, работы клапанов и т.д.) требует значительных финансовых и временных затрат, поэтому при их настройке чаще всего применяют методы математического моделирования. Авторами [18-20] предприняты попытки разработки модели работы центробежных концентратов на базе классических регрессионных подходов. Однако предложенные решения не всегда подходят для получения достоверной модели на хвостах обогащения, поскольку существенно нелинейные зависимости при применении классических методов не позволяют учитывать скрытые взаимосвязи между параметрами работы концентратора. Целью данной работы является описание применения метода опорных векторов (относящегося к методам машинного обучения) к задаче построения нелинейных моделей работы центробежного концентратора на базе полиномиальных радиально-базисных функций ядра.
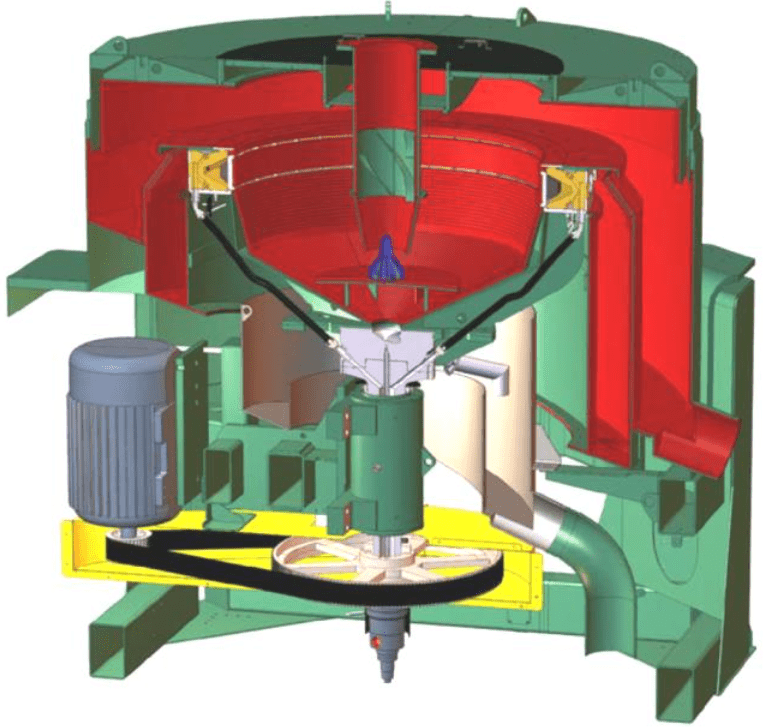
Рис.2. Концентратор Knelson KC-CVD64
Концентратор Knelson с непрерывной регулируемой разгрузкой (CVD) – это центробежный гравитационный сепаратор, предназначенный для извлечения больших масс полезного минерала, в котором применяются запатентованная FLSmidth Knelson технология флюидизации и система пережимных пневматических клапанов, обеспечивающих непрерывный выход концентрата одновременно с добавлением свежего питания (рис.2). Технология CVD используется преимущественно для извлечения основных металлов и промышленных минералов (самородной меди, ртути, танталита, касситерита, хромита и шеелита [21-23], а также благородных металлов [24, 25].
Объектами исследований в данной работе являлись продукты, полученные в результате работы гидроциклонов (гидравлических классификаторов), а также технологические параметры работы центробежных концентраторов. В работе применялись классические методы математической статистики, метод наименьших квадратов для построения модели линейной регрессии,
метод опорных векторов, реализованный на базе библиотеки Scikit-learn, а также метод верификации получаемых моделей на базе библиотеки ShuffleSplit.
Методика
Технологические исследования проводились на трех технологических потоках обогатительной фабрики, а именно на разгрузке нескольких спигот гидравлического классификатора. После подачи питания на полупромышленную установку были настроены промежуточные параметры, после чего подготовительный этап был завершен.
Разгрузка первого и второго спигота гидравлического классификатора
Объединенный продукт самотеком подавался на установку. Содержание твердого в данном потоке составляло около 40-50 %, максимальная крупность частиц 4 мм. Для соблюдения требований к потоку питания, поступающему на полупромышленную установку, в трубопровод подачи питания была добавлена вода сопровождения и часть потока была отведена через байпас установки.
Этап 1. G-ускорение
Испытания проводились на разных скоростях вращения ротора – 60, 70, 80 и 90 G; производительность по твердому составила 1,73 т/ч; средний объемный поток 1,44 м3/ч; содержание олова в питании 1,24 %; время закрытия клапана было остановлено на 8 с. На основании проведенного комплекса испытаний была установлена оптимальная скорость вращения ротора, которая составила 80 G, и зафиксировано минимальное значение содержания Sn в хвостах концентрации – 0,31 %. Максимальное содержание Sn в хвостах установлено при скорости 90 G – 0,44 %.
Этап 2. Расход флюидизационной воды
Испытания с различным значением уставки расхода флюидизационной воды во время цикла обогащения концентратора проводились при скорости вращения ротора 80 G, времени закрытия клапана 12 с, времени открытия клапана 0,32 с. Содержание твердого в питании составляло 25 %, олова – 1,24 %. Расход флюизационной воды варьировался от 25 до 45 л/мин.
Наилучшие результаты были зафиксированы при расходе воды 35 и 45 л/мин – извлечение составило 75,75 и 88,45 % соответственно. Однако содержание в концентрате более 2 % достигнуто только при расходе 45 л/мин. Для дальнейших тестов было принято использовать значение расхода флюидизационной воды, равное 45 л/мин.
Этап 3. Периодичность открытия пережимных клапанов
Следующим этапом являлось установление оптимального значения периодичности открытия пережимных клапанов концентратора. Время открытия 0,32 с; время закрытия клапана – 18, 24, 32, 48, 64 с; содержание Sn в питании 1,24 %.
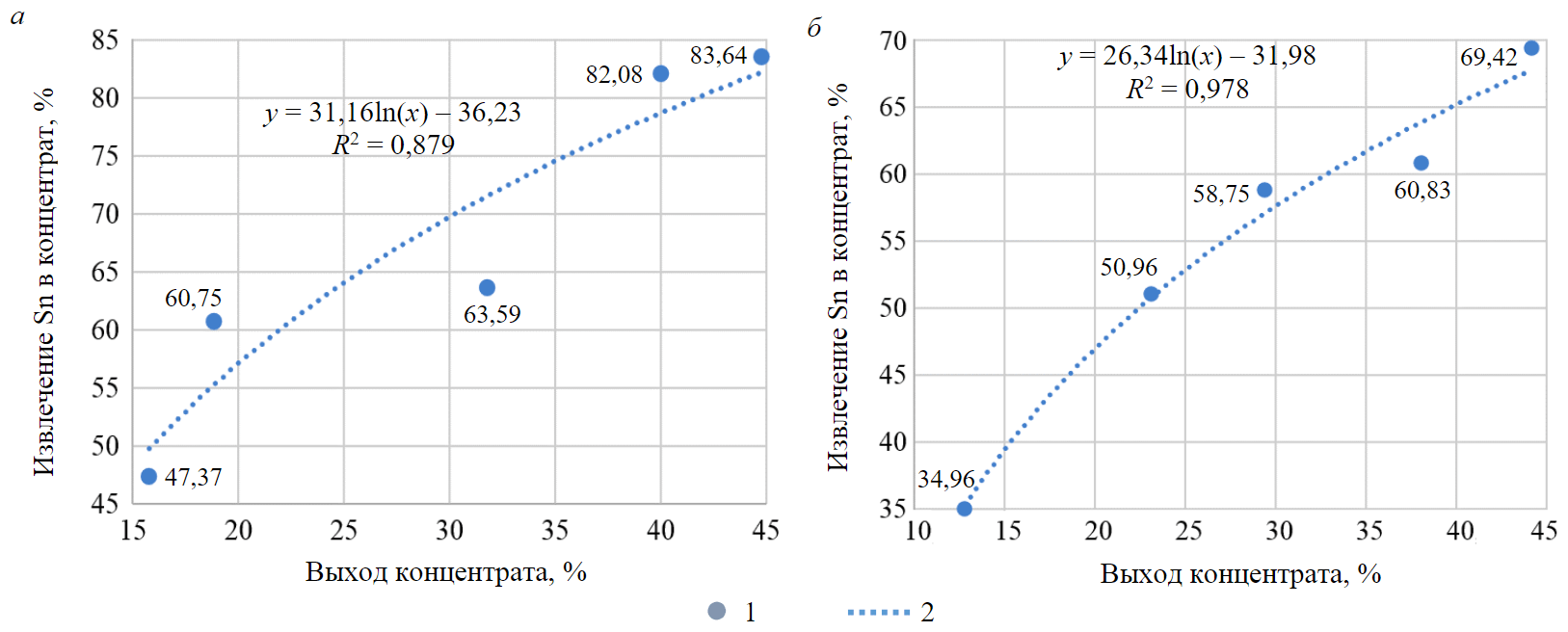
Рис.3. Зависимости извлечения Sn в концентрат от выхода концентрата при разгрузке первого и второго (а) и четвертого (б) спиготов гидравлического классификатора 1 – зависимость извлечения Sn от выхода; 2 – логарифмическая зависимость извлечения Sn в концентрат от выхода
В результате эксперимента установлено, что при увеличении уставки времени закрытия клапана содержание олова в концентрате линейно возрастает. Максимальное значение содержания в концентрате 3,23 % зафиксировано при значении уставки времени закрытия клапана 64 с. Однако при увеличении времени наблюдается повышение концентрации ценного компонента в хвостах. На основании полученных данных был построен график зависимости извлечения олова от выхода продукта (рис.3, а). В результате полупромышленных испытаний, коэффициент концентрации варьировался от 1,7 до 3, извлечение олова составило 60-83 %.
Разгрузка третьего спигота гидравлического классификатора
На данном технологическом потоке была обеспечена стабильная подача материала на концентратор со средним содержанием твердого в потоке 20-21 % крупностью частиц –1+0 мм. Извлечение не опускалось ниже 80 % при степени концентрации 1,51-1,76 и содержании олова в концентрате 1,12-1,31 %. Наилучшие показатели извлечения в концентрат зафиксированы при скорости вращения ротора в 70 G и составили 87,84 %.
По результатам выполнения данного теста было выбрано значение уставки расхода флюидизационной воды, равное 35 л/мин. Извлечение олова в концентрат составило 88,93 %. Наиболее низкое извлечение ценного компонента (80,55 %) зафиксировано при расходе 40 л/мин.
С увеличением времени закрытия пережимных клапанов извлечение олова в концентрат уменьшается с 82,6 до 42,35 %, при этом значительно снижается выход концентрата – с 44 до 9 %.
Установлено, что на технологические показатели работы концентратора значительное влияние оказывает крупность питания. Для эффективного обогащения представленного сырья со снижением крупности необходимо снижать скорость вращения ротора и расход флюидизационной воды.
Разгрузка четвертого спигота гидравлического классификатора
Аналогичный комплекс исследований проведен на разгрузке четвертого спигота гидравлического классификатора (рис.3, б). На различных технологических потоках установлено изменение коэффициента концентрации от 1,5 до 2,7, при этом извлечение фиксировалось в диапазоне 34-70 %; содержание олова в концентрате варьировалось от 2,78 до 3,65 г/т.
Обсуждение результатов
В результате испытаний был получен массив данных 33 экспериментов (см. таблицу). В качестве независимых переменных выступают скорость вращения ротора х1, расход флюидизационной воды х2, время, в течение которого клапан открыт, х3 и содержание ценного компонента в питании х4. В качестве выходных переменных принимается содержание ценного компонента в концентрате у1 и хвостах у2.
Результаты опробования после применения процедуры нормирования
|
Скорость вращения |
Расход флюид. воды х2 |
Время х3 |
Питание (Sn) х4, % |
Концентрат (Sn) у1, % |
Хвосты (Sn) у2, % |
|
–1,90502 |
–1,20829 |
–0,73582 |
0,449332 |
–0,85767 |
–0,10721 |
|
–0,64771 |
–1,20829 |
–0,73582 |
1,326049 |
–0,43093 |
–0,2532 |
|
0,609607 |
–1,20829 |
–0,73582 |
0,830513 |
–0,49494 |
–0,69117 |
|
1,866921 |
–1,20829 |
–0,73582 |
1,402285 |
–0,69764 |
0,257765 |
|
0,609607 |
–0,69045 |
–0,47726 |
–0,92292 |
–0,18556 |
0,841728 |
|
0,609607 |
–0,17261 |
–0,47726 |
1,859703 |
–0,50561 |
0,038779 |
|
0,609607 |
0,345225 |
–0,47726 |
1,211695 |
0,35852 |
–0,54518 |
|
0,609607 |
0,863064 |
–0,47726 |
–0,80857 |
0,145154 |
–0,39919 |
|
0,609607 |
1,380902 |
–0,47726 |
0,373096 |
1,094632 |
–0,2532 |
|
0,609607 |
1,380902 |
0,292669 |
1,135458 |
0,134485 |
0,33076 |
|
0,609607 |
1,380902 |
0,805954 |
2,317121 |
0,582554 |
1,133709 |
|
0,609607 |
1,380902 |
1,832523 |
–0,54174 |
1,382676 |
2,812602 |
|
0,609607 |
1,380902 |
2,859092 |
1,09734 |
1,553369 |
1,790667 |
|
0,609607 |
0,863064 |
0,804671 |
–0,84668 |
0,347851 |
1,644676 |
|
–1,90502 |
–0,69045 |
–0,47854 |
–0,84668 |
–0,49494 |
–1,05615 |
|
–0,64771 |
–0,69045 |
–0,47854 |
–0,69421 |
–0,54829 |
–1,34813 |
|
0,609607 |
–0,69045 |
–0,47854 |
–0,92292 |
–0,69764 |
–1,20214 |
|
1,866921 |
–0,69045 |
–0,47854 |
–1,07539 |
–0,58029 |
–1,20214 |
|
–0,64771 |
–1,20829 |
–0,47854 |
0,296859 |
–0,10022 |
–0,39919 |
|
–0,64771 |
–0,17261 |
–0,47854 |
0,525568 |
–0,14289 |
–0,10721 |
|
–0,64771 |
0,345225 |
–0,47854 |
0,525568 |
–0,12155 |
–0,69117 |
|
–0,64771 |
0,863064 |
–0,47854 |
–0,80857 |
–0,6123 |
–0,69117 |
|
–0,64771 |
1,380902 |
–0,47854 |
–0,73233 |
–0,6123 |
–0,98316 |
|
–0,64771 |
0,345225 |
–0,09358 |
0,030032 |
0,070475 |
–0,69117 |
|
–0,64771 |
0,345225 |
0,291386 |
–0,35115 |
–0,53762 |
–2,95403 |
|
–0,64771 |
0,345225 |
0,804671 |
–0,35115 |
0,742578 |
0,257765 |
|
–0,64771 |
0,345225 |
1,83124 |
–0,12244 |
2,438838 |
0,841728 |
|
–0,64771 |
0,345225 |
2,857809 |
0,220623 |
3,238961 |
1,863662 |
|
–1,90502 |
–1,20829 |
–0,47854 |
–0,80857 |
–0,85767 |
–0,39919 |
|
–0,64771 |
–1,20829 |
–0,47854 |
–1,15163 |
–1,02836 |
–0,2532 |
|
0,609607 |
–1,20829 |
–0,47854 |
–1,53281 |
–1,18838 |
–0,2532 |
|
1,866921 |
–1,20829 |
–0,47854 |
–1,45657 |
–1,07103 |
–0,83717 |
|
0,609607 |
1,380902 |
–0,73582 |
0,373096 |
–0,32425 |
0,549746 |
Обработка полученных результатов для поиска наиболее адекватной модели, связывающей входные х1, х2, х3, х4 и выходные у1, у2 параметры процесса, проходила с использованием двух наиболее распространенных метрик: коэффициента детерминации R2 и объясненной дисперсии EV. Применение подобной метрики подразумевает разделение исходного набора данных на две части – обучающую и тестовые выборки:
где m – количество векторов в тестирующей выборке; уi – истинные значения параметра; < – значение, рассчитанное на основе модели; – среднее значение параметра при расчете по тестирующей выборке; D – дисперсия.
Для исключения влияния содержания выборок (обучающей и тестовой) на оценки моделей применяется кросс-валидация [26], когда из исходной выборки случайным образом k раз выбирается два подмножества без повторений. При этом расчет оценок также проводится k раз, и, таким образом, можно получить не зависящую от входных данных оценку эффективности модели. Ввиду небольшого объема исходных данных разобьем исходную выборку в отношении 80:20 для обучающей и тестирующей части соответственно, а k примем равным пяти.
При использовании таких моделей наиболее целесообразным представляется применение уравнений регрессии. Сначала рассмотрим простую линейную модель для переменной y1 (коэффициент детерминации R2 = 0,74 на обучающей выборке):
при этом p-значения коэффициентов регрессии, рассчитанные на основе t-статистики равны 0,69; 0,8; 0,14; 1,34·10–6; 0,15. Поскольку все коэффициенты, кроме коэффициента при х3, существенно больше 0,05, то, несмотря на то, что зависимость между исследуемыми переменными существует, оценить ее количественные характеристики по данному уравнению невозможно.
Поэтому для поиска регрессионной зависимости между исследуемыми переменными предлагаем использовать другие методы, позволяющие установить не только качественную, но и количественную связь между факторами [27]. Так, наряду с классическим методом наименьших квадратов, для решения задач регрессионного анализа и конструирования сложных нелинейных моделей используется один из алгоритмов машинного обучения, называемый методом опорных векторов (SVM). Данный подход широко применяется для решения задачи классификации, однако в работах [28-30] показана его применимость к решению задач регрессии.
Метод опорных векторов применяется для отображения исходного пространства R4 e x = (х1, х2, х3, х4)T в некоторое гиперпространство H. В этом гиперпространстве строятся две параллельные плоскости, положение которых различается на значение параметра b. Однако для того, чтобы построить эти гиперплоскости, начиная с некоторого приближения, из обучающей выборки выбираются векторы и добавляются в множество опорных SV. После чего определяется целевая функция решаемой задачи оптимизации – минимизация отклонения для всех векторов, не попавших в «зазор» между построенными гиперплоскостями, а также определяется двойственная задача к данной прямой задаче [30, 31].
Итоговое уравнение регрессии выглядит так:
где Di – коэффициенты двойственной задачи (по отношению к прямой, заключающейся в поиске коэффициентов гиперплоскости, минимизирующей функцию штрафа); SV – множество индексов опорных векторов; – ядро, используемое при построении гиперпространства.
Рассмотрим функции K , применяемые в данном алгоритме в качестве ядер. Так, любая функция, применяемая в качестве ядра должна удовлетворять условия теоремы Мерсера [32], которая требует неотрицательной определенности и симметричности функции в пространстве Rn. Cуществует несколько стандартных функций , используемых в программных библиотеках, реализующих метод опорных векторов. Поскольку установлено, что линейная регрессия не принесла удовлетворительного результата, используются два типа нелинейных ядер:
- полиномиальное ядро , где – скалярное произведение векторов и ; p – максимальная степень полинома;
- радиально-базисное ядро , где – метрика расстояния между векторами; γ – параметр.
При использовании полиномиального ядра и размерности пространства признаков n = 4 с раскрытием скобок функция ядра предстает в следующем виде:
где x1i … x4i – координаты i-го опорного вектора.
Поскольку мы располагаем всего 33 наблюдениями, применение степени p > 2 не будет оправдано ввиду того, что уже при p= 3 количество коэффициентов в уравнении регрессии будет равно 33, поэтому для нашей задачи используется p = 2. Тогда при раскрытии скобок и подставлении ядра в выражение (1) получим уравнение регрессии для полиномиального ядра второй степени
где α1 … α14 – коэффициенты, получаемые из координат i-го опорного вектора.
Для радиально-базисного ядра функция записывается в таком виде:
Подставляя в выражение (1) уравнения регрессии, получим:
где αij – коэффициенты, получаемые из координат i-го опорного вектора.
Полученная регрессионная функция не содержит отдельных коэффициентов для квадратов переменных x1, x2, x3, x4, что затрудняет идентификацию влияния на выход каждого параметра в отдельности, однако такая функция может учесть существенную нелинейную зависимость между входами и выходами процесса.
Для программной реализации метода опорных векторов к задаче обработки результатов испытаний технологии CVD6 при обогащении оловянных руд воспользуемся библиотекой Scikit-learn для языка программирования Python. В качестве стратегии разбиения на обучающую и тестирующую выборки использовался метод ShuffleSplit, а для обработки массивов данных библиотека Numpy.
Данные, полученные в результате работы программы: при линейной регрессии R2 = 0,614, EV = 0,722; при полиномиальном ядре SVM R2 = 0,693, EV = 0,781; при радиально-базисном ядре SVM R2 = 0,742, EV = 0,781. Для метрик R2 и EV показаны усредненные результаты, полученные после пяти запусков.
Использование обеих метрик метода SVM показало лучшие результаты относительно простой линейной регрессии, при этом для метрики R2 радиально-базисное ядро выявило несколько лучший результат.
Особенностью метода опорных векторов является наличие гиперпараметра регуляризации C, определение которого индивидуально как для каждой применяемой функции ядра, так и для каждой решаемой задачи [30, 33, 34]. Для поиска наилучшего значения C воспользуемся регулярным поиском по отрезку C ∈ [0,0001; 10,0001] с шагом 0,0001 (рис.4).
Итоговые уравнения регрессии, полученные при лучших значениях гиперпараметра C метода SVM: для полиномиального ядра второй степени значение, соответствующее максимальному значению метрики EV, C = 0,0401, для радиально-базисного C = 2,943. Таким образом, уравнение регрессии при полиномиальном ядре представлено выражением:
Значение метрики R2, рассчитанное на тестирующей выборке для данного уравнения, равно 0,858, что является высоким результатом.
После применения метода опорных векторов с радиально-базисным ядром к решаемой задаче количество опорных векторов оказалось равным 20 и, соответственно, уравнение (2) содержит 20 слагаемых, поэтому представим его в общем виде:
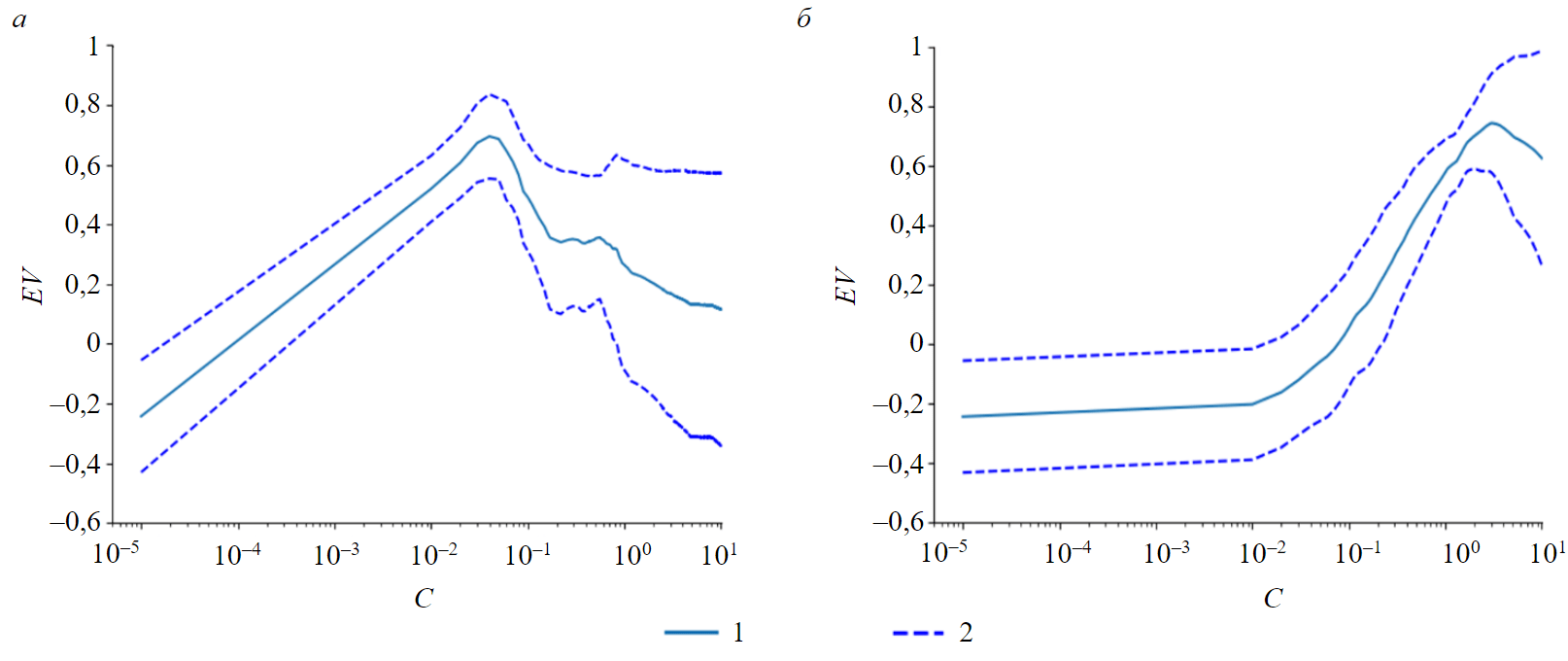
Рис.4. Графики подбора гиперпараметра С метода SVM для полиноминального (а) и радиально-базисного (б) ядер 1 – зависимость метрики от значения; 2 – среднеквадратичное отклонение
Представим в виде массива значения коэффициентов Bi = (–0,24; –0,13; –0,9; –2,19; –1,81; 2,45, 2,43; –1,17; 0,62; 1,39; –1,82; –0,53; –2,41; –5,96; 1,93; 3,47; –2,08; 3,36; 0,1; 2,81).
Поскольку общее количество коэффициентов αi1; αi2; αi3; αi4 равно 80, в статье их приводить не следует. Значение метрики R2, рассчитанное на тестирующей выборке для данного уравнения, равно 0,923, что соответствует высокой прогностической способности модели.
Представим аналогичные исследования для хвостов. При использовании полиномиального ядра получено следующее уравнение регрессии:
Коэффициент детерминации R2, рассчитанный на тестирующей выборке, равен 0,59, что является низким результатом.
Для радиально-базисного ядра общая форма уравнения совпадает с выражением (4), а Bi имеем следующий набор коэффициентов: Bi = (–0,33; 0,03; 0,54; 0,41; 0,64; 0,56; –0,75; –0,25; –0,49; 1,36; 0,19; 0,78; –1,51; –1,43; 0,14; –2,11; –2,23; –0,40; 0,05; 1,29; 1,11; –0,24; –0,58).
Значение свободного коэффициента b = 0,296, при этом R2 = 0,846.
Полученные результаты хорошо согласуются с результатами, полученными при работе на обогатительных фабриках с иным ценным компонентом [18-20]. Так, модели (3), (4) для концентрата y1 показали очень хорошую прогностическую способность на тестовых выборках (R2 > 0,85), при этом использование полиномиального ядра предпочтительнее, так как позволяет исследовать полученное уравнение для поиска экстремальных точек.
В результате была найдена стационарная точка M0 (–2,8; –3,47; –1,83; 0,23), соответствующая данной точке матрица Гессе является знакопеременной. При этом детерминант наибольшего минора не равен нулю, что говорит о том, что найденная точка M0 является седловой, т.е. максимальные значения в концентрате следует искать с учетом ограничений накладываемых на значения переменных х1, х2, х3, х4.
При использовании полиномиального ядра в модели для хвостов получаются неудовлетворительные результаты, однако модель, полученная на основе радиально-базисного ядра, подтвердила тезис о нелинейной зависимости содержания ценного компонента в хвостах от настраиваемых параметров.
Заключение
Установлено, что метод опорных векторов применим к задаче обработки результатов обогатительных испытаний и показывает достаточно интересные результаты. В частности, полученная модель хвостов при использовании радиально-базисного ядра убедительно свидетельствует о существенной нелинейности взаимосвязи между содержанием ценного компонента и настраиваемыми параметрами, что будет накладывать дополнительные ограничения в случае параметрической оптимизации работы установки. Применяя метод опорных векторов SVR с радиально-базисным ядром RBF, удалось получить модель, прогностическая способность которой имеет достаточно высокий результат (R2 = 0,846).
Применение полиномиального ядра для поиска зависимости между содержанием ценного компонента в концентрате и настраиваемыми параметрами позволило получить не зависящую от входных данных высокую прогностическую способность R2 = 0,858. При этом использование полиномиального ядра позволило проводить с полученным уравнением стандартную процедуру поиска экстремума функции многих переменных. Полученные значения коэффициентов регрессии позволяют утверждать, что наиболее влиятельным фактором на выход концентрата является время, в течение которого открыт пережимной клапан, поскольку полученные коэффициенты уравнения (3) имеют наибольшие абсолютные значения слагаемых, в которых присутствует переменная х3.
Литература
- Чантурия В.А., Бочаров В.А. Современное состояние и основные направления развития технологии комплексной переработки минерального сырья цветных металлов // Цветные металлы. 2016. № 11. С. 11-18. DOI: 10.17580/tsm.2016.11.01
- Aleksandrova T.N., Orlova A.V., Taranov V.A. Enhancement of copper concentration efficiency in complex ore processing by the reagent regime variation // Journal of Mining Science. 2020. Vol. 56. Iss. 6. P. 982-989. DOI: 10.1134/S1062739120060101
- Федотов П.К., Сенченко А.Е., Федотов К.В., Бурдонов А.Е. Исследования обогатимости сульфидных и окисленных руд золоторудных месторождений Алданского щита // Записки Горного института. 2020. Т. 242. С. 218-227. DOI: 10.31897/PMI.2020.2.218
- Angadi S.I., Sreenivas T., Ho-Seok Jeon et al. A review of cassiterite beneficiation fundamentals and plant practices // Minerals Engineering. 2015. Vol. 70. P. 178-200. DOI: 10.1016/j.mineng.2014.09.009
- Matveeva T.N., Chanturiya V.A., Getman V.V. et al. The Effect of Complexing Reagents on Flotation of Sulfide Minerals and Cassiterite from Tin-Sulfide Tailings // Mineral Processing and Extractive Metallurgy Review. 2022. Vol. 43. Iss. 3. P. 346-359. DOI: 10.1080/08827508.2020.1858080
- Leistner T., Embrechts M., Leißner T. A study of the reprocessing of fine and ultrafine cassiterite from gravity tailing residues by using various flotation techniques // Minerals Engineering. 2016. Vol. 96-97. P. 94-98. DOI: 10.1016/j.mineng.2016.06.020
- Matveeva T.N., Getman V.V., Karkeshkina A.Yu. Flotation extraction of tin from tailings of sulfide-tin ore dressing using thermomorphic polymer // Eurasian Mining. 2021. № 2. P. 46-49. DOI: 10.17580/em.2021.02.10
- Hassanzadeh A., Safari M., Duong H. Hoang et al. Technological assessments on recent developments in fine and coarse particle flotation systems // Minerals Engineering. 2022. Vol. 180. № 107509. DOI: 10.1016/j.mineng.2022.107509
- Angadi S.I., Eswaraiah C., Ho-Seok Jeon et al. Selection of Gravity Separators for the Beneficiation of the Uljin Tin Ore // Mineral Processing and Extractive Metallurgy Review. 2017. Vol. 38. Iss. 1. P. 54-61. DOI: 10.1080/08827508.2016.1262856
- Tong Yue, Haisheng Han, Yuehua Hu et al. Beneficiation and purification of tungsten and cassiterite minerals using Pb-BHA complexes flotation and centrifugal separation // Minerals. 2018. Vol. 8. Iss. 2. № 566. DOI: 10.3390/min8120566
- Zhang Jin-Lu, Ge Bao-Liang, Wang Xian-Qiang, Yang Chun-Gang. Study on Beneficiation of a Stanniferous Multi-metallic Sulphide Ore in Yunnan // The Chinese Journal of Process Engineering. 2015. Vol. 15. Iss. 6. P. 945-953. DOI: 10.12034/j.issn.1009-606X.215282
- Юсупов Т.С., Кондратьев С.А., Бакшеева И.И. Структурно-химические и технологические свойства минералов касситерит-сульфидного техногенного сырья // Обогащение руд. 2016. № 5. С. 26-31. DOI: 10.17580/or.2016.05.05
- Yong Cheng Zhou, Xiong Tong, Xiao Wang et al. Beneficiation of Ultrafine Cassiterite from a Tin Tailings by Flotation // Advanced Materials Research. 2013. Vol. 616-618. P. 643-648. DOI: 10.4028/www.scientific.net/AMR.616-618.643
- Yongcheng Zhou, Xiong Tong, Shaoxian Song et al. Beneficiation of Cassiterite Fines from a Tin Tailing Slime by Froth Flotation // Separation Science and Technology. Vol. 49. Iss. 3. P. 458-463. DOI: 10.1080/01496395.2013.818036
- Murthy Y.R., Tripathy S.K. Process optimization of a chrome ore gravity concentration plant for sustainable development // Journal of the Southern African Institute of Mining and Metallurgy. 2021. Vol. 120. № 4. P. 261-268. DOI: 10.17159/2411-9717/990/2020
- Basnayaka L., Albijanic B., Subasinghe N. Performance evaluation of processing clay-containing ore in Knelson concentrator // Minerals Engineering. 2020. Vol. 152. № 106372. DOI: 10.1016/j.mineng.2020.106372
- Nayak A., Jena M.S., Mandre N.R. Application of Enhanced Gravity Separators for Fine Particle Processing: An Overview // Journal of Sustainable Metallurgy. 2021. Vol. 7. Iss. 2. P. 315-339. DOI: 10.1007/s40831-021-00343-5
- Пелих В.В., Салов В.М., Бурдонов А.Е., Лукьянов Н.Д. Модель извлечения бадделеита из отвальных продуктов апатито-бадделеитовой обогатительной фабрики на концентраторе CVD6 // Записки Горного института. 2021. Т. 248. С. 281-289. DOI: 10.31897/PMI.2021.2.12
- Пелих В.В., Салов В.М., Бурдонов А.Е., Лукьянов Н.Д. Установление технологических зависимостей работы концентратора KC-CVD6 с помощью метода группового учета аргументов // Известия Томского политехнического университета. Инжиниринг георесурсов. 2020. Т. 331. № 2. С. 139-150. DOI: 10.18799/24131830/2020/2/2500
- Пелих В.В., Салов В.М., Бурдонов А.Е., Лукьянов Н.Д. Применение Knelson CVD-технологии для обогащения золото-свинцовой руды // Обогащение руд. 2019. № 1. С. 3-11. DOI: 10.17580/or.2019.01.01
- Sakuhuni G., Emre Altun N., Klein B. Modelling of continuous centrifugal gravity concentrators using a hybrid optimization approach based on gold metallurgical data // Minerals Engineering. 2022. Vol. 179. № 107425. DOI: 10.1016/j.mineng.2022.107425
- Койжанова А.К., Кенжалиев Б.К., Магомедов Д.Р., Абдылдаев Н.Н. Разработка комбинированной технологии обогащения малосульфидных золотосодержащих руд // Обогащение руд. 2021. № 2. С. 3-8. DOI: 10.17580/or.2021.02.01
- Majumder A.K., Barnwal J.P. Modeling of enhanced gravity concentrators – Present status // Mineral Processing and Extractive Metallurgy Review. 2006. Vol. 27. Iss. 1. P. 61-86. DOI: 10.1080/08827500500339307
- Fedotov P.K., Senchenko A.E., Fedotov K.V., Burdonov A.E. Integrated Technology for Processing Gold-Bearing Ore // Journal of The Institution of Engineers (India): Series D. 2021. Vol. 102. Iss. 2. P. 397-411. DOI: 10.1007/s40033-021-00291-0
- Jordens A., Sheridan R.S., Rowson N.A., Waters K.E. Processing a rare earth mineral deposit using gravity and magnetic separation // Minerals Engineering. 2014. Vol. 62. P. 9-18. DOI: 10.1016/j.mineng.2013.09.011
- Ojala M., Garriga G.C. Permutation Tests for Studying Classifier Performance // Journal of Machine Learning Research. 2010. Vol. 11. P. 1833-1863.
- Tie-Yan Liu. Learning to rank for Information Retrieval // Foundations and Trends in Information Retrieval. 2009. Vol. 3. № 3. P. 225-231. DOI: 10.1561/1500000016
- Vapnik V.N. An overview of statistical learning theory // IEEE Transactions on Neural Networks. 1999. Vol. 10. Iss. 5. P. 988-999. DOI: 10.1109/72.788640
- Ghanbari E., Shakery A. A Learning to rank framework based on cross-lingual loss function for cross-lingual information retrieval // Applied Intelligence. Vol. 52. P. 3156-3174. DOI: 10.1007/s10489-021-02592-z
- Sacks J., Welch W.J., Mitchell T.J., Wynn H.P. Design and analysis of computer experiments // Statistical Science. 1989. Vol. 4. Iss. 4. P. 409-423. DOI: 10.1214/ss/1177012413
- Smola A.J., Schölkopf B. A tutorial on support vector regression // Statistics and Computing. 2004. Vol. 14. P. 199-222. DOI: 10.1023/B:STCO.0000035301.49549.88
- Bartlett P., Shawe-Taylor J. Generalization Performance of Support Vector Machines and Other Pattern Classifiers // Advances in Kernel Methods. Cambridge: MIT Press, 1998. P. 43-54.
- Vapnik V., Izmailov R. V-matrix method of solving statistical inference problems // Journal of Machine Learning Research. 2015. Vol. 16. P. 1683-1730.
- Burdonov I.B., Vinarskii E.M., Yevtushenko N.V., Kossatchev A.S. Perfect Sets of Paths in the Full Graph of SDN Switches // Programming and Computer Software. 2021. Vol. 47. Iss. 7. P. 505-514. DOI: 10.1134/S0361768821070033
