Развитие методологии сценарного анализа инвестиционных проектов предприятий минерально-сырьевого комплекса

Введение

Инвестирование средств в отрасли сферы недропользования в странах с ресурсоориентированной экономикой имеет чрезвычайно важное значение для развития национального хозяйства – экономического роста, социального развития и в конечном итоге роста конкурентоспособности макроэкономической системы [1]. Эффективность принятия инвестиционных решений в области реализации инвестиционных проектов в соответствующих минерально-сырьевых отраслях экономики во многом зависит от процессов управления этими проектами, в частности снижения их информационной неопределенности. На сегодняшний день задача снижения информационной неопределенности при оценке рисков инвестиционных проектов является одной из наиболее сложных и актуальных задач инвестиционного проектирования [2]. Сложность принимаемых в этой области решений обусловлена тем, что величины денежных потоков от операционной, финансовой и инвестиционной деятельности предприятия имеют прогнозный характер. Это в свою очередь ограничивает применение детерминированных методов и требует учета факторов случайности и неопределенности при оценке параметров внутренней и внешней среды проекта [3-5].

Риск-менеджмент инвестиционных проектов на предприятиях минерально-сырьевого комплекса не может не учитывать отраслевые особенности сферы недропользования, вытекающие из содержания производственно-коммерческой деятельности ее хозяйствующих субъектов [6-8]. Процессы воспроизводства хозяйственной деятельности ресурсодобывающих компаний протекают на основе природно-технологических факторов развития сферы недропользования и действия экономических законов [9]. Конечной целевой установкой управления рисками на предприятии следует считать рост его конкурентоспособности на внутреннем и внешнем рынках [10-12].

Одним из ключевых элементов системы управления проектными рисками являются количественные методы их оценки [13, 14]. Среди них наиболее известными являются методы: анализа чувствительности критериев эффективности проекта; корректировки нормы дисконта; анализа показателей предельного уровня; анализа сценариев развития проекта; построения «дерева решений»; имитационного статистического моделирования (метод Монте-Карло) [15-17].

При принятии инвестиционных решений в условиях существенной неопределенности факторов внешней среды широкое распространение получил метод анализа сценариев развития проекта [18-20]. Данный метод основывается на экспертных суждениях, связанных с построением нескольких прогнозных моделей денежных потоков проекта и указанием вероятностей их реализации.  Главным недостатком сценарного прогнозирования является субъективизм вынесенных экспертных суждений. Для снижения степени субъективизма, как правило, привлекается дополнительная информация. В методе анализа сценариев такая информация может быть получена путем установления отношений предпочтения для возможных значений исследуемых параметров проекта, что позволяет построить их вероятностные распределения и в качестве оценки использовать максимально правдоподобные значения в смысле максимума априорной вероятности.

Таким образом, целью данной работы является снижение информационной неопределенности при сценарном анализе рисков инвестиционных проектов. Данная цель достигается за счет ряда модификаций типовой процедуры сценарного анализа, а именно применения интервально-вероятностного подхода при оценке стохастических параметров проекта и введения дополнительного показателя оценки риска для снижения субъективизма экспертных суждений.

Методы

Во всем мире сфера недропользования считается высокорисковой. Риски являются как следствием результатов производственно-коммерческой деятельности ее субъектов, так и инвестиционной привлекательности соответствующих предприятий и уровня активности инвесторов. В результате анализа инвестиционных проектов в сфере недропользования были выявлены специфические для минерально-сырьевых отраслей экономики факторы риска, которые условно можно сгруппировать на правовые, горно-геологические, финансовые, производственные, территориальные. В международной практике окончательное решение в области утверждения (отклонения) инвестиционного проекта принимается по финансовым индикаторам и показателям бизнес-планов проектов, их технико-экономического обоснования [21]. Именно поэтому модифицированный сценарный анализ инвестиционных проектов опирается [22, 23] прежде всего на финансовые характеристики проектов с использованием соответствующего экономико-математического инструментария. В процессе принятия инвестиционных решений современные традиционные методики управления рисками включают: самострахование рисков (образование финансовых резервов «в качестве подушки безопасности»), страхование риска страховой компанией, хеджирование риска конкретными субъектами фондового рынка, «долевое» распределение риска внутри участников инвестиционного проекта.

Развитие методологии сценарного анализа инвестиционных проектов в минерально-сырьевом секторе экономики должно строиться на учете отраслевых особенностей хозяйствующих субъектов сферы недропользования [24]:

1. На предынвестиционной фазе управления проектом имеет место высокая неопределенность значений его основных технико-экономических параметров. Это вызвано тем, что для каждого месторождения полезных ископаемых всегда сложно определить с высокой точностью их запасы в связи с особенностями залегания запасов, постоянной динамики и сложности горно-геологических условий. Поэтому при разработке и реализации соответствующих инвестиционных решений необходимо учитывать специфику конкретного месторождения так же, как и целесообразный срок функционирования горнодобывающих предприятий, который напрямую зависит от срока разработки соответствующих месторождений, зависящий от объема запасов полезных ископаемых и рентабельности добычи [25].
2. Существует постоянный рост потребности и спроса на сырьевые ресурсы и конечную продукцию в результате их обогащения и переработки. Все это в конечном итоге повышает инвестиционную активность минерально-сырьевого комплекса и актуализирует вопросы инвестиционного проектирования в рамках создания новых производств и развития материально-технической базы сферы недропользования [26, 27].
3. Реализация инвестиционных проектов в сфере недропользования, как правило, характеризуется длительным циклом, отличается высоким уровнем сложности и капиталоемкости [28, 29]. Это вызвано тем, что функционирование горнодобывающих предприятий всегда ориентировано на развитую инфраструктуру, создание которой и поддержание в необходимом состоянии невозможны без строительства и логистики [30, 31]. Также велики расходы не только на его приобретение, но и эксплуатацию и ремонт. Необходимо учитывать и размещение предприятий недропользования относительно соответствующих месторождений. Эффективные решения в этой области способствуют снижению неоправданных издержек – транспортно-логистических, связанных с созданием и функционированием инженерной и социальной инфраструктуры. Стоит отметить и то, что длительный производственный цикл распространяется и на всю цепочку создания добавленной стоимости – от геологоразведки, добычи и до создания конечного продукта [32, 33].
4. Соблюдение принципов рационального недропользования предполагает разработку широкомасштабных мероприятий в области минимизации потерь сырьевых ресурсов и, как следствие, величины штрафных санкций. Кроме этого, горная промышленность связана с экологически вредными производствами, которые в современных условиях предполагают использование природоохранного оборудования, существенно увеличивающего потребность в объеме инвестиционных ресурсов [34].
5. Дополнительные инвестиционные риски вызваны высокой неопределенностью в сфере правового регулирования недропользования. Законодательство в этой области постоянно совершенствуется, претерпевает изменения. Основополагающим документом остаются Методические рекомендации по оценке эффективности инвестиционных проектов.

Например, инвестиционные проекты, утвержденные ПАО «Газпром», диверсифицированы и охватывают разные отрасли топливно-энергетического комплекса. Только в настоящее время компания реализует несколько десятков широкомасштабных проектов не только на территории Российской Федерации, но и за ее пределами:

• Восточная газовая программа, ориентированная на создание полномасштабной газовой промышленности на Востоке Сибири, – пять месторождений в стадии промышленной эксплуатации, длина газопровода «Сила Сибири» около 3 тыс. км;
• Ямал, новый центр газодобычи – 32 месторождения, 36,5 трлн м³ газа, 1,6 млрд т газового конденсата, 300 млн т нефти;
• СПГ – проекты сжиженного природного газа – Сахалин-2, Владивосток-СПГ, комплекс по переработке этансодержащего газа и производству СПГ в Ленинградской обл., проект поставок СПГ в Калининградскую обл.

Метод анализа сценариев развития проекта состоит в вариативном расчете показателей эффективности проекта и их последующей агрегации в обобщенный показатель с учетом риска. При этом следует отметить, что, в отличие от метода анализа чувствительности, в методе анализа сценариев предполагается совместное и взаимоувязанное изменение нескольких параметров проекта.

Под сценарием развития проекта понимается правдоподобная непротиворечивая комбинация параметров проекта, а также факторов его внешнего окружения. В общем случае процедура анализа сценариев предполагает выполнение следующих этапов:

• Генерируется несколько вариантов (сценариев) изменений исходных параметров проекта в соответствии с представлениями его участников о возможных рисках.
• Для каждого сценария указывается вероятностная оценка его реализации.
• По каждому сценарию рассчитываются показатели эффективности и риска проекта (как правило, NPV – чистый дисконтированный доход и s – стандартное отклонение).

Типовая процедура метода предполагает рассмотрение трех возможных сценариев развития проекта – пессимистического, наиболее вероятного и оптимистического, а в качестве критерия эффективности выступает чистый дисконтированный доход NPV. В этом случае интегральный показатель эффективности проекта рассчитывается по формуле математического ожидания (Методические рекомендации. С. 48):

где NPV₁, NPV₂, NPV₃ – чистый дисконтированный доход для пессимистического, наиболее вероятного и оптимистического сценариев соответственно; p_i – вероятность осуществления сценария.

В качестве показателя риска обычно используется стандартное отклонение

Чем меньше стандартное отклонение, тем менее рискованным считается проект.

Использование формул (1) и (2) связано с определением точечных оценок априорных вероятностей p_i, что на практике часто вызывает существенные затруднения. Это обусловлено тем, что инвестиционные проекты в минерально-сырьевом секторе экономики являются, как правило, уникальными и невозможно подобрать статистический массив данных, пригодный для объективного установления вероятностей p_i. Поэтому для получения точечных значений вероятностей p_i часто рекомендуется использовать экспертные оценки. Так как в основе любой экспертной процедуры лежат субъективные соображения, то вероятности p_i получили название субъективных вероятностей.

Ряд исследователей высказывают серьезные критические замечания относительно использования вероятностного подхода для оценки ожидаемой эффективности и риска проекта как раз в силу субъективной природы вероятностей p_i [35]. Следует отметить, что в ситуациях, связанных с оценкой неопределенности глобальных факторов внешнего окружения проекта (природно-климатических, политических, макроэкономических и др.), найти альтернативу вероятностному подходу достаточно затруднительно.

Когда имеет место информационная неопределенность внутренних количественных параметров проекта и нет группы экспертов, высказавших согласованное мнение о вероятностях реализации отдельных сценариев, более предпочтительным, на наш взгляд, является использование интервального подхода для оценки ожидаемой эффективности проекта. В этом случае для расчета интегрального показателя эффективности проекта рекомендуется использовать формулу Гурвица:

где NPV_min, NPV_max – чистый дисконтированный доход для наиболее пессимистического и наиболее оптимистического сценариев соответственно; λ – коэффициент, отражающий систему предпочтений лица, принимающего решение (ЛПР), λ∈[ 0 , 1 ].

Обоснование формулы (3), а также ее обобщение применительно к оценке эффективности инвестиционных проектов можно найти в работе П.Л.Виленского.

При λ = 0 в формуле (3) реализуется система предпочтений, соответствующая крайнему пессимизму, при λ = 1 – крайнему оптимизму, при λ = 0,5 – нет выраженной склонности ни в сторону пессимизма, ни в сторону оптимизма. В инвестиционном проектировании обычно λ∈[ 0 , 0 , 5 ], что отражает предпочтения инвесторов, не склонных к риску. Чаще всего можно встретить значение λ = 0,3, что соответствует умеренно-пессимистической системе предпочтений инвестора. В Методических рекомендациях (С. 89) также рекомендуется использовать значение λ = 0,3.

Доминирование умеренно-пессимистического подхода при оценке эффективности инвестиционных проектов, по всей видимости, можно объяснить тем обстоятельством, что желательно по возможности предотвращать ситуации, при которых из-за естественных отклонений фактических значений денежных потоков от их расчетных значений проекты, оцененные как эффективные, такими не окажутся. Чтобы этого избежать, исходные данные, используемые при расчетах, должны быть несколько «ухудшены», что придаст оценке проекта некоторый «запас прочности». Однако указанные «ухудшения» не должны быть слишком велики, так как иначе в результате расчета могут быть необоснованно отброшены и «хорошие» (эффективные) проекты. Таким образом, умеренный пессимизм отражает разумное, по мнению авторов, отношение инвесторов к риску, поэтому именно данный принцип и был положен в основу последующих рассуждений. При поступлении дополнительной информации о факторах, влияющих на реализацию проекта, значение l может быть пересмотрено в сторону увеличения.

В рамках вероятностного подхода к оценке ожидаемой эффективности проекта ключевой методологической проблемой является субъективная природа вероятностей p_i в формулах (1) и (2). Для снижения степени субъективизма в определении этих вероятностей предлагается использовать метод анализа иерархий.

Суть предлагаемой процедуры состоит в следующем. ЛПР выносит качественные суждения о степени предпочтения одного сценария перед другим в соответствии со шкалой Саати. В результате формируется матрица предпочтений сценариев развития проекта (рис.1).

Элементы матрицы a_ij характеризуют степень предпочтения i-го сценария перед j-м сценарием в соответствии со шкалой Саати.

Матрица предпочтений обрабатывается в соответствии со схемой

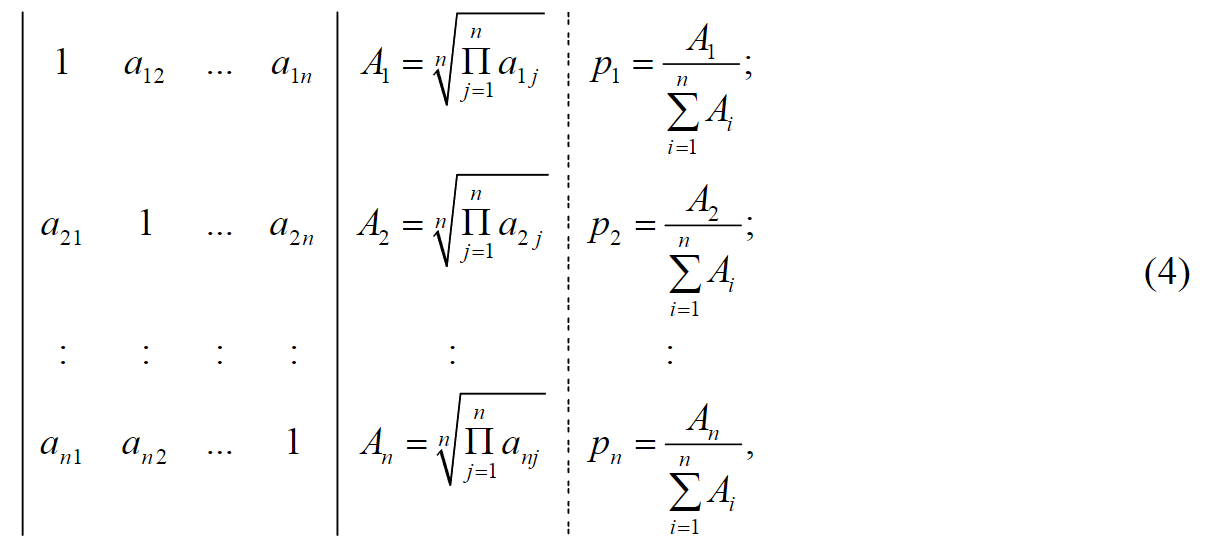
где p_i  – i-й элемент вектора приоритетов (вероятность осуществления i-го сценария).

В качестве вероятностного показателя риска наибольшее распространение получило стандартное отклонение σ. Чем меньше стандартное отклонение, тем «уже» вероятностное распределение и тем меньше риск. Однако этим показателем удобно пользоваться при сравнении нескольких инвестиционных проектов друг с другом. При анализе одного проекта этот показатель становится менее информативным. Поэтому предлагается в типовую процедуру анализа сценариев развития проекта ввести дополнительный показатель, оценивающий вероятность события, что NPV примет значение меньше заданного значения x:

Если принять допущение о нормальном распределении NPV, то формулу (5) можно записать в виде

где $\Phi =\frac{1}{\sigma \sqrt{2\pi }}{\displaystyle \underset{-\infty }{\overset{x}{\int }}{e}^{-\frac{{(t-\overline{x})}^2}{2{\sigma }^2}}dt}$ ;– функция Лапласа.

Часто интерес представляет вероятность события, что проект окажется убыточным:

В этом случае с учетом принятого допущения о нормальном распределении NPV получим

Рассмотрим интервально-вероятностный подход к оценке ожидаемой эффективности проекта.Пусть имеются два проекта A и B с одинаковыми значениями NPV для пессимистического и оптимистического сценариев, например NPV^A_min= NPV^B_min= 10, а NPV^A_max= NPV^B_max= 20. Для этих проектов определены значения наиболее вероятного сценария развития, допустим NPV^A_prob=17, а  NPV^B_prob=12. При использовании формулы (3) значения ${\overline{NPV}}^A$ и ${\overline{NPV}}^B$ не изменятся, так как в формуле Гурвица учитываются только экстремальные значения NPV. Можно ожидать, что получение дополнительной информации должно привести к изменению  NPV^¯, причем для рассматриваемой ситуации ${\overline{NPV}}^A>{\overline{NPV}}^B$ .

В работе [27] доказывается, что при использовании формулы Гурвица введение дополнительных промежуточных значений NPV не должно приводить к изменению $\overline{NPV}$, но при этом делается важное уточнение, что ничего не известно о вероятностях отдельных исходов (сценариев).

Определение априорных вероятностей является одной из ключевых методологических проблем при оценке ожидаемой эффективности проекта на основе метода анализа сценариев. В практической деятельности ЛПР, как правило, всегда устанавливает некоторое отношение предпочтения относительно сценариев, используя свой опыт, интуицию и знания. Установление отношения предпочтения является более естественной и простой операцией, чем непосредственное определение вероятностей осуществления сценариев.

С формальной точки зрения отношение предпочтения представляет собой бинарное отношение порядка на множестве допустимых альтернатив. Отношения порядка достаточно подробно исследованы в работе Фишберна.

К основным типам отношений порядка на компонентах вектора p = (p₁, p₂, ..., p_n) относятся следующие:

• простое линейное отношение порядка

• частично-усиленное линейное отношение порядка

• усиленное линейное отношение порядка

где α_i > 0 – заданное целое число.

При сравнении сценариев развития проекта ЛПР задает, как правило, простое линейное отношение порядка.

Пусть задана область возможных значений оцениваемого показателя:

На компонентах ω_i ЛПР устанавливает бинарное отношение предпочтения:

где ${\text{ω}}_i⊳{\text{ω}}_j$ означает, что ω_i более вероятно, чем ω_j.

Тогда естественно предположить, что ${\text{ω}}_i⊳{\text{ω}}_j$ только при p_i≥p_j, т.е. бинарное отношение предпочтения (13) индуцирует линейное отношение порядка (9).

В этом случае в качестве точечных оценок априорных вероятностей p_i можно использовать оценки Фишберна $\widehat{p}$_i:

которые образуют убывающую арифметическую прогрессию. Переменная k в формуле (14) обозначает порядковый номер (позицию) сценария в установленном бинарном отношении предпочтения (для наиболее вероятного сценария k = 1).

Обоснование оценок Фишберна для отношений порядка (10) и (11) можно найти в работе [35].

В подавляющем большинстве рекомендаций по оценке эффективности инвестиционных проектов закладываются умеренно-пессимистические значения для всех параметров проекта, что, как показала практика, дает наиболее удовлетворительные результаты [36, 37]. Опираясь на данное положение, найдем оценки Фишберна $\widehat{p}$_i для случаев точечного и интервального определения NPV.

В формуле (1) предполагается нахождение NPV для трех сценариев развития проекта. Установим бинарное отношение предпочтения на компонентах NPV_i, приняв за основу умеренно-пессимистический подход:

В установленном бинарном отношении для NPV₂ значение переменной k = 1, для NPV₁ – k = 2, для NPV₃ – k = 3.

Тогда получим следующие оценки Фишберна $\widehat{p}$_i:

В случае интервального определения NPV будем исходить из того, что ЛПР дает три интервальные оценки сценариям развития проекта:

• [NPV_min1, NPV_min2] – для пессимистического сценария;
• [NPV_prob1, NPV_prob2] – для наиболее вероятного сценария;
• [NPV_max1, NPV_max2] – для оптимистического сценария.

Рассмотрим наиболее типичную ситуацию, когда данные оценки образуют пять непересекающихся интервалов (рис.2).

В этом случае возможны два подхода к построению бинарного отношения предпочтений – на основе трех и пяти интервалов.

Приняв во внимание умеренно-пессимистический подход, бинарное отношение предпочтений на основе трех интервалов будет иметь следующий вид:

Оценки Фишберна $\widehat{p}$_i в этом случае будут соответствовать оценкам (16). Точечные оценки NPV при умеренно-пессимистической системе предпочтений могут быть найдены по формуле (3).

Бинарное отношение предпочтений на основе пяти интервалов будет иметь следующий вид:

В этом случае получим следующие оценки Фишберна:

где $\widehat{p}$₁ – вероятность пессимистического сценария, соответствующего интервалу [NPV_min1, NPV_min2]; $\widehat{p}$₂ – вероятность умеренно-пессимистического сценария, соответствующего интервалу [NPV_min2, NPV_prob1]; $\widehat{p}$₃ – вероятность наиболее ожидаемого сценария, соответствующего интервалу [NPV_prob1, NPV_prob2]; $\widehat{p}$₄ – вероятность умеренно-оптимистического сценария, соответствующего интервалу [NPV_prob2, NPV_max1]; $\widehat{p}$₅ – вероятность оптимистического сценария, соответствующего интервалу [NPV_max1, NPV_max2].

Точечные оценки NPV также могут быть найдены по формуле (3), если в качестве базовой принята умеренно-пессимистическая системе предпочтений.

Если вероятности сценариев развития проекта, полученные на основе нахождения оценок Фишберна, по каким-либо соображениям не устраивают ЛПР, он может воспользоваться методом анализа иерархий.

Результаты

Для понимания данной методологии предлагается рассмотреть следующую задачу.

Постановка задачи

Рассматривается проект дочернего предприятия ПАО «Газпром» по выпуску специального оборудования для технического обслуживания и ремонта цистерн, предназначенных для перевозки сжиженных углеводородных газов и легкого углеводородного сырья (цистерны моделей 15-908R, 15-1407-01, 15-1519-01 и др.) с исходными параметрами, заданными в виде точечных оценок: начальные инвестиции I₀ – 3000,00 у.д.е.; горизонт планирования n – 5 лет; ставка дисконтирования r – 20 %; налог на прибыль T – 20 %; цена P за единицу оборудования – 45,00 у.д.е.; переменные издержки на единицу оборудования AVC – 28,00 у.д.е.; амортизационные отчисления А – 1500 у.д.е.; а также интервальных оценок: объем выпуска Q по сценарию, у.е.: пессимистическому – 90-110, наиболее вероятному – 210-240, оптимистическому – 310-320; постоянные издержки FC по сценарию, у.д.е.: пессимистическому – 820-850, наиболее вероятному – 750-770, оптимистическому – 700-730.

Требуется провести сценарный анализ проекта при умеренно-пессимистической системе предпочтений ЛПР.

Сценарный анализ проекта

Необходимо построить непротиворечивые комбинации его параметров и рассчитать значения NPV. Для рассматриваемого проекта были рассчитаны шесть значений NPV, исходя из возможных комбинаций параметров Q и FC (табл.1). Для расчета NPV использовались соотношения, рассмотренные в работе [3].

Таблица 1

Расчетные значения NPV

Рассчитанные значения NPV разбивают отрезок [NPV_min1, NPV_max2] на пять интервалов (рис.2). Приняв за основу умеренно-пессимистическую систему предпочтений, по формуле (3) были рассчитаны значения M(NPV_i) для каждого интервала (табл.2). Вероятности попадания в интервал (вероятности сценариев развития проекта) могут быть получены на основе нахождения оценок Фишберна.

Таблица 2

Расчетные значения M(NPV_i) и p_i

Длярасчета интегрального показателя эффективности проекта воспользуемся формулой

Приняв допущение о нормальном распределении NPV, проведем вероятностный анализ риска проекта: дисперсия D(NPV) – 7961807,78 у.д.е.; стандартное отклонение σ (NPV) – 2821,67 у.д.е.; P(NPV < 0) – 0,083; P(NPV < M (NPV) – 50 % х M (NPV)) – 0,244.

При построении бинарного отношения предпочтений на основе трех интервалов получим:

Значения показателей, рассчитанных в рамках вероятностного анализа риска проекта (при трехинтервальном бинарном отношении предпочтений): дисперсия D(NPV) – 11572491,88 у.д.е.; стандартное отклонение σ (NPV) – 3401,84 у.д.е.; P (NPV < 0) – 0,135; P (NPV < M (NPV) – 50 % х M(NPV)) – 0,290.

При умеренно-пессимистическом подходе к построению бинарных отношений предпочтений уменьшение числа оцениваемых сценариев ведет к получению более «жестких» пессимистических оценок для показателей эффективности и риска проекта. Введение в рассмотрение дополнительных сценариев в определенной степени сглаживает «жесткий» пессимизм и вызывает больше доверия к значениям оцениваемых параметров. При этом следует заметить, что увеличение числа рассматриваемых сценариев также имеет ограничения, связанные с психологическим законом Миллера, используемым во многих шкалах экспертного оценивания, а также с определенной сложностью построения непротиворечивых комбинаций исходных параметров проекта для достаточно большого числа возможных сценариев его развития.

Обсуждение

Предложенный интервально-вероятностный подход к сценарному анализу развития проектов предполагает, что интервальная оценка исходных параметров проекта проводится или одним экспертом, или группой экспертов путем совместного открытого обсуждения. Во втором случае выработанная коллективная экспертная оценка с точки зрения ее последующей обработки эквивалентна оценке, вынесенной одним экспертом.

Если эксперты проводят интервальное оценивание параметров проекта независимо друг от друга, то бинарные отношения предпочтений могут быть построены на основе обработки заданных интервальных оценок. При этом возможны три варианта:

• все интервальные оценки взаимно противоречивы

• все интервальные оценки взаимно непротиворечивы

• некоторые интервальные оценки взаимно противоречивы

где m – количество экспертов.

Для варианта (22) могут быть применены различные методы обработки независимых экспертных оценок [38]. При условии, что эксперты имеют равную квалификацию, наиболее простым решением является выбор медианного интервала или интервала $[a^{*},b^{*}]={\displaystyle \underset{j=1}{\overset{m}{\cap }}[a_j,b_j]}$ . При m ≥ 3 могут быть отброшены крайний левый и правый интервалы. Возможны другие варианты обработки.

Для варианта (23) отношение предпочтения может быть построено на основе рассуждения, что наиболее предпочтительны интервалы с наибольшим правдоподобием. Такими являются интервалы, образованные пересечением наибольшего числа экспертных интервальных оценок. Например, относительно границ параметра A вынесены четыре независимых экспертных оценки: эксперт 1 → [ 4000 , 8000 ]; эксперт 2 → [ 5000 , 9000 ]; эксперт 3 → [ 6000 , 8000 ]; эксперт 4 → [ 400 , 8000 ]).

Интерпретируя пересечение интервальных оценок как области наибольшего правдоподобия, произведем их упорядочение по вероятности при умеренно-пессимистической системе предпочтений:

В этом случае получим следующие оценки Фишберна (вероятности попадания в интервал):

Если оценки Фишберна по каким-либо соображениям не устраивают в качестве вероятностей сценариев развития проекта, то для получения правдоподобных субъективных вероятностей p_i можно использовать метод анализа иерархий. Если в разработке проекта принимают участие несколько аналитиков, имеющих одинаковый вес, то для агрегирования их суждений может использоваться формула среднего геометрического:

Логичность формулы (27) становится очевидной, если два равноценных эксперта указывают при сравнении показателей соответственно оценки a_ij и 1/a_ij, что при вычислении агрегированной оценки дает единицу и свидетельствует об эквивалентности сравниваемых показателей. Агрегированные суждения a^A_ij обрабатываются по схеме (4).

Для сравнения типового и модифицированного метода анализа сценариев был поставлен эксперимент по оценке обоснованности разработанных с использованием этих методов инвестиционных решений. Суть эксперимента состояла в том, что восьми аналитикам было предложено решить шесть задач по инвестиционному проектированию с использованием типового и модифицированного методов. Затем, используя шкалу Саати, выявили степень предпочтительности разработанных решений по отношению друг к другу. Результатом обработки полученных экспертных суждений явились шесть векторов приоритетов, элементы которых интерпретировались в качестве коэффициентов обоснованности разработанных решений (табл.3).

Таблица 3

Коэффициенты обоснованности

Так как значения коэффициентов обоснованности зависят не только от использованных методов решения, но также и от ряда других факторов, то следует полагать, что они являются случайными величинами. Таким образом, возникает задача оценки значимости различия между средними коэффициентами обоснованности двух выборок.

Дисперсионное отношение F_р = S²_ф/S²₀ = 21,13, где S²_ф – выборочная межгрупповая (факторная) дисперсия; S²₀ – выборочная внутригрупповая (остаточная) дисперсия. На уровне значимости α = 0,01 табличное (критическое) значение критерия Фишера F = 10,04. Так как F_р > F, то с высоким уровнем надежности можно утверждать, что значение коэффициента обоснованности зависит от используемого метода.

Выборочный коэффициент детерминации ρˆ²=σ²_ф/σ²_у=0,679, где σ²_ф – сумма квадратов между группами; σ²_у – полная сумма квадратов отклонения общего среднего. Таким образом, около 68 % общей вариации коэффициента обоснованности связано с используемым методом. Ошибка коэффициента детерминации S_p² = 0,032. Так как ρˆ²/S_p²> F, то полученная оценка выборочного коэффициента детерминации является достоверной на уровне значимости α = 0,01.

Заключение

Задача снижения информационной неопределенности в процессе оценки рисков инвестиционных проектов является одной из наиболее сложных задач финансового менеджмента.

Разработанный авторами модифицированный метод сценарного анализа направлен на снижение степени субъективизма при оценке прогнозируемых параметров инвестиционных проектов в условиях неопределенности факторов внешней среды и тем самым позволяет повысить обоснованность разрабатываемых инвестиционных решений. Метод предлагается использовать в системе риск-менеджмента инвестиционных проектов минерально-сырьевого комплекса.

Научная новизна метода состоит в том, что он основан на умеренно-пессимистической системе предпочтений при получении точечных значений исходных параметров инвестиционного проекта и, в отличие от известных, использует метод анализа иерархий и оценки Фишберна для интервально-вероятностной оценки прогнозируемых параметров сценариев развития проекта. Дальнейшее развитие метода видится в его комплексном применении с методом SWOT-анализа для обоснованного выявления факторов внутреннего и внешнего окружения проекта. Особый интерес может представлять построение иерархического дерева факторов и оценка степени их влияния на сценарии развития проекта.

Для сравнения типового и предложенного модифицированного метода была проведена оценка обоснованности разработанных с использованием этих методов инвестиционных решений. Результаты статистической обработки позволяют с достаточно высоким уровнем надежности сделать вывод, что модифицированный метод позволяет получить более обоснованные инвестиционные решения по сравнению с типовым методом.

Важно отметить, что использование какого-то одного метода оценки рисков инвестиционных проектов затрагивает решение только одной составляющей этой сложной многоаспектной задачи. Эффективным является комплексный подход к оценке рисков, предполагающий применение разноплановых экономико-математических методов, в том числе и методов имитационного статистического моделирования, позволяющих генерировать тысячи случайных сценариев. Такой подход на более качественном уровне способствует принятию инвестиционных решениий в условиях неопределенности внешней среды, что является характерным для крупных проектов в минерально-сырьевом секторе экономики.

Литература

1. Litvinenko V.S. Digital Economy as a Factor in the Technological Development of the Mineral Sector // Natural Resources Research. 2020. Vol. 28. P. 1521-1541. DOI: 10.1007/s11053-019-09568-4
2. Sobieraj J., Metelski D. Project Risk in the Context of Construction Schedules – Combined Monte Carlo Simulation and Time at Risk (TaR) Approach: Insights from the Fort Bema Housing Estate Complex // Applied Sciences. 2022. Vol. 12. Iss. 3. № 1044. DOI: 3390/app12031044
3. Batkovskiy A.M., Semenova E.G., Trofimets V.Ya. et al. Modified method for sensitivity analysis of investment projects efficiency criteria // Journal of Applied Economic Sciences. 2017. Vol. 12. Iss. 4. P. 1116-1131.
4. Chrysafis K.A., Papadopoulos B.K. Decision Making for Project Appraisal in Uncertain Environments: A Fuzzy-Possibilistic Approach of the Expanded NPV Method // 2020. Vol.13. Iss. 1. № 27. DOI: 10.3390/sym13010027
5. Yoo Hwan Lee, Young Wook Seo. Strategies for Sustainable Business Development: Utilizing Consulting and Innovation Activities // Sustainability. 2020. 10. Iss. 11. № 4122. DOI: 10.3390/su10114122
6. Kuś A., Dorota G.-Pl. A Model of Innovation Activity in Small Enterprises in the Context of Selected Financial Factors: The Example of the Renewable Energy Sector // 2021. Vol. 14. Iss. 10. № 2926. DOI: 10.3390/en14102926
7. Saługa P.W., Katarzyna S.-W., Miśkiewicz R., Mateusz Ch. Cost of Equity of Coal-Fired Power Generation Projects in Poland: Its Importance for the Management of Decision-Making Process // 2020.Vol. 13. Iss. 18. № 4833. DOI: 10.3390/en13184833
8. Tobisova A., Senova A., Izarikova G. et al. Proposal of a Methodology for Assessing Financial Risks and Investment Development for Sustainability of Enterprises in Slovakia // 2022. Vol.14. Iss. 9. № 5068. DOI: 10.3390/su14095068
9. Vertakova Y., Izmalkova I., Leontyev E. Cluster Enterprise Comprehensive Risk Assessment: Methodology Based on the Functional-Target Approach // Journal of Risk and Financial Management.Vol. 15. Iss. 1. № 15. DOI: 10.3390/jrfm15010015
10. Недосекин А.О., Рейшахрит Е.И., Козловский А.Н. Стратегический подход к оценке экономической устойчивости объектов минерально-сырьевого комплекса России // Записки Горного института. 2019. Т. 237. C. 354-360. DOI: 10.31897/PMI.2019.3.354
11. Сметанкин А.В.Распределение затрат на управление рисками по критерию воздействия // Записки Горного института. 2004. Т. 159 (1). С. 197-199.
12. Carayannis E.G., Ilinova A., Cherepovitsyn A. The future of energy and the case of the arctic offshore: The role of strategic management // Journal of Marine Science and Engineering. 2021. Vol. 9. Iss. 2. № 134. DOI: 10.3390/jmse9020134
13. Зайцев А.Ю. Методический подход к обоснованию капитальных вложений золоторудных месторождений на основе удельных затрат // Записки Горного института. 2019. Т. 238. C. 459-464. DOI: 10.31897/PMI.2019.4.459
14. Королёв В.Ю., Бенинг В.Е., Шоргин С.Я. Математические основы теории риска. М.: Физматлит, 2011. 591 с.
15. Kruk M.N., Nikulina A.Y. Economic estimation of project risks when exploring sea gas and oil deposits in the Russian arctic // International Journal of Economics and Financial Issues. 2016. Vol. 6. Iss. 2. P. 138-150.
16. Nada A.N., Abdel-Basset M., Gamal A., Chang V. Evaluation of Production of Digital Twins Based on Blockchain Technology // 2022. Vol. 11. Iss. 8. № 1268. DOI: 10.3390/electronics11081268
17. Wei-Ling Tseng, Ian-Lin Lai, Wing-Huen Ip et al. The 3D Direct Simulation Monte Carlo Study of Europa’s Gas Plume // 2022. Vol. 8. Iss. 5. № 261. DOI: 10.3390/universe8050261
18. Cherepovitsyn A.E., Ilinova A.A. Methods and tools of scenario planning in areas of natural resources management // European Research Studies Journal. 2018. Vol. 21. Iss. 1. P. 434-446.
19. Dicorato M., Gioacchino T., Giuseppe F., Marasciuolo Fr. Technical Indicators for the Comparison of Power Network Development in Scenario Evaluations // 2021. Vol. 14. Iss. 14. № 4179. DOI: 10.3390/en14144179
20. van Leeuwen R., Annelies E., Edmund W. et al. Model Supported Business Case Scenario Analysis for Decentral Hydrogen Conversion, Storage and Consumption within Energy Hubs // Energies. 2022.  Vol. Iss. 6. № 2065. DOI: 10.3390/en15062065
21. Ponomarenko T.V., Reshneva E.A., Mosquera Urbano A.P. Assessment of Energy Sustainability Issues in the Andean Community: Additional Indicators and Their Interpretation // Energies. 2022. Vol. 15. Iss. 3. № 1077. DOI: 10.3390/en15031077
22. Reizenbuk K., Sarapulova T., Shchedrin S. et al. Application of distributed computing in developing architecture of intelligent information system for automated stock exchange trading // Journal of Advanced Research in Dynamical and Control Systems (discontinued). 2019. Vol. 11. Iss. 8. Special Issue. P. 2549-2555.
23. Rudakov M., Gridina E., Kretschmann Jü. Risk-based thinking as a basis for efficient occupational safety management in the mining industry // Sustainability. 2021. Vol. 13. Iss. 2. № 470. DOI: 10.3390/su13020470
24. Daniluk P. Strategic Analysis of Energy Security. Methodological Aspects of the Scenario Approach //  2021. Vol.14. Iss. 15. № 4639. DOI: 10.3390/en14154639
25. Gridina E.B., Rudakov M.L., Rumiantseva A.M. Evaluation of stability of sides of quarries and dumps on the basis of a risk-oriented approach // Naukovyi Visnyk Natsionalnoho Hirnychoho Universytetu. 2020. Vol. 4. P. 47-52. DOI: 10.33271/nvngu/2020-4/047
26. Cherepovitsyn A., Evseeva O. Parameters of sustainable development: Case of arctic liquefied natural gas projects // Resources. 2021. Vol. 10. Iss. 1. № 1. DOI: 10.3390/resources10010001
27. Vasilenko N., Khaykin M., Kirsanova N. et al. Issues for development of economic system for subsurface resource management in Russia through lens of economic process servitization // International Journal of Energy Economics and Policythis link is disabled. 2020. Vol. 10. Iss. 1. P. 44-48. DOI: 10.32479/ijeep.8303
28. Nisula A.-M., Blomqvist K., Bergman J.-P., Seppo Y. Organizing for knowledge creation in a strategic interorganizational innovation project // International Journal of Project Management. 2022. Vol. 40. Iss. 4. P. 398-410. DOI: 1016/j.ijproman.2022.03.011
29. Szczepankiewicz E.I., Loopesko W.E., Ullah F. A Model of Risk Information Disclosures in Non-Financial Corporate Reports of Socially Responsible Energy Companies in Poland // 2022. Vol.15. Iss. 7. № 2601. DOI: 10.3390/en15072601
30. Stroykov G.A., Babyr N.V., Ilin I.V. et al. System of comprehensive assessment of project risks in energy industry // International Journal of Engineering, Transactions A: Basics. 2021. Vol. 34. Iss. 7. P. 1778-1784. DOI: 10.5829/IJE.2021.34.07A.22
31. Vayas-Ortega G., Soguero-Ruiz G., Rodríguez-Ibáñez M. et al. On the Differential Analysis of Enterprise Valuation Methods as a Guideline for Unlisted Companies Assessment (II): Applying Machine-Learning Techniques for Unbiased Enterprise Value Assessment // Applied Science. 2020. Vol. 10. Iss. 17. № 5334. DOI: 3390/app10155334
32. Ponomarenko T., Marin E., Galevskiy S. Economic Evaluation of Oil and Gas Projects: Justification of Engineering Solutions in the Implementation of Field Development Projects // Energies. Vol. 15. Iss. 9. № 3103. DOI: 10.3390/en15093103
33. Providakis S., Rogers C.D.F., Chapman D.N. Assessing the Economic Risk of Building Damage due to the Tunneling-Induced Settlement Using Monte Carlo Simulations and BIM // Sustainability. 2020. Vol. 12. Iss. 23. № 10034. DOI: 3390/su122310034
34. Коршунов Г.И., Еремеева А.M., Дребенштедт К. Обоснование применения растительной добавки к дизельному топливу в качестве способа защиты подземного персонала угольных шахт от воздействия вредных выбросов дизель-гидравлических локомотивов // Записки Горного института. 2021. Т. 247. С. 39-47. DOI: 10.31897/PMI.2021.1.5
35. Сигал А.В., Ремесник Е.С. Точечные оценки Фишберна и их обобщения // Моделирование и анализ безопасности и риска в сложных системах. 2019. С. 85-92.
36. Si-Yong L., Hnottavange-Telleen K., Wei Jia et al. Risk Assessment and Management Workflow – An Example of the Southwest Regional Partnership // 2021.Vol. 14. Iss. 7. № 1908. DOI: 10.3390/en14071908
37. Solovyova V.M., Ilinova A.A., Cherepovitsyn A.E. Strategic forecasting of REE mining projects development in Russian Arctic // Advances in Raw Material Industries for Sustainable Development Goals. 2021. P. 456-464. DOI: 10.1201/9781003164395-57
38. Kuo T. An Ordinal Consistency Indicator for Pairwise Comparison Matrix // Symmetry. Vol. 13. Iss. 11. № 2183. DOI: 10.3390/sym13112183