Development of methodology for scenario analysis of investment projects of enterprises of the mineral resource complex

Introduction

Investing in subsoil use in countries with a resource-based economy is extremely important for the development of the national economy – economic growth, social development and, ultimately, growth of the competitiveness of the macroeconomic system [1]. The efficiency of investment decision-making in the field of implementation of investment projects in the relevant mineral and raw materials sectors of the economy largely depends on the processes of managing these projects, in particular, reducing their information uncertainty. To date, the task of reducing information uncertainty in assessing the risks of investment projects is one of the most complex and urgent tasks of investment design [2]. The complexity of the decisions made in this area is because the amount of cash flows from the operating, financial and investment activities of the enterprise are predictive. This, in turn, limits the use of deterministic methods and requires taking into account the factors of randomness and uncertainty assessing the parameters of the internal and external environment of the project [3-5].

Risk management of investment projects at enterprises of the mineral resource complex cannot ignore the industry-specific features of the subsoil use sphere, arising from the content of the production and commercial activities of its economic entities [6-8]. The processes of reproduction of the economic activity of resource extracting companies proceed on the basis of natural and technological factors in the development of the sphere of subsoil use and the operation of economic laws [9]. The growth of enterprise competitiveness in the domestic and foreign markets should be considered as the ultimate goal of risk management in a company [10-12].

One of the key elements of the project risk management system is quantitative methods for their assessment [13, 14]. Among them, the most well-known methods are: sensitivity analysis of project performance criteria; discount rate adjustments; analysis of indicators of the limiting level; analysis of project development scenarios; building a “decision tree”; simulation statistical modeling (Monte Carlo method) [15-17].

When making investment decisions under conditions of significant uncertainty of environmental factors, the method of analyzing project development scenarios has become widespread [18-20]. This method is based on expert judgments related to the construction of several predictive models of project cash flows and indicating the probabilities of their implementation. The main disadvantage of scenario forecasting is the subjectivity of expert judgments. To reduce the degree of subjectivity, as a rule, additional information is involved. In the scenario analysis method, such information can be obtained by establishing preference relations for the possible values of the project parameters under study, which makes it possible to construct their probability distributions and use the maximum likelihood values in the sense of the maximum a priori probability as an estimate.

Thus, the purpose of this work is to reduce information uncertainty in scenario risk analysis of investment projects. This goal is achieved through a number of modifications of the typical scenario analysis procedure, namely, the use of an interval-probabilistic approach in assessing the stochastic parameters of the project and the introduction of an additional risk assessment indicator to reduce the subjectivity of expert judgments.

Methods

All over the world, the sphere of subsoil use is considered high-risk. Risks are both a consequence of the results of the production and commercial activities of its subjects, and investment attractiveness of the relevant enterprises and the level of investor activity. As a result of the analysis of investment projects in the field of subsoil use, risk factors specific to the mineral and raw materials sectors of the economy were identified, they can be conditionally grouped into legal, mining and geological, financial, industrial, and territorial ones. In international practice, the final decision in the field of approval (rejection) of an investment project is made in accordance with financial indicators and indicators of project business plans, their feasibility study [21]. That is why the modified scenario analysis of investment projects relies [22, 23] primarily on the financial characteristics of projects using the appropriate economic and mathematical tools. In the process of making investment decisions, modern traditional risk management methods include self-insurance of risks (formation of financial reserves “as a safety cushion”), risk insurance by an insurance company, risk hedging by specific stock market entities, “share” distribution of risk within the participants of the investment project.

The development of a methodology for scenario analysis of investment projects in the mineral resource sector of the economy should be based on the industrial specifics of economic entities in the sphere of subsoil use [24]:

1. At the pre-investment phase of project management, there is a high uncertainty in the values of its main technical and economic parameters. This is due to the fact that for each mineral deposit it is always difficult to determine their reserves with high accuracy due to the peculiarities of the reserves occurrence, constant dynamics and complexity of mining and geological conditions. Therefore, when developing and implementing appropriate investment decisions, it is necessary to take into account the specifics of a particular deposit, as well as the expedient period of mining enterprises operation, which directly depends on the development period of the corresponding deposits, depending on the volume of mineral reserves and the profitability of mining [25].
2. There is a constant growth in need and demand for raw materials and final products as a result of their enrichment and processing. All this ultimately increases the investment activity of the mineral resource complex and actualizes the issues of investment design in the framework of creating new industries and developing the material and technical base of the subsoil use [26, 27].
3. The implementation of investment projects in the field of subsoil use, as a rule, is characterized by a long cycle, a high level of complexity and capital intensity [28, 29]. This is due to the fact that the functioning of mining enterprises is always focused on a developed infrastructure, the creation and maintenance of which is impossible without construction and logistics [30, 31]. In addition, the costs are high not only for its acquisition, but also for operation and repair. It is also necessary to take into account the location of subsoil use enterprises in relation to the corresponding deposits. Effective solutions in this area contribute to the reduction of unjustified costs – transport and logistics associated with the creation and operation of engineering and social infrastructure. It is also worth noting that a long production cycle extends to the entire value chain – from exploration, production to the creation of the final product [32, 33].
4. Compliance with the principles of rational subsoil use implies the development of large-scale measures in the field of minimizing the loss of raw materials and, as a result, the amount of penalties. In addition, mining industry is associated with environmentally harmful industries, which in modern conditions involve the use of environmental protection equipment that significantly increases the need for investment resources [34].
5. Additional investment risks are caused by high uncertainty in the field of legal regulation of subsoil use. Legislation in this area is constantly being improved and undergoes changes. The Guidelines for evaluating the effectiveness of investment projects remain the fundamental document.

For example, investment projects approved by PAO Gazprom are diversified and cover different sectors of the fuel and energy complex. Only at the present time, the company is implementing several dozen large-scale projects not only in the Russian Federation, but also abroad:

• Eastern Gas Program, focused on the creation of a full-scale gas industry in the East of Siberia – five fields in the stage of industrial operation, the length of “The Power of Siberia” gas pipeline is about 3 thousand km;
• Yamal, a new gas production center – 32 fields, 36.5 trillion m³ of gas, 1.6 billion tons of gas condensate, 300 million tons of oil;
• LNG – liquefied natural gas projects – Sakhalin-2, Vladivostok-LNG, complex for processing ethane-containing gas and production of LNG in Leningrad region, LNG supply project in Kaliningrad region.

The method for analyzing project development scenarios consists in the variable calculation of project performance indicators and their subsequent aggregation into a generalized indicator taking into account risk. At the same time, it should be noted that, unlike the sensitivity analysis method, the scenario analysis method assumes a joint and interconnected change in several project parameters.

A project development scenario is understood as a plausible consistent combination of project parameters, as well as factors of its external environment. In general, the scenario analysis procedure involves the following steps:

• A project development scenario is understood as a plausible consistent combination of project parameters, as well as factors of its external environment. In general, the scenario analysis procedure involves the following steps:

• For each scenario, a probabilistic assessment of its implementation is indicated.
• Efficiency and risk indicators of the project are calculated for each scenario (as a rule, NPV – net present value and s – standard deviation).

The standard procedure of the method involves consideration of three possible scenarios for development of the project – pessimistic, most probable and optimistic, and the net present value NPV acts as an efficiency criterion. In this case, the integral indicator of the project's effectiveness is calculated according to the mathematical expectation formula (Methodological recommendations, p. 48):

where NPV₁, NPV₂, NPV₃ – net present value for the pessimistic, most probable and optimistic scenarios, respectively; p_i – the probability of the scenario.

Standard deviation is usually used as a measure of risk

The lower the standard deviation, the less risky the project is considered.

The use of formulas (1) and (2) is associated with the determination of point estimates of a priori probabilities p_i, which in practice often causes significant difficulties. This is due to the fact that investment projects in the mineral resource sector of the economy are, as a rule, unique and it is impossible to select a statistical data set suitable for objectively establishing the probabilities p_i. Therefore, to obtain point values of probabilities p_i, it is often recommended to use expert estimates. Since any expert procedure is based on subjective considerations, the probabilities p_i are called subjective probabilities.

A number of researchers express serious criticisms regarding the use of a probabilistic approach to assess the expected effectiveness and risk of a project, precisely because of the subjective nature of the probabilities p_i [35]. It should be noted that in situations related to the assessment of the uncertainty of global factors of the external project environment (natural-climatic, political, macroeconomic, etc.), it is quite difficult to find an alternative to the probabilistic approach.

When there is information uncertainty of the internal quantitative parameters of the project, and there is no group of experts who expressed an agreed opinion on the probabilities of the implementation of individual scenarios, it is more preferable, in our opinion, to use the interval approach to assess the expected effectiveness of the project. In this case, to calculate the integral indicator of project efficiency, it is recommended to use the Hurwitz formula:

where NPV_min, NPV_max – net present value for the most pessimistic and most optimistic scenarios, respectively; λ – coefficient reflecting the system of preferences of the decision maker (DM), λ∈[ 0 , 1 ].

The substantiation of formula (3), as well as its generalization in relation to the evaluation of the effectiveness of investment projects, can be found in the work of P.L.Vilensky.

When λ = 0 in formula (3), a system of preferences is realized corresponding to extreme pessimism, when λ = 1 – extreme optimism, when λ = 0.5 – there is no pronounced inclination either towards pessimism or towards optimism. In investment planning, usually  which reflects the preferences of risk-averse investors. Most often, you can meet the value λ = 0.3, which corresponds to a moderately pessimistic system of investor preferences. In the Guidelines (p. 89) it is also recommended to use the value λ = 0.3.

The dominance of a mode­rately pessimistic approach in evaluating the effectiveness of investment projects, apparently, can be explained by the fact that it is desirable, if possible, to prevent situations in which, due to natural deviations of the actual values of cash flows from their calculated values, projects rated as effective, they will not be like that. To avoid this, the initial data used in the calculations should be somewhat “degraded”, which will give the project assessment some “margin of safety”. However, these “deteriorations” should not be too great, since otherwise, as a result of the calculation, “good” (effective) projects may be unreasonably discarded. Thus, moderate pessimism reflects a reasonable, in the opinion of the authors, investors' attitude to risk, which is why this principle was the basis for subsequent reasoning. Upon receipt of additional information about the factors affecting the implementation of the project, the value of l may be revised upwards.

Within the framework of the probabilistic approach to assessing the expected project effectiveness, the key methodological problem is the subjective nature of the probabilities p_i in formulas (1) and (2). To reduce the degree of subjectivity in determining these probabilities, it is proposed to use the method of analyzing hierarchies.

The essence of the proposed procedure is as follows. The decision maker gives qualitative judgments about the degree of preference for one scenario over another in accordance with the Saaty scale. As a result, a preference matrix of project development scenarios is formed (Fig.1).

The elements of the matrix a_ij characterize the degree of preference for the i-th scenario over the j-th scenario in accordance with the Saaty scale.

The preference matrix is processed according to the scheme

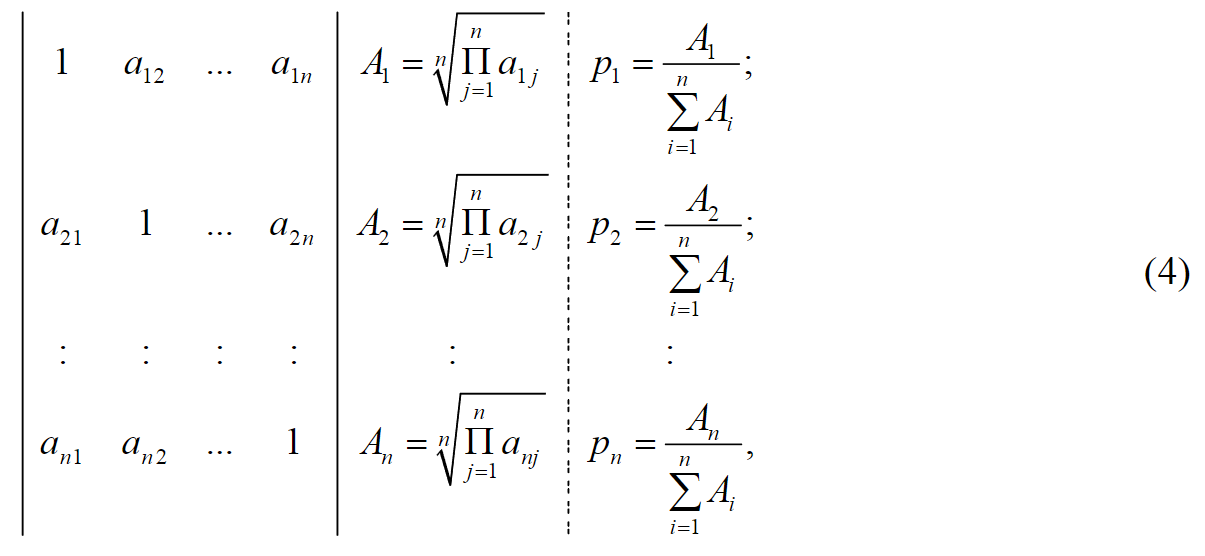
where p_i  – i-th element of the vector of priorities (probability of the implementation of the i-thscenario).

As a probabilistic indicator of risk, standard deviation s is the most widely used. The smaller the standard deviation, the “narrower” the probability distribution and the lower is the risk. However, this indicator is convenient to use when comparing several investment projects with each other. When analyzing one project, this indicator becomes less informative. Therefore, it is proposed to introduce an additional indicator into the standard procedure for analyzing project development scenarios, which assesses the probability of an event that NPV will take a value less than a given value x:

If we accept the assumption of the normal distribution of NPV, then formula (5) can be written as

where $\Phi =\frac{1}{\sigma \sqrt{2\pi }}{\displaystyle \underset{-\infty }{\overset{x}{\int }}{e}^{-\frac{{(t-\overline{x})}^2}{2{\sigma }^2}}dt}$ – Laplace function.

Often of interest is the probability of the event that the project will be unprofitable:

In this case, taking into account the accepted assumption about the normal distribution of NPV, we obtain:

Consider the interval-probabilistic approach to assessing the expected efficiency project. Let there be two projects A and B with the same NPV values for the pessimistic and optimistic scenarios, for example. NPV^A_min= NPV^B_min= 10, and NPV^A_max= NPV^B_max= 20. For these projects, the values of the most probable development scenario are determined, for example NPV^A_prob=17, and  NPV^B_prob=12. When using formula (3), the values ${\overline{NPV}}^A$ and ${\overline{NPV}}^B$ will not change, since only extreme values of NPV are taken into account in the Hurwitz formula. It can be expected that obtaining more information should lead to a change NPV ¯ , and for the situation under consideration ${\overline{NPV}}^A>{\overline{NPV}}^B$.

In the work [27], it is proved that when using the Hurwitz formula, the introduction of additional intermediate values of NPV should not lead to a change of , but at the same time, an important clarification is made that nothing is known about the probabilities of individual outcomes (scenarios).

Determining a priori probabilities is one of the key methodological problems in assessing the expected effectiveness of a project based on the scenario analysis method. In practical activities DM, as a rule, always establish a certain preference relation regarding scenarios, using his experience, intuition and knowledge. Establishing a preference relation is a more natural and simple operation than directly determining the probabilities of scenarios.

From a formal point of view, the preference relation is a binary order relation on the set of admissible alternatives. Order relations are studied in sufficient detail in the work of Fishburn.

The main types of order relations on the components of the vector p = (p₁, p₂, ..., p_n) include the following:

• simple linear order relation

• partial-strengthened linear order relation

• strengthened linear order relation

where α_i > 0 – is a given integer.

When comparing project development scenarios DM sets a simple linear order relation as a rule.

Let the range of possible values of the estimated indicator be given:

DM establishes a binary preference relation on the components ω_i:

where ω i ⊳ ω j means that ω_i is more likely than ω_j.

Then it is natural to assume that  ω i ⊳ ω j only for p_i≥p_j, binary preference relation (13) induces a linear order relation (9).

In this case, as point estimates of a priori probabilities p_i, one can use the Fishburn estimates $\widehat{p}$_i:

which form a decreasing arithmetic progression. The variable k in formula (14) denotes the ordinal number (position) of the scenario in the established binary preference relation (for the most probable scenario k = 1).

Justification of the Fishburn estimates for the order relations (10) and (11) can be found in the work [35].

The vast majority of recommendations for evaluating the effectiveness of investment projects include moderately pessimistic values for all project parameters, which, as practice has shown, give the most satisfactory results [36, 37]. Based on this provision, we find the Fishburn estimates $\widehat{p}$_i for the cases of point and interval determination of NPV.

Formula (1) assumes finding NPV for three project development scenarios. Let us establish a binary preference relation on the NPVicomponents, taking a moderately pessimistic approach as a basis:

In the established binary relation for  the value of the variable k = 1, for  – k = 2, for  – k = 3.

Then we obtain the following Fishburn estimates $\widehat{p}$_i:

In the case of an interval determination of NPV, we will proceed from the fact that DM gives three interval estimates for the project development scenarios:

• [NPV_min1, NPV_min2] – for a pessimistic scenario;
• [NPV_min1, NPV_min2] – for a pessimistic scenario;
• [NPV_min1, NPV_min2] – for a pessimistic scenario;

Let us consider the most typical situation, when these estimates form five non-overlapping intervals (Fig.2).

In this case, two approaches to constructing a binary preference relation, based on three and five intervals, are possible.

Taking into account a moderately pessimistic approach, a binary preference relation based on three intervals will have the following form:

Fishburn estimates $\widehat{p}$_i in this case will correspond to estimates (16). Point estimates of NPV with a moderately pessimistic system of preferences can be found using formula (3).

A binary preference relation based on five intervals will have the following form:

In this case, we obtain the following Fishburn estimates:

where $\widehat{p}$₁ – probability of a pessimistic scenario corresponding to the interval [NPV_min1, NPV_min2]; $\widehat{p}$₂ – probability of a moderately pessimistic scenario corresponding to the interval [NPV_min2, NPV_prob1]; $\widehat{p}$₃ - is the probability of the most expected scenario corresponding to the interval [NPV_prob1, NPV_prob2]; $\widehat{p}$₄ – probability of a moderately optimistic scenario corresponding to the interval [NPV_prob2, NPV_max1]; $\widehat{p}$₅ - is the probability of an optimistic scenario corresponding to the interval [NPV_max1, NPV_max2].

Point estimates of NPV can also be found using formula (3), if a moderately pessimistic system of preferences is taken as the base one.

If the probabilities of project development scenarios, obtained on the basis of finding Fishburn estimates, for some reason do not suit DM, he can use the hierarchy analysis method.

Results

To understand this methodology, it is proposed to consider the following problem.

Formulation of the problem

The project of a subsidiary of PAO Gazprom for the production of special equipment for the maintenance and repair of tanks intended for the transportation of liquefied hydrocarbon gases and light hydrocarbon raw materials (tanks models 15-908R, 15-1407-01, 15-1519-01 and etc.) with initial parameters given in the form of point estimates: initial investment I₀ – 3000.00 conventional monetary unit (c.m.u.); planning horizon n – 5 years; discount rate r – 20 %; income tax T – 20 %; price P per unit of equipment – 45.00 c.m.u.; variable costs per unit of equipment AVC – 28.00 c.m.u.; depreciation deductions А – 1500 c.m.u.; as well as interval estimates: the volume of output Q according to the scenario, c.u.: pessimistic – 90-110, most probable – 210-240, optimistic – 310-320; fixed costs FC under the scenario, c.m.u.: pessimistic – 820-850, most probable – 750-770, optimistic – 700-730.

It is required to conduct a scenario analysis of the project with moderately pessimistic system DM preferences.

Scenario analysis of the project

It is necessary to build consistent combinations of its parameters and calculate the NPV values. For the project under consideration, six NPV values were calculated based on possible combinations of Q and FC parameters (Table 1). The ratios considered in [3] were used to calculate NPV

Table 1

Estimated values NPV

The calculated NPV values divide the segment  into five intervals (Fig.2). Taking as a basis a moderately pessimistic system of preferences, according to formula (3), the values of M (NPV_i) were calculated for each interval (Table 2). The probabilities of falling into the interval (the probabilities of project development scenarios) can be obtained based on finding Fishburn estimates.

Table 2

Estimated values M(NPV_i) и p_i

Having accepted the assumption of the normal distribution of NPV, we will carry out a probabilistic analysis of the project risk: variance D (NPV) – 7961807.78 c.m.u.; standard deviation σ (NPV) – 2821.67 c.m.u.; P (NPV < 0) – 0.083; P (NPV < M (NPV) – 50 % X M (NPV)) – 0.244.

When constructing a binary preference relation based on three intervals, we obtain:

Values of indicators calculated as part of the probabilistic risk analysis of the project (with a three-interval binary preference relation): variance D (NPV) – 11572491.88 c.m.u.; variance s (NPV) – 3401.84 c.m.u.; P (NPV < 0) – 0.135; P (NPV < M (NPV) – 50 % х M (NPV)) – 0.290.

With a moderately pessimistic approach to building binary preference relations, a decrease in the number of evaluated scenarios leads to more “strict” pessimistic estimates for project efficiency and risk indicators. The introduction of additional scenarios to a certain extent smooths out the “strict” pessimism and inspires more confidence in the values of the estimated parameters. At the same time, it should be noted that the increase in the number of scenarios under consideration also has limitations associated with Miller's psychological law used in many scales of expert assessment, as well as with a certain complexity of constructing consistent combinations of initial project parameters for a sufficiently large number of possible scenarios for its development.

Discussion

The proposed interval-probabilistic approach to scenario analysis of the development of projects assumes that the interval assessment of the initial parameters of the project is carried out either by one expert or by a group of experts through a joint open discussion. In the second case, the developed collective expert assessment from the point of view of its subsequent processing is equivalent to the assessment made by one expert.

If experts conduct interval estimation of project parameters independently of each other, then binary preference relations can be built based on processing given interval estimates. In this case, three options are possible:

• all interval estimates are mutually inconsistent

• all interval estimates are mutually consistent

• some interval estimates are mutually inconsistent

where m is the number of experts.

For option (22), various methods for processing independent expert assessments can be applied [38]. Provided that the experts have equal qualifications, the simplest solution is to choose a median interval or interval $[a^{*},b^{*}]={\displaystyle \underset{j=1}{\overset{m}{\cap }}[a_j,b_j]}$. For m ≥ 3, the leftmost and rightmost intervals can be discarded. Other processing options are possible.

For option (23), a preference relation can be constructed based on the reasoning that the intervals with the highest likelihood are most preferred. These are the intervals formed by the intersection of the largest number of expert interval estimates. For example, regarding the boundaries of the para-meter A, four independent expert assessments were made: expert 1 → [ 4000 , 8000 ]; expert 2 → [ 5000 , 9000 ]; expert 3 → [ 6000 , 8000 ]; expert 4 → [ 4000, 8000 ]).

For option (23), a preference relation can be constructed based on the reasoning that the intervals with the highest likelihood are most preferred. These are the intervals formed by the intersection of the largest number of expert interval estimates. For example, regarding the boundaries of the para-meter A, four independent expert assessments were made: expert 1 → [ 4000 , 8000 ]; expert 2 → [ 5000, 9000 ]; expert 3 → [ 6000 , 8000 ]; expert 4 → [ 4000 , 8000 ]).

In this case, we obtain the following Fishburn estimates (the probabilities of falling into the interval):

If, for some reason, Fishburn estimates do not suit the project development scenarios as probabilities, then the hierarchy analysis method can be used to obtain plausible subjective probabilities p_i. If several analysts with the same weight take part in the development of the project, then the geometric mean formula can be used to aggregate their judgments:

The logic of formula (27) becomes obvious if two equal experts indicate, when comparing the indicators, respectively, estimates  and 1/a_ij, which, when calculating the aggregated estimate, gives one and indicates the equivalence of the compared indicators. Aggregated judgments  are processed according to scheme (4).

To compare the standard and modified method of scenario analysis, an experiment was set up to assess the validity of investment decisions developed using these methods. The essence of the experi-ment was that eight analysts were asked to solve six investment planning problems using standard and modified methods. Then, using the Saaty scale, the degree of preference of the developed solutions in relation to each other was revealed. The result of processing the obtained expert judgments were six vectors of priorities, the elements of which were interpreted as the coefficients of the validity of the developed solutions (Table 3).

Table 3

Reasonability coefficients

Since the validity coefficients values depend not only on the solution methods used, but also on a number of other factors, it should be assumed that they are random variables. Thus, the problem arises of assessing the significance of the difference between the average validity coefficients of two samples.

Dispersion ratio F_r = S²_f/S²₀ = 21,13, where S²_f is the sample intergroup (factorial) variance; S²₀ is the sample intragroup (residual) variance. At the significance level α = 0,01, the tabular (critical) value of the Fisher criterion F = 10.04. Since F_r > F, it can be argued with a high level of reliability that the value of the justification factor depends on the method used.

Selective coefficient of determination ρˆ²=σ²_f/σ²_у=0,679, where σ²_f is the sum of squares between groups; σ²_у is the total sum of the squared deviations of the overall mean. Thus, about 68 % of the total variation in the validity factor is due to the method used. Determination coefficient error S_r² = 0,032. Since ρˆ²/S_p²> F, the obtained estimate of the sampling coefficient of determination is reliable at the significance level α = 0.01.

Conclusion

The task of reducing information uncertainty in the process of assessing the risks of investment projects is one of the most difficult tasks of financial management.

The modified method of scenario analysis developed by the authors is aimed at reducing the degree of subjectivity in assessing the predicted parameters of investment projects in the conditions of uncertainty of environmental factors and thereby improves the validity of the developed investment decisions. The method is proposed to be used in the system of risk management of investment projects of the mineral resource complex.

The scientific novelty of the method lies in the fact that it is based on a moderately pessimistic system of preferences when obtaining point values of the initial parameters of an investment project and, unlike the well-known ones, uses the method of analysis of hierarchies and Fishburn's assessment for interval-probabilistic assessment of the predicted parameters of project development scenarios. Further development of the method is seen in its complex application with the SWOT-analysis method for the reasonable identification of factors of the internal and external project environment. Construction of a hierarchical tree of factors and assessing the degree of their influence on project development scenarios may be of particular interest.

To compare the standard and the proposed modified method, an assessment of the validity of the investment decisions developed, using these methods, was made. The results of statistical processing allow us to conclude with a fairly high level of reliability that the modified method allows you to get more reasonable investment decisions compared to the standard method.

It is important to note that the use of a single method for assessing the risks of investment projects affects the solution of only one component of this complex multifaceted task. An integrated approach to risk assessment is effective, which involves the use of diverse economic and mathematical methods, including methods of imitating statistical modeling, which allow generating thousands of random scenarios. Such an approach at a higher quality level contributes to the adoption of investment decisions in the face of uncertainty in the external environment, which is typical for large projects in the mineral resource sector of the economy.

References

1. Litvinenko V.S. Digital Economy as a Factor in the Technological Development of the Mineral Sector. Natural Resources Research. 2020. Vol. 28, p. 1521-1541. DOI: 10.1007/s11053-019-09568-4
2. Sobieraj J., Metelski D.Project Risk in the Context of Construction Schedules – Combined Monte Carlo Simulation and Time at Risk (TaR) Approach: Insights from the Fort Bema Housing Estate Complex. Applied Sciences. 2022. Vol. 12. Iss. 3. N 1044. DOI:3390/app12031044
3. Batkovskiy A.M., Semenova E.G., Trofimets V.Ya. et al. Modified method for sensitivity analysis of investment projects efficiency criteria. Journal of Applied Economic Sciences. 2017. Vol. 12. Iss. 4, p. 1116-1131.
4. Chrysafis K.A., Papadopoulos B.K. Decision Making for Project Appraisal in Uncertain Environments: A Fuzzy-Possibilistic Approach of the Expanded NPV Method. 2020. Vol.13. Iss. 1. N 27. DOI: 10.3390/sym13010027
5. Yoo Hwan Lee, Young Wook Seo. Strategies for Sustainable Business Development: Utilizing Consulting and Innovation Activities. Sustainability. 2020. 10. Iss. 11. N 4122. DOI: 10.3390/su10114122
6. Kuś A., Dorota G.-Pl.A Model of Innovation Activity in Small Enterprises in the Context of Selected Financial Factors: The Example of the Renewable Energy Sector. 2021.Vol. 14. Iss. 10. N 2926. DOI: 10.3390/en14102926
7. Saługa P.W., Katarzyna S.-W., Miśkiewicz R., Mateusz Ch. Cost of Equity of Coal-Fired Power Generation Projects in Poland: Its Importance for the Management of Decision-Making Process. Energies.Vol. 13. Iss. 18. N 4833. DOI: 10.3390/en13184833
8. Tobisova A., Senova A., Izarikova G. et al. Proposal of a Methodology for Assessing Financial Risks and Investment Development for Sustainability of Enterprises in Slovakia. Sustainability. 2022. Vol. Iss. 9. N 5068. DOI: 10.3390/su14095068
9. Vertakova Y., Izmalkova I., Leontyev E.Cluster Enterprise Comprehensive Risk Assessment: Methodology Based on the Functional-Target Approach. Journal of Risk and Financial Management.Vol. 15. Iss. 1. N 15. DOI:10.3390/jrfm15010015
10. Nedosekin A.O., Rejshahrit E.I., Kozlovskij A.N. Strategic approach to assessing economic sustainability objects of mineral resources sector of Russia. Journal of Mining Institute. 2019. 237, p. 354-360. DOI: 10.31897/PMI.2019.3.354
11. Smetankin A.V. Allocation of risk management costs by impact criterion. Journal of Mining Institute. 2004. Vol. 159 (1), 197-199 (in Russian).
12. Carayannis E.G., Ilinova A., Cherepovitsyn A. The future of energy and the case of the arctic offshore: The role of strategic management. Journal of Marine Science and Engineering. 2021. Vol. 9. Iss. 2. N 134. DOI: 10.3390/jmse9020134
13. Zaitsev A.Y. Methodological Approach to Substantiation of Capital Investments of Gold Fields Based on Unit Costs. Journal of Mining Institute. 2019. Vol. 238, p. 459-464. DOI: 10.31897/PMI.2019.4.459
14. Korolyov V.Yu., Bening V.E., Shorgin S.Ya. Mathematical foundations of risk theory. Moscow: Fizmatlit, 2011, p. 591 (in Russian).
15. Kruk M.N., Nikulina A.Y. Economic estimation of project risks when exploring sea gas and oil deposits in the Russian International Journal of Economics and Financial Issues. 2016. Vol. 6. Iss. 2, p. 138-150.
16. Nada A.N., Abdel-Basset M., Gamal A., Chang V. Evaluation of Production of Digital Twins Based on Blockchain Technol Electronics. 2022. Vol. 11. Iss. 8. N 1268. DOI: 10.3390/electronics11081268
17. Wei-Ling Tseng, Ian-Lin Lai, Wing-Huen Ip et al. The 3D Direct Simulation Monte Carlo Study of Europa’s Gas Plume. Universe. 2022. Vol. 8. 5. N 261. DOI: 10.3390/universe8050261
18. Cherepovitsyn A.E., Ilinova A.A. Methods and tools of scenario planning in areas of natural resources management. European Research Studies Journal. 2018. Vol. 21. Iss. 1, p. 434-446.
19. Dicorato M., Gioacchino T., Giuseppe F., Marasciuolo Fr. Technical Indicators for the Comparison of Power Network Development in Scenario Evaluations. Energies. Vol. 14. Iss. 14. N 4179. DOI: 10.3390/en14144179
20. van Leeuwen R., Annelies E., Edmund W. et al. Model Supported Business Case Scenario Analysis for Decentral Hydrogen Conversion, Storage and Consumption within Energy Hubs. Energies. 2022.  Vol. Iss. 6. N 2065. DOI: 10.3390/en15062065
21. Ponomarenko T.V., Reshneva E.A., Mosquera Urbano A.P. Assessment of Energy Sustainability Issues in the Andean Community: Additional Indicators and Their Interpretation. Energies. 2022. Vol. 15. Iss. 3. N 1077. DOI: 10.3390/en15031077
22. Reizenbuk K., Sarapulova T., Shchedrin S. et al. Application of distributed computing in developing architecture of intelligent information system for automated stock exchange trading. Journal of Advanced Research in Dynamical and Control Systems (discontinued). 2019. Vol. 11. Iss. 8. Special Issue, p. 2549-2555.
23. Rudakov M., Gridina E., Kretschmann Jü. Risk-based thinking as a basis for efficient occupational safety management in the mining industry. Sustainability. 2021. Vol. 13. Iss. 2. N 470. DOI: 10.3390/su13020470
24. Daniluk P. Strategic Analysis of Energy Security. Methodological Aspects of the Scenario Approach. Energies. 2021.Vol. Iss. 15. N 4639. DOI: 10.3390/en14154639
25. Gridina E.B., Rudakov M.L., Rumiantseva A.M. Evaluation of stability of sides of quarries and dumps on the basis of a risk-oriented approach. Naukovyi Visnyk Natsionalnoho Hirnychoho Universytetu. 2020. Vol. 4, p. 47-52. DOI: 10.33271/nvngu/2020-4/047
26. Cherepovitsyn A., Evseeva O. Parameters of sustainable development: Case of arctic liquefied natural gas projects. Resources. 2021. Vol. 10. Iss. 1. № 1. DOI: 10.3390/resources10010001
27. Vasilenko N., Khaykin M., Kirsanova N. et al. Issues for development of economic system for subsurface resource management in Russia through lens of economic process servitization. International Journal of Energy Economics and Policythis link is disabled. 2020. Vol. 10. Iss. 1, p. 44-48. DOI: 10.32479/ijeep.8303
28. Nisula A.-M., Blomqvist K., Bergman J.-P., Seppo Y. Organizing for knowledge creation in a strategic interorganizational innovation project. International Journal of Project Management. 2022. Vol. 40. Iss. 4, p. 398-410. DOI: 1016/j.ijproman.2022.03.011
29. Szczepankiewicz E.I., Loopesko W.E., Ullah F.A Model of Risk Information Disclosures in Non-Financial Corporate Reports of Socially Responsible Energy Companies in Poland. 2022. Vol.15. Iss. 7. N 2601. DOI: 10.3390/en15072601
30. Stroykov G.A., Babyr N.V., Ilin I.V. et al. System of comprehensive assessment of project risks in energy industry. International Journal of Engineering, Transactions A: Basics. 2021. Vol. 34. Iss. 7, p. 1778-1784. DOI: 10.5829/IJE.2021.34.07A.22
31. Vayas-Ortega G., Soguero-Ruiz G., Rodríguez-Ibáñez M. et al. On the Differential Analysis of Enterprise Valuation Methods as a Guideline for Unlisted Companies Assessment (II): Applying Machine-Learning Techniques for Unbiased Enterprise Value Assessment. Applied Science. 2020. Vol. 10. Iss. 17. N 5334. DOI: 3390/app10155334
32. Ponomarenko T., Marin E., Galevskiy S. Economic Evaluation of Oil and Gas Projects: Justification of Engineering Solutions in the Implementation of Field Development Projects. Energies. Vol. 15. Iss. 9. N 3103. DOI: 10.3390/en15093103
33. Providakis S., Rogers C.D.F., Chapman D.N. Assessing the Economic Risk of Building Damage due to the Tunneling-Induced Settlement Using Monte Carlo Simulations and BIM. Sustainability. 2020. Vol. 12. Iss. 23. N 10034. DOI: 3390/su122310034
34. Korshunov G.I., Eremeeva A.M., Drebenstedt P. Justification of the use of a vegetal additive to diesel fuel as a method of protecting underground personnel of coal mines from the impact of harmful emissions of diesel-hydraulic locomotives. Journal of Mining Institute. Vol. 247. P. 39-47. DOI: 10.31897/PMI.2021.1.5
35. Sigal A.V., Remesnik E.S. Fishburn point estimates and their generalizations. Modeling and analysis of safety and risk in complex systems. 2019, p. 85-92 (in Russian).
36. Si-Yong L., Hnottavange-Telleen K., Wei Jia et al.Risk Assessment and Management Workflow – An Example of the Southwest Regional Partnership. Energies. 2021.Vol. Iss. 7. N 1908. DOI: 10.3390/en14071908
37. Solovyova V.M., Ilinova A.A., Cherepovitsyn A.E. Strategic forecasting of REE mining projects development in Russian Advances in Raw Material Industries for Sustainable Development Goals. 2021, p. 456-464. DOI: 10.1201/9781003164395-57
38. Kuo T. An Ordinal Consistency Indicator for Pairwise Comparison Matrix. Symmetry. Vol. 13. Iss. 11. N 2183. DOI: 10.3390/sym13112183