Вероятностное исследование оптимизации промывки скважины
- Ph.D. доцент Технологический университет Саханда ▪ Orcid
Аннотация
Промывка ствола скважины считается одной из самых важных функций бурового раствора. Качественная промывка ствола скважины обеспечивает эффективное бурение скважины с минимальными осложнениями. В исследовании на основе данных бурения сланцевого пласта рассматриваются два основных этапа промывки ствола скважины: удаление шлама из-под долота и его перенос на поверхность. Представлены традиционные модели для оптимизации каждого этапа. Поскольку модели требуют различных входных данных, которые обычно подвержены некоторой степени погрешности и неопределенности, выходные данные модели также являются неопределенным параметром. С помощью моделирования методом Монте-Карло было проведено простое вероятностное исследование для количественной оценки степени достоверности полученных результатов. Результаты данного исследования подтверждают качественную промывку ствола рассматриваемой скважины. Однако более надежное решение по дальнейшей оптимизации промывки скважины должно приниматься с учетом результатов анализа неопределенности.
Введение
Буровые растворы выполняют различные важные функции, включая очистку скважины, контроль порового давления пласта, охлаждение долота, смазку бурильной колонны, сбор данных о пласте и обеспечение стабильности ствола скважины [1-4]. Эффективность процесса бурения сильно зависит от степени очистки ствола скважины от шлама. Эффективная очистка ствола скважины приводит к повышению механической скорости проходки (МСП) и может предотвратить такие осложнения при бурении, как прихват труб, потеря циркуляции, некачественное первичное цементирование, неправильная работа бурового долота, чрезмерный крутящий момент
и т.д. [5-7].
Понятие «очистка скважины» иногда неверно интерпретируется как перенос шлама, хотя это двухэтапный процесс – удаление шлама из-под долота и перенос удаленного шлама на поверхность.
Эффективность процесса промывки скважины зависит от рабочих параметров бурения (расход бурового раствора в скважине), геометрии скважины (угол наклона, эксцентриситет бурильной колонны, размер скважины, внешний диаметр бурильной колонны, внутренний диаметр обсадной колонны и т.д.), свойств бурового раствора (плотность и реологические характеристики) и свойств шлама (плотность, средний диаметр, объем и т.д.) [6-8].
Ряд исследователей разработали экспериментальные, численные и аналитические модели для прогнозирования и оптимизации процесса промывки скважины. В этих работах исследуется влияние состава и свойств бурового раствора [9-11], типа бурового раствора [12, 13], рабочих параметров бурения [14-16], геометрии скважины [8, 17, 18], состава шлама и его свойств [19-21], а также свойств потока [22, 23] на процесс промывки скважины. В некоторых исследованиях различные факторы рассматриваются с помощью средств вычислительной гидродинамики (CFD) [6, 24].
Как правило, для моделей промывки скважины требуется разнообразный набор исходных данных. Количество и точность этих входных данных определяют эффективность разработанных моделей. Тот факт, что большинство входных данных подвержены ошибкам, приводит к некоторому уровню неопределенности в выходных данных модели. Человеческий фактор, неправильная интерпретация и упрощение являются основными источниками ошибок входных данных [25].
В данной работе показатели бурения в сланцевом пласте используются в традиционных моделях для оценки эффективности промывки скважин. Кроме того, проводится вероятностное исследование для измерения степени неопределенности в выходных данных моделей промывки скважин.
Методология
Представлены и проанализированы традиционные методы оптимизации промывки скважин, а также набор данных по бурению в сланцевом пласте. Эти данные используются для оценки эффективности промывки скважины, т.е. эффективности удаления шлама из-под долота и переноса шлама на поверхность. Проводится вероятностное исследование с использованием моделирования методом Монте-Карло для количественной оценки степени неопределенности в процессе оптимизации промывки скважины.
Поскольку очистка скважины – это двухэтапный процесс (удаление шлама из-под долота и перенос удаленного шлама на поверхность), уравнения и традиционные методы оптимизации представлены отдельно для каждой части.
Удаление шлама из-под долота
Для оптимизации удаления шлама из-под долота обычно исследуются и оптимизируются гидравлические параметры долота для эффективного удаления шлама. Однако при оптимизации следует учитывать эксплуатационные ограничения, например, расход бурового насоса. Основными гидравлическими параметрами долота являются скорость раствора на выходе гидромониторной насадки (скорость в гидромониторе), гидравлическая мощность долота и сила удара струи, которые могут быть рассчитаны следующим образом [26, 27]:
- скорость раствора в гидромониторе
где Q – расход бурового раствора в стволе скважины, м3/с; ОПП – общая площадь потока в поперечном сечении гидромонитора долота, м2;
- гидравлическая мощность долота
где ∆Pb – перепад давления бурового раствора в долоте; ПБР – плотность бурового раствора, кг/м3; Cd – коэффициент расхода (обычно принимается равным 0,95);
- сила удара струи
Перенос шлама на поверхность
Во время транспортировки шлам, как правило, осаждается в скважине, в то время как буровой раствор движется вверх по кольцевому пространству к поверхности. Из-за сложной природы процесса транспортировки шлама трудно найти точные аналитические решения для анализа эффективности выносящей способности бурового раствора. Для решения этой проблемы обычно используются два подхода.
В первом приближении используются корреляции, которые доступны для вертикальных, наклонно-направленных и горизонтальных скважин. Одна из корреляций, которая обычно используется для оценки выносящей способности бурового раствора в вертикальных или почти вертикальных скважинах, была определена Робинсоном и Морганом, уравнение имеет следующий вид [28]:
где ПВС – показатель выносящей способности; СКП – скорость бурового раствора в кольцевом пространстве, м/с; k – константа в степенном законе, Па·с.
Значения ПВС, равные или больше единицы, указывают на хорошее условие промывки скважины [28, 29].
Во втором приближении сравниваются скорость восходящего потока бурового раствора в кольцевом пространстве (кольцевая скорость) и скорость осаждения шлама (скорость осаждения), при этом скорость транспортировки шлама определяется как разность между кольцевой скоростью и скоростью осаждения:
где Va – кольцевая скорость бурового раствора; Vs – скорость осаждения шлама.
Кроме того, на основе кольцевой скорости и скорости осаждения может быть определен коэффициент переноса
Более высокие значения коэффициента переноса указывают на более эффективный перенос шлама. Основная проблема данного подхода заключается в сложности расчета скорости осаждения. В случае ньютоновских жидкостей и для частиц правильной формы скорость осаждения может быть рассчитана путем уравновешивания тягового усилия и силы тяжести. Однако для буровых растворов со сложным реологическим поведением и частиц шлама неправильной формы расчет скорости осаждения будет гораздо сложнее [30, 31].
В данной работе для расчета скорости осаждения используется упрощенная корреляция
Чиена. Данная корреляция, основанная на расчете кажущейся вязкости бурового раствора и числа Рейнольда частиц, имеет следующий вид для промежуточных и турбулентных режимов течения [32, 33]:
где ρс – плотность шлама, кг/м3; dc – средний диаметр частиц шлама, м.
На основании представленных формул видно, что любая оптимизация процесса промывки скважин требует тщательной адаптации рабочих и технологических параметров, таких как расход бурового раствора, реологические свойства и плотность.
Входные данные бурения
Необходимые данные для вероятностного исследования промывки скважин, включая рабочие параметры бурения (расход бурового раствора), свойства бурового раствора (плотность и реологические характеристики) и свойства шлама (плотность и средний диаметр), были получены на основе опыта бурения в сланцевом пласте. Используемые буровые растворы характеризуются реологическим поведением, согласно пластическому закону Бингама. Пласт был пробурен несколькими скважинами с различными рабочими параметрами и свойствами жидкости, исходя из имеющихся геологических и технических условий.
Диапазоны значений каждого параметра, полученные на основе реальных данных бурения:
- Свойства бурового раствора: ПБР 1025,7-1090,4 кг/м3; пластическая вязкость 0,005-0,007 Па·с; предел текучести 7,18-9,58 Па; расход бурового раствора 0,028-0,054 м3/с.
- Свойства долота: ОПП = 6,41×10–4 м2; Cd = 0,95.
- Геометрия скважины: диаметр скважины 0,4445 м; внешний диаметр бурильной колонны 0,127 м.
- Свойства частиц шлама: средний диаметр 1,996×10–3 м; плотность 2498,4 кг/м3.
Моделирование методом Монте-Карло
Моделирование методом Монте-Карло – это численный метод, в котором случайные выборки входных данных генерируются на основе их функции распределения. Выходные данные модели (скорость осаждения, скорость переноса, коэффициент переноса, скорость в гидромониторе, гидравлическая мощность долота, сила удара струи) рассчитываются для каждого случайного массива входных данных. Таким образом, вместо одного выходного значения получается распределение выходных данных модели, на основе которого рассчитывается вероятность появления каждого выходного значения [25, 34, 35]. В данной работе для вероятностного исследования эффективности промывки скважины используется программное обеспечение Oracle Crystal Ball.
Функция распределения неопределенных входных данных представлена в таблице. Для входных данных выбрано треугольное распределение, так как были известны минимальное, максимальное и наиболее вероятное значение каждого параметра. Выбор треугольного распределения основан на том, что точная функция распределения не могла быть определена из-за недостаточного количества входных данных. Однако имелись представления о минимальном, максимальном и наиболее вероятном значениях, что оправдывает использование треугольной функции распределения.
Функция распределения неопределенных входных данных
|
Параметр |
Тип распределения |
Параметры распределения |
||
|
Минимальное |
Максимальное |
Наиболее вероятное |
||
|
ПБР, кг/м3 |
Треугольный |
1025,7 |
1090,4 |
1054,5 |
|
Пластическая вязкость, Па·с |
Треугольный |
0,005 |
0,007 |
0,006 |
|
Предел текучести, Па |
Треугольный |
7,18 |
9,58 |
8,38 |
|
Выход бурового раствора Q, м3/с |
Треугольный |
0,028 |
0,054 |
0,044 |
Результаты исследований
Для исследования процесса удаления шлама из-под долота анализируются скорость в гидромониторе, гидравлическая мощность долота и сила удара струи. На рис.1 показаны вероятные значения этих параметров на основе моделирования методом Монте-Карло. Представленные на графиках результаты подтверждают, что в случае неопределенных входных данных на выходе будет получено не одно значение, а распределение возможных значений, которое можно использовать для количественной оценки неопределенности.
Для количественной оценки диапазонов определенности, связанных с расчетной скоростью
в гидромониторе, гидравлической мощностью долота и силой удара струи, представлены графики трендов с диапазонами определенности на рис.2.
Представленные данные могут быть использованы для определения выходного значения с конкретной степенью определенности. Например, на рис.2, в видно, что в случае неопределенных входных данных значение силы удара струи лежит в диапазоне 1732-4199 Н с вероятностью 90 %. Повышение уровня определенности исходных данных сузит 90 %-ный диапазон определенности. Учитывая проведенный анализ неопределенности, следует отметить, что для дальнейшей оптимизации гидравлических параметров долота необходимо учитывать уровень определенности выходных данных.
Для исследования переноса шлама анализируются ПВС, скорость переноса и коэффициент переноса. На рис.3 показаны вероятные значения этих параметров на основе моделирования методом Монте-Карло. Подтверждается, что в случае неопределенных входных данных на выходе
будет получено не одно значение, а распределение возможных значений, которое можно использовать для количественной оценки неопределенности.
Для количественной оценки диапазонов определенности, связанных с рассчитанными ПВС и коэффициентом переноса, на рис.4 представлены графики трендов с указанными диапазонами определенности.
Графики трендов позволяют оценить степень определенности выходных данных. Как видно из рис.4, а, значение ПВС превышает 1,42 с достоверностью 90 %. Это свидетельствует об эффективном переносе шлама в рассматриваемой скважине. Анализ скорости переноса и коэффициента переноса также подтверждает эффективный перенос шлама. Для дальнейшей оптимизации ПВС или любого другого показателя переноса шлама необходимо учитывать определенность результатов, особенно когда исходные данные являются неопределенными, как в данном исследовании.
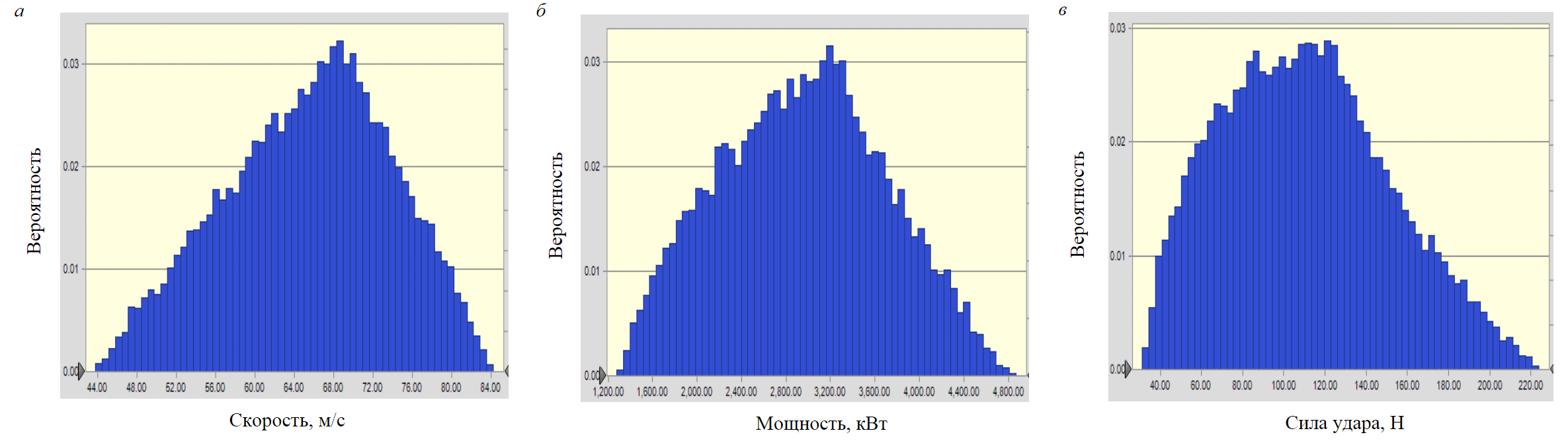
Рис.1. Вероятности значений скорости в гидромониторе (a), гидравлической мощности долота (б) и силы удара струи (в)
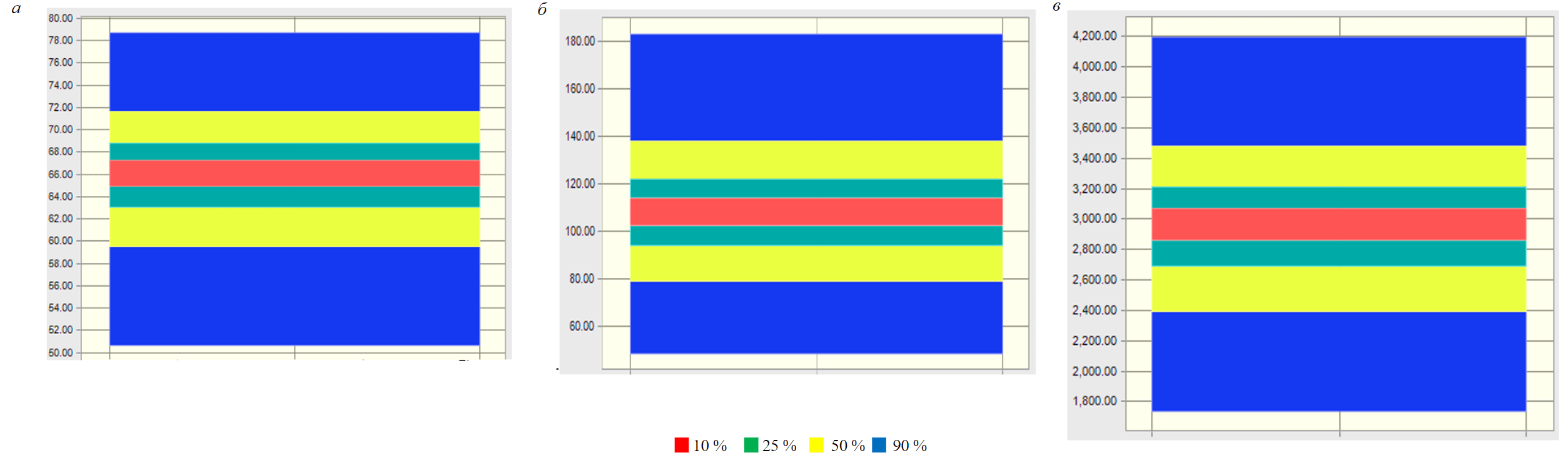
Рис.2. Диапазоны определенности значений скорости в гидромониторе (а), долота (б) и силы удара струи (в)
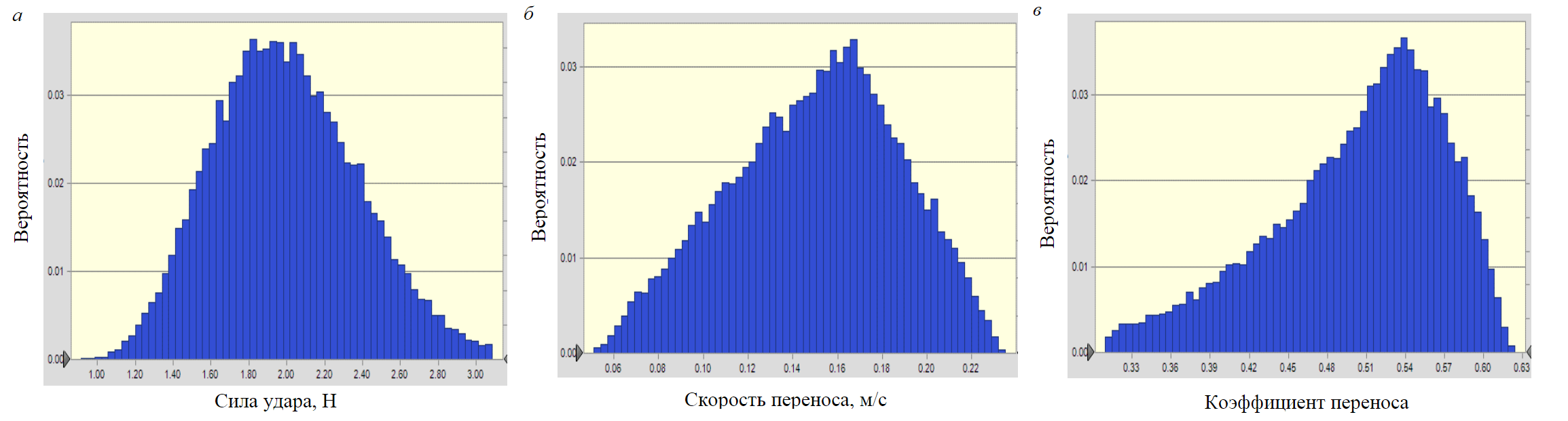
Рис.3. Вероятности значений ПВС (a), скорости переноса (б) и коэффициента переноса (в)

Рис.4. Диапазоны определенности значений ПВС (а) и коэффициента переноса (б)
Заключение
Одной из наиболее важных функций бурового раствора является качественная очистка скважины, которая необходима для эффективного бурения с минимальными осложнениями. Поскольку все модели оптимизации промывки ствола скважины требуют множества неопределенных входных данных, выходной результат также будет иметь неопределенное значение. В данной работе, используя моделирование методом Монте-Карло, было проведено простое вероятностное исследование традиционных моделей промывки скважин для количественной оценки уровня определенности/неопределенности в процедуре расчета. Такой подход может обеспечить принятие более надежного решения об оптимизации. На основании полученных результатов можно сделать следующие выводы:
- Результаты подтверждают, что в случае неопределенных входных данных будет существовать некоторая степень неопределенности в параметрах оптимизации промывки скважин, т.е. скорости в гидромониторе, гидравлической мощности долота, силе удара струи, ПВС, скорости переноса и коэффициенте переноса.
- При известном уровне определенности каждого параметра можно принять более надежное решение для дальнейшей оптимизации промывки скважин.
- ПВС превышает 1,42 с достоверностью 90 %, что свидетельствует об эффективном переносе шлама в рассматриваемой скважине.
- Полученные вероятности значений скорости переноса и коэффициента переноса также подтверждают эффективный перенос шлама в рассматриваемой скважине.
Литература
- Abbas A.K., Alsaba M.T., Al Dushaishi M.F. Improving hole cleaning in horizontal wells by using nanocomposite water-based mud // Journal of Petroleum Science and Engineering. 2021. Vol. 203. № 108619. DOI: 10.1016/j.petrol.2021.108619
- Andrade G.M.P., Oechsler B.F., Coelho J.S.C. et al. Evaluation of characteristic diameter on barite settling in drilling fluids by Monte Carlo method // Journal of Petroleum Science and Engineering. 2021. Vol. 206. № 109072. DOI: 10.1016/j.petrol.2021.109072
- Ashena R., Hekmatinia A.-A., Ghalambor A. et al. Improving drilling hydraulics estimations – a case study // Journal of Petroleum Exploration and Production Technology. 2021. Vol. 11. P. 2763-2776. DOI: 10.1007/s13202-021-01203-4
- Assi A.H. Enhancing the Lifting Capacity of Drilling Fluids in Vertical Oil Wells // Iraqi Journal of Chemical and Petroleum Engineering. 2017. Vol. 18. P. 13-29.
- Awad A.M., Hussein I.A., Nasser M.S. et al. A CFD-RSM study of cuttings transport in non-Newtonian drilling fluids: Impact of operational parameters // Journal of Petroleum Science and Engineering. 2022. Vol. 208. Part C. № 109613. DOI: 10.1016/j.petrol.2021.109613
- Badrouchi F., Rasouli V., Badrouchi N. Impact of hole cleaning and drilling performance on the equivalent circulating density // Journal of Petroleum Science and Engineering. 2022. Vol. 211. № 110150. DOI: 10.1016/j.petrol.2022.110150
- Barooah A., Khan M.S., Khaled M.S. et al. Investigation of cutting transport in horizontal/deviated annulus using visualization and pressure drop techniques for two-phase slurry flow // Journal of Natural Gas Science and Engineering. 2022. Vol. 100. № 104460. DOI: 10.1016/j.jngse.2022.104460
- Boyou N.V., Ismail I., Wan Sulaiman W.R. et al. Experimental investigation of hole cleaning in directional drilling by using nano-enhanced water-based drilling fluids // Journal of Petroleum Science and Engineering. 2019. Vol. 176. P. 220-231. DOI: 10.1016/j.petrol.2019.01.063
- Choupani M.A., Tabatabaee Moradi S.Sh., Tabatabaei Nejad S.A. Study on Attapulgite as Drilling Fluid Clay Additive in Persian Gulf Seawater // International Journal of Engineering. Transactions C: Aspects. 2022. Vol. 35. № 3. P. 587-595. DOI: 10.5829/ije.2022.35.03C.12
- Dvoynikov M.V., Nutskova M.V., Blinov P.A. Developments Made in the Field of Drilling Fluids by Saint Petersburg Mining University // International Journal of Engineering. Transactions A: Basics. 2020. Vol. 33. Iss. 4. P. 702-711. DOI: 10.5829/ije.2020.33.04a.22
- Epelle E.I., Obande W., Okolie J.A., Wilberforce T. CFD modelling and simulation of drill cuttings transport efficiency in annular bends: Effect of particle size polydispersity // Journal of Petroleum Science and Engineering. 2022. Vol. 208. Part E. № 109795. DOI: 10.1016/j.petrol.2021.109795
- Ferroudji H., Rahman M.A., Hadjadj A., Ntow Ofei T. 3D numerical and experimental modelling of multiphase flow through an annular geometry applied for cuttings transport // International Journal of Multiphase Flow. 2022. Vol. 151. № 104044. DOI: 10.1016/j.ijmultiphaseflow.2022.104044
- Gbadamosi A.O., Junin R., Abdalla Y., Agi A. Experimental investigation of the effects of silica nanoparticle on hole cleaning efficiency of water-based drilling mud // Journal of Petroleum Science and Engineering. 2019. Vol. 172. Р. 1226-1234. DOI: 10.1016/j.petrol.2018.09.097
- Gorji M., Kazemi A., Ganji D.D. Uncertainties due to fuelheating value and burner efficiency on performance functionsof turbofan engines using Monte Carlo simulation // International Journal of Engineering. Transactions A: Basics. 2014. Vol. 27. № 7. P. 1139-1148. DOI: 10.5829/idosi.ije.2014.27.07a.16
- Gulraiz S., Gray K.E. Study on the combined effect of thixotropy, particle shape, and particle size on cuttings transport in horizontal annuli // Powder Technology. 2021. Vol. 392. P. 703-716. DOI: 10.1016/j.powtec.2021.07.041
- Heshamudin N.S., Katende A., Rashid H.A., Ismail I. Experimental investigation of the effect of drill pipe rotation on improving hole cleaning using water-based mud enriched with polypropylene beads in vertical and horizontal wellbores // Journal of Petroleum Science and Engineering. 2019. Vol. 179. Р. 1173-1185. DOI: 10.1016/j.petrol.2019.04.086
- Huque M.M., Rahman M.A., Zendehboudi S., Butt S. Experimental and numerical study of cuttings transport in inclined drilling operations // Journal of Petroleum Science and Engineering. 2022. Vol. 208. Part B. № 109394. DOI: 10.1016/j.petrol.2021.109394
- Issoufou M.K., Song X., Zhu Z., Xu Z. Predicting cuttings settling velocity in drilling muds and in rising-bubbles-containing muds // Journal of Petroleum Science and Engineering. 2021. Vol. 204. DOI: 10.1016/j.petrol.2021.108766
- Jafarifar I., Karimi Dehkordi B., Abbasi H., Schaffie M. Evaluation and optimization of water-salt based drilling fluids for slim-hole wells in one of Iranian central oil fields // Upstream Oil and Gas Technology. 2020. Vol. 5. DOI: 10.1016/j.upstre.2020.100010
- Leusheva E, Morenov V., Tabatabaee Moradi S.Sh. Effect of Carbonate Additives on Dynamic Filtration Index of Drilling Mud // International Journal of Engineering Transactions B: Applications. 2020. Vol. 33. Iss. 5. P. 934-939. DOI: 10.5829/ije.2020.33.05b.26
- Mahmoud H., Alhajabdalla M., Nasser M.S., Hussein I.A. Settling behavior of fine cuttings in fiber-containing polyanionic fluids for drilling and hole cleaning application // Journal of Petroleum Science and Engineering. 2021. Vol. 199. № 108337. DOI: 10.1016/j.petrol.2020.108337
- Mahmoud H., Hamza A., Nasser M.S., Hussein I.A. Hole cleaning and drilling fluid sweeps in horizontal and deviated wells: Comprehensive review // Journal of Petroleum Science and Engineering. 2020. Vol. 186. № 106748. DOI: 10.1016/j.petrol.2019.106748
- Mazen A.Z., Mujtaba I.M., Hassanpour A., Rahmanian N. Mathematical modelling of performance and wear prediction of PDC drill bits: Impact of bit profile, bit hydraulic, and rock strength // Journal of Petroleum Science and Engineering. 2020. Vol. 188. № 106849. DOI: 10.1016/j.petrol.2019.106849
- Mohamed A., Salehi S., Ahmed R. Significance and complications of drilling fluid rheology in geothermal drilling: A review // Geothermics. 2021. Vol. 93. № 102066. DOI: 10.1016/j.geothermics.2021.102066
- Mohammadsalehi M., Malekzadeh N. Application of New Hole Cleaning Optimization Method within All Ranges of Hole Inclinations // International Petroleum Technology Conference, 15-17 November 2011, Bangkok, Thailand, 2012. DOI: 10.2523/IPTC-14154-MS
- Muherei M.A., Basaleh S.S. True Power Law Drilling Fluid Model: Effect of Its Rheological Parameters on Static Particle Settling Velocity // International Research Journal of Engineering and Technology (IRJET). 2016. Vol. 3. Iss. 1. P. 77-88.
- Robinson L., Morgan M. Effect of Hole Cleaning on Drilling Rate and Performance // AADE 2004 Drilling Fluids Conference, 6-7 April 2004, Houston, Texas, 2004. P. 1-7.
- Salubi V., Mahon R., Oluyemi G., Oyeneyin B. Effect of two-phase gas-liquid flow patterns on cuttings transport efficiency // Journal of Petroleum Science and Engineering. 2022. Vol. 208. Part A. № 109281. DOI: 10.1016/j.petrol.2021.109281
- Sayindla S., Lund B., Ytrehus J.D., Saasen A. Hole-cleaning performance comparison of oil-based and water-based drilling fluids // Journal of Petroleum Science and Engineering. 2017. Vol. 159. P. 49-57. DOI: 10.1016/j.petrol.2017.08.069
- Khaled M.Sh., Khan M.S., Ferroudji H. et al. Dimensionless data-driven model for optimizing hole cleaning efficiency in daily drilling operations // Journal of Natural Gas Science and Engineering. 2021. Vol. 96. № 104315. DOI: 10.1016/j.jngse.2021.104315
- Sun X., Zhang K., Chen Y., Li W. Study on the settling velocity of drilling cuttings in the power law // Powder Technology. 2020. Vol. 362. P. 278-287. DOI: 10.1016/j.powtec.2019.11.025
- Tabatabaee Moradi S.Sh., Nikolaev N.I. Uncertainty assessment of wellbore stability analysis in horizontal sections // SN Applied Sciences. 2020. Vol. 2. № 437. DOI: 10.1007/s42452-020-2237-y
- Yan T., Qu J., Sun X., Chen Y. Numerical investigation on horizontal wellbore hole cleaning with a four-lobed drill pipe using CFD-DEM method // Powder Technology. 2020. Vol. 375. P. 249-261. DOI: 10.1016/j.powtec.2020.07.103005
- Yan T., Qu J., Sun X., Li W. A novel predictive model of drag coefficient and settling velocity of drill cuttings in non-Newtonian drilling fluids // Petroleum Science. 2021. Vol. 18. Iss. 6. P. 1729-1738. DOI: 10.1016/j.petsci.2021.09.003
- Yeo L., Feng Y., Seibi A., Temani A. Optimization of hole cleaning in horizontal and inclined wellbores: A study with computational fluid dynamics // Journal of Petroleum Science and Engineering. 2021. Vol. 205. № 108993. DOI: 10.1016/j.petrol.2021.108993
