Модель шагающего пробоотборника для исследования донной поверхности подледникового озера Восток
- 1 — канд. техн. наук ведущий научный сотрудник Санкт-Петербургский горный университет ▪ Orcid
- 2 — канд. техн. наук научный руководитель лаборатории НЦ «Арктика» Санкт-Петербургский горный университет ▪ Orcid
- 3 — д-р техн. наук профессор Санкт-Петербургский горный университет ▪ Orcid
- 4 — канд. техн. наук ассистент Санкт-Петербургский горный университет ▪ Orcid
- 5 — лаборант-исследователь Санкт-Петербургский горный университет ▪ Orcid
Аннотация
Технологии и технические средства исследования подледниковых озер Антарктиды – новое развивающееся научно-техническое направление, которое на сегодняшний день не имеет четко установленной методологии. На основании разрабатываемой технологии бурения новой скважины доступа к озеру Восток и его вскрытия, а также анализа существующих способов и устройств для отбора проб донных отложений, предложена принципиальная модель пробоотборника с движителем шагающего типа, обладающего способностью передвигаться по различным траекториям и позволяющего вести работы в широком технологическом диапазоне. В предложенной модели устройства предусмотрена его оснастка различными исполнительными органами для взятия проб донной поверхности с разными физико-механическими характеристиками. На основании представленной принципиальной модели шагающего пробоотборника разработана математическая модель устройства на основе методов теоретической механики. В результате выполненных исследований получены зависимости, позволяющие осуществить научно обоснованный выбор оптимальных значений геометрических и силовых параметров шагающего устройства. Разработан концептуальный дизайн шагающего пробоотборника, учитывающий взаимное расположение и сопряжение его основных компонентов, габаритные размеры доставочного снаряда, а также эстетическую составляющую устройства.
Введение
Уже более 50 лет станция «Восток» является центром отечественных научных исследований в Антарктиде, за результатами которых следит все мировое научное сообщество [1].
Открытие озера Восток во второй половине ХХ века [2] поставило новые научно-технические задачи, решение которых направлено на его вскрытие и дальнейшее изучение. За все время проведения работ были получены приближенные данные и выдвинуты предположения о морфометрических характеристиках водоема [3-5], составе, возрасте и мощности осадочных отложений [6-8], а также о циркуляции воды в нем [9].
Переход бурения на конжеляционный лед, представляющий собой слой намерзшей воды озера, а также взятие из скважины проб замерзшей воды озера после его вскрытия позволили оценить многие параметры водной толщи [10]. Однако наибольший интерес представляют донные осадочные отложения, их состав и мощность [11-13]. Получение даже небольшого объема материала со дна подледникового озера позволит решить множество научных задач [11-16], главной из которых является поиск признаков наличия в озере живых организмов [17].
На сегодняшний день были успешно реализованы два проекта по отбору проб донных отложений подледниковых водоемов Антарктиды – WISSARD [18, 19] и SALSA [20]. Однако примененные в данных проектах технические решения [21, 22] не могут быть использованы при исследовании реликтового озера Восток из-за его уникальных характеристик.
Анализ существующих технических средств для исследования водоемов и разработки подводных месторождений позволил сформулировать основные требования к конструкции пробоотборника с учетом разработанной ранее технологии вскрытия подледникового озера [23-25], параметров скважины доступа, технологии доставки устройства к донной поверхности, технологии связи устройства с поверхностью ледника [26, 27], а также характеристик озера Восток: глубины, рельефа дна, наличия и скорости подводных течений [28, 30].
Одним из этапов создания экспериментального образца пробоотборника для исследования донных отложений озера Восток является разработка цифрового прототипа устройства для имитации процессов его доставки к донной поверхности и отбора проб донных отложений. Полученная информация позволит оценить предлагаемые технические решения с точки зрения надежности, экологической безопасности и т.п. и по результатам исследования внести соответствующие коррективы в конструкцию экспериментального образца пробоотборника.
Существующие устройства для отбора проб донных отложений подледниковых озер Антарктиды представлены, главным образом, колонковыми пробоотборниками, которые можно классифицировать по принципу действия на гравитационные и гравитационно-поршневые, ударные, поршневые, самосинхронизирующиеся вибрационные, динамически-уравновешенные [31-33].
Несмотря на экспериментально установленные достоинства колонковых пробоотборников, они имеют общий недостаток – за одну спуско-подъемную операцию, достигающую в условиях станции «Восток» иногда нескольких часов, на поверхность доставляется проба, отобранная непосредственно под скважиной. Таким образом, полученная информация не является репрезентативной и не дает полного представления о донной поверхности. Поэтому с учетом достаточной несущей способности дна озера, а также его предположительно пологого рельефа непосредственно под станцией «Восток», целесообразно применение движителей, способных обеспечить перемещение устройства и многократный отбор проб донных отложений.
Для исследования донной поверхности и разработки месторождений полезных ископаемых морей и океанов в качестве средств передвижения используются движители гусеничного, колесного, шнекового, вибрационного, шагающего и других типов [34]. Однако указанные условия эксплуатации делают практически непригодными или малоэффективными большинство перечисленных движителей из-за невозможности гарантировать сохранение целостности реликтовой экосистемы дна озера Восток вследствие агрессивного механического воздействия на грунт, приводящего к разрушению поверхностного слоя и замутнению воды.
Анализ известных способов передвижения донных агрегатов [34] показал перспективность использования двухопорных шагающих устройств (шагающих движителей), обеспечивающих работу на любых грунтах, в том числе и на грунтах со сложным рельефом, обладающих высокой проходимостью, экологичностью, простотой управления и позволяющих вести работы в широком технологическом диапазоне [35, 36]. При этом процесс шагания устройства может быть обеспечен путем изменения положения центра масс системы за счет перемещения противовеса, в качестве которого может быть использован рабочий орган устройства.
Методология
Зависимость веса рабочего органа (противовеса) от геометрических и силовых параметров шагающего устройства
При проектировании шагающего пробоотборника (шагающего устройства) необходимо увязать конструктивные параметры данного устройства с габаритами доставочного модуля и способом его транспортирования до донной поверхности подледникового озера Восток [26]. Учитывая отсутствие опыта конструирования и эксплуатации пробоотборников данного типа, поставлена задача разработать методику расчета, на базе которой, по мере накопления опыта конструирования и эксплуатации, в дальнейшем реализовалось бы проектирование подобных устройств.
В качестве базового варианта принята модель шагающего двухопорного пробоотборника, полный цикл шагания которого включает три этапа: поворот (подъем) несущей рамы относительно одной из опор в вертикальной плоскости, поворот несущей рамы относительно данной опоры в горизонтальной плоскости и поворот (опускание) несущей рамы относительно той же опоры в вертикальной плоскости [34-36]. В статье рассматривается только первый этап движения устройства.

Рис.1. Расчетная схема шагающего пробоотборника
Расчетная схема силового нагружения шагающего пробоотборника представлена на рис.1. Здесь 1 – рабочий орган (противовес); 2 – опора; 3 – донная поверхность; 4 – несущая рама; 5 – опорный башмак; С, В – центры шарниров левой и правой опор; L – общая длина несущей рамы, м; lк – длина консоли, м; lцм – длина участка несущей рамы от ее конца до центра масс рабочего органа, м; хцм – расстояние от центра шарнира опоры С до центра масс рабочего органа, м; l – длина рабочего участка несущей рамы, м; Gор – сила тяжести рабочего органа, Н; Gоп – сила тяжести опоры, Н; G¯'p – сила тяжести консоли, расположенной слева от центра С, Н; q – вес 1 м несущей рамы, Н/м; G¯''p – сила тяжести части несущей рамы, расположенной справа от центра С, Н; hп – высота подъема опоры при шагании, м; h¯''p – расстояние по вертикали от донной поверхности до несущей рамы, м; h¯'p – расстояние по вертикали от донной поверхности до опускаемой части несущей рамы при шагании, м; φ – угол поворота несущей рамы в вертикальной плоскости при шагании пробоотборника относительно ее исходного (горизонтального) положения, град.
В устройстве данного типа поворот рамы осуществляется за счет изменения положения центра масс системы (несущая рама, опоры и рабочий орган) перемещением рабочего органа на левую или правую консоли. Вес рабочего органа, необходимый для создания опрокидывающего момента относительно центров С или В, определяется при равенстве нулю силы, с которой одна из опор действует на донную поверхность.
Уравнение равновесия шагающего пробоотборника при равенстве нулю силы, с которой правая опора действует на донную поверхность (предельное состояние, характеризующее начало процесса шагания) (рис.1) имеет вид:
где xцм=lк-lцм; G'p=qlк; G''p=q(l+lк) .
Зависимость веса рабочего органа от геометрических и силовых параметров шагающего пробоотборника с учетом уравнения (1) представляется в виде:
Выражение для нормированного веса рабочего органа, полученное делением уравнения (2) на длину рабочего участка несущей рамы, имеет вид:
где gор = Gор/l – нормированный вес рабочего органа, Н/м; αк = lк/l – безразмерный коэффициент консоли; αцм = lцм/l – безразмерный коэффициент положения рабочего органа; gоп = Gоп/l – нормированный вес опоры, Н/м.

Рис.2. Графики зависимости нормированного веса рабочего органа gор (1-3) и общего нормированного веса шагающего устройства gшп (4-6) от безразмерного коэффициента консоли αк при gоп/q = 0,05 и αцм = 0 (1,4); 0,1 (2,5); 0,2 (3,6)
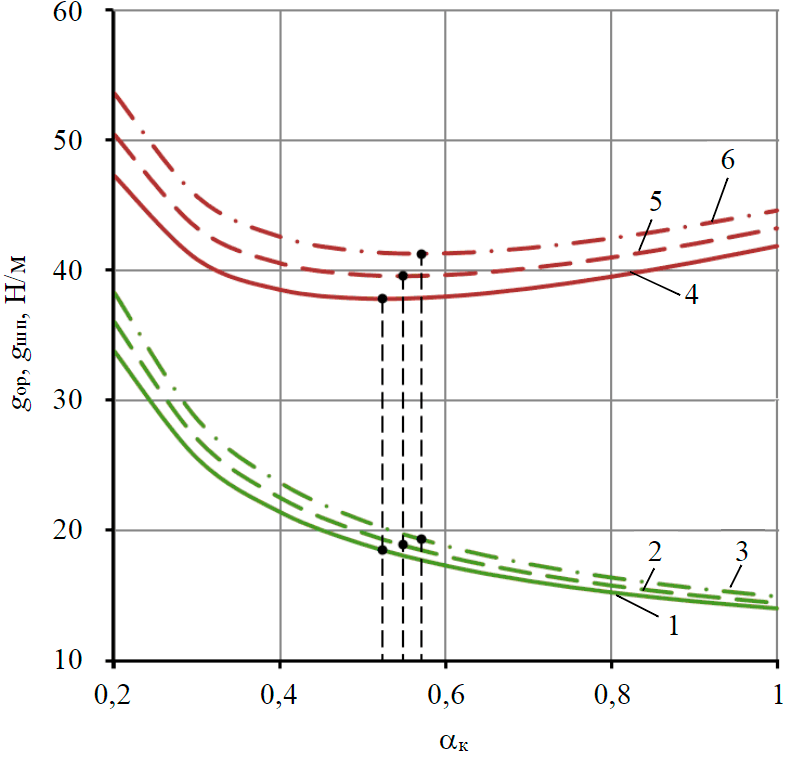
Рис.3. Графики зависимости нормированного веса рабочего органа gор (1-3) и общего нормированного веса шагающего устройства gшп (4-6) от безразмерного коэффициента консоли αк при αцм = 0 и gоп/q = 0,05 (1,4); 0,1 (2,5); 0,15 (3,6)
Под безразмерным коэффициентом консоли подразумевается отношение длины консоли к длине рабочего участка несущей рамы. При αк = 0 длина консоли равна нулю, при αк = 1 – длине рабочего участка несущей рамы. Под безразмерным коэффициентом положения рабочего органа подразумевается отношение длины участка несущей рамы от ее конца до центра масс рабочего органа к длине рабочего участка несущей рамы. При αцм = 0 центр масс рабочего органа находится на конце несущей рамы, т.е. в крайнем левом положении (рис.1). При αцм = 1 центр масс рабочего органа совпадает с центром шарнира левой опоры С.
Отметим, что коэффициент положения рабочего органа косвенно характеризует габаритные размеры рабочего органа, контуры которого, исходя из конструктивных соображений, не должны выступать за пределы несущей рамы.
На основании выражения (3) установлено, что нормированный вес рабочего органа шагающего пробоотборника при заданной длине несущей рамы зависит от безразмерных коэффициентов консоли αк и положения рабочего органа αцм. Минимальный размер шагающего устройства обеспечивается при средних значениях веса 1 м несущей рамы q = 9 Н/м и отношения нормированного веса опоры к весу 1 м несущей рамы gоп/q = 0,05.
Графики зависимости нормированного веса рабочего органа gор при изменении коэффициента консоли αк в пределах от 0 до 1 для трех значений коэффициента положения рабочего органа αцм: 0; 0,1; 0,2 с учетом принятых значений q и gоп/q представлены на рис.2 (кривые 1-3).
Анализ кривых 1-3 на рис.2 показывает, что с увеличением длины консоли, т.е. безразмерного коэффициента αк, нормированный вес рабочего органа gор гиперболически снижается. При αк = 0,2, aцм = 0 и принятых ранее значениях q и gоп/q нормированный вес рабочего органа gор = 33,8 Н/м, а при αк = 0,6 gор = 17,3 Н/м.
С перемещением рабочего органа к центру шарнира левой опоры С, т.е. с увеличением коэффициента αцм, нормированный вес рабочего органа возрастает. При αк = 0,6, αцм = 0 и принятых ранее значениях q и gоп/q, gор = 17,3 Н/м, но при αцм = 0,1 gор = 20,7 Н/м, а при αцм = 0,2 gор = 25,9 Н/м.
При совпадении положения центра масс рабочего органа с левым концом несущей рамы (αцм = 0) и при среднем значении веса 1 м несущей рамы q = 9 Н/м построены графики зависимости нормированного веса рабочего органа gор при изменении коэффициента консоли αк в пределах от 0 до 1 и трех значениях отношения нормированного веса опоры к весу 1 м несущей рамы gоп/q: 0,05; 0,1; 0,15 (рис.3, кривые 1-3).
Из графиков на рис.3, видно, что нормированный вес рабочего органа gор с увеличением безразмерного коэффициента αк резко снижается. Так при αк = 0,2, gоп/q = 0,05 и принятых ранее значениях q и αцм gор = 33,8 Н/м, но при αк = 0,6 gор = 17,3 Н/м. Кроме того, увеличение значения отношения gоп/q приводит к увеличению нормированного веса рабочего органа. При αк = 0,6, gоп/q = 0,05 и принятых значениях q и αцм gор = 17,3 Н/м, но при gоп/q = 0,1 gор = 18 Н/м, а при gоп/q = 0,15 gор = 18,8 Н/м.
На основании анализа кривых на рис.2 и 3 установлено, что величину нормированного веса рабочего органа gор следует выбирать в зависимости от отношения длины консоли к длине рабочего участка несущей рамы αк. При αк → 0 длина консолей уменьшается, при этом нормированный вес рабочего органа увеличивается и соответственно увеличивается общий вес устройства. При αк → 1 длина консолей увеличивается, при этом нормированный вес рабочего органа уменьшается, однако общий вес устройства увеличивается из-за увеличения длины консолей. Вследствие этого оптимальные значения коэффициента консоли следует определять, исходя из условия обеспечения минимального значения общего веса устройства.
Выражение для определения общего веса шагающего пробоотборника имеет вид:
где Gшп – общий вес шагающего пробоотборника, Н; Gр = qL – вес несущей рамы, Н.
После приведения равенства (4) к нормированным величинам (делением на l) с учетом формулы (3) и принятых ранее обозначений выражение для определения общего нормированного веса шагающего устройства принимает вид:
где gшп=Gшп/l – общий нормированный вес шагающего устройства, Н/м.
С учетом принятых ранее значений q = 9 Н/м, gоп/q = 0,05 при αцм = 0-0,2 и q = 9 Н/м, αцм = 0 при gоп/q = 0,05-0,15 построены графики изменения общего нормированного веса шагающего пробоотборника gшп в зависимости от коэффициента консоли αк (рис.2 и 3, кривые 4-6). Полученные кривые носят нелинейный (параболический) характер, значения минимумов на которых соответствуют оптимальным значениям коэффициента консоли.
Для вычисления оптимальных значений коэффициента консоли, соответствующих минимальным значениям общего нормированного веса шагающего устройства, необходимо первую производную от общего нормированного веса шагающего пробоотборника (5) по безразмерному коэффициенту консоли приравнять к нулю:
В результате дифференцирования оптимальное значение коэффициента консоли определяется по формуле:
Выбор оптимального значения коэффициента консоли зависит от конструктивной компоновки устройства и геометрических параметров модуля доставки шагающего пробоотборника до поверхности озера Восток [26]. При изменении положения центра масс рабочего органа xцм (см. рис.1), т.е. перемещении рабочего органа от конца несущей рамы к центру шарнира левой опоры С (αцм → 1), значение коэффициента консоли αк увеличивается, что приводит к увеличению нормированного веса рабочего органа gор и общего нормированного веса шагающего пробоотборника gшп (см. рис.2). При αцм = 0 и принятых значениях q = 9 Н/м и gоп/q = 0,05 αк = 0,52, gор = 18,4 Н/м, gшп = 37,8 Н/м, но при αцм = 0,1 αк = 0,67, gор = 19,3 Н/м, gшп = 41,2 Н/м, а при αцм = 0,2 αк = 0,81, gор = 20 Н/м, gшп = 44,5 Н/м. Коэффициент консоли, а вместе с ним нормированный вес рабочего органа и общий нормированный вес устройства увеличиваются за счет увеличения отношения gоп/q (рис.3). При gоп/q = 0,05 и принятых значениях q = 9 Н/м и αцм = 0 αк = 0,52, gор = 18,4 Н/м, gшп = 37,8 Н/м, но при gоп/q = 0,1 αк = 0,55, gор = 18,9 Н/м, gшп = 39,5 Н/м, а при gоп/q = 0,15 αк = 0,57, gор = 19,3 Н/м, gшп = 41,2 Н/м.
В процессе отбора проб донных отложений нормированный вес рабочего органа gор и общий нормированный вес шагающего пробоотборника gшп увеличиваются за счет присоединенной массы взятых проб. Вследствие этого при одном и том же ранее выбранном оптимальном значении коэффициента консоли αк происходит увеличение коэффициента положения рабочего органа αцм (рис.2 и 3). Следовательно, при заданной длине консоли lк уменьшается расстояние xцм, необходимое для создания увеличившимся нормированным весом рабочего органа gор опрокидывающего момента относительно центра С (см. рис.1). Например, до отбора проб донных отложений (см. рис.2) при αк = 0,52, gор = 18,4 Н/м, gшп = 37,8 Н/м, αцм = 0, xцм = lк, но с учетом взятых проб при αк = 0,52, gор = 22,8 Н/м, gшп = 42,1 Н/м, αцм = 0,1, xцм = 0,81lк или gор = 29,8 Н/м, gшп = 49,2 Н/м, αцм = 0,2, xцм = 0,62lк.
Уравнения угла поворота несущей рамы шагающего устройства в вертикальной плоскости
На реализацию стабильного процесса шагания помимо перечисленных ранее параметров существенное влияние оказывает угол поворота несущей рамы шагающего пробоотборника относительно опоры в вертикальной плоскости. Угол поворота несущей рамы в вертикальной плоскости при шагании устройства ограничивается условием свободного переноса поднятой опоры над неровностями донной поверхности и условием несоприкосновения рабочего органа или несущей рамы с грунтом в момент, когда рабочий орган находится на конце консоли (см. рис.1). При несоблюдении хотя бы одного из этих условий следует изменить траекторию движения устройства для обеспечения дальнейшего процесса шагания.
Для реализации первого условия необходимо, чтобы между башмаками опор и гребнями неровностей дна оставался достаточный зазор. Поэтому высота подъема опоры hп включает в себя максимальную высоту неровностей дна, протяженность которых в направлении перемещения опоры меньше длины (шага) самого перемещения, и минимальный зазор между башмаками опоры и гребнем неровности при поднятой опоре. По высоте hп определяется угол поворота несущей рамы в вертикальной плоскости при шагании (см. рис.1):
Условие несоприкосновения рабочего органа и несущей рамы с грунтом выполняется, если наибольшее опускание консоли ограничивается расстоянием по вертикали h'p от донной поверхности до опускаемой части несущей рамы при шагании. В этом случае допустимый угол поворота несущей рамы в вертикальной плоскости при шагании равен
Отметим, что расстояние h'p включает в себя максимальную высоту неровностей, протяженность которых вдоль несущей рамы не превышает длины консоли (башмаки опоры упираются в ровную донную поверхность), и минимально допустимый зазор между рабочим органом или
несущей рамой и гребнем неровности.
Для обеспечения процесса шагания устройства требуется единовременное выполнение условий (7) и (8). В выражениях (7) и (8) исходными параметрами следует считать характеристику рельефа донной поверхности и длину рабочего участка несущей рамы, являющиеся основными расчетными параметрами.
Таким образом, предварительное определение диапазона значений угла поворота несущей рамы в вертикальной плоскости позволит не только эффективно управлять процессом шагания, но и корректно спроектировать узел сопряжения опоры с несущей рамой для обеспечения ее поворота относительно опоры на требуемый угол.
Зависимость безразмерного коэффициента подъема от безразмерного коэффициента зазора
Ввиду ограниченности габаритных размеров шагающего пробоотборника необходимо найти оптимальные соотношения между расстоянием по вертикали от донной поверхности до несущей рамы в исходном (горизонтальном) положении несущей рамы h''p, высотой подъема опоры hп и расстоянием по вертикали от донной поверхности до опускаемой части несущей рамы при шагании h'p (см. рис.1):
После преобразования соотношений (9) имеем окончательное выражение в безразмерном виде для определения высоты подъема опоры при шагании:
где βп=hп/h''p – безразмерный коэффициент подъема; βp=h'p/h''p – безразмерный коэффициент зазора.
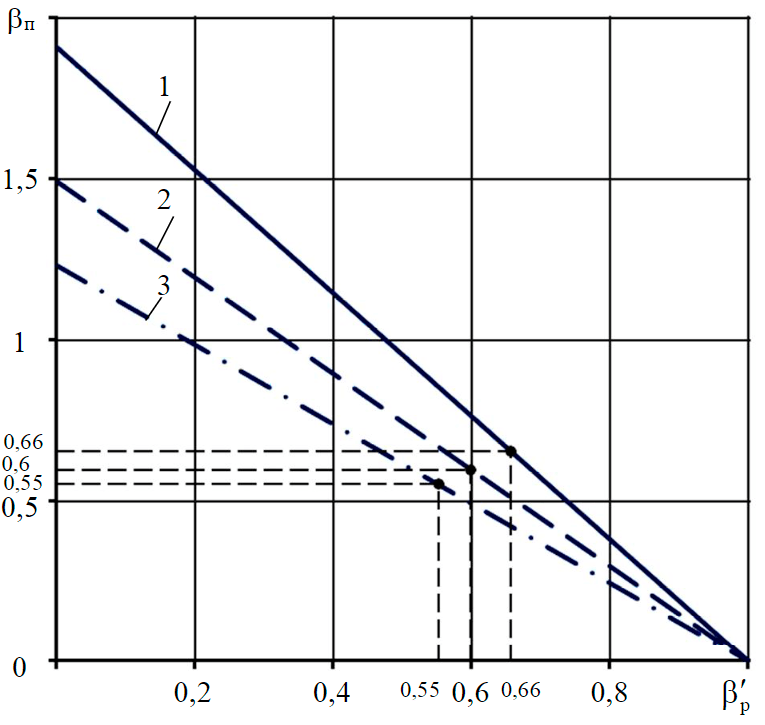
Рис.4. Графики зависимости безразмерного коэффициента подъема βп от безразмерного коэффициента зазора βрʹ при gоп/q = 0,05 и αк = 0,52 (1); 0,67 (2); 0,81 (3)
Под безразмерным коэффициентом подъема подразумевается отношение высоты подъема опоры при шагании к расстоянию по вертикали от донной поверхности до несущей рамы. Под безразмерным коэффициентом зазора подразумевается отношение расстояния по вертикали от донной поверхности до опускаемой части несущей рамы при шагании к расстоянию по вертикали от донной поверхности до несущей рамы.
Согласно выражению (10) графики изменения коэффициента подъема βп при изменении коэффициента зазора β'p в пределах от 0 до 1 и при трех вычисленных ранее оптимальных значениях коэффициента консоли αк, равных 0,52; 0,67 и 0,81, представлены на рис.4.
Анализ графиков на рис.4 показывает, что при β'p=1(h'p=h''p) когда несущая рама находится в исходном (горизонтальном) положении и опирается на обе опоры, βп = 0 (hп = 0) (см. рис.1). С уменьшением коэффициента β'p=(h'p→0) значение коэффициента βп увеличивается (hп > 0), т.е. начинается поворот (подъем) несущей рамы относительно левой опоры в вертикальной плоскости. В случае β'p=0 (h'p=0) левая консоль несущей рамы упирается в грунт, а значение коэффициента подъема βп является максимальным для данного типоразмера шагающего устройства. В этом случае процесс шагания невозможен, так как не выполняется условие несоприкосновения рабочего органа и несущей рамы с грунтом.
Представленные на рис.4 кривые носят линейный характер и позволяют определять высоту подъема опоры в зависимости от расстояния по вертикали между донной поверхностью и опускающейся консолью. С увеличением коэффициента консоли αk при одних и тех же расстояниях по вертикали от донной поверхности до несущей рамы h''p и опускаемой части несущей рамы h'p высота подъема опоры при шагании hп уменьшается. При равных h''p и hп с увеличением коэффициента консоли αк расстояние по вертикали от донной поверхности до опускаемой части несущей рамы h'p уменьшается. При постоянных h'p и hп расстояние по вертикали от донной поверхности до несущей рамы h''p с увеличением коэффициента консоли αк увеличивается.
Графики на рис.4 имеют характерные точки совпадения значений безразмерных коэффициентов подъема и зазора в зависимости от коэффициента консоли: при αк = 0,52 β'p=βп=0,66; при αк = 0,67 β'p=βп=0,6 и при αк = 0,81 β'p=βп=0,55, что соответствует равенству h'p = hп.
Таким образом, кривые на рис.4 позволяют определить для заданных значений коэффициента консоли αк оптимальные соотношения между расстояниями по вертикали от донной поверхности до несущей рамы h''p и опускаемой части несущей рамы h'p, а также высотой подъема опоры hп, необходимые для выбора рациональных параметров шагающего устройства, имеющего ограничения, как по длине, так и по высоте.
Цифровая модель шагающего пробоотборника
На основании построенной математической модели шагающего пробоотборника, описываемой зависимостями (3), (6)-(8), (10), проведено твердотельное моделирование шагающего устройства в системе автоматизированного проектирования Autodesk Inventor. В процессе создания 3D модели шагающего устройства учитывались размеры доставочного модуля (внутренний диаметр 220 мм и длина 1 м) с учетом его размещения в ограниченном пространстве скважины.
Учитывая рассчитанные на основании математической модели средние значения безразмерного коэффициента консоли αк = 0,67 и угла поворота несущей рамы при подъеме опоры в процессе шагания φ = 10°, данную задачу удалось решить за счет контекстного создания 3D моделей элементов шагающего пробоотборника в режиме сборки. Ключевыми инструментами стали функция копирования объектов (рис.5) и проецирование геометрии в режиме создание эскизов (рис.6).
Работа по созданию 3D модели осуществлялась с применением функции параметрического моделирования. Например, для определения расположения ног опор менялись такие параметры, как «длина ног» и «угол ног», что позволило, комбинируя эти параметры, выбрать оптимальную для заданных условий конструкцию (рис.7).
В дальнейшем такой подход позволит менять геометрические параметры всех элементов шагающего пробоотборника, изменяя исходные данные.
Результаты исследований
В ходе проведенных исследований, целью которых являлся научно обоснованный выбор геометрических и силовых параметров устройства для отбора проб донных отложений подледникового озера Восток, получены следующие результаты:
- на основе анализа существующих способов и устройств для взятия проб донных отложений принята в качестве базового варианта модель двухопорного шагающего пробоотборника;
- составлена расчетная схема силового нагружения шагающего устройства;
- для обоснованной расчетной схемы шагающего пробоотборника, с учетом разрабатываемой технологии бурения скважины доступа к озеру Восток, его вскрытия, а также геоморфологических характеристик самого озера разработана математическая модель шагающего устройства;
- анализ полученных математических формул, в частности для нормированного веса рабочего органа и общего нормированного веса шагающего пробоотборника, указывает на необходимость выбора рациональных геометрических и силовых параметров устройства в зависимости от его конструктивной компоновки и геометрических параметров доставочного модуля, ограничивающих габаритные размеры шагающего устройства;
- в соответствии с результатами математического моделирования начата разработка полного цифрового прототипа шагающего пробоотборника, являющегося виртуальным опытным образцом готового устройства и служащего для его оптимизации и проверки;
- в результате 3Dмоделирования шагающего пробоотборника в системе автоматического проектирования Autodesk Inventor получена параметрическая цифровая модель шагающего устройства. Подобраны геометрические параметры устройства, оптимальные для заданных условий эксплуатации.
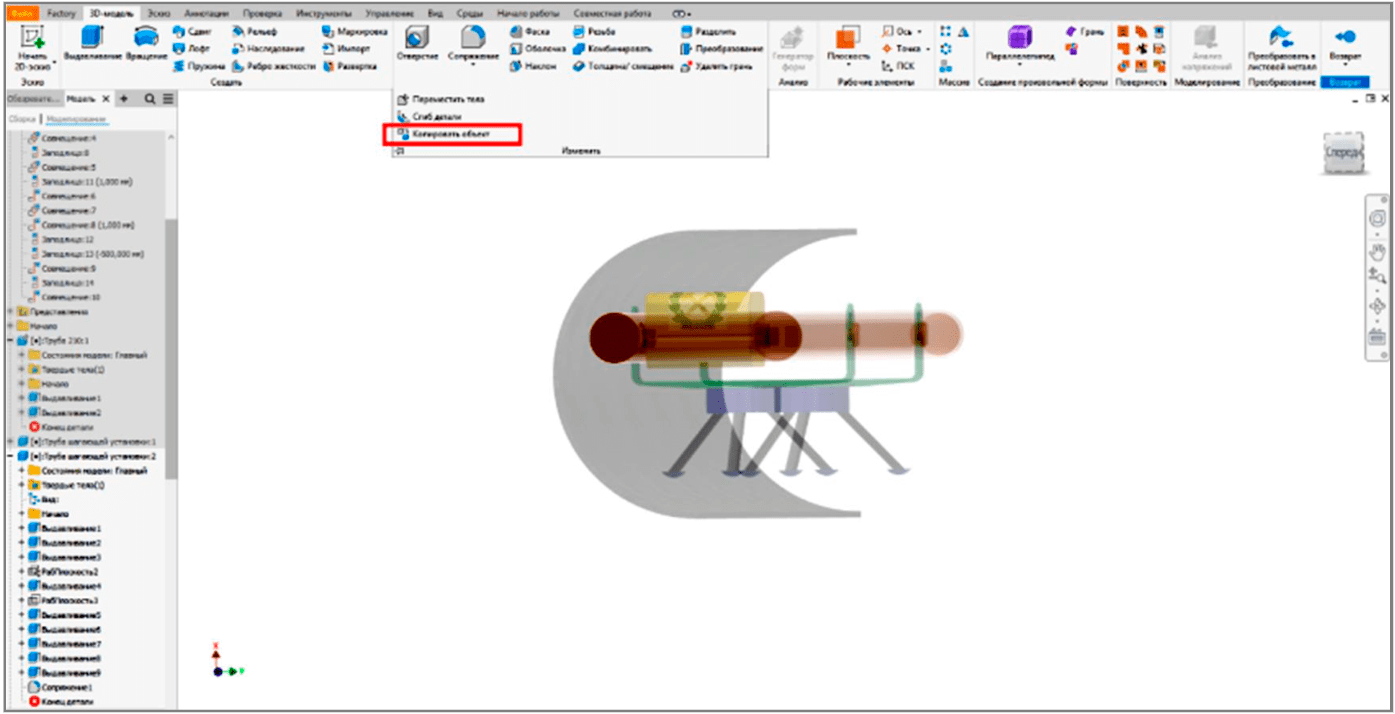
Рис.5. Операция «Копировать объект»

Рис.6. Проецирование геометрии
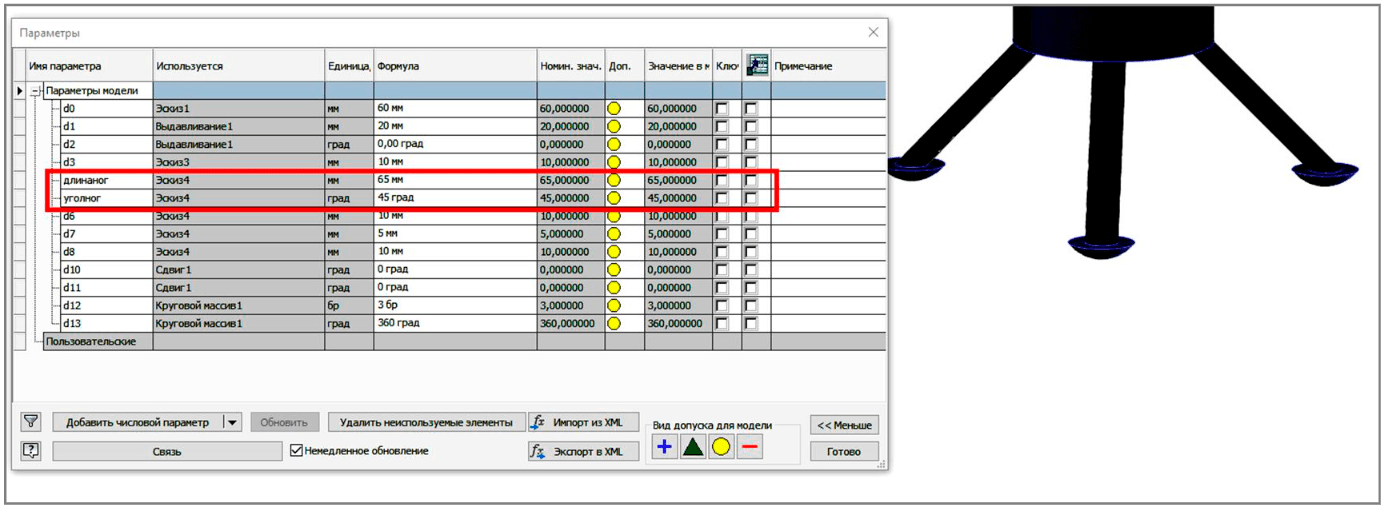
Рис.7. Параметрическое моделирование опоры
Выводы
Необходимость проведения комплексных исследований подледникового озера
Восток и палеоклимата Земли в районе российской антарктической станции «Восток» отмечена в Стратегии развития деятельности Российской Федерации в Антарктике до 2030 г., утвержденной распоряжением Правительства РФ от 30 июня 2021 г. № 1767-р.
Полученные пробы донных отложений послужат уникальным первичным материалом для проведения фундаментальных исследований в геологии, биологии, палеоклиматологии и т.д., позволяющим укрепить первенство российской науки в исследовании Антарктиды.
При разработке технических средств для проведения исследований необходим критический подход к использованию существующего опыта создания механических и других типов устройств для взятия проб со дна морей и океанов.
Подледниковое озеро Восток является уникальной природной системой, проведение исследований которой требует обеспечения экологической безопасности проводимых работ, а также надежной и безотказной работы технических средств. Одной из главных проблем является создание придонного устройства, обеспечивающего наряду с эффективной работой по взятию проб экологическую безопасность и безаварийное перемещение при наличии возможных (неопознанных) препятствий на дне в зоне сбора, при этом габаритные размеры устройства строго ограничены диаметром скважины (от 129 до 250 мм).
Разработанная математическая модель шагающего пробоотборника позволяет оптимизировать его конструкцию, приняв за критерий оптимизации минимальный вес устройства с учетом вписывания конструкции в заданные габариты, ограниченные размерами доставочного модуля, и обеспечения процесса шагания по донной поверхности. Дальнейшее математическое моделирование шагающего пробоотборника связано с анализом его динамики и выполнением расчетов на прочность его основных элементов с учетом присоединенной массы отобранных проб донных отложений.
Использование технологии цифровых прототипов при создании 3D модели шагающего устройства позволит провести большую часть испытаний и тестов шагающего пробоотборника в виртуальном режиме, прежде чем он станет реальным объектом. Возможность выявления ошибок на ранних стадиях проектирования позволит сэкономить значительное количество времени и средств при создании физических опытных образцов устройства.
Одними из ближайших этапов работы над твердотельной цифровой моделью шагающего пробоотборника станут динамическое моделирование, параметрический расчет напряженно-деформированного состояния, визуализация, автоматическое получение и обновление конструкторской документации.
Литература
- Litvinenko V. Foreword: Sixty-year Russian history of Antarctic sub-glacial lake exploration and Arctic natural resource development // Chemie der Erde. 2020. Vol. 80. Iss. 3. № 125652. DOI: 10.1016/j.chemer.2020.125652
- Kapitsa A.P., Ridley J.K., de Q.Robin G. Large deep freshwater lake beneath the ice of central East Antarctica // Nature. 1996. Vol. 381. № 6584. Р. 684-686. DOI: 10.1038/381684a0
- Попов С.В., Шереметьев А.Н., Масолов В.Н., Лукин В.В. Береговая черта подледникового озера Восток и прилегающие водоемы: интерпретация данных радиолокационного профилирования // Материалы гляциологических исследований. 2005. Вып. 98. С. 73-80.
- Попов С.В., Лунев П.И. Орография коренного рельефа района подледникового озера Восток (Восточная Антарктида) // Геоморфология. 2012. № 1. С. 81-91. DOI: 10.15356/0435-4281-2012-1-81-91
- Масолов В.Н., Попов С.В., Лукин В.В., Попков А.М. Рельеф дна и водное тело подледникового озера Восток, Восточная Антарктида // Доклады Академии наук. 2010. Т. 433. № 5. С. 693-698.
- Лейченков Г.Л., Беляцкий Б.В., Попков А.М., Попов С.В. Геологическая природа подледникового озера Восток в Восточной Антарктиде // Материалы гляциологических исследований. 2005. № 98. С. 81-91.
- Попов С.В., Масолов В.Н., Лукин В.В., Попков А.М. Отечественные сейсмические, радиолокационные и сейсмологические исследования подледникового озера Восток, Восточная Антарктида // Лед и снег. 2012. Т. 52. № 4. С. 31-38. DOI: 10.15356/2076-6734-2012-4-31-38
- Leitchenkov G.L., Antonov A.V., Luneov P.I., Lipenkov V.Y. Geology and environments of subglacial Lake Vostok // Philosophical Transactions of The Royal Society. A Mathematical Physical and Engineering Sciences. 2016. Vol. 374. Iss. 2059. № 0302. DOI: 10.1098/rsta.2014.0302
- Казко Г.В., Саватюгин Л.М., Сократова И.Н. Моделирование циркуляции воды в антарктическом подледниковом озере Восток // Лед и снег. 2012. Т. 52. № 4. С 86-91. DOI: 10.15356/2076-6734-2012-4-86-91
- Липенков В.Я., Екайкин А.А., Алехина И.А. и др. Эволюция климата, оледенения и подледниковой среды Антарктиды по данным исследований ледяных кернов и проб воды озера Восток (Основные итоги работ по проекту РНФ, 2014-2016 гг.) // Лед и снег. 2017. Т. 57. № 1. С. 133-141. DOI: 10.15356/2076-6734-2017-l-133-141
- Лейченков Г.Л., Попков А.М. Прогнозный осадочный разрез подледникового озера Восток // Лед и снег. 2012. Т. 52. № 4. С. 21-30. DOI: 10.15356/2076-6734-2012-4-21-30
- Попов С.В., Масолов В.Н., Лукин В.В. Озеро Восток, Восточная Антарктида: мощность ледника, глубина озера, подледный и коренной рельеф // Лед и снег. 2011. № 1 (113). С. 25-35.
- Васильев Н.И., Липенков В.Я., Дмитриев А.Н. и др. Результаты и особенности бурения скважины 5Г и первого вскрытия озера Восток // Лед и cнег. 2012. Т. 52. № 4. С. 12-20. DOI: 10.15356/2076-6734-2012-4-12-20
- Васильев Н.И., Лейченков Г.Л., Загривный Э.А. Перспективы получения образцов донных отложений подледникового озера Восток // Записки Горного института. 2017. Т. 224. С. 199-208. DOI: 10.18454/PMI.2017.2.199
- Васильев Н.И., Дмитриев А.Н., Липенков В.Я. Результаты бурения скважины 5Г на российской станции «Восток» и исследования кернов льда // Записки Горного института. 2016. Т. 218. С. 161-171.
- Лукин В.В. Путь к изучению вод озера Восток // Проблемы Арктики и Антарктики. 2012. № 1 (91). С. 5-19.
- Булат С.А., MarieD., PetitJ. Перспективы поиска жизни в подледниковом озере Восток // Лед и снег. 2012. Т.52. №4. С. 92-96. DOI: 10.15356/2076-6734-2012-4-92-96
- Siegert M. Proposed Exploration of Subglacial Lake Ellsworth. Antarctica Final Comprehensive Environmental Evaluation. British Antarctic Survey. Technical report. Lake Ellsworth Antarctica, 2012. 87 p.
- Fricker H., Powell R., Priscu J. et al. Siple Coast Subglacial Aquatic Environments: The Whillans Ice Stream Subglacial Access Research Drilling Project // Antarctic Subglacial Aquatic Environments (Geophysical Monograph Series). 2011. Vol. 192. P. 199-219. DOI: 10.1002/9781118670354.ch12
- Priscu J., Kalin J., Winans J. et al. Scientific access into Mercer Subglacial Lake: Scientific objectives, drilling operations and initial observations // Annals of Glaciology. 2021. Vol. 62. Iss. 85-86. Р. 340-352. DOI: 10.1017/aog.2021.10
- Siegert M., Clarke R., Mowlem M. Clean access, measurement, and sampling of Ellsworth Subglacial Lake: A method for exploring deep Antarctic subglacial lake environments // Reviews of Geophysics. 2012. Vol. 50. Iss. 1. RG000361. DOI: 10.1029/2011RG000361
- Tulaczyk S., Mikucki J., Siegfried M. et al. WISSARD at Subglacial Lake Whillans, West Antarctica: Scientific operations and initial observations // Annals of Glaciology. 2014. Vol. 55. Iss. 65. P. 51-58. DOI: 10.3189/2014AoG65A009
- Васильев Н.И., Дмитриев А.Н., Блинов П.А. Бурение глубокой скважины на российской антарктической станции «Восток» // Вестник ОНЗ РАН. 2012. Т. 4. № NZ2001. DOI: 10.2205/2012NZ000111
- Литвиненко В.С. Уникальная техника и технологии бурения скважин во льдах Антарктиды // Записки Горного института. 2014. Т. 210. С. 5-10.
- Litvinenko V.S., Vasiliev N.I., Lipenkov V.Ya. et al. Special aspects of ice drilling and results of 5G hole drilling at Vostok station, Antarctica // Annals of Glaciology. 2014. Vol. 55. Iss. 68. P. 173-178. DOI: 10.3189/2014AoG68A040
- БольшуновА.В., ВасильевН.И., ТимофеевИ.П. идр. Перспективное технологическое решение по отбору проб донных отложений подледникового озера Восток: актуальность и постановка задач исследований // Записки Горного института. 2021. Т. 252. С. 779-787. DOI: 10.31897/PMI.2021.6.1
- Litvinenko V.S., Leitchenkov G.L., Vasiliev N.I. Anticipated sub-bottom geology of Lake Vostok and technological approaches considered for sampling // Geochemistry. 2020. Vol. 80. Iss. 3. № 125556. DOI: 10.1016/j.chemer.2019.125556
- Масолов В.Н., Лукин В.В., Шереметьев А.Н., Попов С.В. Геофизические исследования подледникового озера Восток в Восточной Антарктиде // Доклады Академии наук. 2001. Т. 379. № 5. C. 680-685.
- Ласточкин А.Н., Попов С.В., Попков А.М. Рельеф подледниковой котловины оз. Восток (Восточная Антарктида) // Вестник Санкт-Петербургского университета. 2003. № 3. С. 38-50.
- Попов С.В., Черноглазов У.Б. Подледниковое озеро Восток, Восточная Антарктида: береговая линия и окружающие водоемы // Лед и снег. 2011. № 1. С. 13-24.
- Калинин И.С., Бутов И.И., Журавлев А.С., Буянов М.И. Обоснование выбора подводного колонкового пробоотборника для опробования морских россыпей // Горный информационно-аналитический бюллетень. 2015. № 11. С. 250-256.
- Смолов Ю.С. Техника для отбора проб донных осадков. Опыт работ и перспективы // Геология и полезные ископаемые Мирового океана. 2015. № 1 (39). С. 80-90.
- Da Gong, Xiaopeng Fan, Yazhou Li et al. Coring of Antarctic Subglacial Sediments // Journal of Marine Science and Engineering. 2019. Vol. 7. Iss. 6. № 194. DOI: 10.3390/jmse7060194
- Тимофеев И.П. Шагающие машины для освоения ресурсов морского дна. Л.: Изд-во Ленинградского университета, 1987. 176 с.
- Патент № 2601880 РФ. Шагающее устройство для подводной добычи полезных ископаемых / И.П.Тимофеев, Г.В.Соколова, И.А.Королев и др. Опубл. 10.11.2016. Бюл. № 31.
- Патент № 166446 РФ. Шагающая буровая установка / И.П.Тимофеев, Г.В.Соколова, Г.А.Колтон и др. Опубл. 27.11.2016. Бюл. № 33.
