Прогнозирование динамического пластового давления методами искусственного интеллекта
- 1 — инженер Филиал ООО «ЛУКОЙЛ-Инжиниринг» «ПермНИПИнефть» в г. Перми ▪ Orcid ▪ Elibrary ▪ Scopus
- 2 — канд. техн. наук доцент Пермский национальный исследовательский политехнический университет ▪ Orcid
- 3 — д-р техн. наук профессор Пермский национальный исследовательский политехнический университет ▪ Orcid ▪ Elibrary ▪ Scopus ▪ ResearcherID
Аннотация
Определение пластового давления в зонах отбора скважин является ключевой задачей мониторинга разработки месторождений углеводородов. Непосредственные измерения пластового давления требуют продолжительной остановки скважин, что приводит к недобору в добыче сырья и вероятности возникновения технических проблем с последующим запуском скважин. Невозможность одномоментной остановки всех скважин фонда затрудняет оценку реального энергетического состояния залежи. В статье приводятся исследования, направленные на разработку косвенной методики определения пластового давления без остановки скважин на исследование, позволяющей определять его величину в любой момент времени. В качестве математической основы используются два метода искусственного интеллекта – многомерный регрессионный анализ и нейронная сеть. Методика, основанная на построении уравнений множественной регрессии, демонстрирует достаточную работоспособность, но высокую чувствительность к исходным данным. Данная методика позволяет также исследовать процесс формирования пластового давления в различные периоды разработки залежей. Ее применение целесообразно при регулярных фактических определениях значений показателей, используемых в качестве исходных данных. Методика, основанная на искусственной нейронной сети, позволяет достоверно определять пластовое давление даже при минимальном наборе исходных данных и реализована в виде специально разработанного программного продукта. Актуальной задачей продолжения исследований является оценка перспективных прогностических особенностей методов искусственного интеллекта для оценки энергетического состояния залежей в зонах отбора углеводородов.
Введение
Контроль за пластовым давлением в зонах дренирования скважин является приоритетной задачей мониторинга разработки месторождений углеводородов. По данным источников [1-3] актуальная и достоверная информация о значениях пластового давления необходима на всех этапах разработки месторождения. Пластовое давление является важнейшим входным параметром, используемым при планировании и проектировании эксплуатации скважин. С точки зрения строительства скважины данные по пластовому давлению используются для определения размеров буровой установки, глубины обсадной колонны для проектирования цементирования, расчета бурового раствора и жидкости для заканчивания, выбора устьевого и глубиннонасосного оборудования. Данные о значениях пластового давления используются для прогноза добычи и анализа производительности скважин, моделирования разработки и геомеханического анализа [4-6].
На практике данная задача решается, в основном, посредством проведения гидродинамических исследований (ГДИ) при неустановившихся режимах. За величину пластового принимается давление, установившееся на забое скважины после ее длительной остановки. Процесс восстановления давления продолжается от нескольких часов до нескольких недель и в любом случае приводит к потерям в добыче углеводородов, что является основным фактором, ограничивающим повсеместное и регулярное проведение исследований [7]. Кроме того, часто возникает техническая проблема запуска скважин после их продолжительной остановки по причине образовавшихся в стволе скважины отложений асфальтенов, смол и парафинов.
Необходимость регулярного контроля за энергетическим состоянием залежи в комплексе с невозможностью массового проведения гидродинамических исследований обуславливают целесообразность разработки косвенных методов определения пластового давления, исключающих технологический этап продолжительной остановки скважин. Разработке косвенных методов определения динамического пластового давления посвящен ряд научных работ.
Например, в работе [8] предложен способ оценки пластового давления при разведочном бурении, позволяющий выявить зоны аномально высокого пластового давления при наличии сейсмических данных о глубинах залегания ловушек. Указанный способ оценки базируется на методиках с использованием d- и σ-экспонент, учитывающих механическую скорость бурения, скорость вращения ротора, нагрузку на долото и его диаметр, литологическую константу и степень уплотнения пород, плотность бурового раствора и горных пород. Очевидно, основным недостатком способа является возможность его практического применения только на этапе строительства скважины. Также на этапе строительства скважины пластовое давление определяют в рамках опробования коллектора [9].
В статье [10] авторы предлагают прогнозировать поровое давление пласта с применением модифицированной модели Аташбари по данным каротажа на кабеле. Этот метод основан на использовании зависимости пористости и сжимаемости горных пород от пластового давления. Метод апробирован на газонасыщенном карбонатном коллекторе формации Аполлония среднего эоцена бассейна Абу Эль-Гарадиг, Египет.
Способ определения пластового давления при ремонте скважин предложен в работе [11]. При расчете предлагается использовать точку начала притока жидкости из пласта к скважине по заранее известной, однородной по плотности, жидкости глушения при выводе скважины на режим после глушения по математической формуле.
Метод определения пластового давления по данным вывода скважин на режим после ремонта предложен в статье [12]. Сущность метода заключается в использовании карт вывода скважин на режим. Метод применим только для скважин, которые были подвержены глушению при текущем или капитальном ремонте, и только для скважин, оборудованных установками электроцентробежных насосов.
Новый метод расчета давления в любой точке одного источника и одного стока с использованием устьевого давления, апробированный и активно применяющийся на нефтяных месторождениях Китая, описан в источнике [13].
Алгоритм косвенного определения пластового давления в условиях трехфазного притока воды, нефти и выделившегося растворенного газа с использованием методов Data Mining, системного и статистического дескриптивного анализа предложен в статье [14].
Метод определения пластового давления, основанный на сочетании обобщенной формулировки материального баланса и теории псевдостационарного состояния, предложен в работе [15]. Возможности метода продемонстрированы авторами на примере пяти вертикальных и горизонтальных скважин, во всех случаях получена удовлетворительная сходимость расчетных и фактических значений пластового давления. Однако недостатком метода следует считать его применимость только в условиях стационарных дебитов или забойных давлений. Схожий метод, основанный на материальном балансе, предлагается в работе [16]. Недостатком метода является возможность его применения для скважин с радиальным режимом течения.
Способ определения пластового давления в глубинно-насосных нефтяных скважинах без их остановки представлен в источнике [17]. Суть метода сводится к тому, что в затрубное пространство подливается или закачивается агрегатом жидкость, и ее уровень поднимается выше статического положения, по данным падения уровня строится соответствующая кривая и характеристика насоса. Далее проводится касательная к характеристике насоса. Точка касания является глубиной статического уровня, который впоследствии пересчитывается в пластовое давление. Данный метод усовершенствован в работе [18], его особенностью является сокращение продолжительности исследований.
В работе [19] предлагается определять пластовое давление по данным измерений в скважине, остановленной для проведения капитального ремонта, например с целью реализации гидравлического разрыва пласта. По сути данный метод (АСА) является аналогом гидродинамических исследований, поскольку предусматривает необходимость остановки скважины, как следствие характеризуется всеми его недостатками.
Метод, который можно использовать для определения среднего пластового давления как функции времени истощения, предложен в статье [7]. Данный метод основан на совместном использовании уравнения псевдостационарного состояния с его интегральной функцией. В результате возможно построение графика, при обработке которого определяется разница между средним пластовым давлением и забойным давлением. В свою очередь, при известном значении забойного давления определение пластового не сопровождается затруднениями.
Новый метод, который позволяет определять текущее пластовое давление в зоне работы скважины, предложен в работе [20]. Метод сводится к построению графика, который представляет собой прямую линию, отсекающую на оси ординат значение давления, соответствующее величине пластового. Авторы указывают, что метод разработан для горизонтальных скважин, но может быть адаптирован для вертикальных скважин без особых затруднений. Используемая в методе математическая процедура основана на выборе соответствующего источника и функций Грина для горизонтальной скважины во время неограниченно действующего потока и при условии, что скважина является чисто линейным источником.
Новый математический метод определения продуктивности и пластового давления, основанный на теории баланса энергии жидкости в псевдостационарном состоянии, предлагается в статье [21]. Метод сводится к нелинейному регрессионному анализу, выполняемому с использованием компьютерного языка VB. Схожие методы, основанные на теории материального баланса, представлены также в работе [22].
Работа [23] посвящена проблеме оценки пластового давления в залежи, представленной несколькими продуктивными пластами. Для расчета среднего давления в отдельных пластах авторы предлагают использовать метод избирательного притока (SIP) для оптимального распределения добычи и мониторинга эффектов истощения энергетики пласта с течением времени. Метод избирательного притока реализован на некоторых добывающих скважинах на севере Пакистана. Данный метод следует рассматривать как некоторый аналог известного метода определения гидродинамических характеристик пластов, основанного на анализе кривой добычи (по Фетковичу и др.). Аналогичный метод, основанный на анализе динамики производительности скважин, представлен в работе [24].
Все описанные методы условно можно разделить на три группы. К первой группе относятся методы определения пластового давления, основанные на использовании данных бурения или ремонта скважин, что ограничивает их применимость [25]. Вторая группа включает методы той или иной модификации метода материального баланса. Соответственно, все недостатки и ограничения данного метода, разработанного для подсчета запасов, следует отнести и к разработанным на его основе косвенным методикам определения пластового давления. Третья группа объединяет методы математической обработки исторических данных эксплуатации скважин [26, 27]. Корректность определения пластового давления этими методами напрямую зависит от достоверности использования математического аппарата для описания процессов фильтрации в тех или иных индивидуальных геолого-физических условиях [28, 29].
Новым направлением при оценке энергетического состояния залежей углеводородов следует считать применение методов искусственного интеллекта [30-32]. Данные методы в настоящее время находят все большее применение для решения самых различных задач [33-35]. Так, в статье [36] авторы предлагают использовать нечеткую самоорганизующуюся нейронную сеть, которая может автоматически выполнять неконтролируемую кластеризацию и классификацию сейсмических атрибутов. Далее параметры пласта оцениваются с помощью другой нейронной сети. На основе синтетической модели, построенной на реальных данных, рассчитывается изменение порового (пластового) давления в газовом пласте [37, 38].
Множественный регрессионный анализ, по сути являющийся одним из методов искусственного интеллекта, предложено использовать авторами источников [39, 40] для оценки пластового давления в любой период эксплуатации скважин без их остановки на исследование. Преимуществами метода являются использование в качестве исходных данных только тех параметров, которые определяются в практике геолого-промыслового сопровождения разработки нефтяных месторождений, простота вычислений и высокие статистические оценки достоверности моделей при определении пластового давления. Множественная регрессия – известный и широко распространенный, но не единственный метод искусственного интеллекта [41-43]. Поэтому в данной статье приводятся результаты исследований, направленных на разработку косвенной методики определения пластового давления, основанной на применении нейросетей (другого распространенного метода искусственного интеллекта), а также ее сопоставления с методикой, основанной на применении множественной регрессии и фактическими измерениями искомого параметра.
Методология
Исследования выполнены для одного из нефтяных месторождений Пермского края, в пределах которого выделены три объекта разработки. Два объекта приурочены к карбонатным турнейско-фаменским и башкирским отложениям, а также к визейским терригенным коллекторам. Для продуктивных отложений характерна различающаяся газонасыщенность пластовой нефти (68,1, 21,3 и 66,5 м3/т соответственно) и, как следствие, отличающиеся условия и закономерности процессов выработки запасов.
При построении моделей прогноза пластового давления с применением множественной регрессии и нейросети использован один и тот же промысловый материал – результаты 200 исследований 25 добывающих скважин за период их эксплуатации.
При построении уравнений множественной регрессии в качестве исходных данных использованы следующие параметры: фактическое текущее пластовое давление, определенное при проведении ГДИ Pтпл МПа; начальное пластовое давление, определяемое по первому ГДИ скважины Pнпл МПа; продолжительность эксплуатации скважины после ввода из бурения Т, сут; текущие дебиты жидкости Qж м3/сут и нефти Qн т/сут; текущее забойное давление Pзаб МПа; коэффициент проницаемости начальный, определяемый по первому ГДИ скважины kнузп мД; коэффициент проницаемости текущий kтузп мД; скин-фактор S; накопленная добыча нефти Qнн т; накопленная добыча жидкости Qнж м3; накопленная добыча воды Qнв т; газовый фактор Гф м3/сут. Значения всех параметров характеризуют работу скважины в период, соответствующий фактическому измерению пластового давления (ГДИ).
При построении уравнений множественной регрессии использован многоуровневый подход. На первом уровне построены модели с использованием всей выборки (для всех пластов). На втором уровне модели построены дифференцированно для каждого продуктивного объекта, на третьем – для характерных интервалов пластового давления, выделение которых обосновано и подтверждено применением дискриминантного анализа. К практическому применению предложена модель, комплексирующая результаты моделирования на всех трех уровнях. Для каждой модели рассчитаны и приведены ее статистические оценки: коэффициент множественной корреляции R, уровень значимости р, стандартная ошибка S0.
В качестве примера представлены модели, разработанные для турнейско-фаменского пласта.
Первый уровень моделирования:
при R = 0,892, р < 0,0000, S0 = 1,38 МПа.
Второй уровень моделирования:
при R =0,919, р <0,0000, S0 = 1,47 МПа.
Третий уровень моделирования, первый диапазон пластового давления:
при R = 0,958, р < 0,0000, S0 = 0,55 МПа.
Третий уровень моделирования, второй диапазон пластового давления:
при R = 0,924, р < 0,0000, S0 = 0,95 МПа.
Результирующая модель имеет следующий вид:
при R = 0,979, р < 0,0000, S0 = 0,74 МПа.
Диапазоны применимости всех моделей соответствуют исходной выборке и приведены в статье [39].
Большой набор исходных данных, используемых при построении уравнений множественной регрессии, с одной стороны, обеспечивает максимально возможную точность прогнозных оценок пластового давления, но, с другой стороны, получаемые уравнения являются громоздкими и чувствительными к качеству исходных данных. Поэтому при разработке моделей определения пластового давления с использованием нейросети стоит задача минимизации количества исходных данных при сохранении высокой точности прогнозных оценок искомого параметра.
При разработке методики определения пластового давления подобраны оптимальные значения гиперпараметров методом поиска по сетке [44, 45]. Решение данной задачи с помощью модели искусственной нейронной сети заключается в подборе ее оптимальной архитектуры и определении функцией активации ее весов. В рамках воспроизведения и прогноза параметра пластового давления выбрана архитектура полносвязанной нейронной сети, которая наилучшим образом выделяет и использует взаимовлияние факторов, рассматривая всевозможные связи между признаками. При определении весов нейронной сети использовался метод градиентной оптимизации ADAM. Построенная модель состоит из трех слоев, где первый слой содержит 64 нейрона, второй – 32 и третий – 16. В качестве функции активации на каждом слое выбран гиперболический тангенс, который увеличивает чувствительность модели к изменениям значений. Слой, отображающий величину пластового давления имеет линейную функцию активации для связи с предыдущим слоем. В процессе обучения нейронной сети в качестве функции потерь использовалась метрика абсолютного отклонения.
Сравнительная оценка достоверности прогнозирования пластового давления с использованием множественной регрессии и искусственной нейросети выполнена посредством сопоставления рассчитанных значений с данными фактических измерений при использовании соответствующих статистических критериев (коэффициента и графика корреляции, уровня значимости и др.).
Результаты
Методика определения пластового давления, основанная на применении искусственной нейросети, реализована в виде программного продукта. В качестве исходных данных использованы такие параметры как дебиты жидкости, а также коэффициенты эксплуатации каждой скважины.
Результаты вычислений для удобства восприятия визуализированы в виде таблиц, а также графика (рис.1), отражающего динамику пластового давления в процессе эксплуатации скважины, на который также нанесены данные фактических измерений (красные точки). Сравнение рассчитанных и фактически измеренных пластовых давлений для скважин всех объектов разработки приведено на рис.2.
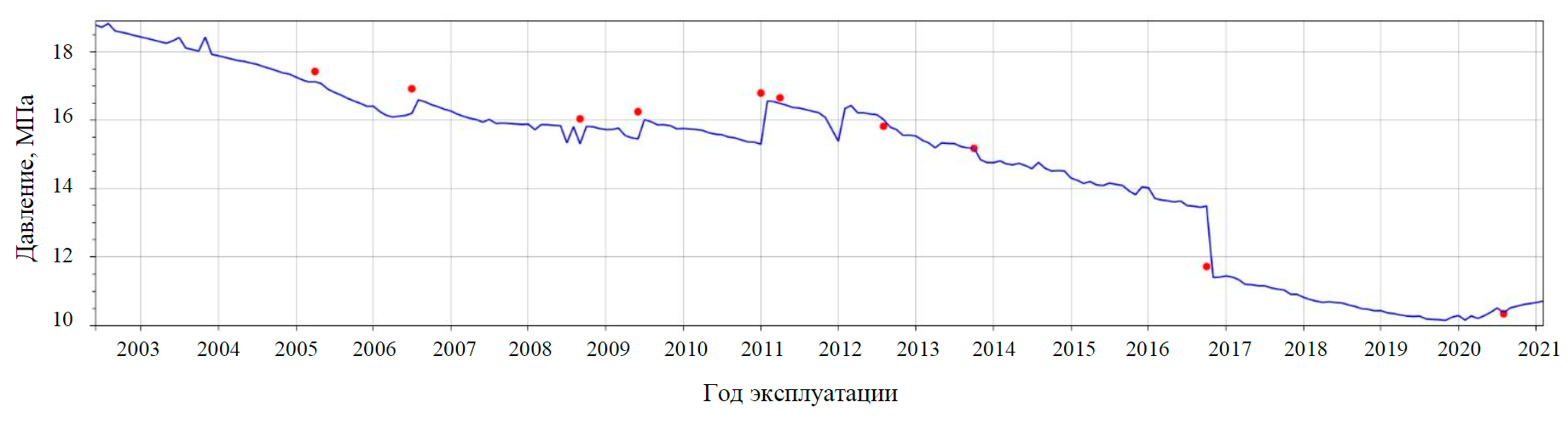
Рис.1. Сопоставление динамики фактического и модельного пластовых давлений за всю историю эксплуатации скважины
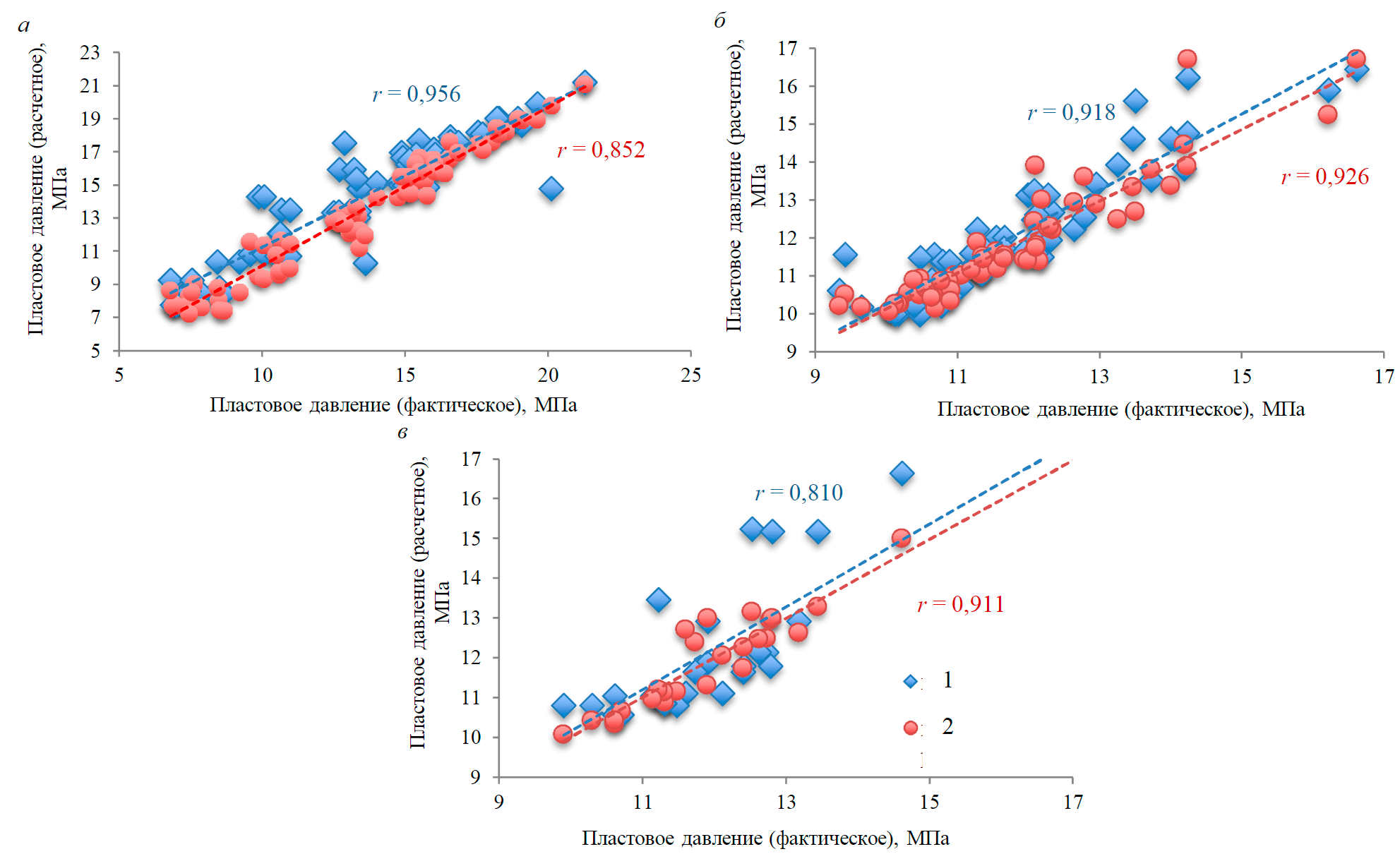
Рис.2. Сопоставление расчетных и фактических пластовых давлений для скважин турнейско-фаменского (а), бобриковского (б) и башкирского (в) объектов разработки
1 – нейросеть; 2 – множественная регрессия
Как следует из анализа представленных на рис.2 данных, во всех случаях оба метода демонстрируют высокую достоверность определения пластового давления для скважин, эксплуатирующих как терригенные, так и карбонатные отложения рассматриваемого месторождения. Меньшая работоспособность модели, основанная на применении искусственной нейросети, для определения пластового давления в зонах отбора скважин башкирских отложений, может быть объяснена незначительным объемом используемой выборки и невысокой степенью обученности сети. Абсолютные средние отклонения от фактического измерения для турнейско-фаменского, бобриковского и башкирского объектов разработки, полученные в результате применения методов нейронной сети, составили 0,72; 0,86; 0,83 МПа, при применении метода множественной регрессии 0,75; 0,87; 0,81 МПа.
Методы нейронной сети и множественной регрессии имеют равное минимальное отклонение прогнозируемых значений пластового давления от фактических, что указывает на эффективность и перспективность использования данных методов.
Обсуждение
В ходе выполненного аналитического обзора отечественных и зарубежных исследований, направленных на определение пластового давления косвенными методами (без остановки скважин на гидродинамические иссле-дования), установлено, что выбранное направление по-прежнему является актуальным. Разработанные в настоящее время методики оценки показателей энергетического состояния характеризуются рядом недостатков.
В данной работе в качестве математического инструмента выбраны методы искусственного интеллекта – множественная регрессия и нейросеть. Для решения поставленной задачи оба метода апробированы применительно к одному из нефтяных месторождений Пермского края, продуктивные объекты которого представлены терригенными и карбонатными коллекторами с различающейся газонасыщенностью пластовой нефти.
При реализации выбранных методов разработаны методики определения пластового давления без остановки скважин на исследования. Методики основаны на математической обработке накопленного опыта фактических определений пластового давления и других промысловых характеристик. Обе методики продемонстрировали высокую достоверность определения пластового давления для всех трех рассматриваемых продуктивных отложений.
Методика, основанная на построении многомерных статистических моделей – уравнений множественной регрессии – демонстрирует несколько более высокую работоспособность по сравнению с нейросетью. Вероятной причиной этого является использование оригинального многоуровневого подхода к построению статистических моделей. При этом особенностью построенных статистических моделей является использование довольно большого количества исходных данных и, как следствие, зависимость от точности их определения. Например, уравнение (4) включает величину газового фактора. При оценке чувствительности модели к его величине получен график, представленный на рис.3.
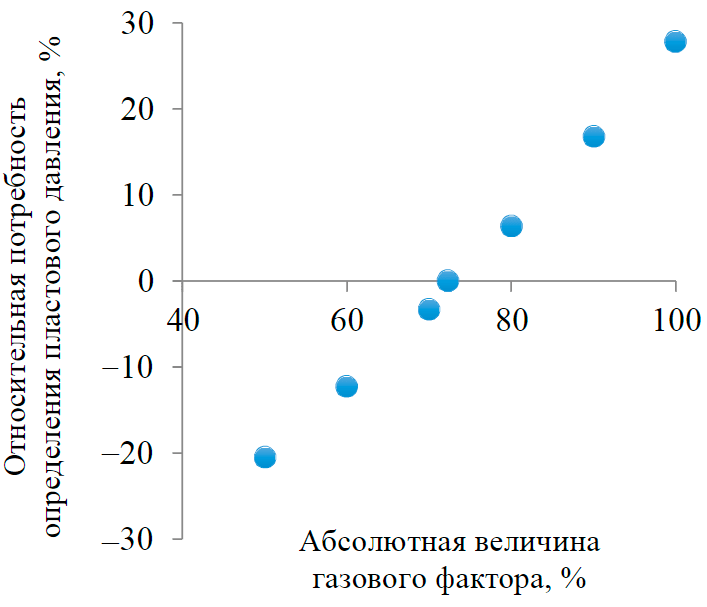
Рис.3. Чувствительность многомерной статистической модели к величине газового фактора
Как следует из представленной на рис.3 диаграммы, использование недостоверных значений газового фактора приводит к значительной погрешности в определении пластового давления при использовании методики, основанной на применении многомерных статистических моделей. В условиях резкой динамики газового фактора, характерной для рассматриваемого месторождения, данная проблема может ограничивать применение многомерных статистических моделей в условиях отсутствия фактических замеров количества добываемого газа. Аналогичная высокая чувствительность установлена применительно и к другим параметрам, используемым в качестве исходных данных в многомерных статистических моделях.
Данный недостаток отсутствует в методике, основанной на применении искусственной нейросети. В качестве исходных данных в этом случае используются только дебиты и коэффициенты эксплуатации, регистрация которых осуществляется с достаточной точностью и регулярностью.
В то же время, методика, основанная на применении искусственной нейросети, лишена возможности исследования и анализа процесса формирования пластового давления при разработке месторождения. Данная задача успешно решается при построении многомерных статистических моделей. В частности, применительно к рассматриваемому объекту установлено, что основными параметрами, управляющими величиной текущего пластового давления, являются его начальное значение и продолжительность периода эксплуатации скважины. Также при статистическом моделировании обоснованы два характерных периода поведения пластового давления. В начальный период за формирование пластового давления отвечают, в основном, геологические факторы (начальное пластовое давление, время эксплуатации скважины и накопленная добыча воды), что следует из анализа уравнения (3). Второй диапазон поведения пластового давления описывается уравнением (4), которое включает в себя ряд технологических параметров (забойное давление, начальное пластовое давление, скин-фактор и газовый фактор, коэффициент проницаемости начальный, определяемый по первому ГДИ скважины) [39].
Заключение
Статья посвящена разработке и сравнительному анализу методик определения динамического пластового давления без остановки скважин на исследование с применением методов искусственного интеллекта – множественной регрессии и нейросети. Обе методики основаны на анализе накопленного опыта проведенных ранее исследований, они позволяют с высокой степенью достоверности определять пластовое давление по комплексу промысловых данных.
Методика, основанная на применении множественной регрессии, позволяет также исследовать процесс формирования пластового давления в различные периоды разработки залежей. Ее применение целесообразно при регулярных фактических определениях значений показателей, используемых в качестве исходных данных. Представленную методику не следует рассматривать в качестве альтернативы ГДИ. Ее использование и применение целесообразно для экспресс-оценки пластового давления либо в условиях невозможности остановки скважины на исследование по технологическим причинам.
Методика, использующая методы машинного обучения, основана на непараметрической многомерной модели, связывающей показатели эксплуатации скважины во времени. Предлагаемый метод учитывает динамику показателей, характеризующих эксплуатацию скважин, а прогнозируемое пластовое давление хорошо коррелируется с измеренными посредством ГДИ значениями. Кроме того, предлагаемый метод позволяет избежать утомительной процедуры калибровки коэффициентов по сравнению с методами, основанными на параметрических преобразованиях.
На основе рассчитанного значения пластового давления с помощью машинного обучения можно определить режим разработки залежи в данный момент, заблаговременно спроектировать систему поддержания пластового давления или оценить ее эффективность, а также обоснованно принимать дальнейшие рациональные решения по разработке нефтяных месторождений.
Литература
- Escobar F.H., Hernandez Y.A., Hernandez C.M. Pressure transient analysis for long homogeneous reservoirs using TDS technique // Journal of Petroleum Science and Engineering. 2007. Vol. 8(1-2). P.68-82. DOI: 10.1016/j.petrol.2006.11.010
- Hazim Al-Attar. A Simple Method For Estimating Average Reservoir Pressure and Well Flow Efficiency in Volumetric Oil Reservoirs // Conference: Second ADRAC, February 2014, Abu Dhabi, United Arab Emirates.
- Oloruntobi O., Butt S. Energy-based formation pressure prediction // Journal of Petroleum Science and Engineering. 2019. Vol. 173. P. 955-964. DOI: 10.1016/j.petrol.2018.10.060
- Guoyi Yu, Feng Xu, Yingzhi Cui et al. A new method of predicting the saturation pressure of oil reservoir and its application // International Journal of Hydrogen Energy. 2020. Vol. 45. Iss. 55. P. 30244-30253. DOI: 10.1016/j.ijhydene.2020.08.042
- Lichun Kuang, He Liu, Yili Ren et al. Application and development trend of artificial intelligence in petroleum exploration and development // Petroleum Exploration and Development. 2021. Vol. 48. Iss. 1. P. 1-14. DOI: 10.1016/S1876-3804(21)60001-0
- Clement Afagwu, Isah Abubakar, Shams Kalam et al. Pressure-transient analysis in shale gas reservoirs: A review // Journal of Natural Gas Science and Engineering. 2020. Vol. 78. № 103319. DOI: 10.1016/j.jngse.2020.103319
- Mohammed S., Enty G.S., Amarfio E.M. Determination of Average Reservoir Pressure from Constant-Rate Drawdown Tests // SPE Nigeria Annual International Conference and Exhibition, August 2014, Lagos, Nigeria. SPE-172424-MS. DOI: 10.2118/172424-MS
- Шакиров А.А. Определение пластового давления аппаратурой АГИП-К по технологии многоциклового зондирования // Каротажник. 2017. № 3 (273). С. 62-66.
- Грищенко М.Н., Харисов Р.Ф. Якупов и др. Анализ результатов косвенного определения пластового давления по изменению режимов работы скважин с использованием генетического алгоритма // Геология, геофизика и разработка нефтяных и газовых месторождений. 2021. № 8 (356). С. 36-41.
- Weiqiang Li, Longxin Mu, Lun Zhao et al. Pore-throat structure characteristics and its impact on the porosity and permeability relationship of Carboniferous carbonate reservoirs in eastern edge of Pre-Caspian Basin // Petroleum Exploration and Development. 2020. Vol. 47. Iss. 5. P. 1027-1041. DOI: 10.1016/S1876-3804(20)60114-8
- Патент № 2539445 РФ. Способ определения пластового давления в нефтяной скважине, оборудованной погружным электронасосом / Л.Н.Баландин, О.А.Грибенников. Опубл. 20.01.2015. Бюл. № 2.
- Фатихов С.З., Федоров В.Н. Анализ методов определения пластового давления в низкопроницаемых коллекторах // Нефтяное хозяйство. 2018. № 4. С. 62-65. DOI: 10.24887/0028-2448-2018-4-62-65
- Xiaoyong Wen, Jing Yang, Shaoyang Geng, Ke Li. Study on new method for evaluating reservoir formation pressure by wellhead pressure // IOP Conference Series: Earth and Environmental Science. 2019. Vol. 384. № 012037. DOI: 10.1088/1755-1315/384/1/012037
- Харисов М.Н., Юнусова Э.А., Майский Р.А. Алгоритм косвенного определения пластового давления с использованием методов DATAMINING // Проблемы сбора, подготовки и транспорта нефти и нефтепродуктов. 2018. № 3 (113). С. 40-48. DOI: 10.17122/ntj-oil-2018-3-40-48
- Ziyuan Cong, Yuwei Li, Yishan Pan et al. Study on CO2 Foam Fracturing Model and Fracture Propagation Simulation // Energy. 2022. Vol. 238. № 121778. DOI: 10.1016/j.energy.2021.121778
- Zhiliang Hea Jianfang Sunb Panhong Guo. Construction of carbonate reservoir knowledge base and its application in fracture-cavity reservoir geological modeling // Petroleum Exploration and Development. 2021. Vol. 48. Iss. 4. P. 824-834. DOI: 10.1016/S1876-3804(21)60069-1
- Elmahdy M., Farag A.E., Tarabees E., Bakr A. Pore Pressure Prediction in Unconventional Carbonate Reservoir // Paper presented at the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, April 2018, Dammam, Saudi Arabia. SPE-194224-MS. DOI: 10.2118/194224-MS
- Царенко А.В., Гиранов Р.Г. Численное моделирование для определения пластового давления на Пильтунском участке Пильтун-Астохского месторождения // Газовая промышленность. 2018. № 12 (778). С. 32-36.
- Bobreneva Yu. O., Davletbaev A.Y., Makhota N.A., Kamalova Z.K. Estimation of Reservoir Pressure from the Sensor Data Before and After Injection Tests in Low-Permeability Formations // Paper presented at the SPE Russian Petroleum Technology Conference, October 2017, Moscow, Russia. SPE-187763-MS. DOI: 10.2118/187763-MS
- Idudje H., Adewole S. A Method of Estimating Reservoir Pressure using Drawdown Test Data // SPE Nigeria Annual International Conference and Exhibition, Virtual, August 2020. SPE-203700-MS. DOI: 10.2118/203700-MS
- Adel M. Salem. Determination of Average Reservoir Pressure using Pressure buildup Test: Analytical and Simulation Approach for Egyptian Oil Fields // Journal of Petroleum and Mining Engineering. 2019. Vol. 21. Iss. 1. P. 9-16. DOI: 10.21608/JPME.2020.73176
- Zhang A., Fan Z., Song H., Zhang H. Reservoir pressure prediction of gas condensate reservoir with oil rim // Journal of China University of Petroleum (Edition of Natural Science). 2014. Vol. 38(5). P.124-129. DOI: 10.3969/j.issn.1673-5005.2014.05.017
- Аsad Ilyas, Safwan Arshad, Jawad Ahmed et al. Determining Average Reservoir Pressures in Multilayered Completed Wells Using Selective Inflow Performance (SIP) Technique // SPE/PAPG Annual Technical Conference, December 2012, Islamabad, Pakistan. SPE-163131-MS. DOI: 10.2118/163131-MS
- Bobby Poe, Gottumukkala Varma. Novel methodology to estimate reservoir pressure and productivity index in unconventional and conventional reservoirs using production data // Offshore Technology Conference Asia, March 2016, Kuala Lumpur, Malaysia. № OTC-26429-MS. DOI: 10.4043/26429-MS
- Ахметова А.А., Пименов Е.Д., Горин А.Н. идр. Оценка применимости данных мини-ГРП для определения пластового давления и гидропроводности // Нефтяное хозяйство. 2018. № 7. С. 90-94. DOI: 10.24887/0028-2448-2018-7-90-94
- Ладейщикова Т.С., Волков В.А., Собянин Н.Н., Митрошин А.В. Косвенные способы оценки текущего пластового давления в скважине для использования при построении интегрированных моделей месторождений // Нефтепромысловое дело. 2021. № 7 (631). С. 39-45. DOI: 10.33285/0207-2351-2021-7(631)-39-45
- Кузнецова Е.А., Шилов А.В., Никулин С.Е., Черных И.А. Определение и прогноз пластового давления, продуктивности и фильтрационных параметров пласта без остановок скважин по результатам анализа истории добычи скважин в программном обеспечении KAPPA TOPAZE, оснащенных глубинными манометрами на приеме насоса и телеметрической системой, для месторождений ООО «ЛУКОЙЛ-ПЕРМЬ» // Нефтепромысловое дело. 2019. № 12 (612). С. 82-84. DOI: 10.30713/0207-2351-2019-12(612)-82-84
- Belhouchet H.E., Benzagouta M.S., Dobbi A. et al. A new empirical model for enhancing well log permeability prediction, using nonlinear regression method: Case study from Hassi-Berkine oil field reservoir – Algeria // Journal of King Saud University – Engineering Sciences. 2021. Vol. 33. Iss. 2. P. 136-145. DOI: 10.1016/j.jksues.2020.04.008
- Ahmed ElGibaly, Mohamed Abdalla Osman. Perforation friction modeling in limited entry fracturing using artificial neural network // Egyptian Journal of Petroleum. 2019. Vol. 28. Iss. 3. P. 297-305. DOI: 10.1016/j.ejpe.2019.08.001
- Бобб И.Ф. Международный опыт создания нефтегазовых IT-технологий для моделирования месторождений // Георесурсы. 2018. Т. 20. № 3. С. 193-196. DOI: 10.18599/grs.2018.3.193-196
- Евсюткин И.В. Марков Н.Г. Глубокие искусственные нейронные сети для прогноза значений дебитов добывающих скважин // Известия Томского политехнического университета. Инжиниринг георесурсов. 2020. Т. 331. № 11. С. 88-95. DOI: 10.18799/24131830/2020/11/2888
- RanJia, YikaiLv, GongwenWang etal. A stacking methodology of machine learning for 3D geological modeling with geological-geophysical datasets, Laochang Sn camp, Gejiu (China) // Computers & Geosciences. 2021. Vol. 151. № 104754. DOI: 10.1016/j.cageo.2021.104754
- Герке К.М., Корост Д.В., Карсанина М.В. идр. Изучение и анализ современных подходов к построению цифровых моделей керна и методов моделирования многофазной фильтрации в масштабах порового пространства // Георесурсы. 2021. Т. 23. № 2. С. 197-213. DOI: 10.18599/grs.2021.2.20
- Черников А.Д., Еремин Н.А., Столяров В.Е. и др. Применение методов искусственного интеллекта для выявления и прогнозирования осложнений при строительстве нефтяных и газовых скважин: проблемы и основные направления решения // Георесурсы. 2021. Т. 22. № 3. С. 87-96. DOI: 10.18599/grs.2020.3.87-96
- Попов Н.А., Путилов И.С., Гуляева А.А., Винокуров Е.Е. Применение технологий глубокого обучения для изучения шлифов на примере Усинского месторождения нефти // Известия Томского политехнического университета. Инжиниринг георесурсов. 2020. Т. 331. № 6. С. 100-112. DOI: 10.18799/24131830/2020/6/2681
- ZhuZhenyu, LiuZhipeng, MiFang, SangShuyun. Reservoir pressure prediction using time-lapse seismic multi-attribute analysis // SEG Technical Program Expanded Abstracts. 2013. P. 5036-5040. DOI: 10.1190/segam2013-1436.1
- Anirbid Sircar, Kriti Yadav, Kamakshi Rayavarapu et al. Application of machine learning and artificial intelligence in oil and gas industry // Petroleum Research. 2021. Vol. 6. Iss. 4. P. 379-391. DOI: 10.1016/j.ptlrs.2021.05.009
- Ghareb Hamada, Veronique Joseph. Developed correlations between sound wave velocity and porosity, permeability and mechanical properties of sandstone core samples // Petroleum Research. 2020. Vol. 5. Iss. 4. P. 326-338. DOI: 10.1016/j.ptlrs.2020.07.001
- Галкин В.И., Пономарева И.Н., Мартюшев Д.А. Прогноз пластового давления и исследование его поведения при разработке нефтяных месторождений на основе построения многоуровневых многомерных вероятностно-статистических моделей// Георесурсы. 2021. Т. 23. № 3. С. 73-82. DOI: 10.18599/grs.2021.3.10
- Патент № 2715490 РФ. Способ определения текущего пластового давления в эксплуатирующейся скважине турнейско-фаменской залежи без ее остановки / В.И.Галкин, И.Н.Пономарева, И.А. Черных. Опубл. 28.02.2020. Бюл. № 7.
- Hanqin Shi, Liang Tao. Visual comparison based on linear regression model and linear discriminant analysis // Journal of Visual Communication and Image Representation. 2018. Vol. 57. P. 118-124. DOI: 10.1016/j.jvcir.2018.10.026
- Gomaa Sayed, Emara Ramadan, Mahmoud Omar, El-hoshoudy A.N. New correlations to calculate vertical sweep efficiency in oil reservoirs using nonlinear multiple regression and artificial neural network // Journal of King Saud University – Engineering Sciences. 2021. DOI: 10.1016/j.jksues.2021.07.010
- Mohaghegh Shahab D. Subsurface analytics: Contribution of artificial intelligence and machine learning to reservoir engineering, reservoir modeling, and reservoir management // Petroleum Exploration and Development. 2020. Vol. 47. Iss. 2. P. 225-228. DOI: 10.1016/S1876-3804(20)60041-6
- Daniel Asante Otchere, Tarek Omar Arbi Ganata, Raoof Gholami, Syahrir Ridha. Application of supervised machine learning paradigms in the prediction of petroleum reservoir properties: Comparative analysis of ANN and SVM models // Journal of Petroleum Science and Engineering. 2021. Vol. 200. № 108182. DOI: 10.1016/j.petrol.2020.108182
- Farno E., Coventry K., Slatter P., Eshtiaghi N. Role of regression analysis and variation of rheological data in calculation of pressure drop for sludge pipelines // Water Research. 2018. Vol. 137. P. 1-8. DOI: 10.1016/j.watres.2018.02.059
