Development of a methodology to assess the hydrocyclone process with account of the rheological properties of the mineral slurry
- 1 — Ph.D., Dr.Sci. Professor Saint Petersburg Mining University ▪ Orcid ▪ Elibrary ▪ Scopus
- 2 — Postgraduate Student Saint Petersburg Mining University ▪ Orcid
Abstract
The paper studies the possibility of assessing the separation of mineral raw materials, taking into account the rheology of the mineral slurry. The ores of the Mayskoye deposit were chosen as the object of the study, characterized by a thin impregnation of the valuable component – gold in the host minerals, which determines the use of fine and ultrafine milling. This fact is essential because the presence of a fine grade seriously affects the rheology of the mineral slurry used in subsequent mineral processing stages. This predetermines the necessity to take into account rheological parameters. The research performed provides the development of a methodology for assessing the separation of minerals in the hydrocyclone based on the interpretation of numerical and mathematical modeling data. using the object-oriented programming language Python, a program for calculating empirical coefficients of the rheological equation, theoretically describing the dynamics of internal transformations of the mineral slurry, was developed. Taking into account the process parameters of the laboratory unit with hydrocyclone and ore properties, three concentrations of solids in the mineral slurry were selected, conditionally corresponding to the minimum, average and maximum values. Rheological equations successively composed for three concentrations, i.e., 400, 500, and 700 g/l, made it possible to calculate the critical shear rates corresponding to the maximum dispersion of the mineral slurry in the hydrocyclone flow. Subsequent numerical simulation using Ansys Fluent software, as well as statistical evaluation of the shear rates at different levels of solids content showed that the shear rate profile in the cross-section of the hydrocyclone corresponding to the maximum dispersion of the mineral slurry is obtained at the content of 400 g/l.
Introduction
The availability of easy-to-process ores is decreasing, which makes it necessary to process complex or low-grade ores, as well as, for example, ash and slag waste [16]. This poses new challenges for the mineral processing industry, since these types of raw materials often have to be milled to much finer grades than the conventional ores; or they contain organic carbon, which changes the refractory properties of the ores [4]. The presence of organic carbon significantly affects the rheological properties of the mineral slurry, as well as the content of clay minerals [29]. One of the decarbonization methods, along with flotation, is hydrocyclone classification, which is less expensive and more productive.
When a continuous liquid and a discrete solid media are mixed, a new continuous medium, i.e. a slurry, is formed, which properties differ from the properties of its individual components [17].
The correlation between the shear stress and shear rate is reflected by the flow curve (Fig.1) [10, 15]. Shear stress is the force that causes the fluid layers to move relative to each other. Shear rate is the ratio of incremental displacement of the layers to the time interval. Non-Newtonian slurries are classified into pseudoplastic, plastic (Bingham), dilatant, etc., with most mineral slurries exhibiting pseudoplastic behavior. The bingham plastic fluids are characterized with a certain initial shear stress value (τ0) [23] due to the presence of fine particles interacting with each other. This behavior creates a weak structure that must be destroyed by overcoming the critical shear stress in order to force the particles to move together with the fluid under the action of the viscous forces.
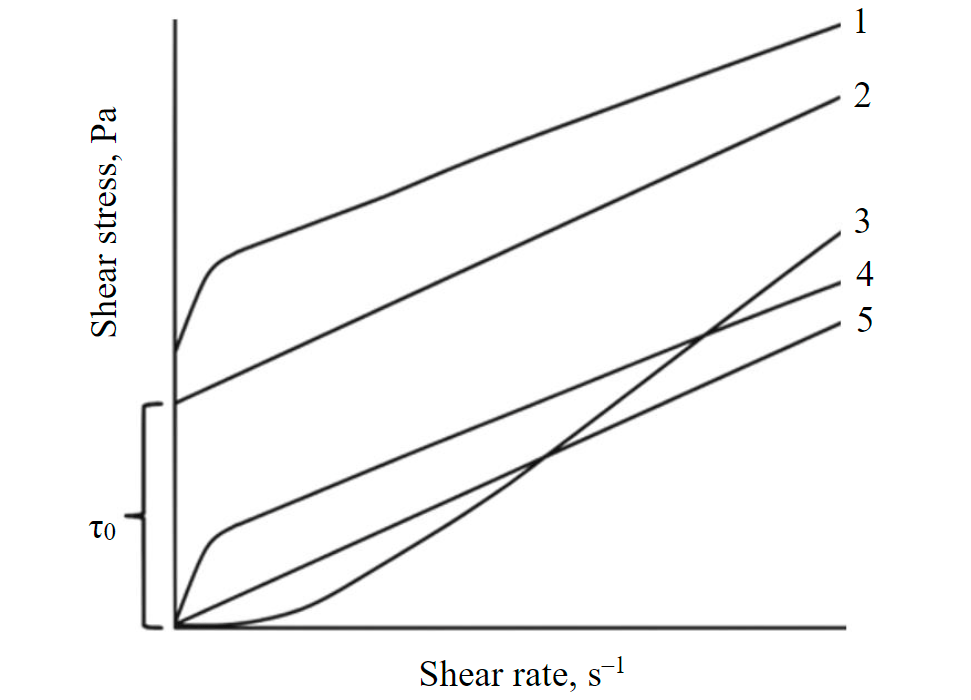
Fig.1. Flow curves for different fluids 1 – pseudoplastic with initial shear stress; 2 – plastic (Bingham); 3 – dilatant; 4 – pseudoplastic; 5 – normal (Newtonian)
A large number of rheological models exist to describe the behavior of such fluids, e.g. the Newtonian, Bingham, Herschel – Bulkley, Sisko, Carreau and other models [13, 21].
The rheological parameters of mineral slurries have a significant impact on the concentration processes, including the milling [31, 34], handling [18] and flotation [22, 30, 33] stages.
The classification processes are no exception, in particular, the classification in hydrocyclones. Many works are dedicated to studying the impact of rheological properties of mineral slurries on the hydrocyclone separation process [8, 21, 27]. The difficulties in understanding the rheology of the slurry inside the hydrocyclone are explained by the complex character of the flows formed, and, therefore, many researchers have been working on this problem for many years [1, 7, 11, 32].
Viscosity of the medium affects formation of the air column along the hydrocyclone axis. The impact of viscosity on the hydrocyclone separation efficiency has been repeatedly confirmed by CFD modeling [20, 26, 28,]. The hydrocyclone performance is quite sensitive to changes in rheological properties of the mineral slurry, i.e. a relatively low viscosity is more preferable for optimum operation.
Gold-bearing ores of the Mayskoye deposit are of the carbonaceous type and belong to a particularly refractory gold-bearing variety. Gold is of primary value [2, 5]. The following sulfide-group minerals prevail: pyrite, arsenopyrite, and stibnite. Quartz, hydromica, feldspar and other minerals make up the most part of the ore (about 90 %) [3, 14]. Gold extracted in processing is mainly associated with sulfides in the form of solid solutions, which requires application of fine and ultrafine milling to unlock the mineral aggregates. Presence of fine grades in the slurry significantly affects the subsequent processing stages.
In this connection, the development of technology to process gold-sulfide carbonaceous ores with account of rheological properties is a major objective, which can be achieved by conducting experimental and theoretical studies using dedicated software.
Evolution of the existing and new technologies to process raw materials is impossible without application of these tools, which explains a wide choice of computational tools, the effectiveness of which is confirmed by a significant number of papers dedicated to numerical and mathematical modeling [6, 9, 33]. Combining these tools within a unified approach makes it possible to develop a methodology to assess the mineral separation process, taking into account the rheological properties of the slurry in order to select the process parameters that contribute to the efficiency of the concentration processes.
Methodology
The impact of the slurry rheology on the hydrocyclone classification process is addressed using an experimental and theoretical approach with application of object-oriented programming and hydrodynamic simulation software.
A unit shown in Fig.2 was used to perform experimental tests on slurry separation.
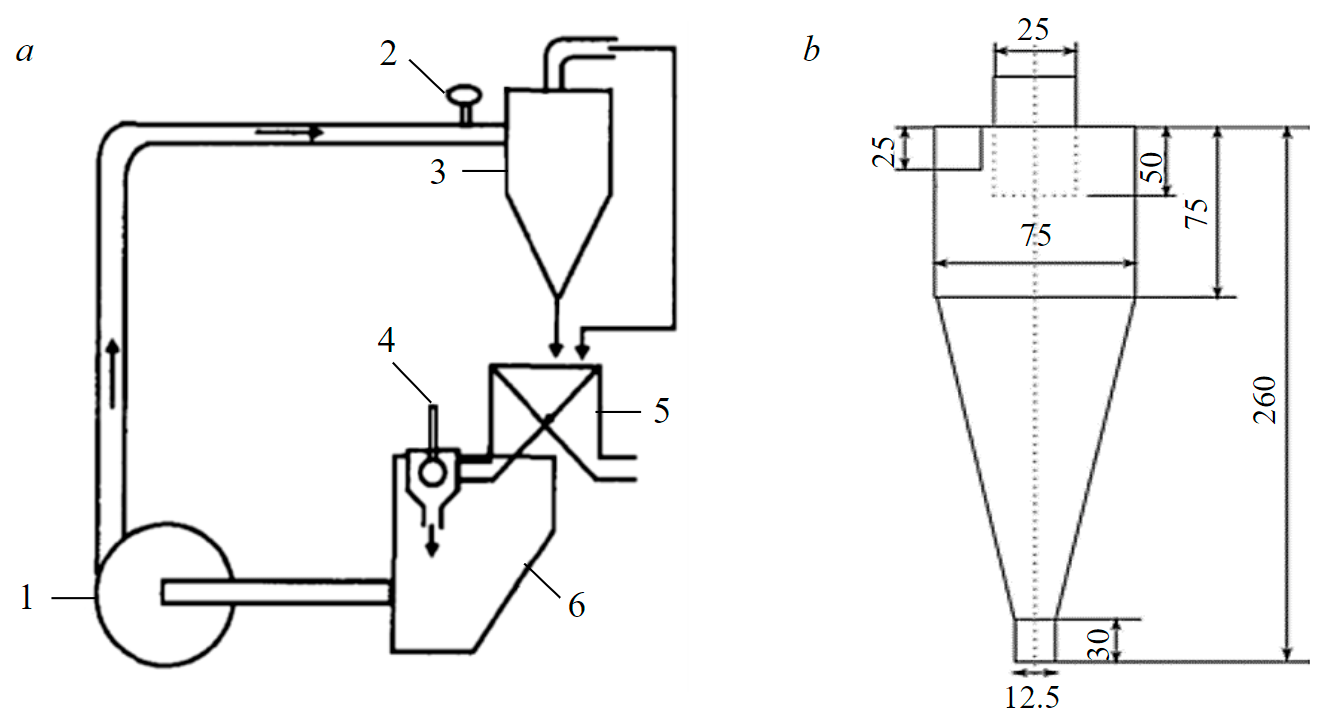
Fig.2. A schematic diagram of the hydrocyclone classification unit (a) and geometrical parameters of the hydrocyclone (b) 1 – pump; 2 – pressure sensor; 3 – hydrocyclone; 4 – rheometer; 5 – sample splitter; 6 – settling sump
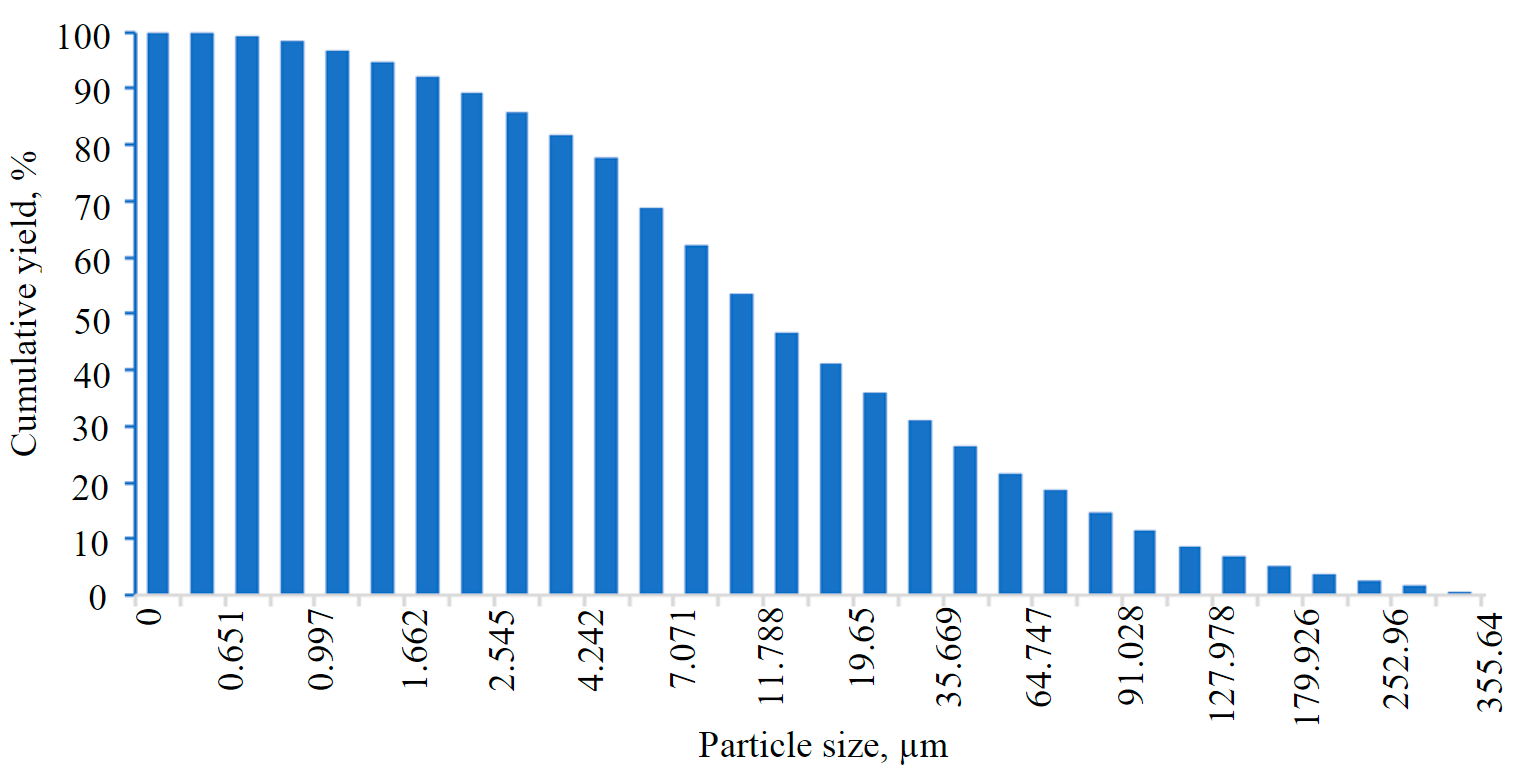
Fig.3. Particle size distribution of initial ore for plus
Testing on the laboratory unit was performed using the gold-sulfide ore (Fig.3) of the Mayskoye deposit, which had been milled for 20 min.
The particle size distribution of the feed and end products was examined using the Malvern Mastersizer 2000 Hydro S laser diffraction particle size analyzer.
Numerical simulation of the hydrocyclone operation was done using the Ansys Fluent software, which is based on the control volume method. The physical aspect of the classification process is complex because many forces act on the particle during its motion. Also the nature of the turbulent flow formed during the unit's operation is of great importance.
The turbulence model was based on the Reynolds stress model (1), in which the transport equation is solved for individual Reynolds stresses [19, 25]. This model is characterized by the fact that, as opposed to the range of conventional k-ε models, it involves solution of six equations for each component of the Reynolds stress tensor rather than two, thus increasing the accuracy of the result. At the same time, in contrast to the LES model, which is considered as the most accurate [28], the RSM model is not as resource-intensive:
where φij is the stress-strain state; Pij are arising stresses; DT,ij is the mass, heat or momentum transfer within the system due to random and chaotic time-dependent motions; εij is energy dissipation.
The gas-liquid phase interaction was described using the Volume of Fluid model, where the interface between the phases is traced by solving the continuity equation for the volume fraction of one (or several) phases [24]. For the q-phase, this equation takes the following form:
where ai is the phase volume fraction; ρi is the phase density; V is the velocity; Sa is the user-defined phase mass index; mpq is the mass transfer from the p-phase to the q-phase; mqp is the mass transfer from the q-phase to the p-phase.
The equation of the mineral slurry motion can be derived from the fluid dynamics equation in stresses:
where ρ is liquid density; v→ is vector of absolute flow velocity; t is time; F→ is vector of mass forces; P is stress tensor in liquid.
The deviator part of the tensor can be represented by a shear stress function, which can be described by a rheological equation, that reflects the dynamics of internal structural transformations in the mineral slurries and makes it possible to determine the shear stresses depending on the velocity gradients. Then the equation can be redefined taking into account the decomposition into parts:
where p is average hydrostatic pressure in the flow; φ is coefficient of the rheological equation; μ is coefficient of dynamic viscosity; γij is shear rate.
Equation (4) is a modified Navier – Stokes equation with member $\sum_{k=1}^{n+1}\phi _ke^{-t_k\gamma_{ij}}$ that takes properties of the mineral slurry into account. This equation can be taken as a vector equation of motion:
where μТ is dynamic viscosity coefficient of the dispersed slurry.
Equation (5) is the defining equation for the shear stress within the slurry as a function of the velocity gradient, which includes the shear stress, the stress characterizing the internal strength of the structure, and the viscosity stress of the dispersed slurry.
The section of the curve between 0 and γcr reflects the anomalous viscosity, which is related to the presence of a structured flow. When the threshold value of the shear rate is exceeded, the slurry follows the laws of motion for a Newtonian fluid. This modification of the Navier – Stokes equation was applied in the Ansys Fluent software to the hydrocyclone classification task.
The coefficients of the rheological equation were calculated using the software developed in Python 3.8 [12] (Fig.4).
The data obtained with a rheometer, i.e. the shear rate and the shear stress, were used as the input for the calculations. A RHEOTEST RN 4.1 rotational rheometer, designed to determine the dynamic viscosity of Newtonian and non-Newtonian liquids was used for this purpose.
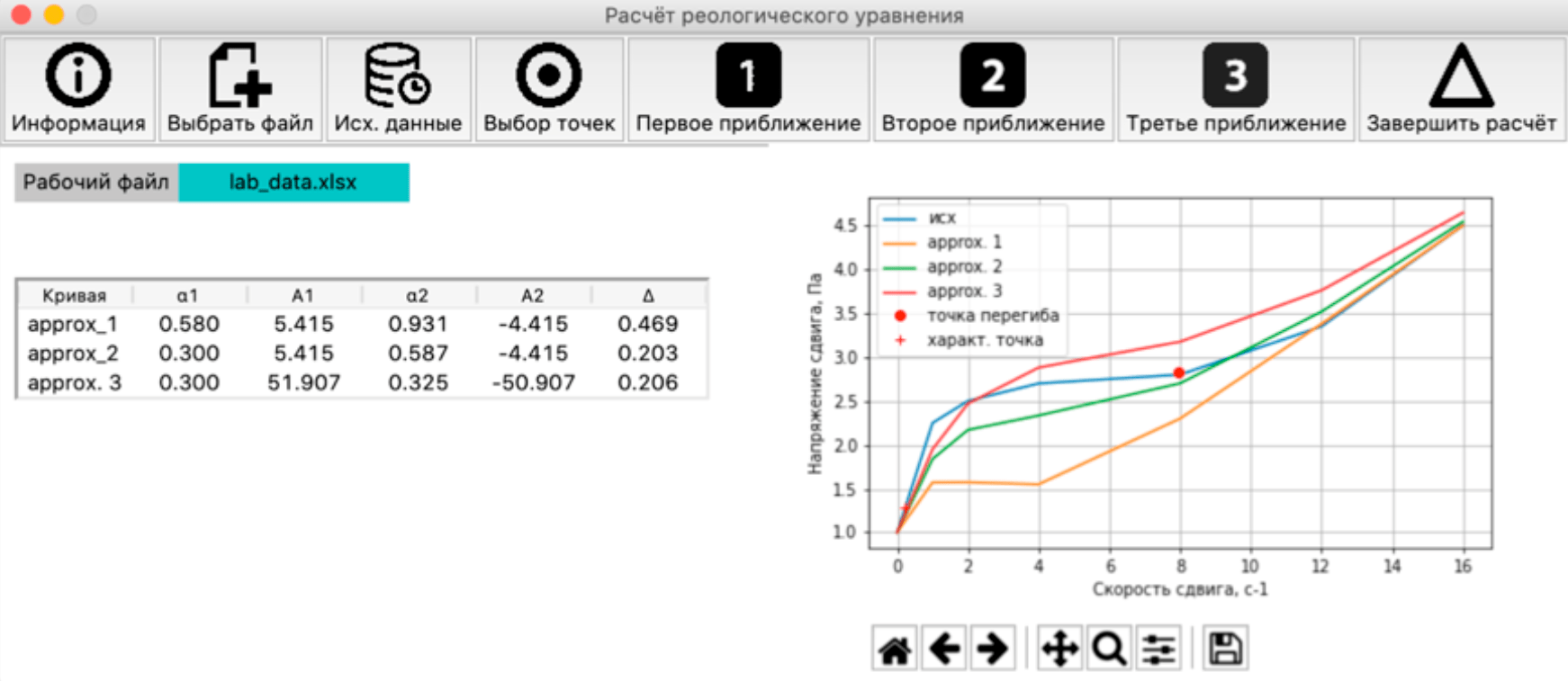
Fig.4. GUI of the developed software
The software (Fig.5) operating principle is to successively approximate the theoretical curve to the experimental data. As the result, a set of curves is obtained, out of which the curve that best describes initial data is selected based on statistical conclusions.
Discussion
Three concentrations of solids in the slurry were selected taking into account properties of the investigated ore type and process parameters of the laboratory equipment in order to assess the influence of the slurry rheology on the classification process. Since the aim of the research is to develop a methodology to assess the separation, the selected concentrations correspond to the conventional minimum, average and maximum possible values for the given hydrocyclone type.
Three equations of the form (5) were obtained for different values of solid content in the slurry, i.e. 400, 500, 700 g/l, using the developed software which is based on the algorithm shown in Fig.5. Equations describe interrelation between the rheological parameters of the mineral slurry, i.e. the share stress and the shear rate:
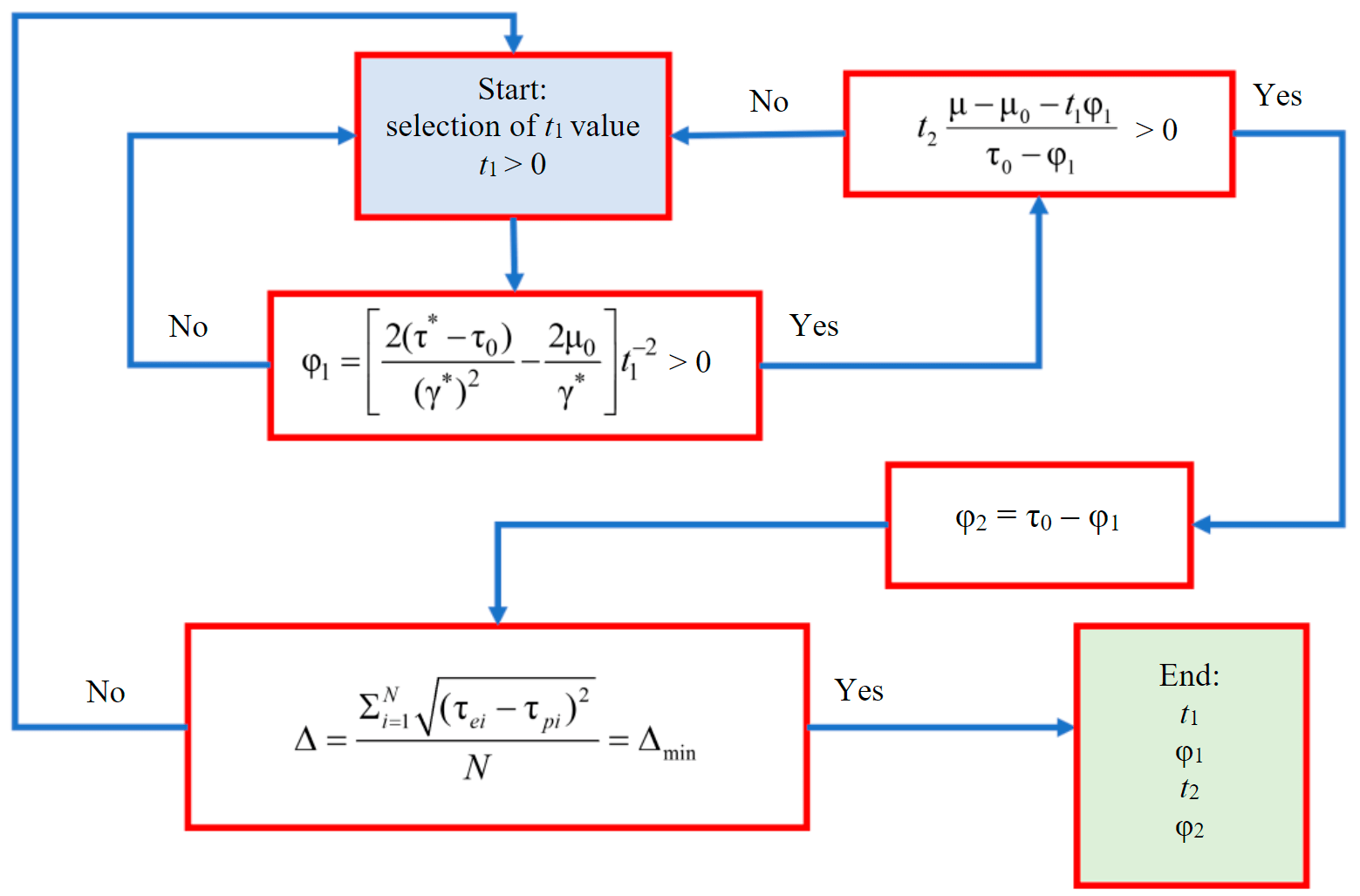
Fig.5. Calculation algorithm for the rheological equation coefficients
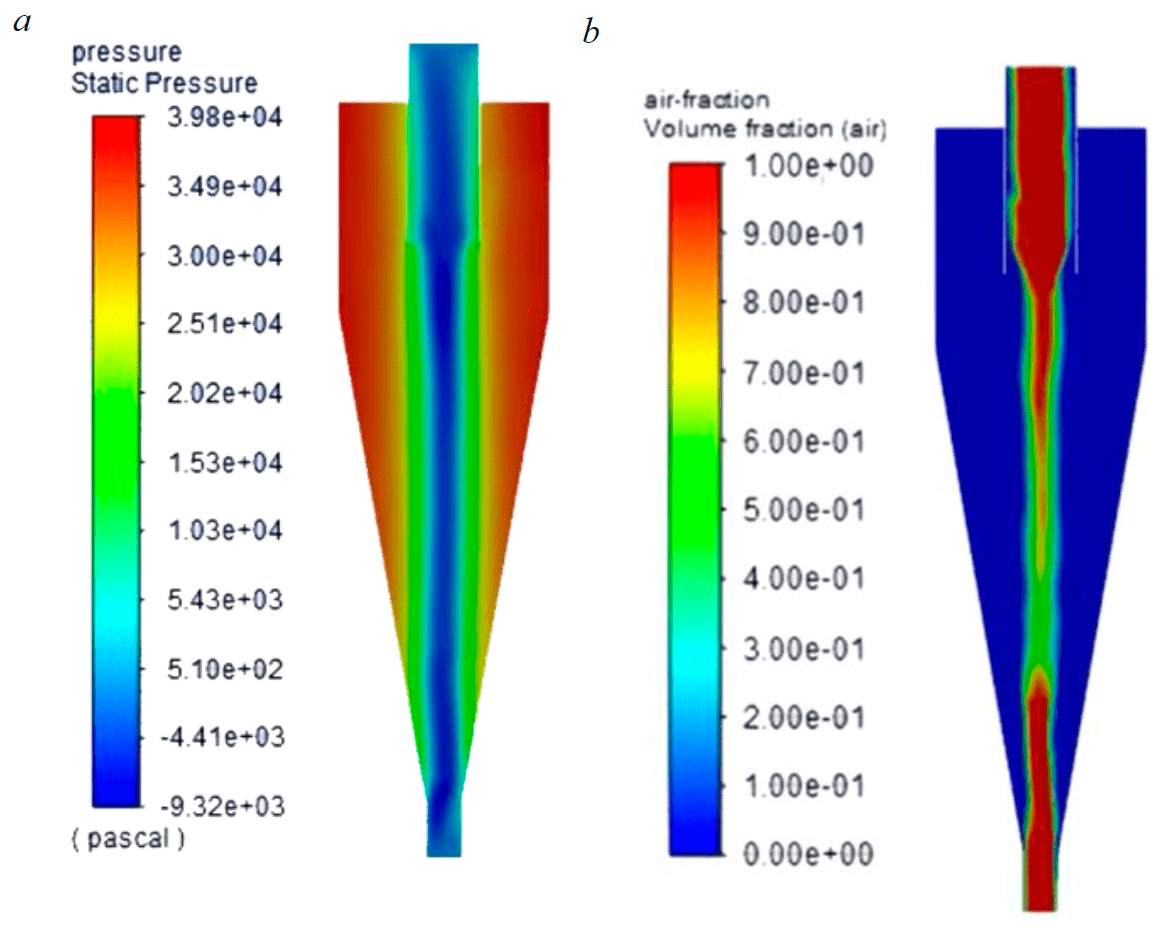
Fig.6. Calculation of a multiphase problem in Ansys Fluent: a – pressure distribution; b – formation of the air column
These equations theoretically describe the dynamics of internal transformations in the slurry and were used as rheological equations in further modeling of the hydrocyclone classification process using the Ansys Fluent software.
Two types of boundary conditions can be used in this software, depending on the type of problem solver, i.e. specification of either the input flow pressure or its initial rate.
Since this model is based on the initial flow rate, the following boundary conditions were used as necessary and sufficient: the input flow rate of 2.28 m/s, the output pressure of 1 atm, the number of phases – 2 and the turbulence intensity of 5 %.
Calculation of the hydrocyclone model in the Ansys Fluent software was done in several stages. The first stage was calculation in the steady-state mode, which is time-independent. A stable representation of the pressure distribution across the unit's profile was obtained using the Reynolds stress model (Fig.6, a). Stability refers to the invariability of a physical value regardless of the number of additional calculation iterations, with the pressure being below the atmospheric pressure.
The next calculation stage was directly time-dependent. An internal air column (Fig.6, b) is formed as the result of reduced pressure along the axis during 104 iterations with the time step of 10–4 s. The model describes this as the “Backflow Volume Fraction” boundary condition on both the apex and the vortex finder. This boundary condition ensures penetration of air inside the hydrocyclone due to reduced pressure along the axis.
The third stage was to calculate the particle motion trajectories. The particle size distribution of the hydrocyclone feed is defined by the Rosin – Rammler distribution when setting the problem in the Ansys Fluent software:
where Yd is the cumulative yield; d is the particle size.
Calculations of the hydrocyclone model for different viscosity values produced distributions of the tangential flow rates, pressures and shear rates within the cross section of the unit. The greatest interest within the research is the value of the shear rate, since the critical value of this parameter, defined through the rheological equation, is the indicator of the slurry dispersion. Approximating curves of these dependences are shown in Fig.7:
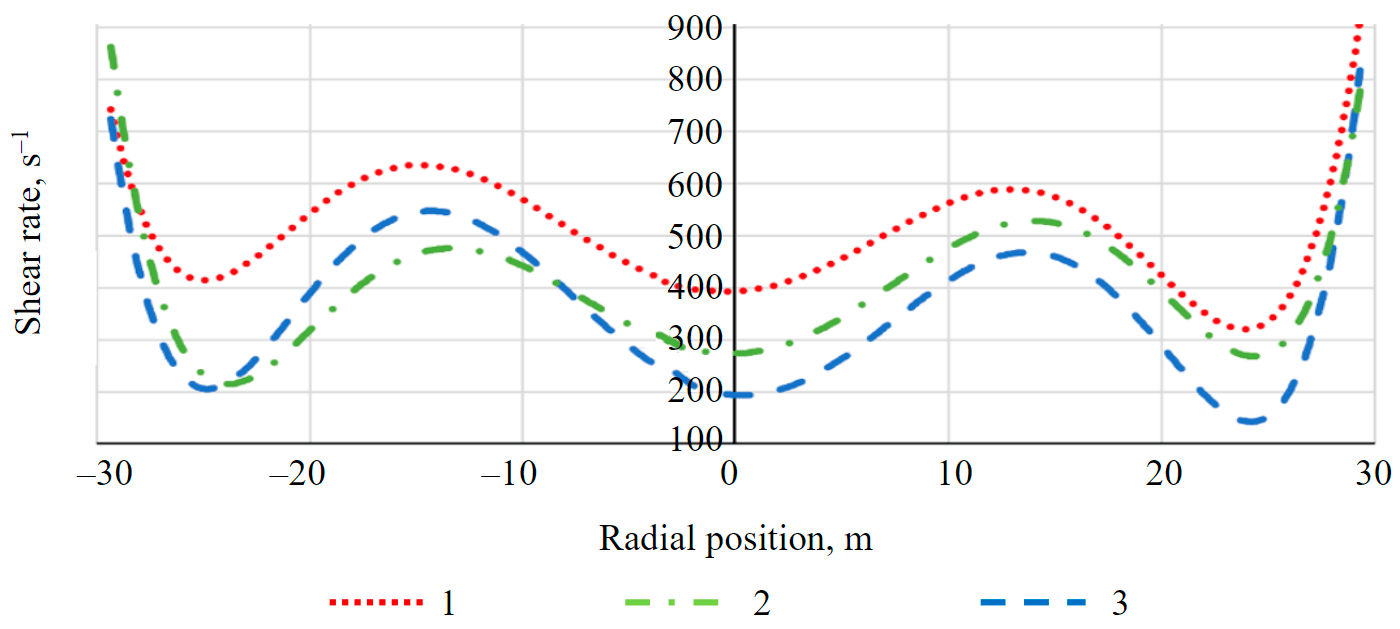
Fig.7. Distribution of shear rates at different solids content in the slurry (approximated by a sixth degree polynomial) 1 – 400; 2 – 500; 3 – 700 g/l
Based on the statistical data presented in the table, it is possible to make a conclusion regarding the viscosity value at which the required velocity profile is formed.
Statistical parameters of shear rate distributions
|
Parameter |
400 g/l |
500 g/l |
700 g/l |
|
Mean value, s–1 |
523.791 |
380.557 |
419.911 |
|
Standard deviation |
134.699 |
173.211 |
158.942 |
|
Minimum value, s–1 |
339.266 |
97.994 |
165.287 |
|
Maximum value, s–1 |
885.536 |
757.120 |
796.984 |
|
Critical shear rate, s–1 |
281 |
602 |
712 |
At the minimum standard deviation the solid content of 400 g/l in the feed enables achievement of the shear rate value in the flow that is greater than the critical one, which is defined by the three-component rheological equation. These conditions provide maximum dispersion of the mineral slurry, and thus higher grading accuracy, which has a positive impact on further concentration processes such as cyanidation and flotation.
For the curves shown in Fig.7 the recurring pattern is evident, so we can combine the three equations obtained earlier for different concentrations of solids in the slurry into one and apply the weighted average coefficients to it. As the result, we get a regression equation, which is a generic case:
Conclusion
The performed experimental and theoretical studies helped to refine the rheological equation of the mineral slurry that describes the relationship between the shear rate and the shear stress. A software application was developed using the Python 3.8 language to calculate the optimal empirical coefficients of the rheological equation.
Then, the problem of hydrocyclone classification of gold-sulfide feed was formulated and solved using the Ansys Fluent software based on a series of full-scale experiments and modification of the Navier – Stokes equation in accordance with the derived rheological equation.
Statistical analysis of the slurry flow inside the hydrocyclone in terms of the shear rate showed that the optimal solid content is 400 g/l, which provides the maximum dispersion of the mineral slurry. Thereby, a method to assess separation of the mineral slurry with account of its rheological properties has been developed and tested, which makes it possible to select optimal technological parameters of the classification process.
References
- Andreev E.E., Lvov V.V., Fadina A.V. Causes and significance of inflections in hydrocyclone efficiency curves. Journal of Mining Institute. 2013. Vol. 202, p. 131-136 (in Russian).
- Artemiev D.S. Features of geological structure and vertical zoning of the Mayskoe gold deposit ore bodies (Central Chukotka). Regional Geology and Metallogeny. 2015. N 64, p. 94-100 (in Russian).
- Artemev D.S., Molchanov A.V., Terekhov A.V. Ore content of hydrothermal-metasomatic formations of the Mayskoye ore field (Chukotka Autonomous Area). Geologiya i mineralno-syrevye resursy Severo-Vostoka Rossii: Materialy Vserossiiskoi nauchnoprakticheskoi konferentsii, 31 marta – 2 aprelya 2015, Yakutsk, Rossiya. Severo-Vostochnyi federalnyi universitet imeni M.K.Ammosova, 2015. Vol. 31, p. 36-39 (in Russian).
- Afanasova A.V. Development of effective technological solutions for processing of gold-bearing ores with account of their refractory properties: Avtoref. dis. … kand. tekhn. nauk. St. Petersburg: Sankt-Peterburgskii gornyi universitet, 2019, p. 20 (in Russian).
- Karchanova A., Asanova I., Myazin V. Towards Improving the Quality of Gold Ore Flotation Concentrate at the Mayskoe Field. Transbaikal State University Journal. 2015. N 10 (125), p. 4-12 (in Russian).
- Kuranov A.D. Application of numerical modeling for design of safety parameters of safety mining method in highly stressed masses. Journal of Mining Institute. 2013. Vol. 206, p. 60-64 (in Russian).
- Lvov V.V., Upraviteleva A.A. Investigation of the magnetic hydrocyclone effect in classification of oxidized ferruginous quartzites. Nauchnye osnovy i praktika pererabotki rud i tekhnogennogo syrya: Materialy XXV Mezhdunarodnoi nauchno-tekhnicheskoi konferentsii, provodimoi v ramkakh XVIII Uralskoi gornopromyshlennoi dekady, 2-11 aprelya 2020, Ekaterinburg, Rossiya. Fort Dialog-Iset, 2020, p. 175-180 (in Russian).
- Lvov V.V., Andreev E.E. Influence of Slurry Rheology on the parameters of classification in washing cyclone. Mining informational and analytical bulletin. 2013. N 2, p. 233-238 (in Russian).
- Zhukov V.V., Sharikov Y.V., Turunen I., Laari A. Modeling of batch gold leaching process by cyanidation. Journal of Mining Institute. 2013. Vol. 202, p. 178-180 (in Russian).
- Pochitalkina I.A., Filenko I.A., Petropavlovskiy I.A., Kondakov D.F. Rheological properties of suspensions at acid treatment of phosphorite of Polpinsky deposit. Izvestiya vysshikh uchebnykh zavedeniy. Khimiya i khimicheskaya tekhnologiya. 2016. Vol. 59. N 10, p. 41-46. DOI: 10.6060/tcct.20165910.5383 (in Russian).
- Savchuk V.A., Valeev S.I. Calculation of effective viscosity in the hydrocyclone. Mechanical engineering technology and materials science. 2020. N 4, p. 16-18. DOI: 10.26160/2542-2146-2020-4-16-18 (in Russian).
- Potemkin V.A., Aleksandrova T.N. Registration Certificate for Computer Software N 2020618724 RF. Software for calculation of empirical coefficients of rheological equations. Opubl. 04.08.2020. Byul. N 8 (in Russian).
- Skulskiy О.I. Rheometric flows of concentrated suspensions of solid particles. Computational Continuum Mechanics. 2020. Vol. 13. N 3, p. 269-278. DOI: 10.7242/1999-6691/2020.13.3.21
- Ignatov P.A., Novikov K.V., Shmonov A.M. et al. Comparative Analysis of Ore-Bearing Structures in Maiskoe, Markha, and Ozernoe Kimberlite Bodies at the Nakyn Field, Yakutia. Geology of Ore Deposits. 2015. Vol. 57. N 2, p. 125. DOI: 10.1134/S1075701515020038
- Trukhanov K.A., Ryabinin M.V. Method for determining rheological properties of non-Newtonian liquids with a rotational viscometer. Globalnyi nauchnyi potentsial. 2015. N 6, p. 67 (in Russian).
- Shabarov A.N., Nikolaeva N.V. Complex utilization of treatment wastes from thermal power plants. Journal of Mining Institute. 2016. Vol. 220, p. 607-610. DOI: 10.18454/PMI.2016.4.607
- Avksentiev S.Y., Makharatkin P.N. Influence of rheology on pressure losses in hydrotransport system of iron ore tailings. Journal of Industrial Pollution Control. 2017. Vol. 33. Iss. 1, p. 741-748.
- Avksentiev S.Y., Nikolaev A.K. Influence of Rheology on Pressure Losses in Hydrotransport System of Polymetallic Ores Tailings. IOP Conference Series: Earth and Environmental Science. 2017. Vol. 87. Iss 5. N 052019. DOI: 10.1088/1755-1315/87/5/052019
- Ding Feng, Si Huang, Li Luo, Wei Guo Ma. CFD analysis of two-phase flow in a solid-liquid hydrocyclone. Applied Mechanics and Materials. 2012. Vol. 130-134, p. 3640-3643. DOI: 10.4028/www.scientific.net/AMM.130-134.3640
- Durango-Cogollo M., Garcia-Bravo J., Newell B., Gonzalez-Mancera A. CFD modeling of hydrocyclones-A study of efficiency of hydrodynamic reservoirs. Fluids. 2020. Vol. 5. N 3. DOI: 10.3390/fluids5030118
- Cruz N., Forster J., Bobicki E.R. Slurry rheology in mineral processing unit operations: A critical review. Canadian Journal of Chemical Engineering. 2019. Vol. 97. Iss. 7, p. 2102-2120. DOI: 10.1002/cjce.23476
- Genc A.M., Kilickaplan I., Laskowski J.S. Effect of pulp rheology on flotation of nickel sulphide ore with fibrous gangue particles. Canadian Metallurgical Quarterly. 2012. Vol. 51. Iss. 4, p. 368-375. DOI: 10.1179/1879139512Y.0000000006
- Koblitz A.R., Lovett S., Nikiforakis N. Direct numerical simulation of particle sedimentation in a Bingham fluid. Physical Review Fluids. 2018. Vol. 3. Iss. 9. DOI: 10.1103/PhysRevFluids.3.093302
- Mahady K., Afkhami S., Kondic L. A volume of fluid method for simulating fluid/fluid interfaces in contact with solid boundaries. Journal of Computational Physics. 2015. Vol. 294, p. 243-257. DOI: 10.1016/j.jcp.2015.03.051
- Vakamalla T.R., Vadlakonda B., Aketi V.A.K., Mangadoddy N. Multiphase CFD Modelling of Mineral Separators Performance: Validation Against Tomography Data. Transactions of the Indian Institute of Metals. 2017. Vol. 70. Iss. 2, p. 323-340. DOI: 10.1007/s12666-016-0995-4
- Narasimha M., Brennan M., Holtham P.N. Large eddy simulation of hydrocyclone-prediction of air-core diameter and shape. International Journal of Mineral Processing. 2006. Vol. 80. Iss. 1, p. 1-14. DOI: 10.1016/j.minpro.2006.01.003
- Lin Yang, Jia-Lin Tian, Zhi Yang et al. Numerical analysis of non-Newtonian rheology effect on hydrocyclone flow field. Petroleum. 2015. Vol. 1. Iss. 1, p. 68-74. DOI: 10.1016/j.petlm.2015.05.001
- Karimi M., Akdogan G., Bradshaw S., Mainza A. Numerical Modelling of Air Core in Hydrocyclones. 9th International Conference in the Minerials and Process Industries, 10-12 December 2012, Melbourne, Australia. CSIRO, 2012. N 12, p. 1-6.
- Rosenkranz J., Lamberg P. Sustainable processing of mineral resources. International Journal of the Society of Material Engineering for Resources. 2014. Vol. 20. Iss. 1, p. 17-22. DOI: 10.5188/ijsmer.20.17
- Taner H.A., Onen V. Control of clay minerals effect in flotation. A review. Minerals Engineering, Held 25-28 September 2016, Swieradow-Zdroj, Poland. E3S Web of Conferences, 2016. Vol. 8. DOI: 10.1051/e3sconf/20160801062
- Cruz N., Peng Y., Wightman E., Xu N. The interaction of clay minerals with gypsum and its effects on copper-gold flotation. Minerals Engineering. 2015. Vol. 77, p. 121-130. DOI: 10.1016/j.mineng.2015.03.010
- Lanyue Jiang, Peikun Liu, Yuekan Zhang The performance prediction model of W-shaped hydrocyclone based on experimental research. Minerals. 2021. Vol. 11. N 2, p 118. DOI: 10.3390/min11020118
- Kaartinen J., Pietilä J., Remes A., Torttila S. Using a virtual flotation process to track a real flotation circuit. IFAC Proceedings Volumes. 2013. Vol. 46. Iss. 16, p. 116-121. DOI: 10.3182/20130825-4-US-2038.00061
- Vieira M.G., Peres A.E.C. Effect of rheology and dispersion degree on the regrinding of an iron ore concentrate. Journal of Materials Research and Technology. 2013. Vol. 2. Iss. 4, p. 332-339. DOI: 10.1016/j.jmrt.2013.07.002
