Разработка методики оценки процесса гидроциклонирования  c учетом реологических параметров минеральной суспензии

Т. Н. Александрова; В. А. Потемкин

doi:10.31897/PMI.2021.6.12

Том 252

Страницы:

908-916

Скачать том:

RUS ENG

Научная статья

Металлургия и обогащение

Разработка методики оценки процесса гидроциклонирования c учетом реологических параметров минеральной суспензии

Авторы:

Т. Н. Александрова¹

В. А. Потемкин²

Об авторах

1 — д-р техн. наук профессор Санкт-Петербургский горный университет ▪ Orcid ▪ Elibrary ▪ Scopus
2 — аспирант Санкт-Петербургский горный университет ▪ Orcid

Дата отправки:

2021-06-24

Дата принятия:

2021-11-30

Дата публикации:

2021-12-17

Аннотация

Рассмотрена возможность оценки сепарации минерального сырья с учетом реологии пульпы. В качестве объекта исследования были выбраны руды Майского месторождения, отличающиеся тонкой вкрапленностью ценного компонента – золота – в минералы-носители, что обуславливает применение тонкого и сверхтонкого измельчения. Данный факт имеет важное значение, поскольку наличие тонкого класса серьезно влияет на реологию минеральной пульпы, применяемой в дальнейших операциях обогатительного цикла. Это предопределяет необходимость учета реологических параметров. Проведенное исследование обеспечивает разработку методики оценки сепарации минерального сырья в гидроциклоне на основе интерпретации данных численного и математического моделирования. С применением объектно-ориентированного языка программирования Python была разработана программа расчета эмпирических коэффициентов реологического уравнения, теоретически отражающего динамику внутренних преобразований минеральной пульпы. Принимая во внимание технологические параметры лабораторной установки с гидроциклоном и свойства руды, было выбрано три концентрации твердого в пульпе, условно соответствующих минимальному, среднему и максимальному значениям.Последовательное получение реологических уравнений для трех вариантов концентрации (400, 500 и 700 г/л) позволило вычислить критические скорости сдвига, соответствующие максимальной диспергации минеральной суспензии в потоке гидроциклона. Последующее численное моделирование с применением ПО Ansys Fluent, а также статистическая оценка скоростей сдвига при различном содержании твердого показали, что при содержании 400 г/л обеспечивается профиль скоростей сдвига в поперечном сечении гидроциклона, соответствующий максимальной диспергации минеральной суспензии.

Ключевые слова:

реология гидроциклон Ansys Fluent Python гидродинамическое моделирование золотосодержащее сырье

10.31897/PMI.2021.6.12

Введение

Доступность легких к переработке руд снижается, что приводит к тому, что перерабатывать приходится сложные или с низким содержанием полезного компонента руды, а также, например, золошлаковые отходы [16]. В результате появляются новые вызовы обогатительной промышленности, поскольку зачастую руды такого типа должны подвергнуться более глубокой стадии измельчения, чем обычные; либо они содержат органический углерод, что является одним из факторов упорности [4]. Наличие органического углерода значительно влияет на реологические параметры минеральных суспензий, так же, как и содержание глинистых минералов [29]. Один из методов обезуглероживания, наряду с флотацией, – классификация в гидроциклоне, которая является менее затратной и более производительной.

При смешивании жидкой непрерывной и твердой дискретной среды образуется новая непрерывная среда – суспензия, – свойства которой отличаются от свойств отдельно взятых компонентов [17].

Соотношение между напряжением и скоростью сдвига отражается кривой течения (рис.1) [10, 15]. Напряжение сдвига – сила, под действием которой слои жидкости двигаются относительно друг друга. Скорость сдвига – это отношение приращения смещения слоев к интервалу времени. Неньютоновские суспензии подразделяются на псевдопластичные, бингамовские, дилатантные и др., причем большинство минеральных суспензий проявляют псевдопластичное поведение. У бингамовских жидкостей определенное начальное напряжение сдвига (τ₀) [23], обусловленное наличием тонкого класса частиц, взаимодействующих между собой. Такое поведение создает слабую структуру, которая должна быть разрушена преодолением критического напряжения сдвига, чтобы заставить частицы двигаться вместе с жидкостью под действием вязких сил.

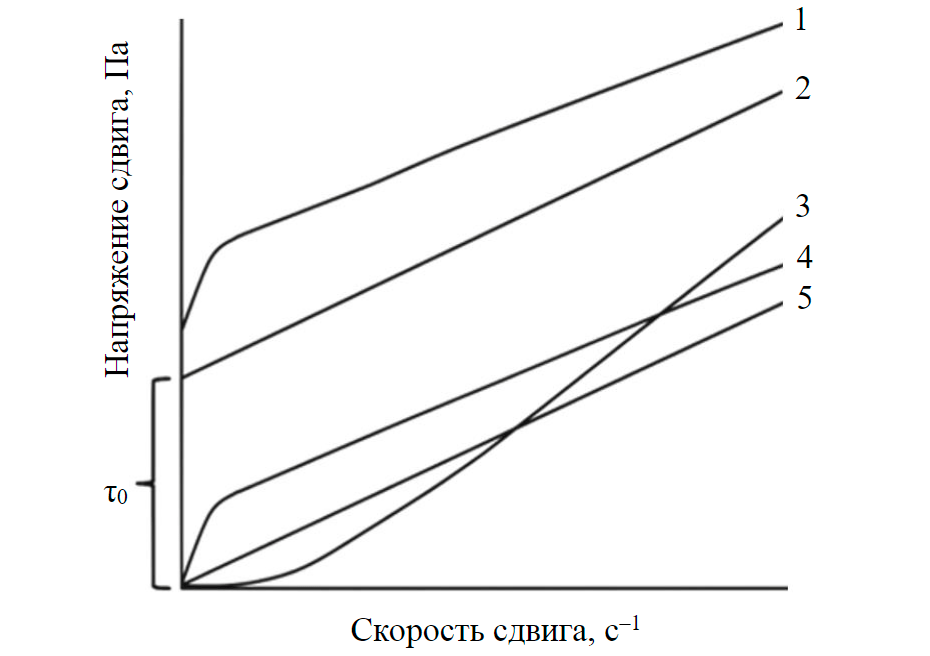
Рис.1. Кривые течения для различных жидкостей 1 – псевдопластики с начальным напряжением; 2 – бингамовские; 3 – дилатантные; 4 – псевдопластичные; 5 – ньютоновские

Для описания поведения таких жидкостей существует большое количество реологических моделей: Ньютоновская, Бингама, Гершела – Балкли, Сиско, Каро и др. [13, 21].

Реологические параметры минеральных суспензий оказывают значительное влияние на процессы обогащения, в том числе на измельчение [31, 34], транспорт [18] и флотацию [22, 30, 33].

Процессы классификации не являются исключением, в частности, классификация с использованием гидроциклона. Вопросу изучения влияния реологии минеральной суспензии на процесс разделения в гидроциклоне посвящено множество работ [8, 21, 27]. Сложность понимания реологии суспензии в гидроциклоне обусловлена сложностью формирующихся потоков, в связи с чем множество ученых работают над этой проблемой долгие годы [1, 7, 11, 32].

Вязкость среды влияет на формирование воздушного столба вдоль оси гидроциклона. Влияние вязкости на эффективность разделения в гидроциклоне было неоднократно подтверждено CFD-моделированием [20, 26, 28,]. Эффективность работы гидроциклона достаточно чувствительна к изменениям реологии минеральной суспензии: относительно низкое значение вязкости более предпочтительно для оптимального режима работы.

Золотосодержащие руды Майского месторождения – это углеродистые руды, которые относятся к особо упорной золотосодержащей разновидности. Основную ценность представляет золото [2, 5]. Из группы сульфидов преобладают такие минералы, как пирит, арсенопирит и стибнит. Кварц, гидрослюды, полевой шпат и другие составляют большую часть руды (порядка 90 %) [3, 14]. Золото, извлекаемое при переработке, в основном связано с сульфидами в виде твердых растворов, что обуславливает применение тонкого и сверхтонкого измельчения для раскрытия минеральных сростков. Наличие тонкого класса в пульпе значительно влияет на последующие стадии переработки.

В этой связи развитие технологии обогащения золотосульфидных углеродистых руд, с учетом реологических особенностей, является важнейшей задачей, которая может быть решена проведением экспериментально-теоретических исследований с помощью специализированного ПО.

Развитие существующих и новых технологий обогащения сырья невозможно без применения данных средств, что обуславливает широкий выбор вычислительных инструментов, подтверждением эффективности которых служит масса работ, посвященных численному и математическому моделированию [6, 9, 33]. Комбинирование данных инструментов в рамках единого подхода делает возможным разработку методики оценки процесса сепарации минерального сырья с учетом реологических свойств пульпы с целью выбора технологических параметров, способствующих эффективности процессов обогащения.

Методология

Влияние реологии пульпы на процесс классификации в гидроциклоне рассматривается с помощью экспериментально-теоретического подхода с использованием объектно-ориентированного программирования и ПО для гидродинамического моделирования.

Для проведения экспериментальных опытов по разделению суспензии была использована установка, представленная на рис.2.

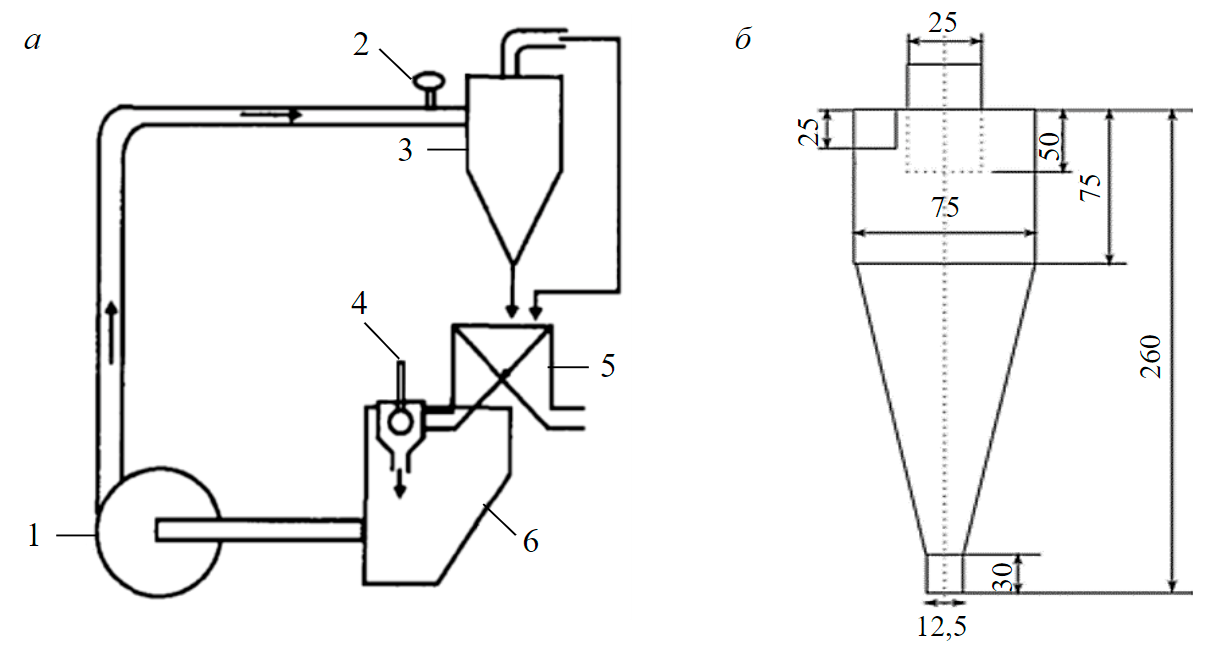
Рис.2. Принципиальная схема установки классификации на гидроциклоне (а) и геометрические параметры гидроциклона (б) 1 – насос; 2 – манометр; 3 – гидроциклон; 4 – вискозиметр; 5 – делитель проб; 6 – зумпф

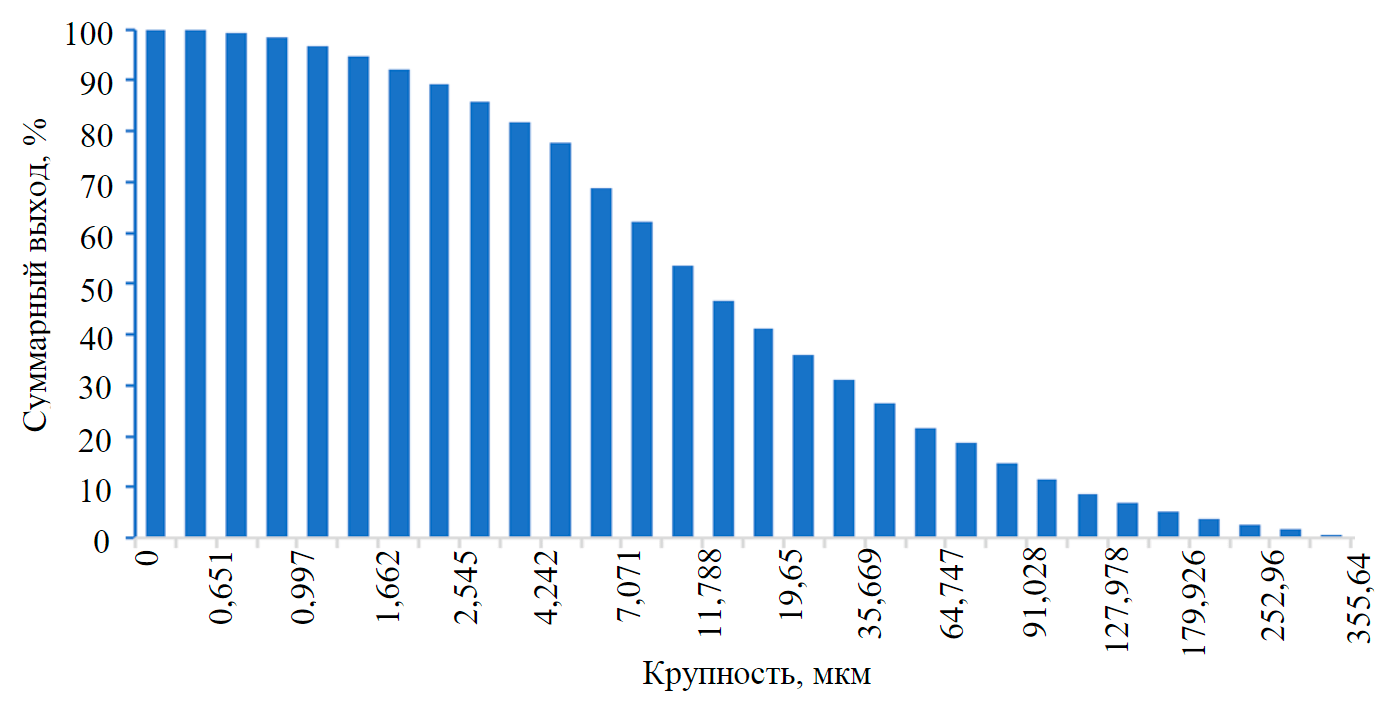
Рис.3. Гранулометрический состав исходной руды по плюсу

Эксперимент на лабораторной установке проводился с использованием золотосульфидной руды (рис.3) Майского месторождения, прошедшей стадию измельчения в течение 20 мин.

Гранулометрический состав продуктов разделения и исходного материала исследовался с помощью лазерного дифракционного анализатора крупности Malvern Mastersizer 2000 Hydro S.

Численное моделирование работы гидроциклона было выполнено с помощью ПО Ansys Fluent, в основе работы которого лежит метод контрольных объемов. Физика процесса классификации является сложной, поскольку во время движения на частицу действует множество сил. Также большое значение имеет характер турбулентного потока, формирующегося во время работы аппарата.

В качестве модели турбулентности была выбрана модель рейнольдсовских напряжений (1), в которой уравнение транспорта решается для индивидуальных напряжений Рейнольдса [19, 25]. Данная модель характерна тем, что в отличие от семейства стандартных k-ε моделей, она предусматривает решение не двух, а шести уравнений для каждого компонента тензора напряжений Рейнольдса, чем повышает точность результата. При этом, в отличие от модели LES, которая считается наиболее точной [28], RSM-модель не такая ресурсоемкая:

\frac{\partial}{\partial t} (ρ \bar{{u^{'}}_{j} {u^{'}}_{j}}) + \frac{\partial}{\partial x_{k}} (u_{k} ρ \bar{{u^{'}}_{j} {u^{'}}_{j}}) = φ_{i j} + P_{i j} + D_{T, i j} + D_{L, i j} - ε_{i j} + F_{i j} (1)

где φ_ij – напряженно-деформированное состояние; P_ij – возникающие напряжения; D_T,ij – перенос массы, тепла или импульса в системе из-за случайных и хаотичных движений, зависящих от времени; ε_ij – диссипация энергии.

Для описания взаимодействия фаз газ – жидкость использовалась модель Volume of Fluid, в которой отслеживание границы раздела между фазами осуществляется путем решения уравнения неразрывности для объемной доли одной (или нескольких) фаз [24]. Для q-фазы это уравнение имеет следующий вид:

\frac{1}{ρ_{q}} [\frac{\partial}{\partial t} (α_{q} ρ_{q}) + \nabla (α_{q} ρ_{q} {\vec{V}}_{q}) = S_{a_{q}} + \sum_{p = 1}^{n} ({\dot{m}}_{p q} - {\dot{m}}_{q p})] (2)

где α_i– объемная доля фазы; ρ_i – плотность фазы; V – скорость; S_a – определяемый пользователем массовый показатель фазы; m_pq – массоперенос от p-фазы к q-фазе; m_qp – массоперенос от q-фазы к p-фазе.

Уравнение движения минеральной суспензии может быть получено из уравнения динамики жидкости в напряжениях:

ρ \frac{d \vec{v}}{d t} = ρ \vec{F} + d i v P, (3)

где ρ – плотность жидкости; $\vec{v}$ – вектор абсолютной скорости потока; t – время; $\vec{F}$ – вектор массовых сил; P – тензор напряжений в жидкости.

Девиаторную часть тензора можно представить функцией напряжения сдвига, которая может быть описана реологическим уравнением, отражающим динамику внутренних структурных преобразований в минеральных суспензиях и позволяющим определить напряжения сдвига в зависимости от градиентов скорости. Тогда уравнение может быть переписано с учетом разложения на части:

ρ \frac{d \vec{v}}{d t} = ρ \vec{F} - g r a d p + d i v (\sum_{k = 1}^{n + 1} φ_{k} e^{- t_{k} \dot{γ_{i j}}} + μ \dot{γ_{i j}}), (4)

где p – среднее гидростатическое давление в потоке; φ – коэффициент реологического уравнения; μ – коэффициент динамической вязкости; γ_ij – скорость сдвига.

Уравнение (4) представляет собой модифицированное уравнение Навье – Стокса с членом $\sum^{n+1}_{k=1}\phi_ke^{-t_k\gamma_{ij}}$, учитывающее свойства минеральной суспензии, и может быть принято за уравнение движения в векторной форме:

$$ \tau=A_1e^{-\alpha_1\dot{\gamma}}+A_2e^{-\alpha_2 \dot{\gamma}}+\mu_T\dot{\gamma} \qquad(5) $$

где μ_Т – коэффициент динамической вязкости диспергированной суспензии.

Уравнение (5) является определяющим для напряжения сдвига внутри суспензии в зависимости от градиента скорости, в который входят напряжение сдвига, напряжение, характеризующее внутреннюю прочность структуры, и напряжение вязкости диспергированной суспензии.

Участок кривой между 0 и γ_кр отражает аномальную вязкость, которая обусловлена наличием структурированного потока. При превышении порогового значения скорости сдвига суспензия подчиняется законам движения ньютоновской жидкости. Данная модификация уравнения Навье –Стокса была применена при постановке задачи классификации в гидроциклоне в ПО Ansys Fluent.

Расчет коэффициентов реологического уравнения осуществлялся с применением разработанной программы на языке Python 3.8 [12] (рис.4).

Исходными для вычислений являются данные, получаемые с помощью вискозиметра, – скорость и напряжение сдвига. В данном случае использовался ротационный вискозиметр RHEOTEST RN 4.1, предназначенный для определения динамической вязкости ньютоновских и неньютоновских жидкостей.

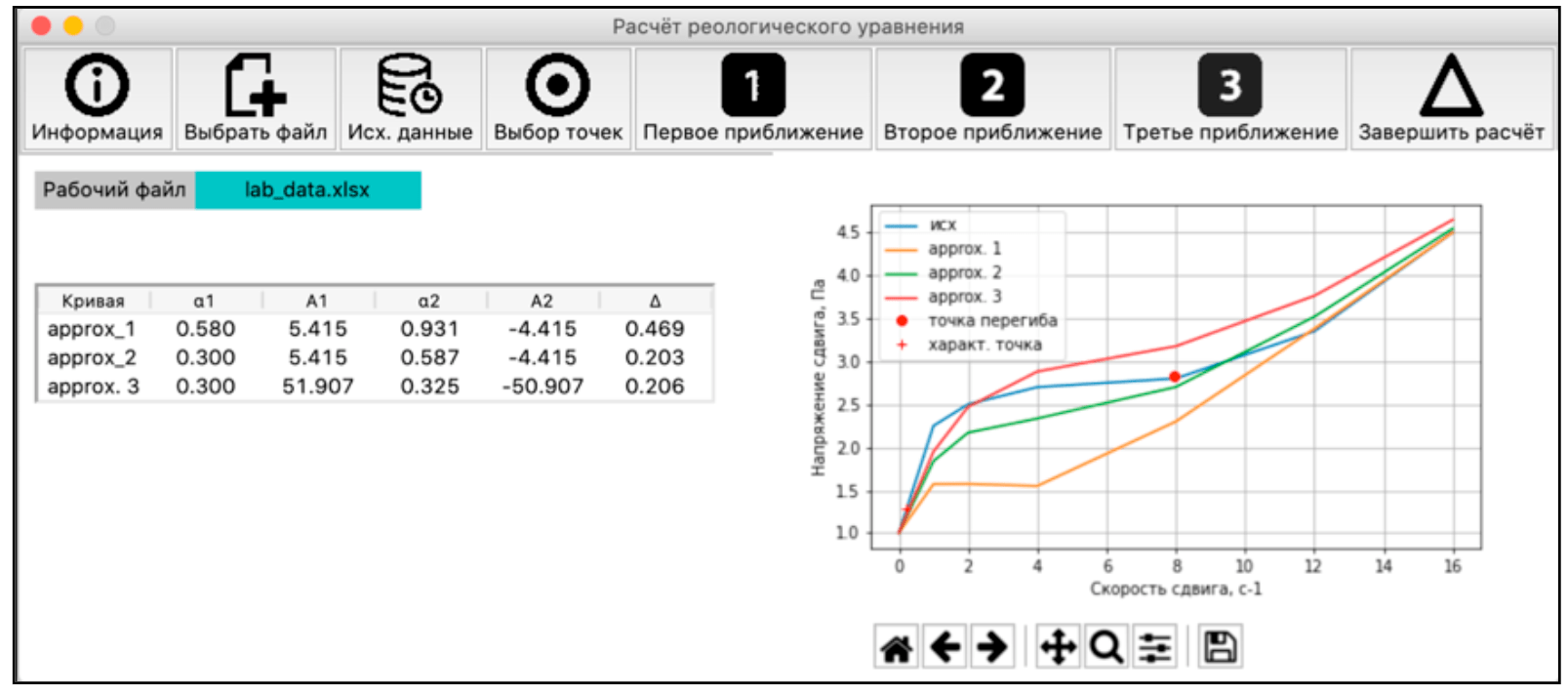
Рис.4. Интерфейс разработанной программы

Принцип работы программы (рис.5) заключается в последовательном приближении теоретической кривой к экспериментальным данным. В результате получается семейство кривых, из которых на основе статистических выводов выбирается та, которая наилучшим образом описывает исходные данные.

Обсуждение

Принимая во внимание свойства исследуемого типа руд и технологические параметры лабораторного оборудования, было выбрано три концентрации твердого в пульпе для оценки влияния реологии пульпы на процесс классификации. Поскольку целью статьи является именно разработка методики оценки сепарации, выбранные концентрации условно соответствуют минимальному, среднему и максимального возможному значению для данного типа гидроциклона.

Для различных значений содержания твердого в пульпе (400, 500, 700 г/л) было получено три уравнения вида (5) с использованием разработанной программы, в основе которой лежит алгоритм, представленный на рис.5. Взаимосвязь между реологическими параметрами минеральной пульпы – напряжением и скоростью сдвига – описывают уравнения:

τ_{400} = 5,415 e^{0,580 γ} - 4,415 e^{0,931 γ} + 0,281 γ; (6)

τ_{500} = 3,120 e^{0,411 γ} - 2,190 e^{0,881 γ} + 0,602 γ; (7)

τ_{700} = 2,919 e^{0,901 γ} - 1,989 e^{0,765 γ} + 0,712 γ . (8)

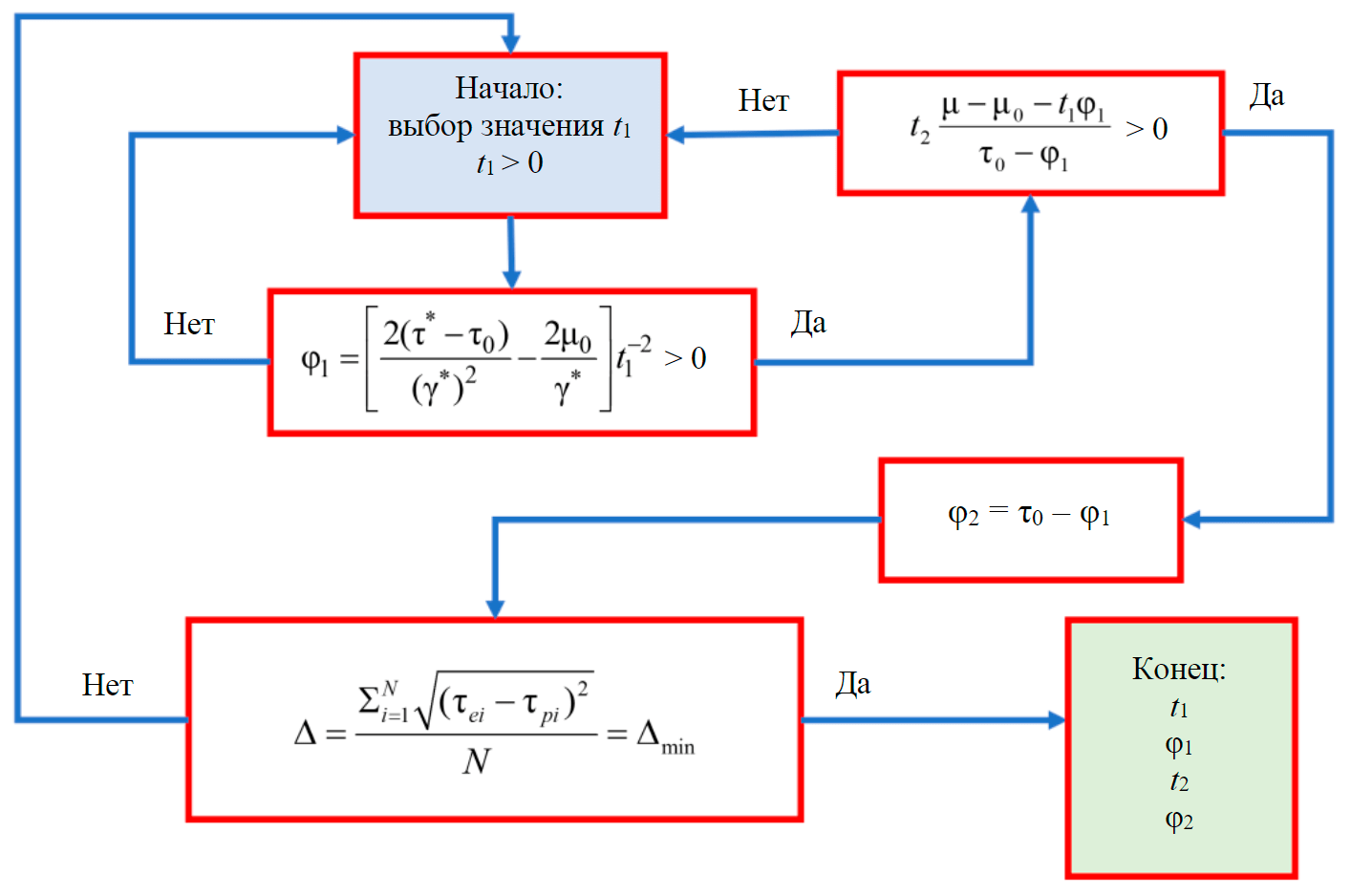
Рис.5. Алгоритм расчета коэффициентов реологического уравнения

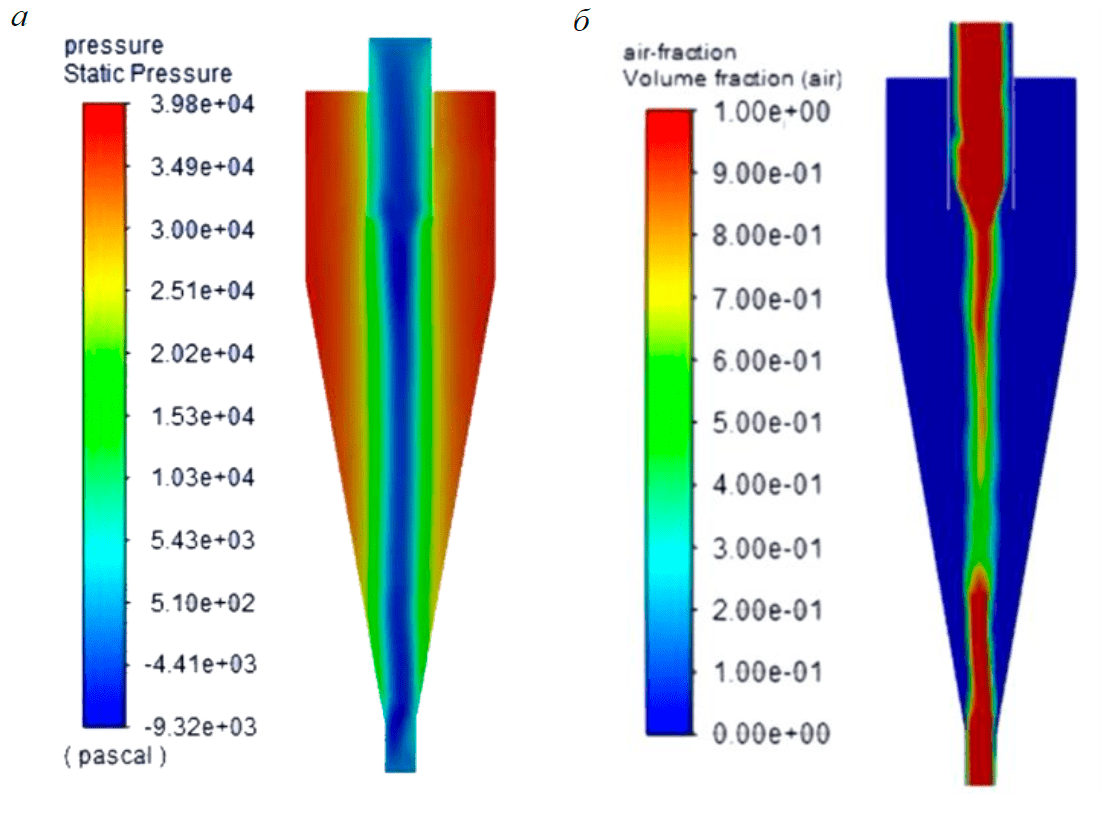
Рис.6. Расчет многофазной задачи в Ansys Fluent: а – распределение давления; б – формирование воздушного столба

Данные уравнения теоретически отражают динамику внутренних преобразований в пульпе и были использованы как реологические уравнения при дальнейшем моделировании процесса классификации в гидроциклоне c применением ПО Ansys Fluent. В данном ПО может быть использовано два вида граничных условий, в зависимости от типа решателя, – заданием давления входного потока или начальной скорости.

Поскольку в рамках данной модели использовалась постановка на основе начальной скорости потока, следующие граничные условия были использованы как необходимые и достаточные: скорость потока на входе – 2,28 м/с; давление на выходе – 1 атм.; количество фаз – 2; интенсивность турбулентности – 5 %.

Расчет модели гидроциклона в ПО Ansys Fluent осуществлялся в несколько этапов. Первым этапом был расчет в стационарном режиме «Steady State», т.е. независящем от времени. С применением модели рейнольдсовских напряжений была получена стабильная картина по давлению в профиле аппарата (рис.6, а). Под стабильностью подразумевается неизменность физической величины вне зависимости от количества дополнительных расчетных итераций, при этом давление должно быть ниже атмосферного.

Следующим был этап расчета, напрямую зависящий от времени. На протяжении 10⁴ итераций с временным шагом 10^–4 с формируется внутренний воздушный столб (рис.6, б) в результате пониженного давления вдоль оси. В модели это описывается в виде граничного условия «Backflow Volume Fraction» на обеих насадках – песковой и сливной. Данное граничное условие обеспечивает проникновение воздуха внутрь гидроциклона из-за пониженного давления вдоль оси.

На третьем этапе рассчитывались траектории движения частиц. Гранулометрический состав питания гидроциклона при постановке задачи в ПО Ansys Fluent задается распределением Розина – Раммлера:

Y_{d} = e^{- {(\frac{d}{49})}^{0,853}}, (9)

где Y_d – суммарный выход; d – крупность частицы.

Результатами расчета модели гидроциклона для различных значений вязкости являлись распределения тангенциальной скорости потока, давления и скорости сдвига в поперечном сечении аппарата. Наибольший интерес в рамках исследования представляет значение скорости сдвига, так как именно критическое значение этой величины, определяемое через реологическое уравнение, является показателем диспергации суспензии. На рис.7 представлены аппроксимирующие кривые следующих зависимостей:

y = 8,451 \cdot 10^{12} x^{6} - 10,235 \cdot 10^{9} x^{5} - 9,714 \cdot 10^{9} x^{4} + 5,763 \cdot 10^{6} x^{3} + 2,737 \cdot 10^{6} x^{2} + 1204,42 x + 274,61; (10)

y = 7,387 \cdot 10^{12} x^{6} + 28,502 \cdot 10^{9} x^{5} - 8,698 \cdot 10^{9} x^{4} - 23,045 \cdot 10^{6} x^{3} + 2,521 \cdot 10^{6} x^{2} + 1689,66 x + 394; (11)

y = 10,109 \cdot 10^{12} x^{6} + 11,009 \cdot 10^{9} x^{5} - 12,072 \cdot 10^{9} x^{4} - 4,941 \cdot 10^{6} x^{3} + 3,573 \cdot 10^{6} x^{2} - 2285,56 x + 194,91. (12)

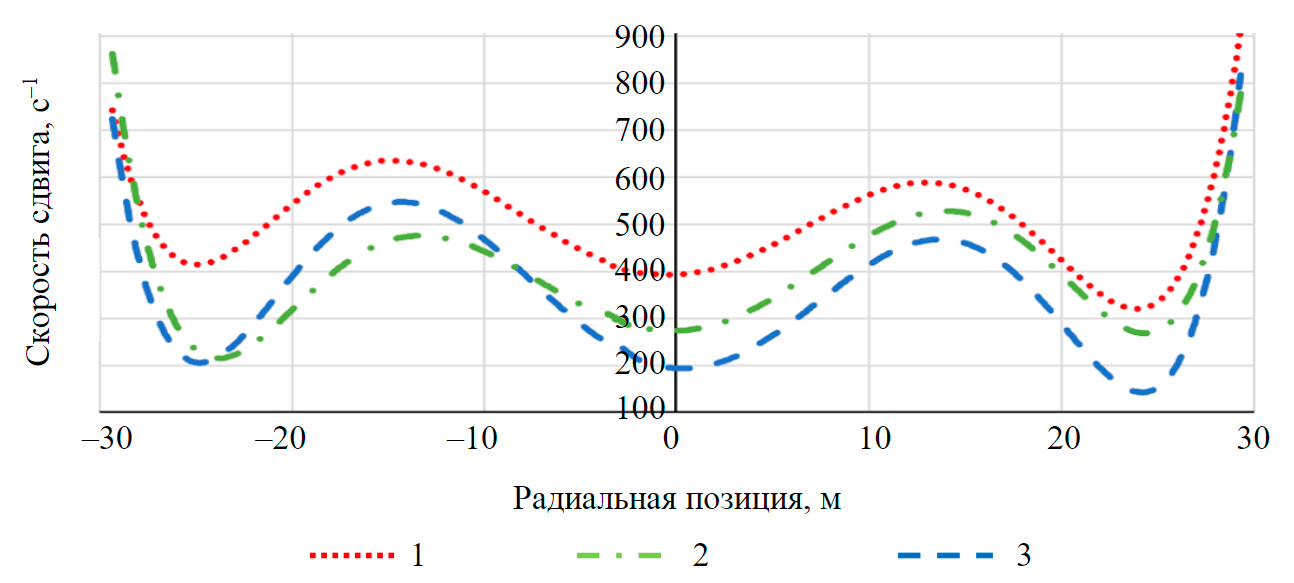
Рис.7. Распределение скоростей сдвига при различном содержании твердого в пульпе (аппроксимация с помощью полинома шестой степени) 1 – 400; 2 – 500; 3 – 700 г/л

На основе статистических данных, представленных в таблице, можно сделать вывод о значении вязкости, при котором формируется необходимый скоростной профиль.

Статистические параметры распределений скоростей сдвига

Параметр	400 г/л	500 г/л	700 г/л
Среднее значение, с^–1	523,791	380,557	419,911
Стандартное отклонение	134,699	173,211	158,942
Минимальное значение, с^–1	339,266	97,994	165,287
Максимальное значение, с^–1	885,536	757,120	796,984
Критическая скорость сдвига, с^–1	281	602	712

При минимальном стандартном отклонении содержание твердого в питании 400 г/л обеспечивает достижение значения скорости сдвига в потоке большего, чем критическое, которое определяется трехкомпонентным реологическим уравнением. При таких условиях обеспечивается максимальная диспергированность минеральной суспензии, а значит более точное разделение по классам крупности, что оказывает положительное влияние на дальнейшие процессы обогащения, такие как цианирование и флотация.

Для представленных на рис.7 кривых очевиден повторяющийся паттерн, вследствие чего можно объединить три полученных ранее уравнения для разных концентраций твердого в пульпе в одно и применить к нему средневзвешенные коэффициенты. В результате получаем регрессионное уравнение, являющееся общим случаем:

y = 8,65 \cdot 10^{12} x^{6} + 2,42 \cdot 10^{9} x^{5} - 1,02 \cdot 10^{10} x^{4} - 7,41 \cdot 10^{6} x^{3} + 2,94 \cdot 10^{6} x^{2} + 202,84 x + 288. (13)

Заключение

В результате проведенного экспериментально-теоретического исследования было уточнено реологическое уравнение минеральной суспензии, описывающее взаимосвязь скорости и напряжения сдвига. С этой целью была разработана программа на языке Python 3.8, позволяющая вычислить оптимальные эмпирические коэффициенты реологического уравнения.

Затем с использованием ПО Ansys Fluent была поставлена и решена задача классификации золотосульфидного сырья в гидроциклоне на основе серии натурных экспериментов и модификации уравнения Навье – Стокса в соответствии с выведенным реологическим уравнением.

Статистический анализ течения пульпы в гидроциклоне с позиции скорости сдвига показал, что оптимальным является содержание твердого 400 г/л, в результате чего достигается максимальная диспергация минеральной суспензии. Таким образом, разработана и опробована методика оценки сепарации минеральной суспензии с учетом ее реологических свойств, позволяющая подобрать оптимальные технологические параметры процесса классификации.

Литература

Андреев Е.Е. Причины и значение изгибов кривых эффективности гидроциклона / Е.Е.Андреев, В.В.Львов, А.В.Фадина // Записки Горного института. 2013. Т. 202. С. 131-136.
Артемьев Д.С. Особенности геологического строения и вертикальной зональности рудных тел Майского золоторудного месторождения (Центральная Чукотка) // Региональная геология и металлогения. 2015. № 64. С. 94-100.
Артемьев Д.С. Рудоносность гидротермально-метасоматических образований майского рудного поля (Чукотский АО) / Д.С.Артемьев, А.В.Молчанов, А.В.Терехов // Геология и минерально-сырьевые ресурсы Северо-Востока России: Материалы Всероссийской научнопрактической конференции, 31 марта – 2 апреля 2015, Якутск, Россия. Северо-Восточный федеральный университет имени М.К.Аммосова, 2015. Т. 31. С. 36-39.
Афанасова А.В. Разработка эффективных технологических решений переработки золотосодержащих руд с учетом их критериев упорности: Автореф. дис. … канд. техн. наук. СПб: Санкт-Петербургский горный университет, 2019. 20 с.
Карчанова А.П. Направление повышения качества флотоконцентрата золотосодержащих руд на майском месторождении / А.П.Карчанова, И.И.Асанова, В.П.Мязин // Вестник Забайкальского государственного университета. 2015. № 10 (125). C. 4-12.
Куранов А.Д. Применение численного моделирования для выбора безопасных параметров систем разработки рудных месторождений в высоконапряженных массивах // Записки Горного института. 2013. Т. 206. С. 60-64.
Львов В.В. Исследование влияния магнитного гидроциклона при классификации окисленных железистых кварцитов / В.В.Львов, А.А.Управителева // Научные основы и практика переработки руд и техногенного сырья: Материалы XXV Международной научно-технической конференции, проводимой в рамках XVIII Уральской горнопромышленной декады, 2-11 апреля 2020, Екатеринбург, Россия. Форт Диалог-Исеть, 2020. С. 175-180.
Львов В.В. Исследование влияния реологии пульпы на параметры классификации в гидроциклоне / В.В.Львов, Е.Е.Андреев // Горный информационно-аналитический бюллетень. 2013. № 2. С. 233-238.
Моделирование периодического процесса выщелачивания золота цианированием / В.В.Жуков, Ю.В.Шариков, Т.Илкка, Л.Арто // Записки Горного института. 2013. Т. 202. С. 178-180.
Реологические характеристики суспензий в процессах кислотной переработки фосфорита Полпинского месторождения / И.А.Почиталкина, И.А.Филенко, И.А.Петропавловский, Д.Ф.Кондаков // Химия и химическая технология. 2016. Т. 59. № 10. C. 41-46. DOI: 10.6060/tcct.20165910.5383
Савчук В.А. Расчет эффективной вязкости в гидроциклоне / В.А.Савчук, С.И.Валеев // Технология машиностроения и материаловедение. 2020. № 4. С. 16-18. DOI: 10.26160/2542-2146-2020-4-16-18
Свидетельство о регистрации программы для ЭВМ № 2020618724 РФ. Программа для расчета эмпирических коэффициентов реологического уравнения / В.А.Потемкин, Т.Н.Александрова. Опубл. 04.08.2020. Бюл. № 8.
Скульский О.И. Реометрические течения концентрированных суспензий твердых частиц // Вычислительная механика сплошных сред. 2020. Т. 13. № 3. С. 269-278. DOI: 10.7242/1999-6691/2020.13.3.21
Сравнительный анализ рудовмещающих структур Майского, Мархинского и Озерного кимберлитовых тел Накынского поля Якутии / П.А.Игнатов, К.В.Новиков, А.М.Шмонов и др. // Геология рудных месторождений. 2015. Т. 57. № 2. С. 125. DOI: 10.7868/S0016777015020033
Труханов К.А. Способ определения реологических характеристик неньютоновских жидкостей ротационным вискозиметром / К.А.Труханов, М.В.Рябинин // Глобальный научный потенциал. 2015. № 6. С. 67.
Шабаров А.Н. Комплексное использование отходов переработки теплоэлектростанций / А.Н.Шабаров, Н.В.Николаева // Записки Горного института. 2016. Т. 220. С. 607-610. DOI: 10.18454/PMI.2016.4.607
Avksentiev S.Y. Influence of rheology on pressure losses in hydrotransport system of iron ore tailings / S.Y.Avksentiev, P.N.Makharatkin // Journal of Industrial Pollution Control. 2017. Vol. 33. Iss. 1. P. 741-748.
Avksentiev S.Y. Influence of Rheology on Pressure Losses in Hydrotransport System of Polymetallic Ores Tailings / S.Y.Avksentiev, A.K.Nikolaev // IOP Conference Series: Earth and Environmental Science. 2017. Vol. 87. Iss. 5. № 052019. DOI: 10.1088/1755-1315/87/5/052019
CFD analysis of two-phase flow in a solid-liquid hydrocyclone / Ding Feng, Si Huang, Li Luo, Wei Guo Ma // Applied Mechanics and Materials. 2012. Vol. 130-134. P. 3640-3643. DOI: 10.4028/www.scientific.net/AMM.130-134.3640
CFD modeling of hydrocyclones-A study of efficiency of hydrodynamic reservoirs / M.Durango-Cogollo, J.Garcia-Bravo, B.Newell, A.Gonzalez-Mancera // Fluids. 2020. Vol. 5. N 3. DOI: 10.3390/fluids5030118
Cruz N. Slurry rheology in mineral processing unit operations: A critical review / N.Cruz, J.Forster, E.R.Bobicki // Canadian Journal of Chemical Engineering. 2019. Vol. 97. Iss. 7. P. 2102-2120. DOI: 10.1002/cjce.23476
Genc A.M. Effect of pulp rheology on flotation of nickel sulphide ore with fibrous gangue particles / A.M.Genc, I.Kilickaplan, J.S.Laskowski // Canadian Metallurgical Quarterly. 2012. Vol. 51. Iss. 4. P. 368-375. DOI: 10.1179/1879139512Y.0000000006
Koblitz A.R. Direct numerical simulation of particle sedimentation in a Bingham fluid / A.R.Koblitz, S.Lovett, N.Nikiforakis // Physical Review Fluids. 2018. Vol. 3. Iss. 9. DOI: 10.1103/PhysRevFluids.3.093302
Mahady K. A volume of fluid method for simulating fluid/fluid interfaces in contact with solid boundaries / K.Mahady, S.Afkhami, L.Kondic // Journal of Computational Physics. 2015. Vol. 294. P. 243-257. DOI: 10.1016/j.jcp.2015.03.051
Multiphase CFD Modelling of Mineral Separators Performance: Validation Against Tomography Data / T.R.Vakamalla, B.Vadlakonda, V.A.K.Aketi, N.Mangadoddy // Transactions of the Indian Institute of Metals. 2017. Vol. 70. Iss. 2. P. 323-340. DOI: 10.1007/s12666-016-0995-4
Narasimha M. Large eddy simulation of hydrocyclone-prediction of air-core diameter and shape / M.Narasimha, M.Brennan, P.N.Holtham // International Journal of Mineral Processing. 2006. Vol. 80. Iss. 1. P. 1-14. DOI: 10.1016/j.minpro.2006.01.003
Numerical analysis of non-Newtonian rheology effect on hydrocyclone flow field / Lin Yang, Jia-Lin Tian, Zhi Yang et al. // Petroleum. 2015. Vol. 1. Iss. 1. P. 68-74. DOI: 10.1016/j.petlm.2015.05.001
Numerical Modelling of Air Core in Hydrocyclones / M.Karimi, G.Akdogan, S.Bradshaw, A.Mainza // 9th International Conference in the Minerials and Process Industries, 10-12 December 2012, Melbourne, Australia. CSIRO, 2012. № 12. С. 1-6.
Rosenkranz J. Sustainable processing of mineral resources / J.Rosenkranz, P.Lamberg // International Journal of the Society of Material Engineering for Resources. 2014. Vol. 20. Iss. 1. P. 17-22. DOI: 10.5188/ijsmer.20.17
Taner H.A. Control of clay minerals effect in flotation. A review / H.A.Taner, V.Onen // Minerals Engineering, Held 25-28 September 2016, Swieradow-Zdroj, Poland. E3S Web of Conferences, 2016. Vol. 8. DOI: 10.1051/e3sconf/20160801062
The interaction of clay minerals with gypsum and its effects on copper-gold flotation / N.Cruz, Y.Peng, E.Wightman, N.Xu // Minerals Engineering. 2015. Vol. 77. P. 121-130. DOI: 10.1016/j.mineng.2015.03.010
The performance prediction model of W-shaped hydrocyclone based on experimental research / Lanyue Jiang, Peikun Liu, Yuekan Zhang // Minerals. 2021. Vol. 11. N 2. № 118. DOI: 10.3390/min11020118
Using a virtual flotation process to track a real flotation circuit / J.Kaartinen, J.Pietilä, A.Remes, S.Torttila // IFAC Proceedings Volumes. 2013. Vol. 46. Iss. 16. P. 116-121. DOI: 10.3182/20130825-4-US-2038.00061
Vieira M.G. Effect of rheology and dispersion degree on the regrinding of an iron ore concentrate / M.G.Vieira, A.E.C.Peres // Journal of Materials Research and Technology. 2013. Vol. 2. Iss. 4. P. 332-339. DOI: 10.1016/j.jmrt.2013.07.002